Methodological Aspects of Welded Joint Quality Assessment
Abstract
1. Introduction
- -
- Development and implementation of high and increased-strength steels and other materials with special physical and mechanical properties accompanied by research into complex issues of weldability;
- -
- Development of new construction solutions with the use of welding methods based on highly concentrated heat sources such as plasma streams, lasers, and electron beams, as well as the mechanization and automation of the welding process;
- -
- Discovery of new phenomena accompanying the processes of welding.
2. Analysis of the Current State of Knowledge
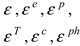 | represent the total strain; represent total, elastic, plastic, heat, creeping, and phase changes. |
- KIth/KIC: stress intensity factor/critical stress intensity factor;
- δ/δc: energy released during fracture/critical energy released during fracture;
- J/Jc: integral value of the parameter/limit value of the parameter.
- K: stress intensity factor;
- v: crack tip propagation velocity;
- cd: velocity of vortex-free wave propagation;
- r: radius;
- Θ: polar coordinates with a beginning situated in the crack tip.
- a: radius of cylindrical opening;
- t: time;
- β: constant (fluidity parameter);
- σo: constant stress.
- ai: radius of the particle;
- bo: the standard value of particle radius;
- sof: coefficient characterizing the particle wrap combination.
3. Components of Welded Joint Assessment Quality
- Kn = p; n p; k, n, r, pN;
- Zi: subsets of characteristics describing the quality of the subsets, including elements of the Ei system;
- Ei: quality subsets of the weld assessment;
- Xi: a set of characteristics that comprehensively describe the weld quality, i = 1, 2, …, p,
- i = {1 < … < k1 < k1 + 1 < … < k2 < k2 + 1 < … < kn − r < … < kn − 1 < kn = p}.
- -
- Analysis of the welding process parameters;
- -
- Evaluation of the welded joint microstructure;
- -
- Microscopic mechanical properties of the weld;
- -
- Macroscopic mechanical properties of the weld.
- Z1(t) = X1(t);
- Z2(t) = X2(t)+ X3(t)+ X4(t)+ X5(t);
- Z3(t) = X6(t)+ X7(t) +X8(t);
- Z4(t) = X9(t)+ X10(t).
+[X2(t) + X3(t) + X4(t) + X5(t)] + [X6(t) + X7(t) + X8(t)] + [X9(t) + X10(t)]
- X1: rate of cooling;
- X2: formation of inclusions;
- X3: parameters of austenite grain;
- X4: phase charts;
- X5: microstructure;
- X6: local strain;
- X7: remaining stress;
- X8: mechanical properties of the weld areas;
- X9: crack resistance;
- X10: bending resistance.
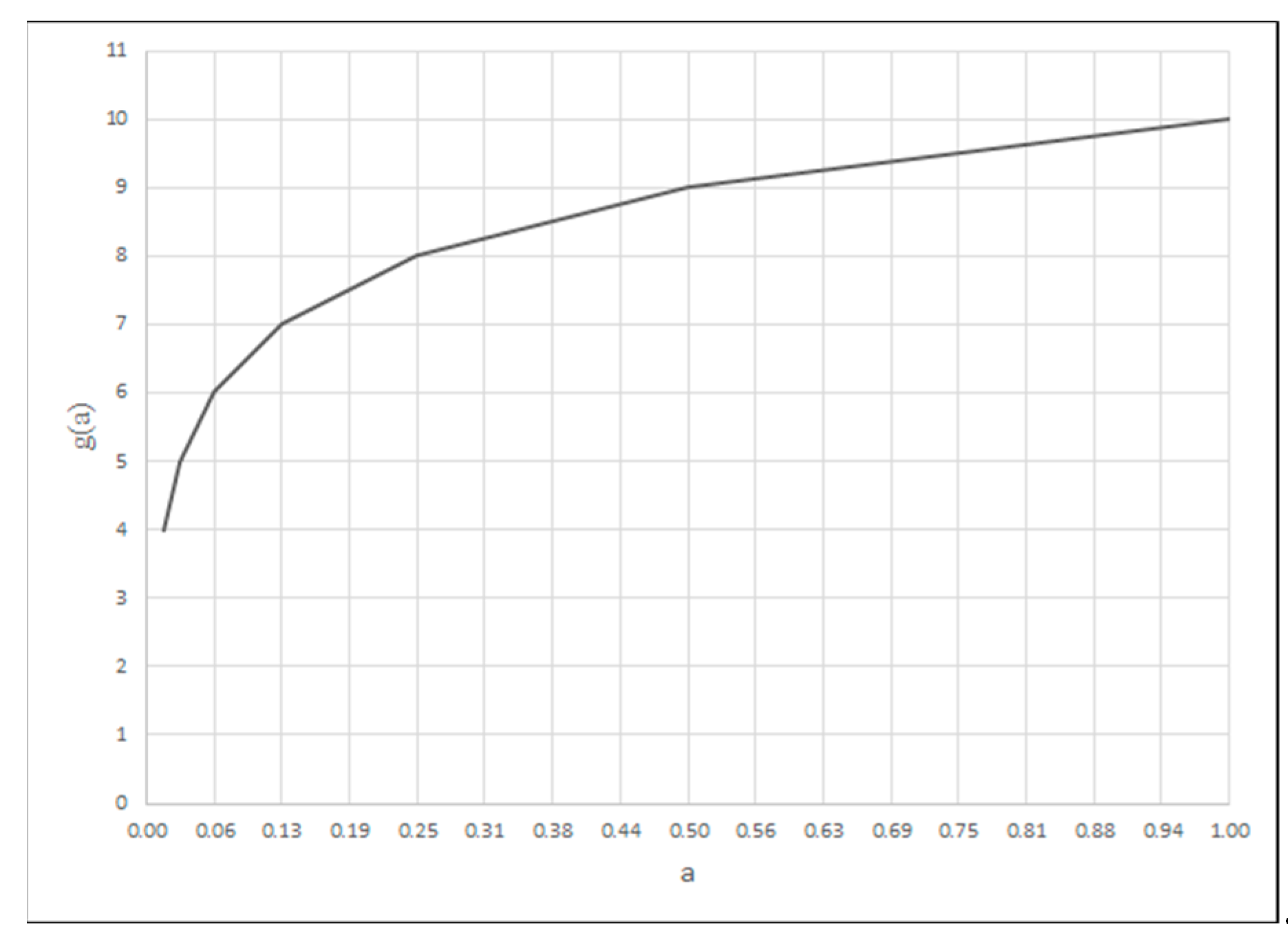
- amax represents the upper range of variability of the criterion argument;
- amin represents the lower range of variability of the criterion argument;
- a represents the value of the criterion argument for the division point;
- fc(a) represents the value of the criterion function for the division point.
- g represents the degree of the criterion fulfilment.
- s represents the total rating of the variant;
- c represents the normalized weight of the criterion;
- g represents the degree of the criterion fulfilment;
- i represents the number of the criterion.
4. Modeling of the Assessment Process of the Welded Joint Characteristics
4.1. Characteristics Describing the Welding Process Parameters
4.2. Characteristics Describing the Weld Microstructure
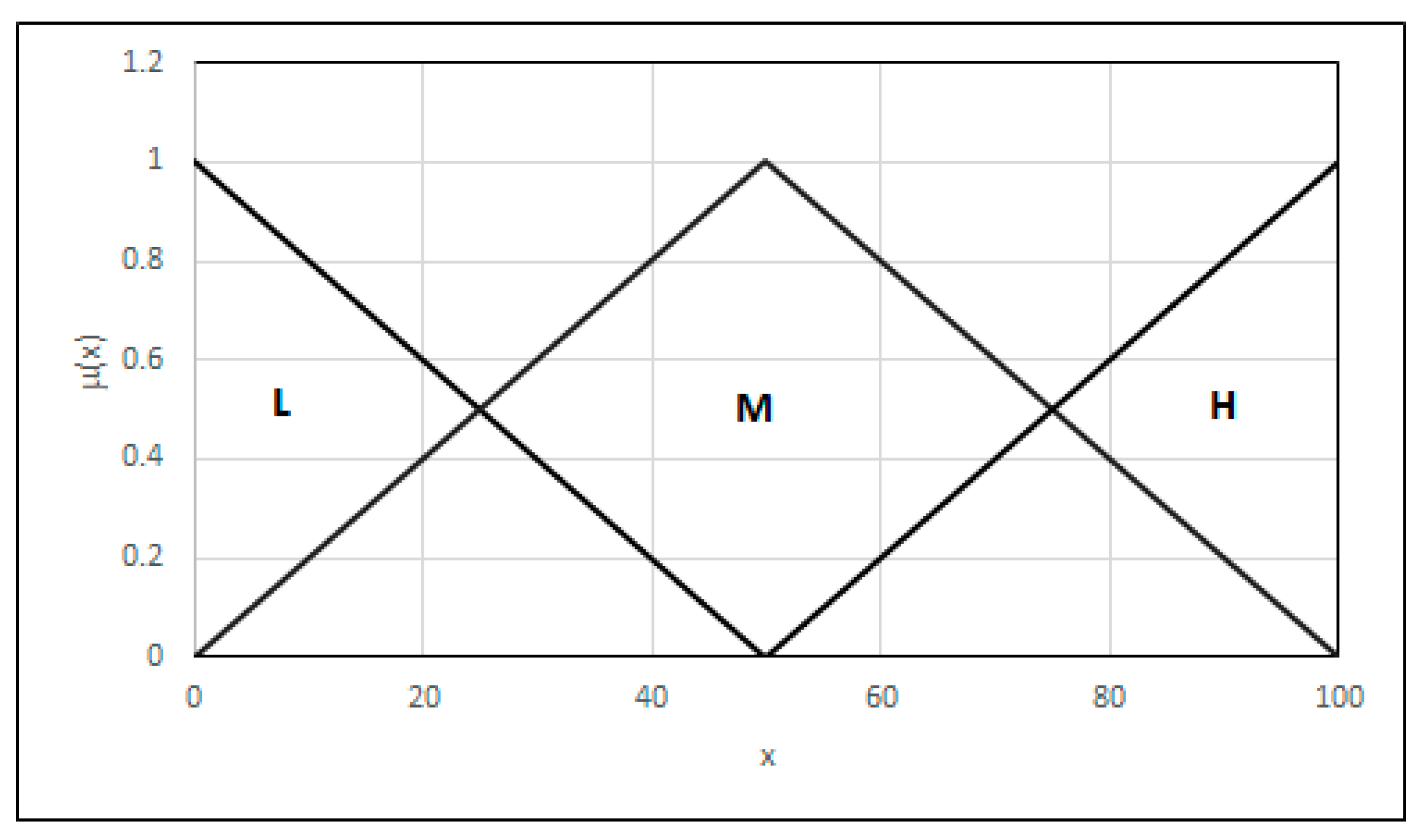
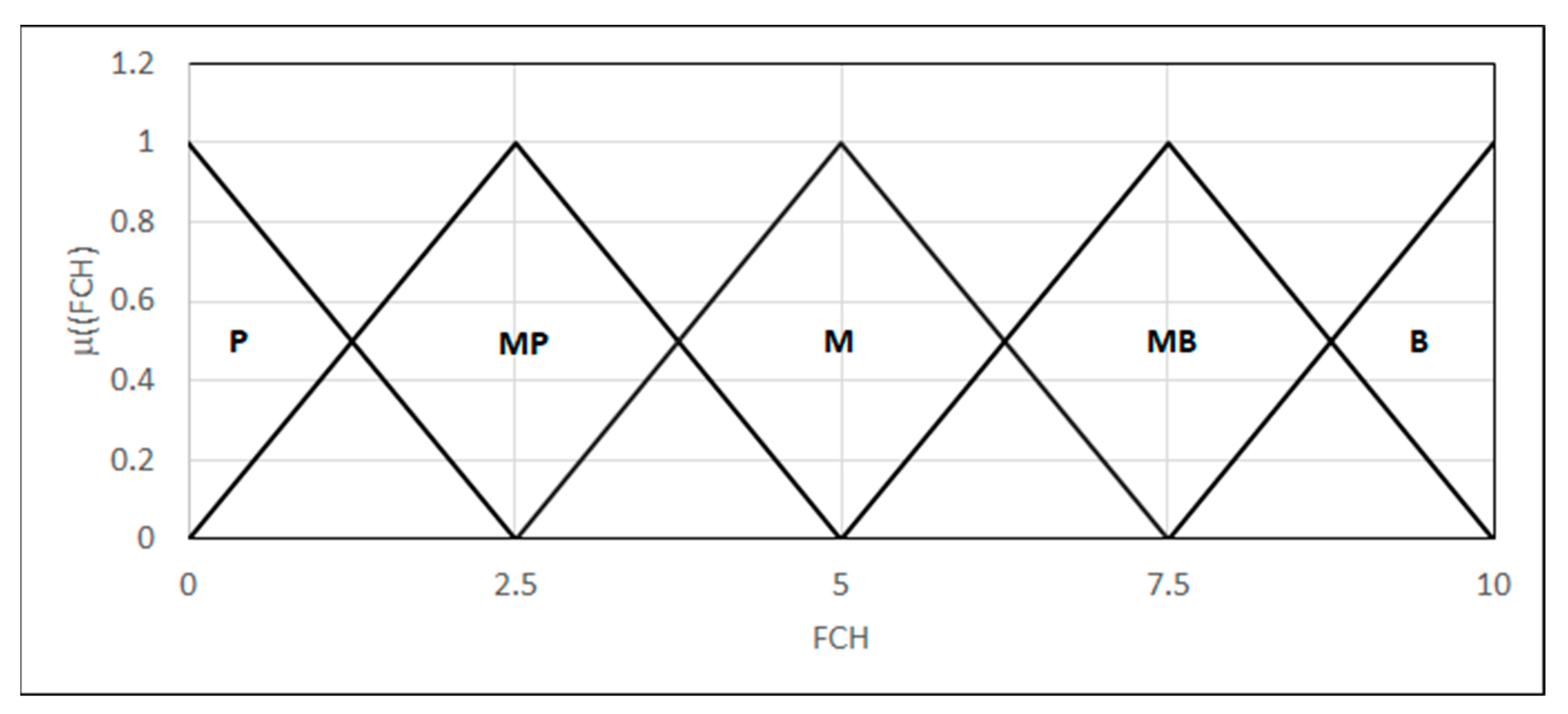
4.2.1. Formation of Inclusions
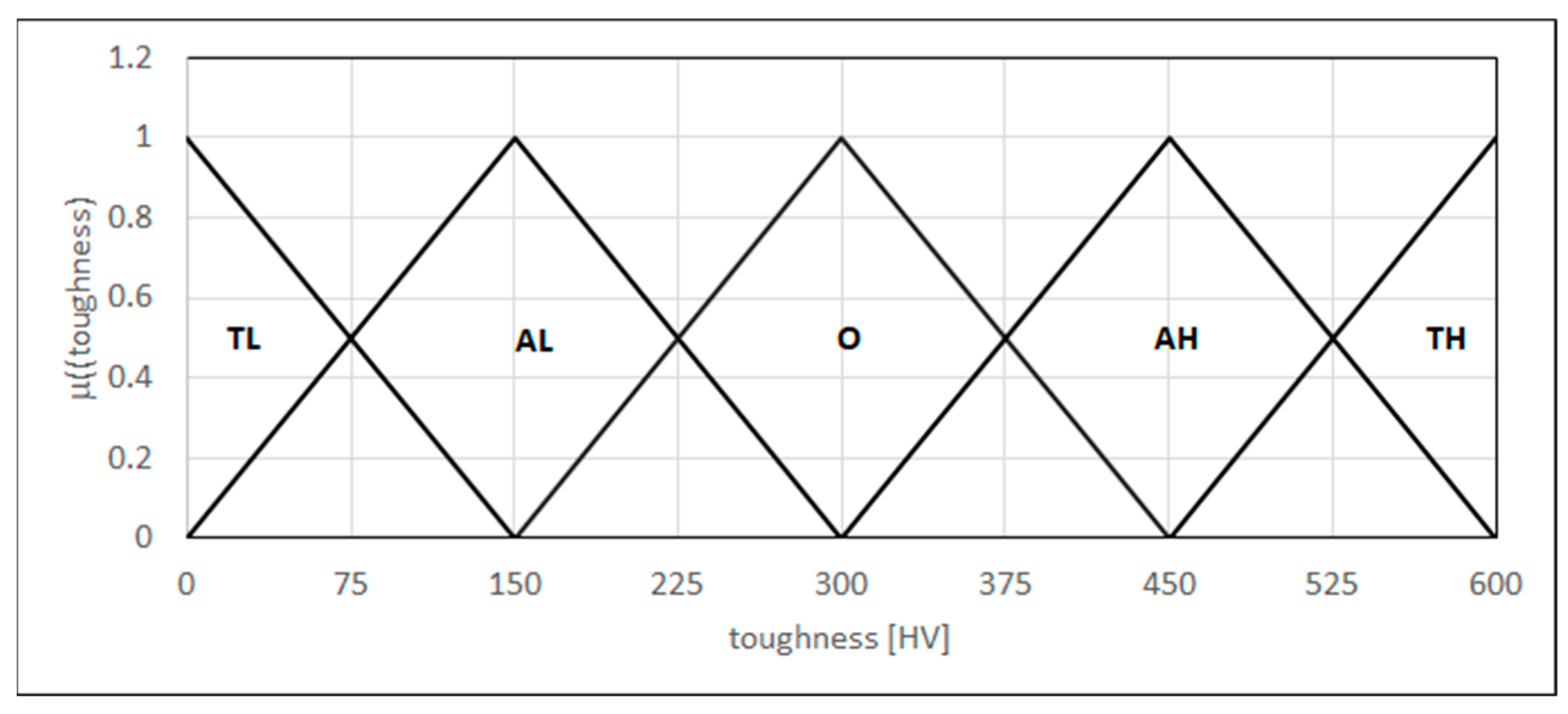
- FS represents the fuzzy set;
- x represents the argument of a fuzzy set;
- lrs represents the left range of the fuzzy set support;
- lrk represents the left range of the fuzzy set kernel;
- rrs represents the right range of the fuzzy set support;
- rrk represents the right range of the fuzzy set kernel.
- d’ represents the transformed distance,
- dmax represents the maximum distance,
- d represents prior to the transformation distance.
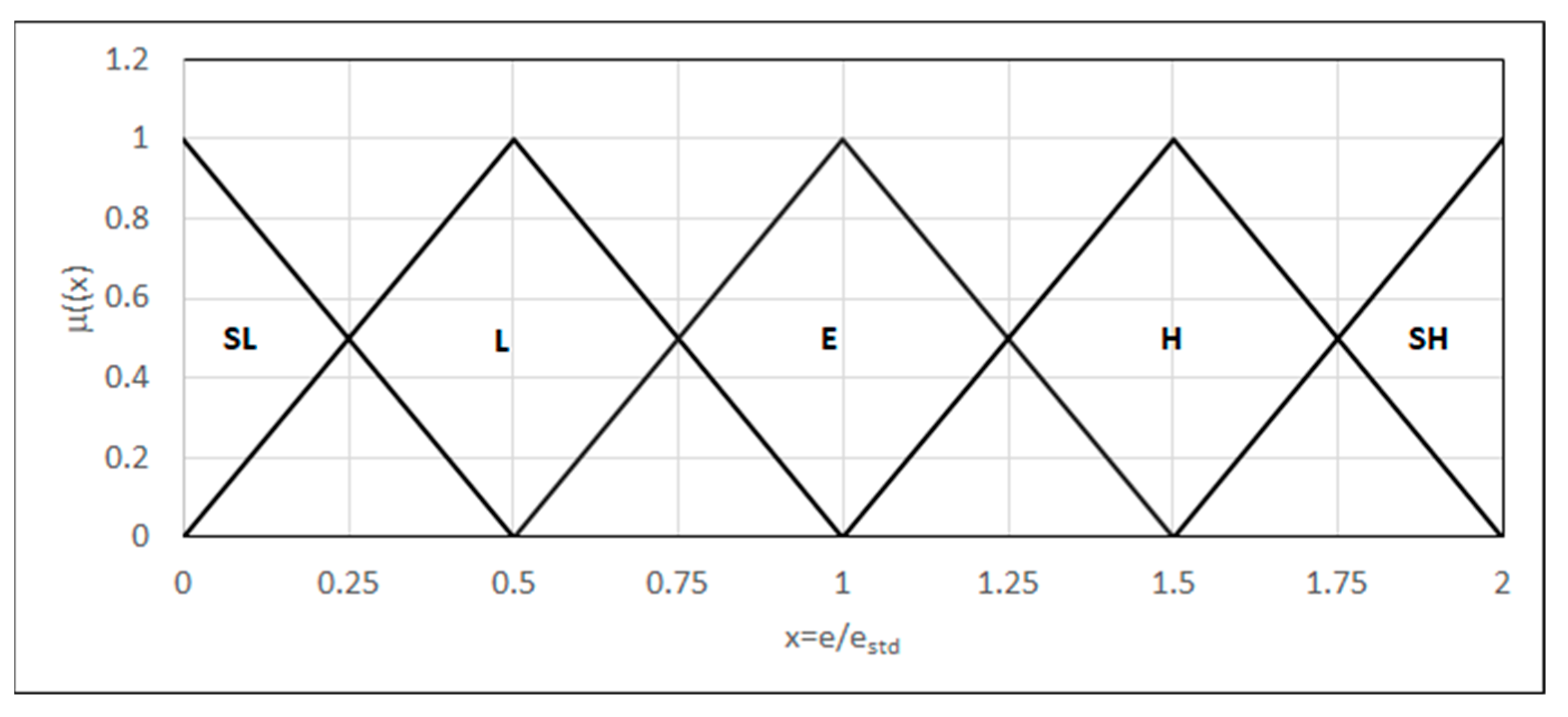
- vc represents the value of the criterion argument,
- FSi represents the i-th fuzzy set,
- μFSi(v) represents the value of the membership function and the value v of the i-th fuzzy set.
4.2.2. Parameters of Austenite Grain
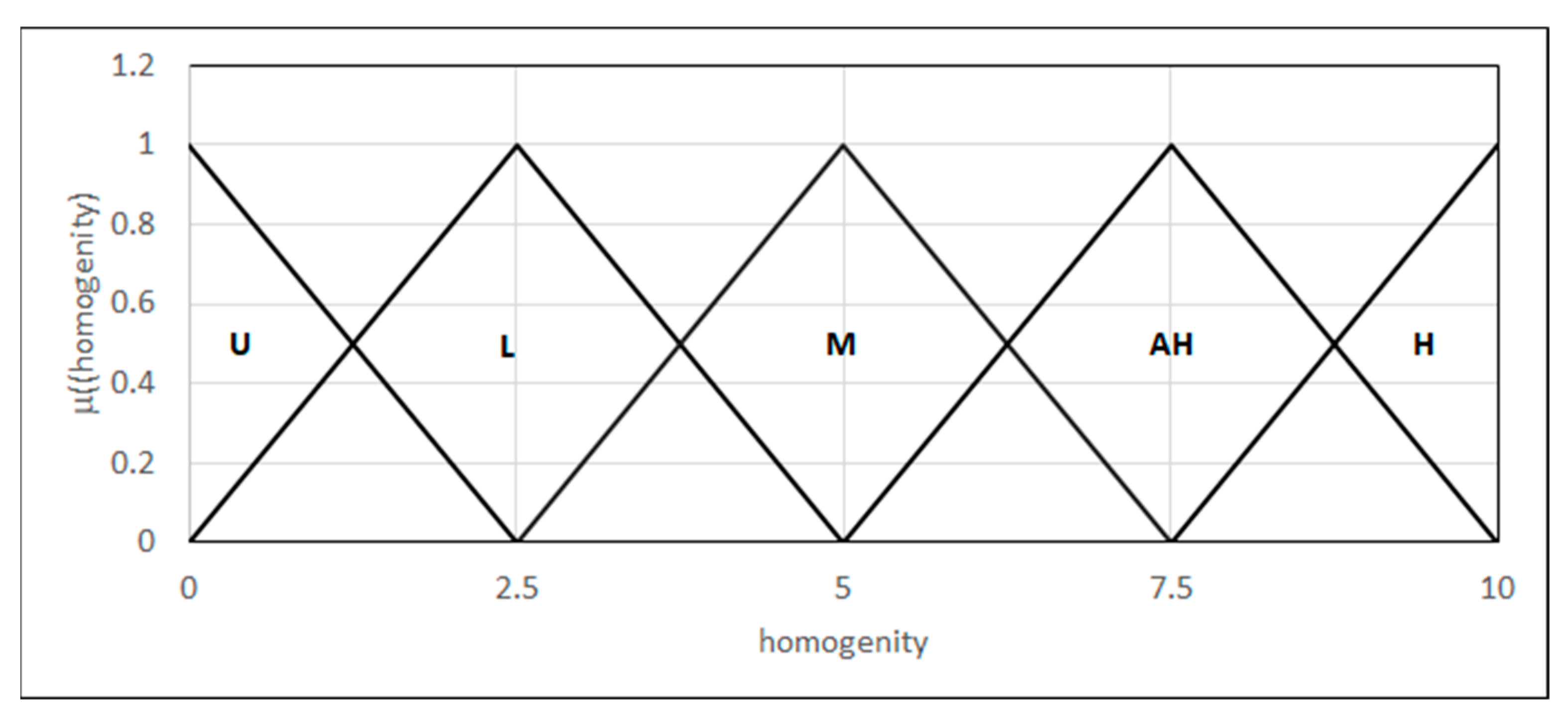
4.2.3. Presence of Each Microstructural Phase in the Joint
- y represents the crisp value,
- FS represents the fuzzy set,
- μ(y) represents the value of the function of membership of the y value in the FS fuzzy set.
4.2.4. Microstructure
4.3. Features Describing the Microscopic Properties of a Mechanical Weld
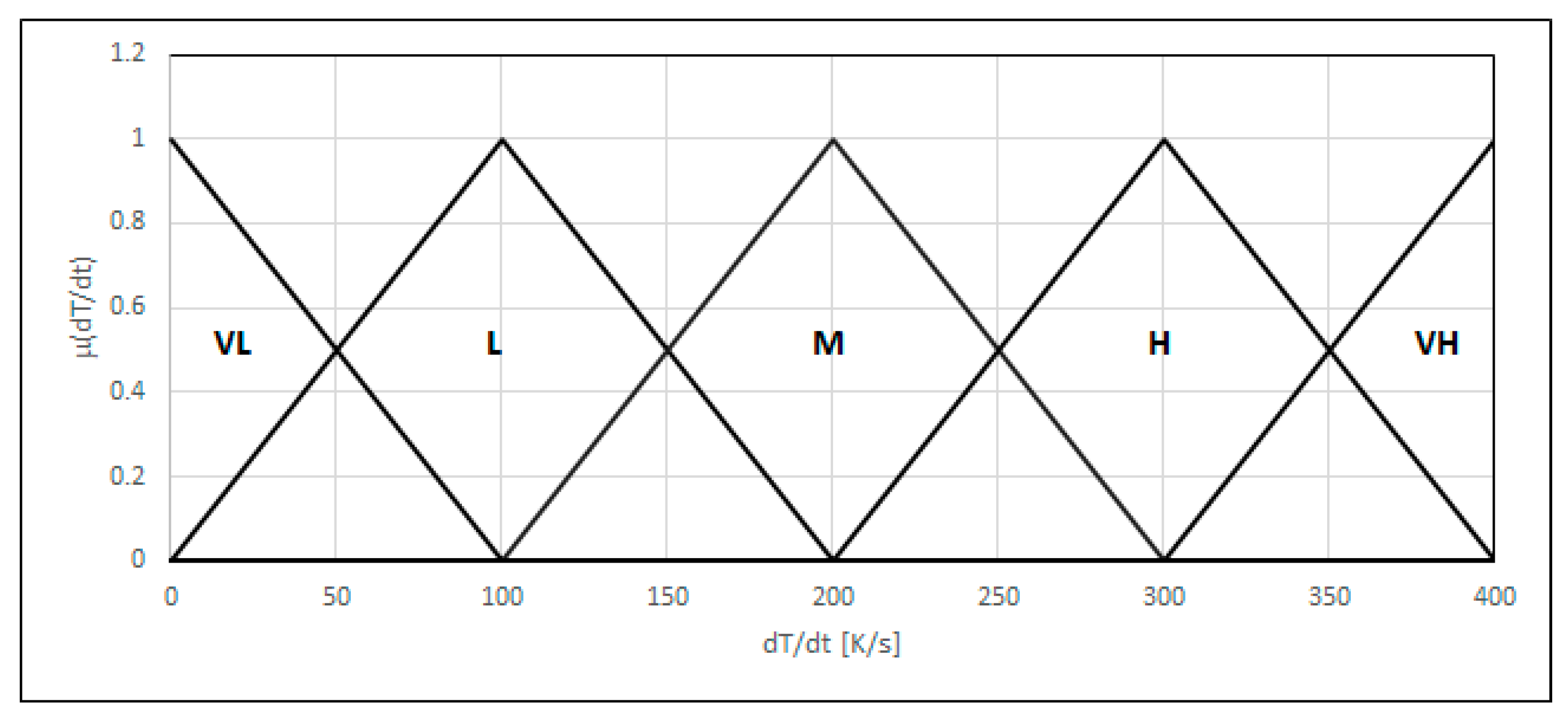
4.3.1. Local Strains
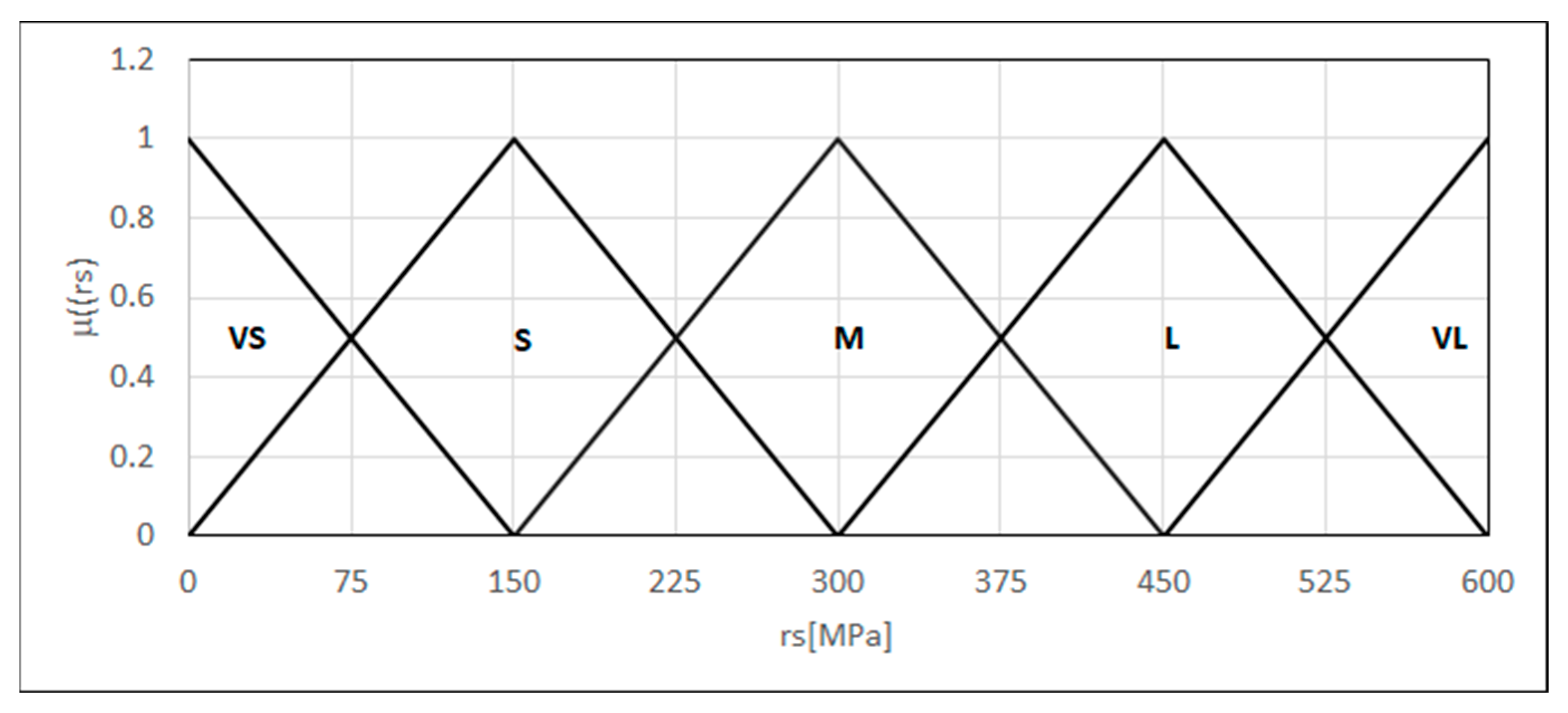
4.3.2. The Residual Stress
4.3.3. Mechanical Properties of the Welded Joint Areas
4.3.4. Tensile Test
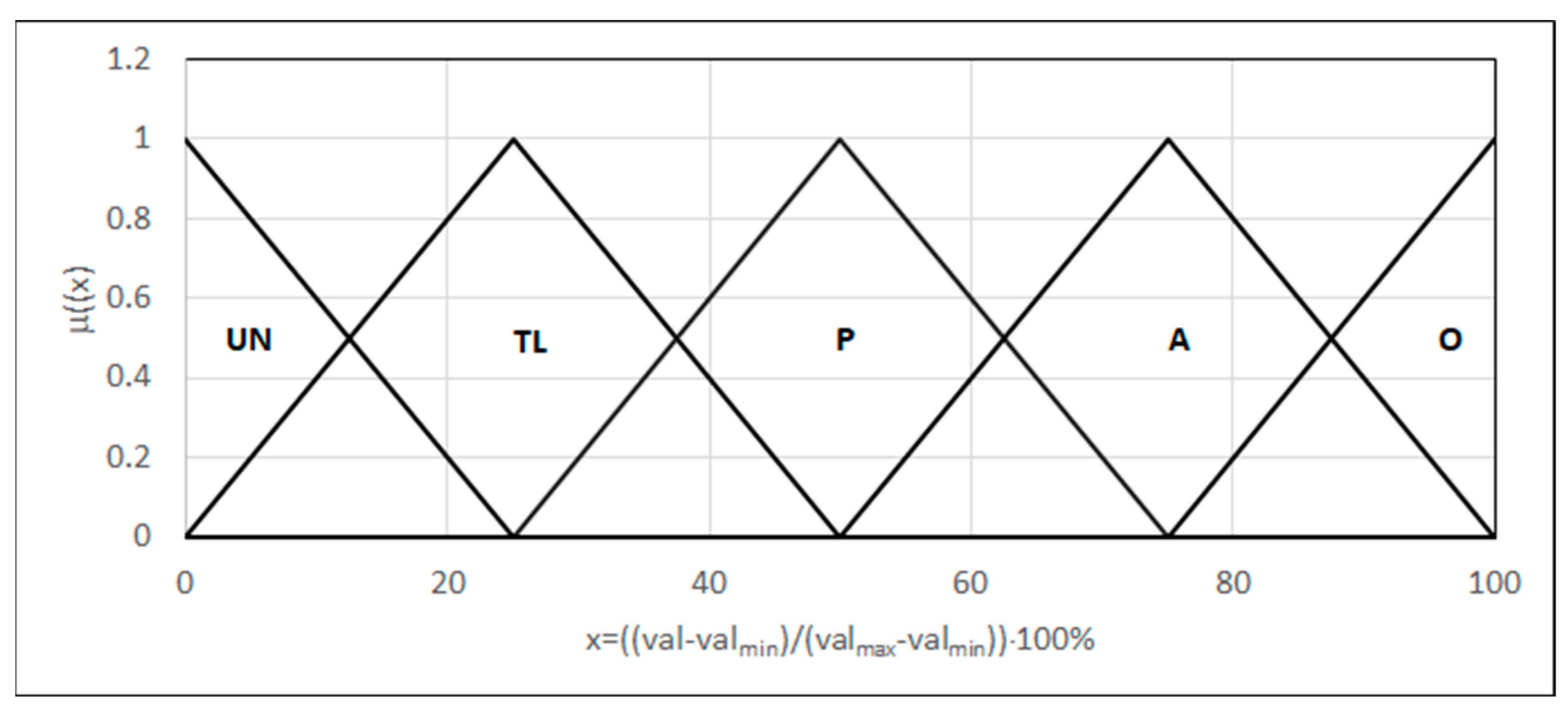
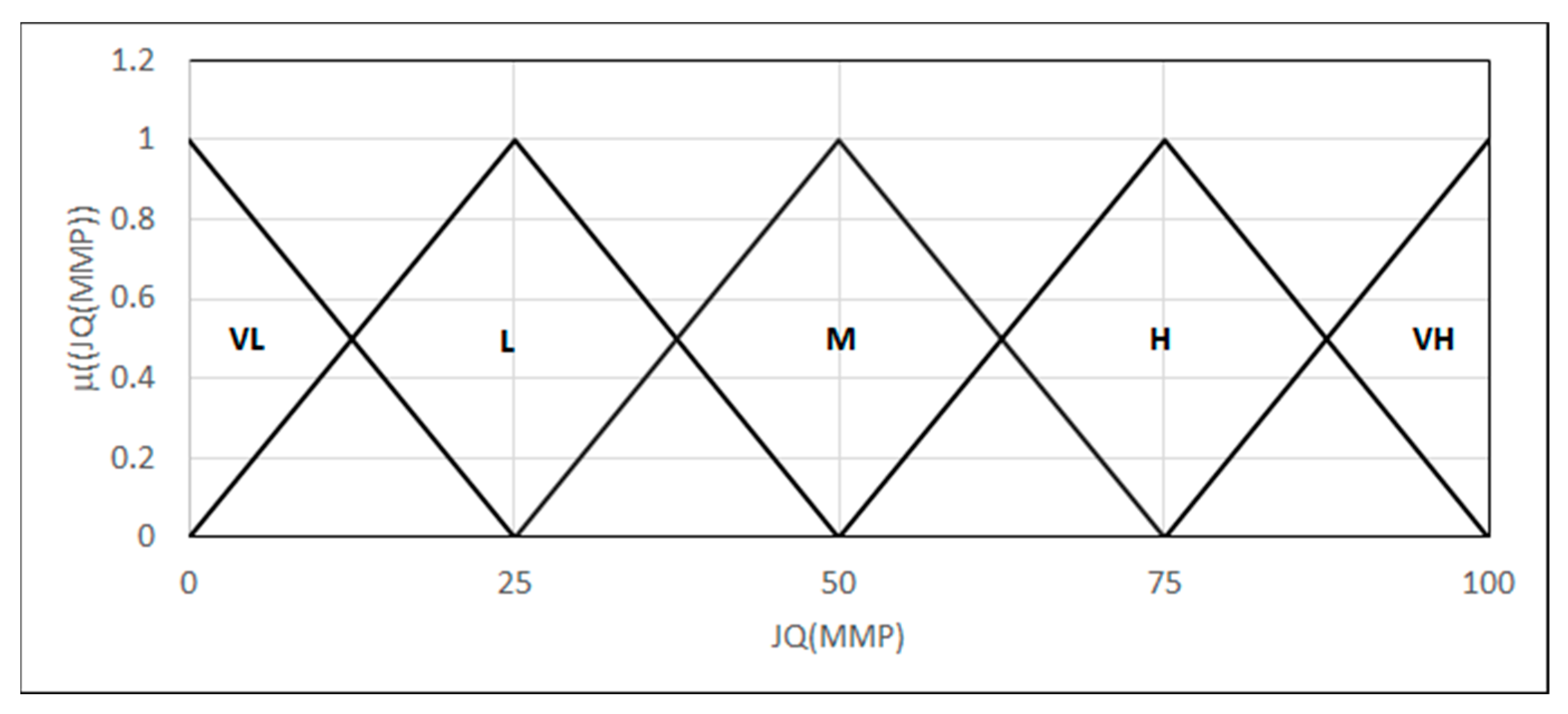
- WQ(TT) represents the weld quality in terms of the tensile test;
- Rm represents the tensile strength;
- A represents the relative extending;
- Sr represents the place of the specimen rupture; i represents the number of fuzzy sets;
- x represents the argument of the fuzzy variable;
- μFSi(x) represents the value of the membership function of the i-th fuzzy set.
4.3.5. Impact Test (Charpy V-Notch)
4.3.6. Micro-Toughness Assessment
4.4. Features Describing the Macroscopic Mechanical Properties of the Weld
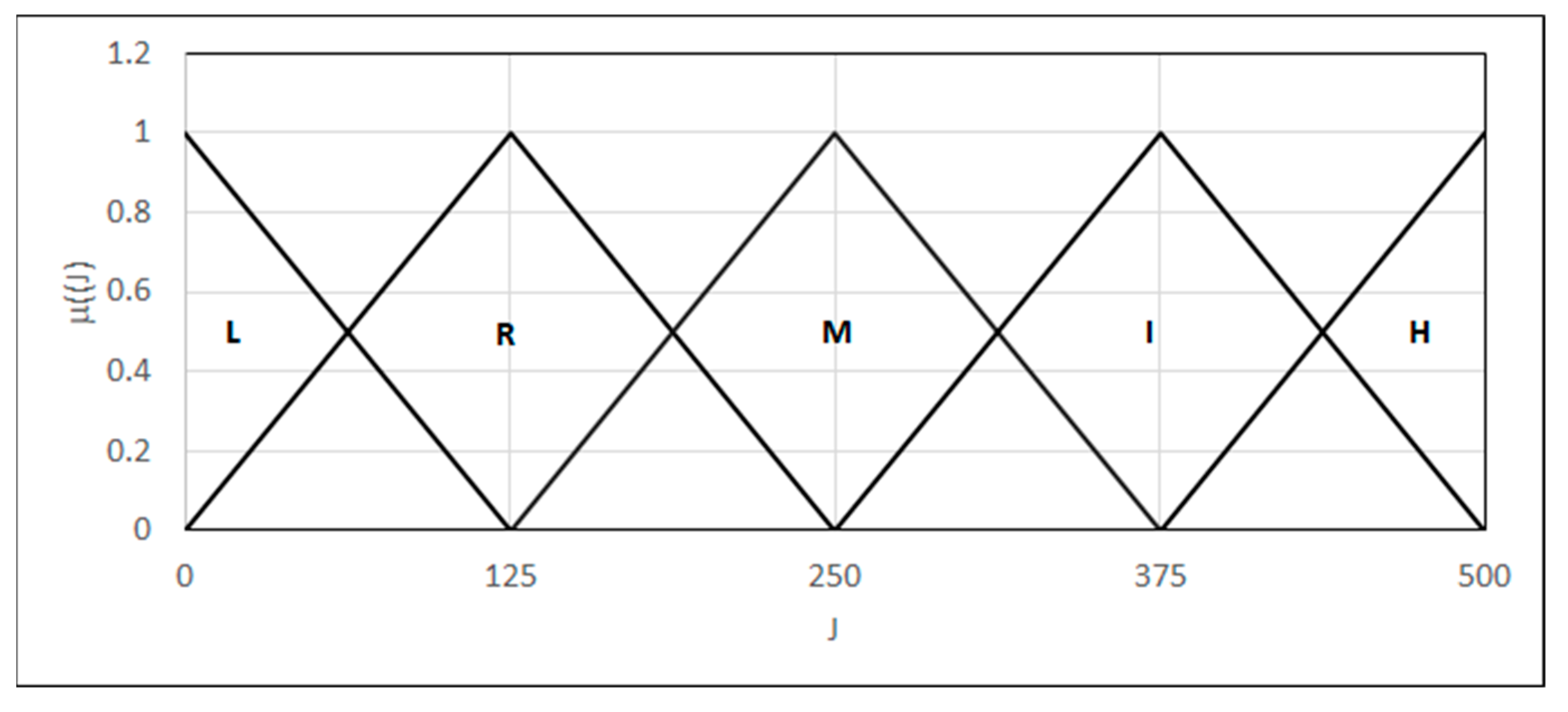
4.4.1. Crack Resistance
4.4.2. Bending Resistance
- -
- Very low surface quality: the presence of large cracks, delaminations, or other defects after bending;
- -
- Low surface quality: the presence of small surface cracks whose lengths or widths do not exceed the acceptable boundaries defined by the norms;
- -
- Medium surface quality: there may be small surface cracks, the length or width of which is within the permissible limits specified by the standards;
- -
- High surface quality;
- -
- Very high surface quality: no cracks or delaminations after the bending test.
- -
- Unacceptable strength: the weld exhibits low ductility and susceptibility to brittle cracking;
- -
- Permissible strength;
- -
- Acceptable strength: small defects that do not affect the weld strength;
- -
- Good strength;
- -
- Very good strength: the joint exhibits high ductility and good adhesion to the parent material.
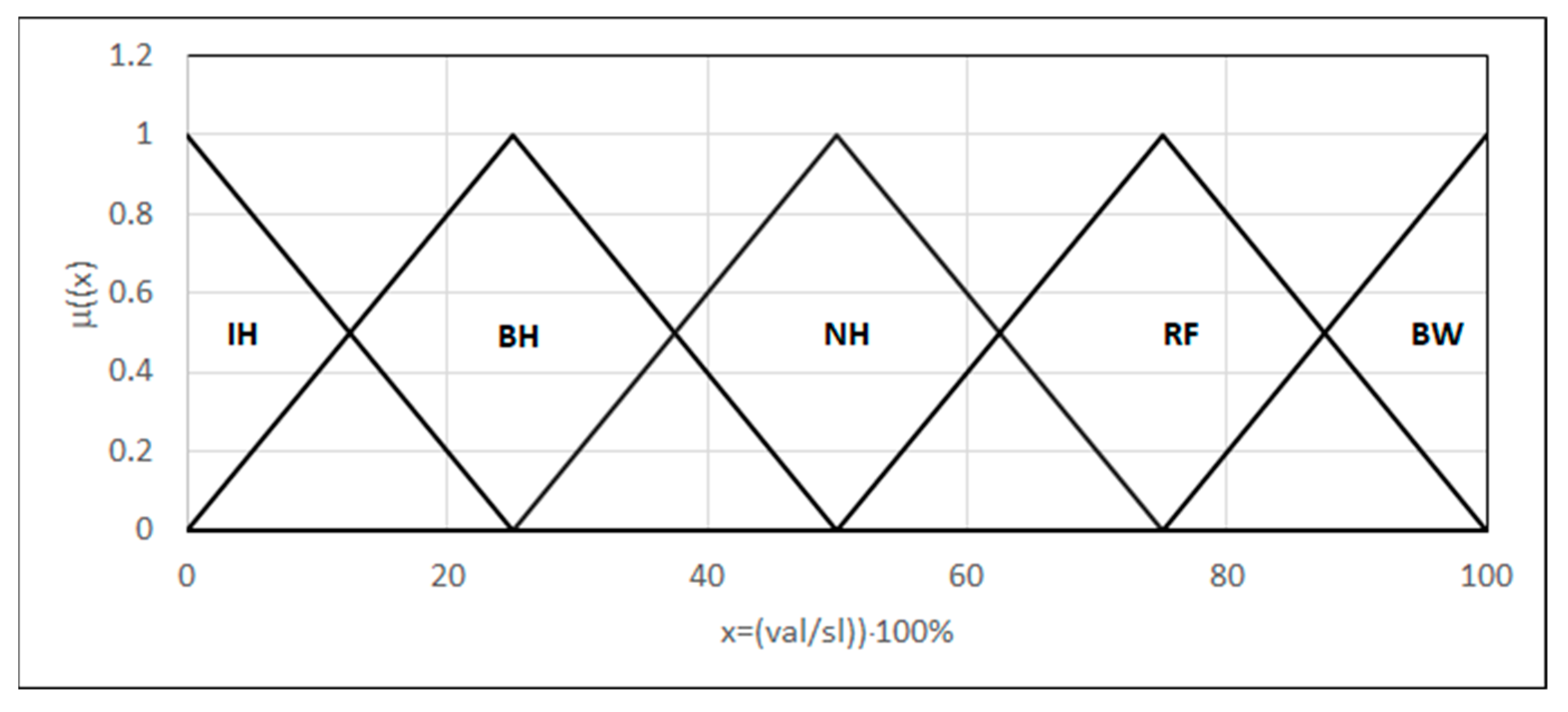
- WQ(BR) represents the weld quality in terms of the bending resistance; sq represents the surface quality;
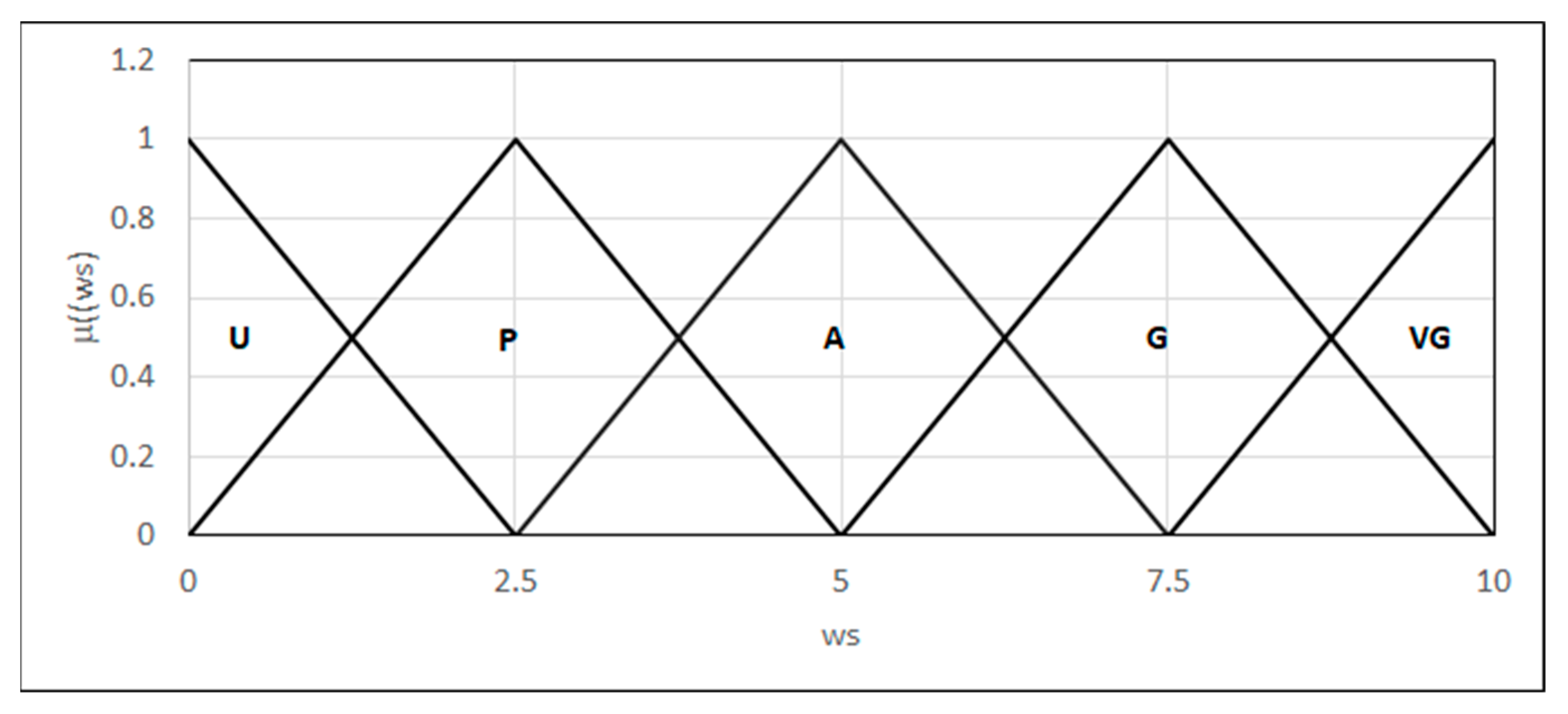
- ws represents the weld strength;
- i represents the number of fuzzy sets;
- x represents the argument of the fuzzy variable;
- μFSi(x) represents the value of the membership function of the i-th fuzzy set.
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- David, S.A.; Babu, S.S. Microstructure Modelling in Weld Metal; Mathematical Modelling of Weld Phenomena 3; Cerjak, H., Ed.; The Institute of Materials: London, UK, 1997. [Google Scholar]
- Ranatowski, E. The Influence of the Constraint Effect on the Mechanical Properties and Weldability of the Mismatched Weld Joints; Mathematical Modelling of Weld Phenomena 8; Cerjak, H., Badeshia, H., Kozeschnik, E., Eds.; TU Graz: Graz, Austria, 2007. [Google Scholar]
- Ranatowski, E.; Muślewski, Ł. The Numerical Analysis of Weldability in the Design and Technological Processes Influence on the Exploitation Condition and Quality. J. KONBiN 2008, 4, 146–164. [Google Scholar]
- Ainsworth, R.A.; Sattari-Far, I.; Sherry, A.H.; Hooton, D.G.; Hadley, I. Methods for Including Constraint effects within the SINTAP procedures. Eng. Fract. Mech. 2000, 67, 563–571. [Google Scholar] [CrossRef]
- Broberg, K.B. Computer demonstration of crack growth. Int. J. Fract. 1990, 42, 277–285. [Google Scholar] [CrossRef]
- Goldak, J.A.; Akhlanghi, M. Computational Welding Mechanics; Springer Science & Business Media: New York, NY, USA, 2005. [Google Scholar]
- Barsoum, Z.; Batti, A.A.; Balawi, S. Computational Weld Mechanics—Towards a Simplified and Cost Effective Approach for Large Welded Structures. Elseviere Procedia Eng. 2015, 114, 62–69. [Google Scholar] [CrossRef]
- Arandelović, M.; Sedmak, S.; Jovićić, R.; Perković, S.; Burzić, Z.; Radu, D.; Radaković, Z. Numerical and Experimental Investigations of Fracture Behaviour of Welded Joints with Multiple Defects. Materials 2021, 14, 4832. [Google Scholar] [CrossRef] [PubMed]
- Lindgren, L.-E.; Lunback, A. Approaches in computational welding mechanics applied to additive manufacturing: Review and outlook. Comptes Rendus Mec. 2018, 346, 1033–1042. [Google Scholar] [CrossRef]
- Goyal, R.; El-zein, M.; Glinka, G. Computational weld analysis and fatigue of welded structures. In Advanced Joining Proceses, Welding, Plastic Deformation, and Adhesion; Elsevier: Amsterdam, The Netherlands, 2021. [Google Scholar]
- Hemer, A.; Milovic, L.; Grabovic, A.; Aleksic, B.; Aleksic, V. Numerical determination and experimental validation of the fracture toughness of welded joints. Eng. Fail. Anal. 2020, 107, 104220. [Google Scholar] [CrossRef]
- EN ISO 5817; Welding-Fusion-Welded Joints in Steel, Nickel, Titanium and Their Alloys (Beam Welding Excluded)-Quality Levels for Imperfections. ISO Copyright Office: Geneva, Switzerland, 2023.
- Radu, D.; Sedmak, A. Welding joints failure assessment—Fracture mechanics approach. Bull. Transilvania. Univ. Brasov. Ser. II For. Wood Ind. Agric. Food Eng. 2016, 9, 121–128. [Google Scholar]
- Stenberg, T.; Barsoum, Z.; Hedlund, J.; Josefsson, J. Development of a computational fatigue model for evaluation of weld quality. Weld. World 2019, 63, 1771–1785. [Google Scholar] [CrossRef]
- Volvo STD 181-0004; Volvo Corporate Standart, Welding of Metallic Materials. Volvo Group: Stockholm, Sweden, 2018.
- Say, D.; Mian, Q.S.; Krichen, M.; Zidi, S. Artificial Intelligence Assistive Non-Destructive Testing of Welding Joints: A Reviev. Preprints 2024. [Google Scholar] [CrossRef]
- Woropay, M.; Muślewski, Ł. Theoretical grounds to evaluate quality of the transport system operation. In Proceedings of the 12th International Maritime Association of the Mediterraean, Lisboa, Portugal, 26–30 September 2005; Guedes Soares, C., Garbatov, Y., Fonseca, N., Eds.; Taylor & Francis Group: Abingdon, UK, 2005; Volume 1. [Google Scholar]
- Pająk, M.; Kluczyk, M.; Muślewski, Ł.; Lisjak, D.; Kolar, D. Ship Diesel Engine Fault Diagnosis Using Data Science and Machine Learning. Electronics 2023, 12, 3860. [Google Scholar] [CrossRef]
- Kostek, R.; Aleksandrowicz, P. Simulation of the right-angle car collision based on identified parameters. In Proceedings of the 11th International Congress of Automotive and Transport Engineering-Mobility Engineering and Environment (CAR) 2017, Pitesti, Romania, 8–10 November 2017. [Google Scholar] [CrossRef]
- ISO 11666; Non-destructive testing of welds-Ultrasonic testing-Acceptance levels, Edition 2. ISO Copyright Office: Geneva, Switzerland, 2018.
- ISO 643; Steels-Micrographic Determination of the Apparent Grain Size. ISO Copyright Office: Geneva, Switzerland, 2019.
- ISO 5817; Welding-Fusion-Welded Joints in Steel, Nickel, Titanium and Their Alloys (Beam Welding Excluded)-Quality Levels for Imperfections. ISO Copyright Office: Geneva, Switzerland, 2014.
- BS EN 10025; Hot Rolled Products of Structural Steels-Part 2: Technical Delivery Conditions for Non-Alloy Structural Steels. BSI Standards Limited: London, UK, 2019.
- ASTM E837; Standard Test Method for Determining Residual Stresses by the Hole-Drilling Strain-Gage Method. ASTM International: West Conshohocken, PE, USA, 2001.
- ISO 12135; Metallic Materials-Unified Method of Test for the Determination of Quasistatic Fracture Toughness. ISO Copyright Office: Geneva, Switzerland, 2021.
- EN ISO 5173; Destructive Tests on Welds in Metallic Materials-Bend Tests. ISO Copyright Office: Geneva, Switzerland, 2023.
- AWS D1.1; Structural Welding Code-Steel an American National Standard. American Welding Society: Miami, FL, USA, 2000.
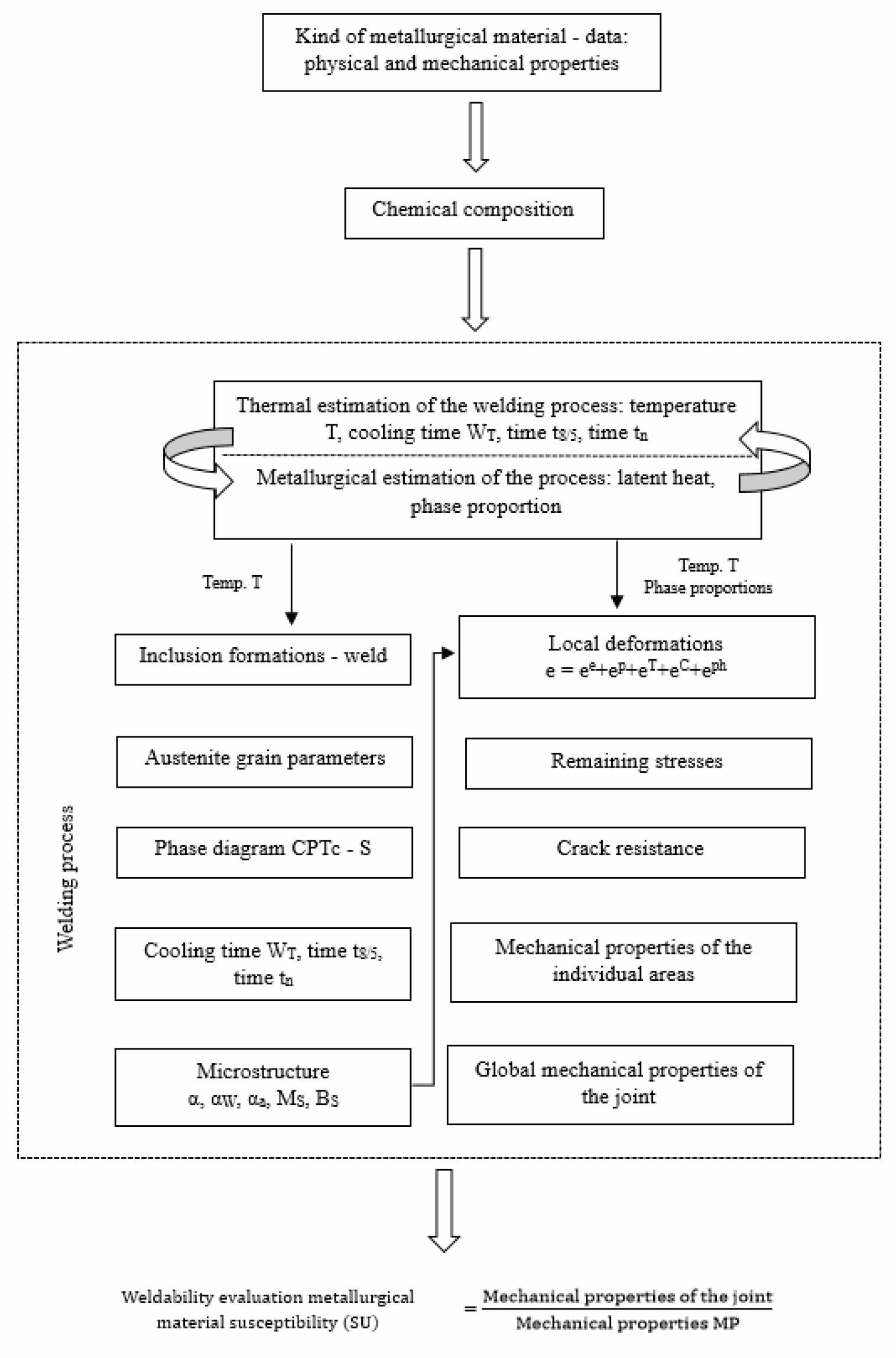
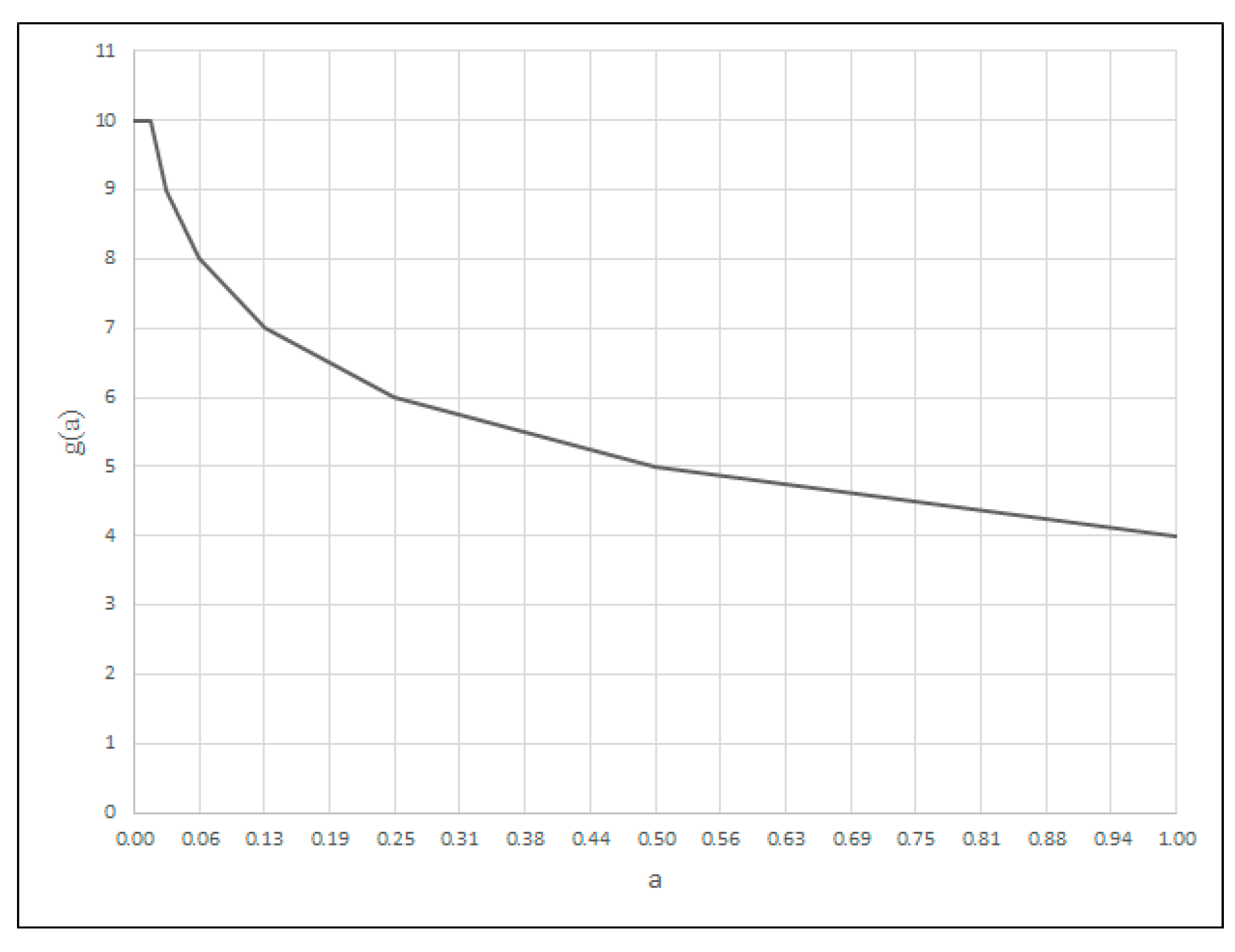



| Total Rating Values | Interpretation |
|---|---|
| 10 | Ideal |
| 9 | Very good |
| 8 | Good |
| 7 | Poor |
| 6 | Very poor |
| 5 | Bad |
| 4 | Very bad |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Muślewski, Ł.; Pająk, M. Methodological Aspects of Welded Joint Quality Assessment. Materials 2025, 18, 2148. https://doi.org/10.3390/ma18092148
Muślewski Ł, Pająk M. Methodological Aspects of Welded Joint Quality Assessment. Materials. 2025; 18(9):2148. https://doi.org/10.3390/ma18092148
Chicago/Turabian StyleMuślewski, Łukasz, and Michał Pająk. 2025. "Methodological Aspects of Welded Joint Quality Assessment" Materials 18, no. 9: 2148. https://doi.org/10.3390/ma18092148
APA StyleMuślewski, Ł., & Pająk, M. (2025). Methodological Aspects of Welded Joint Quality Assessment. Materials, 18(9), 2148. https://doi.org/10.3390/ma18092148






