First-Principles Calculations of Hydrogen Solution and Diffusion in 3C-SiC Grain Boundaries
Abstract
1. Introduction
2. Computational Details
3. Results and Discussion
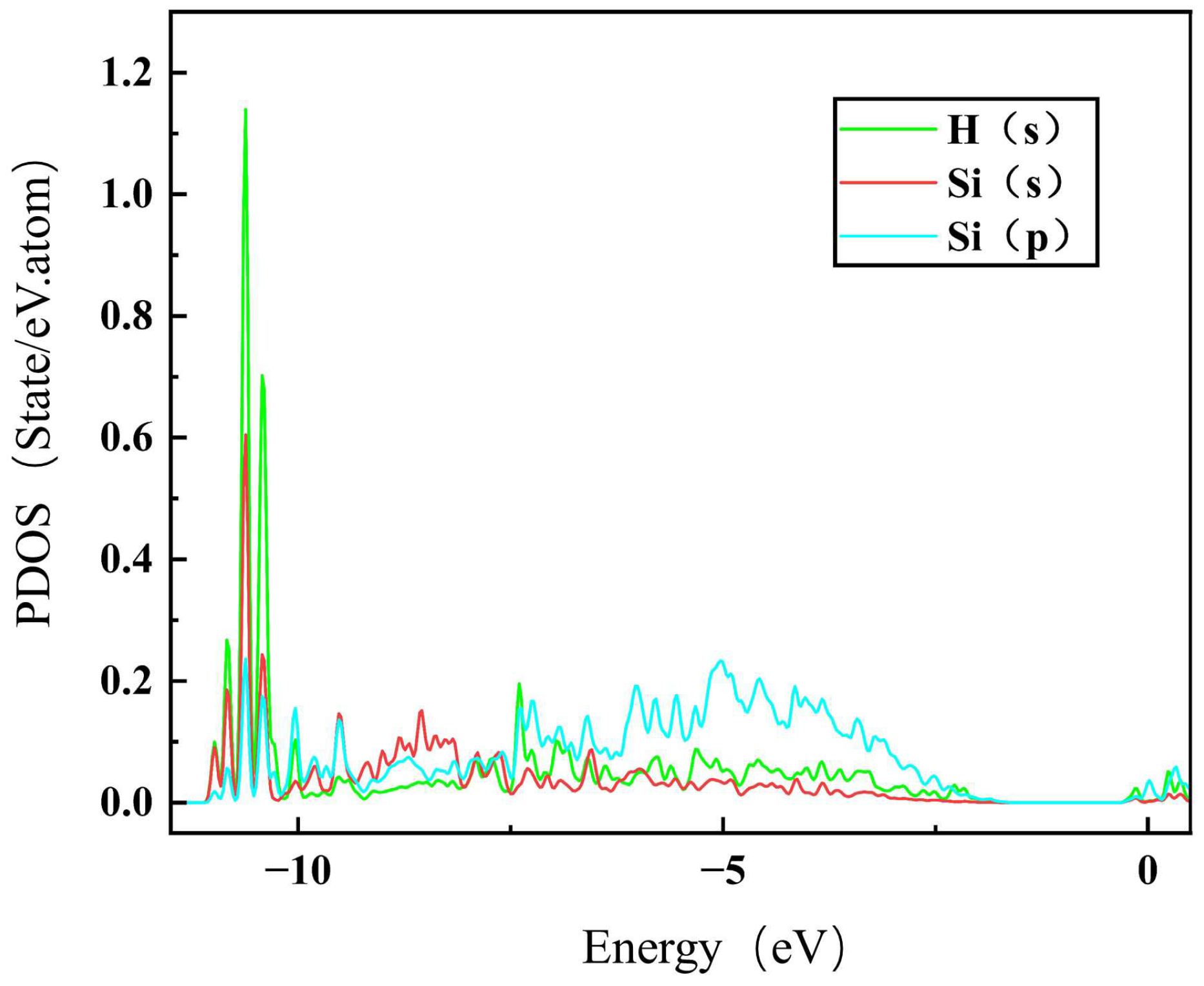
3.1. Hydrogen in Perfect 3C-SiC
3.2. The Structures of Different Grain Boundaries
3.3. The Solution Energy of Hydrogen near the Grain Boundaries
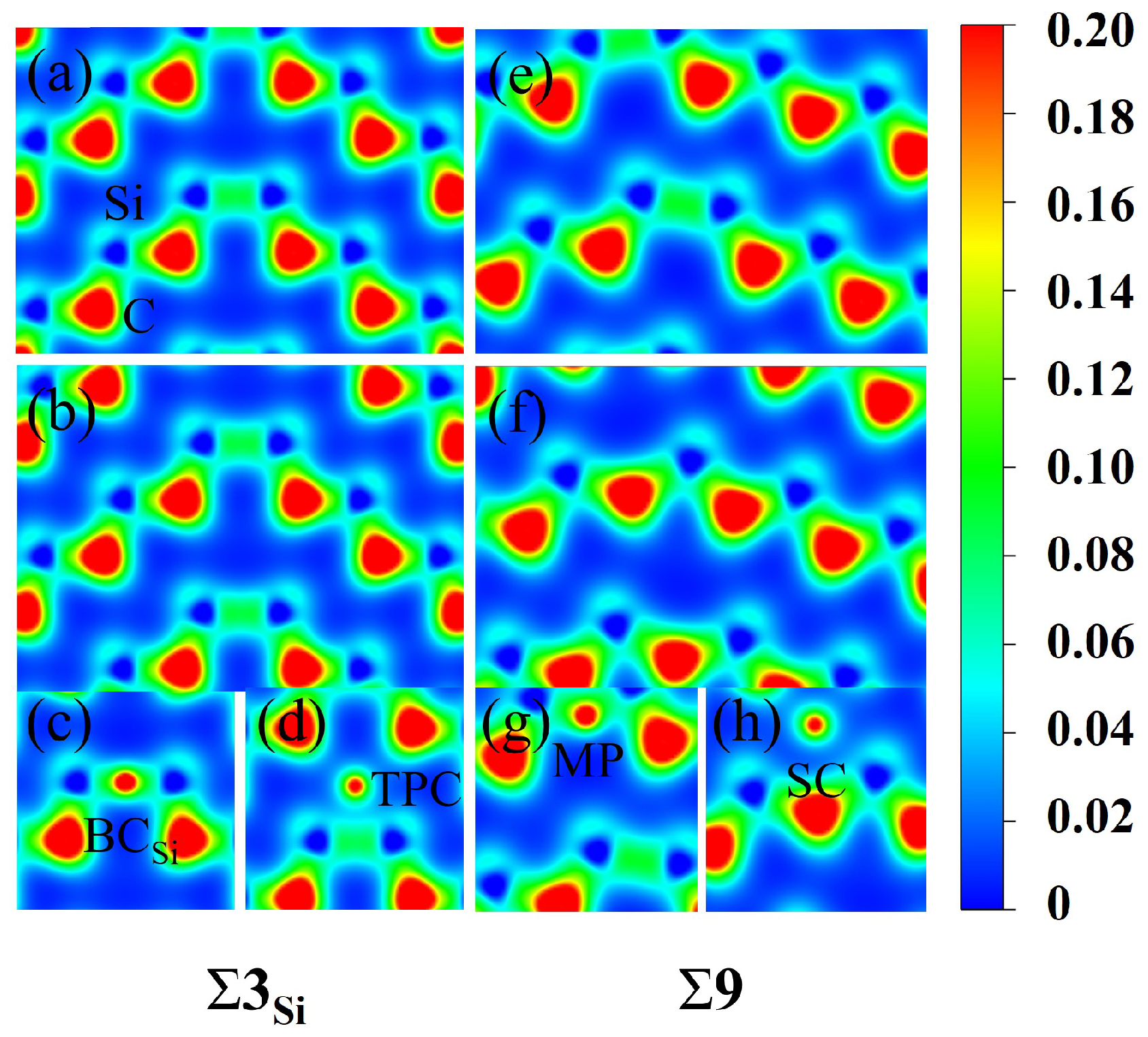
3.4. The Solution and Segregation of Hydrogen at Grain Boundaries
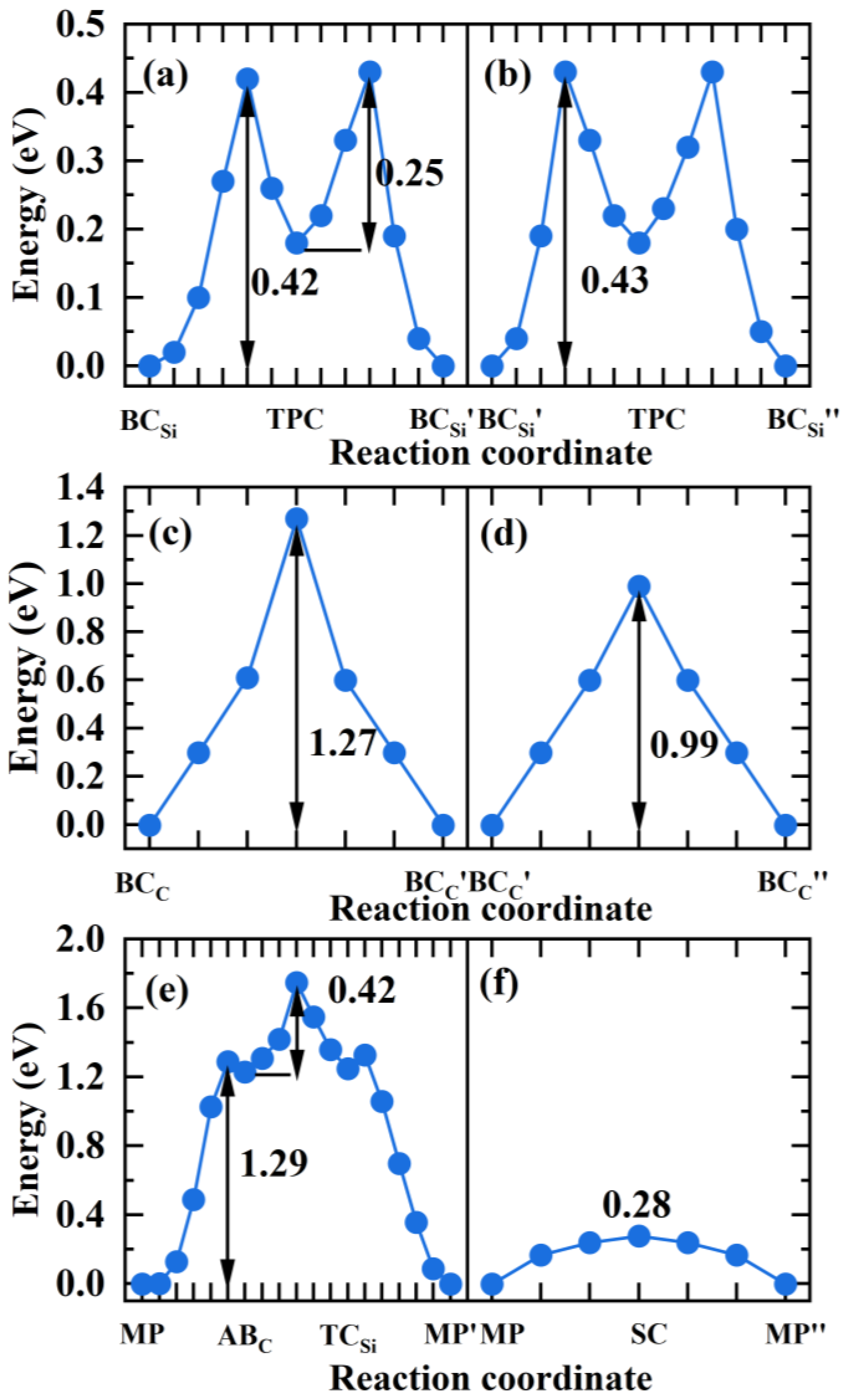
3.5. The Diffusion of Hydrogen in Grain Boundaries
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Cheng, Q.Y.; Chen, Z.Y.; Hu, S.S.; Raghothamachar, B.; Dudley, M. Analysis of Threading Edge Dislocation Low-Angle Grain Boundary Network Distributions in 4H-SiC Wafers Through Synchrotron X-ray Topography and Ray-Tracing Simulation. J. Electron. Mater. 2025, 54. [Google Scholar] [CrossRef]
- Katoh, Y.; Snead, L.L.; Szlufarska, I.; Weber, W.J. Radiation effects in SiC for nuclear structural applications. Curr. Opin. Solid State Mater. Sci. 2012, 16, 143–152. [Google Scholar] [CrossRef]
- Olander, D. Nuclear fuels–Present and future. J. Nucl. Mater. 2009, 389, 1–22. [Google Scholar] [CrossRef]
- Lee, Y.W.; Kim, Y.M.; Kim, W.K.; Kim, W.J.; Park, J.Y.; Cho, M.S. Considerations for Some Properties of Pyrolytic Carbon Coating layers in HTR Coated Particle Fuels. In Proceedings of the Transactions of the Korean Nuclear Society Spring Meeting, Jeju, Republic of Korea, 10–11 May 2007; Available online: https://inis.iaea.org/records/80bg7-0pr80 (accessed on 27 March 2025).
- Gavarini, S.; Baillet, J.; Millard-Pinard, N.; Garnier, V.; Peaucelle, C.; Jaurand, X.; Bernard, C.; Rapegno, R.; Cardinal, S.; Dalverny, C.; et al. Effects of helium irradiation on fine grained β-SiC synthesized by spark plasma sintering. J. Eur. Ceram. Soc. 2020, 40, 1–11. [Google Scholar] [CrossRef]
- Wright, G.M.; Durrett, M.G.; Hoover, K.W.; Kesler, L.A.; Whyte, D.G. Silicon Carbide as a tritium permeation barrier in tungsten plasma-facing components. Curr. Opin. Solid State Mater. Sci. 2015, 458, 272–274. [Google Scholar] [CrossRef]
- Soto, C.; García-Rosales, C.; Echeberria, J.; Martínez-Esnaola, J.M.; Hernández, T.; Malo, M.; Platacis, E.; Muktepavela, F. SiC-based sandwich material for Flow Channel Inserts in DCLL blankets: Manufacturing, characterization, corrosion tests. Fusion. Eng. Des. 2017, 124, 958–963. [Google Scholar] [CrossRef]
- Cai, Z.Q.; Yuan, X.W.; Xu, C.; Li, Y.M.; Shao, Z.; Li, W.J.; Xu, J.X.; Zhang, Q.M. Grain boundary effects on chemical disorders and amorphization-induced swelling in 3C-SiC under high-temperature irradiation: From atomic simulation insight. J. Eur. Ceram. Soc. 2024, 44, 6911–6925. [Google Scholar] [CrossRef]
- Koyanagi, T.; Katoh, Y.; Nozawa, T.; Snead, L.L.; Kondo, S.; Henager, C.H., Jr.; Ferraris, M.; Hinoki, T.; Huang, Q. Recent progress in the development of SiC composites for nuclear fusion applications. J. Nucl. Mater. 2018, 511, 544–555. [Google Scholar] [CrossRef]
- Sawan, M.; Katoh, Y.; Snead, L.L. Transmutation of silicon carbide in fusion nuclear environment. J. Nucl. Mater. 2013, 442, S370–S375. [Google Scholar] [CrossRef]
- Valles, G.; Panizo-Laiz, M.; González, C.; Martin-Bragado, I.; González-Arrabal, R.; Gordillo, N.; Iglesias, R.; Guerrero, C.L.; Perlado, J.M.; Rivera, A. Influence of grain boundaries on the radiation-induced defects and hydrogen in nanostructured and coarse-grained tungsten. Acta Mater. 2017, 122, 277–286. [Google Scholar] [CrossRef]
- Panizo-Laiz, M.; Díaz-Rodríguez, P.; Rivera, A.; Valles, G.; Martín-Bragado, I.; Perlado, J.M.; Munnik, F.; González-Arrabal, R. Experimental and computational studies of the influence of grain boundaries and temperature on the radiation-induced damage and hydrogen behavior in tungsten. Nucl. Fusion 2019, 59, 086055. [Google Scholar] [CrossRef]
- Daghbouj, N.; Li, B.S.; Karlik, M.; Declemy, A. 6H-SiC blistering efficiency as a function of the hydrogen implantation fluence. Appl. Surf. Sci. 2019, 466, 141–150. [Google Scholar] [CrossRef]
- Barcz, A.; Kozubal, M.; Jakieła, R.; Ratajczak, J.; Dyczewski, J.; Gołaszewska, K.; Wojciechowski, T.; Celler, D.G. Diffusion and impurity segregation in hydrogen-implanted silicon carbide. J. Appl. Phys. 2014, 155, 223710. [Google Scholar] [CrossRef]
- O’Connell, J.H.; Neethling, J.H. Investigation of radiation damage and hardness of H− and He− implanted SiC. Radiat. Eff. Defects Solids 2012, 167, 299–306. [Google Scholar] [CrossRef]
- Esteban, G.A.; Perujo, A.; Legarda, F.; Sedano, L.A.; Riccardi, B. Deuterium transport in SiCf/SiC composites. J. Nucl. Mater. 2002, 307, 1430–1435. [Google Scholar] [CrossRef]
- Atkinson, C.M.; Guziewski, M.C.; Coleman, S.P.; Nayak, S.K.; Alpay, S.P. First principles analysis of impurities in silicon carbide grain boundaries. Acta. Mater. 2021, 221, 117421. [Google Scholar] [CrossRef]
- Meng, Z.C.; Wang, C.L.; Wang, Y.L.; Liu, Y.W.; Shu, Y.F.; Yang, L. Screening and manipulation by segregation of dopants in grain boundary of Silicon carbide: First-principles calculations. Ceram. Int. 2023, 49, 32478–32489. [Google Scholar] [CrossRef]
- Leng, B.; Ko, H.; Gerczak, T.J.; Deng, J.; Giordani, A.J.; Hunter, J.L., Jr.; Morgan, D.; Szlufarska, I.; Sridharan, K. Effect of carbon ion irradiation on Ag diffusion in SiC. J. Nucl. Mater. 2016, 471, 220–232. [Google Scholar] [CrossRef]
- Wang, Z.Q.; Zhang, L.M.; AlMotasem, A.T.; Li, B.S.; Polcar, T.; Daghbouj, N. Exploring defect behavior in helium-irradiated single-crystal and nanocrystalline 3C-SiC at 800 °C: A synergy of experimental and simulation techniques. Acta. Mater. 2024, 279, 120281. [Google Scholar] [CrossRef]
- Ding, W.; Lu, P.J.; Xu, Q.F.; Zhang, C.T.F.; Tu, R.; Zhang, S. Grain size and grain boundary characteristics on the out-plane thermal conductivity of <111>-oriented CVD 3C–SiC. Ceram. Int. 2024, 50, 23775–23783. [Google Scholar] [CrossRef]
- Shao, M.Y.; Xu, C.; Hu, R.H.; Lang, Z.; Li, P.W.; Wang, Z.X.; Liu, H.P.; Liu, C.M. Damping effect of (110)<001> symmetric tilt grain boundaries on the shock response of SiC. Surf. Interfaces 2025, 59, 105992. [Google Scholar] [CrossRef]
- Wang, L.; Zhang, L.; Yu, W.S. Revisiting the structures and energies of β-SiC <001> symmetric tilt grain boundaries. J. Mater. Res. 2024, 39, 2166–2175. [Google Scholar] [CrossRef]
- Lillo, T.M.; van-Rooyen, I.J.; Wu, Y.Q. Precession electron diffraction for SiC grain boundary characterization in unirradiated TRISO fuel. Nucl. Eng. Des. 2016, 305, 277–283. [Google Scholar] [CrossRef]
- Lillo, T.M.; van-Rooyen, I.J. Influence of SiC grain boundary character on fission product transport in irradiated TRISO fuel. J. Nucl. Mater. 2016, 473, 83–92. [Google Scholar] [CrossRef]
- Wang, W.Y.; Li, C.; Shang, S.L.; Cao, J.Z.; Liu, Z.K.; Wang, Y.; Fang, C. Diffusion of hydrogen isotopes in 3C-SiC in HTR-PM: A first-principles study. Prog. Nucl. Energ. 2020, 119, 103181. [Google Scholar] [CrossRef]
- Kaukonen, M.; Fall, C.; Lento, J. Interstitial H and H2 in SiC. Appl. Phys. Lett. 2003, 83, 923–925. [Google Scholar] [CrossRef]
- Tam, S.W.; Kopasz, J.P.; Johnson, C.E. Tritium transport and retention in SiC. J. Nucl. Mater. 1995, 219, 87–92. [Google Scholar] [CrossRef]
- Causey, R.A.; Fowler, J.D.; Ravanbakht, C.; Elleman, T.S.; Verghese, K. Hydrogen Diffusion and Solubility in Silicon Carbide. J. Nucl. Mater. 1978, 61, 221–225. [Google Scholar] [CrossRef]
- Kohn, W.; Sham, L.J. Self-Consistent Equations Including Exchange and Correlation Effects. Phys. Rev. 1965, 140, A1133. [Google Scholar] [CrossRef]
- Kresse, G.; Hafner, J. Ab initio molecular dynamics for liquid metals. Phys. Rev. B 1993, 47, 558. [Google Scholar] [CrossRef]
- Kresse, G.; Joubertr, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 1999, 59, 1758. [Google Scholar] [CrossRef]
- Perdew, J.P.; Zunger, A. Self-interaction correction to density-functional approximations for many-electron systems. Phys. Rev. B 1981, 23, 5048. [Google Scholar] [CrossRef]
- Henkelman, G.; Uberuaga, B.P.; Jónsson, H. A climbing image nudged elastic band method for finding saddle points and minimum energy paths. J. Chem. Phys. 2000, 113, 9901–9904. [Google Scholar] [CrossRef]
- Rohrer, G.S. Grain boundary energy anisotropy: A review. J. Mater. Sci. 2011, 46, 5881–5895. [Google Scholar] [CrossRef]
- Uesugi, T.; Higashi, K. First-Principles Calculation of Grain Boundary Excess Volume and Free Volume in Nanocrystalline and Ultrafine-Grained Aluminum. Mater. Trans. 2013, 54, 1597–1604. [Google Scholar] [CrossRef]
- Roberson, M.A.; Estreicher, S.K. Interstitial hydrogen in cubic and hexagonal SiC. Phys. Rev. B 1991, 44, 10578. [Google Scholar] [CrossRef]
- Aradi, B.; Gali, A.; Deák, P.; Lowther, J.E.; Son, N.T.; Janzén, E.; Choyke, W.J. Ab initio density-functional supercell calculations of hydrogen defects in cubic SiC. Phys. Rev. B 2001, 63, 245202. [Google Scholar] [CrossRef]
- Sun, J.; You, Y.W.; Hou, J.; Li, X.Y.; Li, B.S.; Liu, C.S.; Wang, Z.G. The effect of irradiation-induced point defects on energetics and kinetics of hydrogen in 3C-SiC in a fusion environment. Nucl. Fusion 2017, 57, 066031. [Google Scholar] [CrossRef]
- Zhao, S.Q.; Chen, C.Y.; Ran, G. Effect of H and Pd atoms on the migration of He atoms in 3C–SiC. Prog. Nucl. Energ. 2023, 165, 104896. [Google Scholar] [CrossRef]
- Zhang, L.; Zhang, Y.; Lu, G.H. First-principles investigation of site preference and bonding properties of neutral H in 3C–SiC. Nucl. Instrum. Methods Phys. Res. Sect. B 2009, 267, 3087–3089. [Google Scholar] [CrossRef]
- Rabone, J.; López-Honorato, E. Density functional theory metadynamics of silver, caesium and palladium diffusion at β-SiC grain boundaries. J. Nucl. Mater. 2015, 458, 56–63. [Google Scholar] [CrossRef]
- Möller, H.J. <011> tilt boundaries in the diamond cubic lattice. Philos. Mag. A 1981, 43, 1045–1055. [Google Scholar] [CrossRef]
- Liu, Z.J.; Zhang, Y.G.; Li, X.Y.; Xu, Y.C.; Wu, X.B.; Liu, C.S.; Kong, X.S.; Yao, C.F.; Wang, Z.G. Investigation of the dissolution and diffusion properties of interstitial oxygen at grain boundaries in body-centered-cubic iron by the first-principles study. RSC. Adv. 2021, 11, 8643–8653. [Google Scholar] [CrossRef]
- Krawczuk, A.; Macchi, P. Charge density analysis for crystal engineering. BMC Chem. 2014, 8, 68. [Google Scholar] [CrossRef] [PubMed]
- Sun, J.; You, Y.W.; Wu, X.B.; Song, H.Y.; Li, B.S.; Liu, C.S.; Krsjak, V. Segregation and diffusion behaviours of helium at grain boundaries in silicon carbide ceramics: First-principles calculations and experimental investigations. J. Eur. Ceram. Soc. 2022, 42, 4066–4075. [Google Scholar] [CrossRef]
- He, Y.; Su, Y.J.; Yu, H.B.; Chen, C.F. First-principles study of hydrogen trapping and diffusion at grain boundaries in γ-Fe. Int. J. Hydrogen Energ. 2021, 46, 7589–7600. [Google Scholar] [CrossRef]
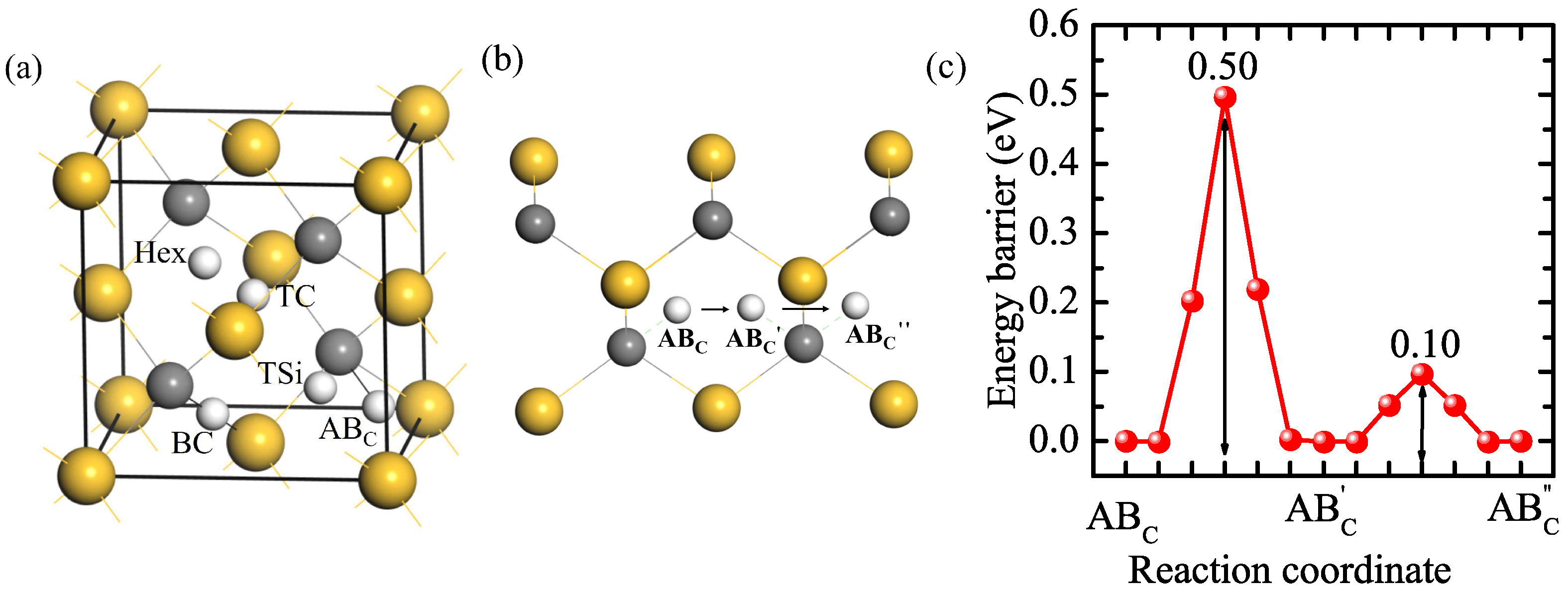
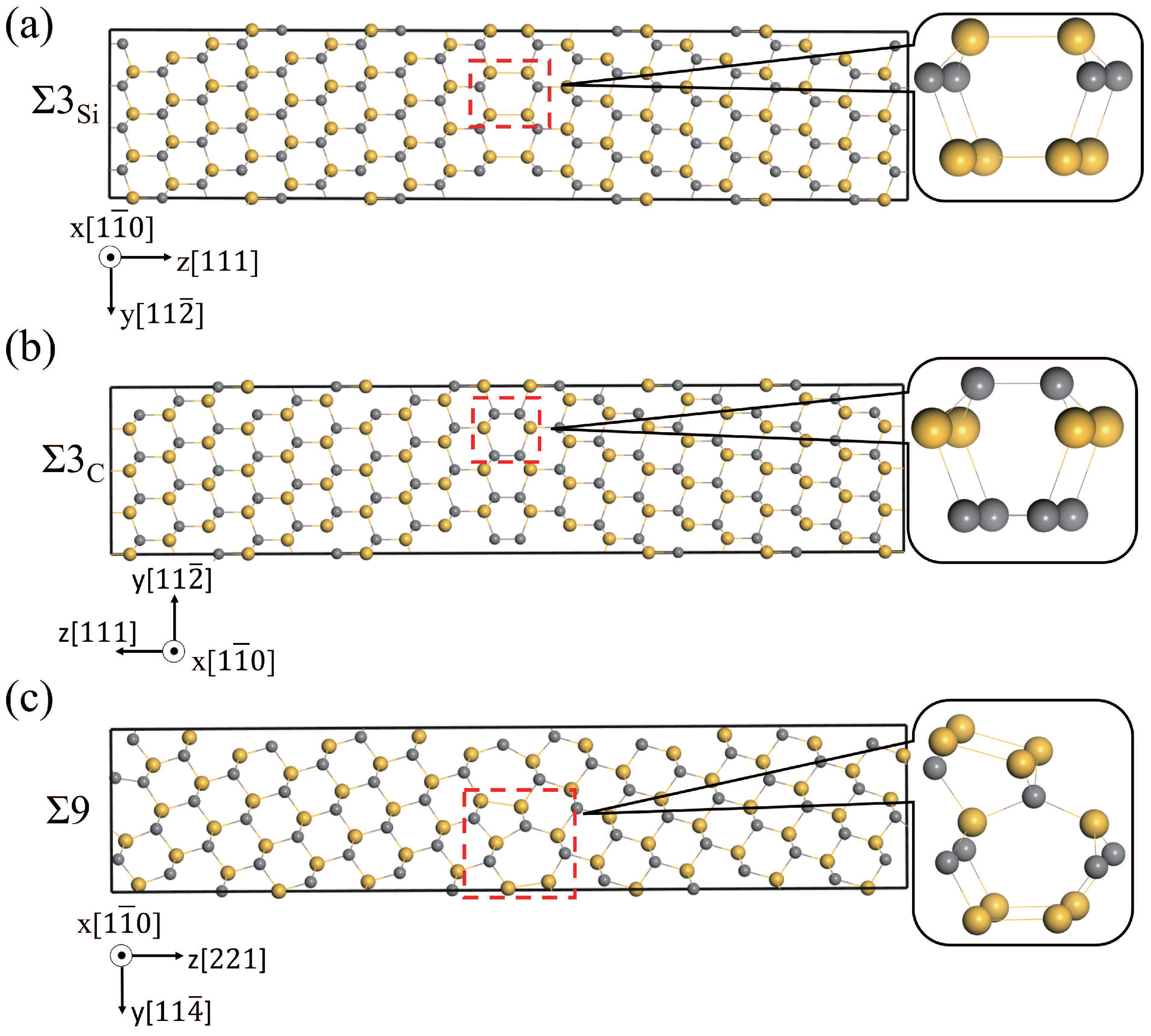
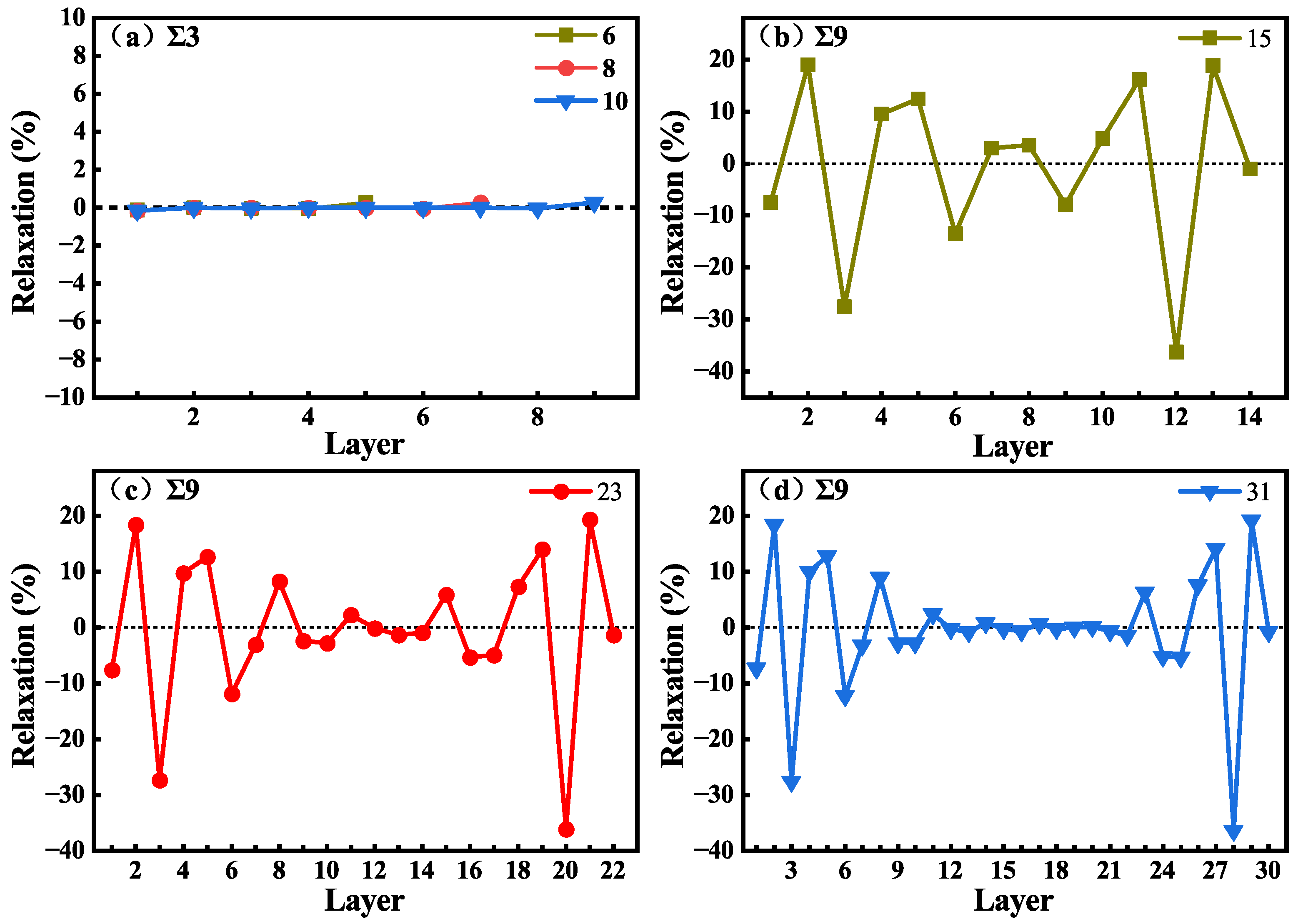
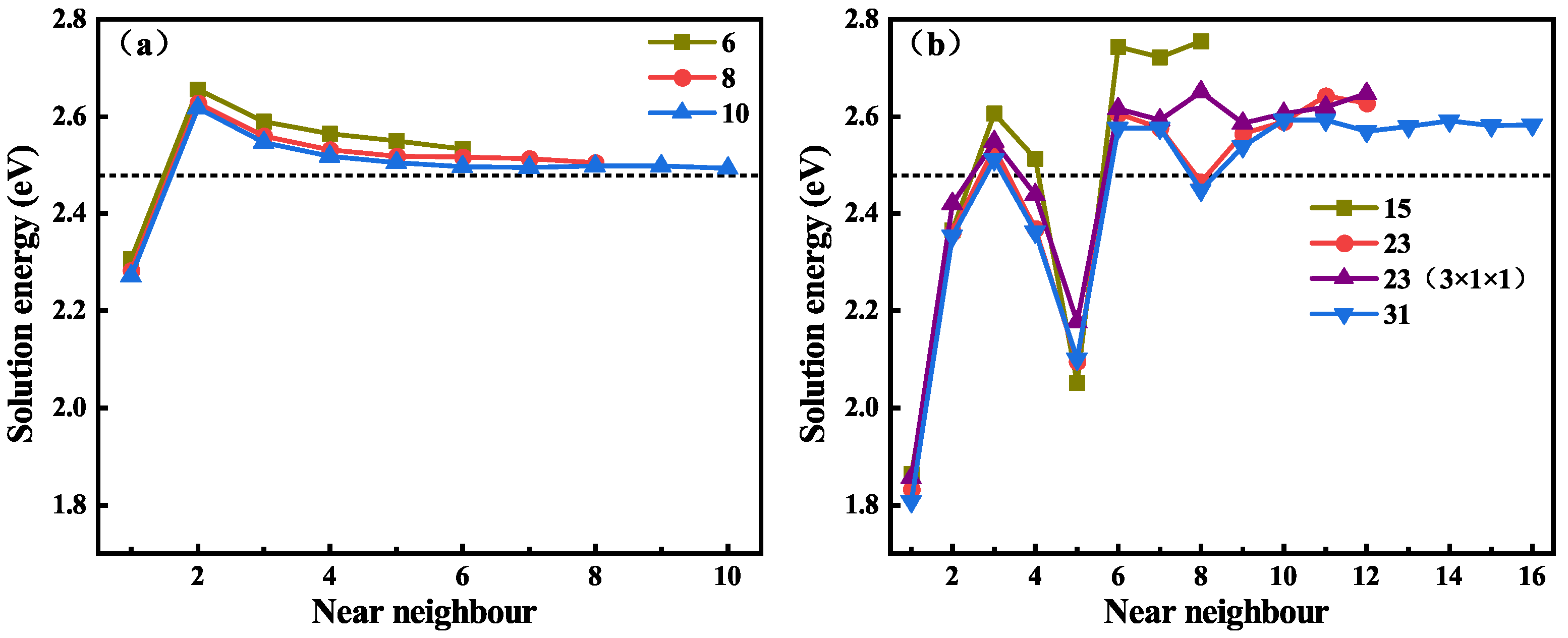


| Site | TC | TSi | Hex | BC | ABC |
|---|---|---|---|---|---|
| This work | 3.61 | 2.93 | TSi | 2.60 | 2.48 |
| Ref. [39] | 3.05 | 2.61 | TSi | 2.41 | 2.05 |
| Ref. [40] | 3.36 | 2.93 | TSi | 2.57 | 2.41 |
| Layer | Lx (Å) | Ly (Å) | Lz (Å) | K Point | Atoms | (J/m2) | |
|---|---|---|---|---|---|---|---|
| 6 | 6.19 | 10.72 | 30.66 | 4 × 2 × 1 | 192 | 1.39 | |
| 8 | 6.20 | 10.72 | 40.77 | 4 × 2 × 1 | 256 | 1.39 | |
| 10 | 6.19 | 10.72 | 50.89 | 4 × 2 × 1 | 320 | 1.39 | |
| 6 | 6.19 | 10.72 | 30.66 | 4 × 2 × 1 | 192 | 1.39 | |
| 8 | 6.20 | 10.72 | 40.77 | 4 × 2 × 1 | 256 | 1.39 | |
| 10 | 6.19 | 10.72 | 50.89 | 4 × 2 × 1 | 320 | 1.39 | |
| 15 | 6.20 | 9.34 | 22.11 | 4 × 3 × 1 | 120 | 1.35 | |
| 23 | 6.20 | 9.32 | 33.79 | 4 × 3 × 1 | 184 | 1.35 | |
| 23 (3 × 1 × 1) | 9.29 | 9.32 | 33.79 | 4 × 3 × 1 | 276 | 1.35 | |
| 31 | 6.20 | 9.31 | 45.47 | 4 × 3 × 1 | 248 | 1.35 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cui, Y.; Sun, J.; Li, M.; Li, B. First-Principles Calculations of Hydrogen Solution and Diffusion in 3C-SiC Grain Boundaries. Materials 2025, 18, 2118. https://doi.org/10.3390/ma18092118
Cui Y, Sun J, Li M, Li B. First-Principles Calculations of Hydrogen Solution and Diffusion in 3C-SiC Grain Boundaries. Materials. 2025; 18(9):2118. https://doi.org/10.3390/ma18092118
Chicago/Turabian StyleCui, Yanan, Jingjing Sun, Meng Li, and Bingsheng Li. 2025. "First-Principles Calculations of Hydrogen Solution and Diffusion in 3C-SiC Grain Boundaries" Materials 18, no. 9: 2118. https://doi.org/10.3390/ma18092118
APA StyleCui, Y., Sun, J., Li, M., & Li, B. (2025). First-Principles Calculations of Hydrogen Solution and Diffusion in 3C-SiC Grain Boundaries. Materials, 18(9), 2118. https://doi.org/10.3390/ma18092118






