Methodological Basis for Reliable Evaluation of Air Void Structure Parameters Using the 2D Method
Abstract
:1. Introduction
2. Materials and Methods
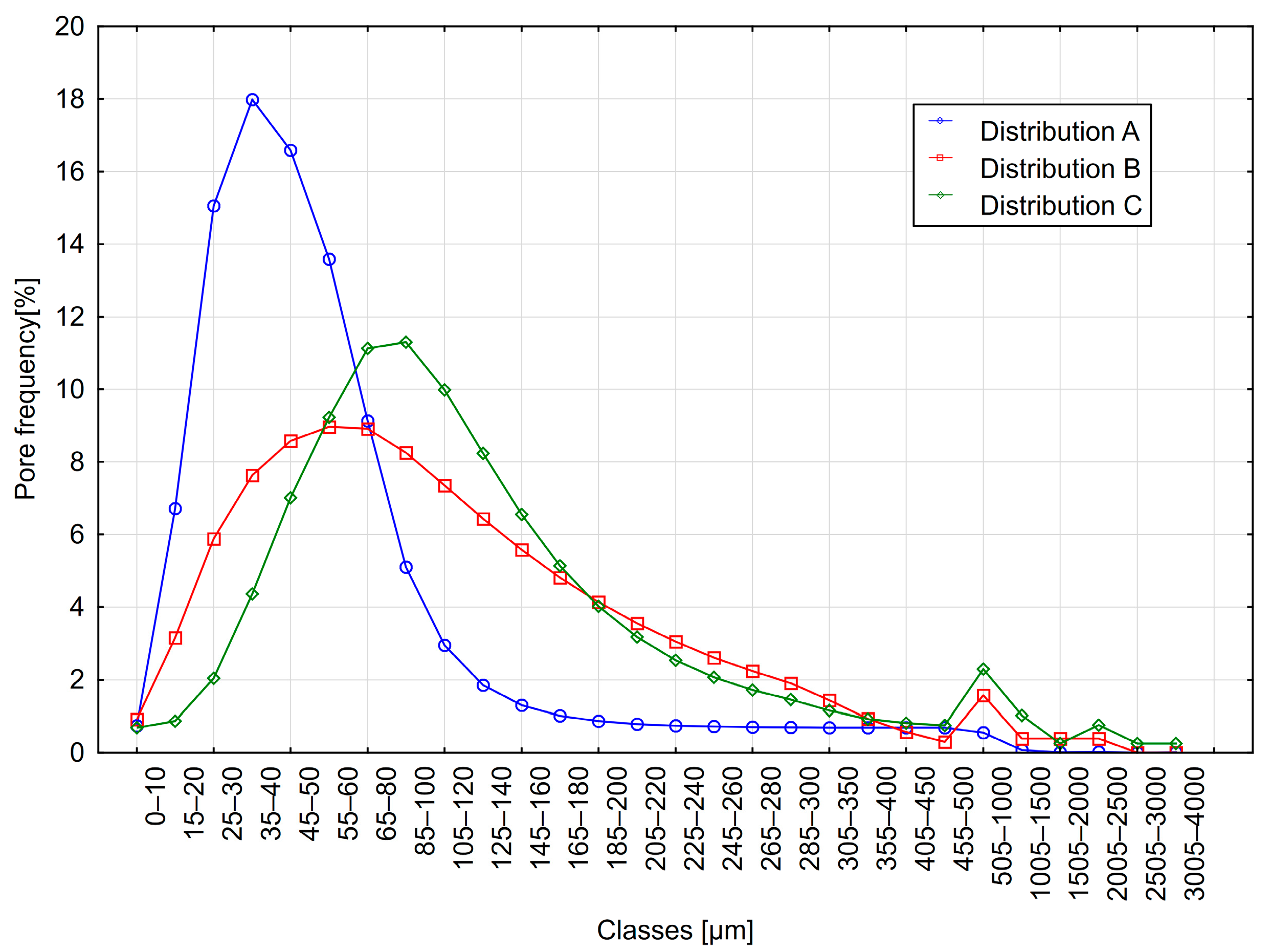
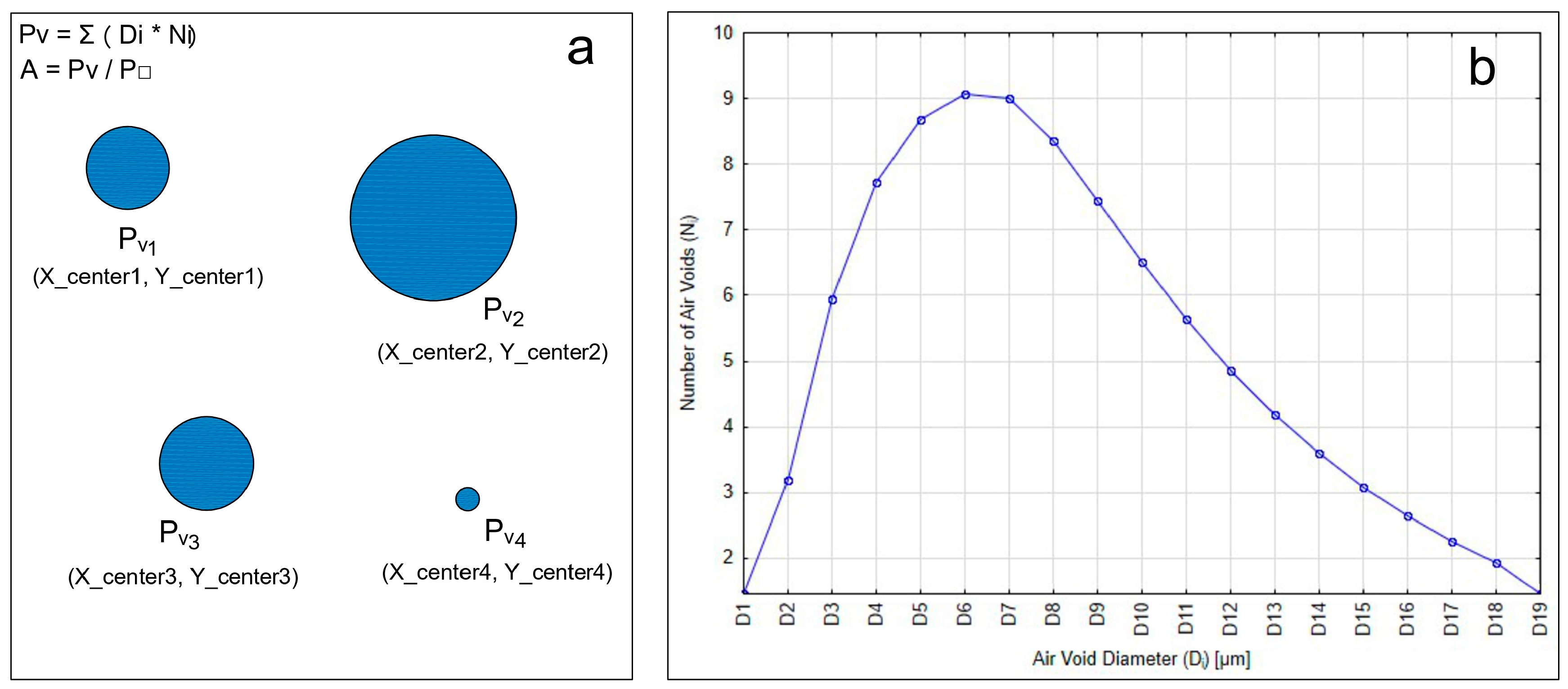
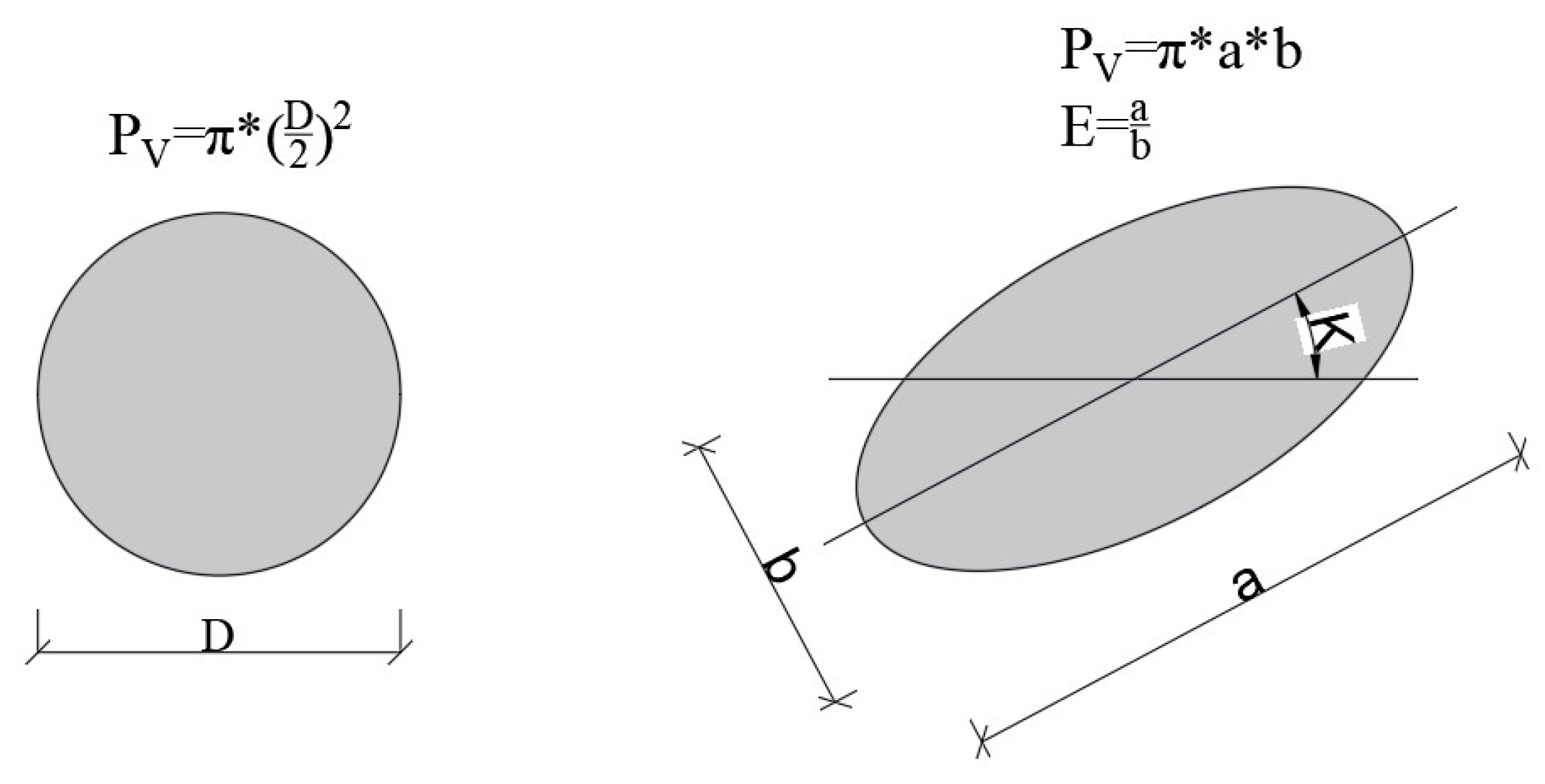
Methodology for Preparing Geometric Models of Air Voids in Concrete
3. Results
3.1. Results of Air Void Structure Parameters Calculated Using the 1D Method
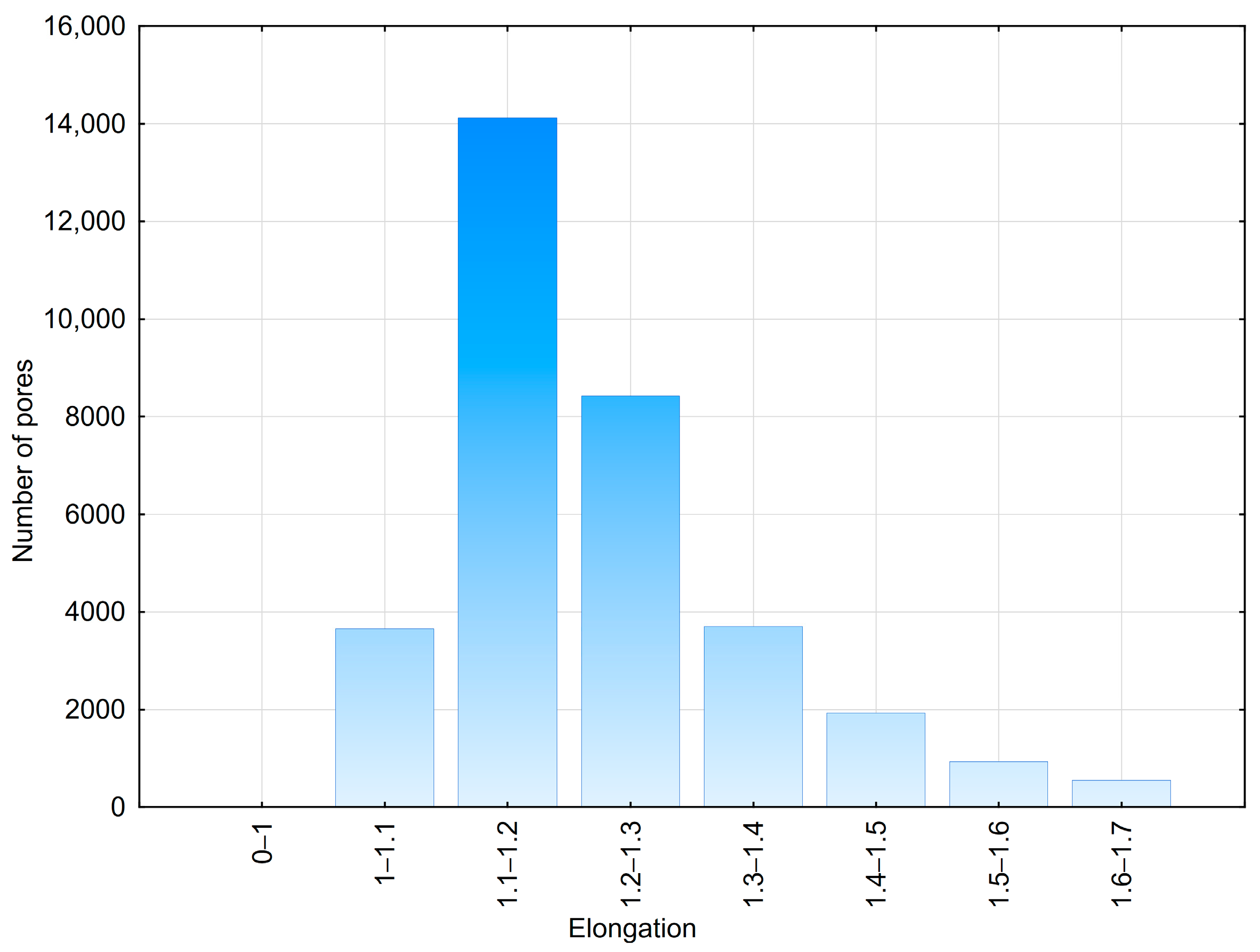
3.2. Results of Air Void Structure Parameters Calculated Using the 2D Method
3.3. Comparison of Results Obtained by the 2D and 1D Methods
3.4. Analysis of the Number, Size, and Resolution of Measurement Frames
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Powers, T.C. A Working Hypothesis for Further Studies of Frost Resistance of Concrete. ACI J. Proc. 1945, 41, 245–272. [Google Scholar]
- ASTM C457/C457M-16; Standard Test Method for Microscopical Determination of Parameters of Air-Void System in Hardened Concrete. ASTM International: West Conshohocken, PA, USA, 2017.
- PN-EN 480-11:2008; Domieszki Do Betonu, Zaprawy I Zaczynu. Metody Badań. CZĘŚĆ 11: Oznaczanie Charakterystyki Porów Powietrznych W Stwardniałym Betonie. PKN: Warszawa, Poland, 2008.
- Beasman, L.E.; McCuen, R.H. Estimating the Distribution of Air Voids in Concrete. Civ. Eng. Dimens. 2011, 13, 15–20. [Google Scholar]
- Snyder, K.; Hover, K.; Natesaiver, K. An Investigation of the Minimum Expected Uncertainty in the Linear Traverse Technique. Cem. Concr. Aggreg. 1991, 13, 3–10. [Google Scholar] [CrossRef]
- Attiogbe, E. Mean spacing of air voids in hardened concrete. ACI Mater. J. 1993, 90, 174–181. [Google Scholar]
- Song, Y.; Zou, R.; Castaneda, D.I.; Riding, K.A.; Lange, D.A. Advances in measuring air-void parameters in hardened concrete using a flatbed scanner. J. Test. Eval. 2017, 45, 1713–1725. [Google Scholar] [CrossRef]
- Zalocha, D. Image analysis as a tool for estimation of air void characteristics in hardened concrete: Example of application and accuracy studies. In Proceedings of the Amas Workshop on Image Analysis in Investigation of Concrete SIAIC, Warsaw, Poland, 21–23 October 2002; pp. 239–257. [Google Scholar]
- Murotani, T.; Igarahshi, S.; Koto, H. Distribution analysis and modeling of air voids in concreto as spatial point processes. Cem. Concr. Res. 2019, 115, 124–132. [Google Scholar] [CrossRef]
- Wawrzerínczyk, J.; Molendowska, A.; Kowalczyk, H. Development of the measuring techniques for estimating the air void system parameters in concrete using 2D analysis method. Materials 2020, 13, 428. [Google Scholar] [CrossRef]
- Fonseca, P.C.; Scherer, G.W. An image analysis procedure to quantify the air void system of mortar and concrete. Mater. Struct. 2015, 48, 3087–3098. [Google Scholar] [CrossRef]
- Das, A.; Song, Y.; Mantellato, S.; Wangler, T.; Lange, D.A.; Flatt, R.J. Effect of processing on the air void system of 3D printed concreto. Cem. Concr. Res. 2022, 156, 106789. [Google Scholar] [CrossRef]
- Pleau, R.; Pigeon, M.; Laurencot, J.L. Some findings on the usefulness of image analysis for determining the characteristics of the air-void system on hardened concrete. Cem. Concr. Compos. 2001, 23, 237–246. [Google Scholar] [CrossRef]
- Sommer, H. The precision of the microscopical determination of the air void system in hardened concrete. Cem. Concr. Aggreg. 1979, 1, 49–55. [Google Scholar] [CrossRef]
- Langan, B.W.; Ward, M.A. Determination of the air-void system parameters in hardened concrete—An error analysis. ACI J. Proc. 1986, 83, 943–952. [Google Scholar]
- Wawrzeńczyk, J.; Kowalczyk, H. Simplified Method of Estimating the A300 Micropore Content in Air-Entrained Concrete. Materials 2023, 16, 2752. [Google Scholar] [CrossRef] [PubMed]
- Pleau, R.; Plante, P.; Gagne, R.; Pigeon, M. Practical considerations pertaining to the microscopical determination of air void characteristics of hardened concrete (ASTM standard). Cem. Concr. Aggreg. 1990, 12, 3–11. [Google Scholar] [CrossRef]
- Konkol, J.; Prokopski, G. The use of fractal geometry for the assessment of the diversification of macro-pores in concrete. Image Anal. Stereol. 2011, 30, 89–100. [Google Scholar] [CrossRef]
- Kim, K.Y.; Yun, T.S.; Choo, J.; Kang, D.H.; Shin, H.S. Determination of air-void parameters of hardened cement-based materials using X-ray computed tomography. Constr. Build. Mater. 2012, 37, 93–101. [Google Scholar] [CrossRef]
- du Plessis, A.; Boshoff, W.P. A review of X-ray computed tomography of concrete and asphalt construction materials. Constr. Build. Mater. 2019, 199, 637–651. [Google Scholar] [CrossRef]
- Snyder, K.A.; Hover, K.C.; Natesaiyer, K.; Simon, M.J. Modeling Air-Void Systems in Hydrated Cement Paste. Microcomput. Civ. Eng. 1991, 6, 35–44. [Google Scholar] [CrossRef]
- Snyder, K.A. A Numerical Test of Air-Void Spacing Equations 1 Introduction; National Institute of Standards and Technology: Gaithersburg, MD, USA, 1998.
- Powers, T.C. The Air Requirement of Frost-Resistant Concrete; The Portland Cement Association: Washington, DC, USA, 1949; Volume 29, pp. 184–202. [Google Scholar]
- Philleo, R.E. A method for analyzing void distribution in air-entrained concrete. Cem. Concr. Aggreg. 1983, 5, 128–130. [Google Scholar] [CrossRef]
- Pleau, R.; Pigeon, M. The use of the flow length concept to assess the efficiency of air entrainment with regards to frost durability: Part I—Description of the test method. Cem. Concr. Aggreg. 1996, 18, 19–29. [Google Scholar] [CrossRef]
- Bažant, Z.P.; Gambarova, P.G. Crack Shear In Concrecte: Crack Band Microplane Model. J. Struct. Eng. 1984, 110, 2015–2035. [Google Scholar] [CrossRef]
- Bažant, Z.P.; Oh, B.H. Microplane Model for Progressive Fracture of Concrete and Rock. J. Eng. Mech. 1985, 111, 559–582. [Google Scholar] [CrossRef]
- Zaitsev, Y.B.; Wittmann, F.H. Simulation of crack propagation and failure of concrete. Matériaux Constr. 1981, 14, 357–365. [Google Scholar] [CrossRef]
- Unger, J.F.; Eckardt, S. Multiscale Modeling of Concrete. Arch. Comput. Methods Eng. 2011, 18, 341–393. [Google Scholar] [CrossRef]
- Nguyen, V.P.; Stroeven, M.; Sluys, L.J. Multiscale failure modeling of concrete: Micromechanical modeling, discontinuous homogenization and parallel computations. Comput. Methods Appl. Mech. Eng. 2012, 201–204, 139–156. [Google Scholar] [CrossRef]
- Fascetti, A.; Bolander, J.E.; Nisticó, N. Lattice Discrete Particle Modeling of Concrete under Compressive Loading: Multiscale Experimental Approach for Parameter Determination. J. Eng. Mech. 2018, 144, 4018058. [Google Scholar] [CrossRef]
- Li, X.N.; Zuo, X.B.; Li, L.; Liu, J.H. Multiscale modeling and simulation on mechanical behavior of fiber reinforced concrete. Int. J. Solids Struct. 2024, 286–287, 112569. [Google Scholar] [CrossRef]
- Wiggers, P.; Moftah, S.O. Mesoscale models for concrete: Homogenisation and damage behaviour. Finite Elem. Anal. Des. 2006, 42, 623–636. [Google Scholar] [CrossRef]
- Stefan, H.; Eckardt, S.; Carsten, K. A geometrical inclusion-matrix model for the finite element analysis of concrete at multiple scales. In Proceedings of the 16th IKM, Weimar, Germany, 10–12 June 2003; Volume 1, pp. 2–10. [Google Scholar]
- Leite, J.P.B.; Slowik, V.; Mihashi, H. Computer simulation of fracture processes of concreto using mesolevel models of lattice structure. Cem. Concr. Res. 2004, 34, 1025–1033. [Google Scholar] [CrossRef]
- Lilliu, G.; van Mier, J.G.M. 3D lattice type fracture model for concrete. Eng. Fract. Mech. 2003, 70, 927–941. [Google Scholar] [CrossRef]
- Wawrzeńczyk, J.; Kozak, W. A method of analyzing porosity structure in air-entrained concrete. Archit. Civ. Eng. Environ. 2015, 8, 77–82. [Google Scholar]
- Song, Y.; Damiani, R.M.; Shen, C.; Castaneda, D.I.; Lange, D.A. A 3D petrographic analysis for concrete freeze-thaw protection. Cem. Concr. Res. 2020, 128, 105952. [Google Scholar] [CrossRef]
- Lu, H. X-Ray Computed Tomography Assessment of Air Void Distribution in Concrete. Ph.D. Thesis, University of Toronto, Toronto, ON, Canada, 2017. [Google Scholar]
- Cnudde, V.; Cwirzen, A.; Masschaele, B.; Jacobs, P.J.S. Porosity and microstructure characterization of building stones and concretes. Eng. Geol. 2009, 103, 76–83. [Google Scholar] [CrossRef]
- Kowalska, D.; Jóźwiak-Niedźwiedzka, D.; Chalimoniuk, M.; Dąbrowski, M. Application of Computed Tomography CT to Evaluate the Air-Entrainment in Concrete. In Proceedings of the International Conference on Vibration Engineering and Technology of Machinery, Manchester, UK, 9–11 September 2014; pp. 907–918. [Google Scholar]
- Chung, S.Y.; Sikora, P.; Rucinska, T.; Stephan, D.; Abd Elrahman, M. Comparison of the pore size distributions of concretes with different air-entraining admixture dosages using 2D and 3D imaging approaches. Mater. Charact. 2020, 162, 110182. [Google Scholar] [CrossRef]
- Wei, Y.; Wei, Z.; Xue, K.; Wang, C.; Hong, Y. Automated detection and segmentation of concrete air voids using zero-angle light source and deep learning. Autom. Constr. 2021, 130, 103877. [Google Scholar] [CrossRef]
- MATLAB, R2023a; The MathWorks Inc.: Natick, MA, USA, 2023.
- NIS-Elements Imaging AR, Version 4.6; Nikon: Tokyo, Japan, 2016.




| Author | Method | Resolution [µm/px] | Size [cm] | |
|---|---|---|---|---|
| 1D | Konkol [18] | Stereoscopic microscope Flatbed scanner | 2.76 6.36 | 6.32 × 3.25 |
| Song [7] | Flatbed scanner | 5.3 | 6.35 × 6.35 | |
| 1D/2D | Murotani [9] | Flatbed scanner | 30 | 6 × 6 |
| Wawrzeńczyk [10,16] | Stereoscopic microscope | 6.75 1.13 | 8.25 × 6.19 | |
| 2D | Arnesh Das [12] | Flatbed scanner | 5.3 | 3 × 5 × 5 |
| Fonseca [11] | Flatbed scanner | 7.94 | 4 × 4 | |
| 3D | Kim [19] | Computer tomography | 200 | 40.96 × 40.96 |
| Du Plessis [20] | Computer tomography | 0.05 | 0.015 |
| P % | Ttot mm | N | A % | A300 % | α mm−1 | L mm | |
|---|---|---|---|---|---|---|---|
| Mean | 28.07 | 2522.56 | 1016 | 5.66 | 2.73 | 29.37 | 0.17 |
| Median | 28.50 | 2537.74 | 937 | 5.59 | 2.55 | 27.19 | 0.17 |
| Sd | 1.94 | 47.74 | 313 | 1.65 | 0.92 | 7.49 | 0.04 |
| Min | 21.00 | 2438.62 | 251 | 0.95 | 0.61 | 15.80 | 0.08 |
| Max | 35.50 | 2643.62 | 2221 | 11.83 | 6.04 | 55.80 | 0.33 |
| 1D | A % | A300 % | α mm−1 | L mm | N |
|---|---|---|---|---|---|
| Distribution A | |||||
| A3_Cr | 2.70 | 1.00 | 23.77 | 0.271 | 186 |
| A3_El | 2.74 | 1.01 | 23.86 | 0.268 | 193 |
| A5_Cr | 4.96 | 1.51 | 21.97 | 0.223 | 339 |
| A5_El | 4.97 | 1.56 | 22.16 | 0.221 | 339 |
| A8_Cr | 7.27 | 2.05 | 22.97 | 0.168 | 486 |
| A8_El | 7.29 | 2.05 | 23.22 | 0.165 | 495 |
| Distribution B | |||||
| B3_Cr | 3.14 | 0.70 | 10.88 | 0.55 | 109 |
| B3_El | 3.17 | 0.76 | 10.93 | 0.55 | 109 |
| B5_Cr | 4.97 | 1.21 | 11.87 | 0.41 | 171 |
| B5_El | 4.96 | 1.25 | 11.96 | 0.41 | 173 |
| B8_Cr | 7.45 | 1.84 | 11.68 | 0.32 | 261 |
| B8_El | 7.42 | 1.90 | 11.97 | 0.32 | 264 |
| Distribution C | |||||
| C3_Cr | 3.37 | 0.30 | 6.18 | 0.94 | 65 |
| C3_El | 3.31 | 0.32 | 6.24 | 0.94 | 65 |
| C5_Cr | 4.94 | 0.60 | 6.55 | 0.75 | 102 |
| C5_El | 4.90 | 0.53 | 6.70 | 0.74 | 103 |
| C8_Cr | 7.74 | 0.63 | 6.00 | 0.60 | 153 |
| C8_El | 7.79 | 0.64 | 6.24 | 0.58 | 156 |
| 2D | A % | A300 % | α1 mm−1 | L1 mm | N |
|---|---|---|---|---|---|
| Distribution A | |||||
| A3_Cr | 3.07 | 0.78 | 22.35 | 0.27 | 8286 |
| A3_El | 3.07 | 0.78 | 22.36 | 0.27 | 8282 |
| A5_Cr | 5.03 | 1.27 | 22.31 | 0.22 | 13656 |
| A5_El | 5.04 | 1.27 | 22.34 | 0.22 | 13651 |
| A8_Cr | 7.77 | 1.94 | 22.31 | 0.18 | 20980 |
| A8_El | 7.78 | 1.94 | 22.33 | 0.18 | 20973 |
| Distribution B | |||||
| B3_Cr | 2.99 | 0.61 | 11.48 | 0.54 | 2216 |
| B3_El | 2.99 | 0.61 | 11.50 | 0.54 | 2218 |
| B5_Cr | 4.98 | 0.98 | 11.27 | 0.43 | 3622 |
| B5_El | 4.98 | 0.98 | 11.29 | 0.43 | 3623 |
| B8_Cr | 7.94 | 1.52 | 11.08 | 0.36 | 5547 |
| B8_El | 7.94 | 1.52 | 11.10 | 0.36 | 5545 |
| Distribution C | |||||
| C3_Cr | 3.09 | 0.28 | 6.60 | 0.92 | 1022 |
| C3_El | 3.09 | 0.28 | 6.61 | 0.92 | 1021 |
| C5_Cr | 5.03 | 0.51 | 6.99 | 0.70 | 1961 |
| C5_El | 5.03 | 0.51 | 6.99 | 0.70 | 1964 |
| C8_Cr | 8.02 | 0.76 | 6.67 | 0.59 | 2920 |
| C8_El | 8.03 | 0.75 | 6.66 | 0.59 | 2917 |
| vk | ||||
|---|---|---|---|---|
| A % | A300 % | α1 mm−1 | L1 mm | |
| Distribution A | 10.89 | 19.60 | 4.82 | 4.90 |
| Distribution B | 5.75 | 20.53 | 6.38 | 8.68 |
| Distribution C | 6.54 | 18.44 | 10.37 | 5.56 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wawrzeńczyk, J.; Kowalczyk, H. Methodological Basis for Reliable Evaluation of Air Void Structure Parameters Using the 2D Method. Materials 2025, 18, 2095. https://doi.org/10.3390/ma18092095
Wawrzeńczyk J, Kowalczyk H. Methodological Basis for Reliable Evaluation of Air Void Structure Parameters Using the 2D Method. Materials. 2025; 18(9):2095. https://doi.org/10.3390/ma18092095
Chicago/Turabian StyleWawrzeńczyk, Jerzy, and Henryk Kowalczyk. 2025. "Methodological Basis for Reliable Evaluation of Air Void Structure Parameters Using the 2D Method" Materials 18, no. 9: 2095. https://doi.org/10.3390/ma18092095
APA StyleWawrzeńczyk, J., & Kowalczyk, H. (2025). Methodological Basis for Reliable Evaluation of Air Void Structure Parameters Using the 2D Method. Materials, 18(9), 2095. https://doi.org/10.3390/ma18092095





