Efficiency of Alternative Reinforcement Methods for Wooden Ceilings and Their Ecological Aspects
Abstract
1. Introduction
2. Materials and Methods
2.1. Procedure
- The geometry of the parts to be joined;
- Their modulus of elasticity;
- Joint stiffness;
- The strength of the composite partners;
- The static framework conditions such as span, load position, and support.
2.2. Materials
2.3. Experimental Studies
2.4. Basic Equations of the Elastic Composite Theory

2.5. Engineering Model for Calculation of Breaking Loads
2.6. Static System
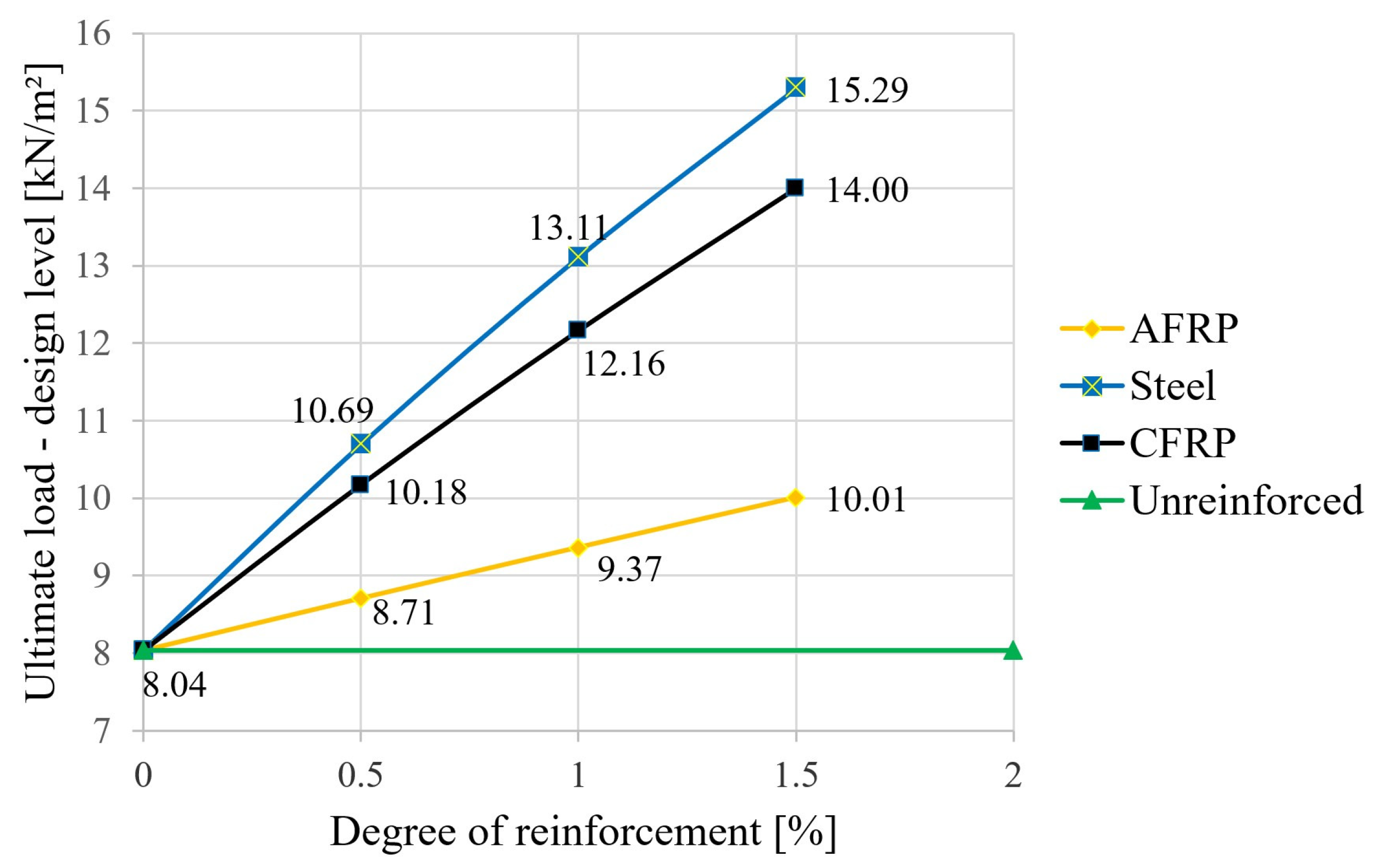
3. Results
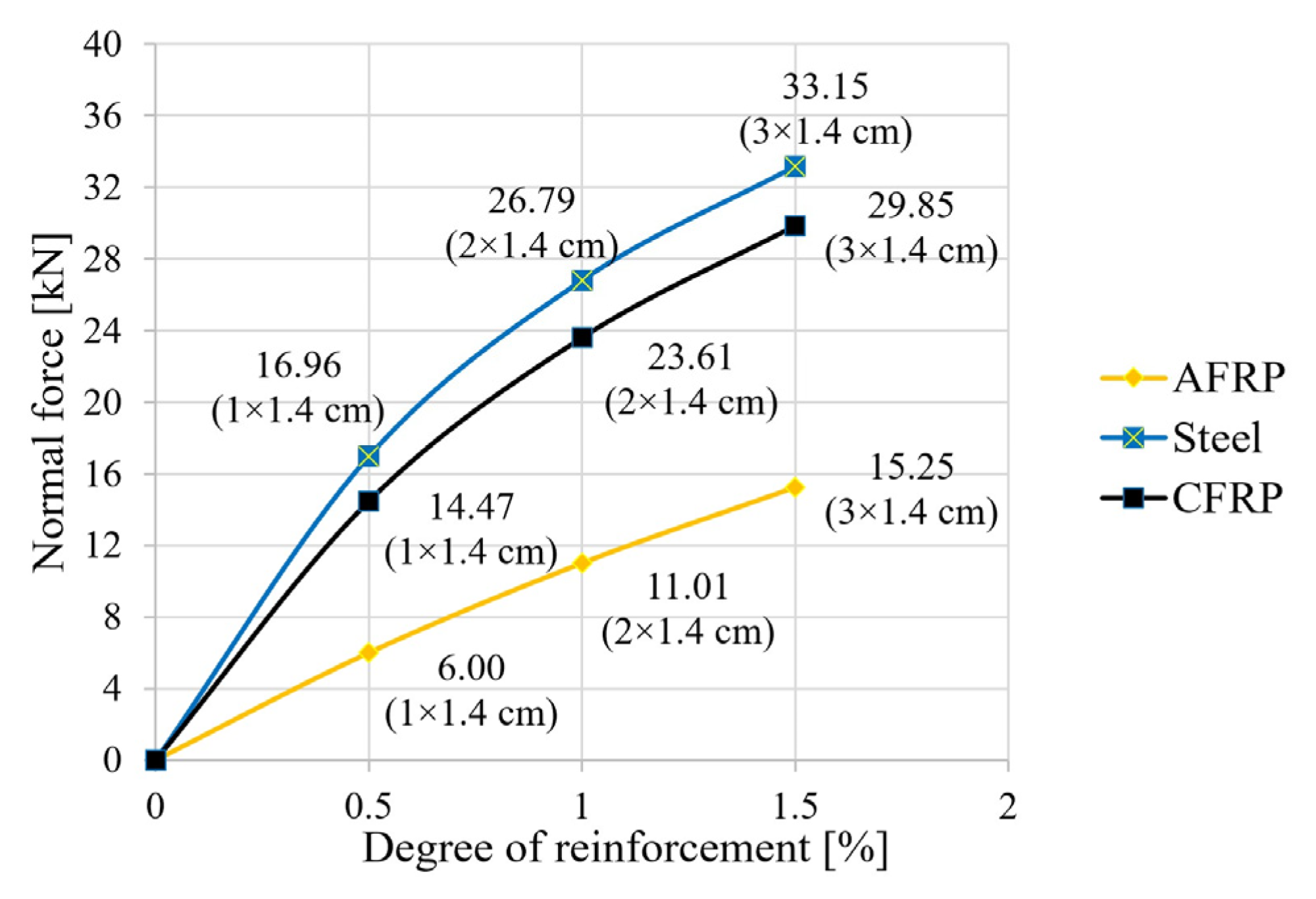
3.1. Internal Forces
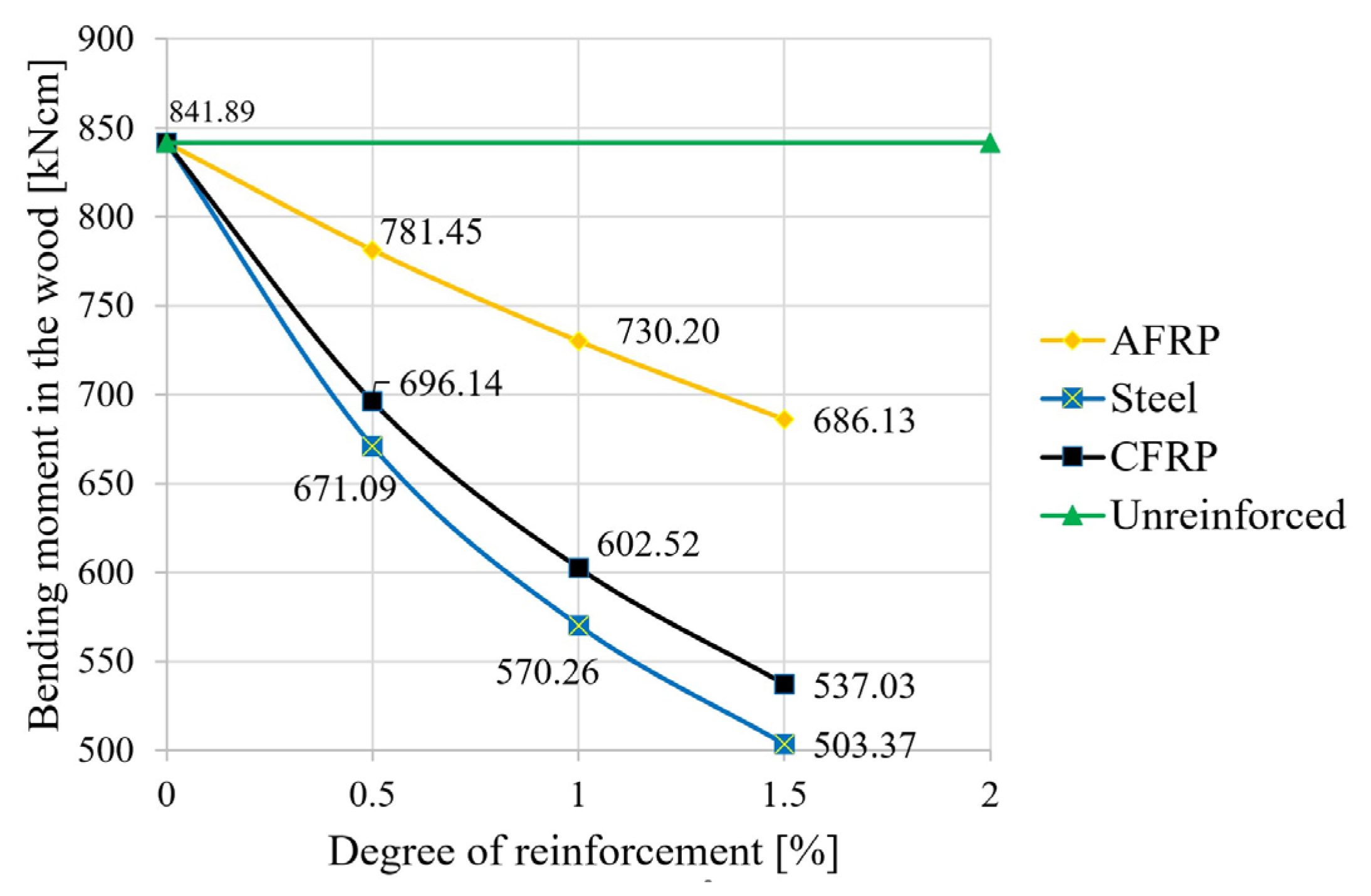
3.2. Deformations
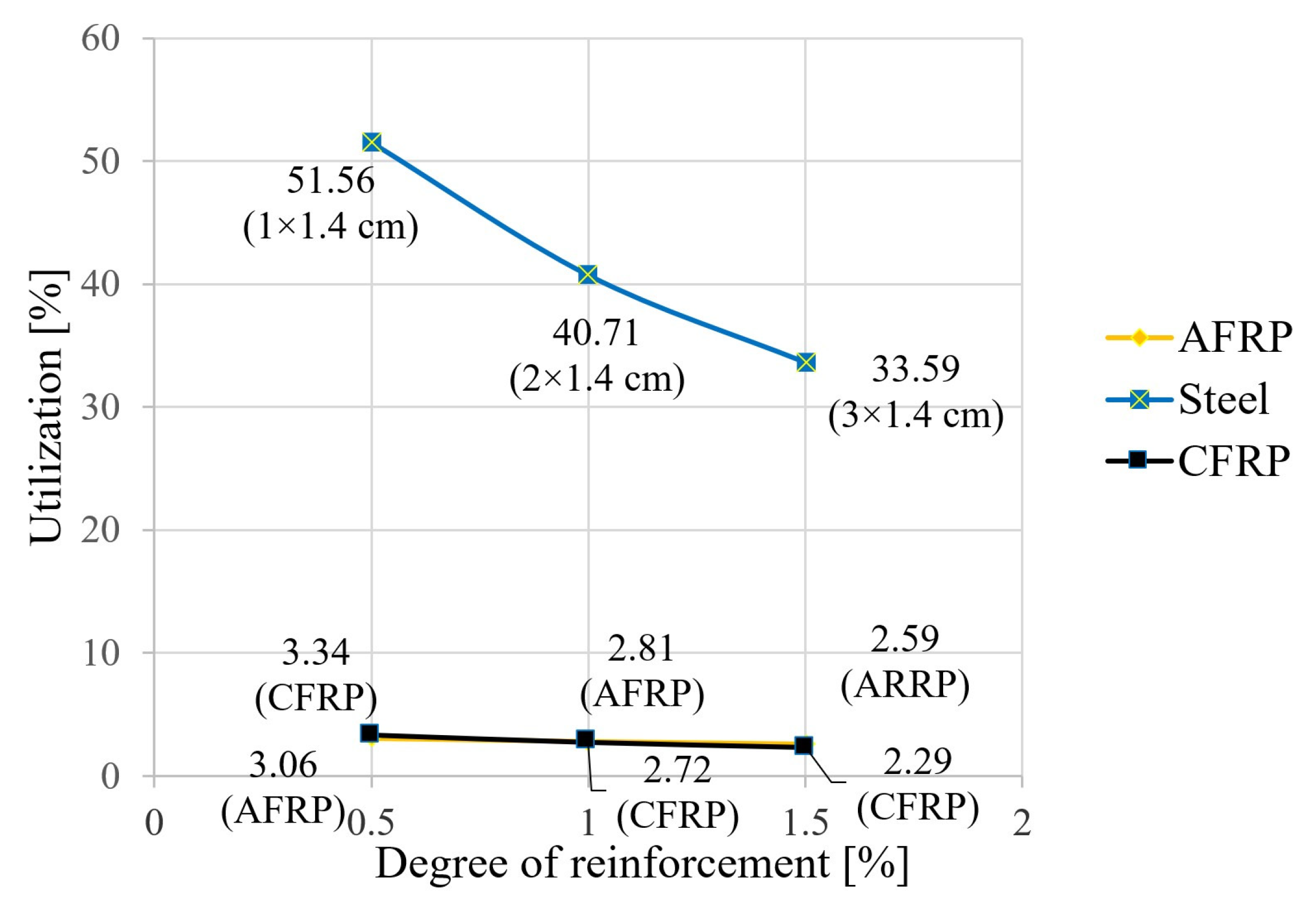
3.3. Results for the Breaking Condition
3.4. Environmental Impact
| Type | Density | GWP | Source |
|---|---|---|---|
| kg/m3 | kg CO2-eq/kg | ||
| CFRP: Sika CarboDur ® S | 1500 | 12.5 | [46] |
| AFRP: Arapree ® | 1450 | 11.2 | [46] |
| Structural steel | 7850 | 1.44 | [47] |
| Concrete | 2400 | 197 1 | [48] |
| Reinforcing steel | 7850 | 0.68 | [48] |
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Dias, A.; Schänzlin, J. Design of Timber-Concrete Composite Structures. In Proceedings of the 4th International Conference on Timber Bridges, Biel, Switzerland, 9 May 2022. [Google Scholar] [CrossRef]
- Holschemacher, K.; Selle, R.; Schmidt, J.; Kieslich, H. Wood-Concrete-Composite; Betonkalender: Berlin, Germany, 2013; pp. 241–287. (In German) [Google Scholar]
- Natterer, J.; Hoeft, M. The Load-Bearing Behavior of Wood-Concrete Composite Structures; Research Paper CERS Nr. 1345; EPFL/IBOIS: Lausanne, Switzerland, 1987. (In German) [Google Scholar]
- Huber, C.; Deix, K. Comparison of Calculation Methods of Elastic Bonding: Limits of the Gamma Method Using an Example of a Wood–Concrete Composite Floor with Single Loads. Materials 2021, 14, 7211. [Google Scholar] [CrossRef] [PubMed]
- Soriano, J.; Pellis, B.P.; Mascia, N.T. Mechanical Performance of Glued-Laminated Timber Beams Symmetrically Reinforced with Steel Bars. Compos. Struct. 2016, 150, 200–207. [Google Scholar] [CrossRef]
- Vosskuehler, J. Expert System for Dimensioning Reinforcement and Connections of Wood with Steel. Master’s Thesis, Ryerson University, Toronto, ON, Canada, 2016. [Google Scholar] [CrossRef]
- Christoforo, A.L.; Gomes, A.F.F.; Arroyo, F.N.; Mascarenhas, F.J.R.; Santos, H.F.D.; Topolniak, L.; Akasaki, J.L. Reinforcement of Timber Beams with Steel Bars: Parametric Analysis Using the Finite Element Method. Buildings 2022, 12, 1036. [Google Scholar] [CrossRef]
- Işleyen, Ü.K.; Kesik, H.İ. Experimental and Numerical Analysis of Compression and Bending Strength of Old Wood Reinforced with CFRP Strips. Structures 2021, 33, 259–271. [Google Scholar] [CrossRef]
- Nadir, Y.; Nagarajan, P.; Ameen, M. Flexural Stiffness and Strength Enhancement of Horizontally Glued Laminated Wood Beams with GFRP and CFRP Composite Sheets. Constr. Build. Mater. 2016, 112, 547–555. [Google Scholar] [CrossRef]
- De Jesus, A.M.; Pinto, J.M.; Morais, J.J. Analysis of Solid Wood Beams Strengthened with CFRP Laminates of Distinct Lengths. Constr. Build. Mater. 2012, 35, 817–828. [Google Scholar] [CrossRef]
- Wdowiak, A. Strengthening of Structural Flexural Glued Laminated Beams of Ashlar with Cords and Carbon Laminates. Materials 2022, 15, 8303. [Google Scholar] [CrossRef]
- Kawecki, B.; Sumorek, A. Study on Profitability of Combining Wood and CFRP into Composite Based on Mechanical Performance of Bent Beams. Appl. Sci. 2022, 12, 10304. [Google Scholar] [CrossRef]
- Koshcheev, A.A.; Roshchina, S.I.; Naichuk, A.Y.; Vatin, N.I. The Effect of Eccentricity on the Strength Characteristics of Glued Rods Made of Steel Cable Reinforcement in Solid Wood. IOP Conf. Ser. Mater. Sci. Eng. 2020, 896, 012059. [Google Scholar] [CrossRef]
- Custódio, J.; Cabral-Fonseca, S. Advanced Fibre-Reinforced Polymer (FRP) Composites for the Rehabilitation of Timber and Concrete Structures: Assessing Strength and Durability. In Advanced Fiber-Reinforced Polymer(FRP) Composites for Structural Applications; Woodhead Publishing: Cambridge, UK, 2013; pp. 814–882. [Google Scholar] [CrossRef]
- Śliwa-Wieczorek, K.; Sadowski, Ł.; Ostrowski, K.; Jaskowska-Lemańska, J.; Karolak, A. The Influence of CFRP Sheets on the Load-Bearing Capacity of the Glued Laminated Timber Beams under Bending Test. Materials 2021, 14, 4019. [Google Scholar] [CrossRef]
- Saad, K.; Lengyel, A. Strengthening Timber Structural Members with CFRP and GFRP: A State-of-the-Art Review. Polymers 2022, 14, 2381. [Google Scholar] [CrossRef] [PubMed]
- Kasal, B.; Yan, L. Fiber-Reinforced Polymers as Reinforcement for Timber Structural Elements. In RILEM State-of-the-Art Reports; Springer: Berlin/Heidelberg, Germany, 2021; pp. 51–78. [Google Scholar] [CrossRef]
- Wang, Z.; Li, H.; Lorenzo, R.; Corbi, I.; Corbi, O.; Fang, C. Review on Bond Properties between Wood and Fiber Reinforced Polymer. J. Renew. Mater. 2020, 8, 993–1018. [Google Scholar] [CrossRef]
- Kawecki, B.; Podgórski, J. The Effect of Glue Cohesive Stiffness on the Elastic Performance of Bent Wood-CFRP Beams. Materials 2020, 13, 5075. [Google Scholar] [CrossRef] [PubMed]
- Kim, K.-H.; Hong, S.-I.; Il, H.S. Bonding Performance of Glulam Reinforced with Textile Type of Glass- and Aramid-Fiber, GFRP and CFRP. J. Korean Wood Sci. Technol. 2011, 39, 156–162. [Google Scholar] [CrossRef][Green Version]
- Karaman, A.; Yildirim, M.N.; Tor, O. Bending characteristics of laminated wood composites constructer with black pine wood and aramid fiber reinforced fabric. Wood Res. 2021, 66, 309–320. [Google Scholar] [CrossRef]
- Zhou, A.; Qin, R.; Chow, C.L.; Lau, D. Bond Integrity of Aramid, Basalt and Carbon Fiber Reinforced Polymer Bonded Wood Composites at Elevated Temperature. Compos. Struct. 2020, 245, 112342. [Google Scholar] [CrossRef]
- Bergmeister, K. Carbon Fibers in Structural Engineering; Ernst & Sohn: Berlin, Germany, 2003. [Google Scholar]
- Nowak, T.; Jasieńko, J.; Czepiżak, D. Experimental Tests and Numerical Analysis of Historic Bent Timber Elements Reinforced with CFRP Strips. Constr. Build. Mater. 2013, 40, 197–206. [Google Scholar] [CrossRef]
- Schober, K.-U.; Harte, A.M.; Kliger, R.; Jockwer, R.; Xu, Q.; Chen, J.F. FRP Reinforcement of Timber Structures. Constr. Build. Mater. 2015, 97, 106–118. [Google Scholar] [CrossRef]
- Gribanov, A.S.; Strekalkin, A.A.; Kudryatseva, A.A.; Zdralovic, N. CFRP Composites for Strengthening Wooden Structures. IOP Conf. Ser. Mater. Sci. Eng. 2020, 896, 012114. [Google Scholar] [CrossRef]
- Ianasi, A.C. On the Role of CFRP Reinforcement for Wood Beams Stiffness. IOP Conf. Ser. Mater. Sci. Eng. 2015, 95, 012015. [Google Scholar] [CrossRef]
- Blaß, H.J.; Romani, M. Load-Bearing and Deformation Behavior of Composite Beams Made of Glulam and Fiber-Reinforced Plastics; Research Paper; Department Ingenieurholzbau, Universität Fridericiana; Karslruhe, Germany, 2000. (In German) [Google Scholar]
- Luggin, W.F. The Application of Prestressed CFRP Laminates to Glulam Beams, Experimental and Computational Studies. Ph.D. Thesis, Universität für Bodenkultur, Wien, Austria, 2000. (In German). [Google Scholar]
- Basha, M.; Wagih, A.; Melaibari, A.A.; Soutis, C.; Lubineau, G.; Abdraboh, A.M. Impact and Post-Impact Response of Lightweight CFRP/Wood Sandwich Composites. Compos. Struct. 2021, 279, 114766. [Google Scholar] [CrossRef]
- Lau, D.; Qiu, Q.; Zhou, A.; Chow, C.L. Long Term Performance and Fire Safety Aspect of FRP Composites Used in Building Structures. Constr. Build. Mater. 2016, 126, 573–585. [Google Scholar] [CrossRef]
- Huber, C.; Deix, K. Reinforcement of wooden beams with aramid and reinforcing steel bars. Osterr. Ing. Und Archit. ÖIAZ 2017, 162, 95–103. (In German) [Google Scholar]
- Product Data Sheet Sika® CarboDur®, S. Carbon Fiber Lamellas for Static Reinforcement; Sika GmbH: Munich, Germany, 2022. (In German) [Google Scholar]
- Aramid Fiber Reinforced Polymer Rod; Technical Data Sheet. Sireg S.p.A.: Milan, Italy, 2007.
- ÖNORM EN 10025-2; Hot Rolled Products of Structural Steels—Part 2: Technical Delivery Conditions for Non-Alloy Structural Steels. Austria Standards: Vienna, Austria, 2019.
- ÖNORM EN 14080; Timber Structures—Glued Laminated Timber and Glued Solid Timber—Requirements. Austria Standards: Vienna, Austria, 2013.
- Sika GmbH. SikaDur-30; Technical Data Sheet; Sika GmbH: Munich, Germany, 2022. [Google Scholar]
- ÖNORM EN 1995-1-1; Eurocode 5. Designs of Timber Structures, Part 1-1: General—Common Rules and Rules for Buildings. Austrian Standards: Vienna, Austria, 2019.
- Heimeshoff, B. For the calculation of flexural beams from flexibly interconnected cross-section parts in engineered timber construction. Holz Als Roh Werkst. 1987, 45, 237–241. (In German) [Google Scholar]
- Schatz, T. Article on the simplified bending design of FRP-reinforced timber beams. Bautechnik 2004, 81, 153–162. (In German) [Google Scholar]
- ÖNORM B 1991-1-1; Eurocode 1—Actions on Structures—Part 1-1: General Actions—Densities, Selfweight and Imposed Loads for Buildings. Austrian Standards: Vienna, Austria, 2017.
- Sobek, W. Non Nobis—On Building in the Future—Volume 1: Start from What Is, 3rd ed.; Avedition GmbH: Stuttgart, Germany, 2022. [Google Scholar]
- BaunetzWissen, Glossar—Treibhauspotenzial. Available online: https://www.baunetzwissen.de/glossar/t/treibhauspotenzial-6305134 (accessed on 5 March 2023).
- Preinstorfer, P.; Huber, T.; Reichenbach, S.; Lees, J.M.; Kromoser, B. Parametric Design Studies of Mass-Related Global Warming Potential and Construction Costs of FRP-Reinforced Concrete Infrastructure. Polymers 2022, 14, 2383. [Google Scholar] [CrossRef]
- ÖNORM EN 15804; Building Sustainability—Environmental Product Declarations—Basic Rules for the Product Category of Building Products. Austrian Standards: Vienna, Austria, 2022.
- Xie, T.; Bennett, B.; Visintin, P. Performance-Based Environmental Assessment of FRP-Confined Concrete Stub Columns: Investigation on FRP Types. J. Compos. Constr. 2023, 27, 04023021. [Google Scholar] [CrossRef]
- Baubook, Baubook—Reference Value Steel. Available online: https://baubook.at/ (accessed on 5 March 2023).
- Ökobaudat, Reference Value. Available online: https://www.oekobaudat.de/no_cache/en/database/search.html (accessed on 5 March 2023).
- Yang, H.; Dongdong, J.; Liu, W.; Weiquing, L.; Weidong, L. Prestressed Glulam Beams Reinforced with CFRP Bars. Constr. Build. Mater. 2016, 109, 73–83. [Google Scholar] [CrossRef]
- Yang, H.; Liu, W.; Lu, W.; Zhu, S.; Geng, Q. Flexural Behavior of FRP and Steel Reinforced Glulam Beams: Experimental and Theoretical Evaluation. Constr. Build. Mater. 2016, 106, 550–563. [Google Scholar] [CrossRef]
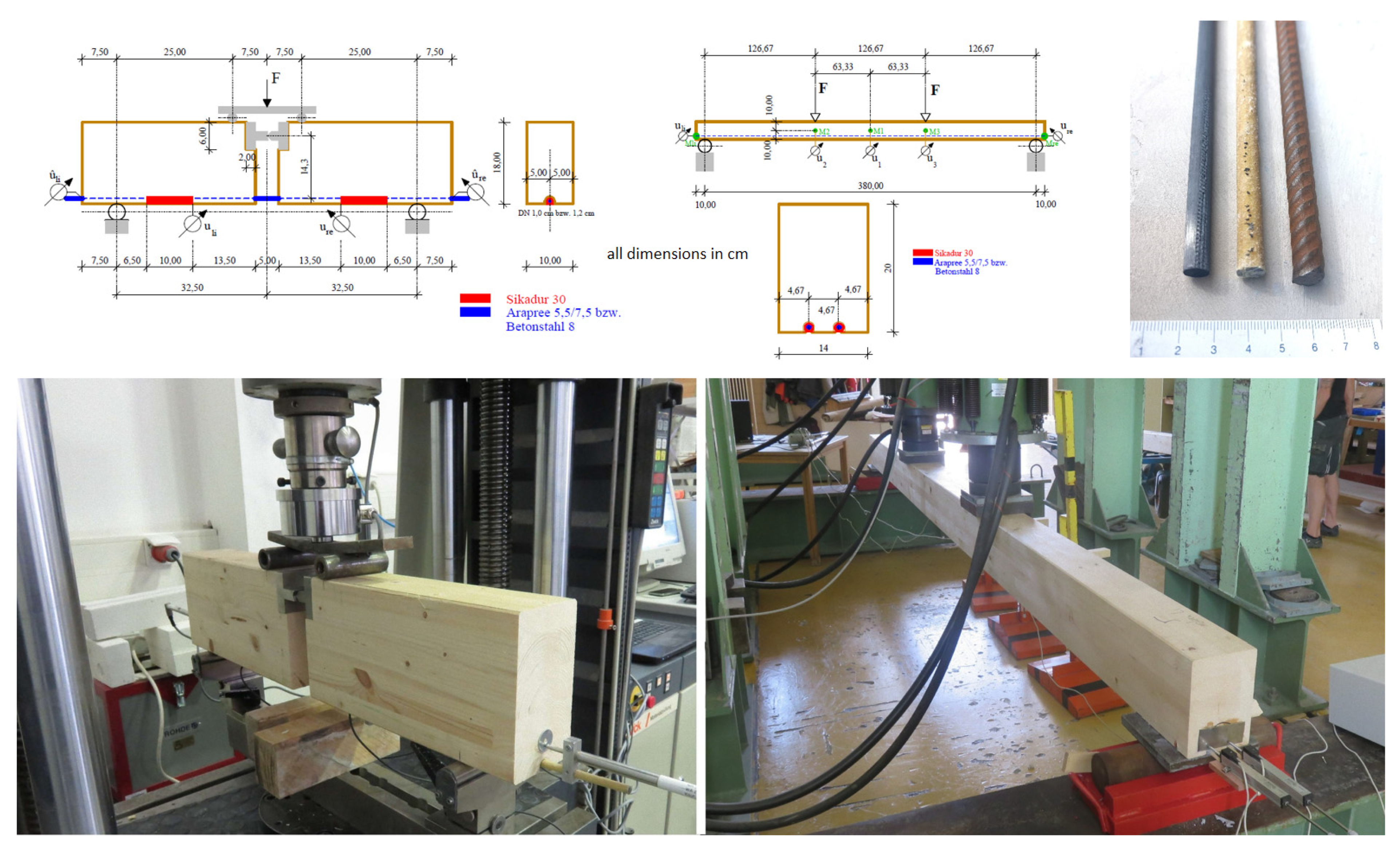


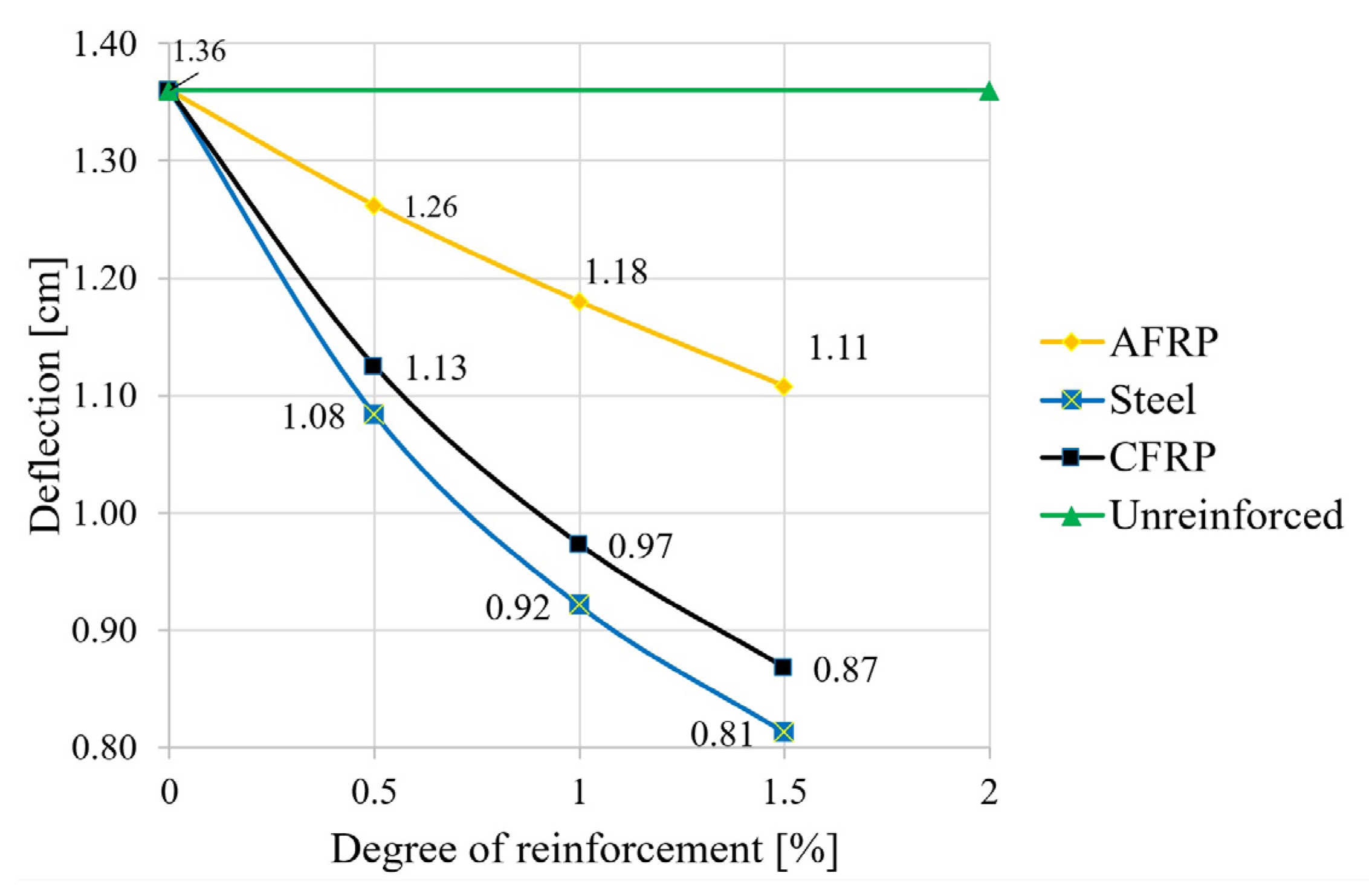
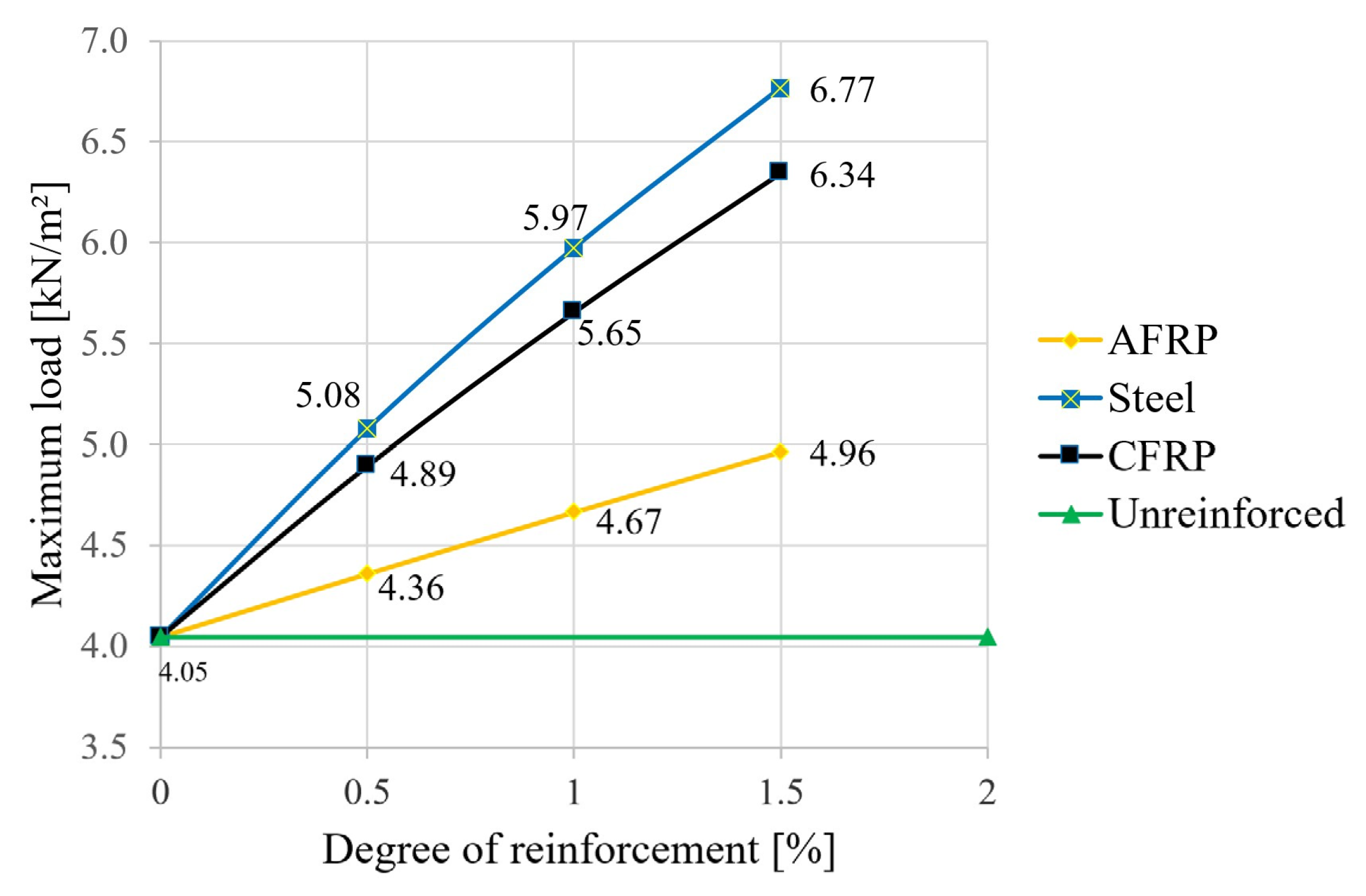
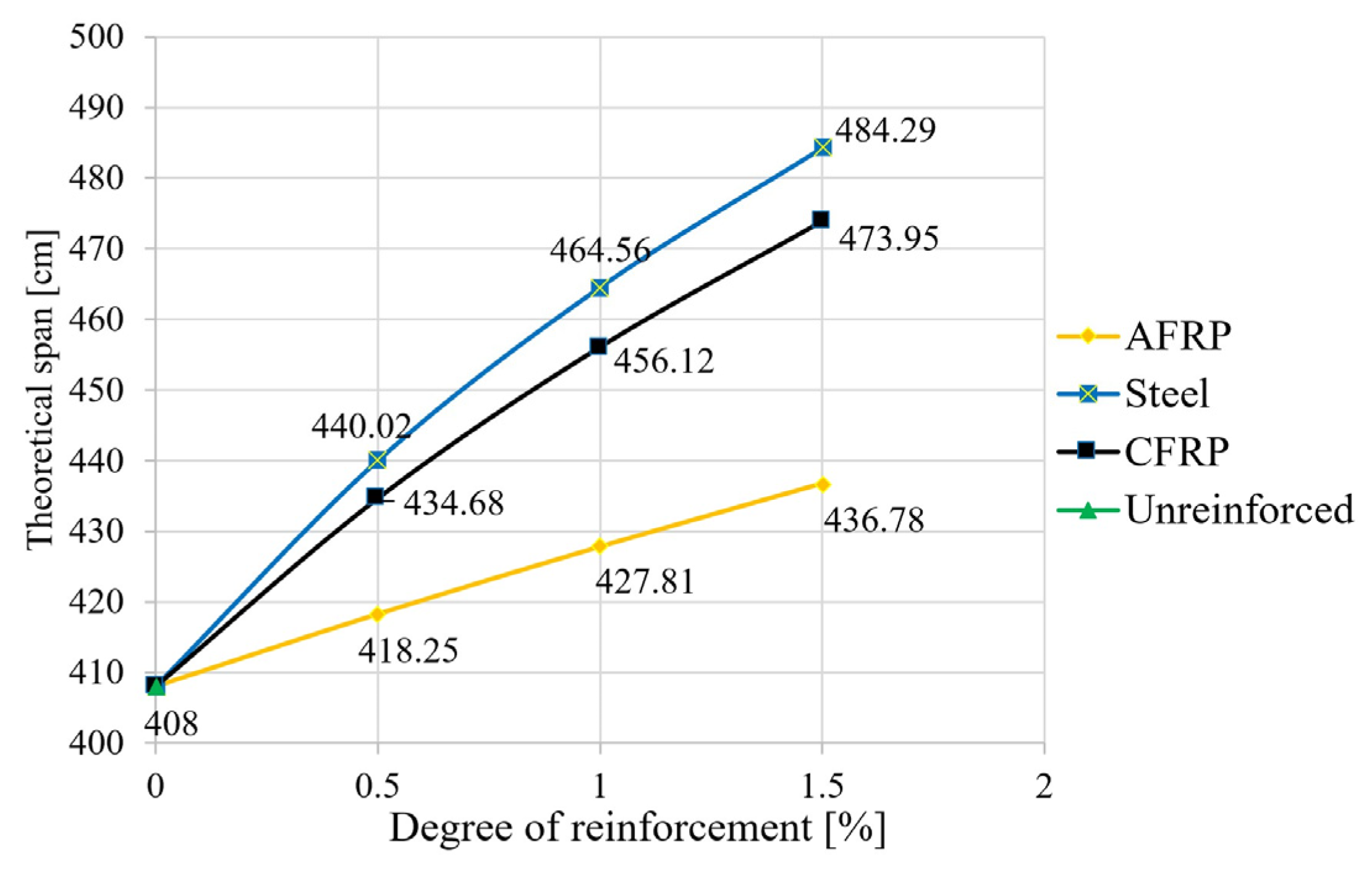
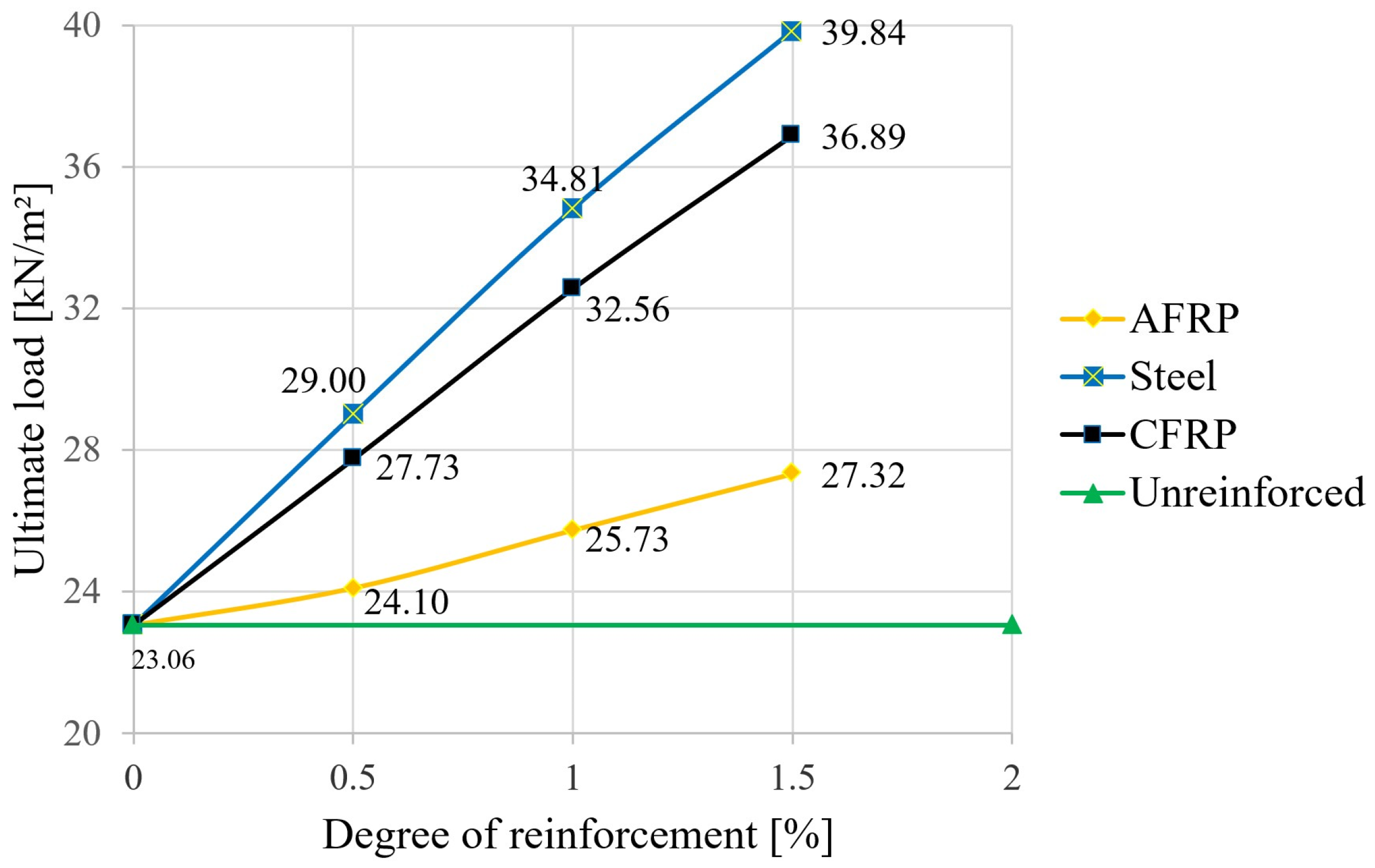

| Type | Elasticity Modulus | Tensile Strength | Source |
|---|---|---|---|
| N/mm2 | N/mm2 | ||
| CFRP: Sika CarboDur ® S | 170,000 | 3100 | Product info [33] |
| AFRP: Arapree ® | 60,000 | 1400 | Product info [34] |
| Structural steel | 210,000 | 235 1 | EN 10025 [35] |
| Glued laminated timber GL 24 h | 11,500 | 51.4 | EN 14080 [36] |
| Type | GWP/Tensile Strength | GWP/Elasticity Modulus |
|---|---|---|
| kg CO2-eq/m/MPa × 106 | kg CO2-eq/m/MPa × 106 | |
| CFRP: Sika CarboDur ® S | 3691 | 67 |
| AFRP: Arapree ® | 5438 | 127 |
| Structural steel | 16,695 | 19 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Deix, K.; Huber, C.; Gogic, J. Efficiency of Alternative Reinforcement Methods for Wooden Ceilings and Their Ecological Aspects. Materials 2025, 18, 2032. https://doi.org/10.3390/ma18092032
Deix K, Huber C, Gogic J. Efficiency of Alternative Reinforcement Methods for Wooden Ceilings and Their Ecological Aspects. Materials. 2025; 18(9):2032. https://doi.org/10.3390/ma18092032
Chicago/Turabian StyleDeix, Karl, Christian Huber, and Josip Gogic. 2025. "Efficiency of Alternative Reinforcement Methods for Wooden Ceilings and Their Ecological Aspects" Materials 18, no. 9: 2032. https://doi.org/10.3390/ma18092032
APA StyleDeix, K., Huber, C., & Gogic, J. (2025). Efficiency of Alternative Reinforcement Methods for Wooden Ceilings and Their Ecological Aspects. Materials, 18(9), 2032. https://doi.org/10.3390/ma18092032






