Deep-Subwavelength Composite Metamaterial Unit for Concurrent Ventilation and Broadband Acoustic Insulation
Abstract
1. Introduction
2. Materials and Methods
2.1. Design and Physical Mechanism of VCMU
2.2. Theoretical Modeling and Methods
3. Results and Discussion
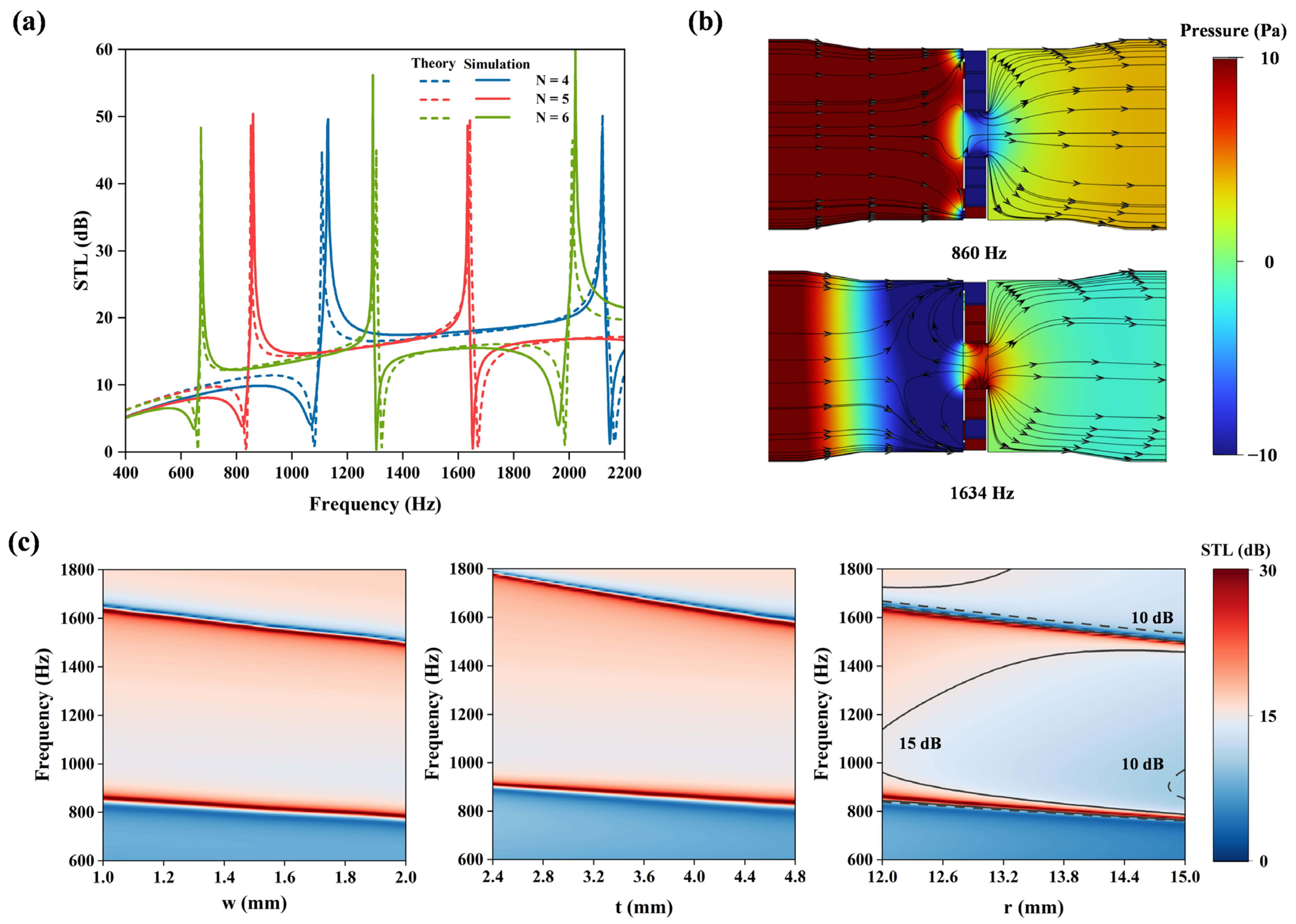
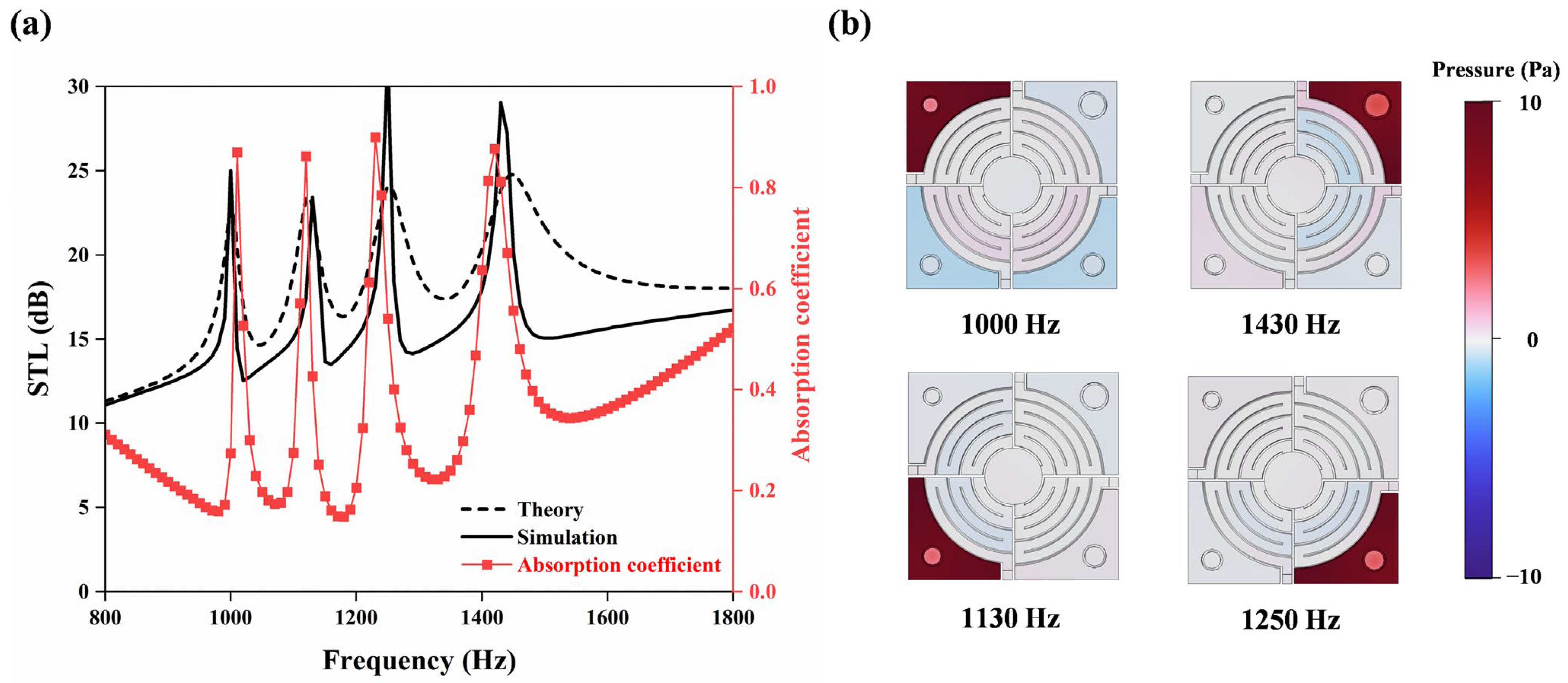
3.1. Finite Element Model and Parametric Analysis
3.2. Experimental Verification
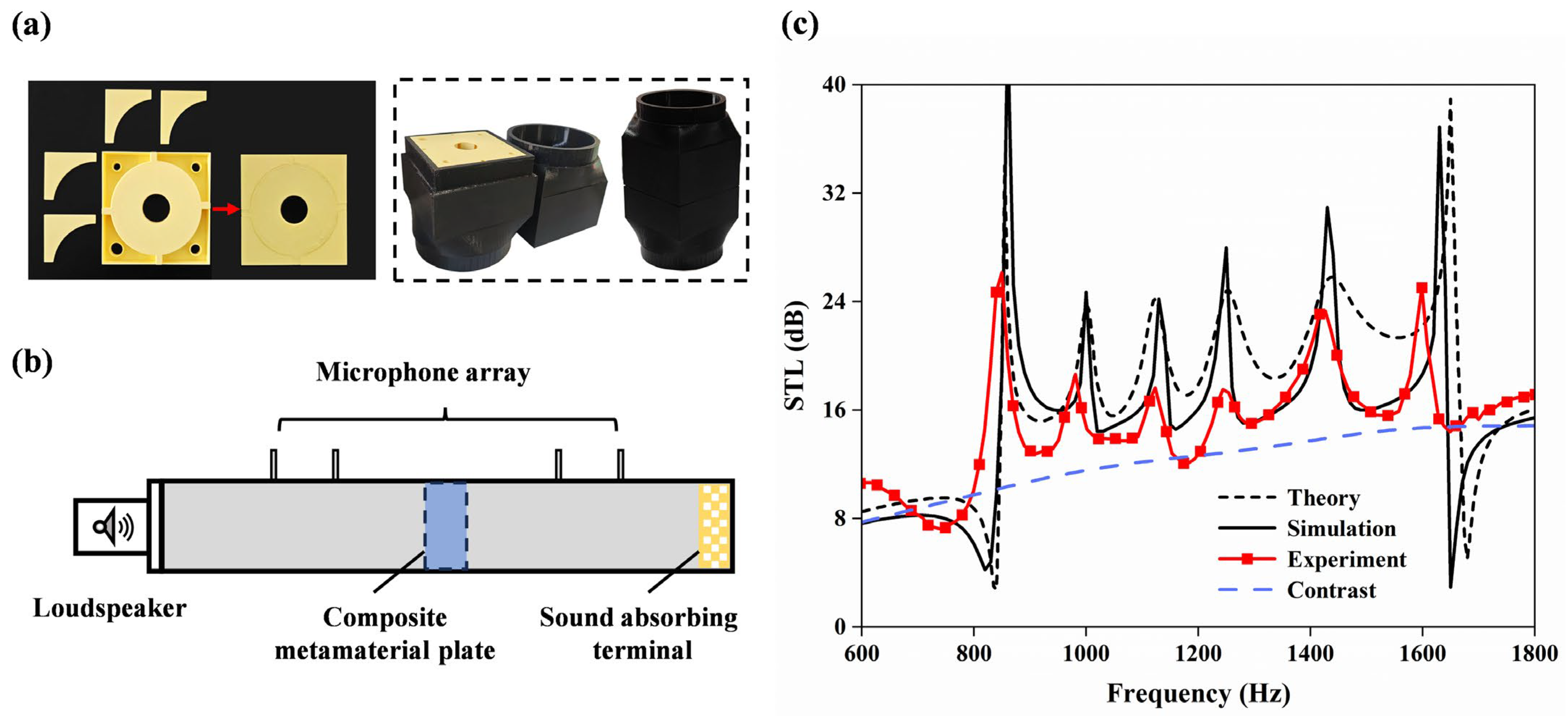
3.2.1. Validation of Acoustic Insulation Models
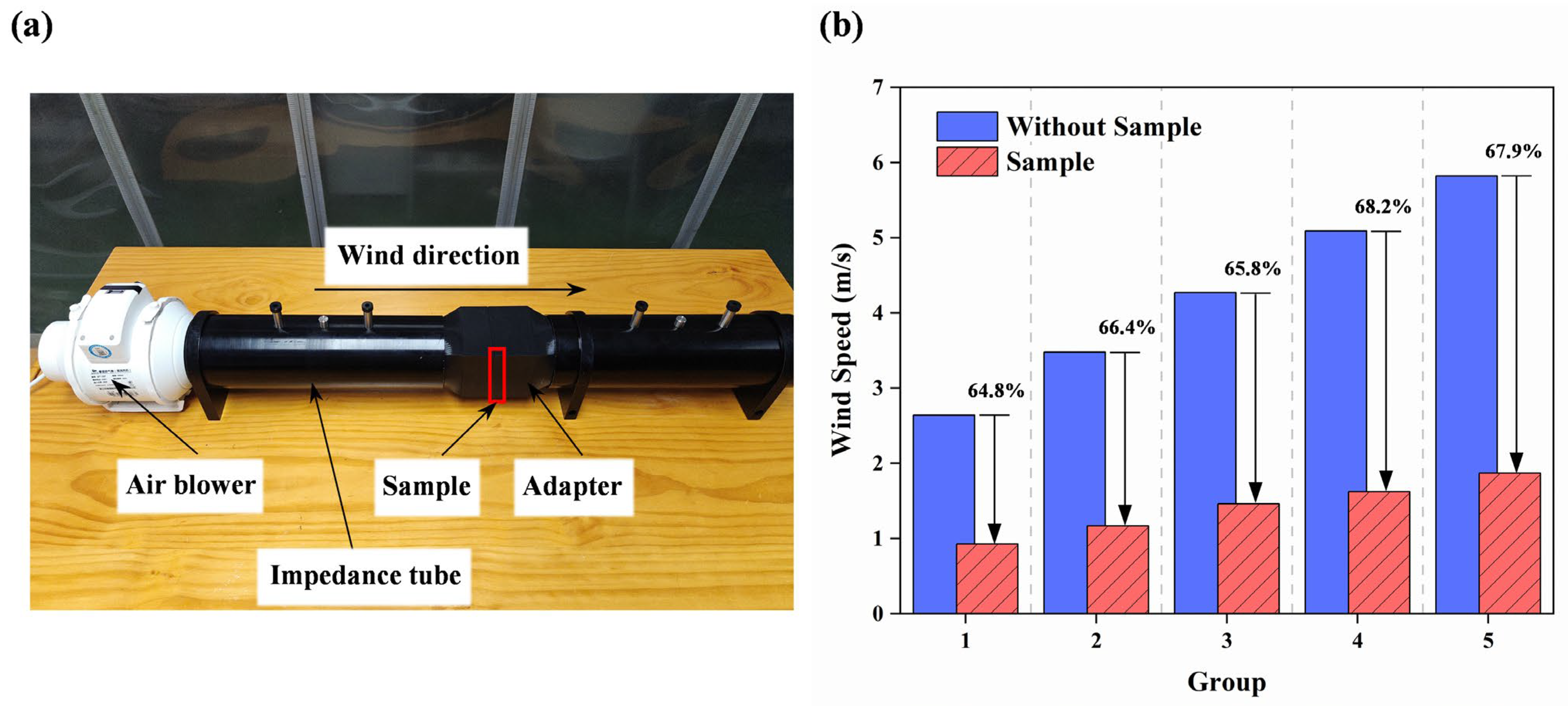
3.2.2. Verification of Ventilation Functionality
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Slabbekoorn, H. Noise Pollution. Curr. Biol. 2019, 29, R957–R960. [Google Scholar] [CrossRef] [PubMed]
- Tadeu, A.; António, J.M.P. Acoustic insulation of single panel walls provided by analytical expressions versus the mass law. J. Sound Vib. 2002, 257, 457–475. [Google Scholar] [CrossRef]
- Berardi, U.; Iannace, G. Acoustic Characterization of Natural Fibers for Sound Absorption Applications. Build. Environ. 2015, 94, 840–852. [Google Scholar] [CrossRef]
- Liu, Z.; Zhang, X.; Mao, Y.; Zhu, Y.Y.; Yang, Z.; Chan, C.T.; Sheng, P. Locally Resonant Sonic Materials. Science 2000, 289, 1734–1736. [Google Scholar] [CrossRef]
- Li, J.; Chan, C.T. Double-Negative Acoustic Metamaterial. Phys. Rev. E 2004, 70, 055602. [Google Scholar] [CrossRef]
- Fang, N.; Xi, D.; Xu, J.; Ambati, M.; Srituravanich, W.; Sun, C.; Zhang, X. Ultrasonic Metamaterials with Negative Modulus. Nat. Mater. 2006, 5, 452–456. [Google Scholar] [CrossRef]
- Yang, Z.; Mei, J.; Yang, M.; Chan, N.H.; Sheng, P. Membrane-Type Acoustic Metamaterial with Negative Dynamic Mass. Phys. Rev. Lett. 2008, 101, 204301. [Google Scholar] [CrossRef]
- Lee, S.H.; Park, C.M.; Seo, Y.M.; Wang, Z.G.; Kim, C.K. Composite Acoustic Medium with Simultaneously Negative Density and Modulus. Phys. Rev. Lett. 2010, 104, 054301. [Google Scholar] [CrossRef]
- Li, Y.; Liang, B.; Gu, Z.; Zou, X.; Cheng, J. Reflected Wavefront Manipulation Based on Ultrathin Planar Acoustic Metasurfaces. Sci. Rep. 2013, 3, 2546. [Google Scholar] [CrossRef]
- Zhao, J.; Li, B.; Chen, Z.; Qiu, C.-W. Manipulating Acoustic Wavefront by Inhomogeneous Impedance and Steerable Extraordinary Reflection. Sci. Rep. 2013, 3, 2537. [Google Scholar] [CrossRef]
- Tang, K.; Qiu, C.; Ke, M.; Lu, J.; Ye, Y.; Liu, Z. Anomalous Refraction of Airborne Sound through Ultrathin Metasurfaces. Sci. Rep. 2014, 4, 6517. [Google Scholar] [CrossRef] [PubMed]
- Mei, J.; Wu, Y. Controllable Transmission and Total Reflection through an Impedance-Matched Acoustic Metasurface. New J. Phys. 2014, 16, 123007. [Google Scholar] [CrossRef]
- Li, J.; Pendry, J.B. Hiding Under the Carpet: A New Strategy for Cloaking. Phys. Rev. Lett. 2008, 101, 203901. [Google Scholar] [CrossRef] [PubMed]
- Farhat, M.; Guenneau, S.; Enoch, S. Ultrabroadband Elastic Cloaking in Thin Plates. Phys. Rev. Lett. 2009, 103, 024301. [Google Scholar] [CrossRef]
- Sanchis, L.; García-Chocano, V.M.; Llopis-Pontiveros, R.; Climente, A.; Martínez-Pastor, J.; Cervera, F.; Sánchez-Dehesa, J. Three-Dimensional Axisymmetric Cloak Based on the Cancellation of Acoustic Scattering from a Sphere. Phys. Rev. Lett. 2013, 110, 124301. [Google Scholar] [CrossRef]
- Sounas, D.L.; Fleury, R.; Alù, A. Unidirectional Cloaking Based on Metasurfaces with Balanced Loss and Gain. Phys. Rev. Appl. 2015, 4, 014005. [Google Scholar] [CrossRef]
- Cai, X.; Guo, Q.; Hu, G.; Yang, J. Ultrathin Low-Frequency Sound Absorbing Panels Based on Coplanar Spiral Tubes or Coplanar Helmholtz Resonators. Appl. Phys. Lett. 2014, 105, 121901. [Google Scholar] [CrossRef]
- Li, Y.; Assouar, B.M. Acoustic Metasurface-Based Perfect Absorber with Deep Subwavelength Thickness. Appl. Phys. Lett. 2016, 108, 063502. [Google Scholar] [CrossRef]
- Huang, S.; Fang, X.; Wang, X.; Assouar, B.; Cheng, Q.; Li, Y. Acoustic Perfect Absorbers via Spiral Metasurfaces with Embedded Apertures. Appl. Phys. Lett. 2018, 113, 233501. [Google Scholar] [CrossRef]
- Zhang, H.; Zhu, Y.; Liang, B.; Yang, J.; Yang, J.; Cheng, J. Omnidirectional Ventilated Acoustic Barrier. Appl. Phys. Lett. 2017, 111, 203502. [Google Scholar] [CrossRef]
- Yang, J.; Lee, J.S.; Lee, H.R.; Kang, Y.J.; Kim, Y.Y. Slow-Wave Metamaterial Open Panels for Efficient Reduction of Low-Frequency Sound Transmission. Appl. Phys. Lett. 2018, 112, 091901. [Google Scholar] [CrossRef]
- Kumar, S.; Lee, H.P. Labyrinthine Acoustic Metastructures Enabling Broadband Sound Absorption and Ventilation. Appl. Phys. Lett. 2020, 116, 134103. [Google Scholar] [CrossRef]
- Ghaffarivardavagh, R.; Nikolajczyk, J.; Anderson, S.; Zhang, X. Ultra-Open Acoustic Metamaterial Silencer Based on Fano-like Interference. Phys. Rev. B 2019, 99, 024302. [Google Scholar] [CrossRef]
- Sun, M.; Fang, X.; Mao, D.; Wang, X.; Li, Y. Broadband Acoustic Ventilation Barriers. Phys. Rev. Appl. 2020, 13, 044028. [Google Scholar] [CrossRef]
- Man, X.; Luo, Z.; Liu, J.; Xia, B. Hilbert Fractal Acoustic Metamaterials with Negative Mass Density and Bulk Modulus on Subwavelength Scale. Mater. Des. 2019, 180, 107911. [Google Scholar] [CrossRef]
- Xiang, L.; Wang, G.; Zhu, C. Controlling Sound Transmission by Space-Coiling Fractal Acoustic Metamaterials with Broadband on the Subwavelength Scale. Appl. Acoust. 2022, 188, 108585. [Google Scholar] [CrossRef]
- Cui, H.; Liu, C.; Hu, H. Research on Low-Frequency Noise Control Based on Fractal Coiled Acoustic Metamaterials. Shock Vib. 2022, 2022, 2083563. [Google Scholar] [CrossRef]
- Seo, S.-H.; Kim, Y.-H. Silencer Design by Using Array Resonators for Low-Frequency Band Noise Reduction. J. Acoust. Soc. Am. 2005, 118, 2332–2338. [Google Scholar] [CrossRef]
- Cai, C.; Mak, C.M. Acoustic Performance of Different Helmholtz Resonator Array Configurations. Appl. Acoust. 2018, 130, 204–209. [Google Scholar] [CrossRef]
- Liu, C.; Wang, H.; Liang, B.; Cheng, J.; Lai, Y. Low-Frequency and Broadband Muffler via Cascaded Labyrinthine Metasurfaces. Appl. Phys. Lett. 2022, 120, 231702. [Google Scholar] [CrossRef]
- Su, Z.; Luo, H.; Gao, S.; Luo, Z.; Zhu, Y.; Zhang, H. Customizable Acoustic Metamaterial Barrier with Intelligent Sound Insulation. Phys. Rev. Appl. 2022, 18, 064029. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, W.; Cao, G.; Zuo, G.; Liu, C.; Ma, F. Ultra-Thin Ventilated Metasurface Pipeline Coating for Broadband Noise Reduction. Thin-Walled Struct. 2024, 200, 111916. [Google Scholar] [CrossRef]
- Lin, D.-K.; Xiao, X.-W.; Yang, C.-C.; Ho, S.-Y.; Chou, L.-C.; Chiang, C.-H.; Chen, J.-S.; Liu, C.-H. An Acoustic Impedance Design Method for Tubular Structures with Broadband Sound Insulations and Efficient Air Ventilation. Appl. Acoust. 2024, 220, 109983. [Google Scholar] [CrossRef]
- Zhang, X.; Yu, Q.; Zhao, C.; Shi, D.; Geng, M.; Zheng, J.; Lu, T.; Wang, P. Modular Reverse Design of Acoustic Metamaterial and Sound Barrier Engineering Applications: High Ventilation and Broadband Sound Insulation. Thin-Walled Struct. 2024, 196, 111498. [Google Scholar] [CrossRef]
- Ma, P.-S.; Seo, Y.-H.; Lee, H.J. Multiband Ventilation Barriers Enabled by Space-Coiling Acoustic Metamaterials. Appl. Acoust. 2023, 211, 109565. [Google Scholar] [CrossRef]
- Yang, C.-C.; Lin, D.-K.; Xiao, X.-W.; Chiang, C.-H.; Lin, Y.-H.; Chou, L.-C.; Chen, J.-S.; Liu, C.-H. A Compact Honeycomb-Based Ventilated Sound Barrier with Broad Bandwidth and a Subwavelength Thickness. Appl. Acoust. 2024, 226, 110182. [Google Scholar] [CrossRef]
- Wang, S.; Li, H.; Liu, Y.; Cao, G.; Yang, Z.; Ma, F. Ultra-Thin Metasurface Meta-Barrier for Integrated Ventilation and Sound Insulation. Appl. Acoust. 2025, 231, 110486. [Google Scholar] [CrossRef]
- Rubino, C.; Liuzzi, S.; Fusaro, G.; Martellotta, F.; Scrosati, C.; Garai, M. Balancing Ventilation and Sound Insulation in Windows by Means of Metamaterials: A Review of the State of the Art. Build. Environ. 2025, 275, 112780. [Google Scholar] [CrossRef]
- Zhang, Y.; Chin, Y.W.; Yu, X.; Shrestha, M.; Lau, G.-K.; Koo, B.C.; Liu, K.; Lu, Z. Ventilated Acoustic Metasurface with Low-Frequency Sound Insulation. JASA Express Lett. 2023, 3, 073602. [Google Scholar] [CrossRef]
- Genet, C.; van Exter, M.P.; Woerdman, J.P. Fano-Type Interpretation of Red Shifts and Red Tails in Hole Array Transmission Spectra. Opt. Commun. 2003, 225, 331–336. [Google Scholar] [CrossRef]
- Munjal, M.L. Acoustics of Ducts and Mufflers with Application to Exhaust and Ventilation System Design; John Wiley & Sons: Hoboken, NJ, USA, 1987; ISBN 978-0-471-84738-0. [Google Scholar]
- Verdière, K.; Panneton, R.; Elkoun, S.; Dupont, T.; Leclaire, P. Transfer Matrix Method Applied to the Parallel Assembly of Sound Absorbing Materials. J. Acoust. Soc. Am. 2013, 134, 4648–4658. [Google Scholar] [CrossRef] [PubMed]
- Verdière, K.; Panneton, R.; Elkoun, S.; Dupont, T.; Leclaire, P. Comparison between Parallel Transfer Matrix Method and Admittance Sum Method. J. Acoust. Soc. Am. 2014, 136, EL90–EL95. [Google Scholar] [CrossRef]
- Karal, F.C. The Analogous Acoustical Impedance for Discontinuities and Constrictions of Circular Cross Section. J. Acoust. Soc. Am. 1953, 25, 327–334. [Google Scholar] [CrossRef]
- Nunes, M.; Silva, G. Effect of Effective Length of the Tube on Transmission Loss of Reactive Muffler; Institute of Noise Control Engineering: Wakefield, MA, USA, 2016. [Google Scholar]
- Kennedy, J.; Flanagan, L.; Dowling, L.; Bennett, G.J.; Rice, H.; Trimble, D. The Influence of Additive Manufacturing Processes on the Performance of a Periodic Acoustic Metamaterial. Int. J. Polym. Sci. 2019, 2019, 7029143. [Google Scholar] [CrossRef]


| Parameter Description | Symbol | Unit (mm) |
|---|---|---|
| Width of the square outer frame | L | 90 |
| Radius of the central circular channel | r | 12 |
| Single-layer thickness of the middle structure | h | 11 |
| Labyrinth channel and inlet width | t | 4 |
| Partition thickness | w | 1 |
| Unit i | di (mm) | Vi (mm3) | fi (Hz) |
|---|---|---|---|
| 1 | 6.3 | 8143.2 | 1002 |
| 2 | 7.3 | 8088.5 | 1124 |
| 3 | 8.4 | 8012.5 | 1252 |
| 4 | 10.1 | 7846.2 | 1443 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, X.; He, J.; Nie, J.; Liu, Y.; Yu, H.; Chen, Q.; Yang, J. Deep-Subwavelength Composite Metamaterial Unit for Concurrent Ventilation and Broadband Acoustic Insulation. Materials 2025, 18, 2029. https://doi.org/10.3390/ma18092029
Zhang X, He J, Nie J, Liu Y, Yu H, Chen Q, Yang J. Deep-Subwavelength Composite Metamaterial Unit for Concurrent Ventilation and Broadband Acoustic Insulation. Materials. 2025; 18(9):2029. https://doi.org/10.3390/ma18092029
Chicago/Turabian StyleZhang, Xiaodong, Jinhong He, Jing Nie, Yang Liu, Huiyong Yu, Qi Chen, and Jianxing Yang. 2025. "Deep-Subwavelength Composite Metamaterial Unit for Concurrent Ventilation and Broadband Acoustic Insulation" Materials 18, no. 9: 2029. https://doi.org/10.3390/ma18092029
APA StyleZhang, X., He, J., Nie, J., Liu, Y., Yu, H., Chen, Q., & Yang, J. (2025). Deep-Subwavelength Composite Metamaterial Unit for Concurrent Ventilation and Broadband Acoustic Insulation. Materials, 18(9), 2029. https://doi.org/10.3390/ma18092029






