Understanding the Adsorption Behavior of Different Crystal Surfaces of Manganese Monoxide to Strontium Nitrate Solutions: A Molecular Dynamics Simulation
Abstract
1. Introduction
2. Materials and Methods
2.1. Models
2.2. Force Field and Molecular Dynamics Simulation Details
2.3. Data Analysis
2.3.1. Particle Density Profile (PDP)
2.3.2. Radial Distribution Function (RDF)
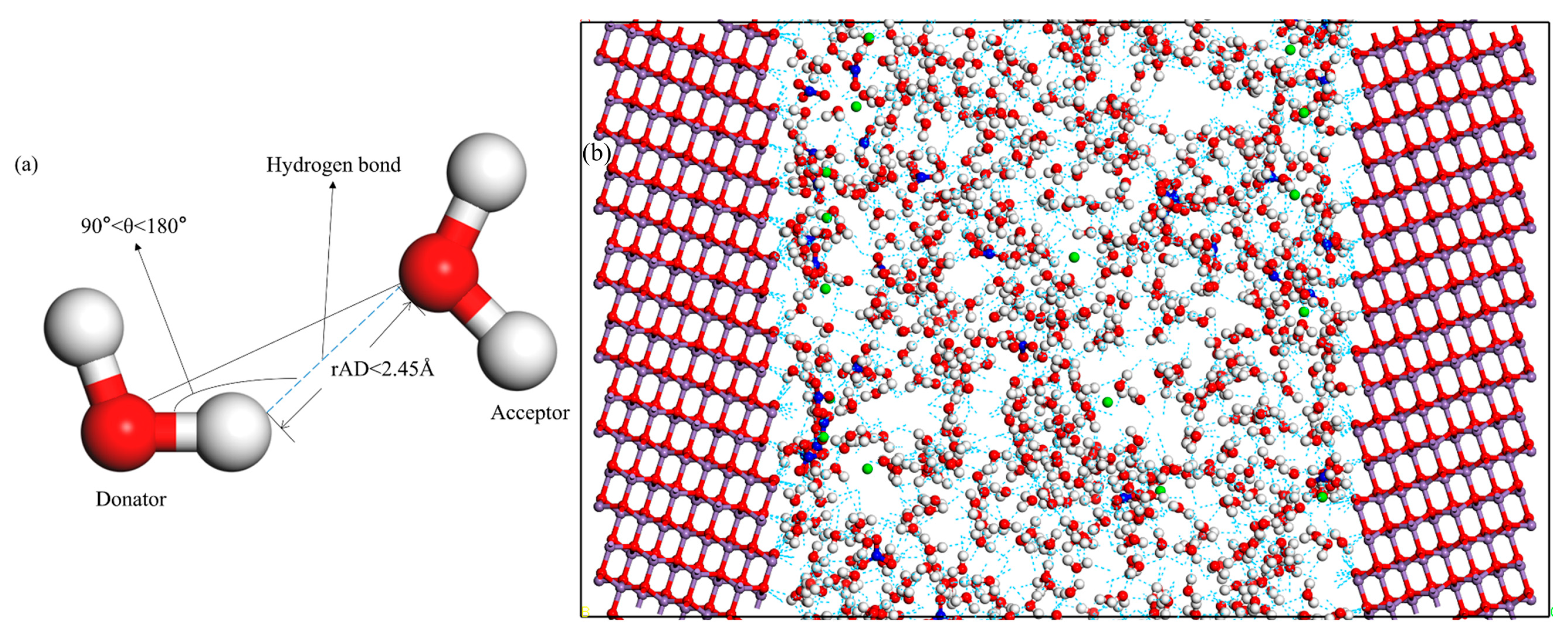
2.3.3. The Network of Hydrogen Bonds
2.3.4. The Non-Bond Interaction Energy (Eint)
2.3.5. Mean Square Displacement (MSD) and Diffusion Coefficient (D)
3. Results and Discussion
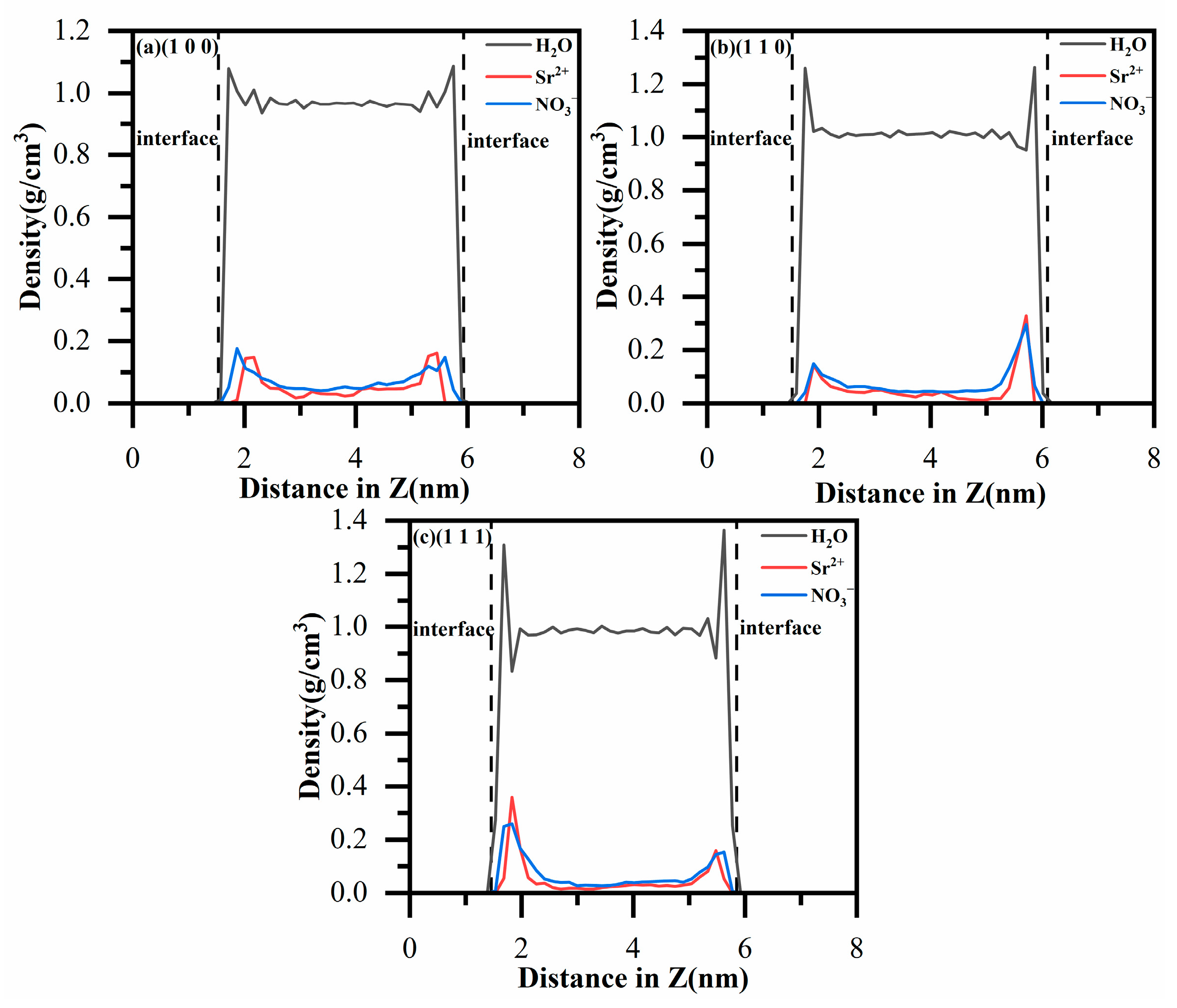
3.1. Density Profiles of Ions and Water Molecules
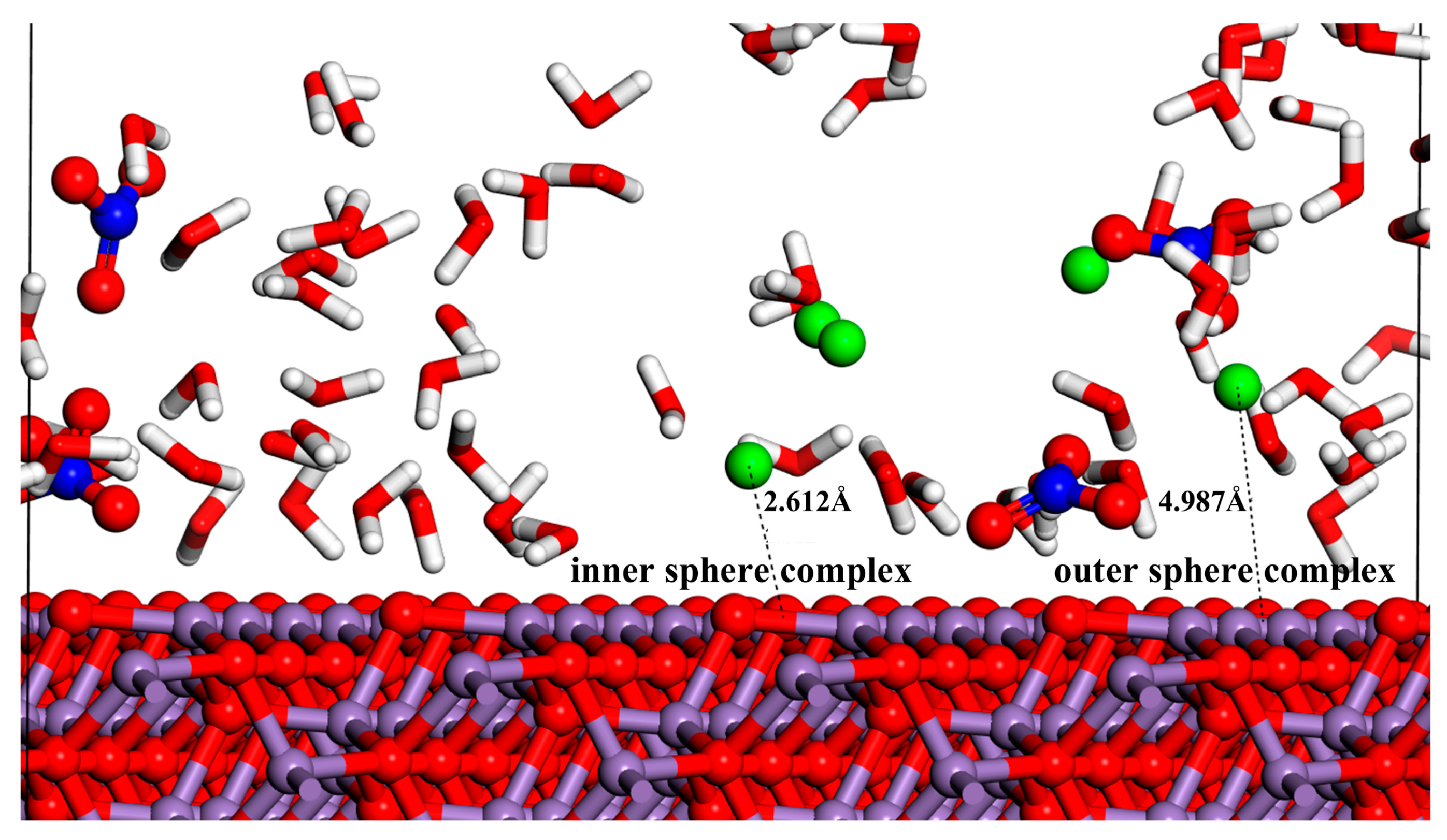
3.2. Radial Distribution Function (RDF)
3.3. The Network of Hydrogen Bonds
3.4. The Non-Bond Interaction Energy
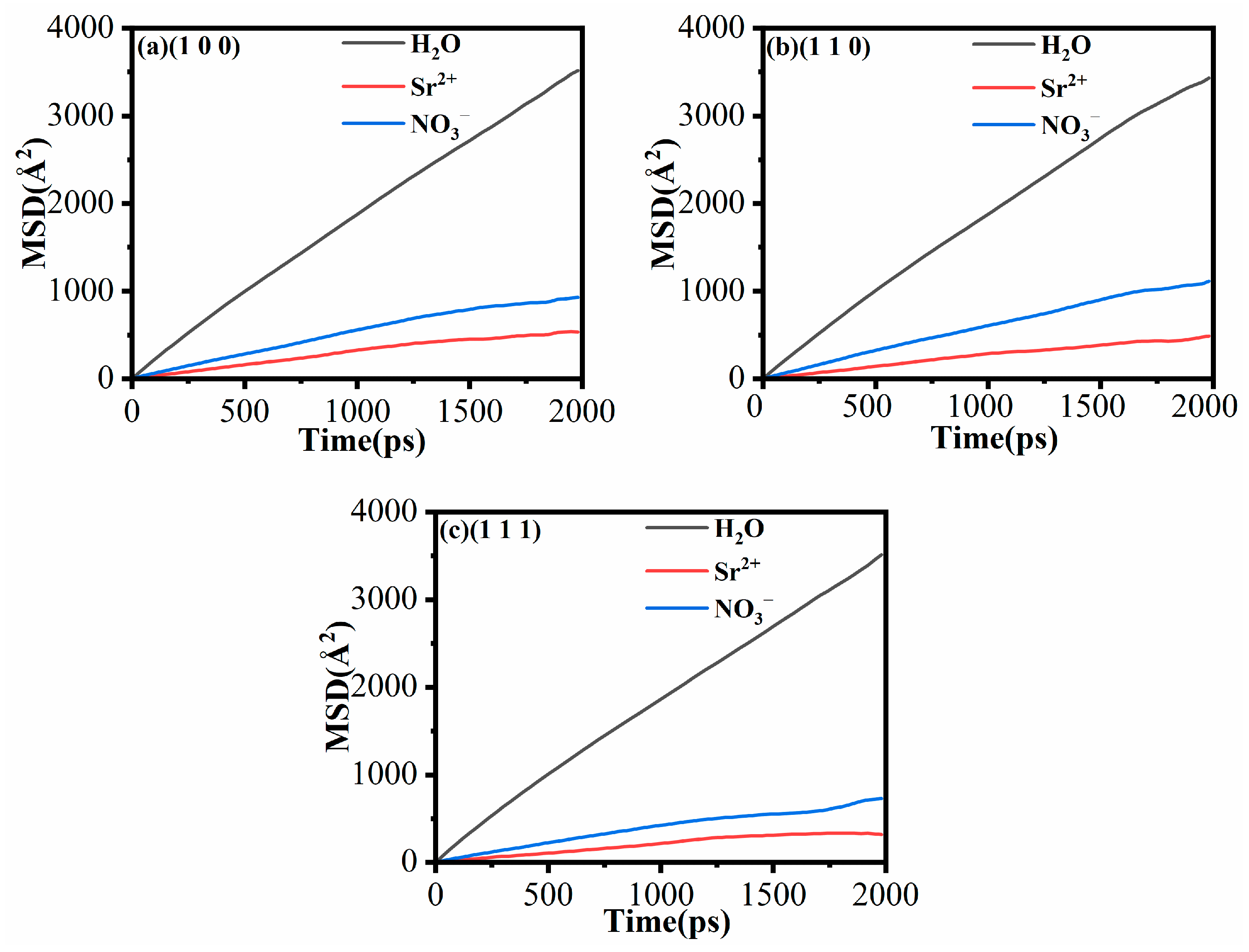
3.5. Mean Square Displacement (MSD) and Diffusion Coefficient (D)
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Li, J.; Jin, J.; Zou, Y.; Sun, H.; Zeng, X.; Huang, X.; Feng, M.; Kanatzidis, M.G. Efficient Removal of Cs+ and Sr2+ Ions by Granulous (Me2NH2)4/3(Me3NH)2/3Sn3S7·1.25H2O/Polyacrylonitrile Composite. ACS Appl. Mater. Interfaces 2021, 13, 13434–13442. [Google Scholar]
- Kim, Y.; Jin, K.; Park, I.-H.; Lee, S.; Park, J.; Park, J. Selective Sr2+ capture in an In3+-based anionic metal-organic framework. Chem. Eng. J. 2024, 484, 149321. [Google Scholar]
- Guo, Y.-L.; Sun, H.-Y.; Zeng, X.; Lv, T.-T.; Yao, Y.-X.; Zhuang, T.-H.; Feng, M.-L.; Huang, X.-Y. Efficient removal of Sr2+ ions by a one-dimensional potassium phosphatoantimonate. Chem. Eng. J. 2023, 460, 141697. [Google Scholar] [CrossRef]
- Lehto, J.; Koivula, R.; Leinonen, H.; Tusa, E.; Harjula, R. Removal of Radionuclides from Fukushima Daiichi Waste Effluents. Sep. Purif. Rev. 2019, 48, 122–142. [Google Scholar]
- Li, Q.; Wang, X.; Song, L.; He, L.; Yu, Q.; Xiao, X.; Ding, S. Cyclohexyl substituted diglycolamide ligands for highly efficient separation of strontium: Synthesis, extraction and crystallography studies. J. Environ. Chem. Eng. 2023, 11, 110495. [Google Scholar]
- Mousavi, S.E.; Kalal, H.S.; Ghorbanian, S.A.; Khamseh, A.A.G.; Khanchi, A.R. A comparison of various XAD-Amberlite resins impregnated with dicyclohexyl-18-crown-6 for strontium removal. J. Prog. Nucl. Energy 2023, 166, 104965. [Google Scholar]
- Liu, B.; Zhu, G.H.; Ma, J.L.; Zhang, L.; Wei, G.J. Equilibrium Fractionation of Stable Strontium Isotopes During Adsorption to Mn Oxides. Geochem. Geophys. Geosyst. 2024, 25, e2024GC011460. [Google Scholar]
- Timofeeva, Y.; Karabtsov, A.; Burdukovskii, M.; Vzorova, D. Strontium and vanadium sorption by iron-manganese nodules from natural and remediated Dystric Cambisols. J. Soils Sed. 2024, 24, 1220–1236. [Google Scholar]
- Saenko, E. Doping birnessite as a method for synthesizing an ion exchanger selective to strontium and repeatedly working in sorption-desorption cycles. J. Solid State Chem. 2024, 329, 124381. [Google Scholar]
- Amesh, P.; Venkatesan, K.A.; Suneesh, A.S.; Maheswari, U. Tuning the ion exchange behavior of cesium and strontium on sodium iron titanate. Sep. Purif. Technol. 2021, 267, 118678. [Google Scholar] [CrossRef]
- Asim, U.; Husnain, S.M.; Abbas, N.; Shahzad, F.; Khan, A.R.; Ali, T. Morphology controlled facile synthesis of MnO2 adsorbents for rapid strontium removal. J. Ind. Eng. Chem. 2021, 98, 375–382. [Google Scholar]
- Shen, Z.; Yan, G.; Chen, G.; Cao, L.; Tang, X.; Sun, Y.; Liu, J.; Yang, S.; Lin, L.; Zeng, X. Preparation and strontium adsorption behaviors of a new sodium manganese silicate material. Sep. Purif. Technol. 2022, 290, 120824. [Google Scholar]
- Zheng, J.; Yang, Y.; Dai, Z.; Wang, J.; Xia, Y.; Li, C. Preparation of manganese dioxide/hollow mesoporous silica spheres (MnO2/HMSS) composites for removal of Sr(II) from aqueous solution. Colloids Surf. A-Physicochem. Eng. Asp. 2023, 666, 131298. [Google Scholar]
- Nugroho, B.S.; Wijayanto, H.; Wihadi, M.N.K.; Nakashima, S. Detection of strontium species and Sr(OH)2 NPs formation via double oxidation effect on coal oxide: Preparation and characterization of new coal oxide and its mixture. Inorg. Chem. Commun. 2023, 157, 111377. [Google Scholar]
- Song, H.; Jeong, S.; Nam, K. Identification of strontium substitution mechanism in hematite via calcium solution. Chemosphere 2023, 340, 139925. [Google Scholar]
- Karasyova, O.N.; Ivanova, L.I.; Lakshtanov, L.Z.; Lövgren, L. Strontium sorption on hematite at elevated temperatures. J. Colloid Interface Sci. 1999, 220, 419–428. [Google Scholar]
- Cao, J.; Kong, L.Y.; Guo, T.; Shi, P.; Wang, C.; Tu, Y.M.; Sas, G.; Elfgren, L. Molecular dynamics simulations of ion migration and adsorption on the surfaces of AFm hydrates. Appl. Surf. Sci. 2023, 615, 156390. [Google Scholar]
- Qin, D.X.; Xue, Z.Y.; Du, M.; Wang, X.; Xue, Y.; Xu, D.G. Molecular dynamics exploration of ion association mechanism of apatite controlled by a nanogrooved hydroxyapatite surface. Appl. Surf. Sci. 2023, 617, 156580. [Google Scholar]
- De Rosa, V.L.D.; Rebaza, A.V.G.; Montes, M.L.; Taylor, M.A.; Alonso, R.E. Sorption of Sr on montmorillonite clays: Theoretical and experimental study. Appl. Surf. Sci. 2022, 592, 153146. [Google Scholar]
- Hou, D.S.; Zhang, J.L.; Pan, W.; Zhang, Y.; Zhang, Z.H. Nanoscale mechanism of ions immobilized by the geopolymer: A molecular dynamics study. J. Nucl. Mater. 2020, 528, 151841. [Google Scholar]
- Wang, R.; Ye, J.Y.; Wang, J.S.; Peng, X.Y. Adsorption and diffusion mechanism of cesium and chloride ions in channel of geopolymer with different Si/Al ratios: Molecular dynamics simulation. J. Radioanal. Nucl. Chem. 2023, 332, 3597–3607. [Google Scholar] [CrossRef]
- Chen, Y.; Wei, M.; Liu, M.; Liu, G.; Li, L.; Yang, Q. Mxene nanosheet membranes for hydrogen isotope separation: An investigation via multi-scale molecular simulations. J. Membr. Sci. 2025, 721, 123814. [Google Scholar]
- Qian, L.; Zhang, Y.; Song, W.; Zhang, S.; Zhang, N.; Nica, V. Construction of high-performance glycoprotein molecularly imprinted polymers using boronic acid-containing imidazolium ionic liquid monomer and UiO-66@wood sponge composite carrier. Chem. Eng. J. 2025, 506, 160283. [Google Scholar] [CrossRef]
- Kim, H.; Kim, J.; Hyun, S.P.; Kwon, K.D. Toward a mechanistic understanding of cesium adsorption to todorokite: A molecular dynamics simulation study. J. Hazard. Mater. 2022, 436, 129250. [Google Scholar] [PubMed]
- Salari, H.; Erami, M.; Dokoohaki, M.H.; Zolghadr, A.R. New insights into adsorption equilibrium of organic pollutant on MnO2 nanorods: Experimental and computational studies. J. Mol. Liq. 2022, 345, 117016. [Google Scholar] [CrossRef]
- Guo, Y.; Zhao, Z.; Zhang, J.; Liu, Y.; Hu, B.; Zhang, Y.; Ge, Y.; Lu, H. High-performance zinc-ion battery cathode enabled by deficient manganese monoxide/graphene heterostructures. Electrochim. Acta 2022, 411, 140045. [Google Scholar]
- Ilyasov, V.V.; Popova, I.G.; Ershov, I.V. Ab initio study of magnetism and interaction of graphene with the polar MnO(111) surface. Appl. Surf. Sci. 2017, 419, 924–932. [Google Scholar]
- Minakshi, M.; Singh, P.; Carter, M.; Prince, K. The Zn-MnO2 battery: The influence of aqueous LiOH and KOH electrolytes on the intercalation mechanism. Electrochem. Solid State Lett. 2008, 11, A145–A149. [Google Scholar]
- Jain, A.; Shyue Ping, O.; Hautier, G.; Chen, W.; Richards, W.D.; Dacek, S.; Cholia, S.; Gunter, D.; Skinner, D.; Ceder, G.; et al. Commentary: The Materials Project: A materials genome approach to accelerating materials innovation. APL Mater. 2013, 1, 011002. [Google Scholar] [CrossRef]
- Nam, K.M.; Kim, Y.-I.; Jo, Y.; Lee, S.M.; Kim, B.G.; Choi, R.; Choi, S.-I.; Song, H.; Park, J.T. New Crystal Structure: Synthesis and Characterization of Hexagonal Wurtzite MnO. J. Am. Chem. Soc. 2012, 134, 8392–8395. [Google Scholar] [CrossRef]
- Tu, Y.; Wang, T.; Wen, R.; Cao, J.; Fang, M.; Wang, C.; Sas, G.; Elfgren, L. Molecular dynamics study on the adsorption of radioactive ions by geopolymers. Adv. Cem. Res. 2023, 36, 129–141. [Google Scholar]
- Zhang, K.; Li, H.; Li, Z.; Qi, S.; Cui, S.; Chen, W.; Wang, S. Molecular dynamics and density functional theory simulations of cesium and strontium adsorption on illite/smectite. J. Radioanal. Nucl. Chem. 2022, 331, 2983–2992. [Google Scholar] [CrossRef]
- Wang, N.; Pei, C.; Zhong, Y.; Zhang, Y.; Liu, X.; Hou, J.; Yuan, Y.; Zhang, R. Molecular Dynamics Simulation of the Compatibility Between Supercritical Carbon Dioxide and Coating Resins Assisted by Co-Solvents. Materials 2024, 17, 6271. [Google Scholar] [CrossRef]
- Li, J.; He, L. Modification and Aging Mechanism of Crumb Rubber Modified Asphalt Based on Molecular Dynamics Simulation. Materials 2025, 18, 197. [Google Scholar] [CrossRef]
- Wang, S.; Chen, Y.; Wang, L.; Cui, N.; Li, C.; Sun, S. Study on Water Damage of Asphalt-Aggregate Based on Molecular Dynamics. Materials 2025, 18, 209. [Google Scholar] [CrossRef] [PubMed]
- Liu, L.; Zhang, C.; Jiang, W.; Li, X.; Dai, Y.; Jia, H. Understanding the sorption behaviors of heavy metal ions in the interlayer and nanopore of montmorillonite: A molecular dynamics study. J. Hazard. Mater. 2021, 416, 125976. [Google Scholar] [PubMed]
- Zhang, W.; Li, J.S.; Chen, S.X.; Huang, K.; Luo, L.J.; Tong, K.W.; Guo, J.H.; Li, S.C.; Zhang, R.; Dai, Z.J. Effect of layer charge density and cation concentration on sorption behaviors of heavy metal ions in the interlayer and nanopore of montmorillonite: A molecular dynamics simulation. Colloids Surf. A-Physicochem. Eng. Asp. 2023, 657, 130553. [Google Scholar]
- You, M.; Yin, X.; Sun, Y.; Wu, H.; Li, J.; Zhou, X. Hydrated Calcium Silicate Erosion in Sulfate Environments a Molecular Dynamics Simulation Study. Materials 2024, 17, 6005. [Google Scholar] [CrossRef]
- Kumar, R.; Schmidt, J.R.; Skinner, J.L. Hydrogen bonding definitions and dynamics in liquid water. J. Chem. Phys. 2007, 126, 204107. [Google Scholar]
- Cao, Z.D.; Wu, Y.D.; Niu, M.S.; Li, Y.; Li, T.; Ren, B.Z. Exploring the solvent effect on risperidone (form I) crystal morphology: A combination of molecular dynamics simulation and experimental study. J. Mol. Liq. 2023, 376, 121358. [Google Scholar]
- Hou, D.; Xu, X.; Ge, Y.; Wang, P.; Chen, J.; Zhang, J. Molecular structure, dynamics and adsorption behavior of water molecules and ions on 010 surface of γ-FeOOH: A molecular dynamics approach. Constr. Build. Mater. 2019, 224, 785–795. [Google Scholar]
- Blickle, V.; Speck, T.; Lutz, C.; Seifert, U.; Bechinger, C. Einstein relation generalized to nonequilibrium. Phys. Rev. Lett. 2007, 98, 210601. [Google Scholar] [PubMed]
- Li, D.; Zhao, W.; Hou, D.; Zhao, T. Molecular dynamics study on the chemical bound, physical adsorbed and ultra-confined water molecules in the nano-pore of calcium silicate hydrate. Constr. Build. Mater. 2017, 151, 563–574. [Google Scholar]
- Tu, Y.; Yu, Q.; Wen, R.; Shi, P.; Yuan, L.; Ji, Y.; Sas, G.; Elfgren, L. Molecular dynamics simulation of coupled water and ion adsorption in the nano-pores of a realistic calcium-silicate-hydrate gel. Constr. Build. Mater. 2021, 299, 123961. [Google Scholar]
- Ghalami, Z.; Ghoulipour, V.; Khanchi, A. Highly efficient capturing and adsorption of cesium and strontium ions from aqueous solution by porous organic cage: A combined experimental and theoretical study. Appl. Surf. Sci. 2019, 471, 726–732. [Google Scholar]
- Yadav, S.; Chandra, A. Transport of hydrated nitrate and nitrite ions through graphene nanopores in aqueous medium. J. Comput. Chem. 2020, 41, 1850–1858. [Google Scholar]
- Zhu, F.; Zhou, H.; Fang, C.; Fang, Y.; Zhou, Y.; Liu, H. Ab Initio Investigation of the Microspecies and Energy in Hydrated Strontium Ion Clusters. Mol. Phys. 2018, 116, 273–282. [Google Scholar]
- Yadav, S.; Chandra, A. Preferential solvation, ion pairing, and dynamics of concentrated aqueous solutions of divalent metal nitrate salts. J. Chem. Phys. 2017, 147, 244503. [Google Scholar]
- Zhu, F.; Zhou, H.; Wang, X.; Zhou, Y.; Liu, H.; Fang, C.; Fang, Y. Raman spectroscopy and ab initio quantum chemical calculations of ion association behavior in calcium nitrate solution. J. Raman Spectrosc. 2018, 49, 852–861. [Google Scholar]
- Quezada, G.R.; Toledo, P.G. Complexation of Alkali and Alkaline-Earth Metal Cations at Spodumene-Saltwater Interfaces by Molecular Simulation: Impact on Oleate Adsorption. Minerals 2021, 11, 12. [Google Scholar]
- Wang, R.; Zhou, X.; Zhang, W.; Ye, J.; Wang, J. Transport mechanism of uranyl nitrate in nanopore of geopolymer with different Si/Al ratios: Molecular dynamics simulation. J. Solid State Chem. 2024, 331, 124542. [Google Scholar]
- Xu, W.-H.; Meng, Q.-Q.; Gao, C.; Wang, J.; Li, Q.-X.; Liu, J.-H.; Huang, X.-J. Investigation of the facet-dependent performance of α-Fe2O3 nanocrystals for heavy metal determination by stripping voltammetry. Chem. Commun. 2014, 50, 5011–5013. [Google Scholar]
- Yang, H.; Boucly, A.; Gabathuler, J.P.; Bartels-Rausch, T.; Artiglia, L.; Ammann, M. Ordered Hydrogen Bonding Structure of Water Molecules Adsorbed on Silver Iodide Particles under Subsaturated Conditions. J. Phys. Chem. C 2021, 125, 11628–11635. [Google Scholar]
- Liu, Y.; Yu, T.; Lai, W.; Ma, Y.; Kang, Y.; Ge, Z. Adsorption behavior of acetone solvent at the HMX crystal faces: A molecular dynamics study. J. Mol. Graph. Model. 2017, 74, 38–43. [Google Scholar]



| Model | a/Å | b/Å | c/Å | α/(deg) | β/(deg) | γ/(deg) | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| (100) | 44.46 | 42.78 | 74.65 | 90.00 | 90.00 | 90.00 | 2080 | 2600 | 28 | 56 | 208 |
| (110) | 42.78 | 41.47 | 76.11 | 90.00 | 90.00 | 90.00 | 2016 | 2600 | 28 | 56 | 224 |
| (111) | 44.91 | 41.47 | 73.06 | 90.00 | 90.00 | 90.00 | 1904 | 2600 | 28 | 56 | 224 |
| Interface | (100) | (110) | (111) |
|---|---|---|---|
| The number of hydrogen bonds (0 ps) | 0 | 0 | 0 |
| The number of hydrogen bonds (6000 ps) | 322 | 204 | 241 |
| MnO | (100) | (110) | (111) |
|---|---|---|---|
| Eint (kcal/mol) | −4257.04 | −2474.91 | −3181.38 |
| Eelec (kcal/mol) | −4112.27 | −1729.95 | −2521.50 |
| Evdw (kcal/mol) | −144.77 | −744.96 | −659.88 |
| MnO | (100) | (110) | (111) |
|---|---|---|---|
| H2O (1 × 10−5 cm2/s) | 2.77 | 2.70 | 2.78 |
| Sr2+ (1 × 10−5 cm2/s) | 0.34 | 0.33 | 0.18 |
| NO3− (1 × 10−5 cm2/s) | 0.61 | 0.88 | 0.46 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xiang, Q.; Yu, X.; Guo, K.; Cheng, C.; Yue, X.; Wang, J.; Liu, Y. Understanding the Adsorption Behavior of Different Crystal Surfaces of Manganese Monoxide to Strontium Nitrate Solutions: A Molecular Dynamics Simulation. Materials 2025, 18, 1752. https://doi.org/10.3390/ma18081752
Xiang Q, Yu X, Guo K, Cheng C, Yue X, Wang J, Liu Y. Understanding the Adsorption Behavior of Different Crystal Surfaces of Manganese Monoxide to Strontium Nitrate Solutions: A Molecular Dynamics Simulation. Materials. 2025; 18(8):1752. https://doi.org/10.3390/ma18081752
Chicago/Turabian StyleXiang, Qingwei, Xingyu Yu, Kuixiang Guo, Chufeng Cheng, Xixiang Yue, Jingsong Wang, and Yaochi Liu. 2025. "Understanding the Adsorption Behavior of Different Crystal Surfaces of Manganese Monoxide to Strontium Nitrate Solutions: A Molecular Dynamics Simulation" Materials 18, no. 8: 1752. https://doi.org/10.3390/ma18081752
APA StyleXiang, Q., Yu, X., Guo, K., Cheng, C., Yue, X., Wang, J., & Liu, Y. (2025). Understanding the Adsorption Behavior of Different Crystal Surfaces of Manganese Monoxide to Strontium Nitrate Solutions: A Molecular Dynamics Simulation. Materials, 18(8), 1752. https://doi.org/10.3390/ma18081752






