Effects of S Doping and Oxygen Vacancy on the Physical Properties of Rutile TiO2 for Photocatalysis Applications Based on Density Functional Theory Study
Abstract
1. Introduction
2. Computational Details
3. Results and Discussion
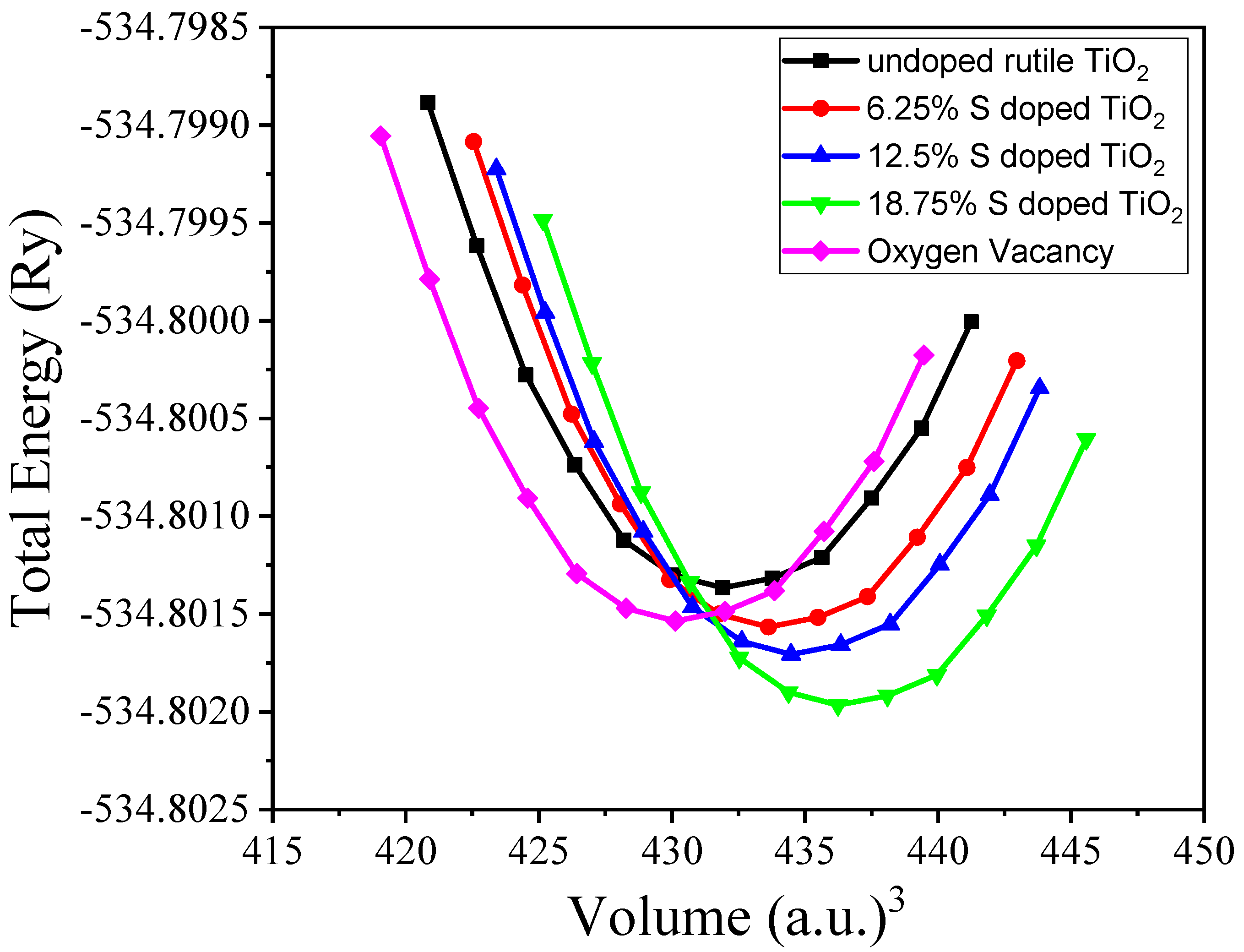
3.1. Structural Properties
| Materials | Lattice Constant (Å) | Vol. (Å)3 | Bond Angle (Å) | Bond Length (°) | |
|---|---|---|---|---|---|
| a = b | c | ||||
| Undoped rutile TiO2 | 4.63 | 2.98 | 63.7 | Ti-O = 1.9518 Ti-O = 1.9796 | Ti-O-Ti = 90 |
| Expt. work [29] | 4.61 | 2.96 | 62.91 | Ti-O = 1.9500 Ti-O = 1.9800 | -- |
| Other DFT [17,30] | 4.68 | 2.98 | -- | Ti-O = 1.961 | -- |
| 6.25% S doped | 4.89 | 3.27 | 73.3 | Ti-S = 2.0080 Ti-S = 2.1050 | Ti-S-Ti = 106.6 |
| 12.5% S doped | 5.14 | 3.69 | 80.4 | Ti-S = 2.0497 Ti-S = 2.4021 | Ti-S-Ti = 113.2 |
| 18.75% S doped | 5.31 | 3.82 | 93.3 | Ti-S = 2.0551 Ti-S = 2.6113 | Ti-S-Ti = 111.4 |
| OV | 4.17 | 2.82 | 53.8 | Ti-S = 1.5887 Ti-S = 1.8430 | Ti-O-Ti = 87.9 |
| Sources | V0 | B0 (GPa) | dB0 |
|---|---|---|---|
| Present work | 63.7 | 229.5 | 4.04 |
| Exp. work [34] | 62.5 | 212 | 6.3 |
| Other DFT [35] | 64.03 | 235 | 4.64 |
| 6.25% S doped | 64.4 | 231.3 | 5.69 |
| 12.5% S doped | 64.6 | 301.9 | 5.81 |
| 18.75% S doped | 65.2 | 305.2 | 5.90 |
| OV | 62.4 | 207.6 | 3.15 |
3.2. Electronic Properties
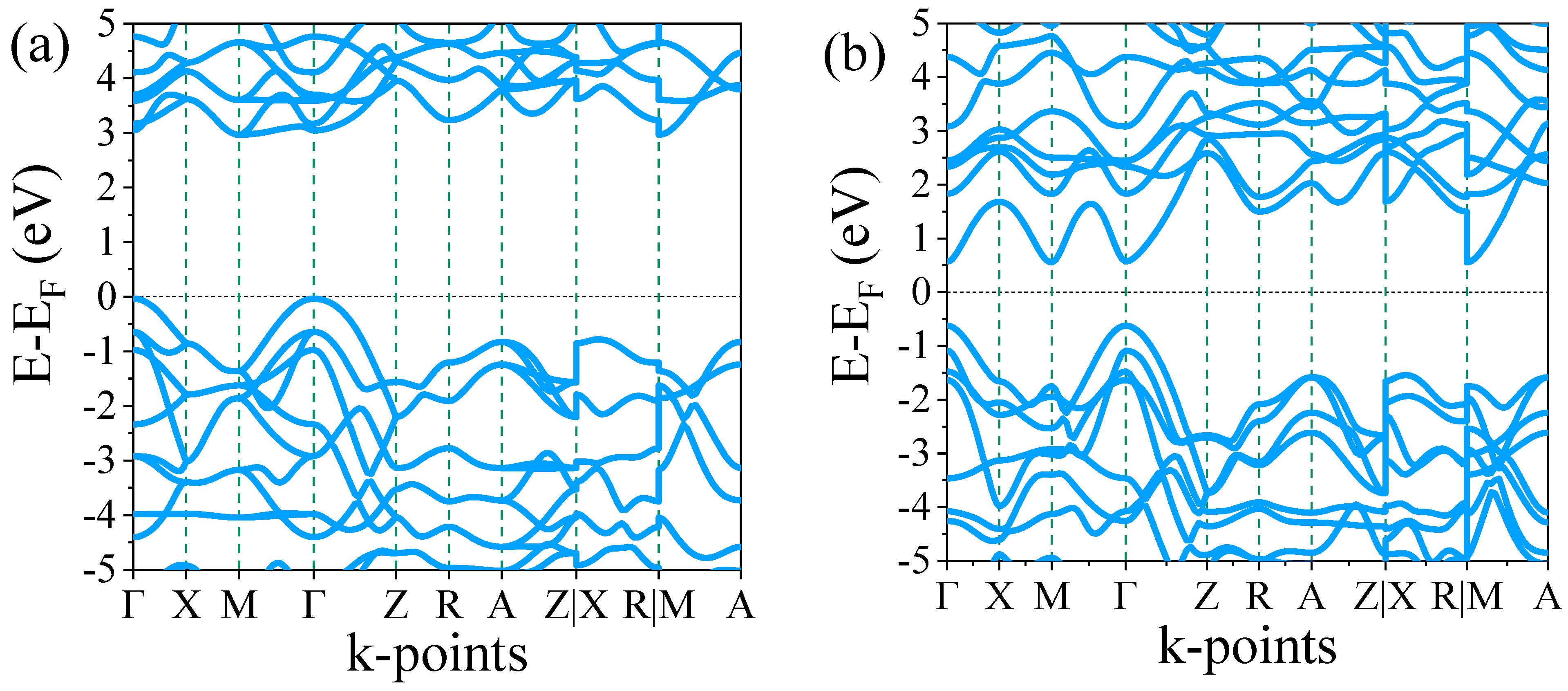
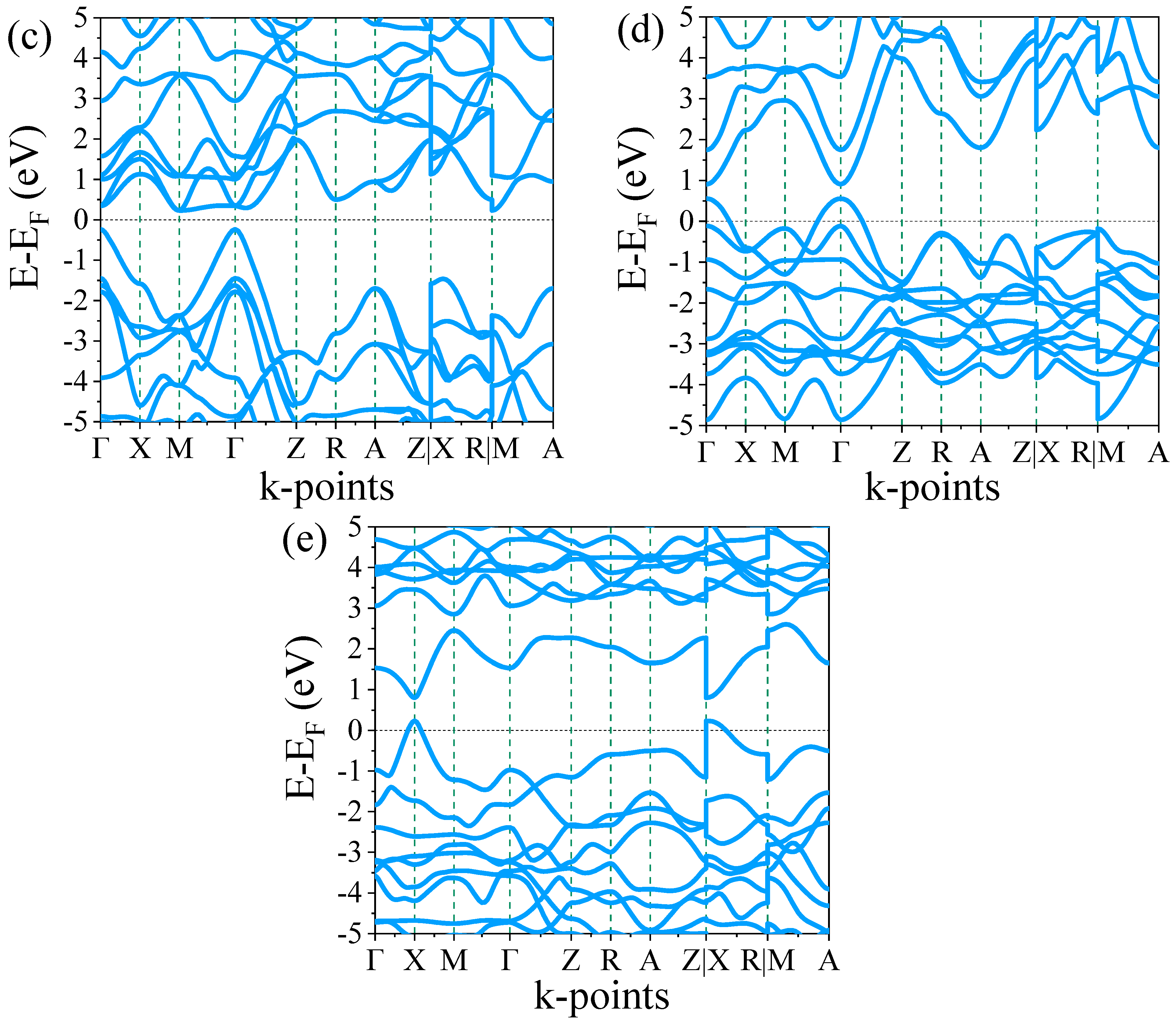
3.2.1. Band Structures
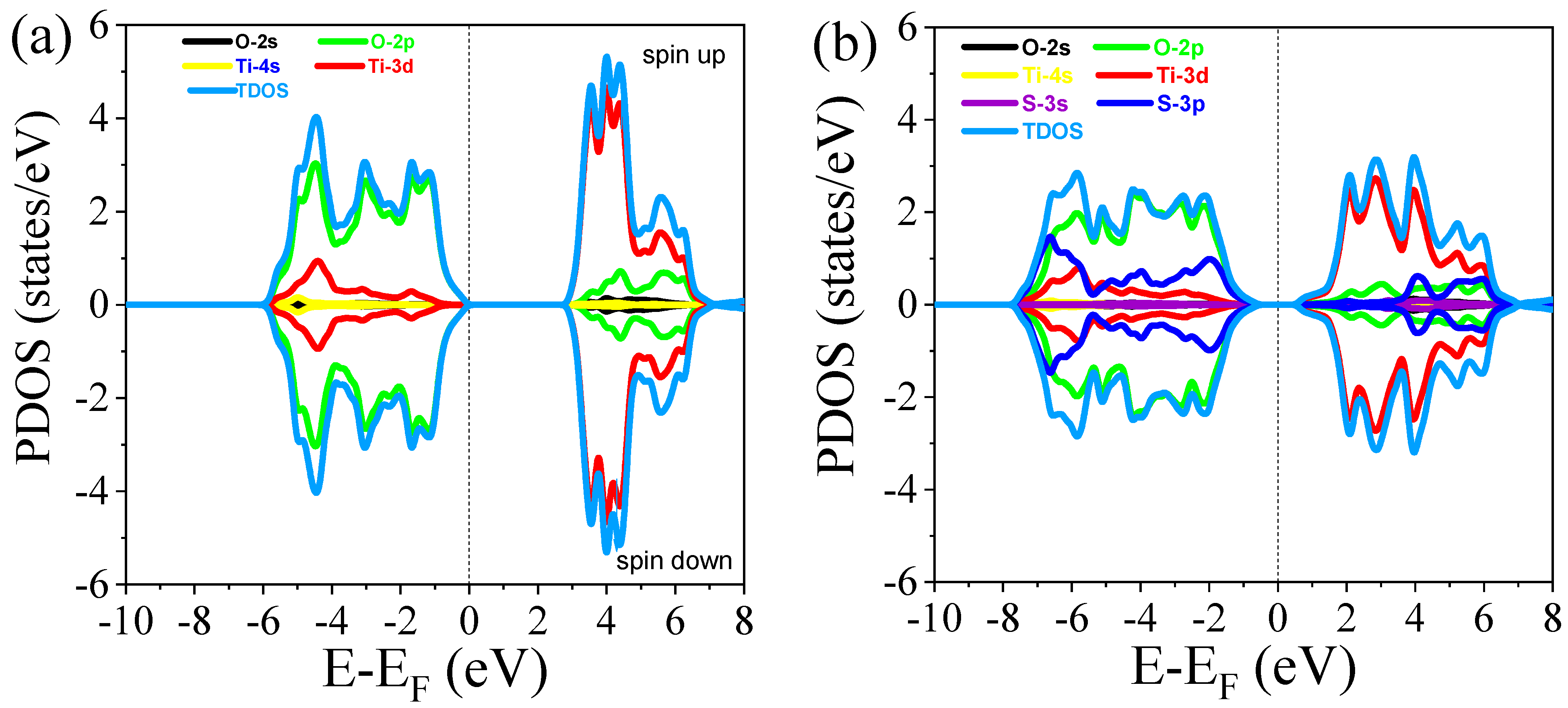
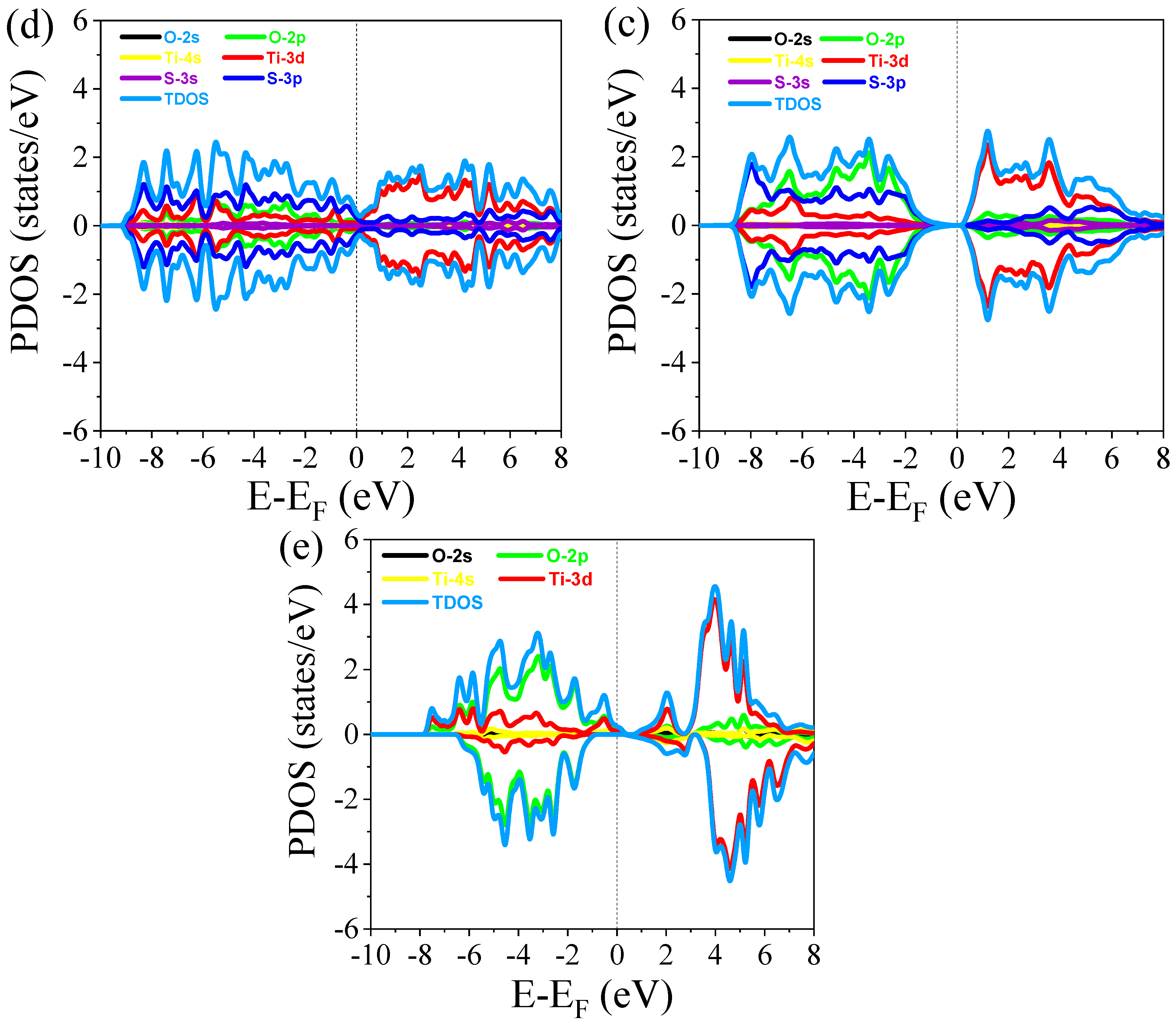
3.2.2. Density of States
3.3. Mechanical Properties
3.4. Optical Properties
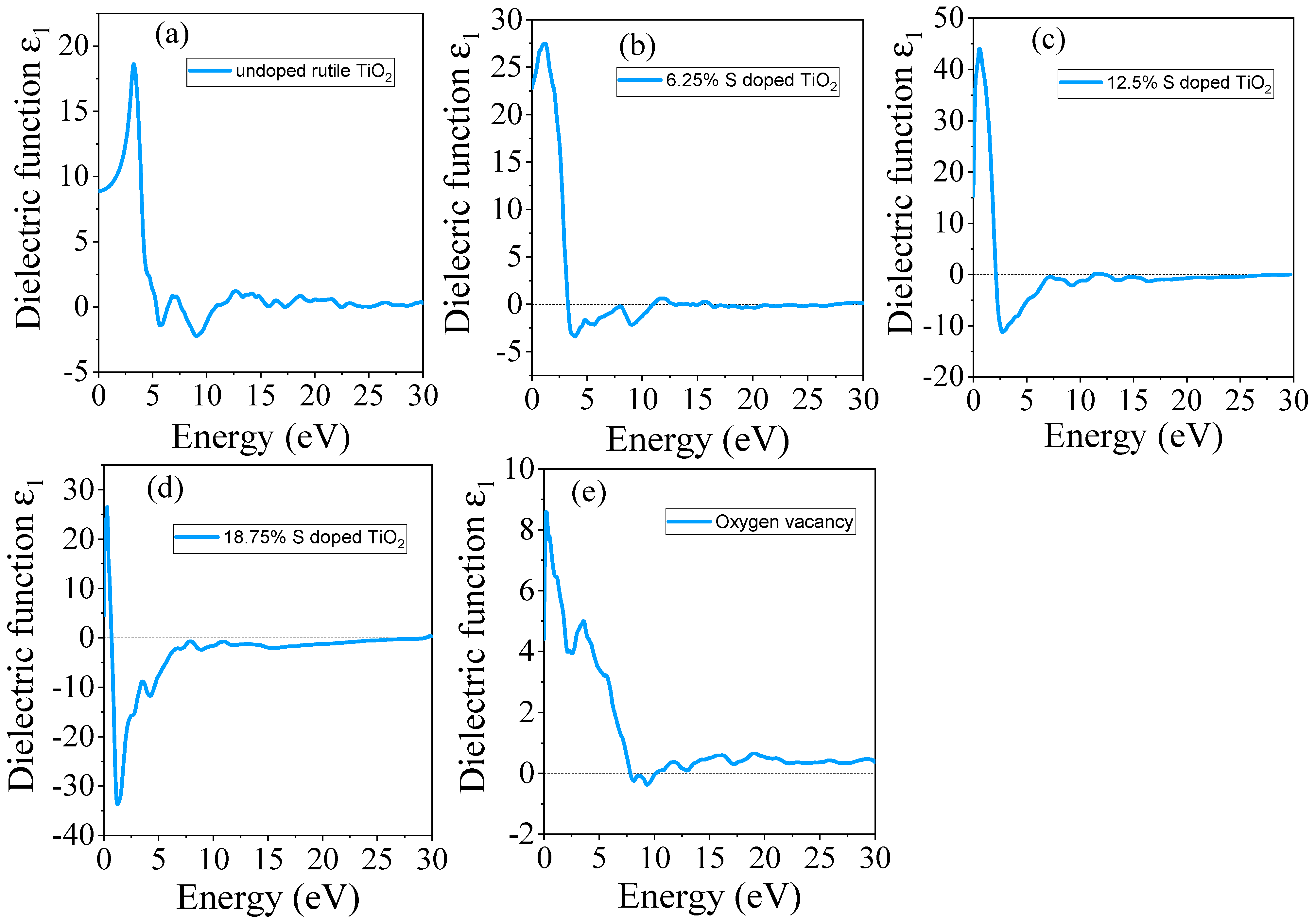
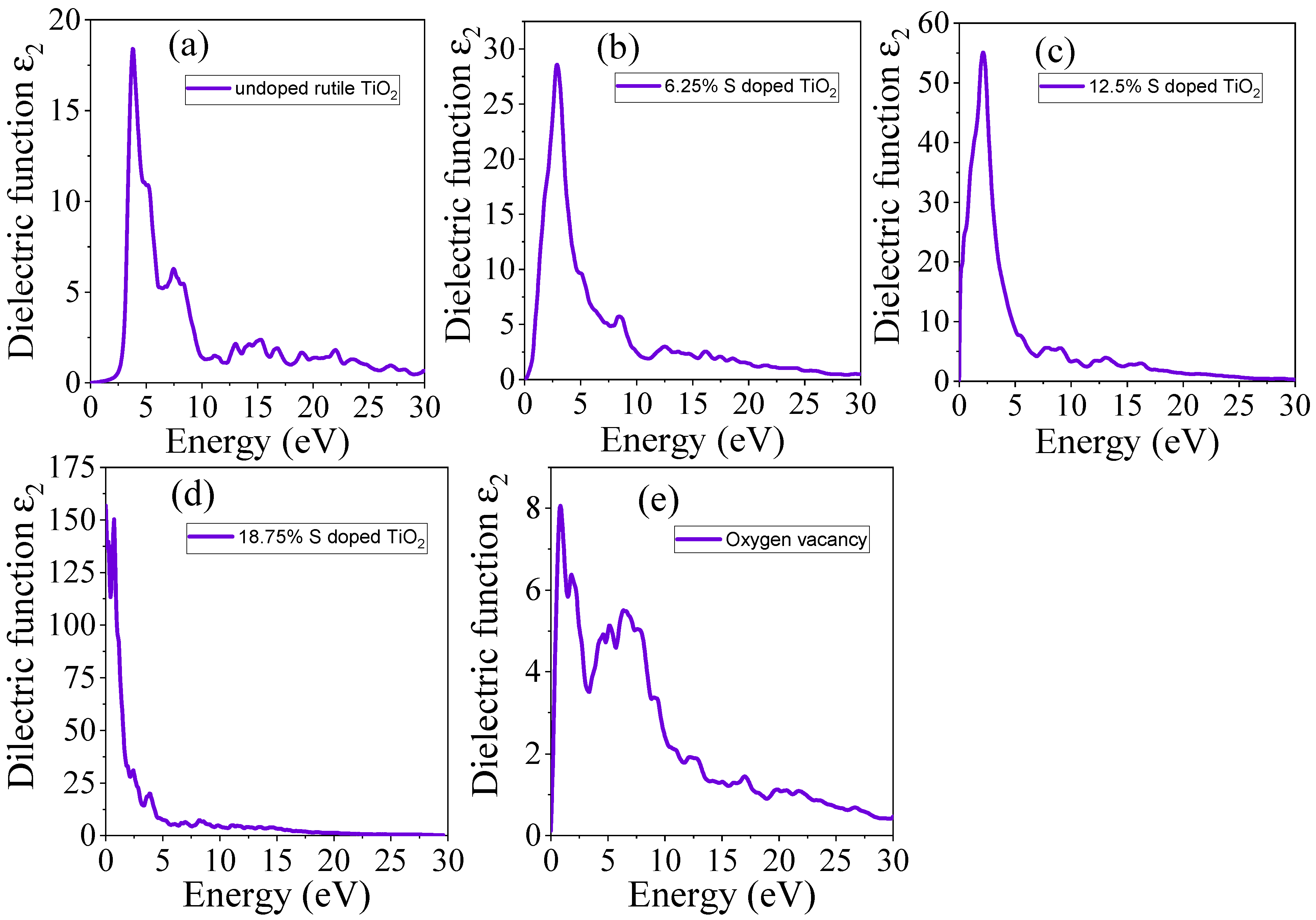
3.4.1. Real Part of Dielectric
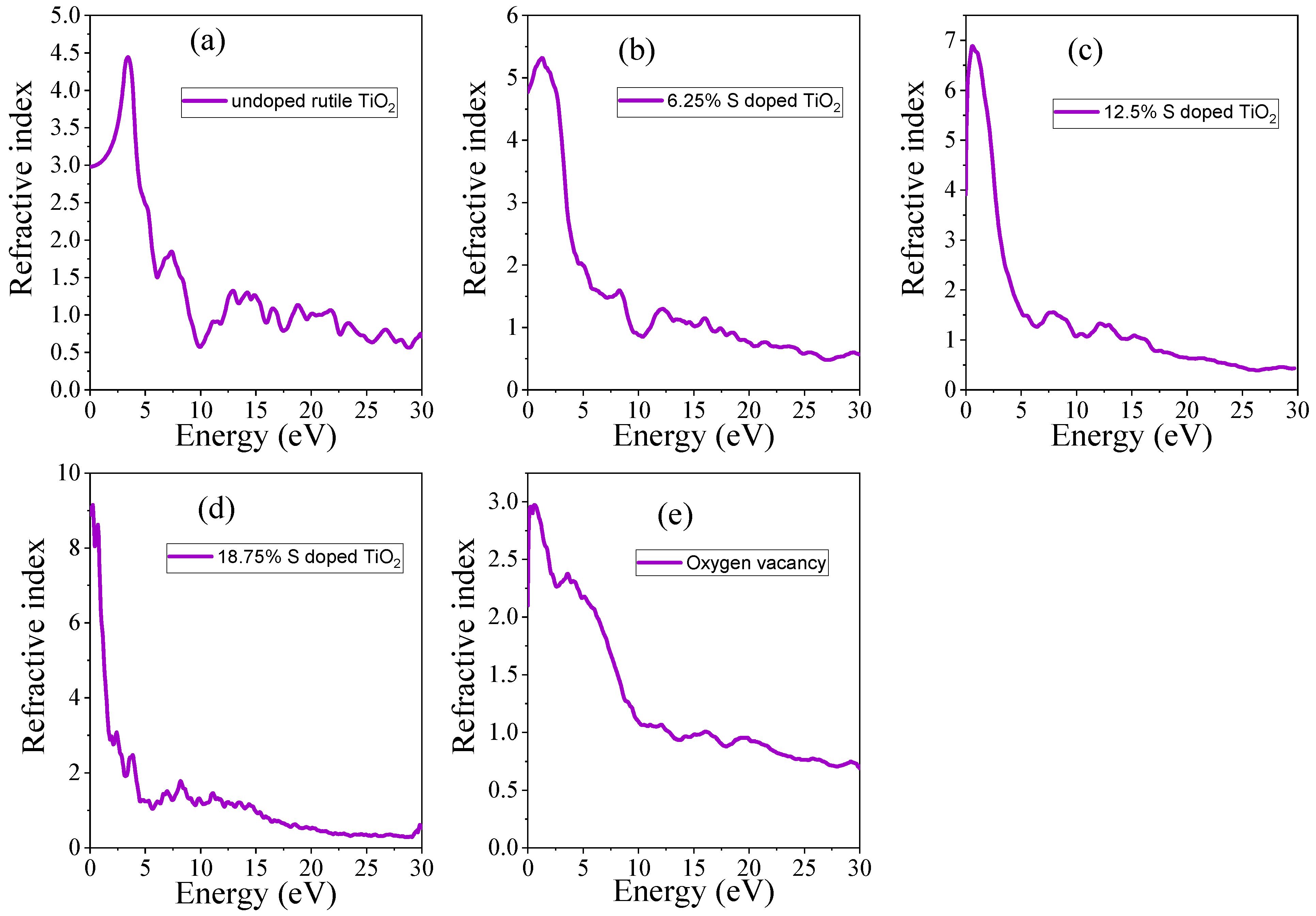
3.4.2. Refractive Index
3.4.3. Absorption Coefficient
3.4.4. Reflectance
3.4.5. Electron Energy Loss Spectrum (EELS)
3.4.6. Optical Conductivity
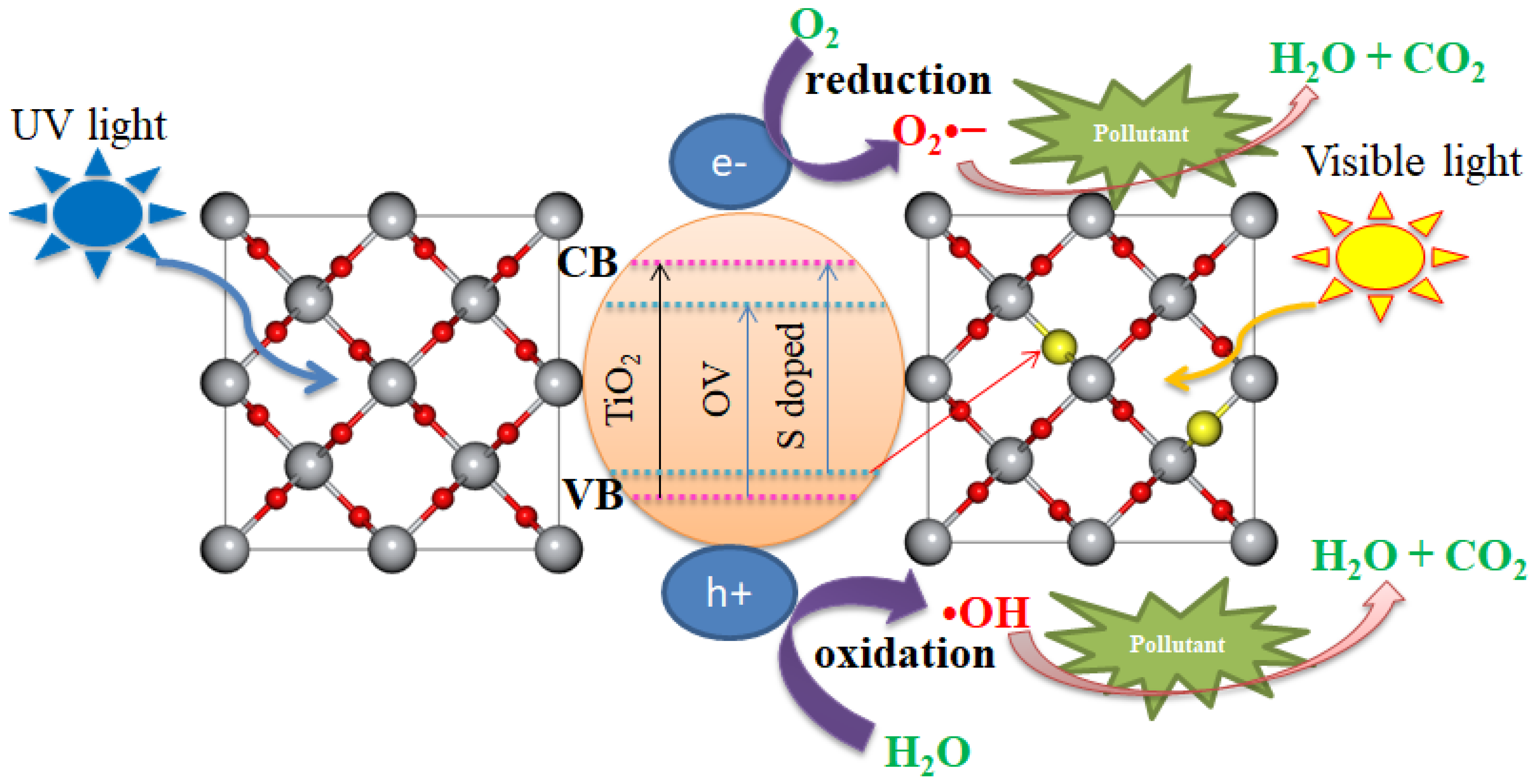
3.5. Photocatalytic Mechanisms
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Cravanzola, S.; Cesano, F.; Gaziano, F.; Scarano, D. Sulfur-doped TiO2: Structure and surface properties. Catalysts 2017, 7, 214. [Google Scholar] [CrossRef]
- Portillo-Vélez, N.S.; Olvera-Neria, O.; Hernández-Pérez, I.; Rubio-Ponce, A. Localized electronic states induced by oxygen vacancies on anatase TiO2 (101) surface. Surf. Sci. 2013, 616, 115–119. [Google Scholar] [CrossRef]
- Zhou, H.; Wang, H.; Yue, C.; He, L.; Li, H.; Zhang, H.; Yang, S.; Ma, T. Photocatalytic degradation by TiO2-conjugated/coordination polymer heterojunction: Preparation, mechanisms, and prospects. Appl. Catal. B Environ. 2024, 344, 123605. [Google Scholar] [CrossRef]
- Geldasa, F.T.; Kebede, M.A.; Shura, M.W.; Hone, F.G. Experimental and computational study of metal oxide nanoparticles for the photocatalytic degradation of organic pollutants: A review. RSC Adv. 2023, 13, 18404–18442. [Google Scholar] [CrossRef] [PubMed]
- Chakravorty, A.; Roy, S. A review of photocatalysis, basic principles, processes, and materials. Sustain. Chem. Environ. 2024, 8, 100155. [Google Scholar] [CrossRef]
- Manzoli, M.; Freyria, F.S.; Blangetti, N.; Bonelli, B. Brookite, a sometimes under evaluated TiO2 polymorph. RSC Adv. 2022, 12, 3322–3334. [Google Scholar] [CrossRef]
- Eddy, D.R.; Permana, M.D.; Sakti, L.K.; Sheha, G.A.N.; Solihudin, G.A.N.; Hidayat, S.; Takei, T.; Kumada, N.; Rahayu, I. Heterophase Polymorph of TiO2 (Anatase, Rutile, Brookite, TiO2(B)) for Efficient Photocatalyst: Fabrication and Activity. Nanomaterials 2023, 13, 704. [Google Scholar] [CrossRef]
- Etafa Tasisa, Y.; Kumar Sarma, T.; Krishnaraj, R.; Sarma, S. Band gap engineering of titanium dioxide (TiO2) nanoparticles prepared via green route and its visible light driven for environmental remediation. Results Chem. 2024, 11, 101850. [Google Scholar] [CrossRef]
- Diao, W.; Xu, J.; Rao, X.; Zhang, Y. Facile Synthesis of Fluorine Doped Rutile TiO2 Nanorod Arrays for Photocatalytic Removal of Formaldehyde. Catal. Letters 2022, 152, 1029–1039. [Google Scholar] [CrossRef]
- Negi, C.; Kandwal, P.; Rawat, J.; Sharma, M.; Sharma, H.; Dalapati, G.; Dwivedi, C. Carbon-doped titanium dioxide nanoparticles for visible light driven photocatalytic activity. Appl. Surf. Sci. 2021, 554, 149553. [Google Scholar] [CrossRef]
- Arunmetha, S.; Dhineshbabu, N.R.; Kumar, A.; Jayavel, R. Preparation of sulfur doped TiO2 nanoparticles from rutile sand and their performance testing in hybrid solar cells. J. Mater. Sci. Mater. Electron. 2021, 32, 28382–28393. [Google Scholar] [CrossRef]
- Mizukoshi, Y.; Ohtsu, N.; Semboshi, S.; Masahashi, N. Visible light responses of sulfur-doped rutile titanium dioxide photocatalysts fabricated by anodic oxidation. Appl. Catal. B Environ. 2009, 91, 152–156. [Google Scholar] [CrossRef]
- Chen, H.; Li, X.; Wan, R.; Kao-Walter, S.; Lei, Y. A DFT study of the electronic structures and optical properties of (Cr, C) co-doped rutile TiO2. Chem. Phys. 2018, 501, 60–67. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, X.; Li, L.; Wu, Y. A theoretical study on the electronic state distribution of Boron/Yttrium single doped or co-doped titanium dioxide based on first principles. Mater. Lett. 2022, 307, 131000. [Google Scholar] [CrossRef]
- Gul, S.R.; Khan, M.; Yi, Z.; Wu, B. DFT Insights into the role of relative positions of Fe and N dopants on the structure and properties of TiO2. Materials 2018, 11, 313. [Google Scholar] [CrossRef]
- Heffner, H.; Faccio, R.; López-Corral, I. Electronic structure properties of boron–doped and carbon–boron–codoped TiO2(B) for photocatalytic applications. J. Phys. Chem. Solids 2022, 165, 110685. [Google Scholar] [CrossRef]
- Chen, H.; Li, X.; Wan, R.; Kao-Walter, S.; Lei, Y.; Leng, C. A DFT study on modification mechanism of (N,S) interstitial co-doped rutile TiO2. Chem. Phys. Lett. 2018, 695, 8–18. [Google Scholar] [CrossRef]
- Elahifard, M.; Sadrian, M.R.; Mirzanejad, A.; Behjatmanesh-Ardakani, R.; Ahmadvand, S. Dispersion of defects in TiO2 semiconductor: Oxygen vacancies in the bulk and surface of rutile and anatase. Catalysts 2020, 10, 397. [Google Scholar] [CrossRef]
- Linh, N.H.; Nguyen, T.Q.; Diño, W.A.; Kasai, H. Effect of oxygen vacancy on the adsorption of O2 on anatase TiO2(001): A DFT-based study. Surf. Sci. 2015, 633, 38–45. [Google Scholar] [CrossRef]
- Hinuma, Y.; Toyao, T.; Kamachi, T.; Maeno, Z.; Takakusagi, S.; Furukawa, S.; Takigawa, I.; Shimizu, K.I. Density Functional Theory Calculations of Oxygen Vacancy Formation and Subsequent Molecular Adsorption on Oxide Surfaces. J. Phys. Chem. C 2018, 122, 29435–29444. [Google Scholar] [CrossRef]
- Panta, R.; Ruangpornvisuti, V. Unusual adsorption behavior of hydrogen molecules on Zr–doped perfect and oxygen–vacancy defective rutile TiO2(110) surfaces: Periodic DFT study. Int. J. Hydrogen Energy 2019, 44, 32101–32111. [Google Scholar] [CrossRef]
- Giannozzi, P.; Andreussi, O.; Brumme, T.; Bunau, O.; Buongiorno Nardelli, M.; Calandra, M.; Car, R.; Cavazzoni, C.; Ceresoli, D.; Cococcioni, M.; et al. Advanced capabilities for materials modelling with Quantum ESPRESSO. J. Phys. Condens. Matter 2017, 29, 465901. [Google Scholar] [CrossRef]
- Meagher, E.P.; Lager, G.A. Polyhedral thermal expansion in the TiO2 polymorphs; refinement of the crystal structures of rutile and brookite at high temperature. Can. Miner. 1979, 17, 77–85. [Google Scholar]
- Kokalj, A. XCrySDen-a new program for displaying crystalline structures and electron densities. J. Mol. Graph. Model. 1999, 17, 176–179. [Google Scholar] [CrossRef] [PubMed]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef]
- Momma, K.; Izumi, F. VESTA 3 for three-dimensional visualization of crystal, volumetric and morphology data. J. Appl. Crystallogr. 2011, 44, 1272–1276. [Google Scholar] [CrossRef]
- Geldasa, F.T.; Kebede, M.A.; Shura, M.W.; Hone, F.G. Density functional theory study of different metal dopants influence on the structural and electronic properties of a tetragonal α-PbO. AIP Adv. 2022, 12, 115302. [Google Scholar] [CrossRef]
- Natarajan, T.S.; Mozhiarasi, V.; Tayade, R.J. Nitrogen Doped Titanium Dioxide (N-TiO2): Synopsis of Synthesis Methodologies, Doping Mechanisms, Property Evaluation and Visible Light Photocatalytic Applications. Photochem 2021, 1, 371–410. [Google Scholar] [CrossRef]
- Zhang, J.; Zhou, P.; Liu, J.; Yu, J. New understanding of the difference of photocatalytic activity among anatase, rutile and brookite TiO2. Phys. Chem. Chem. Phys. 2014, 16, 20382–20386. [Google Scholar] [CrossRef]
- Kesong, Y.; Ying, D.; Baibiao, H.; Shenghao, H. Theoretical study of N-doped TiO2 rutile crystals. J. Phys. Chem. B 2006, 110, 24011–24014. [Google Scholar] [CrossRef]
- Murnaghan, F.D. The compressibility of media under extreme pressures. J. Franklin Inst. 1924, 197, 98. [Google Scholar] [CrossRef]
- Geldasa, F.T.; Dejene, F.B.; Kebede, M.A.; Hone, F.G.; Jira, E.T. Density functional theory study of Chlorine, Fluorine, Nitrogen, and Sulfur doped rutile TiO2 for photocatalytic application. Sci. Rep. 2025, 15, 3390. [Google Scholar] [CrossRef]
- Emery, A.A.; Wolverton, C. High-throughput DFT calculations of formation energy, stability and oxygen vacancy formation energy of ABO3 perovskites. Sci. Data 2017, 4, 170153. [Google Scholar] [CrossRef]
- Isaak, D.G.; Carnes, J.D.; Anderson, O.L.; Cynn, H.; Hake, E. Elasticity of TiO2 rutile to 1800 K. Phys. Chem. Miner. 1998, 26, 31–43. [Google Scholar] [CrossRef]
- Iuga, M.; Steinle-Neumann, G.; Meinhardt, J. Ab-initio simulation of elastic constants for some ceramic materials. Eur. Phys. J. B 2007, 58, 127–133. [Google Scholar] [CrossRef]
- Kim, S.Y.; Saqlain, S.; Cha, B.J.; Zhao, S.; Seo, H.O.; Kim, Y.D. Annealing temperature-dependent effects of fe-loading on the visible light-driven photocatalytic activity of rutile TiO2 nanoparticles and their applicability for air purification. Catalysts 2020, 10, 739. [Google Scholar] [CrossRef]
- Shah, W.H.; Alam, A.; Javed, H.; Rashid, K.; Ali, A.; Ali, L.; Safeen, A.; Ali, M.R.; Imran, N.; Sohail, M.; et al. Tuning of the band gap and dielectric loss factor by Mn doping of Zn1−xMnxO nanoparticles. Sci. Rep. 2023, 13, 8646. [Google Scholar] [CrossRef]
- Erikat, I.; Alkhabbas, M.; Hamad, B.; Alahmad, W. The Chalcogen (S, Se, and Te) Doping Effects on the Structural and Electronic Properties of Anatase (101) TiO2 Thin Surface Layers: DFT Study. Int. J. Photoenergy 2024, 2024, 3489162. [Google Scholar] [CrossRef]
- Li, Z.; Yang, H.; Zhang, D.; Zhou, W.; Gao, N.; Wang, J.; Yang, D. Effects of Bi and S co-doping on the enhanced photoelectric performance of ZnO: Theoretical and experimental investigations. J. Alloys Compd. 2021, 872, 159648. [Google Scholar] [CrossRef]
- Bentour, H.; El Yadari, M.; El Kenz, A.; Benyoussef, A. DFT study of electronic and optical properties of (S–Mn) co-doped SrTiO3 for enhanced photocatalytic hydrogen production. Solid State Commun. 2020, 312, 113893. [Google Scholar] [CrossRef]
- Guan, S.; Cheng, Y.; Hao, L.; Yoshida, H.; Tarashima, C.; Zhan, T.; Itoi, T.; Qiu, T.; Lu, Y. Oxygen vacancies induced band gap narrowing for efficient visible-light response in carbon-doped TiO2. Sci. Rep. 2023, 13, 14105. [Google Scholar] [CrossRef]
- Liu, Q.J.; Liu, Z.T.; Feng, L.P.; Tian, H. First-principles study of structural, elastic, electronic and optical properties of rutile GeO2 and α-quartz GeO2. Solid State Sci. 2010, 12, 1748–1755. [Google Scholar] [CrossRef]
- Mahmood, T.; Cao, C.; Khan, W.S.; Usman, Z.; Butt, F.K.; Hussain, S. Electronic, elastic, optical properties of rutile TiO2 under pressure: A DFT study. Phys. B Condens. Matter 2012, 407, 958–965. [Google Scholar] [CrossRef]
- Mouhat, F.; Coudert, F.X. Necessary and sufficient elastic stability conditions in various crystal systems. Phys. Rev. B-Condens. Matter Mater. Phys. 2014, 90, 224104. [Google Scholar] [CrossRef]
- Mahmood, T.; Malik, H.; Batool, R.; Perveen, Z.; Saleemi, F.; Rasheed, H.; Saeed, M.A.; Cao, C.; Rizwan, M. Elastic, electronic and optical properties of anatase TiO2 under pressure: A DFT approach. Chinese J. Phys. 2017, 55, 1252–1263. [Google Scholar] [CrossRef]
- Li, H.; Chen, Y.; Wang, H.; Wang, H.; Li, Y.; Harran, I.; Li, Y.; Guo, C. First-principles study of mechanical and thermodynamic properties of Ti-Ga intermetallic compounds. J. Alloys Compd. 2017, 700, 208–214. [Google Scholar] [CrossRef]
- Geldasa, F.T.; Kebede, M.A.; Shura, M.W.; Hone, F.G. Different metal dopants effects on the structural, electronic, and optical properties of β-PbO: A density functional theory study. Eur. Phys. J. Plus 2023, 138, 165. [Google Scholar]
- Soussi, A.; Ait Hssi, A.; Boujnah, M.; Boulkadat, L.; Abouabassi, K.; Asbayou, A.; Elfanaoui, A.; Markazi, R.; Ihlal, A.; Bouabid, K. Electronic and Optical Properties of TiO2 Thin Films: Combined Experimental and Theoretical Study. J. Electron. Mater. 2021, 50, 4497–4510. [Google Scholar] [CrossRef]
- Heiba, Z.K.; Mohamed, M.B.; Wahba, A.M. Structural, optical, mechanical, and electronic properties of Cr-doped alumina. J. Mater. Sci. Mater. Electron. 2020, 31, 14645–14657. [Google Scholar] [CrossRef]
- Samat, M.H.; Ali, A.M.M.; Taib, M.F.M.; Hassan, O.H.; Yahya, M.Z.A. Hubbard U calculations on optical properties of 3d transition metal oxide TiO2. Results Phys. 2016, 6, 891–896. [Google Scholar] [CrossRef]
- Geldasa, F.T. The structural, electronic, and optical properties of metals doped litharge PbO: A density functional theory study. Eur. Phys. J. B 2024, 97, 78. [Google Scholar] [CrossRef]
- Etacheri, V.; Di Valentin, C.; Schneider, J.; Bahnemann, D.; Pillai, S.C. Visible-light activation of TiO2 photocatalysts: Advances in theory and experiments. J. Photochem. Photobiol. C Photochem. Rev. 2015, 25, 1–29. [Google Scholar] [CrossRef]
- Du, S.; Lian, J.; Zhang, F. Visible Light-Responsive N-Doped TiO2 Photocatalysis: Synthesis, Characterizations, and Applications. Trans. Tianjin Univ. 2022, 28, 33–52. [Google Scholar] [CrossRef]
- Ma, H.Y.; Zhao, L.; Guo, L.H.; Zhang, H.; Chen, F.J.; Yu, W.C. Roles of reactive oxygen species (ROS) in the photocatalytic degradation of pentachlorophenol and its main toxic intermediates by TiO2/UV. J. Hazard. Mater. 2019, 369, 719–726. [Google Scholar] [CrossRef]

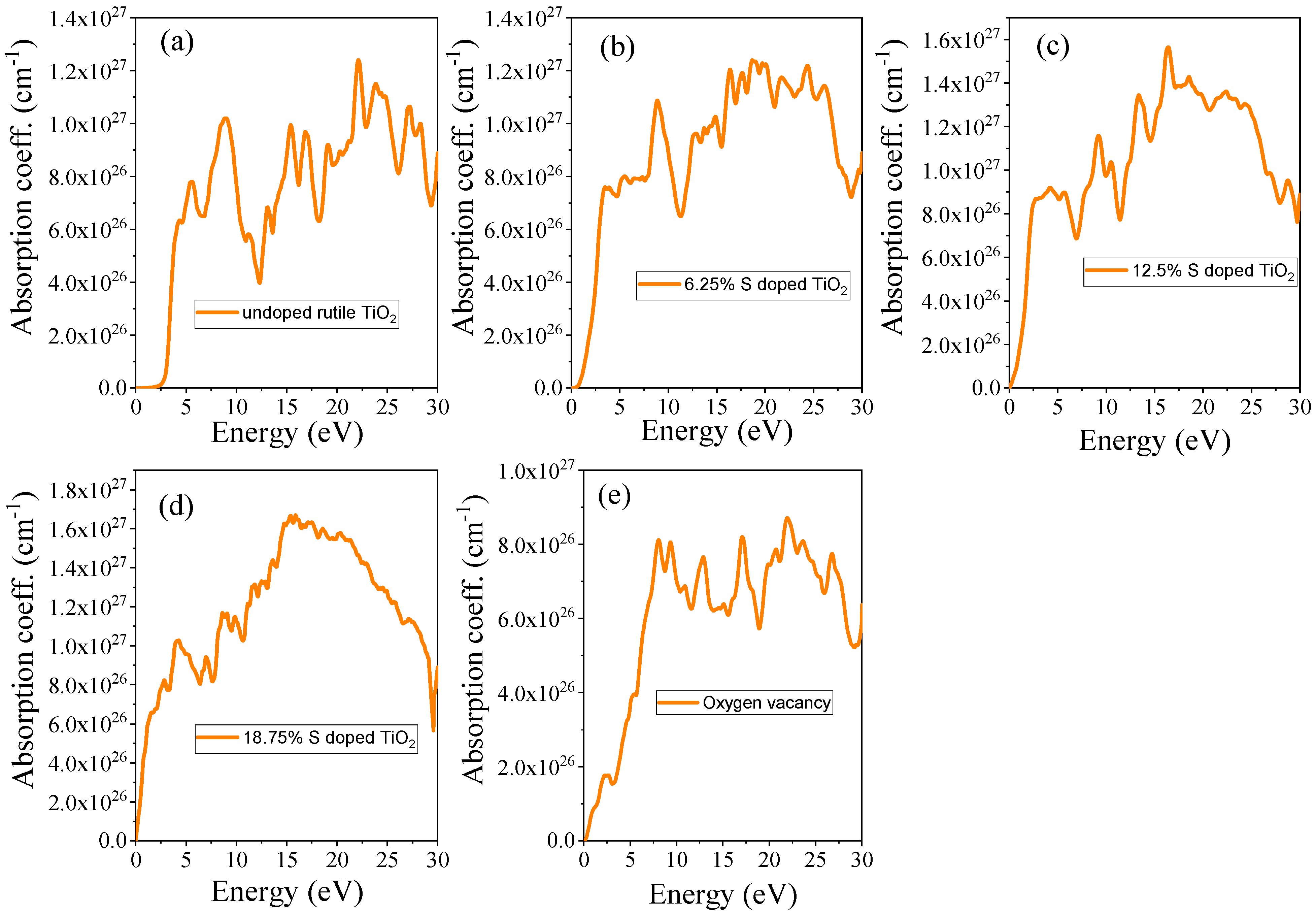
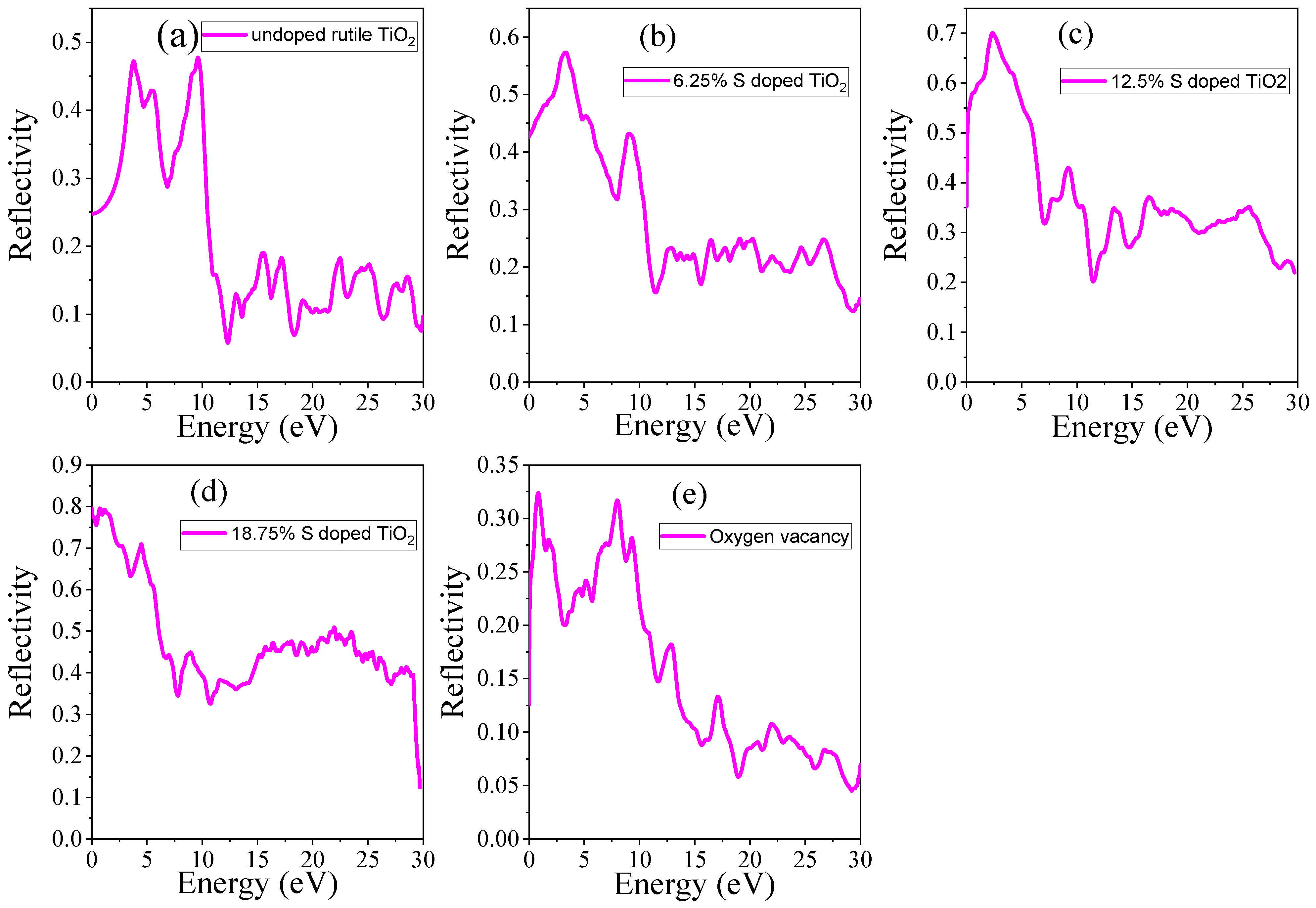
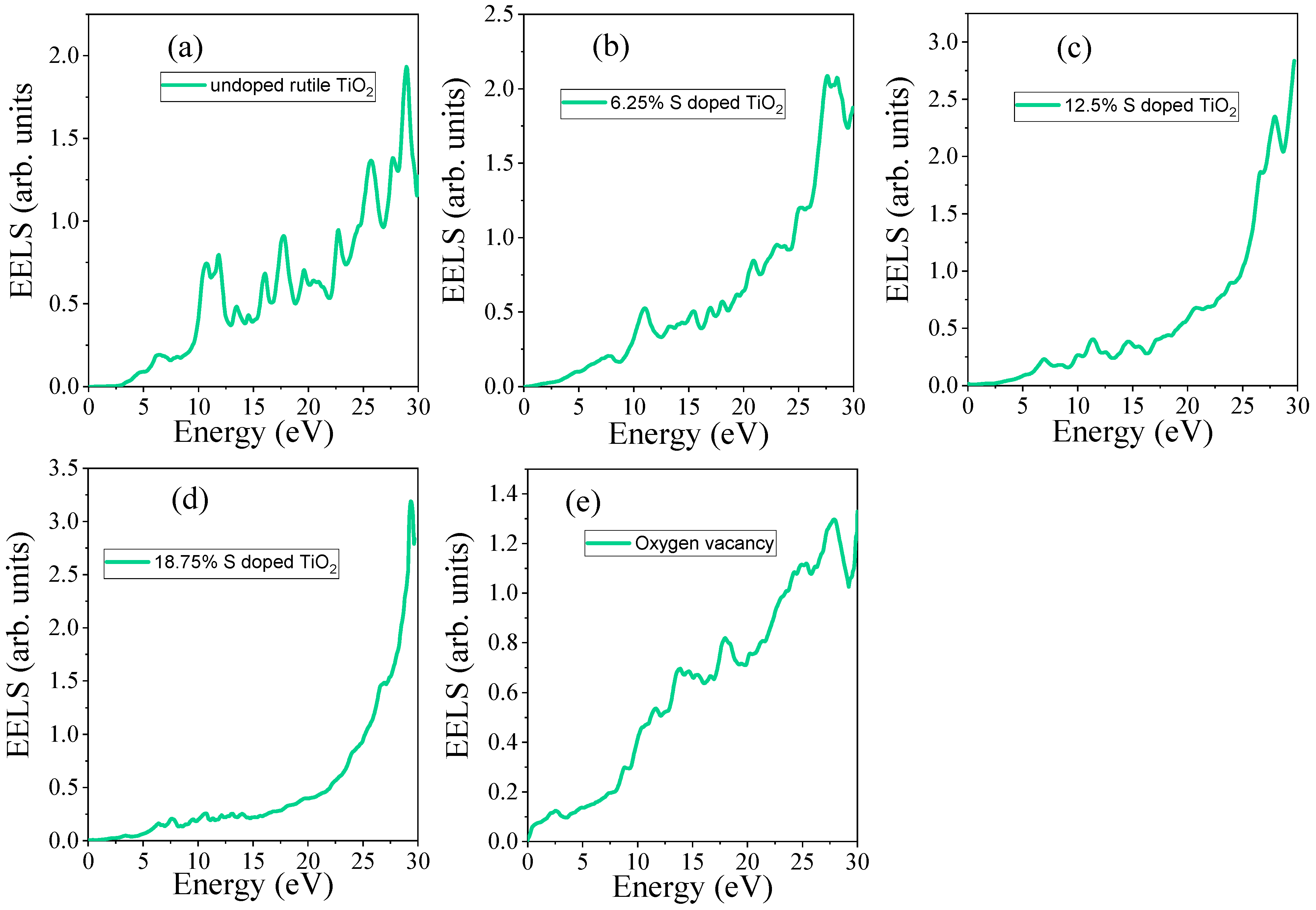
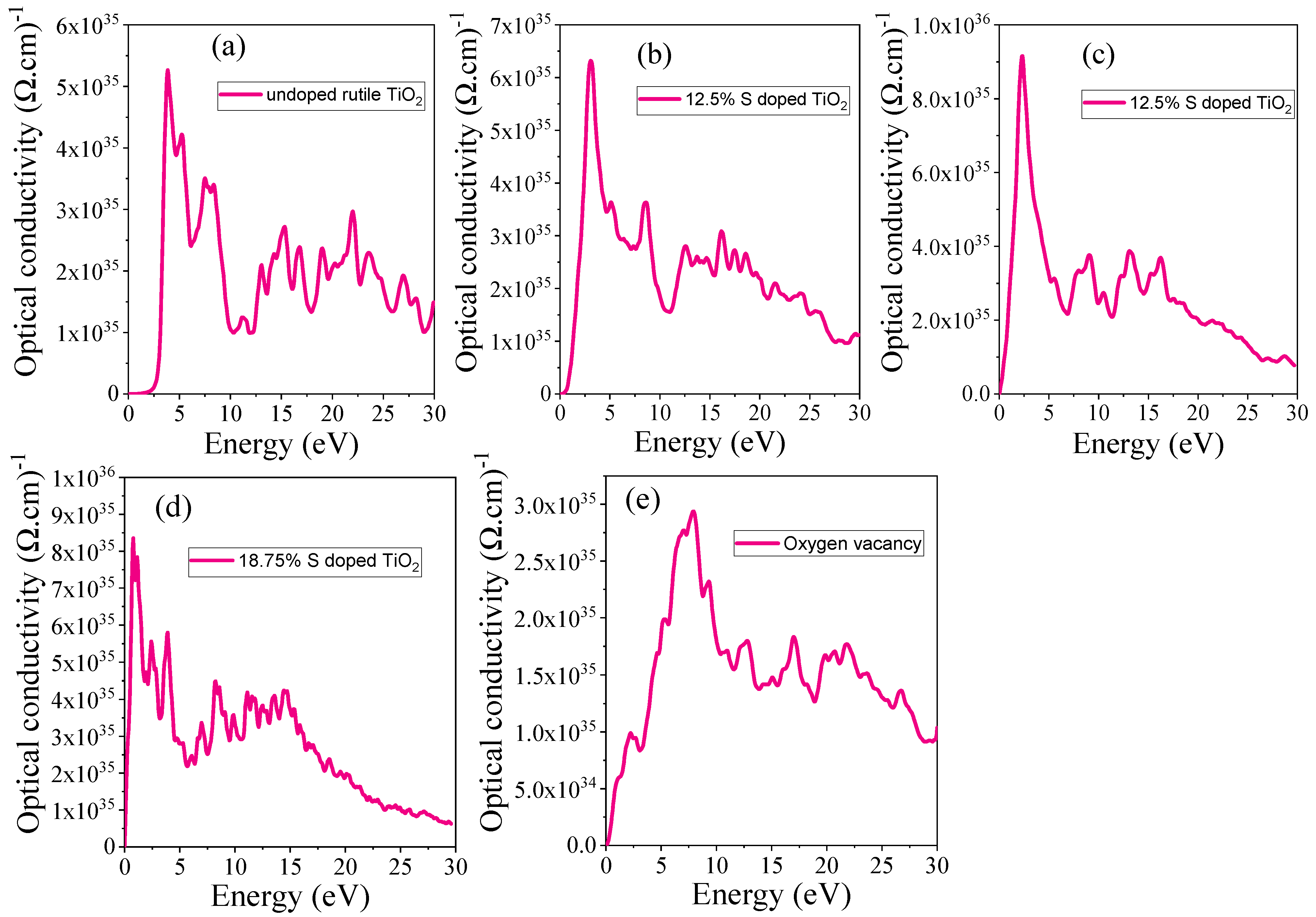
| Systems | S Doping at Ti Sites | S Doping at O Sites | 6.25% Doped TiO2 | 12.5% Doped TiO2 | 18.75 Doped TiO2 | OV |
|---|---|---|---|---|---|---|
| Formation energy (eV) | 2.73 | −3.07 | −4.59 | −3.07 | −1.54 | −1.68 |
| Materials | C11 | C12 | C13 | C33 | C44 | C66 | BH | Y | SH | n |
|---|---|---|---|---|---|---|---|---|---|---|
| Undoped TiO2 | 253.2 | 128.7 | 129.2 | 435.1 | 116.8 | 197.1 | 185.1 | 285.4 | 114.8 | 0.24 |
| Other DFT for TiO2 [43] | 271 | 143 | 144 | 465 | 124 | 188 | 208 | 303.6 | 111 | 0.25 |
| Exp. for TiO2 [34] | 268 | 175 | 147 | 484 | 124 | 190 | 212 | -- | 113 | -- |
| 6.25% doped | 266.4 | 243.3 | 159.9 | 303.1 | 365.1 | 271.4 | 199.3 | 298.4 | 119.3 | 0.27 |
| 12.5% doped | 273.2 | 245.6 | 167.4 | 324.1 | 369.2 | 283.7 | 301.9 | 319.5 | 120.6 | 0.32 |
| 18.75% doped | 291.3 | 253.2 | 174.6 | 341.7 | 374.4 | 286.3 | 305.2 | 314.3 | 118.3 | 0.53 |
| O-Vacancy | 119.0 | 111.4 | 117.9 | 176.0 | 109.2 | 115.3 | 157.1 | 254.1 | 103.3 | 0.46 |
| Materials | ||||||
|---|---|---|---|---|---|---|
| undoped TiO2 | 8.88 | 2.97 | 0.25 | 1.9 | 1.23 | 5.22 |
| 6.25% doped | 22.77 | 4.77 | 0.42 | 2.1 | 1.24 | 6.36 |
| 12.5% doped | 15.34 | 3.91 | 0.35 | 2.8 | 1.57 | 9.08 |
| 18.75% doped | 4.51 | 8.89 | 0.79 | 3.2 | 1.70 | 8.39 |
| Oxygen vacancy | 4.41 | 2.09 | 0.12 | 1.3 | 0.87 | 2.93 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Geldasa, F.T.; Dejene, F.B. Effects of S Doping and Oxygen Vacancy on the Physical Properties of Rutile TiO2 for Photocatalysis Applications Based on Density Functional Theory Study. Materials 2025, 18, 1688. https://doi.org/10.3390/ma18081688
Geldasa FT, Dejene FB. Effects of S Doping and Oxygen Vacancy on the Physical Properties of Rutile TiO2 for Photocatalysis Applications Based on Density Functional Theory Study. Materials. 2025; 18(8):1688. https://doi.org/10.3390/ma18081688
Chicago/Turabian StyleGeldasa, Fikadu Takele, and Francis Birhanu Dejene. 2025. "Effects of S Doping and Oxygen Vacancy on the Physical Properties of Rutile TiO2 for Photocatalysis Applications Based on Density Functional Theory Study" Materials 18, no. 8: 1688. https://doi.org/10.3390/ma18081688
APA StyleGeldasa, F. T., & Dejene, F. B. (2025). Effects of S Doping and Oxygen Vacancy on the Physical Properties of Rutile TiO2 for Photocatalysis Applications Based on Density Functional Theory Study. Materials, 18(8), 1688. https://doi.org/10.3390/ma18081688






