Design, Optimization, and Realization of a Magnetic Multi-Layer Quasi-Zero-Stiffness Isolation Platform Supporting Different Loads
Abstract
1. Introduction
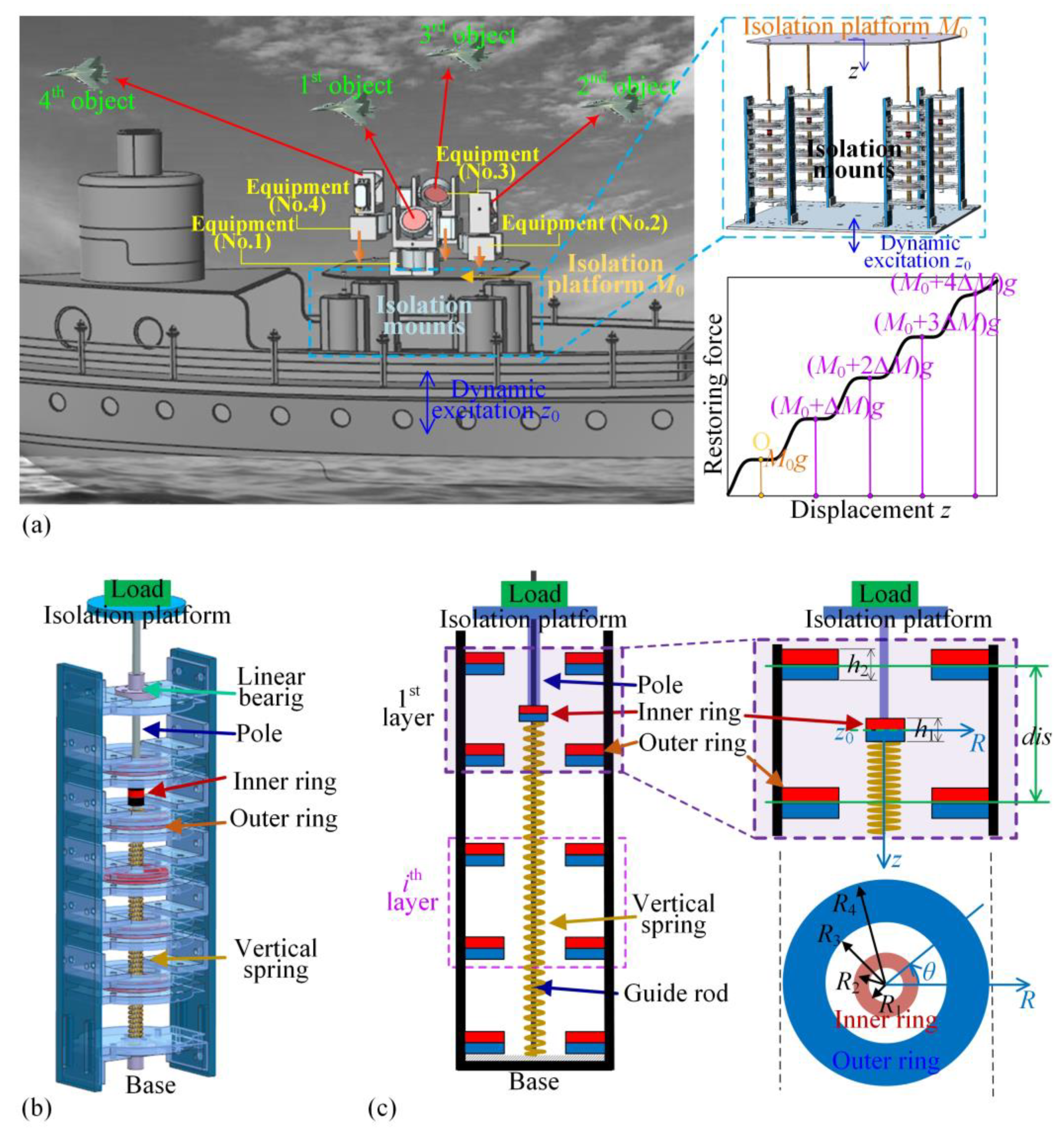
2. Design for ML-QZS Isolation Platform for Variable Loads
2.1. Design Method of the ML-QZS Isolation Mounts
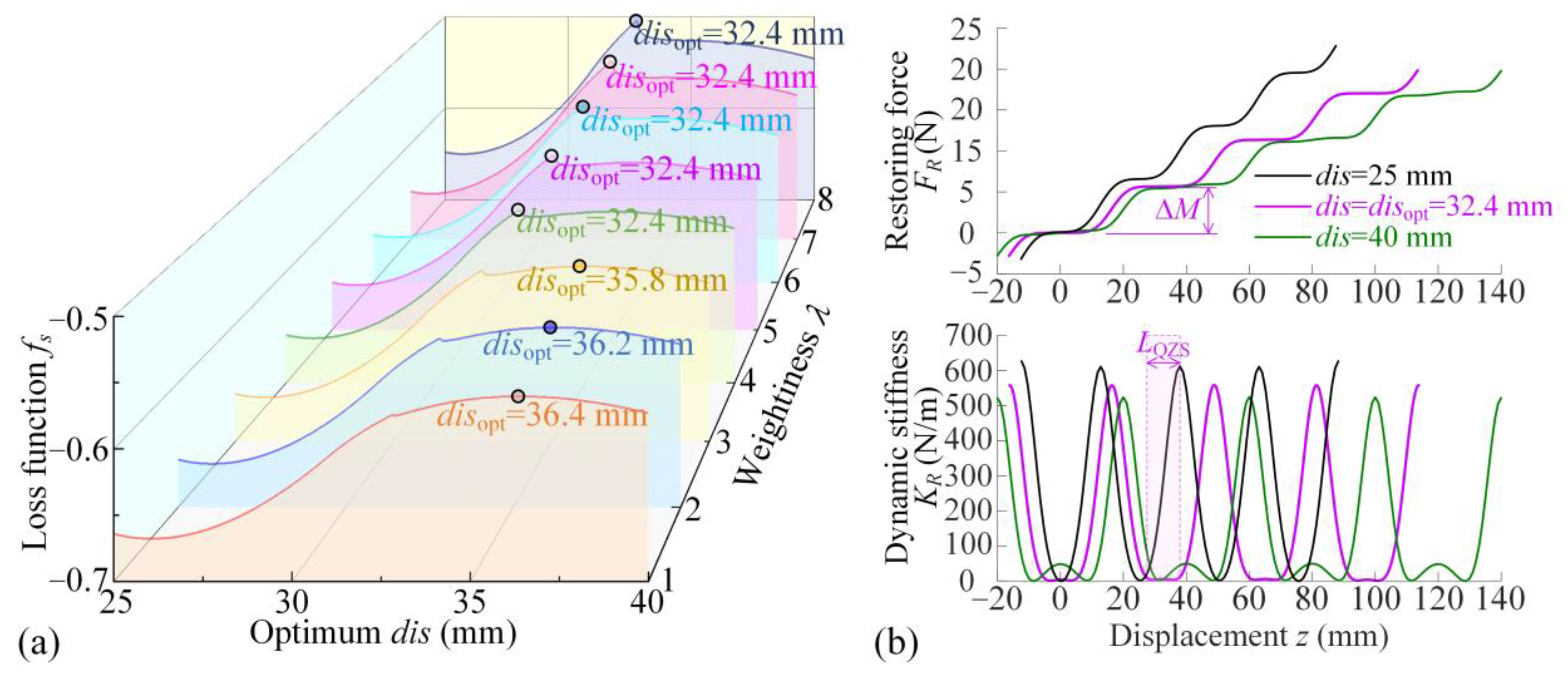
2.2. Structural Optimization for Small-Variation Load Step and Wide-Range QZS Property
3. Optimization for Dynamic Performances
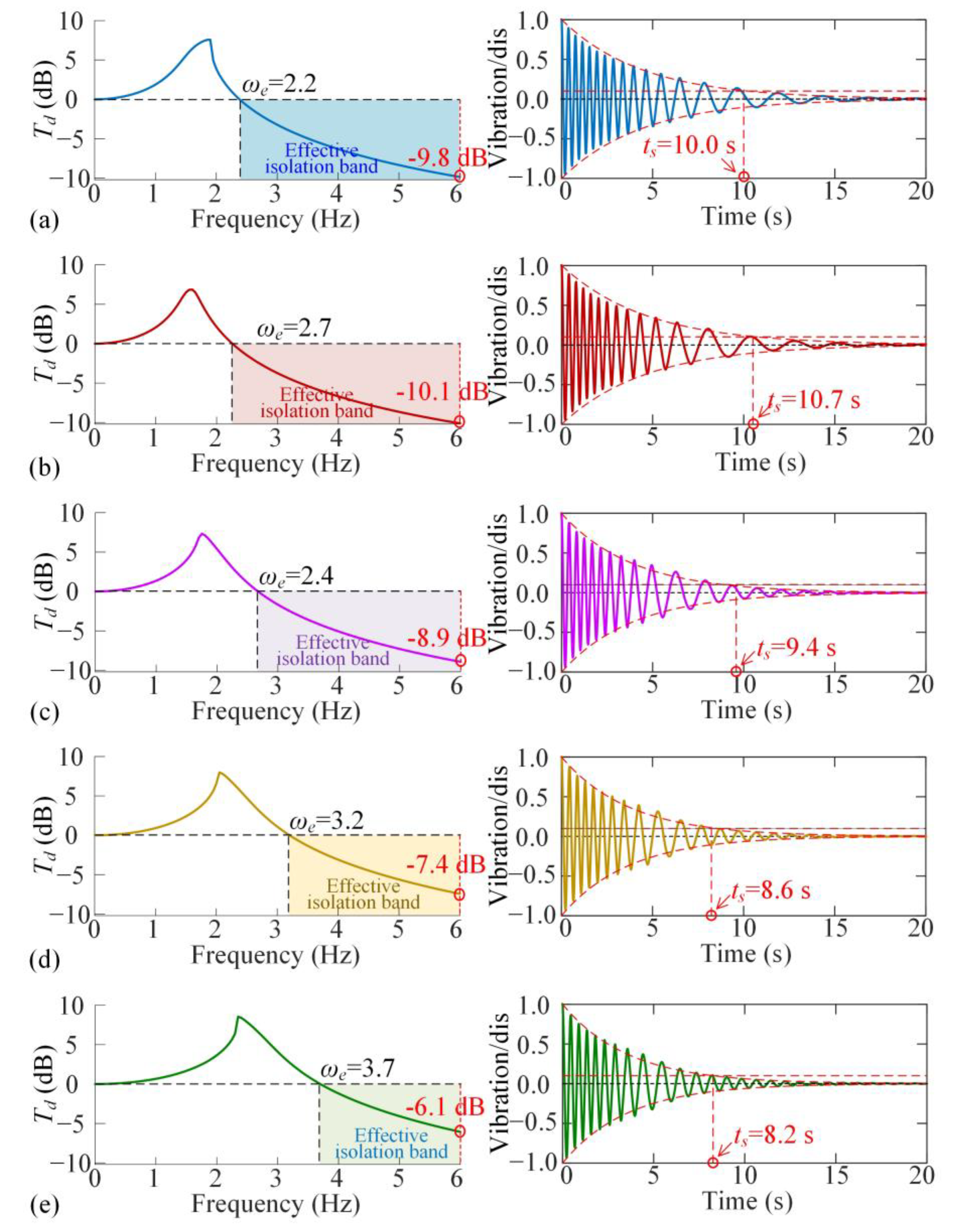
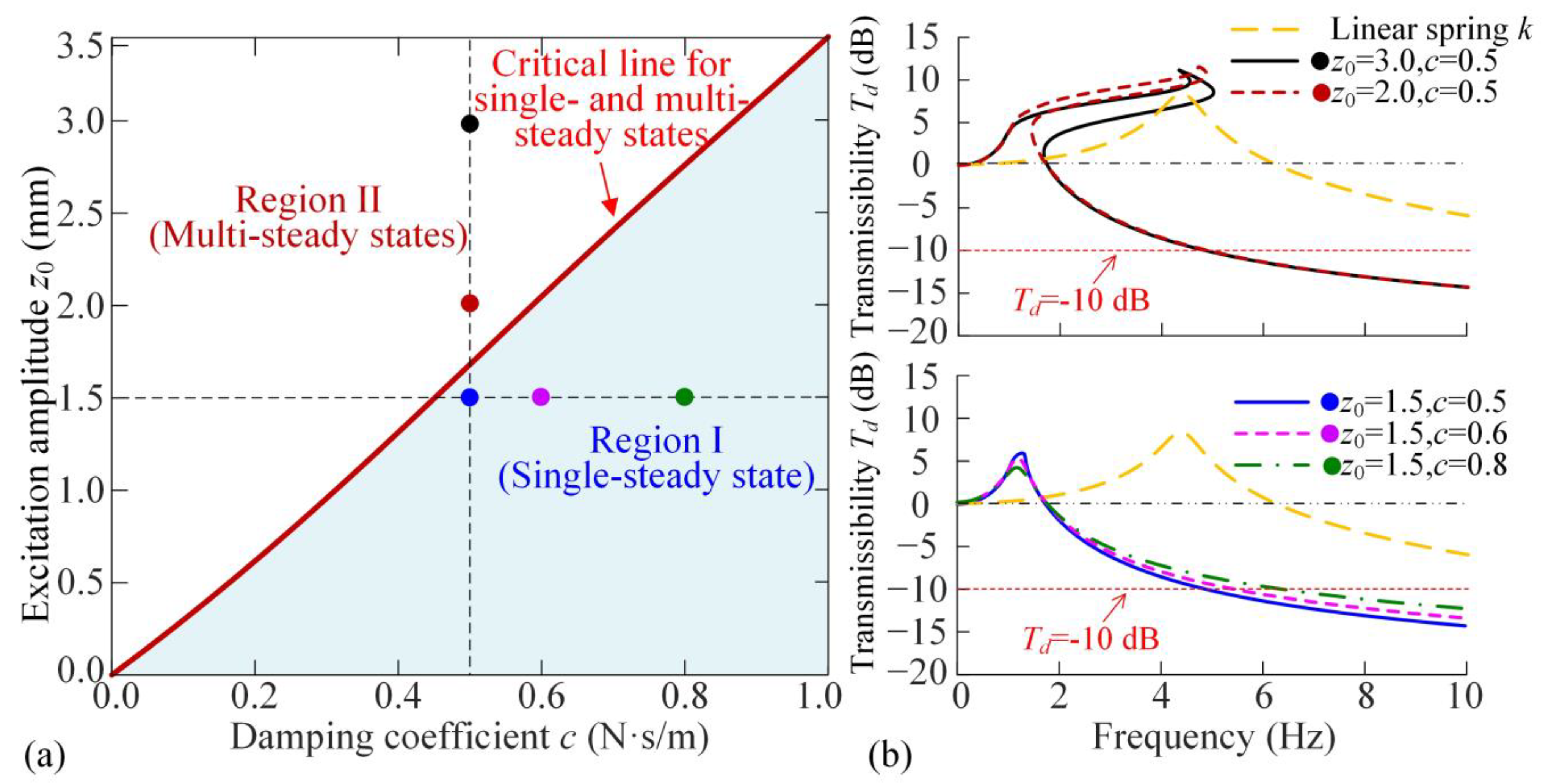
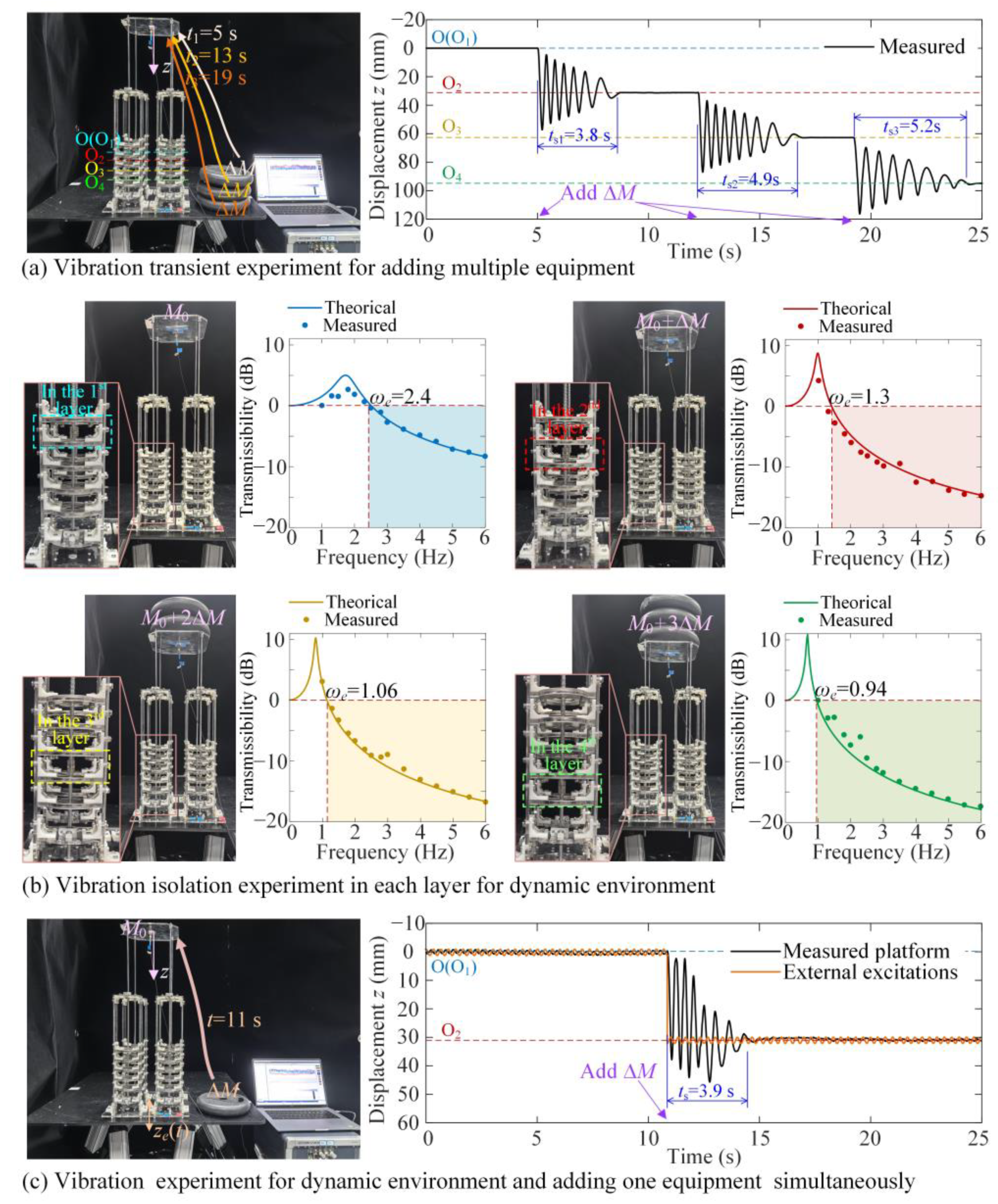
3.1. Bifurcation Condition for Single-Steady State and Displacement Transmissibility Curve
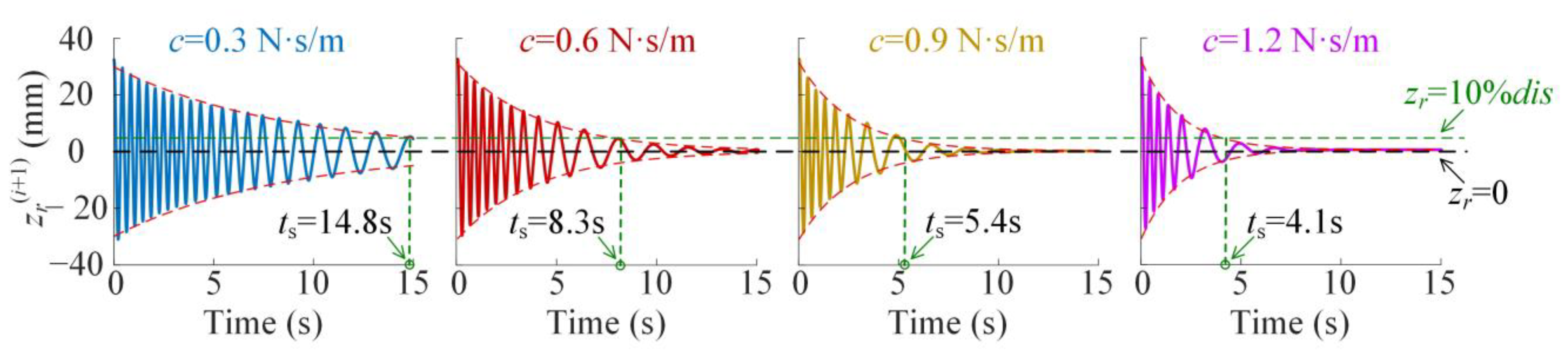
3.2. Transient Vibration Spanning to the Next Layer
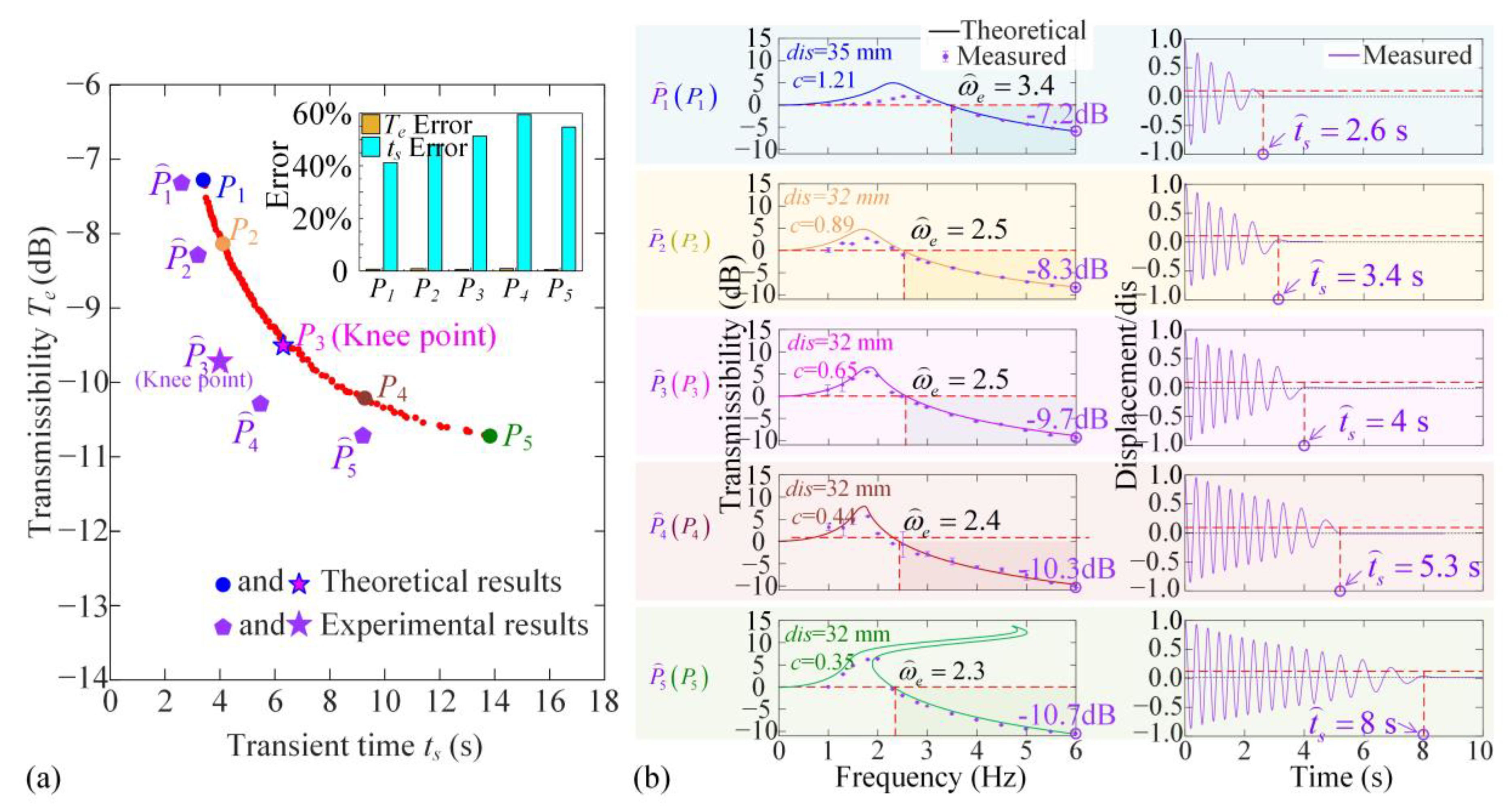
3.3. Optimization Criterion for Dynamic Performances
4. Isolation Platform and Experimental Verification for Structural Optimization
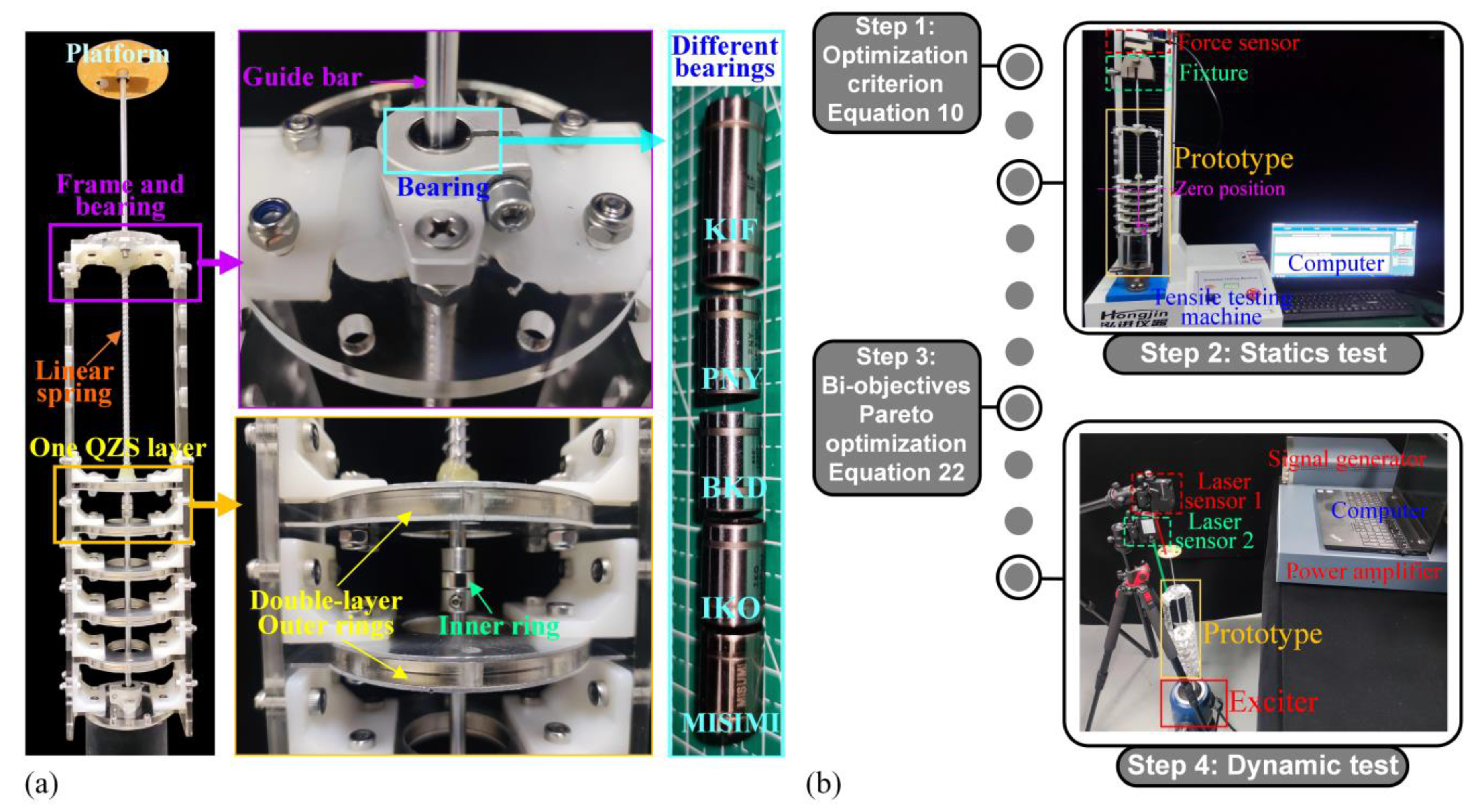
4.1. Experimental Prototype for One ML-QZS Isolation Mount
4.2. Experiment Results
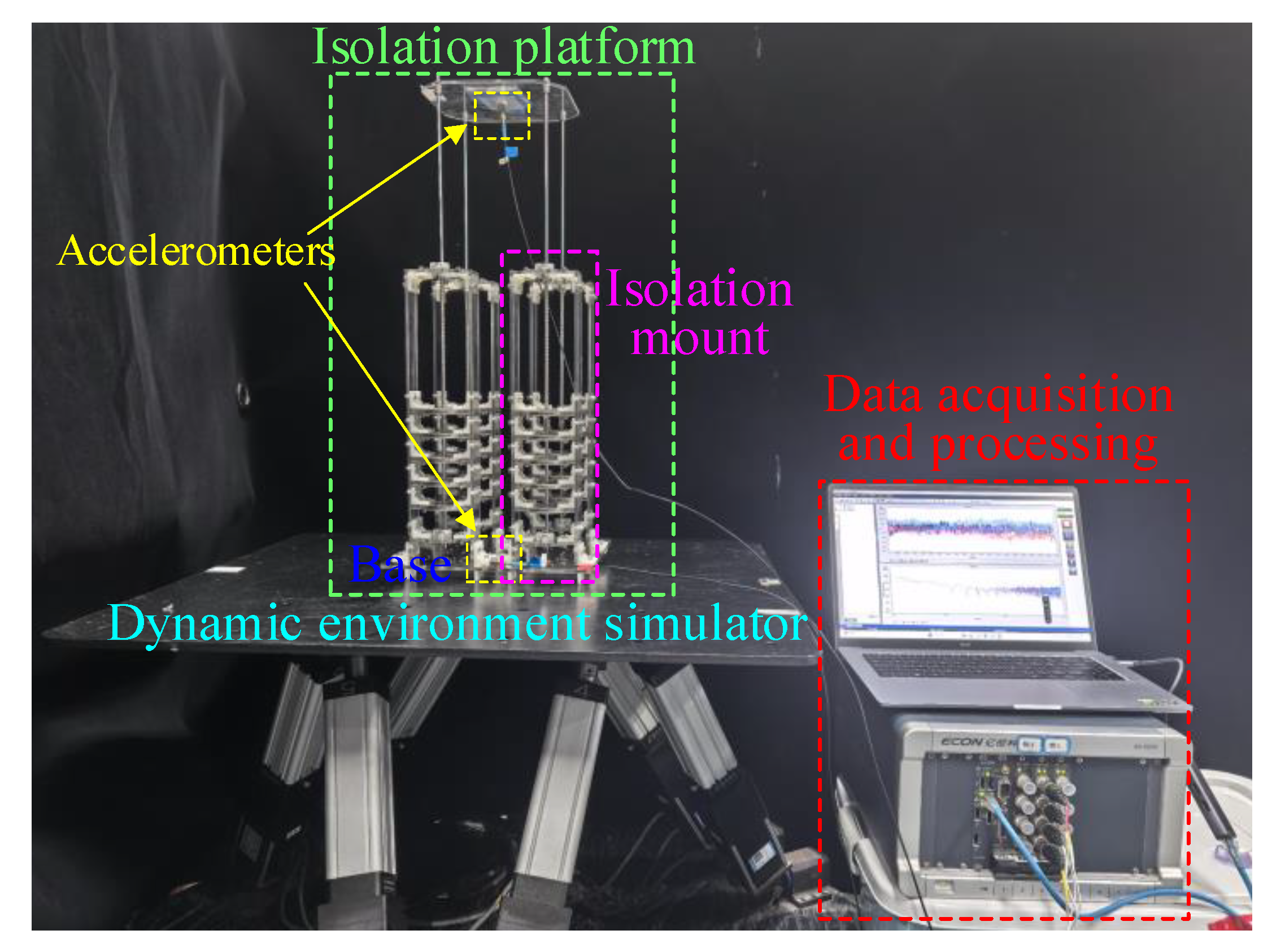
4.3. Isolation Platform with ML-QZS Property for Variable Loads
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
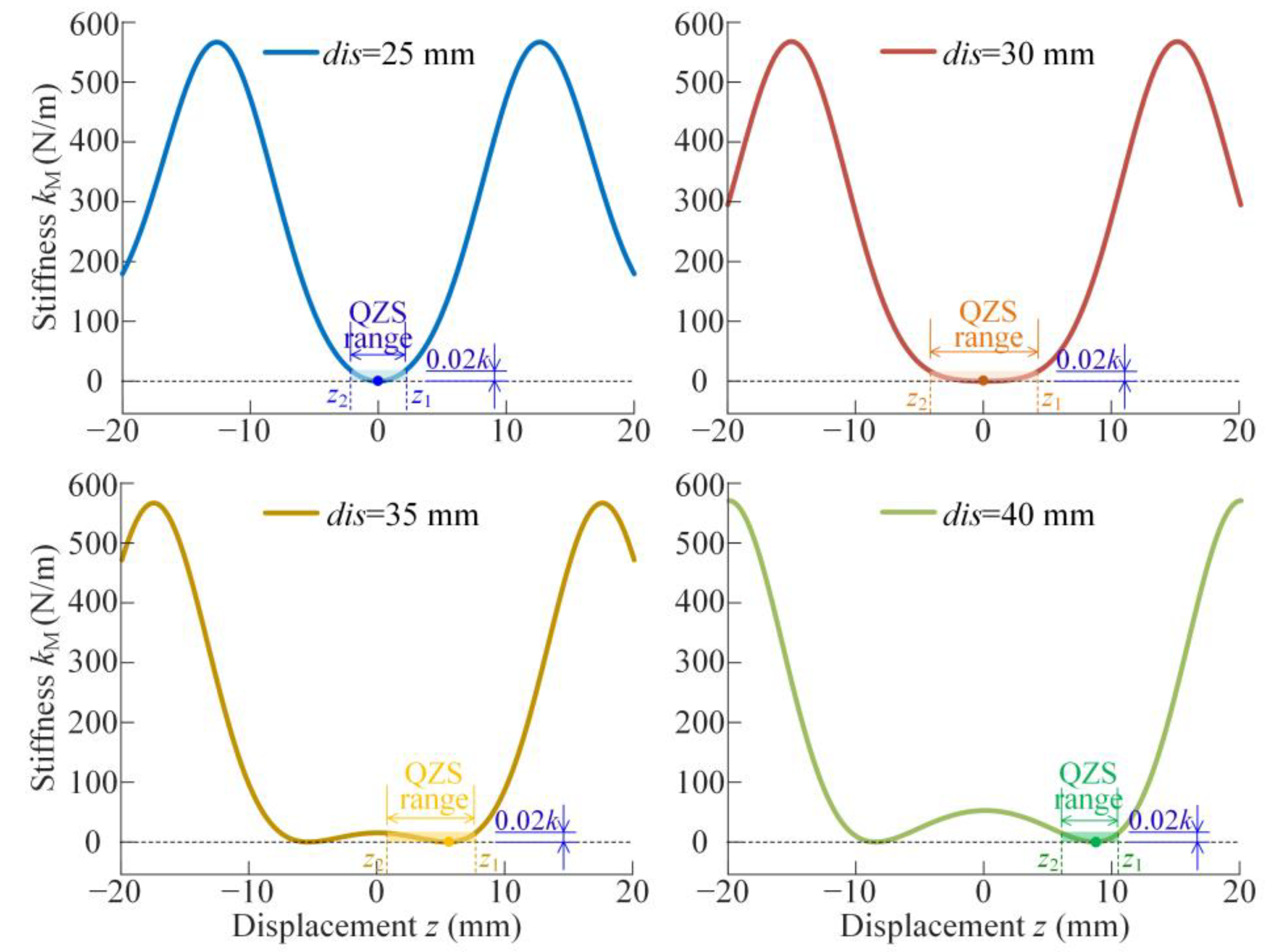
Appendix B
Appendix C

Appendix D
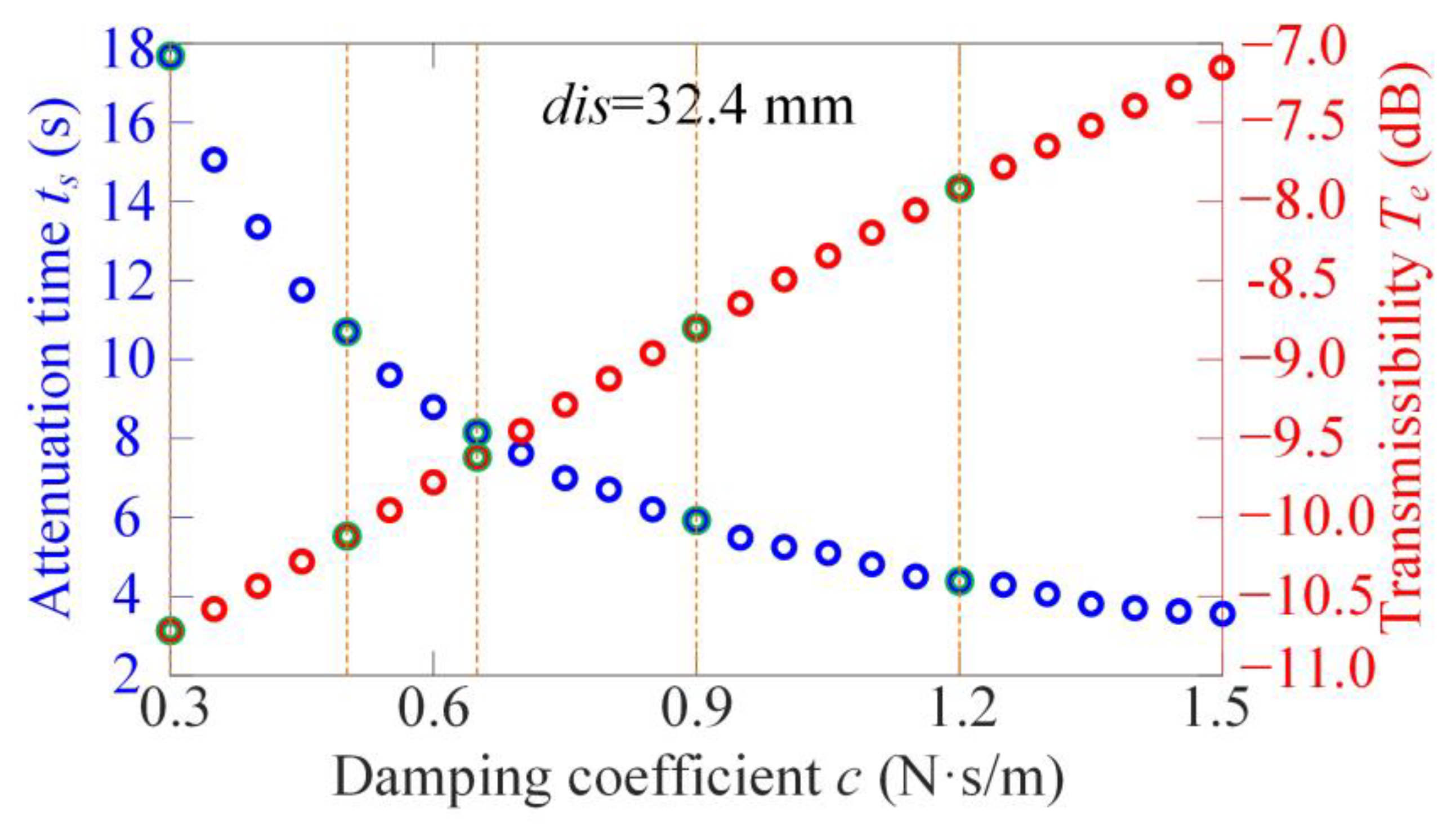
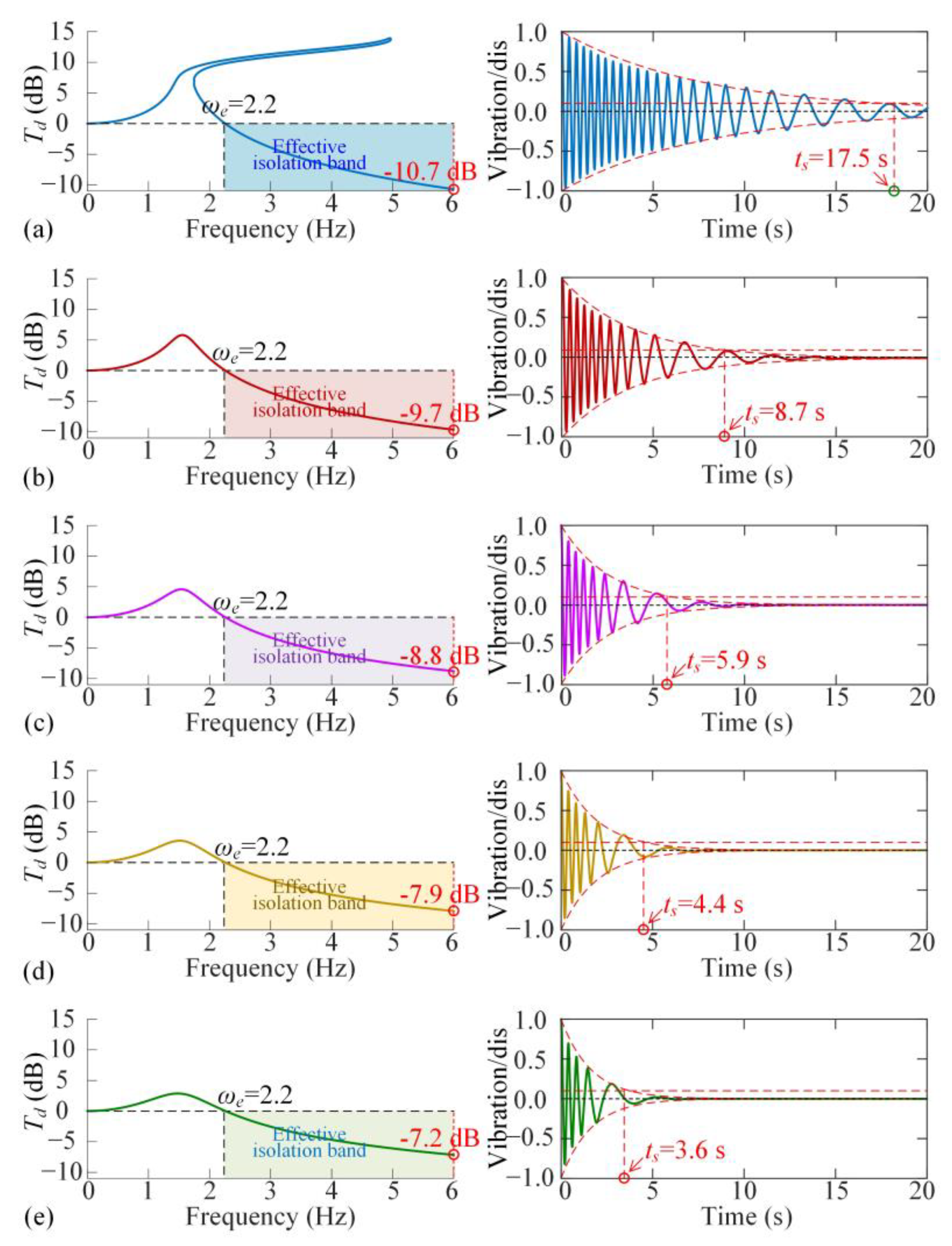
Appendix E
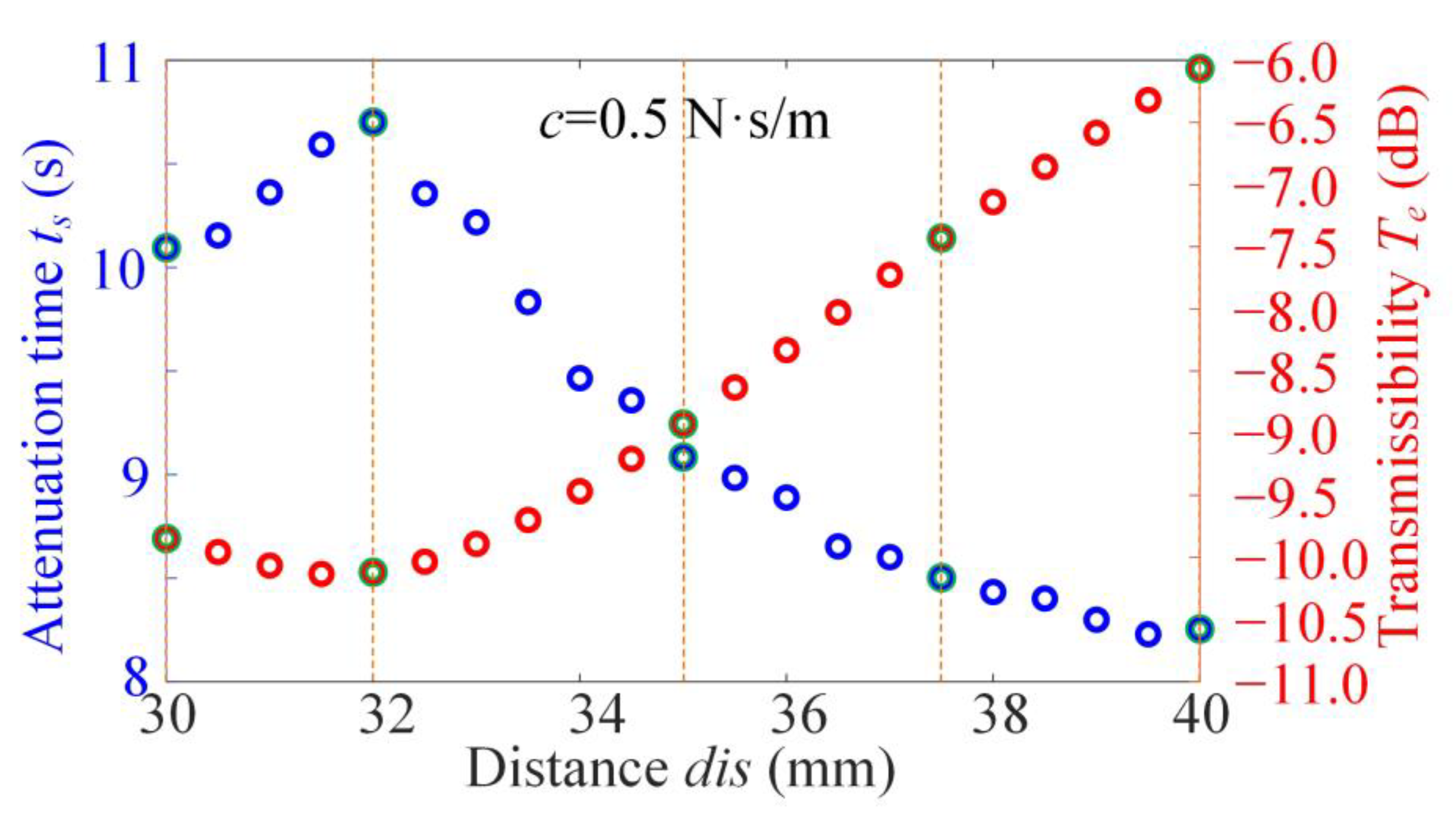
References
- Ding, J.; Chang, Y.; Chen, P.; Zhuang, H.; Ding, Y.; Lu, H.; Chen, Y. Dynamic modeling of ultra-precision fly cutting machine tool and the effect of ambient vibration on its tool tip response. Int. J. Extrem. Manuf. 2020, 2, 025301. [Google Scholar] [CrossRef]
- Miao, H.; Wang, C.; Li, C.; Song, W.; Zhang, X.; Xu, M. Vibration characteristics and reliability analysis of roller linear guideway workbench. Nonlinear Dyn. 2023, 111, 21461–21485. [Google Scholar] [CrossRef]
- Zhang, Q.; Shi, W.; Ouyang, Y. Vibration isolation performance of quasi constant natural frequency isolation pads associated with test verification. Eng. Struct. 2025, 324, 119328. [Google Scholar] [CrossRef]
- Liu, X.L.; Shangguan, W.B.; Jing, X.; Ahmed, W. Vibration isolation analysis of clutches based on trouble shooting of vehicle accelerating noise. J. Sound Vib. 2016, 382, 84–99. [Google Scholar] [CrossRef]
- Shi, X.; Zhou, H.; Zhou, C.; Guo, Z.; Ren, Z. Design and mechanical properties of metal rubber secondary multidirectional vibration isolation system under random vibration. Nonlinear Dyn. 2024, 112, 14805–14828. [Google Scholar] [CrossRef]
- Yu, Y.; Naganathan, N.G.; Dukkipati, R.V. A literature review of automotive vehicle engine mounting systems. Mech. Mach. Theory 2001, 36, 123–142. [Google Scholar] [CrossRef]
- Liu, C.; Jing, X.; Daley, S.; Li, F. Recent advances in micro-vibration isolation. Mech. Syst. Signal Process. 2015, 56, 55–80. [Google Scholar] [CrossRef]
- Yan, B.; Ma, H.; Zhao, C.; Wu, C.; Wang, K.; Wang, P. A vari-stiffness nonlinear isolator with magnetic effects: Theoretical modeling and experimental verification. Int. J. Mech. Sci. 2018, 148, 745–755. [Google Scholar] [CrossRef]
- Carrella, A.; Brennan, M.; Waters, T. Static analysis of a passive vibration isolator with quasi-zero-stiffness characteristic. J. Sound Vib. 2007, 301, 678–689. [Google Scholar] [CrossRef]
- Carrella, A.; Brennan, M.; Waters, T.; Shin, K. On the design of a high-static–low-dynamic stiffness isolator using linear mechanical springs and magnets. J. Sound Vib. 2008, 315, 712–720. [Google Scholar] [CrossRef]
- Tang, B.; Brennan, M.J. On the shock performance of a nonlinear vibration isolator with high-static-low-dynamic-stiffness. Int. J. Mech. Sci. 2014, 81, 207–214. [Google Scholar]
- Hao, Z.; Cao, Q.; Wiercigroch, M. Two-sided damping constraint control strategy for high-performance vibration isolation and end-stop impact protection. Nonlinear Dyn. 2016, 86, 2129–2144. [Google Scholar]
- Li, M.; Li, X.; Gan, C.; Zeng, J.; Zhao, L.; Ding, H.; Wei, K.; Zou, H. Human motion energy harvesting backpack using quasi-zero stiffness mechanism. Energy Convers. Manag. 2023, 288, 117158. [Google Scholar]
- Mao, X.; Yin, M.; Ding, H.; Geng, X.; Shen, Y.; Chen, L. Modeling, analysis, and simulation of X-shape quasi-zero-stiffness-roller vibration isolators. Appl. Math. Mech. 2022, 43, 1027–1044. [Google Scholar] [CrossRef]
- Li, M.; Cheng, W.; Xie, R. A quasi-zero-stiffness vibration isolator using a cam mechanism with user-defined profile. Int. J. Mech. Sci. 2021, 189, 105938. [Google Scholar]
- Zuo, S.; Wang, D.; Zhang, Y.; Luo, Q. An innovative design of parabolic cam-roller quasi-zero-stiffness isolators for ultralow frequency vibration isolation. Nonlinear Dyn. 2024, 112, 18717–18744. [Google Scholar] [CrossRef]
- Wang, Q.; Zhou, J.; Xu, D.; Ouyang, H. Design and experimental investigation of ultra-low frequency vibration isolation during neonatal transport. Mech. Syst. Signal Process. 2020, 139, 106633. [Google Scholar] [CrossRef]
- Guo, M.; Tang, L.; Wang, H.; Liu, H.; Gao, S. A comparative study on transient vibration suppression of magnetic nonlinear vibration absorbers with different arrangements. Nonlinear Dyn. 2023, 111, 16729–16776. [Google Scholar]
- Wang, K.; Zhou, J.; Ouyang, H.; Cheng, L.; Xu, D. A semi-active metamaterial beam with electromagnetic quasi-zero-stiffness resonators for ultralow-frequency band gap tuning. Int. J. Mech. Sci. 2020, 176, 105548. [Google Scholar]
- Hou, S.; Wei, J. A quasi-zero stiffness mechanism with monolithic flexible beams for low-frequency vibration isolation. Mech. Syst. Signal Process. 2024, 210, 111154. [Google Scholar] [CrossRef]
- Liu, J.; Wang, Y.; Yang, S.; Sun, T.; Yang, M.; Niu, W. Customized quasi-zero-stiffness metamaterials for ultra-low frequency broadband vibration isolation. Int. J. Mech. Sci. 2024, 269, 108958. [Google Scholar] [CrossRef]
- Lei, X.; Sun, X.; Cheng, L.; Yu, X. A 3D-printed quasi-zero-stiffness isolator for low-frequency vibration isolation: Modelling and experiments. J. Sound Vib. 2024, 577, 118308. [Google Scholar]
- Gatti, G.; Ledezma-Ramirez, D.F.; Brennan, M.J. Performance of a shock isolator inspired by skeletal muscles. Int. J. Mech. Sci. 2023, 244, 108066. [Google Scholar] [CrossRef]
- Li, H.; Wu, Z.; Jiang, T. A quasi-zero stiffness vibration isolator based on hybrid bistable composite laminate. Chin. J. Theor. Appl. Mech. 2019, 51, 354–363. [Google Scholar]
- Zeng, R.; Wen, G.; Zhou, J.; Zhao, G. Limb-inspired bionic quasi-zero stiffness vibration isolator. Acta Mech. Sin. 2021, 37, 1152–1167. [Google Scholar] [CrossRef]
- Bian, J.; Jing, X. Analysis and design of a novel and compact X-structured vibration isolation mount (X-Mount) with wider quasi-zero-stiffness range. Nonlinear Dyn. 2020, 101, 2195–2222. [Google Scholar] [CrossRef]
- Tian, R.; Wang, M.; Zhang, Y.; Jing, X.; Zhang, X. A concave X-shaped structure supported by variable pitch springs for low-frequency vibration isolation. Mech. Syst. Signal Process. 2024, 218, 111587. [Google Scholar] [CrossRef]
- Yu, C.; Jiang, Q.; Fu, Q.; Yu, K.; Zhang, J.; Zhang, N. The X-shaped structure with nonlinear positive stiffness compensation for low-frequency vibration isolation. Int. J. Mech. Sci. 2023, 259, 108598. [Google Scholar] [CrossRef]
- An, J.; Chen, G.; Deng, X.; Xi, C.; Wang, T.; He, H. Analytical study of a pneumatic quasi-zero-stiffness isolator with mistuned mass. Nonlinear Dyn. 2022, 108, 3297–3312. [Google Scholar] [CrossRef]
- Ye, K.; Ji, J. An origami inspired quasi-zero stiffness vibration isolator using a novel truss-spring based stack Miura-ori structure. Mech. Syst. Signal Process. 2022, 165, 108383. [Google Scholar] [CrossRef]
- Liu, T.; Li, A.; Zhang, H. Quasi-zero stiffness interval optimization design and dynamics analysis of a new bi-directional horizontal isolation system. Mech. Syst. Signal Process. 2024, 206, 110852. [Google Scholar]
- Liu, X.C.; Ding, H.; Geng, X.F.; Wei, K.X.; Lai, S.K.; Chen, L.Q. A magnetic nonlinear energy sink with quasi-zero stiffness characteristics. Nonlinear Dyn. 2024, 112, 5895–5918. [Google Scholar]
- Xu, J.; Yang, X.; Li, W.; Zheng, J.; Wang, Y.; Fan, M.; Zhou, W.; Lu, Y. Design of quasi-zero stiffness joint actuator and research on vibration isolation performance. J. Sound Vib. 2020, 479, 115367. [Google Scholar]
- Sun, X.; Wang, F.; Xu, J. Analysis, design and experiment of continuous isolation structure with Local Quasi-Zero-Stiffness property by magnetic interaction. Int. J. Non-Linear Mech. 2019, 116, 289–301. [Google Scholar]
- Liu, C.; Zhao, R.; Yu, K.; Liao, B. In-plane quasi-zero-stiffness vibration isolator using magnetic interaction and cables: Theoretical and experimental study. Appl. Math. Model. 2021, 96, 497–522. [Google Scholar] [CrossRef]
- Kovacic, I.; Brennan, M.J.; Waters, T.P. A study of a nonlinear vibration isolator with a quasi-zero stiffness characteristic. J. Sound Vib. 2008, 315, 700–711. [Google Scholar] [CrossRef]
- Zuo, S.; Wang, D.; Zhang, Y.; Luo, Q. Design and testing of a parabolic cam-roller quasi-zero-stiffness vibration isolator. Int. J. Mech. Sci. 2022, 220, 107146. [Google Scholar] [CrossRef]
- Sun, Y.; Zhou, J.; Thompson, D.; Yuan, T.; Gong, D.; You, T. Design, analysis and experimental validation of high static and low dynamic stiffness mounts based on target force curves. Int. J. Non-Linear Mech. 2020, 126, 103559. [Google Scholar]
- Zhang, Y.; Wen, H.; Hu, H.; Jin, D. A novel quasi-zero stiffness isolator with designable stiffness using cam-roller-spring-rod mechanism. Acta Mech. Sin. 2025, 41, 524210. [Google Scholar]
- Yu, K.; Chen, Y.; Yu, C.; Zhang, J.; Lu, X. A compact nonlinear stiffness-modulated structure for low-frequency vibration isolation under heavy loads. Nonlinear Dyn. 2024, 112, 5863–5893. [Google Scholar]
- Yan, G.; Wu, Z.Y.; Wei, X.S.; Wang, S.; Zou, H.X.; Zhao, L.C.; Qi, W.H.; Zhang, W.M. Nonlinear compensation method for quasi-zero stiffness vibration isolation. J. Sound Vib. 2022, 523, 116743. [Google Scholar] [CrossRef]
- Yan, G.; Qi, W.H.; Lu, J.J.; Liu, F.R.; Yan, H.; Zhao, L.C.; Wu, Z.Y.; Zhang, W.M. Bio-inspired multi-joint-collaborative vibration isolation. J. Sound Vib. 2024, 568, 118089. [Google Scholar] [CrossRef]
- Zhao, F.; Ji, J.; Ye, K.; Luo, Q. An innovative quasi-zero stiffness isolator with three pairs of oblique springs. Int. J. Mech. Sci. 2021, 192, 106093. [Google Scholar] [CrossRef]
- Pu, H.; Liu, J.; Wang, M.; Ding, J.; Sun, Y.; Peng, Y.; Luo, J. Bio-inspired quasi-zero stiffness vibration isolator with quasilinear negative stiffness in full stroke. J. Sound Vib. 2024, 574, 118240. [Google Scholar] [CrossRef]
- Gatti, G. Statics and dynamics of a nonlinear oscillator with quasi-zero stiffness behaviour for large deflections. Commun. Nonlinear Sci. Numer. Simul. 2020, 83, 105143. [Google Scholar] [CrossRef]
- Zhao, F.; Ji, J.; Luo, Q.; Cao, S.; Chen, L.; Du, W. An improved quasi-zero stiffness isolator with two pairs of oblique springs to increase isolation frequency band. Nonlinear Dyn. 2021, 104, 349–365. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhu, G.; Cao, Q. Isolation performances and optimization of triple quasi-zero stiffness isolators. Sci. China Phys. Mech. Astron. 2024, 67, 274511. [Google Scholar] [CrossRef]
- Zhao, F.; Ji, J.; Cao, S.; Ye, K.; Luo, Q. QZS isolators with multi-pairs of oblique bars for isolating ultralow frequency vibrations. Nonlinear Dyn. 2024, 112, 1815–1842. [Google Scholar] [CrossRef]
- Chen, T.; Zheng, Y.; Song, L.; Gao, X.; Wang, G. Study on a quasi-zero-stiffness isolator for variable mass load. Appl. Math. Model. 2023, 123, 447–463. [Google Scholar] [CrossRef]
- Xu, D.; Yu, Q.; Zhou, J.; Bishop, S. Theoretical and experimental analyses of a nonlinear magnetic vibration isolator with quasi-zero-stiffness characteristic. J. Sound Vib. 2013, 332, 3377–3389. [Google Scholar] [CrossRef]
- Chen, R.; Li, X.; Tian, J.; Yang, Z.; Xu, J. On the displacement transferability of variable stiffness multi-directional low frequency vibration isolation joint. Appl. Math. Model. 2022, 112, 690–707. [Google Scholar]
- Jiao, G.; Zeng, J.; Wang, S. A compact magnetic-curved-spring QZS isolator for supporting uncertain loads. Nonlinear Dyn. 2024, 113, 9217–9238. [Google Scholar] [CrossRef]
- Qi, W.H.; Yan, G.; Lu, J.J.; Liu, F.R.; Zhao, T.Y.; Yan, H.; Zhang, W.M. Local gravity control method for solving load-mismatch issue in isolators. Int. J. Mech. Sci. 2024, 265, 108891. [Google Scholar] [CrossRef]
- Lu, J.J.; Yan, G.; Qi, W.H.; Yan, H.; Liu, F.R.; Zhao, T.Y.; Zhang, W.M. Integrated vibration isolation and actuation via dual nonlinear stiffness regulation. Int. J. Mech. Sci. 2024, 263, 108760. [Google Scholar]
- Ye, K.; Ji, J.; Brown, T. Design of a quasi-zero stiffness isolation system for supporting different loads. J. Sound Vib. 2020, 471, 115198. [Google Scholar]
- Zhou, J.; Zhou, J.; Pan, H.; Wang, K.; Cai, C.; Wen, G. Multi-layer quasi-zero-stiffness meta-structure for high-efficiency vibration isolation at low frequency. Appl. Math. Mech. 2024, 45, 1189–1208. [Google Scholar]
- Zeng, C.; Liu, L.; Hu, Y.; Zhao, W.; Xin, X.; Liu, Y.; Leng, J. Stair-Stepping Mechanical Metamaterials with Programmable Load Plateaus. Adv. Funct. Mater. 2024, 34, 2408887. [Google Scholar]



| Vibration Isolator | QZS Range/Design Parameter (kQZS < 0.02 ks) | (Hz) | Vibrable Load |
|---|---|---|---|
| Linear spring damping isolator | 0 | 6.5 | Yes |
| QZS with triple nonlinear spring [43] | 0.2 | 3.0 | No |
| QZS with single magnetic ring [17] | 0.16 | 3.0 | No |
| QZS with X-shaped structure [28] | 0.105 | 3.5 | No |
| QZS with electromagnetic constant force mechanism [53] | 0.112 | 2.5 | Yes |
| QZS with dual electromagnetic nonlinear stiffness mechanisms [54] | 0.250 | 3.5 | Yes |
| QZS with Multi-layer cam-roller [55] | 0.5 | 3.6 | Yes |
| QZS with mechanical metamaterials [57] | 0.08 | 17.6 | Yes |
| The proposed ML-QZS isolator | 0.32 | 2.5 | Yes |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, S.; Sun, X.; Qian, J.; Xu, J.; Li, K. Design, Optimization, and Realization of a Magnetic Multi-Layer Quasi-Zero-Stiffness Isolation Platform Supporting Different Loads. Materials 2025, 18, 1676. https://doi.org/10.3390/ma18071676
Yang S, Sun X, Qian J, Xu J, Li K. Design, Optimization, and Realization of a Magnetic Multi-Layer Quasi-Zero-Stiffness Isolation Platform Supporting Different Loads. Materials. 2025; 18(7):1676. https://doi.org/10.3390/ma18071676
Chicago/Turabian StyleYang, Shuaijie, Xiuting Sun, Jiawei Qian, Jian Xu, and Kaixiang Li. 2025. "Design, Optimization, and Realization of a Magnetic Multi-Layer Quasi-Zero-Stiffness Isolation Platform Supporting Different Loads" Materials 18, no. 7: 1676. https://doi.org/10.3390/ma18071676
APA StyleYang, S., Sun, X., Qian, J., Xu, J., & Li, K. (2025). Design, Optimization, and Realization of a Magnetic Multi-Layer Quasi-Zero-Stiffness Isolation Platform Supporting Different Loads. Materials, 18(7), 1676. https://doi.org/10.3390/ma18071676







