Fluid Flow and Heat Transfer Performances of Aluminum Alloy Lattices with Triply Periodic Minimal Surfaces
Abstract
1. Introduction
2. Materials and Methods
2.1. Lattice Design
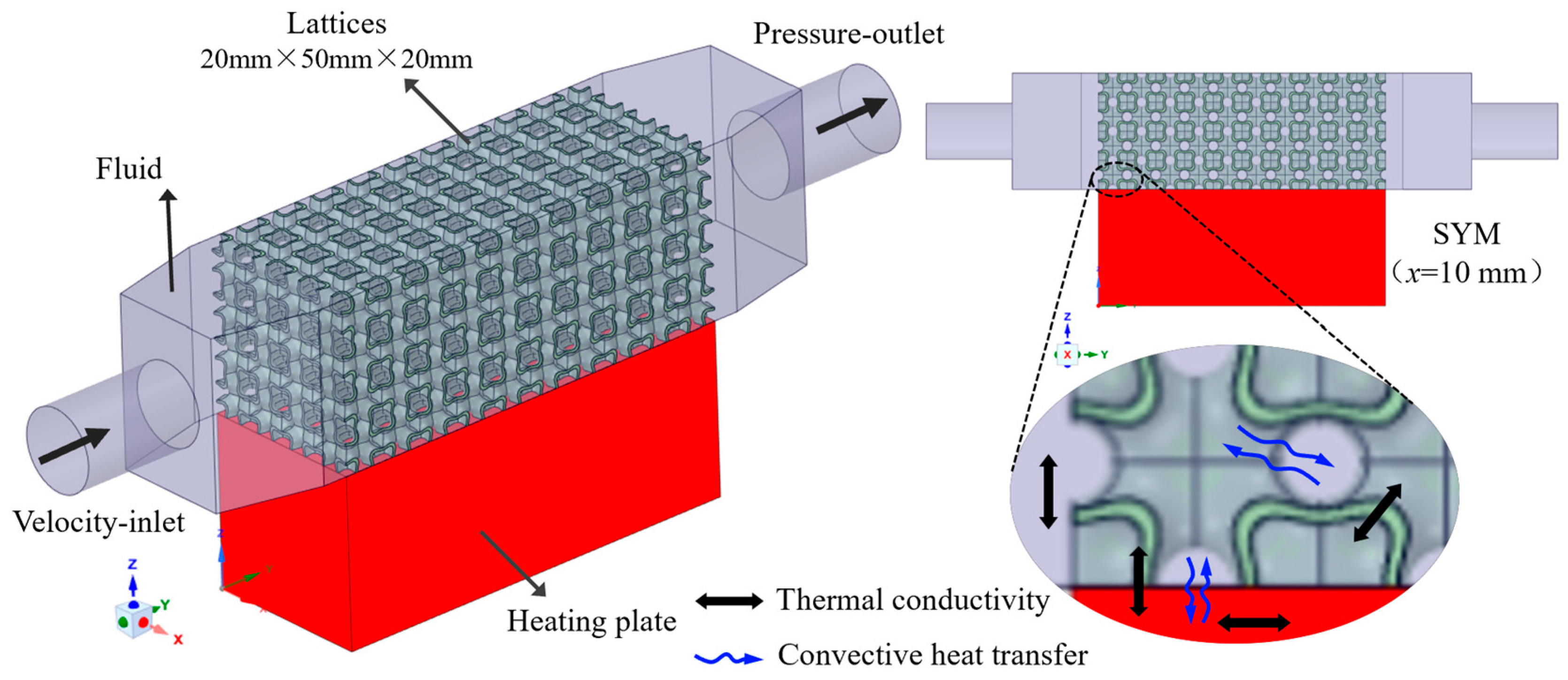
2.2. Numerical Method
2.2.1. Mathematical Model
- Continuity equation:
- Conservation of momentum equation:
- Energy equation:
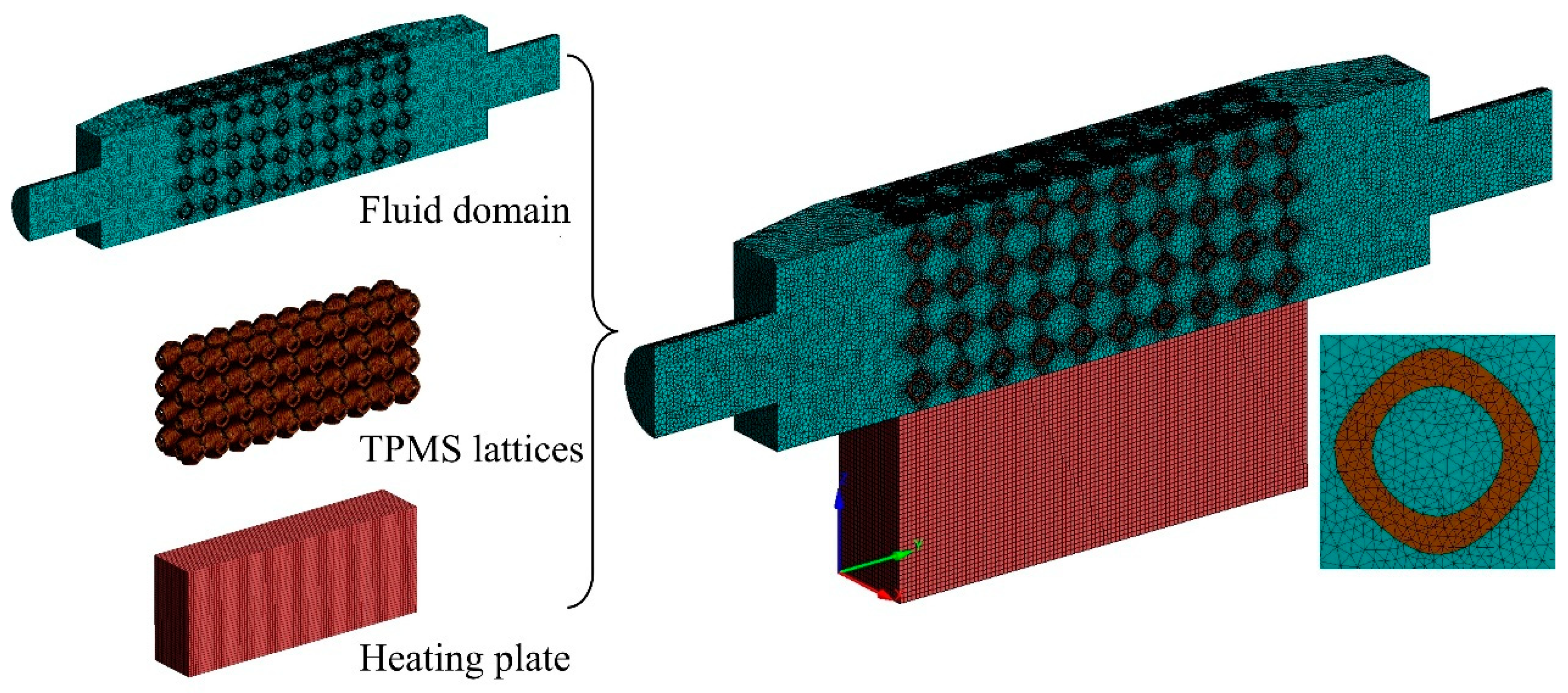
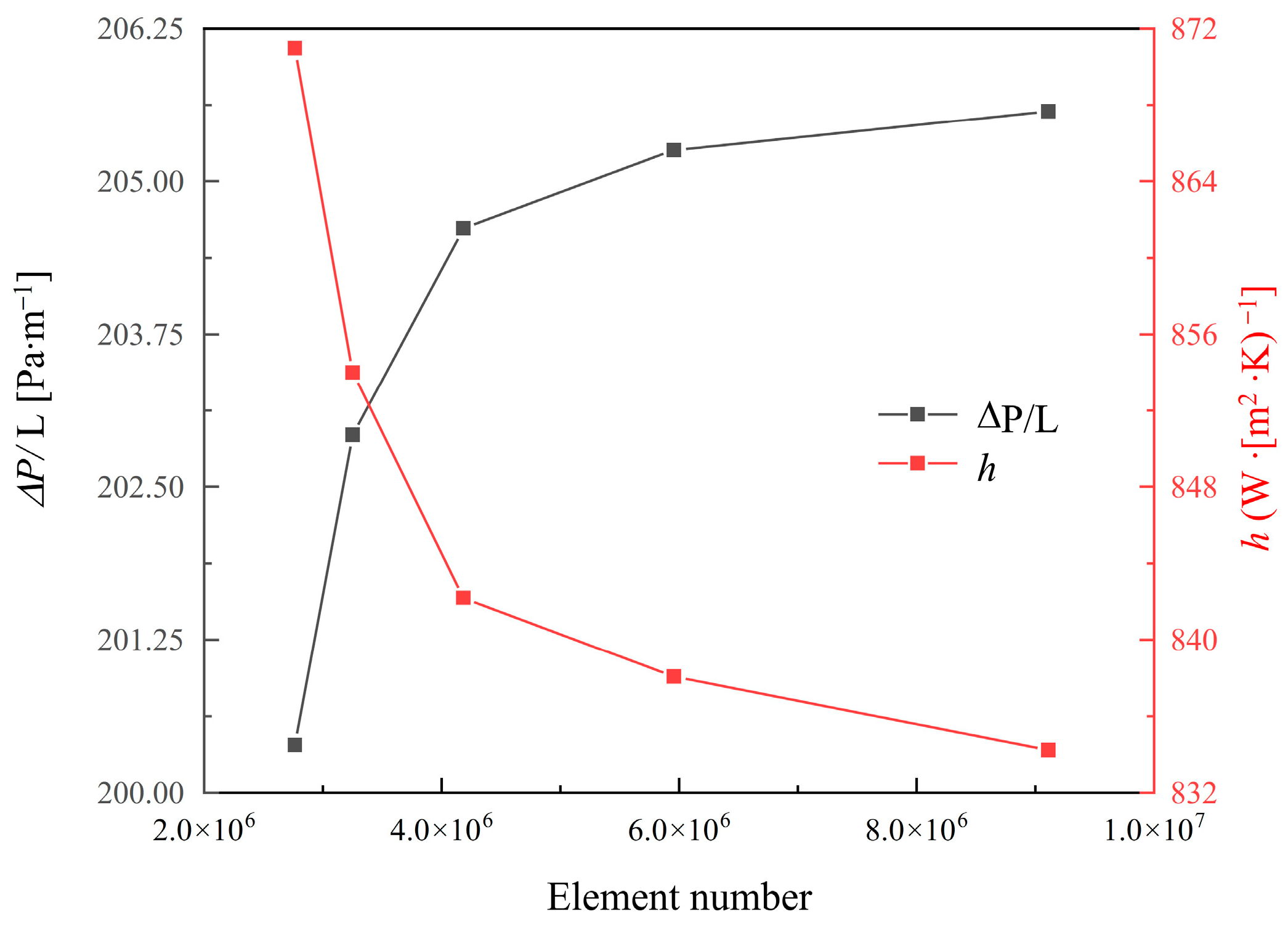
2.2.2. Mesh Independence Study
2.3. Mathematical Analysis
- (1)
- Flow characteristics
- (2)
- Heat transfer characteristics
- (3)
- Overall thermal transfer performance
2.4. Sample Fabrication
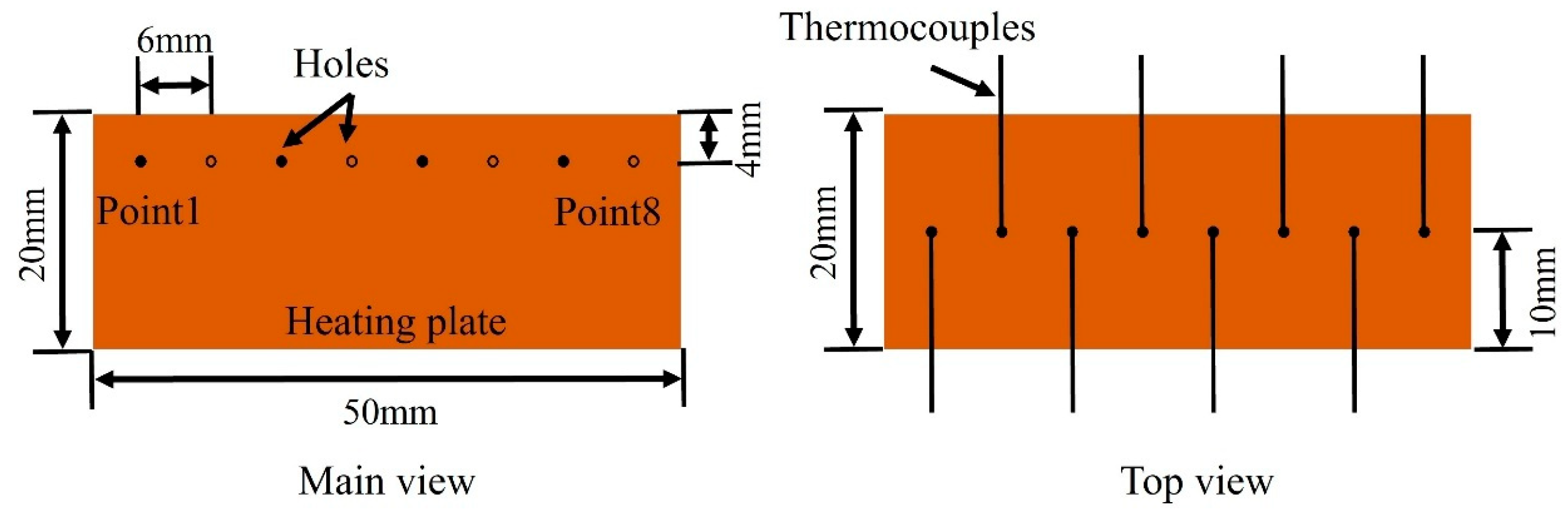
2.5. Experiments Details
3. Results and Discussion
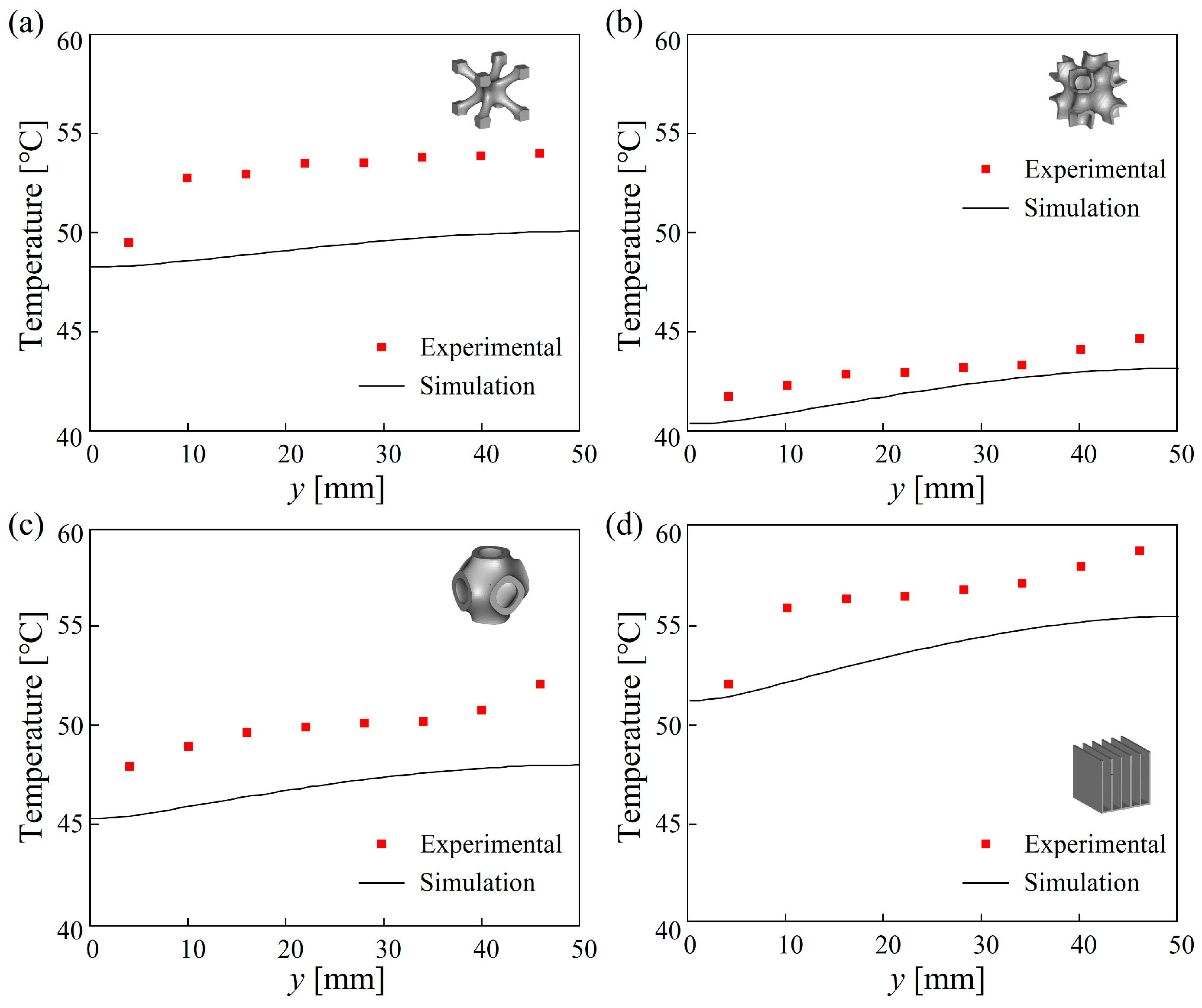
3.1. Validation of Simulations
3.2. Fluid Flow Characteristics
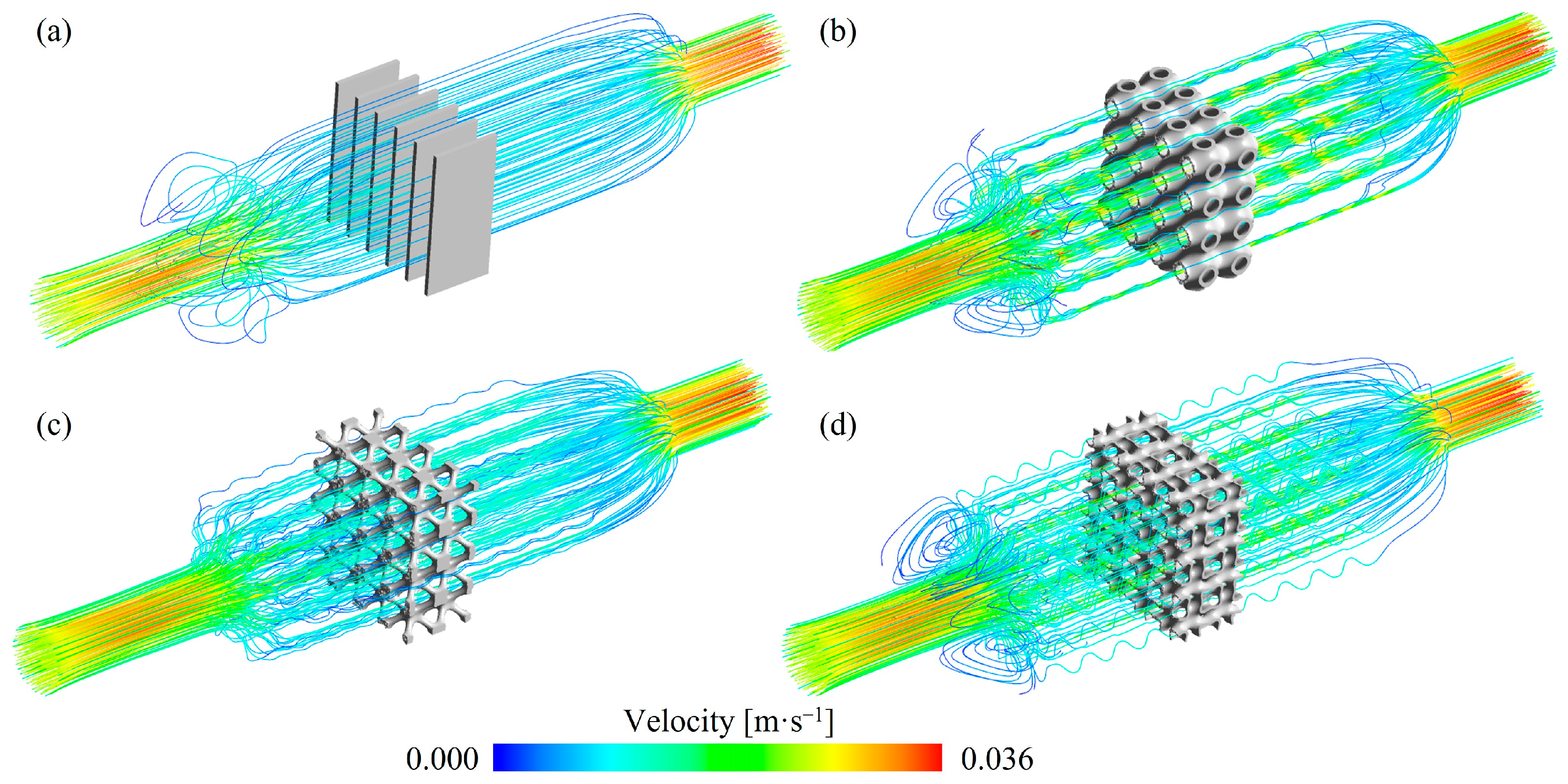
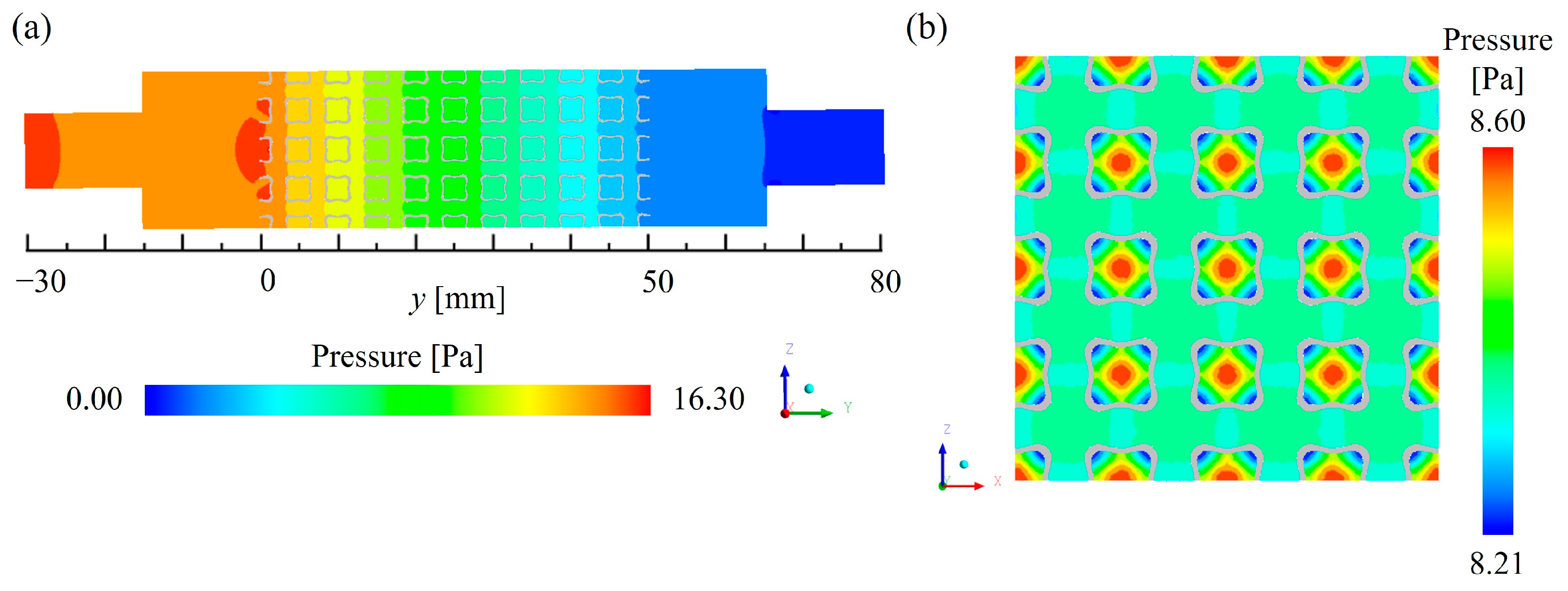
3.2.1. Fluid Flow Mechanisms
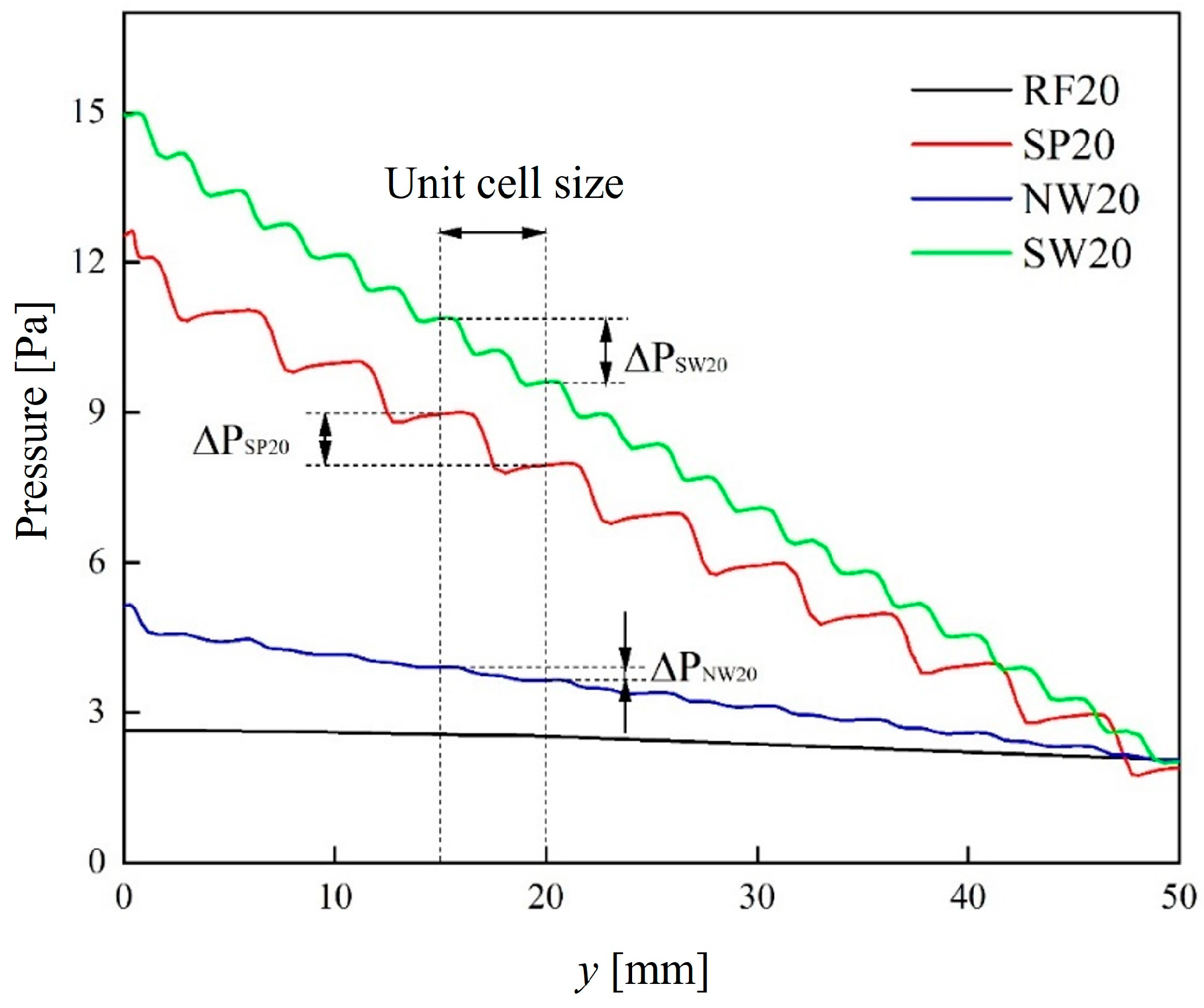
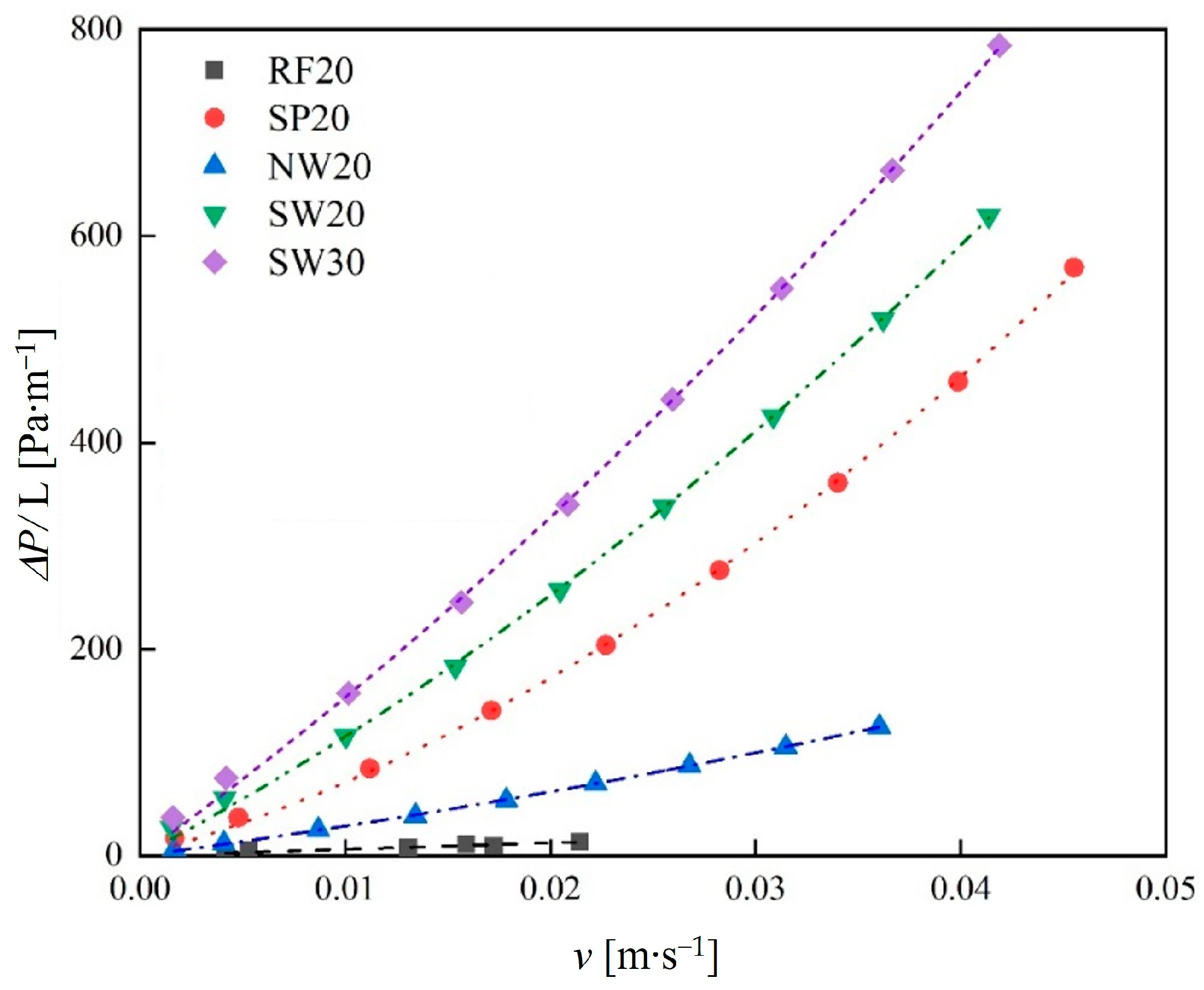
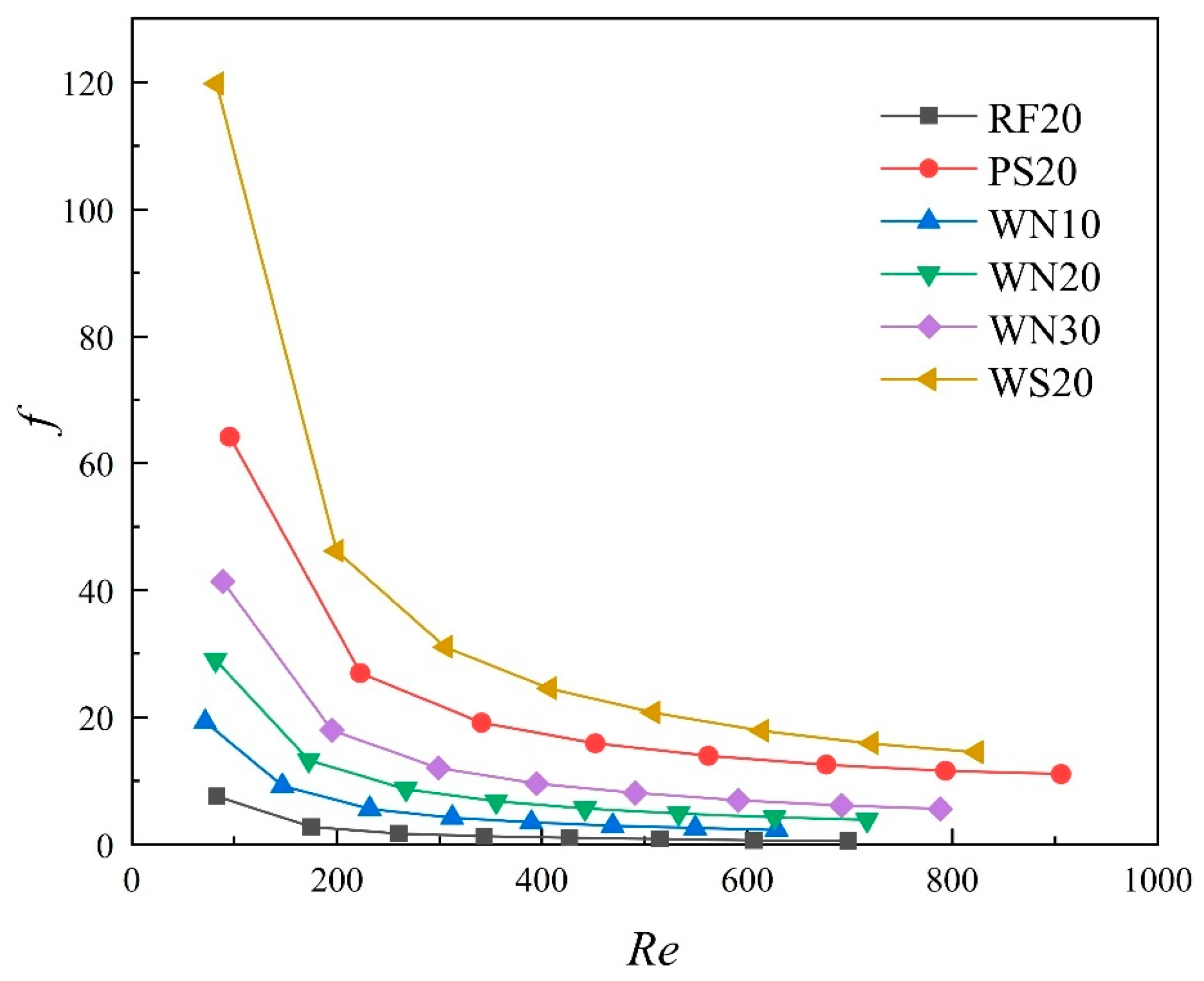
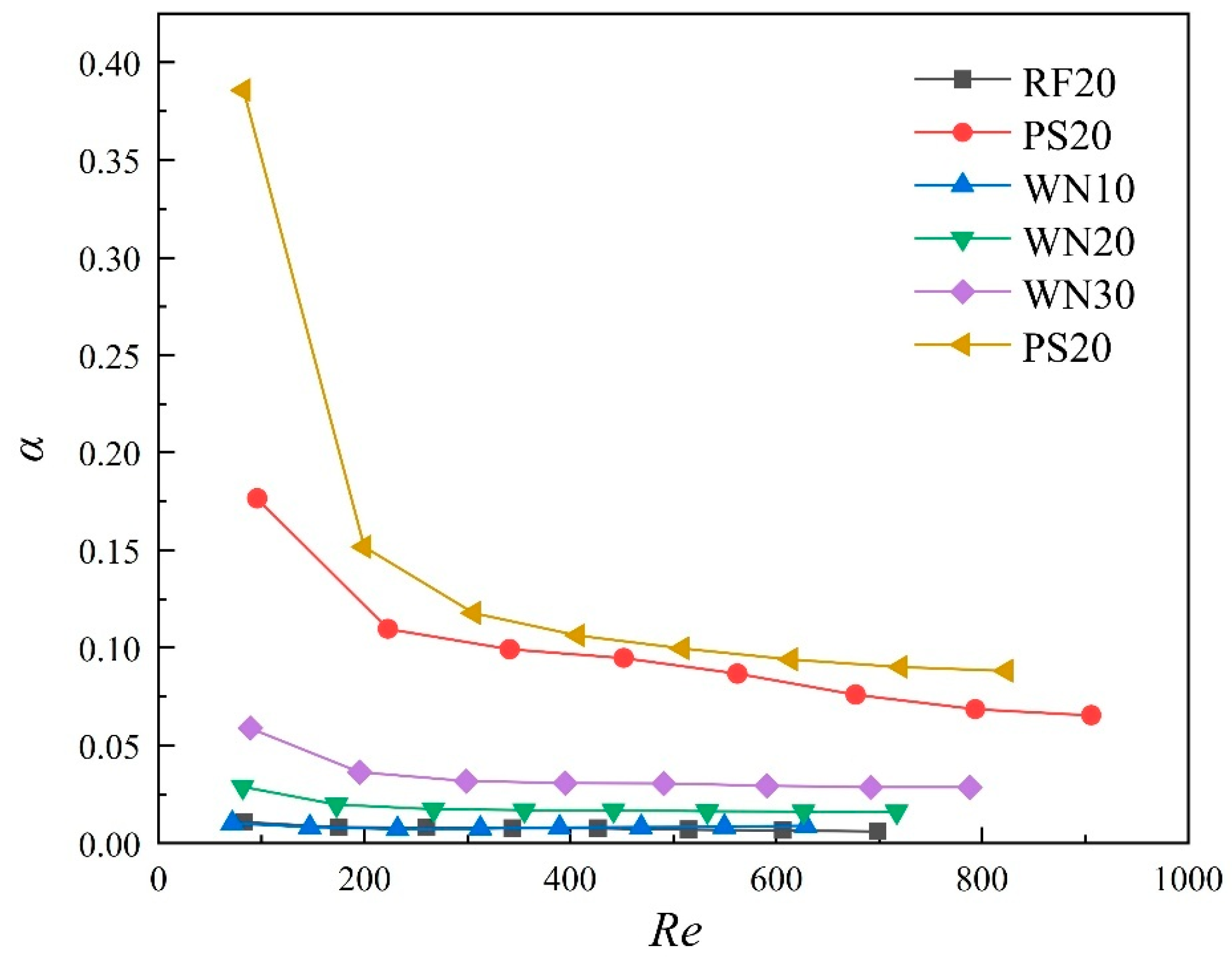
3.2.2. Fluid Flow Resistance
3.3. Heat Transfer Characteristics
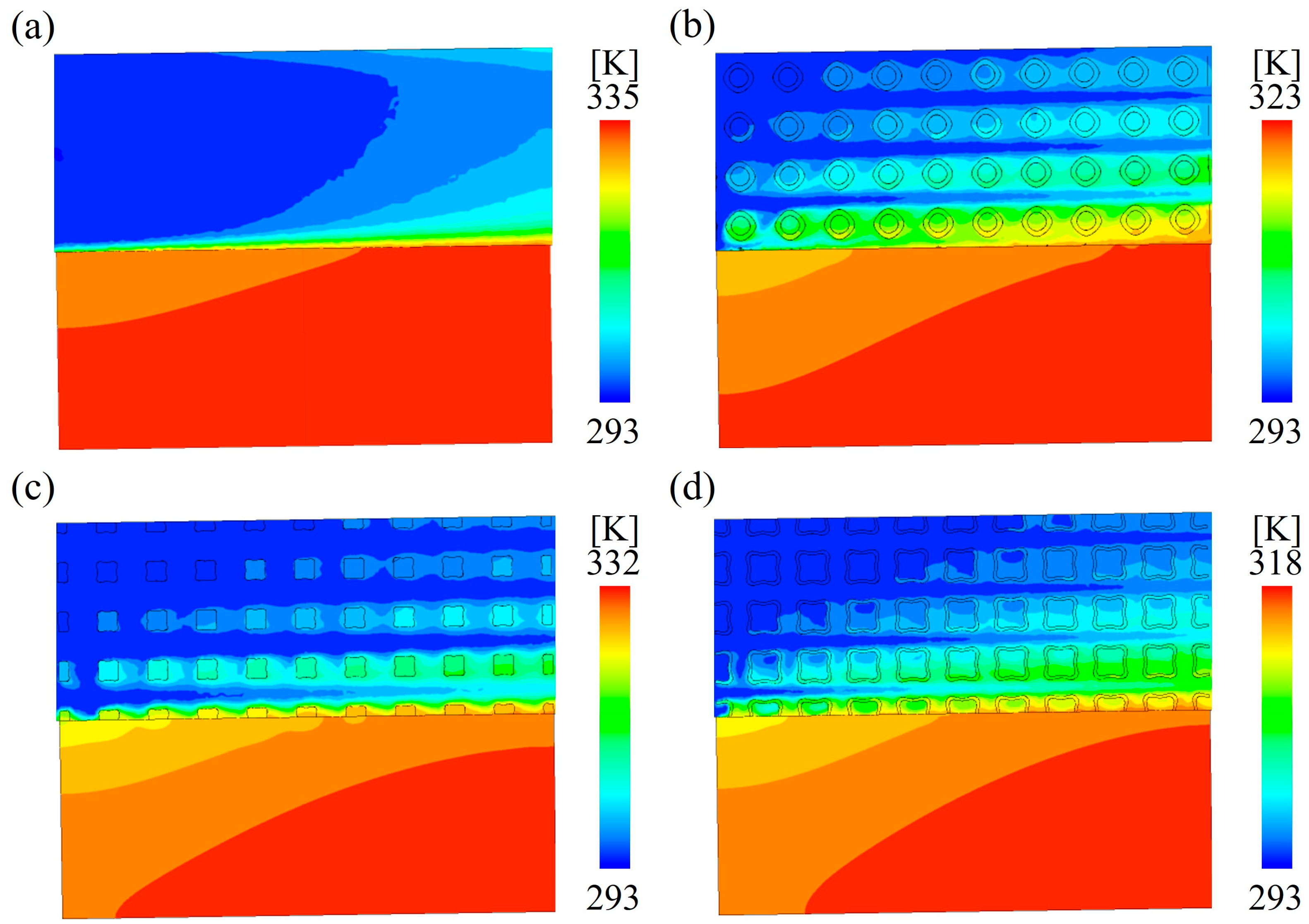
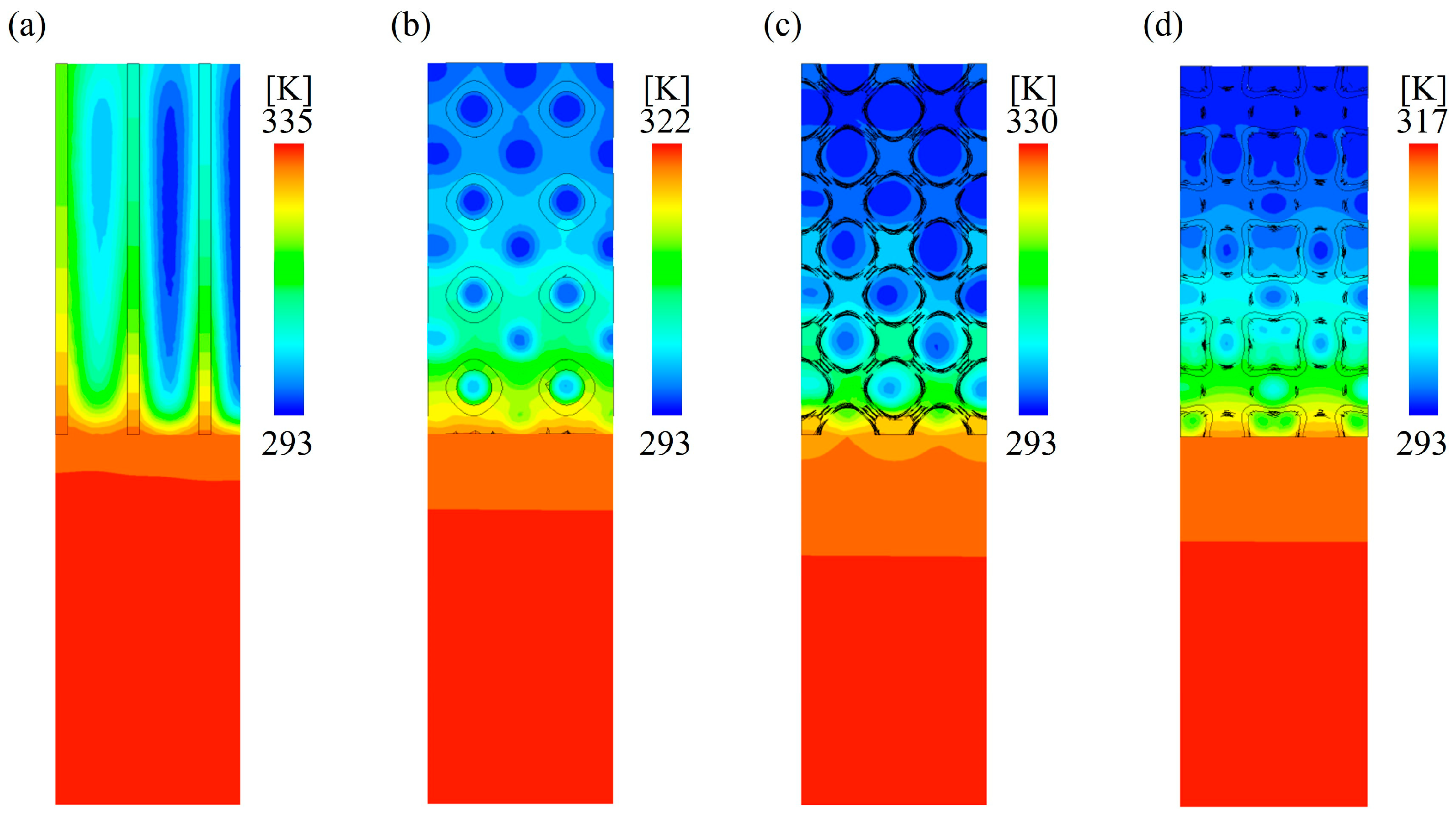
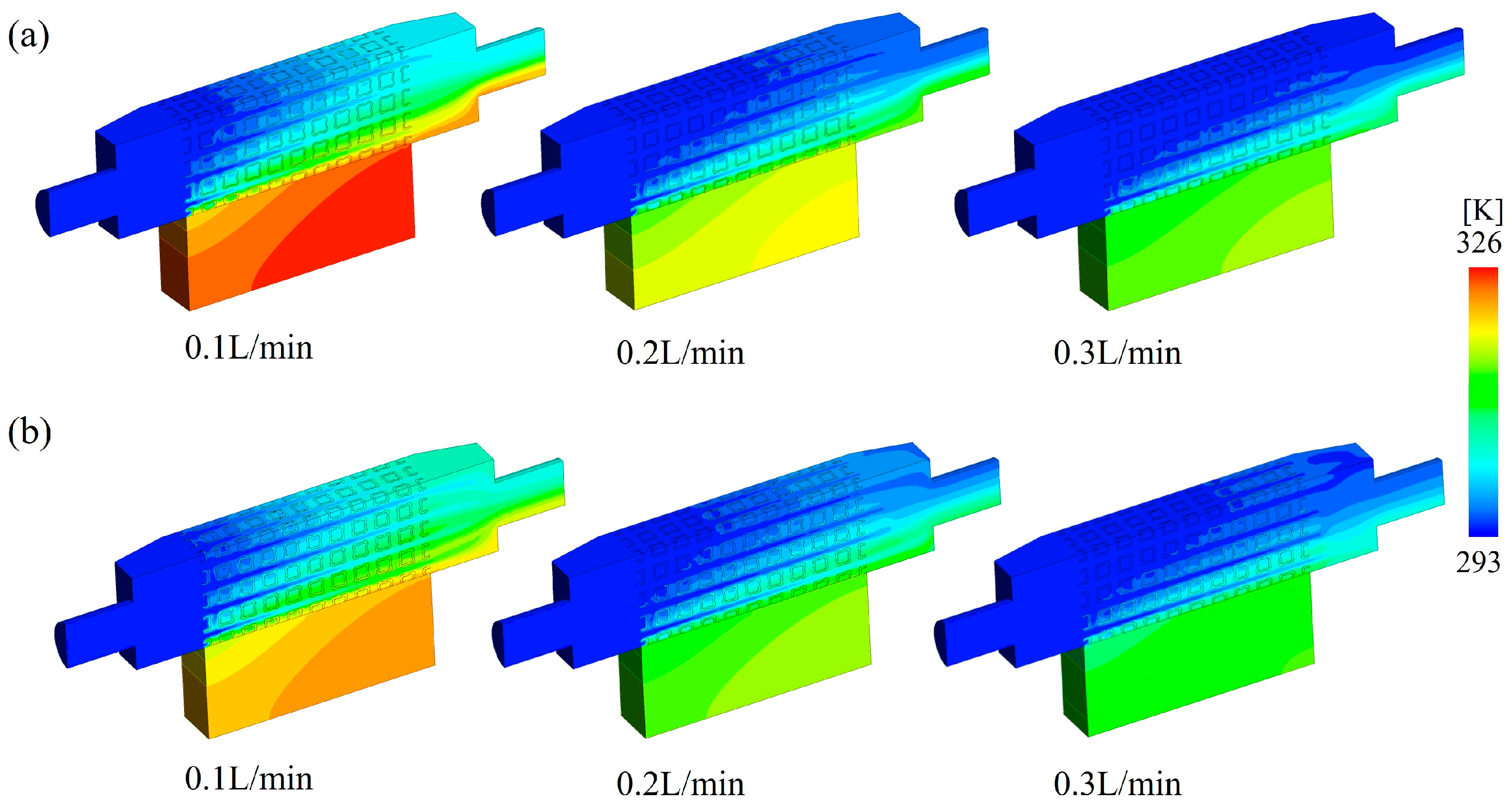
3.3.1. Temperature Distribution
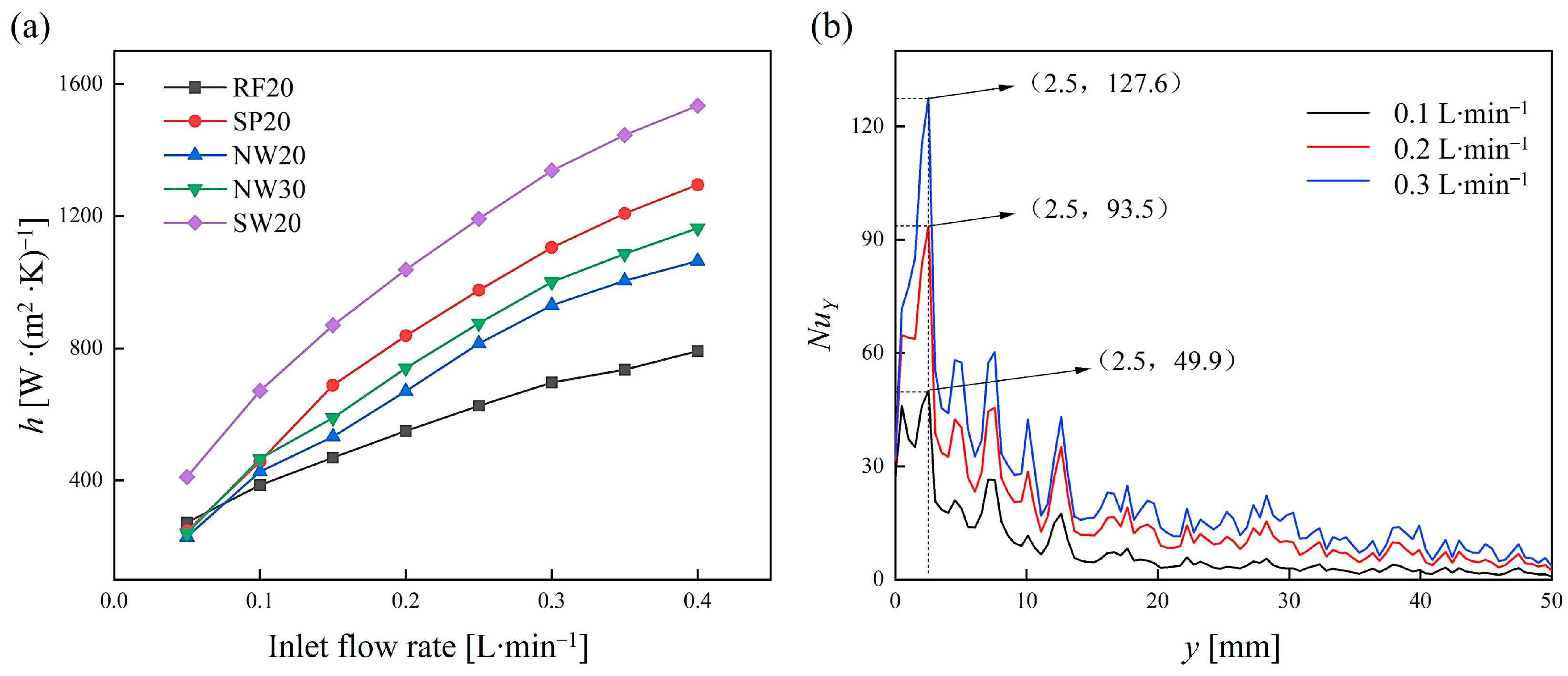
3.3.2. Convective Heat Transfer Properties
3.4. Overall Thermal Transfer Performance
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wang, X.; Li, X.; Li, Z.; Wang, Z.; Zhai, W. Superior Strength, Toughness, and Damage-Tolerance Observed in Microlattices of Aperiodic Unit Cells. Small 2024, 20, e2307369. [Google Scholar] [PubMed]
- Noronha, J.; Dash, J.; Rogers, J.; Leary, M.; Brandt, M.; Qian, M. Titanium Multi-Topology Metamaterials with Exceptional Strength. Adv. Mater. 2023, 36, e2308715. [Google Scholar]
- Sha, W.; Xiao, M.; Wang, Y.; Huang, M.; Li, Q.; Gao, L. Topology optimization methods for thermal metamaterials: A review. Int. J. Heat Mass Transf. 2024, 227, 125588. [Google Scholar]
- Yun, S.; Lee, D.; Jang, D.S.; Lee, M.; Kim, Y. Numerical analysis on thermo-fluid–structural performance of graded lattice channels produced by metal additive manufacturing. Appl. Therm. Eng. 2021, 193, 117024. [Google Scholar]
- Sha, W.; Hu, R.; Xiao, M.; Chu, S.; Zhu, Z.; Qiu, C.-W.; Gao, L. Topology-optimized thermal metamaterials traversing full-parameter anisotropic space. Npj Comput. Mater. 2022, 8, 179. [Google Scholar]
- Mirabolghasemi, A.; Akbarzadeh, A.H.; Rodrigue, D.; Therriault, D. Thermal conductivity of architected cellular metamaterials. Acta Mater. 2019, 174, 61–80. [Google Scholar]
- Kaur, M.; Yun, T.G.; Han, S.M.; Thomas, E.L.; Kim, W.S. 3D printed stretching-dominated micro-trusses. Mater. Des. 2017, 134, 272–280. [Google Scholar]
- Yan, H.; Zhang, Q.; Chen, W.; Xie, G.; Dang, J.; Lu, T.J. An X-lattice cored rectangular honeycomb with enhanced convective heat transfer performance. Appl. Therm. Eng. 2020, 166, 114687. [Google Scholar]
- Liang, D.; He, G.; Chen, W.; Chen, Y.; Chyu, M.K. Fluid flow and heat transfer performance for micro-lattice structures fabricated by Selective Laser Melting. Int. J. Therm. Sci. 2022, 172, 107312. [Google Scholar]
- Ho, J.Y.; Leong, K.C. Cylindrical porous inserts for enhancing the thermal and hydraulic performance of water-cooled cold plates. Appl. Therm. Eng. 2017, 121, 863–878. [Google Scholar]
- Shi, X.; Yang, Z.; Chen, W.; Chyu, M.K. Investigation of the effect of lattice structure on the fluid flow and heat transfer of supercritical CO2 in tubes. Appl. Therm. Eng. 2022, 207, 118132. [Google Scholar]
- Zhao, M.; Zhang, D.Z.; Li, Z.; Zhang, T.; Zhou, H.; Ren, Z. Design, mechanical properties, and optimization of BCC lattice structures with taper struts. Compos. Struct. 2022, 295, 115830. [Google Scholar]
- Ansari, D.; Duwig, C. A gyroid TPMS heat sink for electronic cooling. Energy Convers. Manag. 2024, 319, 118918. [Google Scholar]
- Kim, J.; Yoo, D.-J. 3D printed compact heat exchangers with mathematically defined core structures. J. Comput. Des. Eng. 2020, 7, 527–550. [Google Scholar]
- Zhao, M.; Li, X.; Zhang, D.Z.; Zhai, W. TPMS-based interpenetrating lattice structures: Design, mechanical properties and multiscale optimization. Int. J. Mech. Sci. 2023, 244, 108092. [Google Scholar]
- Singh, A.; Al-Ketan, O.; Karathanasopoulos, N. Mechanical performance of solid and sheet network-based stochastic interpenetrating phase composite materials. Compos. Part B Eng. 2022, 251, 110478. [Google Scholar]
- Gao, S.; Ding, J.; Qu, S.; Liu, H.; Song, X. Numerical and experimental investigation of additively manufactured shell-lattice copper heat exchanger. Int. Commun. Heat Mass Transf. 2023, 147, 106976. [Google Scholar]
- Maskery, I.; Parry, L.A.; Padrão, D.; Hague, R.J.M.; Ashcroft, I.A. FLatt Pack: A research-focussed lattice design program. Addit. Manuf. 2022, 49, 102510. [Google Scholar]
- Guo, X.; Ding, J.; Li, X.; Qu, S.; Hsi Fuh, J.Y.; Lu, W.F.; Song, X.; Zhai, W. Interpenetrating phase composites with 3D printed triply periodic minimal surface (TPMS) lattice structures. Compos. Part B Eng. 2023, 248, 110351. [Google Scholar]
- Qiu, N.; Zhang, J.; Yuan, F.; Jin, Z.; Zhang, Y.; Fang, J. Mechanical performance of triply periodic minimal surface structures with a novel hybrid gradient fabricated by selective laser melting. Eng. Struct. 2022, 263, 114377. [Google Scholar]
- Yang, N.; Du, C.; Wang, S.; Yang, Y.; Zhang, C. Mathematically defined gradient porous materials. Mater. Lett. 2016, 173, 136–140. [Google Scholar]
- Renon, C.; Jeanningros, X. A numerical investigation of heat transfer and pressure drop correlations in Gyroid and Diamond TPMS-based heat exchanger channels. Int. J. Heat Mass Transf. 2025, 239, 126599. [Google Scholar] [CrossRef]
- Moradmand, M.M.; Sohankar, A. Numerical and experimental investigations on the thermal-hydraulic performance of heat exchangers with Schwarz-P and gyroid structures. Int. J. Therm. Sci. 2024, 197, 108748. [Google Scholar]
- Lai, W.-H.; Samad, A. Development and flow optimization of “Gyroid” based additive manufacturing heat exchanger: Both computational and experimental analyses. Int. J. Therm. Sci. 2025, 213, 109835. [Google Scholar] [CrossRef]
- Oh, S.-H.; An, C.-H.; Seo, B.; Kim, J.; Park, C.Y.; Park, K. Functional morphology change of TPMS structures for design and additive manufacturing of compact heat exchangers. Addit. Manuf. 2023, 76, 103778. [Google Scholar] [CrossRef]
- Tang, W.; Zou, C.; Zhou, H.; Zhang, L.; Zeng, Y.; Sun, L.; Zhao, Y.; Yan, M.; Fu, J.; Hu, J.; et al. A novel convective heat transfer enhancement method based on precise control of Gyroid-type TPMS lattice structure. Appl. Therm. Eng. 2023, 230, 120797. [Google Scholar]
- Wang, J.; Qian, C.; Qiu, X.; Yu, B.; Yan, L.; Shi, J.; Chen, J. Numerical and experimental investigation of additive manufactured heat exchanger using triply periodic minimal surfaces (TPMS). Therm. Sci. Eng. Prog. 2024, 55, 103007. [Google Scholar] [CrossRef]
- Maskery, I.; Aremu, A.O.; Parry, L.; Wildman, R.D.; Tuck, C.J.; Ashcroft, I.A. Effective design and simulation of surface-based lattice structures featuring volume fraction and cell type grading. Mater. Des. 2018, 155, 220–232. [Google Scholar]
- Maskery, I.; Aboulkhair, N.T.; Aremu, A.O.; Tuck, C.J.; Ashcroft, I.A. Compressive failure modes and energy absorption in additively manufactured double gyroid lattices. Addit. Manuf. 2017, 16, 24–29. [Google Scholar] [CrossRef]
- Zhang, X.; Jin, X.; Xie, G.; Yan, H. Thermo-Fluidic Comparison between Sandwich Panels with Tetrahedral Lattice Cores Fabricated by Casting and Metal Sheet Folding. Energies 2017, 10, 906. [Google Scholar] [CrossRef]
- Yan, H.; Fang, K.; Wu, W.; Zhao, Z.; Feng, F. Thermal performance enhancement by modifying the spiral flow and turbulence transport in an X-lattice cellular structure. Int. J. Therm. Sci. 2024, 205, 109277. [Google Scholar]
- Hu, X.; Tian, Y.; Yang, K.; Ruan, G. Design and optimization of air-cooled heat dissipation structure of an on-board supercapacitor box. Appl. Therm. Eng. 2024, 249, 123458. [Google Scholar]
- Park, S.-H.; Seo, D.-H.; Jeong, J.H. Experimental and numerical analysis of thermal flow in open-cell porous metal during Darcy-Forchheimer transition regime. Appl. Therm. Eng. 2020, 181, 116029. [Google Scholar] [CrossRef]
- Pati, S.; Borah, A.; Boruah, M.P.; Randive, P.R. Critical review on local thermal equilibrium and local thermal non-equilibrium approaches for the analysis of forced convective flow through porous media. Int. Commun. Heat Mass Transf. 2022, 132, 105889. [Google Scholar]
- Shen, B.; Yan, H.; Xue, H.; Xie, G. The effects of geometrical topology on fluid flow and thermal performance in Kagome cored sandwich panels. Appl. Therm. Eng. 2018, 142, 79–88. [Google Scholar]
- Luis Guillermo, O.-R.; Arturo, G.-O.; James, P.-B.; Saul, P. Computational analysis and engineering modeling for the heat transfer and fluid flow through the gyroid TPMS structure. Appl. Therm. Eng. 2025, 268, 125865. [Google Scholar] [CrossRef]
- Min, R.; Wang, Z.; Yang, H.; Bao, R.; Zhang, N. Heat transfer characterization of waste heat recovery heat exchanger based on flexible hybrid triply periodic minimal surfaces (TPMS). Int. Commun. Heat Mass Transf. 2024, 157, 103007. [Google Scholar]
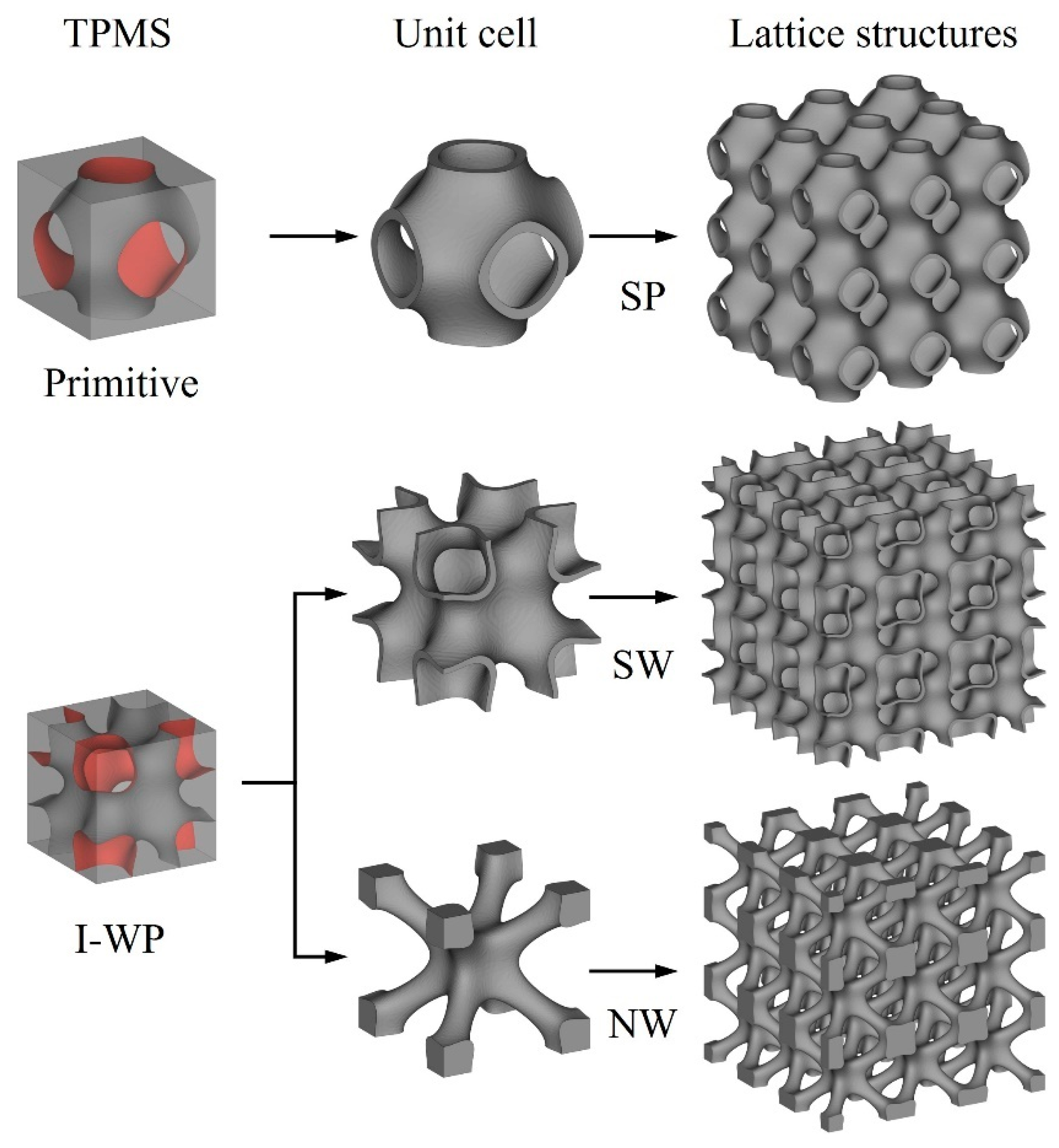

| Sample | Type | VF | Surface Area [mm2] | Dimensions [mm × mm × mm] |
|---|---|---|---|---|
| SP 20 | Sheet primitive (SP) | 0.2 | 18,566 | 20 × 50 × 20 |
| SP 30 | 0.3 | 18,367 | ||
| SW 20 | Sheet I-WP (SW) | 0.2 | 27,969 | |
| SW 30 | 0.2 | 27,228 | ||
| NW 10 | Network I-WP (NW) | 0.1 | 8665 | |
| NW 20 | 0.2 | 11,716 | ||
| NW 30 | 0.3 | 13,321 | ||
| RF10 | Rectangular fins (RF) | 0.1 | 6180 | |
| RF20 | 0.2 | 6360 | ||
| RF30 | 0.3 | 6540 |
| Material | Specific Heat [J·(kg·K)−1] | Thermal Conductivity [W·(m·K)−1] | Density [kg·m−3] | Dynamic Viscosity [Pa·s] |
|---|---|---|---|---|
| Water | 4180 | 0.599 | 998.2 | 1.003 × 10−3 |
| Cast copper | 381 | 387.6 | 8978 | |
| AlSi10Mg | 895 | 151.468 | 2670 |
| Boundary | Velocity | Pressure | Temperature |
|---|---|---|---|
| Inlet | u = w = 0 | - | |
| Outer | - | - |
| Coefficient | SW30 | SW20 | SP20 | NW20 |
|---|---|---|---|---|
| [m2] | 7.23 × 10−8 | 9.31 × 10−8 | 1.72 × 10−7 | 3.72 × 10−7 |
| [m−1] | 117.15 | 99.14 | 143.62 | 24.21 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Z.; Gao, Z.; Dai, M.; Song, B.; Yang, B.; Zhang, T.; Yuan, S.; Liu, G.; Zhao, M. Fluid Flow and Heat Transfer Performances of Aluminum Alloy Lattices with Triply Periodic Minimal Surfaces. Materials 2025, 18, 1407. https://doi.org/10.3390/ma18071407
Liu Z, Gao Z, Dai M, Song B, Yang B, Zhang T, Yuan S, Liu G, Zhao M. Fluid Flow and Heat Transfer Performances of Aluminum Alloy Lattices with Triply Periodic Minimal Surfaces. Materials. 2025; 18(7):1407. https://doi.org/10.3390/ma18071407
Chicago/Turabian StyleLiu, Zhensen, Zetian Gao, Mingqiu Dai, Bingke Song, Biqi Yang, Tao Zhang, Shuangyin Yuan, Gang Liu, and Miao Zhao. 2025. "Fluid Flow and Heat Transfer Performances of Aluminum Alloy Lattices with Triply Periodic Minimal Surfaces" Materials 18, no. 7: 1407. https://doi.org/10.3390/ma18071407
APA StyleLiu, Z., Gao, Z., Dai, M., Song, B., Yang, B., Zhang, T., Yuan, S., Liu, G., & Zhao, M. (2025). Fluid Flow and Heat Transfer Performances of Aluminum Alloy Lattices with Triply Periodic Minimal Surfaces. Materials, 18(7), 1407. https://doi.org/10.3390/ma18071407






