Evolution of the Fatigue Failure Prediction Process from Experiment to Artificial Intelligence: A Review
Abstract
1. Introduction
- -
- For surface defects,
- -
- For defects located just below the surface,
- -
- For the internal defects,
- —the Vickers hardness [Kgf/mm2];
- is the maximum expected size of inclusions contained in a volume.
- —a material-independent constant with value = 3.3 × 10−3;
- —a material-independent constant with value = 120.
- is the fatigue limit in rotational bending or tensile compression;
- —the projection of the fault in the plane perpendicular to the direction of the maximum main stress;
- C—a constant of the material.
- is the stress amplitude in MPa.
- is the critical dimension of inclusion in m2.
- α and C are the adjusted material parameters.
- is a material-dependent constant.
- Nf > 107 cycles.
- —the relative depth of the critical inclusion (d being the diameter of the minimum cross-sectional area of the specimen and dinc being the micro-defect size).
- is the fatigue stress of the material containing a crack.
- —the stress intensity factor.
- —the SIF form factor (threshold voltage intensity factor).
- —the independent variable representing the length of a crack.
- —the El-Haddad parameter represents the critical crack length of the material.
- Discontinuous phase—when nanoscale cracks start to appear.
- Continuous phase—when short, micrometer-scale cracks are formed by the random joining of nanometer-scale cracks.
- Fast phase—when long cracks appear, and the threshold of rupture is imminent.
- is the number of cycles until breakage.
- —crack length at the critical moment of rupture.
- —the length of the crack at the initial time of testing.
- —constants of material.
- —the amplitude of cyclic stress.
- —a dimensionless parameter.
2. Methods
3. Results and Discussion
- n is the number of cycles until the break.
- a and b are the Basquin parameters.
- —the fatigue limit.
- —maximum tensile strength.
- is the parameter of fatigue damage.
- —fatigue damage threshold parameter.
- —the fatigue impairment parameter for the low cycle fatigue regime.
- —the fatigue impairment parameter for the high cycle fatigue regime.
- —number of cycles to failure when strain is ;
- —the number of cycles until the intersection of the tangent of the finite-life region with the horizontal asymptote of the elastic stress.
- is the slope of the region of finite life.
- is the finite lifetime density function.
- —cumulative distribution function for a standard normal variable.
- —variance of the logarithm of finite life.
- —the value of observation.
- —stress range during the fatigue test.
- —maximum tensile strength.
- N—the number of charge cycles to break or end of test.
- —the fatigue limit.
- , —geometrical parameters.
- is the measured value of the size.
- —average value of the size.
- —standard deviation of the size.
4. Conclusions
- 1.
- AI is an important leap in the approach to steel fatigue and lifetime determination. It allows for reducing experimentation time and for obtaining viable conclusions from a smaller number of experiments.
- 2.
- AI is not a substitute for the known physical methods in the field of fatigue, but it increases the confidence in the results obtained by having a higher generalizability than all the methods tried so far.
- 3.
- The application of AI requires the mastery of software that fatigue testing laboratories have not yet generalized, so it will be some time before the methods for measuring and interpreting data obtained based on AI can be standardized.
- 4.
- The emergence of AI does not rule out experiments. It remains the basic linchpin of fatigue testing, so the endeavor to innovate in experiments must continue.
- 5.
- The main problem in using AI is to find a way to incorporate the laws that govern fatigue failure into it.
- 6.
- The results of the application of AI have shown that it cannot substitute for an experiment but can only consider the nonlinearities introduced in an experiment by structural defects.
- 7.
- The application of AI to fatigue rupture prediction in future research requires the establishment of a universally accepted standard. Today, each AI user has his or her own opinion about the variables to be considered. The industry needs certain and reproducible criteria.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| Symbol | Explanation |
| LCF | Low Cycle Fatigue |
| HCF | High Cycle Fatigue |
| VHCF | Very High Cycle Fatigue |
| SIF | Stress Intensity Factor |
| KV | Kohout–Vĕchet Fatigue Model |
| AI | Artificial Intelligence |
| CNN | Convolutional Neural Network |
| RNN | Recurrent Neural Network |
| LSTM | Long Short-Term Memory |
| DBNs | Deep Belief Networks |
| ML | Machine Learning |
| SVM | Support Vector Machine |
| ANN | Artificial Neural Network |
| RMSE | Root Mean Square Error |
| MAPE | Mean Absolute Percentage Error |
| BN | Bayesian Algorithm |
| GA | Genetic Algorithm |
| FL | Fuzzy Logic |
| CBR | Case-Based Reasoning |
| SWT | Smith–Watson–Topper |
References
- Murakami, Y.; Beretta, S. Small Defects and Inhomogeneities in Fatigue Strength: Experiments, Models and Statistical Implications. Extremes 1999, 2, 123–147. [Google Scholar] [CrossRef]
- Murakami, Y.; Endo, M. Effect of hardness and crack geometries on DKth of small cracks emanating from small defects. J. Soc. Mater. Sci. 1986, 35, 911–917. [Google Scholar] [CrossRef]
- Murakami, Y.; Endo, M. Effect of defects, inclusions, and inhomogeneities on fatigue strength. Int. J. Fatigue 1994, 16, 163–181. [Google Scholar] [CrossRef]
- Murakami, Y. Effects of small defects and nonmetallic inclusions on the fatigue strength of metals. JSME Int. Journal. Ser. 1 Solid Mech. Strength Mater. 1989, 32, 167–180. [Google Scholar] [CrossRef]
- Murakami, Y.; Usuki, H. Quantitative evaluation of effects of non-metallic inclusions on fatigue strength of high strength steels I: Basic fatigue mechanism and evaluation of the correlation between the fatigue fracture stress and the size and location of non-metallic inclusions. Int. J. Fatigue 1989, 11, 299–307. [Google Scholar] [CrossRef]
- Murakami, Y. Inclusion rating by statistics of extreme value and its application to fatigue strength prediction and quality control of materials. J. Res. Natl. Inst. Stand. Technol. 1994, 99, 345–351. [Google Scholar] [CrossRef]
- Murakami, Y.; Toryiama, T.; Coudert, E.M. Instructions for a new method of inclusion rating and correlation with the fatigue limit. J. Test. Eval. 1994, 22, 318–326. [Google Scholar] [CrossRef]
- Tanaka, K.; Akiniwa, Y. Fatigue crack propagation behavior derived from S–N data in very high cycle regime. Fatigue Fract. Eng. Mater. Struct. 2002, 25, 775–784. [Google Scholar] [CrossRef]
- Mayer, H.; Haydn, W.; Schuller, R.; Issler, S.; Furtner, B.; Bacher-Höchst, M. Very high cycle fatigue properties of bainitic high carbon–chromium steel. Int. J. Fatigue 2009, 31, 242–249. [Google Scholar] [CrossRef]
- Zhu, M.; Xuan, F.Z.; Du, Y.N.; Tu, S.T. Very high cycle fatigue behavior of a low strength welded joint at moderate temperature. Int. J. Fatigue 2012, 40, 74–83. [Google Scholar] [CrossRef]
- Wu, W.; Zhu, M.L.; Liu, X.; Xuan, F.Z. Effect of temperature on high-cycle fatigue and very high cycle fatigue behaviors of a low-strength CrNiMoV steel welded joint. Fatig. Fract. Eng. Mater. Struct. 2017, 40, 45–54. [Google Scholar] [CrossRef]
- Shiozawa, K.; Morii, Y.; Nishino, S.; Lu, L. Subsurface crack initiation and propagation mechanism in high-strength steel in a very high cycle fatigue regime. Int. J. Fatigue 2006, 28, 1521–1532. [Google Scholar] [CrossRef]
- Zhu, M.L.; Jin, L.; Xuan, F.Z. Fatigue life and mechanistic modeling of interior micro-defect induced cracking in high cycle and very high cycle regimes. Acta Mater. 2018, 157, 259–275. [Google Scholar] [CrossRef]
- Zhu, M.L.; Xuan, F.Z.; Chen, J. Influence of microstructure and micro defects on long-term fatigue behavior of a CreMoeV steel. Mater. Sci. Eng. A. 2012, 546, 90–96. [Google Scholar] [CrossRef]
- El Haddad, M.H.; Topper, T.H.; Smith, K.N. Prediction of non-propagating cracks. Eng. Fract. Mech. 1979, 11, 573–584. [Google Scholar] [CrossRef]
- Kitagawa, H.; Takahashi, S. Applicability of fracture mechanics to very small cracks or the cracks in the early stage. In Proceedings of the 2nd ICM, International Conference on Mechanical Behavior of Materials, Boston, MA, USA, 16–20 August 1976; pp. 627–631. [Google Scholar]
- Miller, K.J. The behavior of short fatigue cracks and their initiation. Part I. A review of two recent books. Fatigue Fract. Eng. Mater. Struct. 1987, 10, 75–91. [Google Scholar] [CrossRef]
- Miller, K.J. The behavior of short fatigue cracks and their initiation. Part II. A general summary. Fatigue Fract. Eng. Mater. Struct. 1987, 10, 93–113. [Google Scholar] [CrossRef]
- Cui, W.C. A state-of-the-art review on fatigue life prediction methods for metal structures. J. Mar. Sci. Technol. 2002, 7, 43–56. [Google Scholar] [CrossRef]
- Kamal, M.; Rahman, M.M. Advances in fatigue life modeling: A review. Renew. Sustain. Energy Rev. 2018, 82, 940–949. [Google Scholar] [CrossRef]
- Yao, W. Stress field intensity approach for predicting fatigue life. Int. J. Fatigue 1993, 15, 243–246. [Google Scholar] [CrossRef]
- Chan, K.S.; Tian, J.W.; Wang, B.; Liaw, P.K. Evolution of slip morphology and fatigue crack initiation in surface grains of Ni200. Met. Mater. Trans. A 2009, 40, 2545–2556. [Google Scholar] [CrossRef]
- Zhu, S.; Yu, Z.; Correia, J.; De Jesus, A.; Berto, F. Evaluation and comparison of critical plane criteria for multiaxial fatigue analysis of ductile and brittle materials. Int. J. Fatigue 2018, 112, 279–288. [Google Scholar] [CrossRef]
- Tong, X.; Wang, D.; Xu, H. Investigation of cyclic hysteresis energy in the fatigue failure process. Int. J. Fatigue 1989, 11, 353–359. [Google Scholar] [CrossRef]
- Liu, K.C. A method based on virtual strain-energy parameters for multiaxial fatigue life reduction. In Advances in Multiaxial Fatigue; McDowell, D.L., Ellis, R., Eds.; ASTM International: West Conshohocken, PA, USA, 1993; pp. 67–84. ISBN 978-0-8031-1862-1. [Google Scholar] [CrossRef]
- Glinka, G.; Shen, G.; Plumtree, A. A multiaxial fatigue strain energy density parameter related to the critical fracture plane. Fatigue Fract. Eng. Mater. Struct. 1995, 18, 37–46. [Google Scholar] [CrossRef]
- Chen, X.; Xu, S.; Huang, D. A critical plane-strain energy density criterion for multiaxial low-cycle fatigue life under non-proportional loading. Fatigue Eng. Mater. Struct. 1999, 22, 679–686. [Google Scholar] [CrossRef]
- Varvani-Farahani, A. A new energy-critical plane parameter for fatigue life assessment of various metallic materials subjected to in-phase and out-of-phase multiaxial fatigue loading conditions. Int. J. Fatigue 2000, 22, 295–305. [Google Scholar] [CrossRef]
- Jahed, H.; Varhani-Farahani, A. Upper, and lower fatigue limits model using energy-based fatigue properties. Int. J. Fatigue 2006, 28, 467–473. [Google Scholar] [CrossRef]
- Zhan, Z.; Li, H.; Lam, K.Y. Development of a novel fatigue damage model with AM effects for life prediction of commonly used alloys in aerospace. Int. J. Mech. Sci. 2019, 155, 110–124. [Google Scholar] [CrossRef]
- Kohout, J.; Věchet, S. New function for fatigue curves characterization and its multiple merits. Int. J. Fatigue 2001, 23, 175–183. [Google Scholar] [CrossRef]
- Karunananda, K.; Ohga, M.; Dissanayake, R.; Siriwardane, S.; Chun, P. New combined high and low-cycle fatigue model to estimate the life of steel bridges considering the interaction of high and low amplitudes loadings. Adv. Struct. Eng. 2012, 15, 287–302. [Google Scholar] [CrossRef]
- Smith, K.N.; Watson, P.; Topper, T.H. A stress-strain function for the fatigue of metals. J. Mater. 1970, 5, 767–778. Available online: https://www.researchgate.net/publication/309476268 (accessed on 5 January 2025).
- Dowling, N.E.; Calhoun, C.A.; Arcari, A. Mean stress effects in stress-life fatigue and the Walker equation. Fatigue Fract. Eng. Mater. Struct. 2009, 32, 163–179. [Google Scholar] [CrossRef]
- Park, J.; Nelson, D. Evaluation of an energy-based approach and a critical plane approach for predicting constant amplitude multiaxial fatigue life. Int. J. Fatigue 2000, 22, 3–18. [Google Scholar] [CrossRef]
- Correiaa, J.A.F.O.; Raposoa, P.; Muniz-Calventeb, M.; Blasónb, S.; Lesiukc, G.; De Jesusa, A.M.P.; Moreiraa, P.M.G.P.; Calçadaa, R.A.B.; Cantelib, A.F. A generalization of the fatigue Kohout-Vechet model for several fatigue damage parameters. Eng. Fract. Mech. 2017, 185, 284–300. [Google Scholar] [CrossRef]
- Loren, S.; Lundstrom, M. Modelling curved S–N curve. Fatigue Fract. Eng. Mater. Struct. 2005, 28, 437–443. [Google Scholar] [CrossRef]
- Qian, G.A.; Lei, W.S. A statistical model of fatigue failure incorporating effects of specimen size and load amplitude on fatigue life. Philos. Mag. 2019, 99, 2089–2125. [Google Scholar] [CrossRef]
- Gong, H.F.; Chen, Z.S.; Zhu, Q.X.; He, Y.L. A Monte Carlo and PSO based virtual sample generation method for enhancing energy prediction and energy optimization on small data problem: An empirical study of petrochemical industries. Appl. Energy. [CrossRef]
- Chen, H.; Yang, Y.L.; Cao, S.L.; Gao, K.; Xu, S.; Li, Y.; Zhang, R. Fatigue life prediction of aluminum alloy 6061 based on defects analysis. Int. J. Fatigue 2021, 147, 106189. [Google Scholar] [CrossRef]
- Ebid, A.M.; Deifalla, A.F.; Mahdi, A.H. Evaluating Shear Strength of Light-Weight and Nor-mal-Weight Concretes through Artificial Intelligence. Sustainability 2022, 14, 14010. [Google Scholar] [CrossRef]
- Badra, N.; Haggag, S.Y.A.; Deifalla, A.F.; Salem, N.M. Development of machine learning models for reliable prediction of the punching shear strength of FRP-reinforced concrete slabs without shear reinforcements. Measurement 2022, 201, 111723. [Google Scholar] [CrossRef]
- Salem, N.M.; Deifalla, A.F. Evaluation of the strength of slab-column connections with FRPs using machine learning algorithms. Polymers 2022, 14, 1517. [Google Scholar] [CrossRef] [PubMed]
- Jia, Y.F.; Fu, R.; Ling, C.; Shen, Z.; Zheng, L.; Zhong, Z.; Hong, Y. Fatigue life prediction based on a deep learning method for Ti-6Al-4V fabricated by laser powder bed fusion up to very-high-cycle fatigue Regime. Int. J. Fatigue 2023, 172, 107645. [Google Scholar] [CrossRef]
- Sun, X.Y.; Zhou, K.; Shi, S.W.; Song, K.; Chen, X. A new cyclical generative adversarial network-based data augmentation method for multiaxial fatigue life prediction. Int. J. Fatigue 2022, 162, 106996. [Google Scholar] [CrossRef]
- Li, J.; Yang, Z.M.; Qian, G.A.; Berto, F. Machine learning based very-high-cycle fatigue life prediction of Ti-6Al-4V alloy fabricated by selective laser melting. in Int. J. Fatigue 2022, 158, 106764. [Google Scholar] [CrossRef]
- Mishra, S.; Molinaro, R. Estimates on the generalization error of physics-informed neural networks for approximating a class of inverse problems for PDEs. IMA J. Numer. Anal. 2022, 42, 981–1022. [Google Scholar] [CrossRef]
- Wang, L.Y.; Zhu, S.P.; Luo, C.; Liao, D.; Wang, Q. Physics-guided machine learning frameworks for fatigue life prediction of AM materials. Int. J. Fatigue 2023, 172, 107658. [Google Scholar] [CrossRef]
- Wang, C.; Yang, Y.; Chen, H.; Xu, S.; Li, Y.; Zhang, R.; Ling, M. Fatigue life prediction is driven by mesoscopic defect data. Eng. Appl. Artif. Intell. 2024, 131, 107773. [Google Scholar] [CrossRef]
- Epremian, E.; Mehl, R.F. A Statistical Interpretation of the Effect of Understressing on Fatigue Strength. In Symposium on Fatigue with Emphasis on Statistical Approach-II; ASTM International: West Conshohocken, PA, USA, 1952; pp. 58–69. ISBN 978-0-8031-6251-8. [Google Scholar] [CrossRef]
- Parmentier, G.; Huther, M.; Huther, I.; Lefebvre, F. Best Practice on Statistical Analysis of Fatigue Data. In Best Practice Guideline for Statistical Analyses of Fatigue Results; Springer: Cham, Switzerland, 2023; ISSN 2365-4368. [Google Scholar]
- Paolino, D.S.; Chiandussi, G.; Rossetto, M. A unified statistical model for S-N fatigue curves probabilistic definition. Fatigue Fract. Eng. Mater. Struct. 2012, 36, 187–201. [Google Scholar] [CrossRef]
- Pascual, F.; Meeker, W. Analysis of fatigue data with runouts based on a model with nonconstant standard deviation and a fatigue limit parameter. J. Test. Eval. 1997, 25, 292–301. [Google Scholar] [CrossRef]
- Castillo, E.; Fernández-Canteli, A. A Unified Statistical Methodology for Modeling Fatigue Damage; Springer: Berlin/Heidelberg, Germany, 2009; ISBN 978-1-4020-9182-7. [Google Scholar] [CrossRef]
- Castillo, E.; López Aenlle, M.; Ramos, A.; Fernández-Canteli, A.; Kieselbach, R.; Esslinger, V. Specimen length effect on parameter estimation in modeling fatigue strength by Weibull distribution. Int. J. Fatigue 2006, 28, 1047–1058. [Google Scholar] [CrossRef]
- Toasa Caiza, P.D.; Ummenhofer, T. Consideration of the runouts and their subsequent retests into S-N curves modeling based on a three-parameter Weibull distribution. Int. J. Fatigue 2018, 106, 70–80. [Google Scholar] [CrossRef]
- Lu, S.; Su, Y.; Yang, M.; Li, Y. A Modified Walker Model Dealing with Mean Stress Effect in Fatigue Life Prediction for Aeroengine Disks. Math. Probl. Eng. 2018, 2018, 5148278. [Google Scholar] [CrossRef]
- Gao, Z.; Jiang, X.; Cui, M. A novel nonlinear fatigue cumulative damage model based on machine learning. Int. J. Fatigue 2024, 188, 201295706. [Google Scholar] [CrossRef]
- Ince, A.; Glinka, G. A generalized fatigue damage parameter for multiaxial fatigue life prediction under proportional and non-proportional loadings. Int. J. Fatigue 2018, 62, 34–41. [Google Scholar] [CrossRef]
- Toasa Caiza, P.D.; Ummenhofer, T.A. A probabilistic Stüssi function for modeling the S-N curves and its application on specimens made of steel S355J2+N. Int. J. Fatigue 2018, 117, 121–134. [Google Scholar] [CrossRef]
- Toasa Caiza, P.D.; Ummenhofer, T. General probability weighted moments for the three-parameter Weibull distribution and their application in S-N curves modeling. Int. J. Fatigue 2011, 33, 1533–1538. [Google Scholar] [CrossRef]
- Lee, J.A.; Almond, D.P.; Harris, B. The use of neural networks for the prediction of fatigue lives of composite materials. Compos. Part. A Appl. Sci. Manuf. 1999, 30, 1159–1169. [Google Scholar] [CrossRef]
- Freire, R.C.S., Jr.; Neto, A.D.D.; Freire de Aquino, E.M. Building of constant life diagrams of fatigue using artificial neural networks. Int. J. Fatigue 2005, 27, 746–751. [Google Scholar] [CrossRef]
- Gurney, K. An Introduction to Neural Networks, 1st ed.; CRC Press: Boca Raton, FL, USA, 1995; ISBN 9780262315883. [Google Scholar] [CrossRef]
- Anthony, M.; Bartlett, P.L. Neural Network Learning: Theoretical Foundations; Cambridge University Press: Cambridge, UK, 2010; ISBN 052157353X. [Google Scholar]
- Kashyzadeh, K.R.; Ghorbani, S. New neural network-based algorithm for predicting the fatigue life of aluminum alloys in terms of machining parameters. Eng. Fail. Anal. 2023, 146, 107128. [Google Scholar] [CrossRef]
- Sherstinsky, A. Fundamentals of recurrent neural network (RNN) and long short-term memory (LSTM) network. Phys. D 2020, 404, 132306. [Google Scholar] [CrossRef]
- Agrawal, A.; Deshpande, P.D.; Cecen, A.; Basavarsu, G.P.; Choudhary, A.N.; Kalidindi, S.R. Exploration of data science techniques to predict fatigue strength of steel from composition and processing parameters. Integr. Mater. Manuf. Innov. 2014, 3, 90–108. [Google Scholar] [CrossRef]
- He, L.; Wang, Z.L.; Akebono, H.; Sugeta, A. Machine learning-based prediction of fatigue life and fatigue limit for steels. J. Mater. Sci. Technol. 2021, 90, 9–19. [Google Scholar] [CrossRef]
- Wang, Z.L.; Ogawa, T.; Adachi, Y. A Machine Learning Tool for Materials Informatics. Adv. Theory Simul. 2020, 3, 1900177. [Google Scholar] [CrossRef]
- Yan, F.; Song, K.; Liu, Y.; Chen, S.; Chen, J. Predictions and mechanism analysis of the fatigue strength of steel based on machine learning. J. Mater. Sci. 2020, 55, 15334–15349. [Google Scholar] [CrossRef]
- Zhou, K.; Sun, X.; Shi, S.; Kai, S.; Xu, C. Machine learning-based genetic feature identification and fatigue life prediction. Fatigue Fract. Eng. Mater. Struct. 2021, 44, 2524–2537. [Google Scholar] [CrossRef]
- Huang, Z.; Yan, J.; Zhang, J.; Han, C.; Peng, J.; Cheng, J.; Wang, Z.; Luo, M.; Yin, P. Deep Learning-Based Fatigue Strength Prediction for Ferrous Alloy. Processes 2024, 12, 2214. [Google Scholar] [CrossRef]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning: An Introduction to a Broad Range of Topics in Deep Learning, Covering Mathematical and Conceptual Background, Deep Learning Techniques Used in Industry, and Research Perspectives; MIT Press: Cambridge, MA, USA, 2016; p. 775. ISBN 9780262035613. [Google Scholar]
- Yang, J.; Kang, G.; Liu, Y.; Kan, Q. A novel method of multiaxial fatigue life prediction based on deep learning. Int. J. Fatigue 2021, 151, 106356. [Google Scholar] [CrossRef]
- Albert, J.H.; Leonard, T.; Hsu, J.S.J. Bayesian methods: An analysis for statisticians and interdisciplinary researchers. J. Am. Stat. Assoc. 2000, 95, 679–680. [Google Scholar] [CrossRef]
- Guo, J.; Zan, X.; Wang, L.; Lei, L.; Ou, C.; Bai, S. A random forest regression with Bayesian optimization-based method for fatigue strength prediction of ferrous alloys. Eng. Fract. Mech. 2023, 293, 109714. [Google Scholar] [CrossRef]
- Fu, G.Z.; Zhang, X.; Li, W.; Guo, J. Bayesian Fusion of Degradation and Failure Time Data for Reliability Assessment of Industrial Equipment Considering Individual Differences. Processes 2024, 12, 268. [Google Scholar] [CrossRef]
- Gan, L.; Wu, H.; Zhong, Z. Fatigue life prediction considering mean stress effect based on random forests and kernel extreme learning machine. Int. J. Fatigue 2022, 158, 2748–2766. [Google Scholar] [CrossRef]

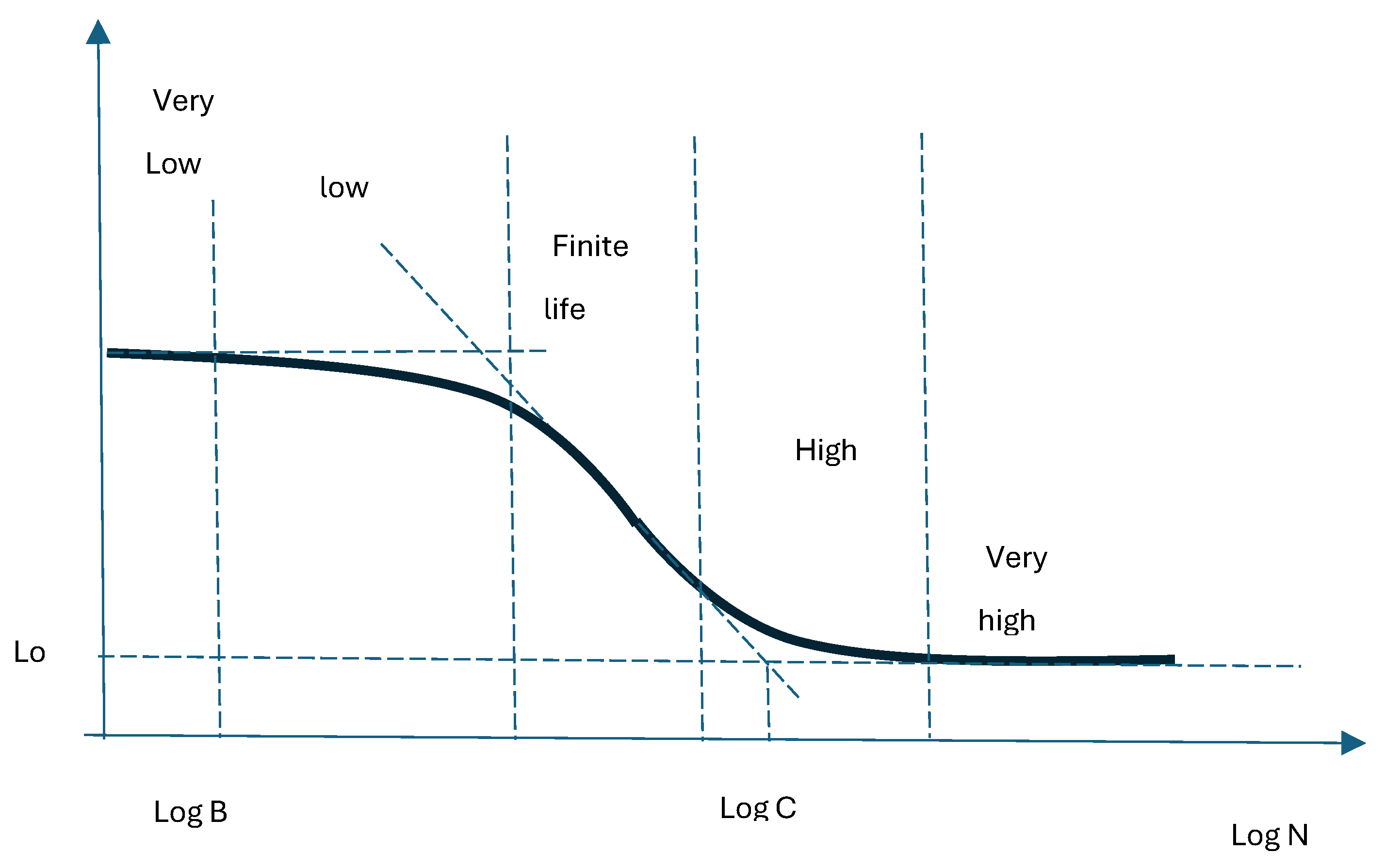

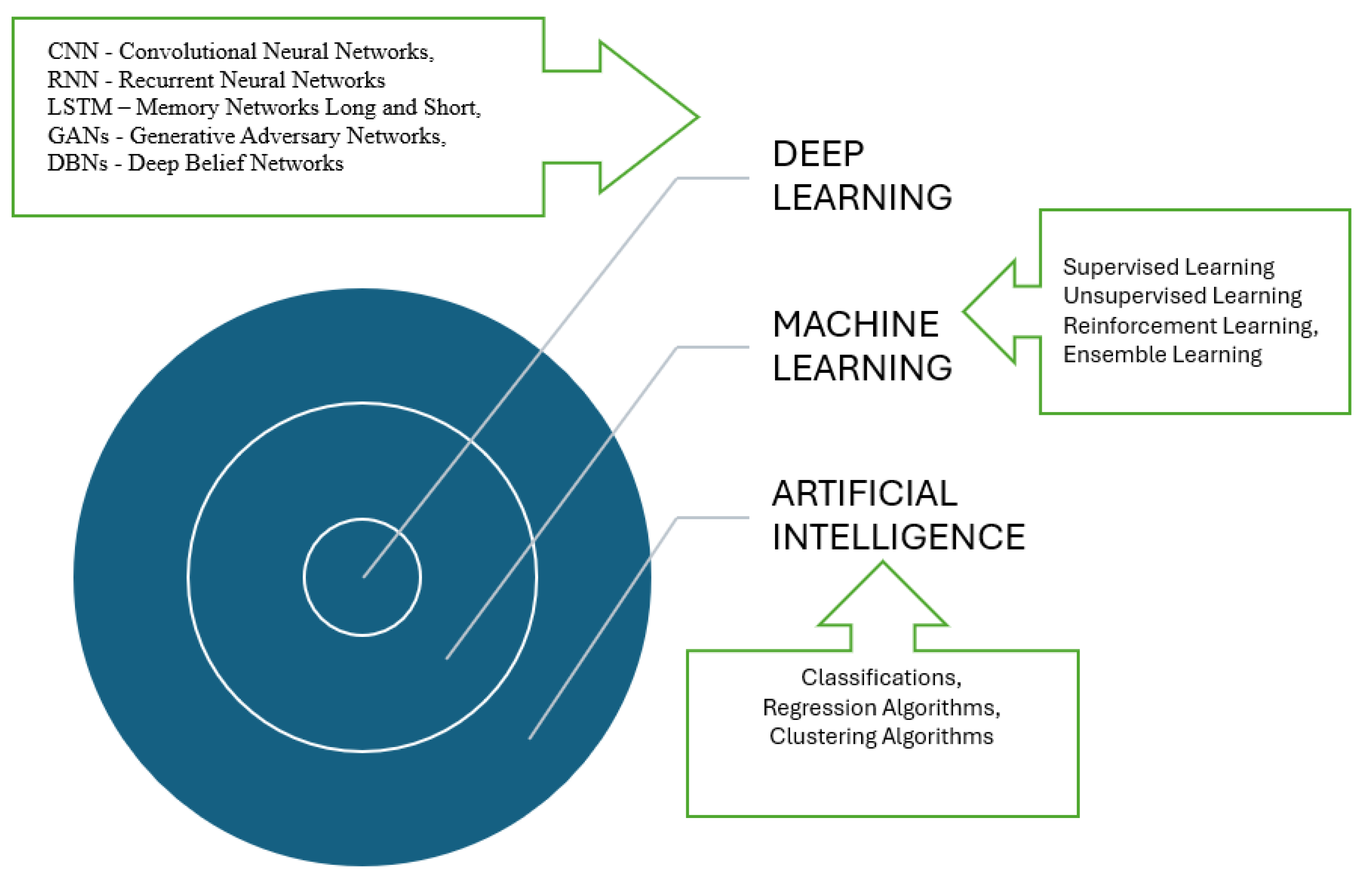
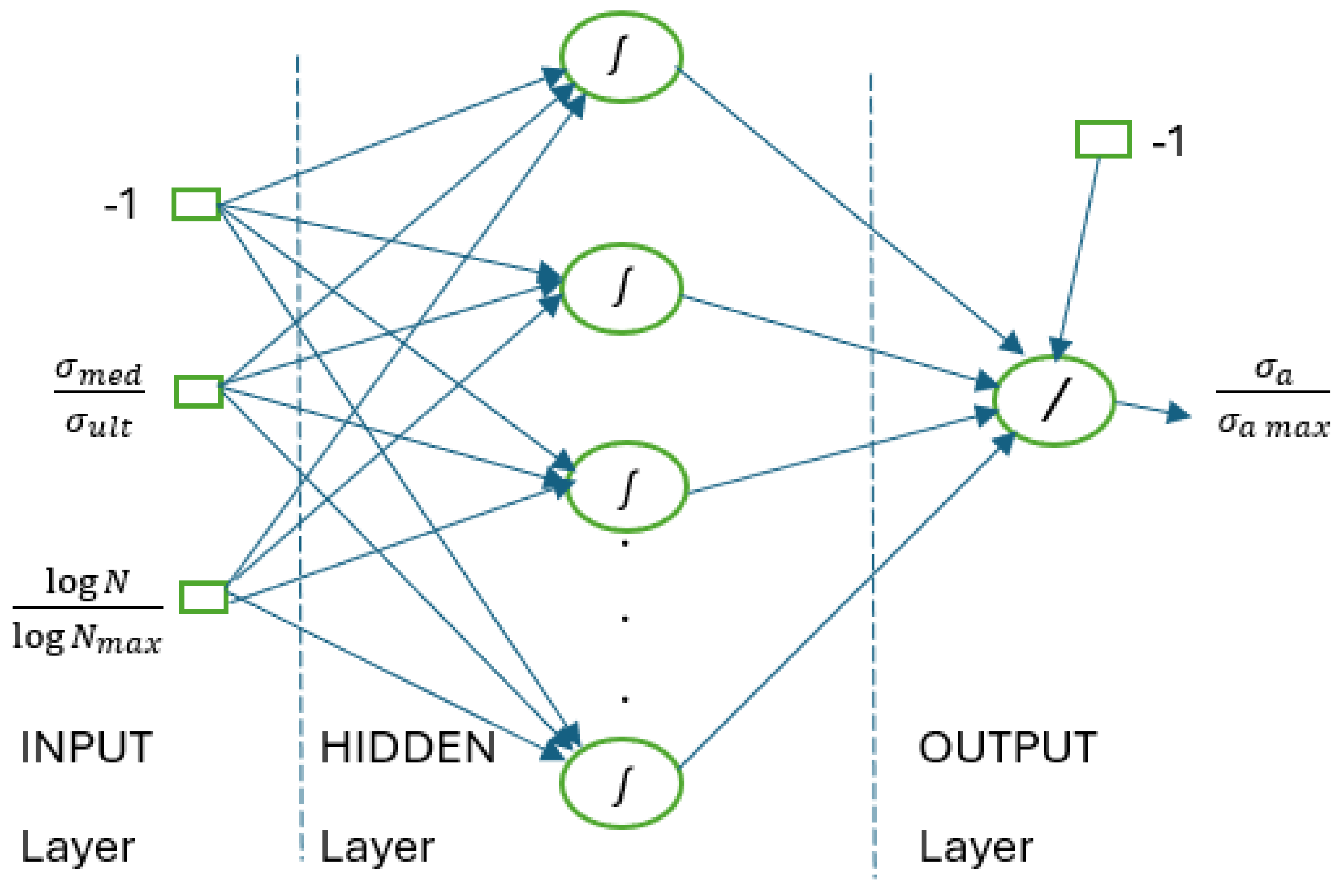

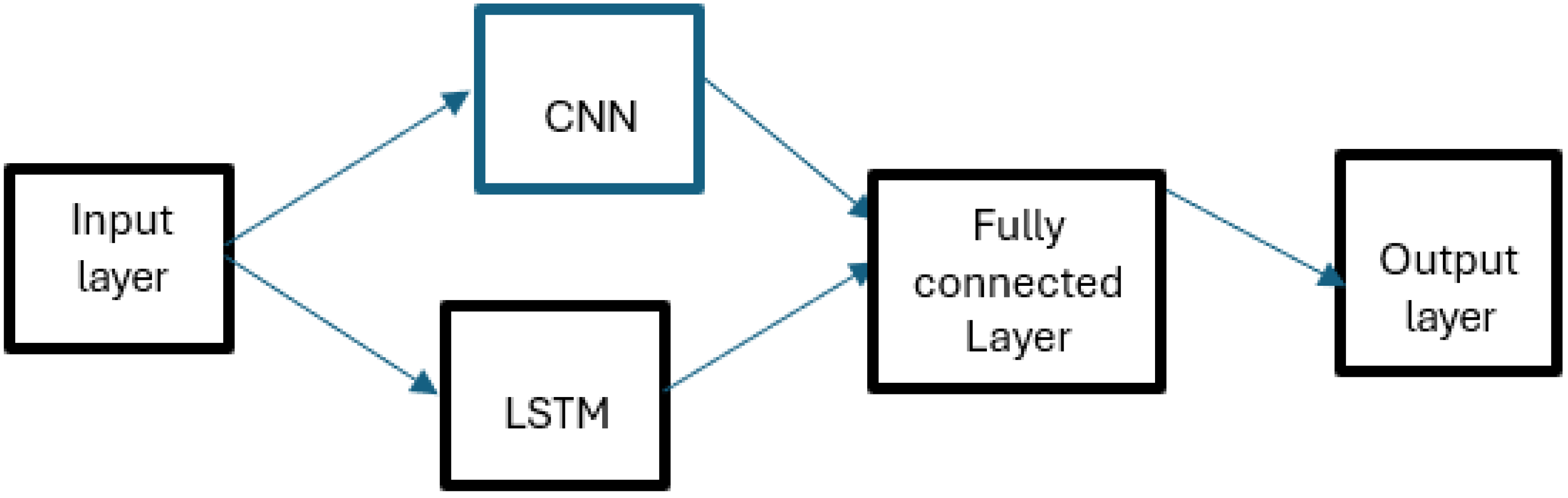
| Nr. Crt. | Forecast Path | Details |
|---|---|---|
| 1 | The inductive method | Experiments were generalized inductively, with approximately valid conclusions for a whole class of steel. Empirical equations were used, but these were limited by idealizations and phenomenological assumptions, which affected their accuracy in relation to real phenomena. |
| 2 | The deductive method | From the experiments, general theories were deduced, with a greater or lesser degree of validity and accuracy in estimating the moment of breaking. |
| 3 | The simulation method | Using powerful software, experimental conditions and important process parameters can be simulated, and predictions have been attempted. The simulations, often based on finite elements, are limited by the reliability of the model and cannot capture variational laws. The simplifications that are resorted to give rise to uncertainties. |
| 4 | The use of Artificial Intelligence (AI) | Starting from big data processing, predictions can be made using artificial intelligence methods, the most widely used of which is machine learning. The biggest flaw of the machine learning method is that it is a kind of “black box” whose correlations and interferences drawn from the processed data are not based on physical interpretation. |
| Nr. Crt. | The Approach | Comment | Formulas |
|---|---|---|---|
| 1 | Applied stress –fatigue life [20] | It is the most commonly used in papers, generating the so-called S-N curves, where S is the test stress symbol and N is the fatigue life expressed in several cycles. Basquin established the formula, which is useful when the tests are in the elastic range. | = —Young’s modulus. —range of elastic deformation. —fatigue resistance coefficient. b—the exponent of fatigue resistance. |
| 2 | Deformation–fatigue life [21] | The method considers both elasticity and plasticity. The Manson–Coffin equation. | —ductile breakage coefficient. c—the exponent of ductile breakup. |
| 3 | Field intensity [22] | It is mainly used for notched parts and considers the stress distribution in the notches, which leads to the formation of fatigue cracks. | —the local region of deterioration. —the deterioration function. —the weight function. V—the volume of the region . |
| 4 | The micro approach [23] | It refers to the motion of slip bands that accumulate energy due to the obstruction of their motion, by granular boundaries, and thus generate a distortion. | Represents the accumulation of plastic deformation stress in the slip band. —the width of the slip band. w - distance. —the plastic deformation range. —the Taylor factor. |
| 5 | The critical plane [24] | The Fatemi Society (FS) model is applied to multi-axial shear fatigue failure considering the shear strain amplitude. | , represent the maximum shear stresses and normal stresses, respectively. , —shear strain and normal strain amplitude. , —shear fatigue and ductile shear strength. —the shear modulus. |
| 6 | The energy approach [25,26,27,28,29,30] | Fatigue is the absorption and accumulation of energy. When the accumulation reaches a critical value, breakdown occurs. The equation describes the energy–life curve. | is the energy of cyclic hysteresis, , —constants. |
| 7 | The mechanics of continuous damage [31] | Fatigue fracture is analyzed with defect formation and propagation. Nonlinear damage evolves by changing the load-carrying capacity. | is the function of the tension state. —a constant. —the state of determination. |
| Calculation Formula | The Meaning of Terms |
|---|---|
| Smith–Watson–Topper (SWT) [33] | —the maximum cycle stress. —the total deformation amplitude. —the fatigue resistance —the number of cycles to failure. —the limit strain for the low-cycle fatigue regime. |
| Walker-like strain [34] | —the stress ratio. —the material parameters. —Walker constant adjustment. —the modulus of elasticity. |
| Energy-based [35] | —the stress range. —the cyclic strain-hardening exponent. —the total deformation energy range. —the range of elastic strain energy. —the plastic strain energy range. —the range of plastic deformation. |
| Calculation Formula | The Meaning of Terms |
|---|---|
| Walker-like strain [31] | —Walker-type deformation parameter. —Walker-type final plastic strain amplitude for the low-cycle fatigue regime. —Walker-type final plastic strain amplitude for the high-cycle fatigue regime. |
| Smith–Watson–Topper (SWT) [31] | —fatigue damage parameter SWT. —the fatigue damage limit parameter. —short cycle fatigue damage parameter. —high cycle fatigue damage parameter. |
| Energy-based [31] | , —low cycle and high cycle fatigue energy parameters, respectively. |
| The Model | Hypotheses | Meaning of Terms |
|---|---|---|
| Goodman [47] | Expresses equivalent stress using the ultimate tensile strength of the material, the stress amplitude, and the average stress. | is the final tensile strength. —the average stress. —the stress amplitude. —the equivalent stress. |
| Morrow–Gerber [47] | Replaces the ultimate tensile strength with breaking strength | —the true breaking strength. |
| Manson–Halford [48] | Based on crack propagation theory. | —the initial crack length. —crack size during fatigue loading, considered 0.18 inches. —number of cycles at which the crack reaches the value an underload S. N—material lifetime under load S. |
| SWT [47] | Calculates the equivalent stress using maximum stress and stress amplitude. | —maximum stress. |
| Walker [48] | The Walker model considers that the average stress is material dependent. It therefore introduces a parameter which varies from 0 to 1, with small values of the intervalue indicating that the material is more dependent on the average stress. | Like above |
| (GSE) Generalized energy damage parameter [49] | It is a parameter that considers both the normal and the shear energy occurring in the experimental plane. | —maximum shear stress. —normal maximum effort. —the strain energy parameter. —elastic shear energy. —shear energy in the plastic state. —normal elastic strain energy. —normal strain energy in the plastic state. |
| Authors | Problem Solved | The Type of AI Utilized |
|---|---|---|
| Gong et al., 2017 [39] | Solving the small dataset problem to improve the accuracy of efficiency analysis. | Virtual sampling generation technology |
| Chen et al., 2021 [40] | Established a fatigue life prediction model by considering defects. | Support Vector Machine (SVR) |
| Ebid et al., 2022 [41]; Badra et al., 2022 [42] | Predicting the compressive and shear strength of a plate. | Artificial Neural Network (ANN) |
| Salem and Deifalla, 2022 [43] | Predicting the bending strength of plates (99% accuracy). | Integrated reinforcement shaft model |
| Jia et al., 2023 [44] | Predicting the relationship between average material stress and stress amplitude. | Deep neural network model |
| Sun et al., 2022 [45] | Predictive data augmentation method that generates high-quality samples based on the original data. | Generative adversarial network (GAN) |
| Li et al., 2022 [46] | Increasing the accuracy of the predictive model by extending the sparse dataset. | Monte Carlo simulation |
| Mishra și Molinaro, 2022 [47] | How neural networks are trained on supervised learning problems concerning the laws of physics. | Physics-based neural networks (PINNs) |
| Wang et al., 2023 [48] | Paris–Erdogan formula and the normalized S-N curve. | Physically guided machine learning frameworks |
| Ratio used | 3R | 4R | 5R | 6R |
| 10 | 10 | 10 | 2 | |
| −2 | −2 | −2 | 10 | |
| 0.1 | 0.1 | −1 | −2 | |
| 0.5 | 0.1 | −1 | ||
| 0.5 | 0.1 | |||
| 0.5 |
| Parameters Working | Working Interval | The Optimal Values | |||
|---|---|---|---|---|---|
| Learning Rate | 0.0001 | 0.001 | 0.01 | 0.001 | |
| Dropout Rate | 0.1 | 0.5 | 0.2 | ||
| Convolution Kernel Size | 2 | 7 | 3 | ||
| Number of Convolution Filters | 8 | 128 | 64 | ||
| Number of LSTM Units | 32 | 160 | 64 | ||
| Number of Fully Connected Layers | 4 | 16 | 2 | ||
| Univoc Mono Systems | |
|---|---|
| BN Bayesian network | It consists of a combination of graph theory and the probability of relationships between network nodes. |
| ANN Artificial Neural Network | See above examples. |
| GA Genetic Algorithm | It has been successfully applied to damage detection in structures. |
| FL Fuzzy Logic | If sufficient experimental tests and measurements are available, FL can contribute to fault diagnosis. |
| CBR Case-Based Reasoning | It is a method that can reduce the dependence of failure analysis on extensive experimental information. |
| Hybrid Systems | |
| ANN + GA + FL | Real-time crack identification. |
| GA + neuro-fuzzy (ANFIS) | It was used to detect bearing faults. With this hybrid method, the average testing accuracy increased by about 60%. |
| ANN + GA | Allows detection, identification, and level of gear failure. |
| CBR + GA | It was used to identify faulty aeronautical components. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Samoila, C.; Ursutiu, D.; Tudorache, I. Evolution of the Fatigue Failure Prediction Process from Experiment to Artificial Intelligence: A Review. Materials 2025, 18, 1153. https://doi.org/10.3390/ma18051153
Samoila C, Ursutiu D, Tudorache I. Evolution of the Fatigue Failure Prediction Process from Experiment to Artificial Intelligence: A Review. Materials. 2025; 18(5):1153. https://doi.org/10.3390/ma18051153
Chicago/Turabian StyleSamoila, Cornel, Doru Ursutiu, and Iuliana Tudorache (Nistor). 2025. "Evolution of the Fatigue Failure Prediction Process from Experiment to Artificial Intelligence: A Review" Materials 18, no. 5: 1153. https://doi.org/10.3390/ma18051153
APA StyleSamoila, C., Ursutiu, D., & Tudorache, I. (2025). Evolution of the Fatigue Failure Prediction Process from Experiment to Artificial Intelligence: A Review. Materials, 18(5), 1153. https://doi.org/10.3390/ma18051153








