Study on the One-Dimensional Impact Compression Characteristics of Coral Sand Under Conditions of Different Relative Density
Abstract
1. Introduction
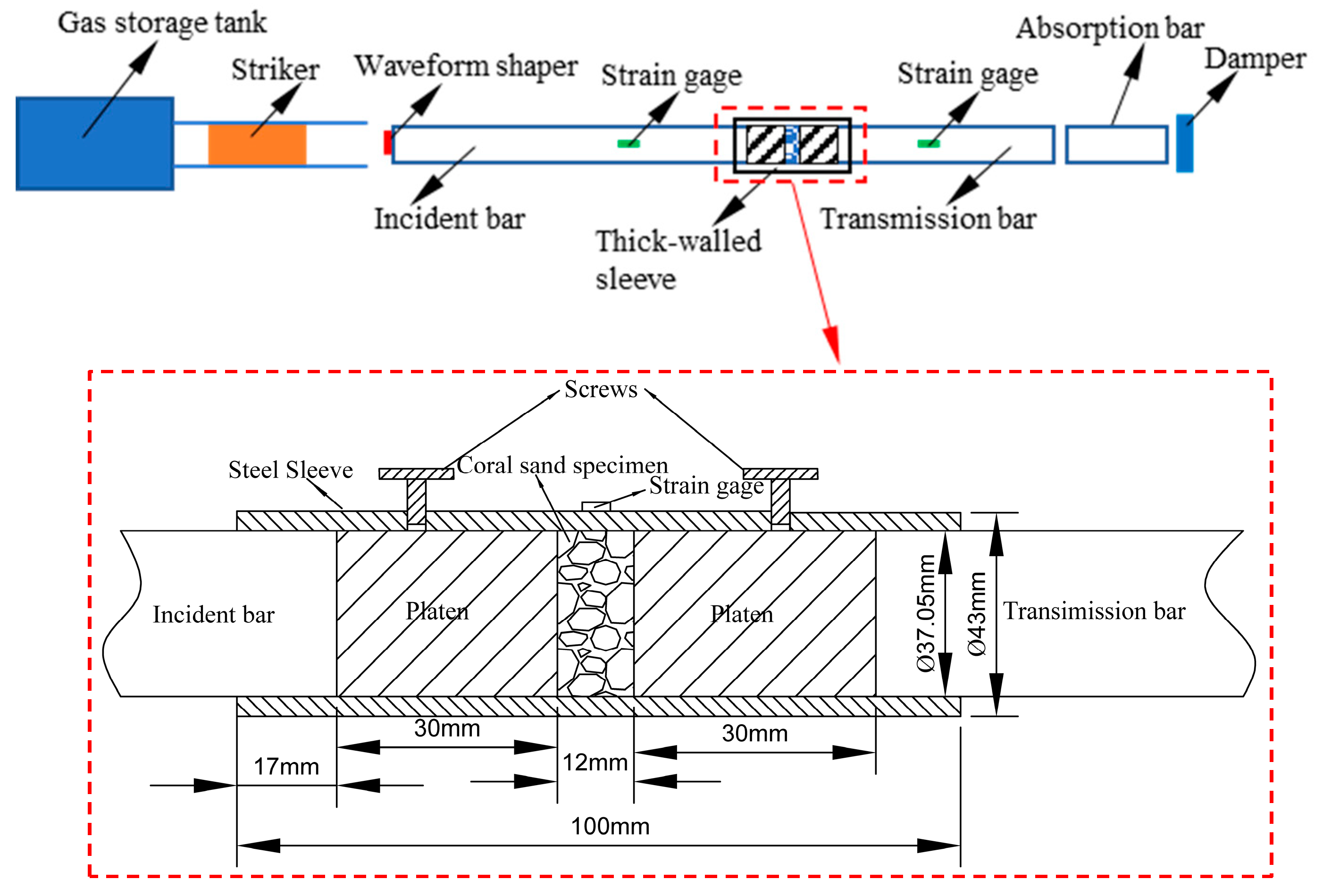
2. Experimental Setup and Specimens
2.1. Experimental Setup
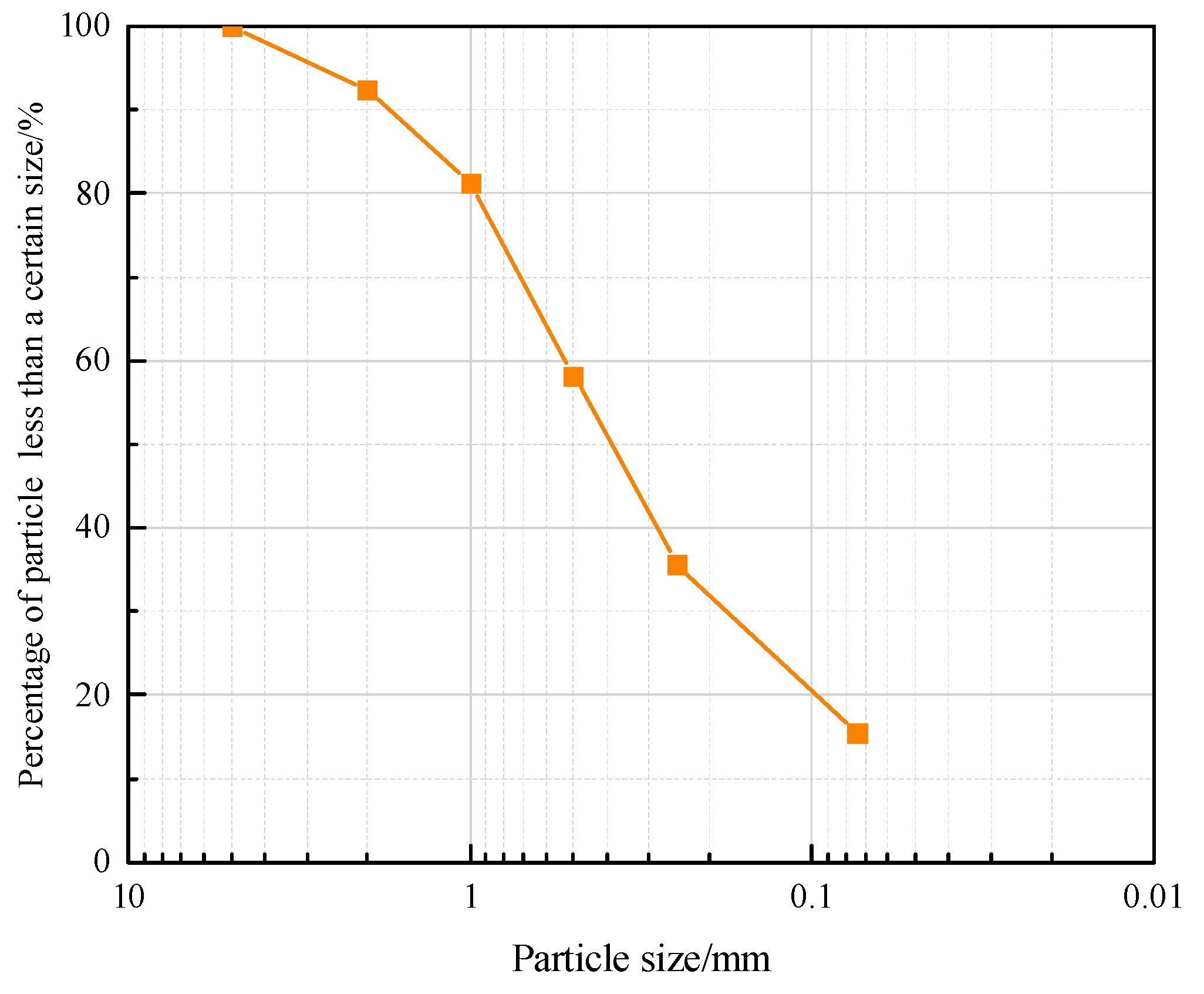
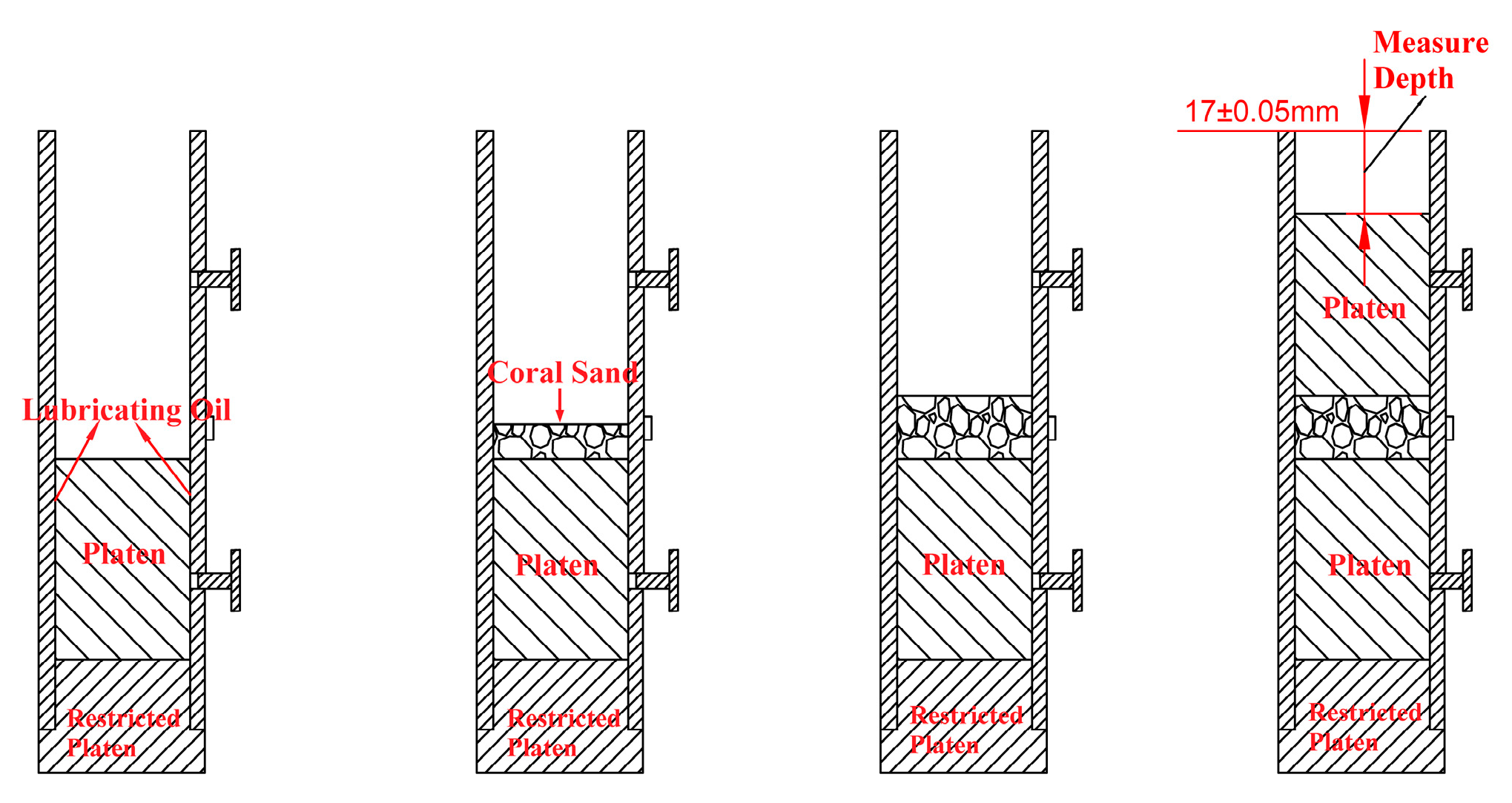
2.2. Specimen Preparation
3. Results and Discussion
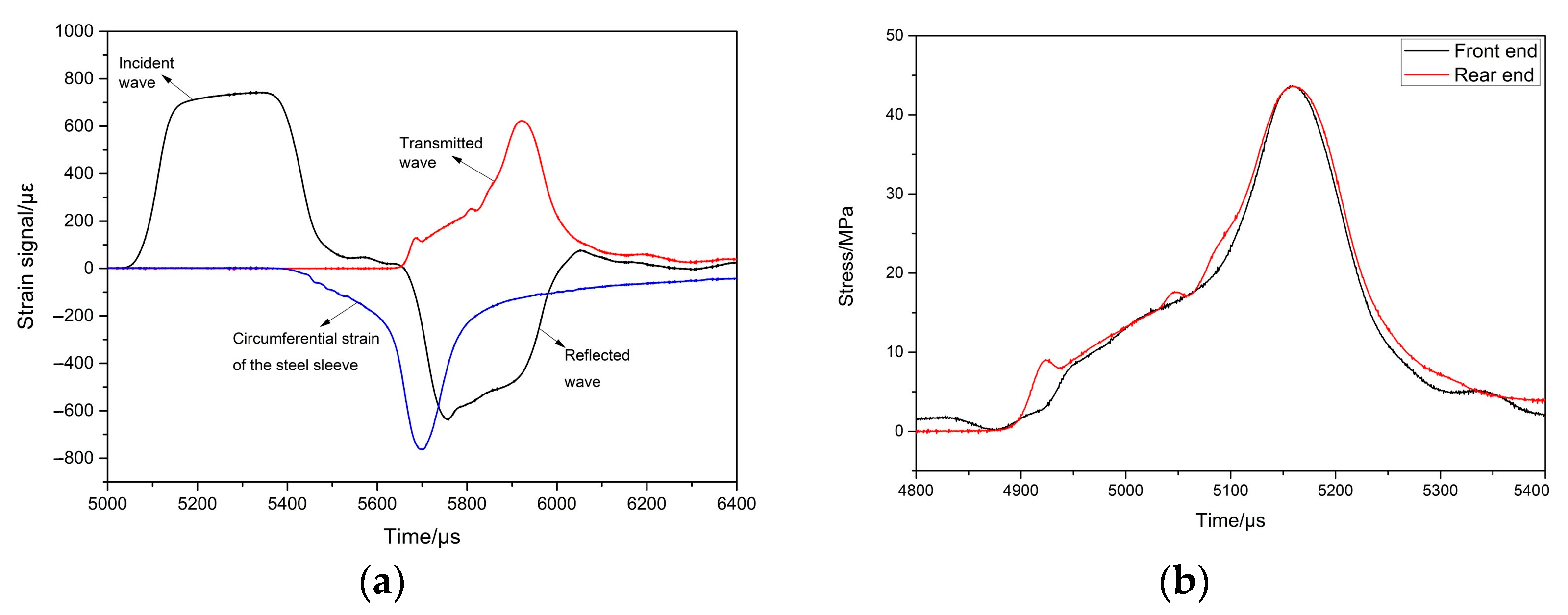
3.1. Validity of Experimental Results
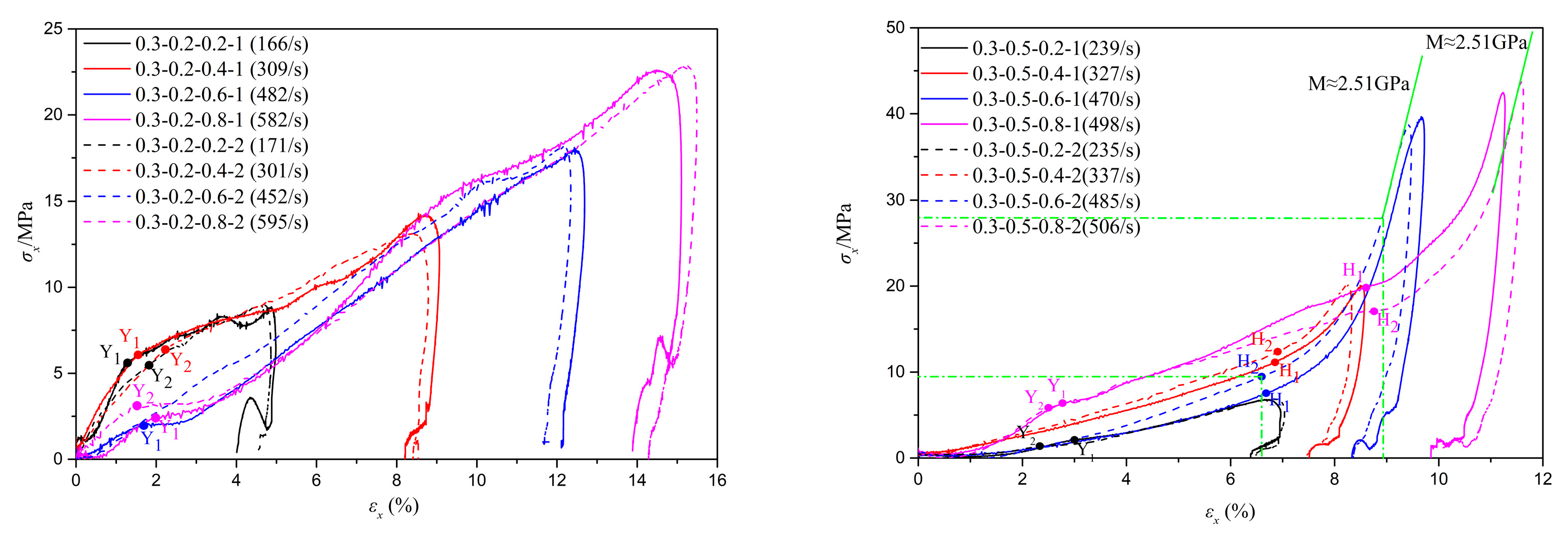
3.2. Typical Test Results
3.3. The Influence of Relative Density
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhang, J.M. Study on the Fundamental Mechanical Characteristics of Calcareous Sand and the Influence of Particle Breakage. Master’s Thesis, Chinese Academy of Science, Beijing, China, 2004. [Google Scholar]
- Wang, X.Z.; Jiao, Y.Y.; Wang, R.; Hu, M.J.; Meng, Q.S.; Tan, F.Y. Engineering characteristics of the calcareous sand in Nansha Islands, South China Sea. Eng. Geol. 2011, 120, 40–47. [Google Scholar] [CrossRef]
- Wang, X.Z.; Wang, X.; Jin, Z.C.; Zhu, C.Q.; Wang, R.; Meng, Q. Investigation of engineering characteristics of calcareous soils from fringing reef. Ocean Eng. 2017, 134, 77–86. [Google Scholar] [CrossRef]
- Wang, X.; Wu, Y.X.; Lu, Y.; Cui, J.; Wang, X.; Zhu, C. Strength and dilatancy of coral sand in the South China Sea. Bull. Eng. Geol. Environ. 2021, 80, 8279–8299. [Google Scholar] [CrossRef]
- Wang, X.; Wu, Y.; Cui, J.; Zhu, C.Q.; Wang, X.Z. Shape Characteristics of Coral Sand from the South China Sea. J. Mar. Sci. Eng. 2020, 8, 803. [Google Scholar] [CrossRef]
- Ma, L.J.; Li, Z.; Luo, Z.M.; Wei, H.Z.; Duan, L.Q. Experimental study of strain rate effects on mechanical properties of coral particles. Chin. J. Rock Soil Mech. 2019, 40, 4637–4643. [Google Scholar] [CrossRef]
- Xiao, Y.; Yuan, Z.X.; Chu, J.; Liu, H.L.; Huang, J.Y.; Luo, S.N.; Wang, S.; Lin, J. Particle breakage and energy dissipation of carbonate sands under quasi-static and dynamic compression. Acta Geotech. 2019, 14, 1741–1755. [Google Scholar] [CrossRef]
- Xiao, Y.; Liu, H.; Xiao, P.; Xiang, J. Fractal crushing of carbonate sands under impact loading. Géotechnique Lett. 2016, 6, 199–204. [Google Scholar] [CrossRef]
- Zhou, B.; Ku, Q.; Li, C.H.; Wang, H.B.; Dong, Y.K.; Cheng, Z. Single-particle crushing behaviour of carbonate sands studied by X-ray microtomography and a combined finite-discrete element method. Acta Geotech. 2022, 17, 3195–3209. [Google Scholar] [CrossRef]
- Lv, Y.R.; Wang, C.; Huang, H.X.; Zuo, D.J. Study on particle structure and crushing behaviors of coral sand. Chin. J. Rock Soil Mech. 2021, 42, 352–360. [Google Scholar] [CrossRef]
- Ma, L.J.; Li, Z.; Wang, M.Y.; Wei, H.Z.; Fan, P.X. Effects of size and loading rate on the mechanical properties of single coral particles. Powder Technol. 2019, 342, 961–971. [Google Scholar] [CrossRef]
- Wang, C.Y.; Ding, X.M.; Xiao, Y.; Peng, Y.; Liu, H.L. Effects of relative densities on particle breaking behaviour of non-uniform grading coral sand. Powder Technol. 2021, 382, 524–531. [Google Scholar] [CrossRef]
- Chen, X.; Shen, J.H.; Wang, X.; Yao, T.; Xu, D.X. Effect of Saturation on Shear Behavior and Particle Breakage of Coral Sand. J. Mar. Sci. Eng. 2022, 10, 1280. [Google Scholar] [CrossRef]
- Gao, R.; Ye, J.H. Mechanical behaviors of coral sand and relationship between particle breakage and plastic work. Eng. Geol. 2023, 316, 107063. [Google Scholar] [CrossRef]
- Wu, Y.; Cui, J.; Li, N.; Wang, X.; Wu, Y.H.; Guo, S.Y. Experimental study on the mechanical behavior and particle breakage characteristics of hydraulic filled coral sand on a coral reef island in the South China Sea. Rock Soil Mech. 2020, 41, 3181–3191. [Google Scholar] [CrossRef]
- Bo, H. Research on the Particle Breakage Mechanical Characteristics and Constitutive Model of Calcareous Sand Under Triaxial Conditions. Master’s Thesis, Chinese Academy of Science, Beijing, China, 2008. [Google Scholar]
- Yu, F.W. Particle breakage in triaxial shear of a coral sand. Soils Found. 2018, 58, 866–880. [Google Scholar] [CrossRef]
- Yu, H.Z. Experimental Research on Dynamic Behavior of Saturated Calcareous Sand under Complex Stress Conditions. Master’s Thesis, Huazhong University of Science and Technology, Wuhan, China, 2006. [Google Scholar]
- Li, J.G. Experimental Research on Dynamical Behavior of Saturated Calcareous Sand Under Wave Loading. Master’s Thesis, Chinese Academy of Science, Beijing, China, 2004. [Google Scholar]
- Wang, G.; Wang, Z.N.; Ye, Q.G.; Zhang, J.J. Particle breakage evolution of coral sand using triaxial compression tests. J. Rock Mech. Geotech. Eng. 2021, 13, 321–334. [Google Scholar] [CrossRef]
- Omidvar, M.; Iskander, M.; Bless, S. Stress-strain behavior of sand at high strain rates. Int. J. Impact Eng. 2012, 49, 192–213. [Google Scholar] [CrossRef]
- Dong, K.; Ren, H.Q.; Ruan, W.J.; Ning, H.J.; Guo, R.Q.; Huang, K. Study on strain rate effect of coral sand. Chin. J. Explos. Shock Waves 2020, 40, 093102-1. [Google Scholar] [CrossRef]
- Wei, J.Q.; Wang, M.Y.; Qiu, Y.Y.; Zhao, Z.Y. Impact compressive response of calcareous sand. Chin. J. Vib. Shock 2018, 37, 7–12. [Google Scholar] [CrossRef]
- Wei, J.Q.; Lv, Y.R.; Liu, G.Q.; Zhang, L.; Li, L. One-dimensional impact responses and energy absorption of calcareous sand. Chin. J. Rock Soil Mech. 2019, 40, 191–198. [Google Scholar] [CrossRef]
- Wen, Z.; Qiu, Y.Y.; Zi, M.; Zhao, Z.Y.; Wang, M.Y. Experimental study on quasi-one-dimensional strain compression of calcareous sand. Chin. J. Explos. Shock Waves 2019, 39, 033101. [Google Scholar] [CrossRef]
- Lv, Y.R.; Wang, M.Y.; Wei, J.Q.; Liao, B. Experimental techniques of SHPB for calcareous sand and its dynamic behaviors. Chin. J. Explos. Shock Waves 2018, 38, 1262–1270. [Google Scholar] [CrossRef]
- Lv, Y.R.; Li, Z.Z.; Li, L. One-dimensional compression behavior of calcareous sand and its experimental technology under high stress conditions. Chin. J. Rock Mech. Eng. 2019, 38, 3142–3150. [Google Scholar] [CrossRef]
- Lv, Y.R.; Liu, J.G.; Xiong, Z.M. One-dimensional dynamic compressive behavior of dry calcareous sand at high strain rates. J. Rock Mech. Geotech. Eng. 2019, 11, 192–201. [Google Scholar] [CrossRef]
- Li, X.; Lv, Y.R.; Su, Y.C.; Zou, K.H.; Wang, Y.; Huang, W.X. Coupling effects of morphology and inner pore distribution on the mechanical response of calcareous sand particles. J. Rock Mech. Geotech. Eng. 2023, 15, 1565–1579. [Google Scholar] [CrossRef]
- Lv, Y.R.; Li, X.; Fan, C.F.; Su, Y.C. Effects of internal pores on the mechanical properties of marine calcareous sand particles. Acta Geotech. 2021, 16, 3209–3228. [Google Scholar] [CrossRef]
- Lv, Y.R.; Wang, Y.; Zuo, D. Effects of particle size on dynamic constitutive relation and energy absorption of calcareous sand. Powder Technol. 2019, 356, 21–30. [Google Scholar] [CrossRef]
- Lv, Y.R.; Li, X.; Wang, Y. Particle breakage of calcareous sand at high strain rates. Powder Technol. 2020, 366, 776–787. [Google Scholar] [CrossRef]
- Lv, Y.R.; Hu, J.M.; Zhang, D.D.; Wang, Y.; Su, Y.C. Particle breakage of calcareous sand from low-high strain rates. J. Rock Mech. Geotech. Eng. 2024, 16, 5249–5263. [Google Scholar] [CrossRef]
- Zhao, Z.Y.; Qiu, Y.Y.; Zi, M.; Xing, H.D.; Wang, M.Y. Experimental study on dynamic compression of unsaturated calcareous sand. Chin. J. Explos. Shock Waves 2020, 40, 023102. [Google Scholar] [CrossRef]
- Song, B.; Chen, W.N.; Luk, V. Impact compressive response of dry sand. Mech. Mater. 2009, 41, 777–785. [Google Scholar] [CrossRef]
- Huang, J.; Xu, S.; Hu, S. Effects of grain size and gradation on the dynamic responses of quartz sands. Int. J. Impact Eng. 2013, 59, 1–10. [Google Scholar] [CrossRef]
- Luo, H.Y.; Cooper, W.L.; Lu, H.B. Effects of particle size and moisture on the compressive behavior of dense Eglin sand under confinement at high strain rates. Int. J. Impact Eng. 2014, 65, 40–55. [Google Scholar] [CrossRef]
- Wang, W.; Zhang, Z.H.; Huo, Q.; Song, X.D.; Yang, J.C.; Wang, X.F.; Wang, J.H.; Wang, X. Dynamic Compressive Mechanical Properties of UR50 Ultra-Early-Strength Cement-Based Concrete Material under High Strain Rate on SHPB Test. Materials 2022, 15, 6154. [Google Scholar] [CrossRef]
- Zhang, H.; Ren, H.Q.; Mu, C.M.; Wu, X.Y.; Huang, K.; Wang, F. Experiment Study on the Influence of Density and Confining Pressure on Triaxial Shear Properties of Calcareous Sand. Materials 2023, 16, 1683. [Google Scholar] [CrossRef]
- Ravi-Chandar, K.; Ma, Z. Inelastic Deformation in Polymers under Multiaxial Compression. Mech. Time-Depend. Mater. 2000, 4, 333–357. [Google Scholar] [CrossRef]
- Veyera, G.E. Uniaxial Stress-Strain Behavior of Unsaturated Soils at High Strain Rates: WR-TL-93-3523; Defense Technical Information Center: Fort Belvoir, VA, USA, 1994. [Google Scholar]
- Barr, A.D.; Clarke, S.D.; Tyas, A.; Warren, J.A. Effect of moisture content on high strain rate compressibility and particle breakage in loose sand. Exp. Mech. 2018, 58, 1331–1334. [Google Scholar] [CrossRef]
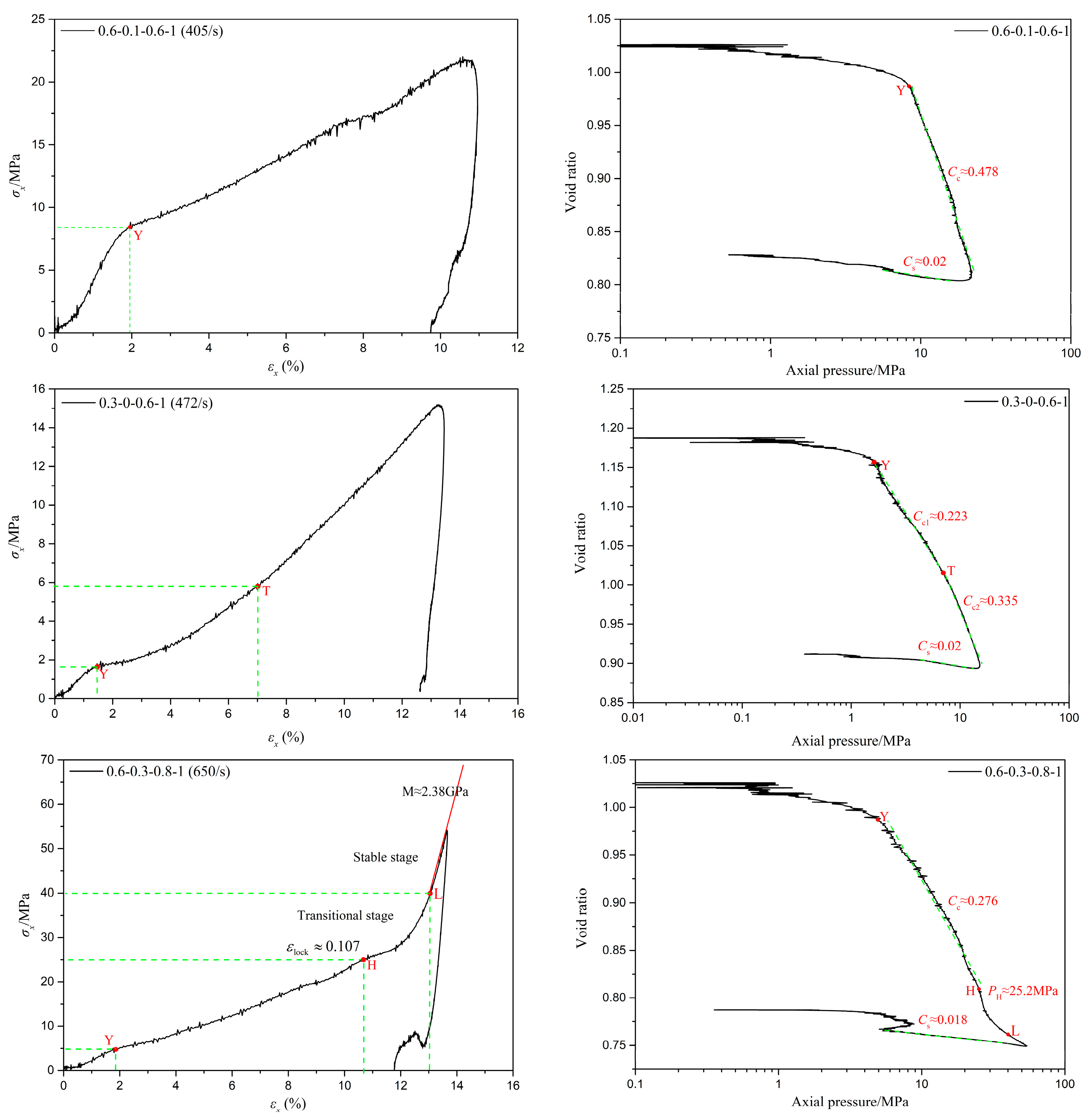
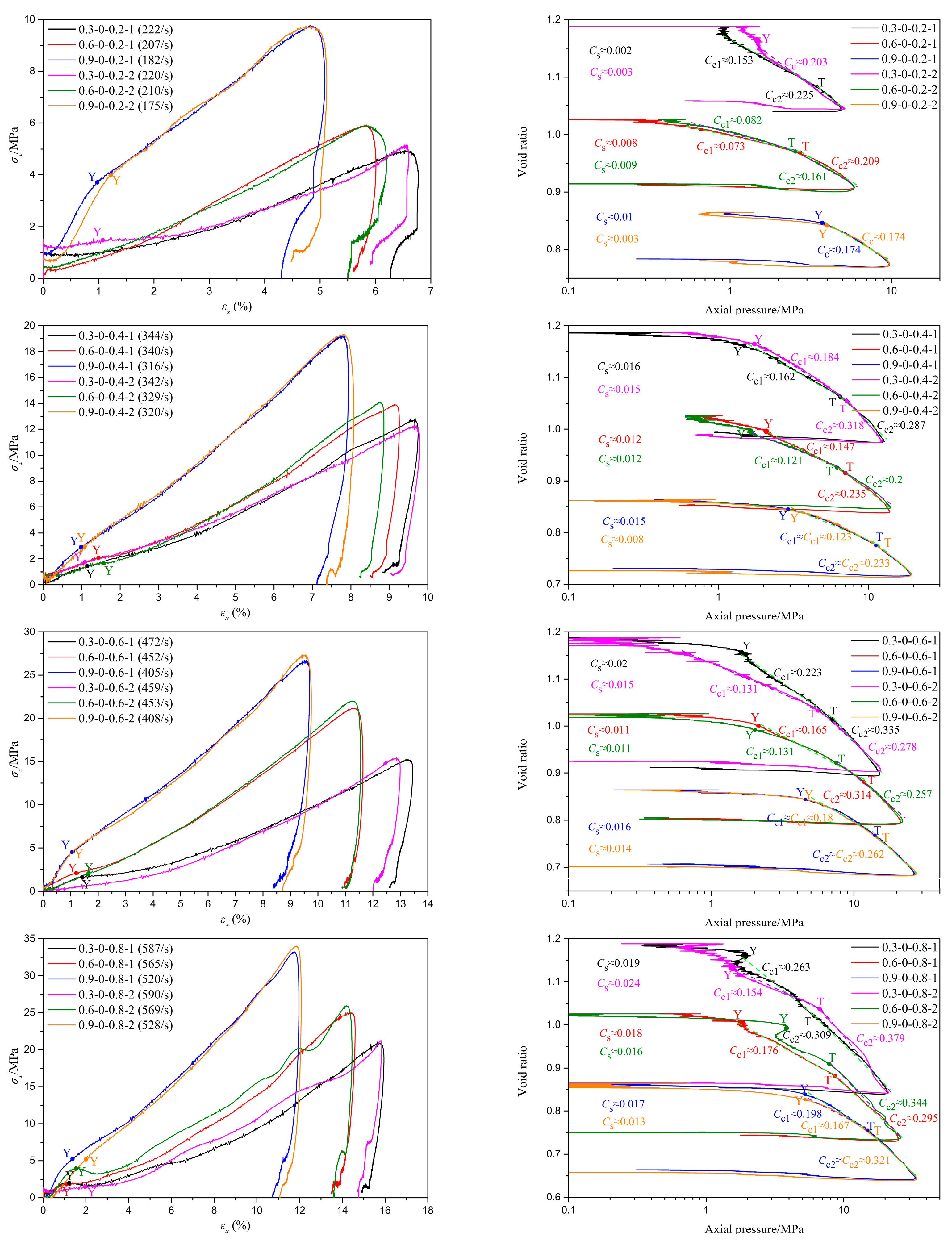
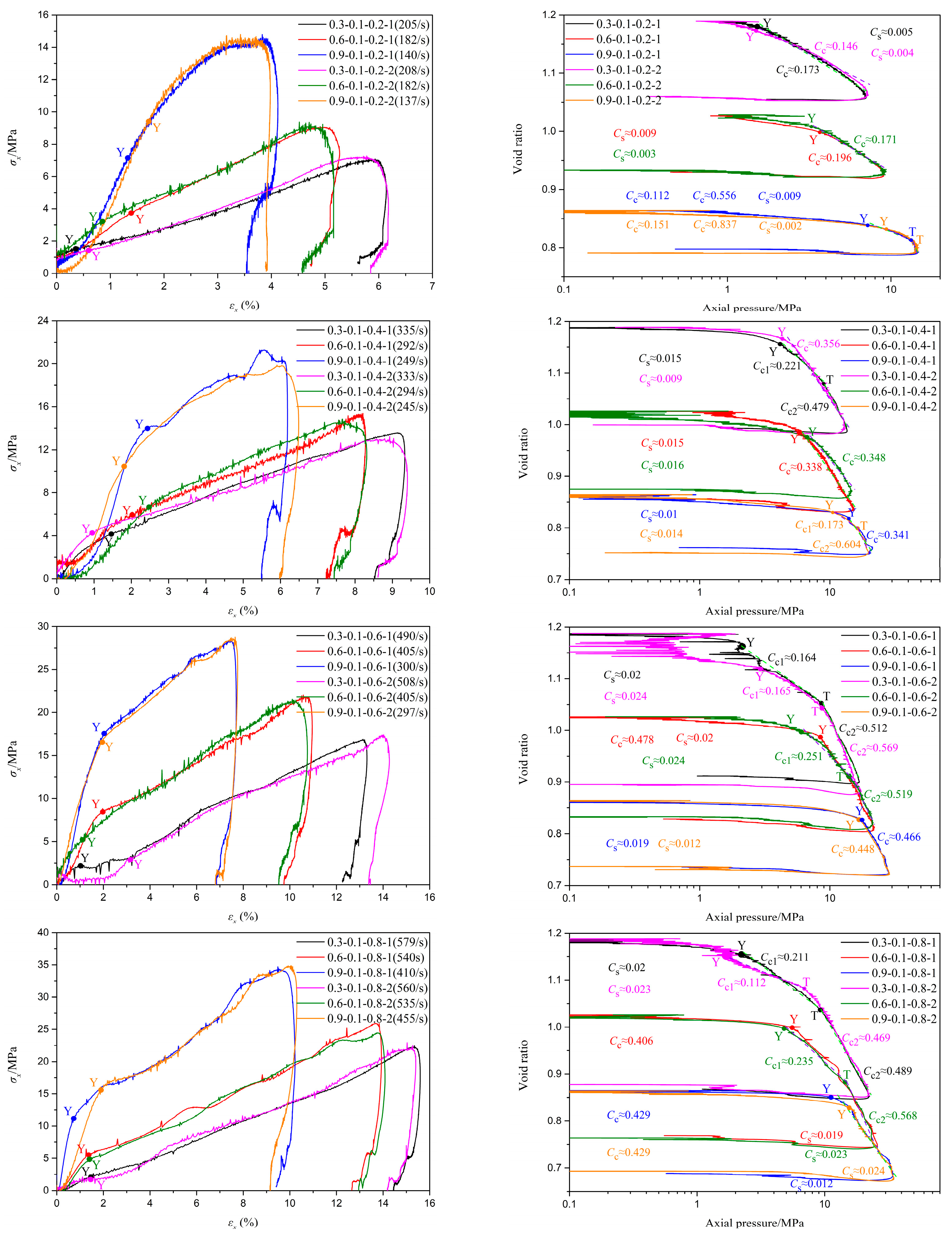
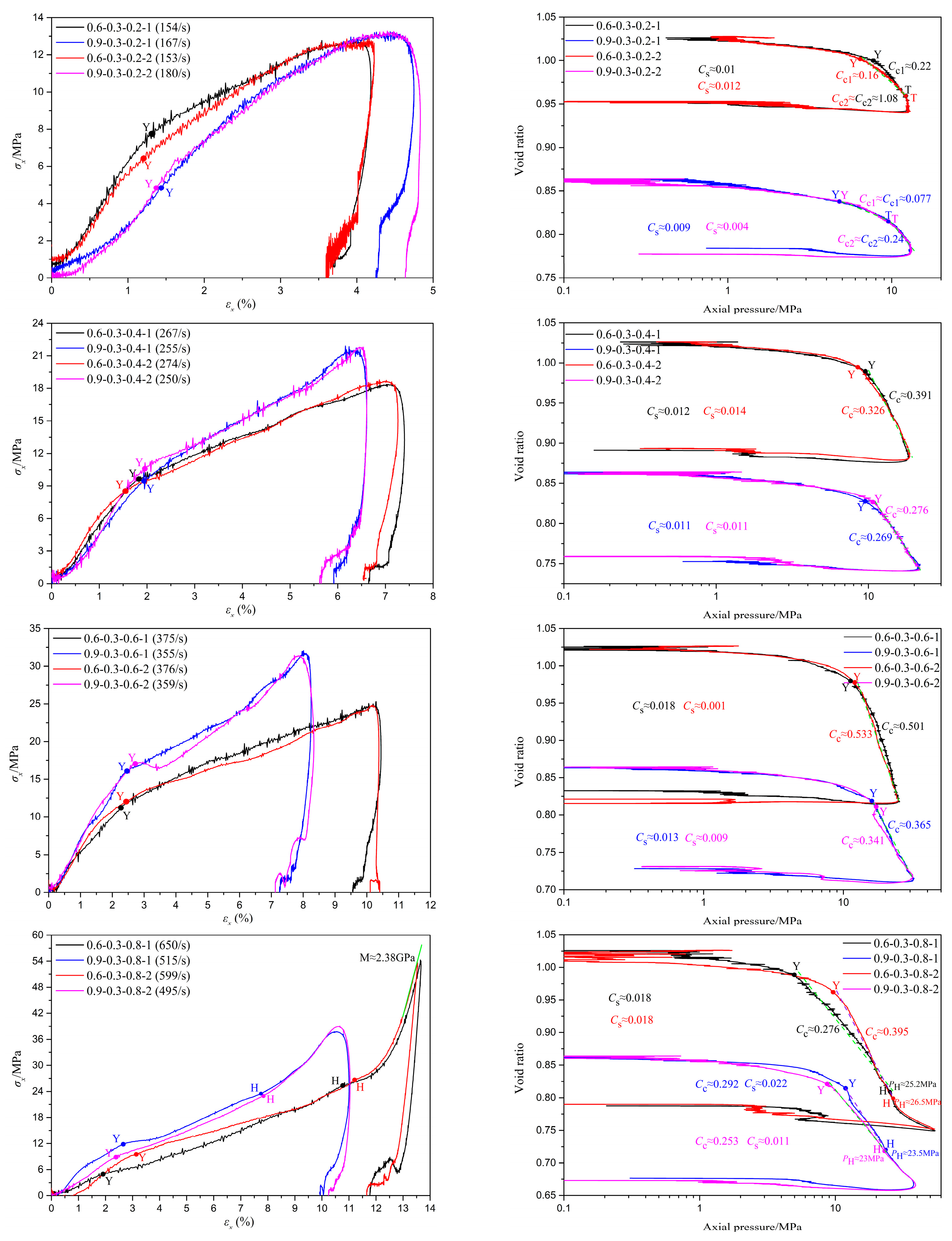
| Test Number (i = 1, 2) | Relative Density | Moisture Content | Gas Storage Tank Pressure/MPa | Test Number | Relative Density | Moisture Content | Gas Storage Tank Pressure/MPa |
|---|---|---|---|---|---|---|---|
| 0.3-0-0.2-i | 0.3 | 0 | 0.2 | 0.6-0.3-0.2 | 0.6 | 0.3 | 0.2 |
| 0.3-0-0.4-i | 0.3 | 0 | 0.4 | 0.6-0.3-0.4 | 0.6 | 0.3 | 0.4 |
| 0.3-0-0.6-i | 0.3 | 0 | 0.6 | 0.6-0.3-0.6 | 0.6 | 0.3 | 0.6 |
| 0.3-0-0.8-i | 0.3 | 0 | 0.8 | 0.6-0.3-0.8 | 0.6 | 0.3 | 0.8 |
| 0.3-0.5-0.2-i | 0.3 | 0.5 | 0.2 | 0.6-0.1-0.2 | 0.6 | 0.1 | 0.2 |
| 0.3-0.5-0.4-i | 0.3 | 0.5 | 0.4 | 0.6-0.1-0.4 | 0.6 | 0.1 | 0.4 |
| 0.3-0.5-0.6-i | 0.3 | 0.5 | 0.6 | 0.6-0.1-0.6 | 0.6 | 0.1 | 0.6 |
| 0.3-0.5-0.8-i | 0.3 | 0.5 | 0.8 | 0.6-0.1-0.8 | 0.6 | 0.1 | 0.8 |
| 0.3-0.2-0.2-i | 0.3 | 0.2 | 0.2 | 0.9-0-0.2 | 0.9 | 0 | 0.2 |
| 0.3-0.2-0.4-i | 0.3 | 0.2 | 0.4 | 0.9-0-0.4 | 0.9 | 0 | 0.4 |
| 0.3-0.2-0.6-i | 0.3 | 0.2 | 0.6 | 0.9-0-0.6 | 0.9 | 0 | 0.6 |
| 0.3-0.2-0.8-i | 0.3 | 0.2 | 0.8 | 0.9-0-0.8 | 0.9 | 0 | 0.8 |
| 0.3-0.1-0.2-i | 0.3 | 0.1 | 0.2 | 0.9-0.3-0.2 | 0.9 | 0.3 | 0.2 |
| 0.3-0.1-0.4-i | 0.3 | 0.1 | 0.4 | 0.9-0.3-0.4 | 0.9 | 0.3 | 0.4 |
| 0.3-0.1-0.6-i | 0.3 | 0.1 | 0.6 | 0.9-0.3-0.6 | 0.9 | 0.3 | 0.6 |
| 0.3-0.1-0.8-i | 0.3 | 0.1 | 0.8 | 0.9-0.3-0.8 | 0.9 | 0.3 | 0.8 |
| 0.6-0-0.2-i | 0.6 | 0 | 0.2 | 0.9-0.1-0.2 | 0.9 | 0.1 | 0.2 |
| 0.6-0-0.4-i | 0.6 | 0 | 0.4 | 0.9-0.1-0.4 | 0.9 | 0.1 | 0.4 |
| 0.6-0-0.6-i | 0.6 | 0 | 0.6 | 0.9-0.1-0.6 | 0.9 | 0.1 | 0.6 |
| 0.6-0-0.8-i | 0.6 | 0 | 0.8 | 0.9-0.1-0.8 | 0.9 | 0.1 | 0.8 |
| Test Number | Pc/MPa | Test Number | Pc/MPa | Test Number | Pc/MPa | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.3-0-0.2-1 | 0.153/0.225 | 0.002 | / | 0.3-0-0.2-2 | 0.203 | 0.003 | 1.49 | 0.3-0.1-0.8-1 | 0.211/0.489 | 0.02 | 2.14 |
| 0.6-0-0.2-1 | 0.073/0.209 | 0.008 | / | 0.6-0-0.2-2 | 0.082/0.161 | 0.009 | / | 0.6-0.1-0.8-1 | 0.406 | 0.019 | 5.51 |
| 0.9-0-0.2-1 | 0.174 | 0.01 | 3.75 | 0.9-0-0.2-2 | 0.174 | 0.003 | 4 | 0.9-0.1-0.8-1 | 0.429 | 0.012 | 11 |
| 0.3-0-0.4-1 | 0.162/0.287 | 0.016 | 1.42 | 0.3-0-0.4-2 | 0.184/0.318 | 0.015 | 1.78 | 0.3-0.1-0.8-2 | 0.112/0.469 | 0.023 | 1.65 |
| 0.6-0-0.4-1 | 0.147/0.235 | 0.012 | 2.14 | 0.6-0-0.4-2 | 0.121/0.2 | 0.012 | 1.56 | 0.6-0.1-0.8-2 | 0.235/0.568 | 0.023 | 4.76 |
| 0.9-0-0.4-1 | 0.123/0.233 | 0.015 | 2.9 | 0.9-0-0.4-2 | 0.123/0.233 | 0.008 | 2.81 | 0.9-0.1-0.8-2 | 0.429 | 0.024 | 15.54 |
| 0.3-0-0.6-1 | 0.223/0.335 | 0.02 | 1.65 | 0.3-0-0.6-2 | 0.131/0.278 | 0.015 | / | 0.6-0.3-0.2-1 | 0.22/1.08 | 0.01 | 7.61 |
| 0.6-0-0.6-1 | 0.165/0.314 | 0.011 | 2.15 | 0.6-0-0.6-2 | 0.131/0.257 | 0.011 | 2 | 0.9-0.3-0.2-1 | 0.077/0.24 | 0.009 | 4.79 |
| 0.9-0-0.6-1 | 0.18/0.262 | 0.016 | 4.64 | 0.9-0-0.6-2 | 0.18/0.262 | 0.014 | 4.5 | 0.6-0.3-0.4-1 | 0.391 | 0.012 | 9.64 |
| 0.3-0-0.8-1 | 0.263/0.309 | 0.019 | 1.96 | 0.3-0-0.8-2 | 0.154/0.379 | 0.024 | 1.46 | 0.9-0.3-0.4-1 | 0.269 | 0.011 | 9.51 |
| 0.6-0-0.8-1 | 0.176/0.295 | 0.018 | 1.79 | 0.6-0-0.8-2 | 0.344 | 0.016 | 3.92 | 0.6-0.3-0.6-1 | 0.501 | 0.018 | 11.27 |
| 0.9-0-0.8-1 | 0.198/0.321 | 0.017 | 5.26 | 0.9-0-0.8-2 | 0.167/0.321 | 0.013 | 5.26 | 0.9-0.3-0.6-1 | 0.365 | 0.013 | 16.08 |
| 0.3-0.1-0.2-1 | 0.173 | 0.005 | 1.44 | 0.3-0.1-0.2-2 | 0.146 | 0.004 | 1.43 | 0.6-0.3-0.8-1 | 0.276 | 0.018 | 4.95 |
| 0.6-0.1-0.2-1 | 0.196 | 0.009 | 3.61 | 0.6-0.1-0.2-2 | 0.171 | 0.003 | 3.22 | 0.9-0.3-0.8-1 | 0.292 | 0.022 | 11.68 |
| 0.9-0.1-0.2-1 | 0.112/0.556 | 0.009 | 7.15 | 0.9-0.1-0.2-2 | 0.151/0.837 | 0.002 | 9.4 | 0.6-0.3-0.2-2 | 0.16/1.08 | 0.012 | 6.4 |
| 0.3-0.1-0.4-1 | 0.221/0.479 | 0.015 | 4.11 | 0.3-0.1-0.4-2 | 0.356 | 0.009 | 4.27 | 0.9-0.3-0.2-2 | 0.077/0.24 | 0.004 | 4.8 |
| 0.6-0.1-0.4-1 | 0.338 | 0.015 | 5.86 | 0.6-0.1-0.4-2 | 0.348 | 0.016 | 6.67 | 0.6-0.3-0.4-2 | 0.326 | 0.014 | 8.51 |
| 0.9-0.1-0.4-1 | 0.341 | 0.01 | 14.16 | 0.9-0.1-0.4-2 | 0.173/0.604 | 0.014 | 10.47 | 0.9-0.3-0.4-2 | 0.276 | 0.011 | 10.63 |
| 0.3-0.1-0.6-1 | 0.164/0.512 | 0.02 | 2.16 | 0.3-0.1-0.6-2 | 0.165/0.569 | 0.024 | 2.91 | 0.6-0.3-0.6-2 | 0.533 | 0.001 | 12 |
| 0.6-0.1-0.6-1 | 0.478 | 0.02 | 8.4 | 0.6-0.1-0.6-2 | 0.251/0.519 | 0.024 | 6.03 | 0.9-0.3-0.6-2 | 0.341 | 0.009 | 17 |
| 0.9-0.1-0.6-1 | 0.466 | 0.019 | 17.62 | 0.9-0.1-0.6-2 | 0.448 | 0.012 | 16.61 | 0.6-0.3-0.8-2 | 0.395 | 0.018 | 9.6 |
| 0.9-0.3-0.8-2 | 0.253 | 0.011 | 8.74 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, X.; Ren, H.; Zhang, H.; Yi, Z. Study on the One-Dimensional Impact Compression Characteristics of Coral Sand Under Conditions of Different Relative Density. Materials 2025, 18, 1113. https://doi.org/10.3390/ma18051113
Liu X, Ren H, Zhang H, Yi Z. Study on the One-Dimensional Impact Compression Characteristics of Coral Sand Under Conditions of Different Relative Density. Materials. 2025; 18(5):1113. https://doi.org/10.3390/ma18051113
Chicago/Turabian StyleLiu, Xin, Huiqi Ren, Hui Zhang, and Zhi Yi. 2025. "Study on the One-Dimensional Impact Compression Characteristics of Coral Sand Under Conditions of Different Relative Density" Materials 18, no. 5: 1113. https://doi.org/10.3390/ma18051113
APA StyleLiu, X., Ren, H., Zhang, H., & Yi, Z. (2025). Study on the One-Dimensional Impact Compression Characteristics of Coral Sand Under Conditions of Different Relative Density. Materials, 18(5), 1113. https://doi.org/10.3390/ma18051113





