Prediction of Grain Structure and Texture in Twin-Roll Cast Aluminum Alloys Using Cellular Automaton–Finite Element Method
Abstract
1. Introduction
2. Materials and Methods
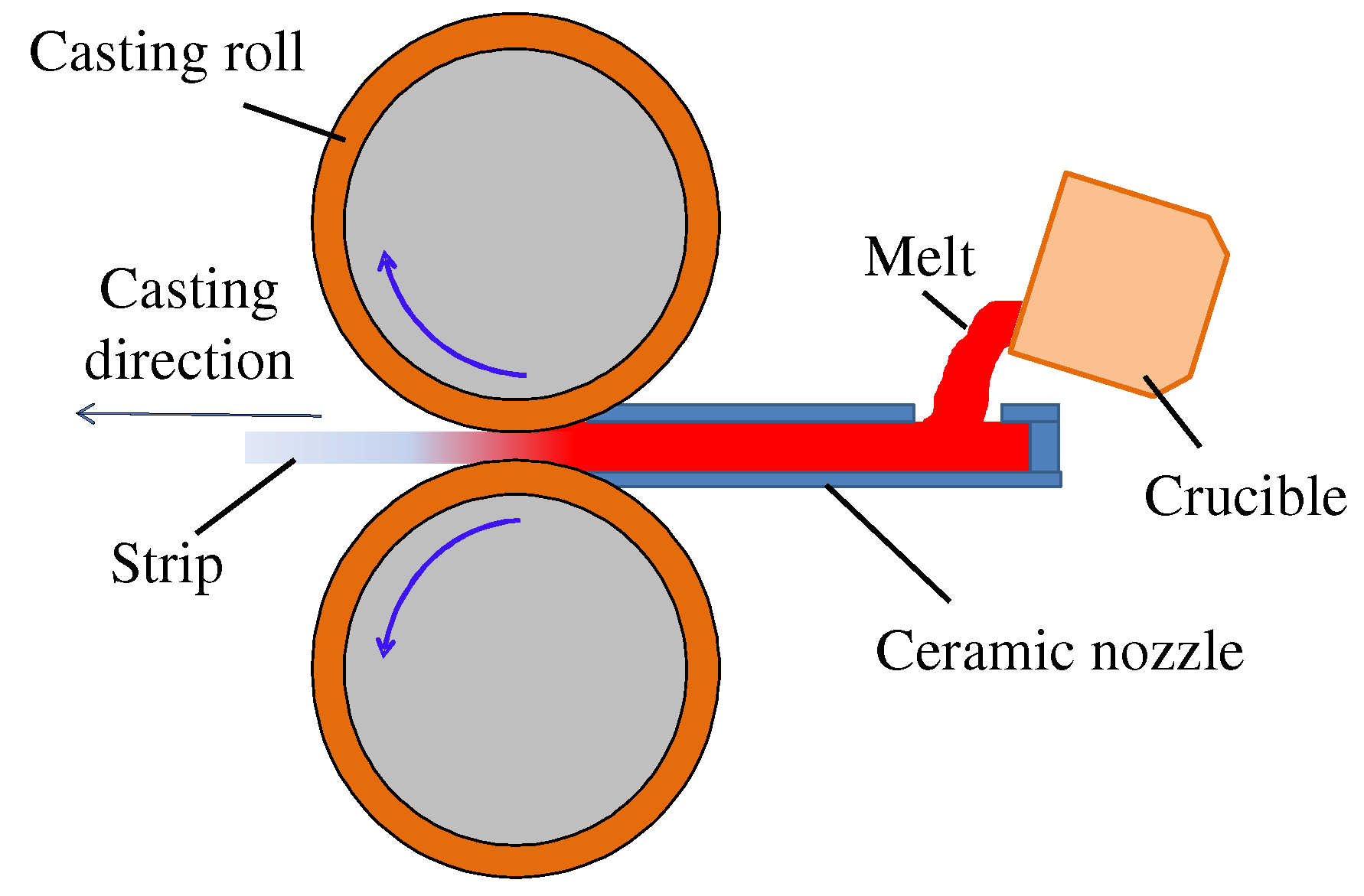
2.1. TRC Process for Strip Fabrication
2.2. Simulation Model for Twin-Roll Casting Process
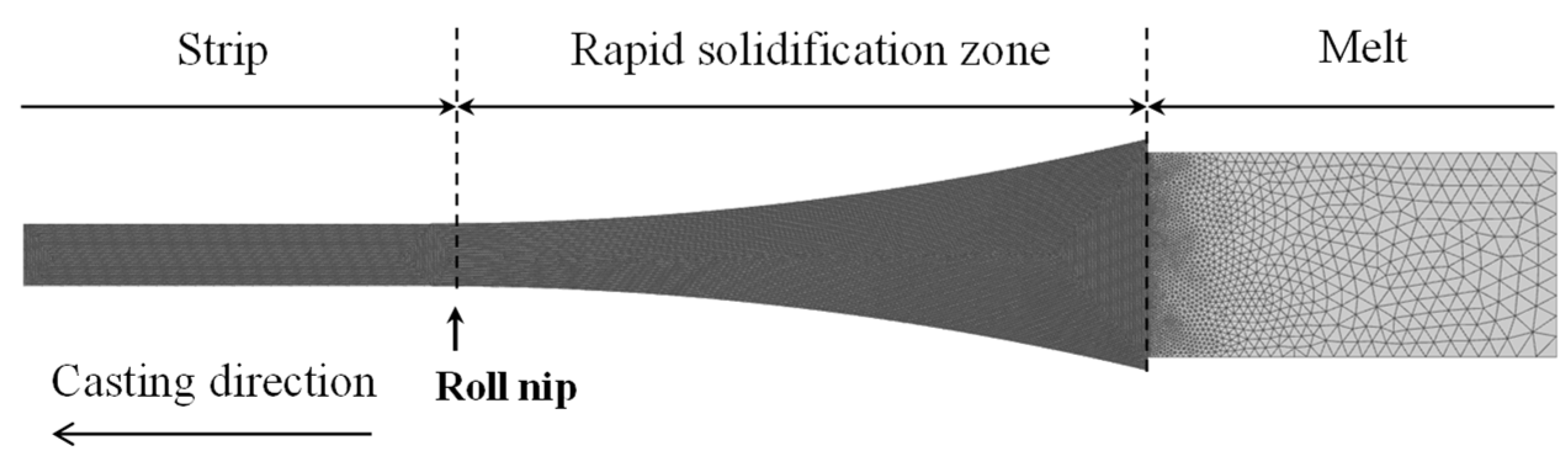
2.2.1. TRC Model Geometry and Boundary Condition
2.2.2. Cellular Automaton (CA) Model
3. Results and Discussion
3.1. Solidification Behavior in Twin-Roll Cast Strips
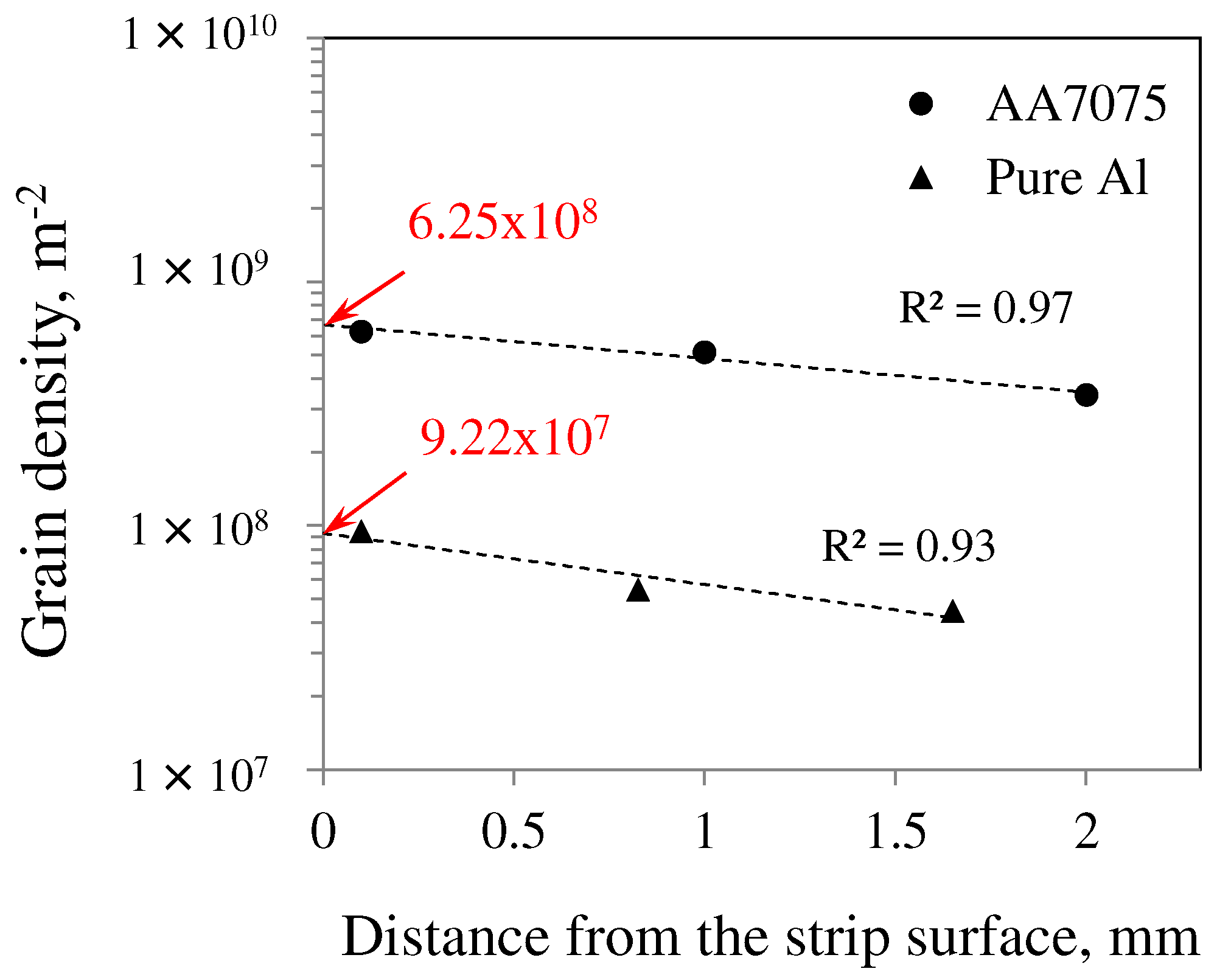
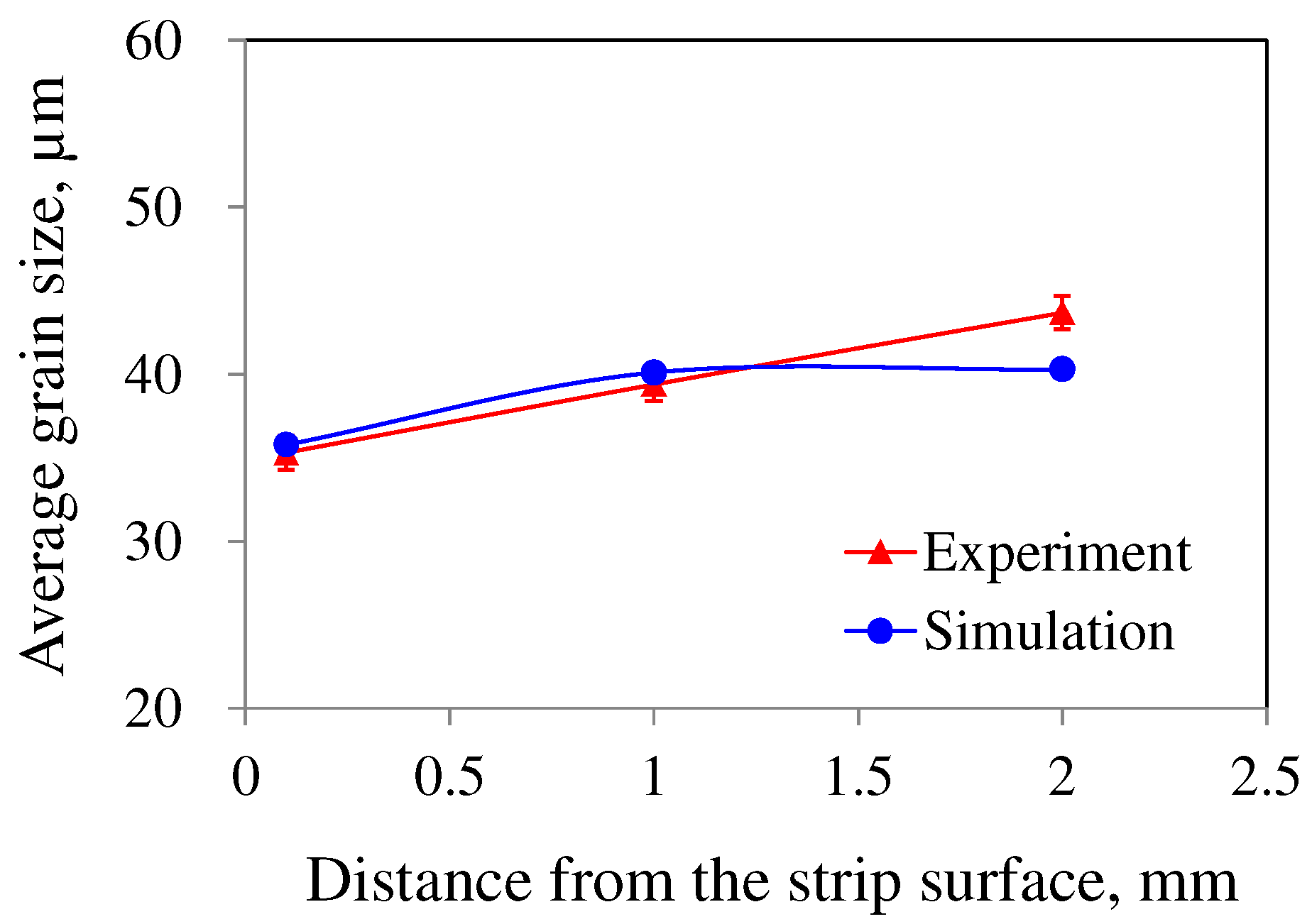
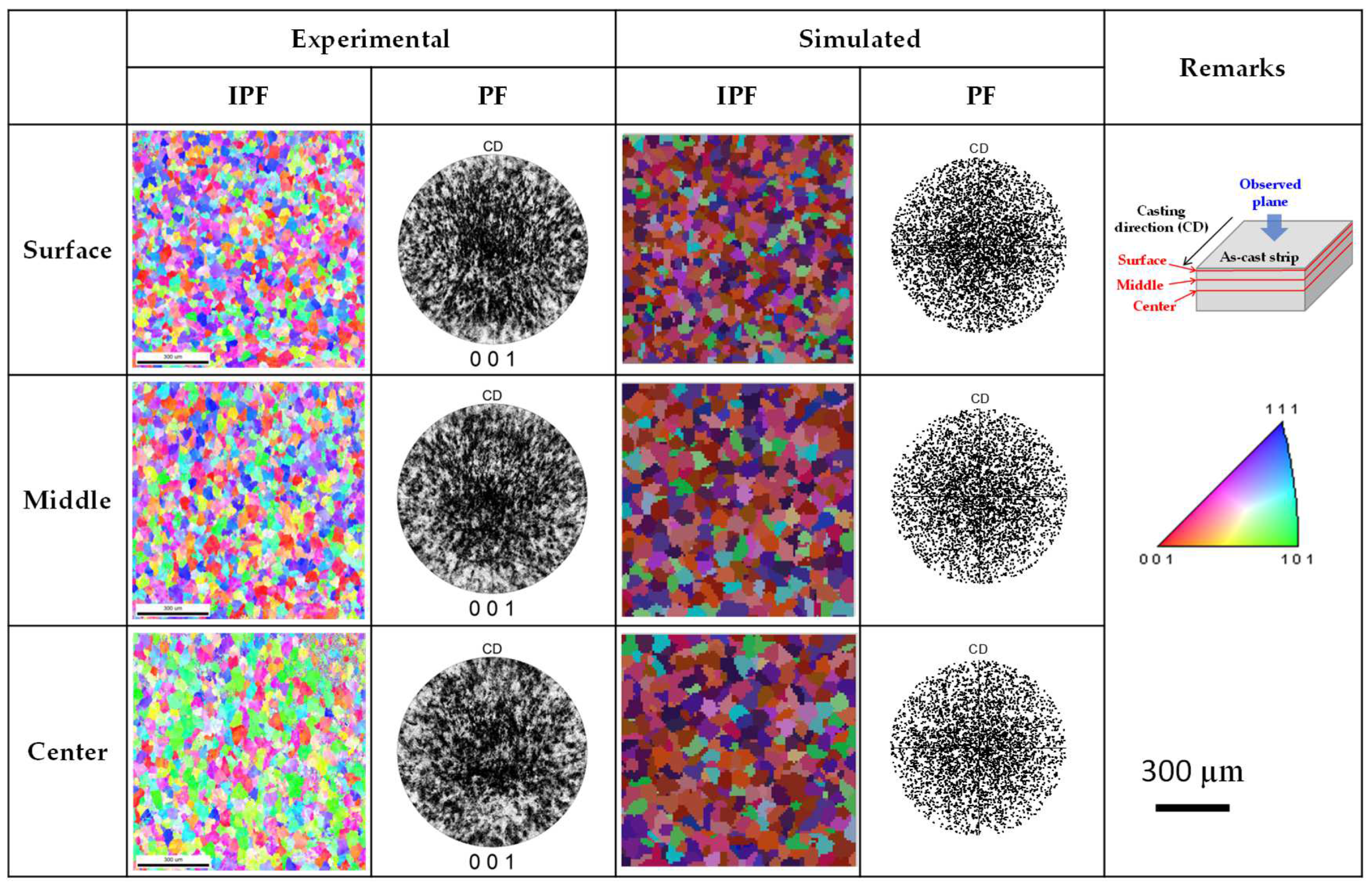
3.2. Prediction of Solidification Grain Structure in TRC Strips
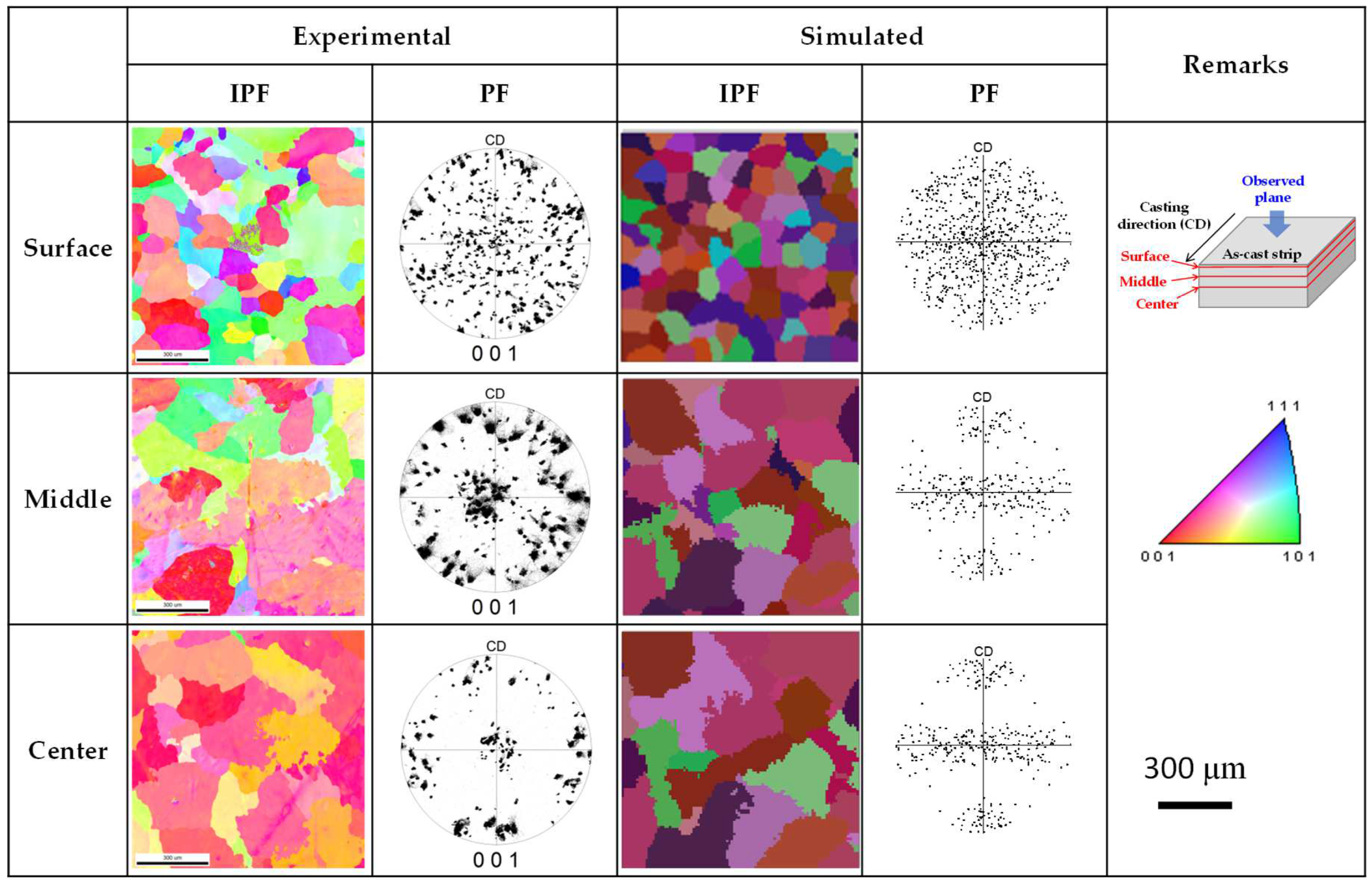
3.3. Prediction of Texture in TRC Strip
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Barekar, N.S.; Dhindaw, B.K. Twin-roll casting of aluminum alloys—An overview. Mater. Manuf. Process. 2014, 29, 651–661. [Google Scholar] [CrossRef]
- Edmonds, D.V. Innovation in the processing of tonnage materials: Examples from the steel and aluminum industries. J. Mater. Process. Technol. 1998, 83, 1–13. [Google Scholar] [CrossRef]
- Kim, M.S. Control of surface inverse segregation in Al-4.5Mg strips produced by industrial twin-roll casting process. Scr. Mater. 2025, 258, 116528. [Google Scholar] [CrossRef]
- Lee, Y.S.; Koh, D.H.; Kim, H.W.; Ahn, Y.S. Improved bake-hardening response of Al-Zn-Mg-Cu alloy through pre-aging treatment. Scr. Mater. 2018, 147, 46–49. [Google Scholar] [CrossRef]
- Jeon, J.; Lee, S.; Jeon, J.; Kang, M.; Kang, H. The influence of as-cast grain sized on the formation of recrystallized grains and the related mechanical properties in Al-Zn-Mg-Cu-based alloys sheets. Materials 2024, 17, 5267. [Google Scholar] [CrossRef]
- Zang, Q.; Feng, D.; Lee, Y.S.; Chen, H.; Kim, M.S.; Kim, H.W. Microstructure and mechanical properties of Al-7.9Zn-2.7Mg-2.0Cu(wt%) alloy strip fabricated by twin roll casting and hot rolling. J. Alloys Compd. 2020, 847, 156481. [Google Scholar] [CrossRef]
- Rappaz, M.; Gandin, C.A. Probabilistic modelling of microstructure formation in solidification processes. Acta Metall. Mater. 1993, 41, 345–360. [Google Scholar] [CrossRef]
- Gandin, C.A.; Pappaz, M. A coupled finite element-cellular automaton model for the prediction of dendritic grain structures in solidification processes. Acta Metall. Mater. 1994, 42, 2233–2246. [Google Scholar] [CrossRef]
- Liu, Q.; Xu, Q. Advances on microstructure modeling of solidification process of shape casting. Tsinghua Sci. Technol. 2004, 9, 497–505. [Google Scholar]
- Gandin, C.A.; Desbiolles, J.L.; Rappaz, M.; Thevoz, P. A three-dimensional cellular automation-finite element model for the prediction of solidification grain structures. Metall. Mater. Trans. A 1999, 30, 3153–3165. [Google Scholar] [CrossRef]
- Liu, D.R.; Yang, Y.; Sun, Q.Y.; Guo, E.J. 2D cellular automaton—Finite element simulation of grain structure and macrosegregation during solidification of Al-4wt% Cu alloy. Int. J. Cast Metals Res. 2016, 29, 393–402. [Google Scholar] [CrossRef]
- Yamazaki, M.; Natsume, Y.; Harada, H.; Ohsasa, K. Numerical simulation of solidification structure formation during continuous casting in Fe-0.7mass%C alloy using automaton method. ISIJ Int. 2006, 46, 903–908. [Google Scholar] [CrossRef]
- Ma, J.; Wang, B.; Zhao, S.; Wu, G.; Zhang, J.; Yang, Z. Incorporating an extended dendritic growth model into the CAFE model for rapidly solidified non-dilute alloys. J. Alloys Compd. 2016, 668, 46–55. [Google Scholar] [CrossRef]
- Ridgeway, C.D.; Gu, C.; Ripplinger, K.; Detwiler, D.; Ji, M.; Soghrati, S.; Luo, A.A. Prediction of location specific mechanical properties of aluminum casting using a new CA-FEA (cellular automaton-finite element analysis) approach. Mater. Des. 2020, 194, 108929. [Google Scholar] [CrossRef]
- Gu, C.; Lu, Y.; Cinkilic, E.; Miao, J.; Klarner, A.; Yang, X.; Luo, A.A. Predicting grain structure in high pressure die casting of aluminum alloys: A coupled cellular automaton and process model. Comput. Mater. Sci. 2019, 161, 64–75. [Google Scholar] [CrossRef]
- Elahi, S.M.; Tavakoli, R.; Romero, I.; Tourret, D. Grain growth competition during melt pool solidification—Comparing phase-field and cellular automaton models. Comput. Mater. Sci. 2023, 216, 111882. [Google Scholar] [CrossRef]
- Andersson, C.; Lundback, A. Modeling the evolution of grain texture during solidification of laser-based powder bed dusion manufactured alloy 625 using a cellular automata finite element model. Metals 2023, 13, 1846. [Google Scholar] [CrossRef]
- Liu, J.; Lv, H.; Xie, S.; Han, R.; Zhang, Z.; Liu, Y.; Chen, H.; Chen, Y.; She, J.; He, D. Solidification microstructure prediction of Ti-6Al-4V alloy produced by laser melting deposition. Coatings 2022, 12, 1610. [Google Scholar] [CrossRef]
- Wang, B.; Zhang, J.Y.; Li, X.M.; Qi, W.H. Simulation of solidification microstructure in twin-roll casting strip. Comput. Mater. Sci. 2010, 49, S135–S139. [Google Scholar] [CrossRef]
- Kim, M.S.; Lee, S.H.; Jung, J.G.; Eah, K. Prediction of grain structure in direct-chill cast Al-Zn-Mg-Cu billets using cellular automaton-finite element method. Prog. Nat. Sci. Mater. Int. 2021, 31, 434–441. [Google Scholar] [CrossRef]
- Chen, Y.; Liu, G.H.; Wang, Y.; Wang, Z.D. Solidification microstructure of Ti-43Al alloy by twin-roll strip casting. China Foundry 2023, 20, 99–107. [Google Scholar] [CrossRef]
- Dantzig, J.; Meydanoglu, O.; Kazazi, A.; Altuner, H.M.; Isiksacan, C.; Serefoglu, M. Microstructure and crystallographic texture in twin-roll casting of AA1050 aluminum alloy: Simulation and industrial validation. Metall. Mater. Trans. A 2022, 53, 4168–4187. [Google Scholar] [CrossRef]
- Kim, M.S.; Kim, H.W.; Kim, S.H.; Kumai, S. Role of roll separating force in high-speed twin-roll casting of aluminum alloys. Metals 2019, 9, 645. [Google Scholar] [CrossRef]
- Seo, S.M.; Kim, I.S.; Lee, J.H.; Jo, C.Y.; Ogi, K. Prediction of solidification grain structure in the Ni-base superalloy CM247LC. J. Korean Inst. Met. Mater. 2006, 44, 44–54. [Google Scholar]
- Seo, S.M.; Kim, I.S.; Jo, C.Y.; Ogi, K. Grain structure prediction of Ni-base superalloy castings using the cellular automaton-finite element method. Mater. Sci. Eng. A 2007, 449–451, 713–716. [Google Scholar] [CrossRef]
- Bolzoni, L.; Xia, M.; Babu, N.H. Formation of equiaxed crystal structures in directionally solidified Al-Si alloys using Nb-based heterogeneous nuclei. Sci. Rep. 2016, 6, 39554. [Google Scholar] [CrossRef]
- Kim, M.S.; Kumai, S. Solidification structure and casting defects in high-speed twin-roll cast Al-2mss% Si alloy strip. Mater. Trans. 2013, 54, 1930–1937. [Google Scholar] [CrossRef]
- Kim, M.S.; Arai, Y.; Hori, Y.; Kumai, S. Formation of internal crack in high-speed twin-roll cast 6022 aluminum alloy strip. Mater. Trans. 2010, 51, 1854–1860. [Google Scholar] [CrossRef]
- Kim, M.S.; Kim, H.W.; Kumai, S. Direct temperature measurement of Al-2mass%Si alloy strips during high-speed twin-roll casting and its application in determining melt/roll heat transfer coefficient for simulation. Mater. Trans. 2017, 58, 967–970. [Google Scholar] [CrossRef]
- Kim, M.S.; Kim, J. Metallurgical method of determining heat transfer coefficient in simulations of twin-roll casting. Metals 2024, 14, 358. [Google Scholar] [CrossRef]
- Thevoz, P.; Desbiolles, J.L.; Rappaz, M. Modeling of equiaxed microstructure formation in casting. Metall. Trans. A 1989, 20, 311–322. [Google Scholar] [CrossRef]
- Kurz, W.; Giovanola, B.; Trivedi, R. Theory of microstructural development during rapid solidification. Acta Metall. 1986, 34, 823–830. [Google Scholar] [CrossRef]
- Bobadilla, M.; Lacaze, J.; Lesoult, G. Influence des conditions de solidification sur le deroulement de la solidification des aciers inoxydables austenitiques. J. Cryst. Growth 1988, 89, 531–544. [Google Scholar] [CrossRef]
- Drozdz, P. Influence of cooling conditions on a slab’s chill zone formation during continuous casting of steel. Arch. Metall. Mater. 2017, 62, 911–918. [Google Scholar] [CrossRef]
- Okauasu, M.; Takeuchi, S. Crystallization characteristics of cast aluminum alloys during a unidirectional solidification process. Mater. Sci. Eng. A 2015, 633, 112–120. [Google Scholar] [CrossRef]




| Alloy | Zn | Mg | Cu | Cr | Si | Fe | Ti | Al | |
|---|---|---|---|---|---|---|---|---|---|
| Pure Al | target | - | - | - | - | - | - | - | Bal. |
| ICP | - | - | - | - | 0.04 | 0.1 | - | Bal. | |
| AA7075 | target | 5.5 | 2.5 | 1.5 | 0.2 | - | - | - | Bal. |
| ICP | 5.18 | 2.27 | 1.49 | 0.22 | 0.11 | 0.23 | 0.05 | Bal. |
| Casting Condition | Value |
|---|---|
| Melt temperature | 680 °C |
| Casting speed | 4 m/min |
| Set-back distance | 35 mm |
| Strip width | 100 mm |
| Condition | Value |
|---|---|
| Melt temperature | 680 °C |
| Ambient temperature | 25 °C |
| Roll temperature | 50 °C |
| Strip/air IHTC, hstrip/air | 12 W/m2K |
| Roll/melt IHTC, hroll/melt | 8600 W/m2K |
| Nozzle/melt IHTC, hnozzle/melt | adiabatic |
| Alloy | Element | C0,i (wt.%) | mi (K/wt.%) | ki |
|---|---|---|---|---|
| Pure Al | Si | 0.04 | −5.80 | 0.11 |
| Fe | 0.1 | −3.22 | 0.02 | |
| AA7075 | Cr | 0.22 | 10.09 | 4.59 |
| Cu | 1.49 | −2.59 | 0.11 | |
| Fe | 0.23 | −4.51 | 0.03 | |
| Mg | 2.27 | −4.65 | 0.30 | |
| Si | 0.11 | −6.55 | 0.09 | |
| Ti | 0.05 | 42.20 | 13.00 | |
| Zn | 5.18 | −1.87 | 0.32 |
| Condition | Surface Nucleation | Volume Nucleation | ||||
|---|---|---|---|---|---|---|
(K) | (K) | (m−2) | (K) | (K) | (m−3) | |
| Pure Al | 1.0 | 0.1 | 9.22 × 107 | 0.5 | 1.0 | 9.50 × 108 |
| AA7075 | 1.0 | 0.1 | 6.25 × 108 | 5 | 1.0 | 2.60 × 1013 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cho, H.-G.; Kim, Y.D.; Kim, M.-S. Prediction of Grain Structure and Texture in Twin-Roll Cast Aluminum Alloys Using Cellular Automaton–Finite Element Method. Materials 2025, 18, 1075. https://doi.org/10.3390/ma18051075
Cho H-G, Kim YD, Kim M-S. Prediction of Grain Structure and Texture in Twin-Roll Cast Aluminum Alloys Using Cellular Automaton–Finite Element Method. Materials. 2025; 18(5):1075. https://doi.org/10.3390/ma18051075
Chicago/Turabian StyleCho, Han-Gyoung, Young Do Kim, and Min-Seok Kim. 2025. "Prediction of Grain Structure and Texture in Twin-Roll Cast Aluminum Alloys Using Cellular Automaton–Finite Element Method" Materials 18, no. 5: 1075. https://doi.org/10.3390/ma18051075
APA StyleCho, H.-G., Kim, Y. D., & Kim, M.-S. (2025). Prediction of Grain Structure and Texture in Twin-Roll Cast Aluminum Alloys Using Cellular Automaton–Finite Element Method. Materials, 18(5), 1075. https://doi.org/10.3390/ma18051075





