The Study of Soliton Mode-Locked and Bound States in Erbium-Doped Fiber Lasers Based on Cr2S3 Saturable Absorbers
Abstract
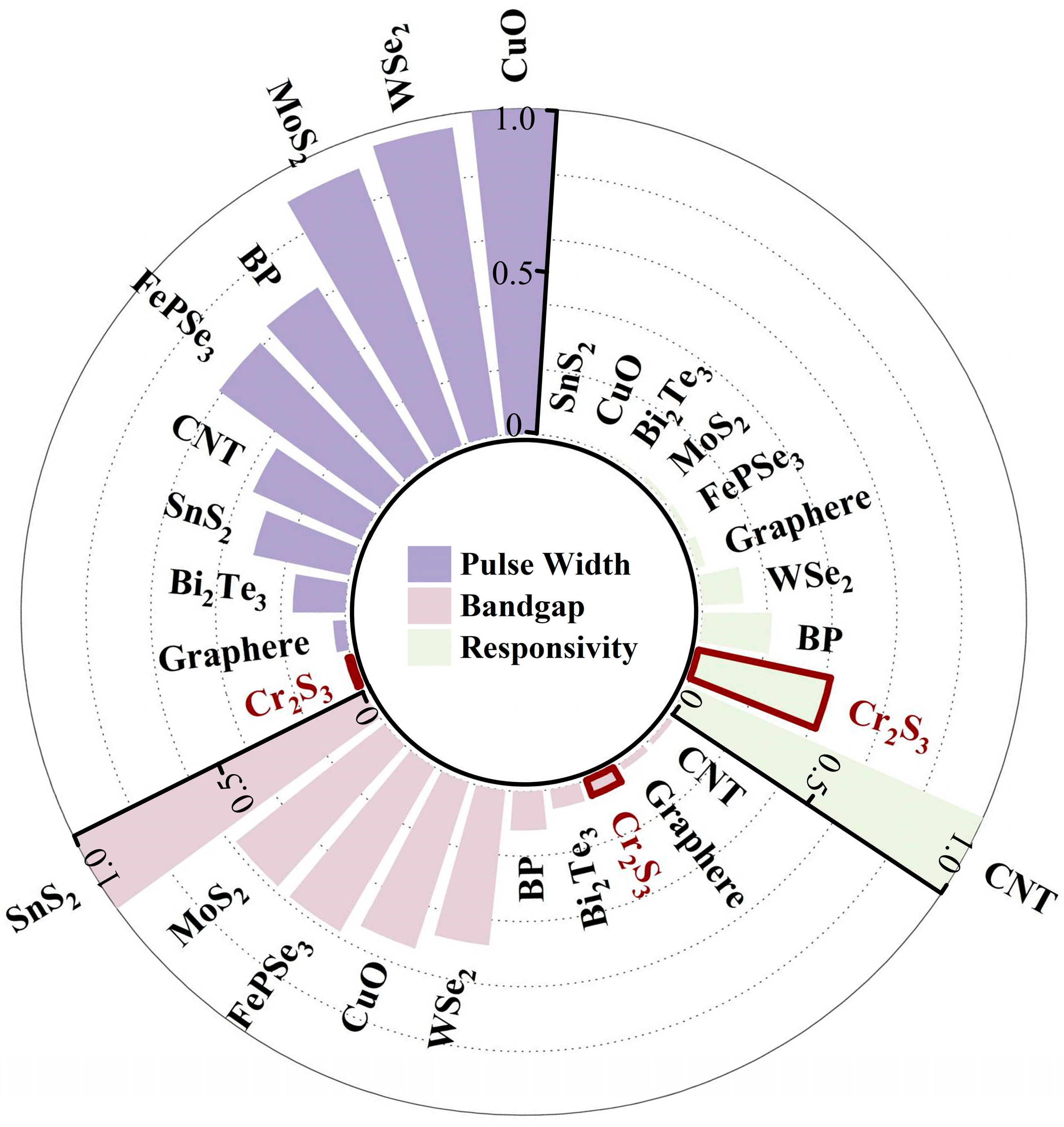
1. Introduction
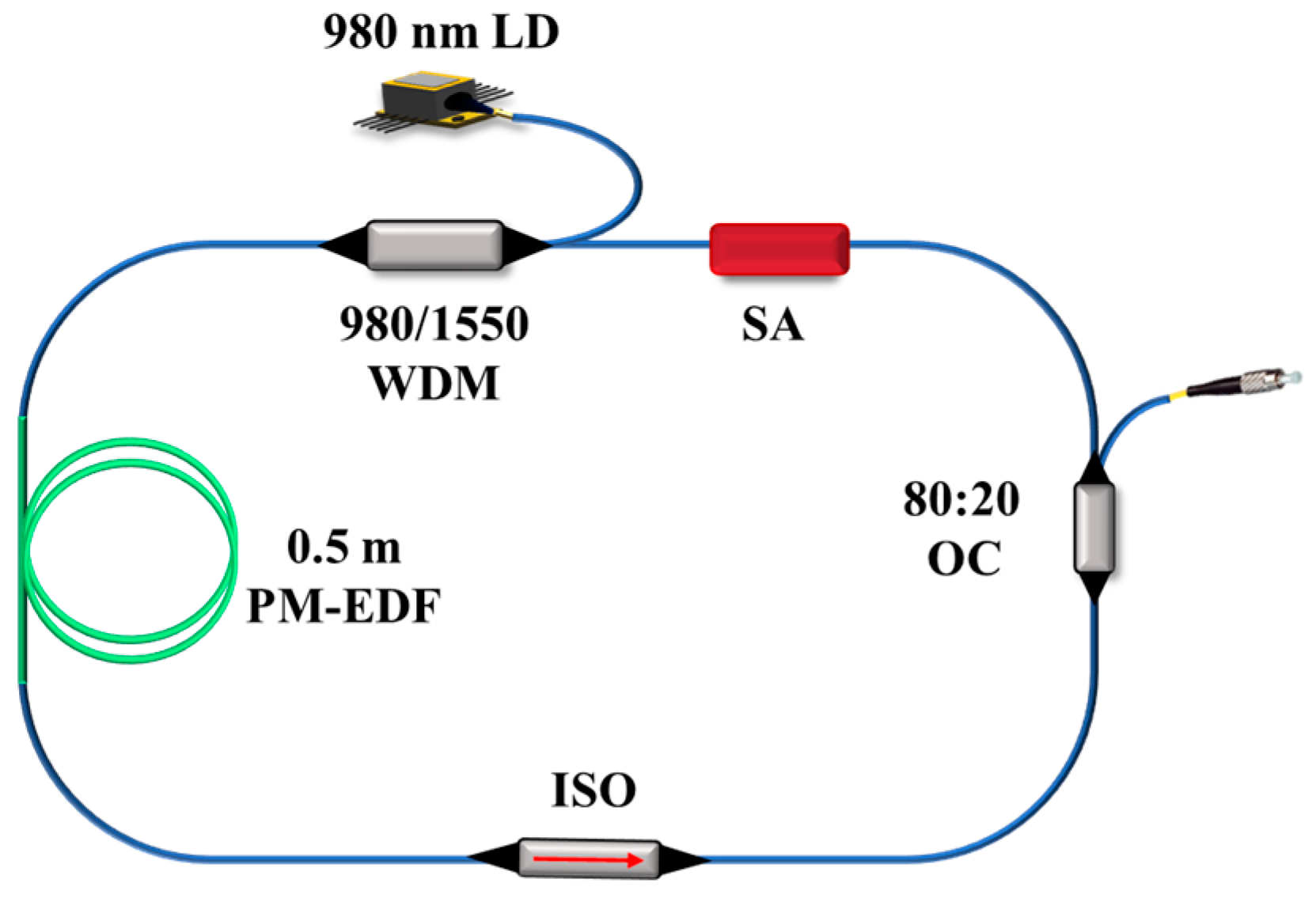
2. Numerical Model of Erbium-Doped Fiber Laser Based on Cr2S3-SA
3. Numerical Simulations and Results
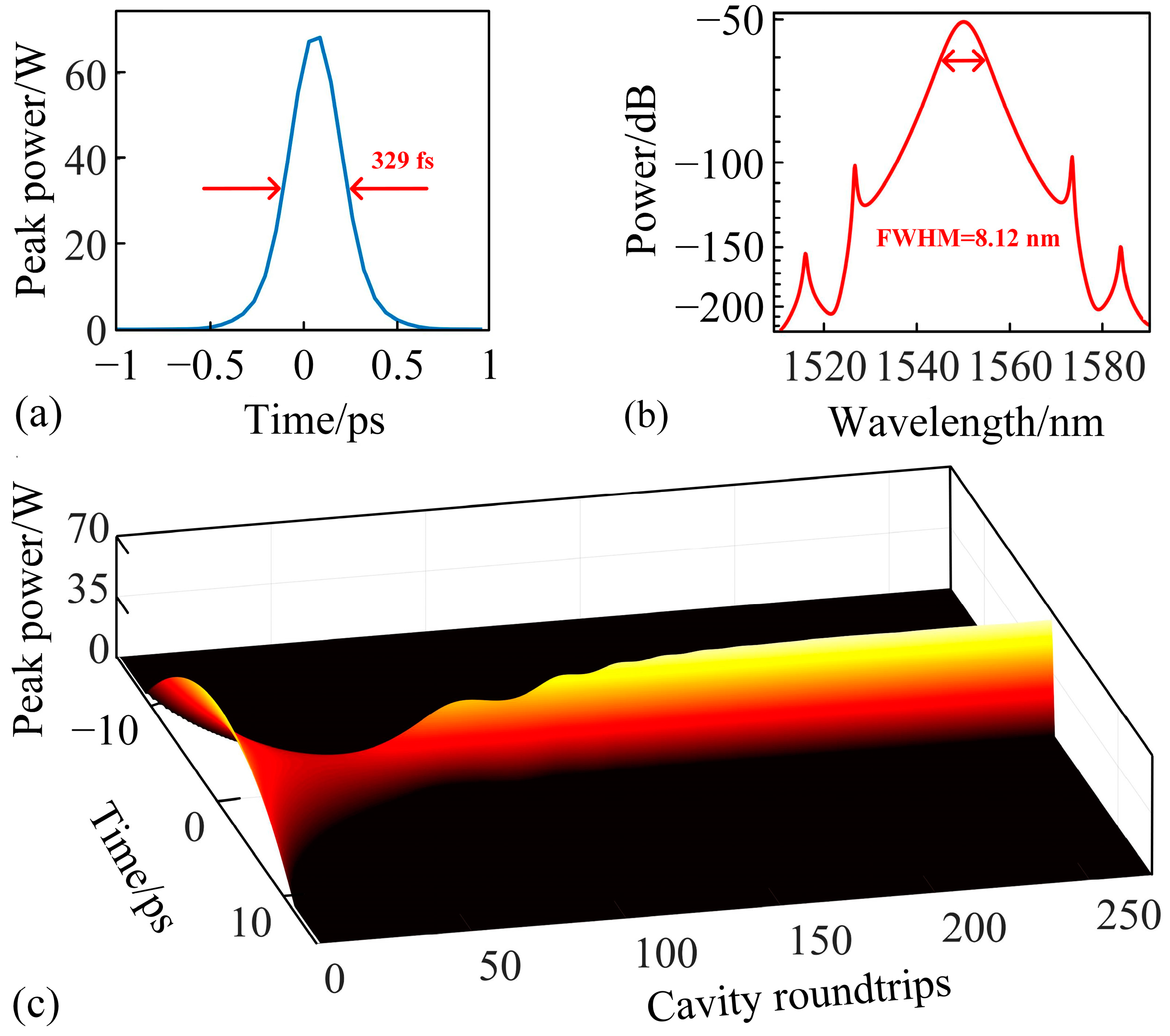
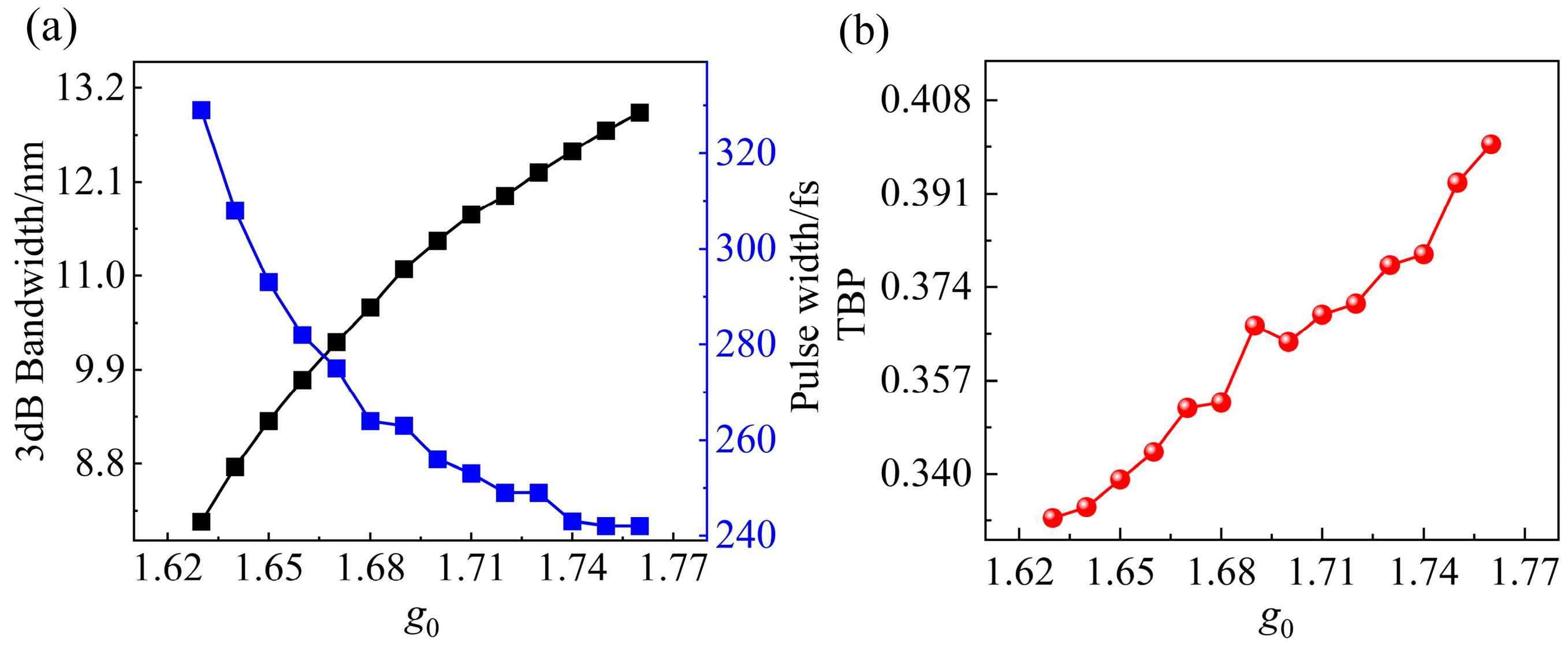
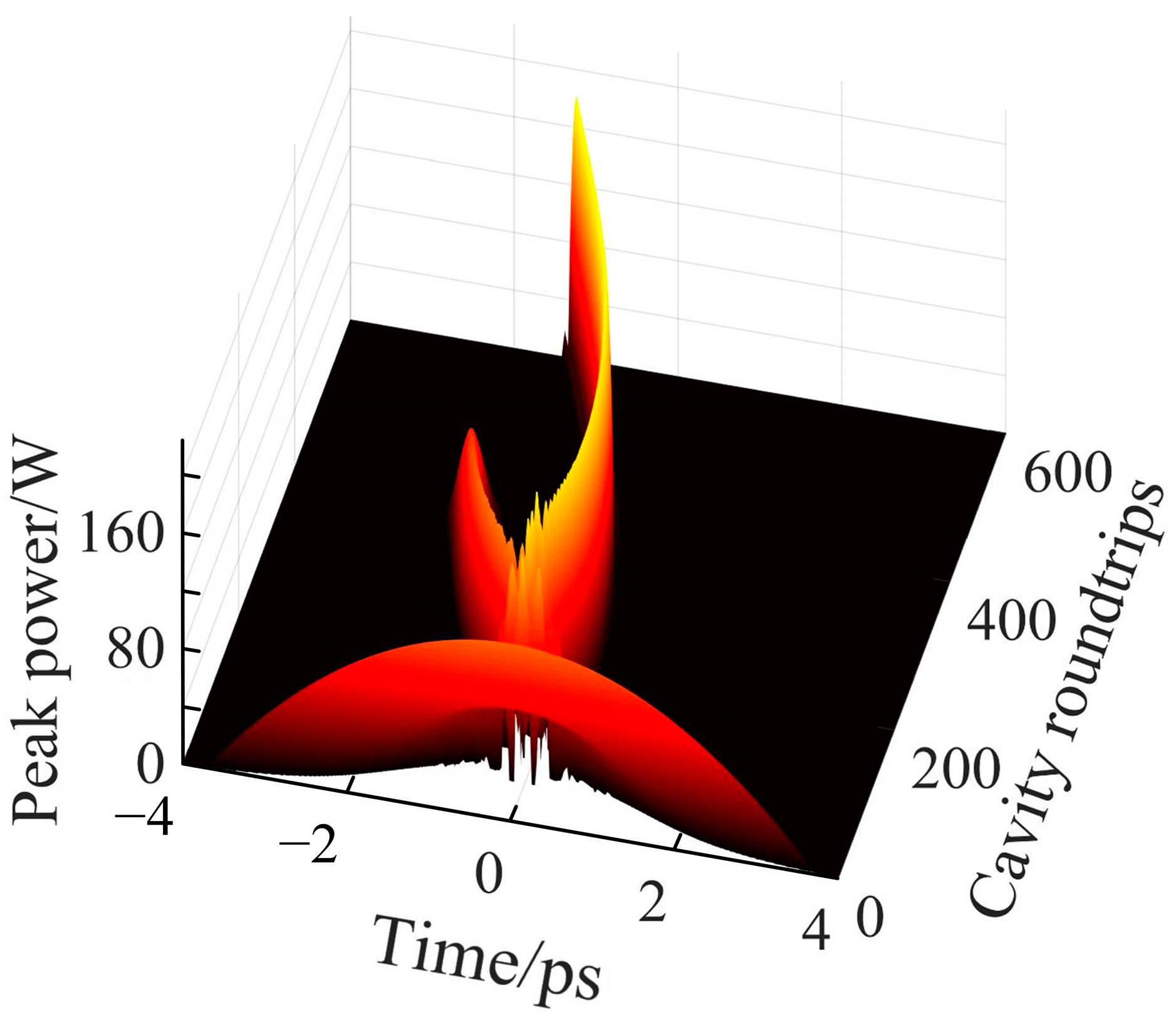
3.1. Soliton Mode-Locking
3.2. Soliton Transition Phase
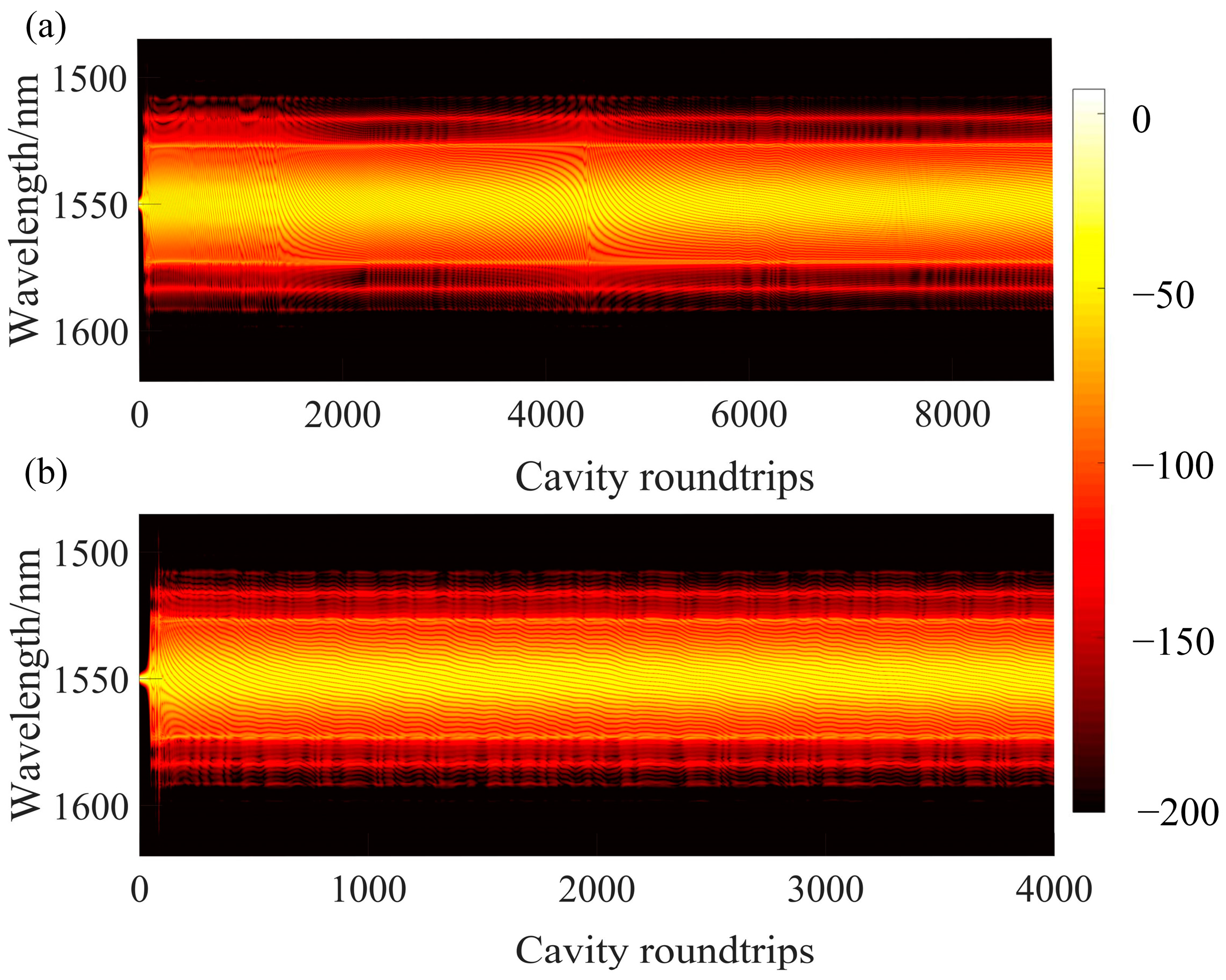
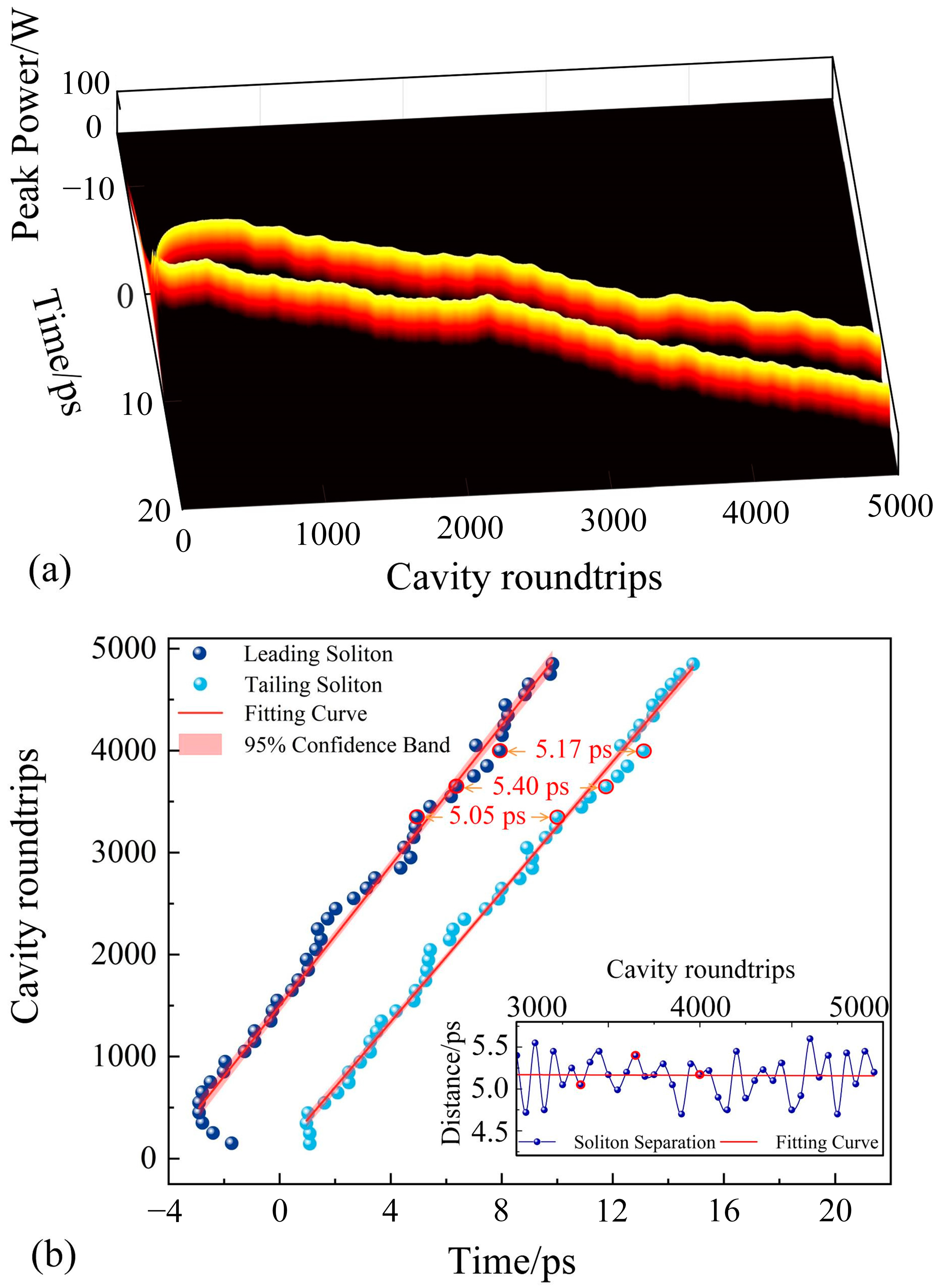
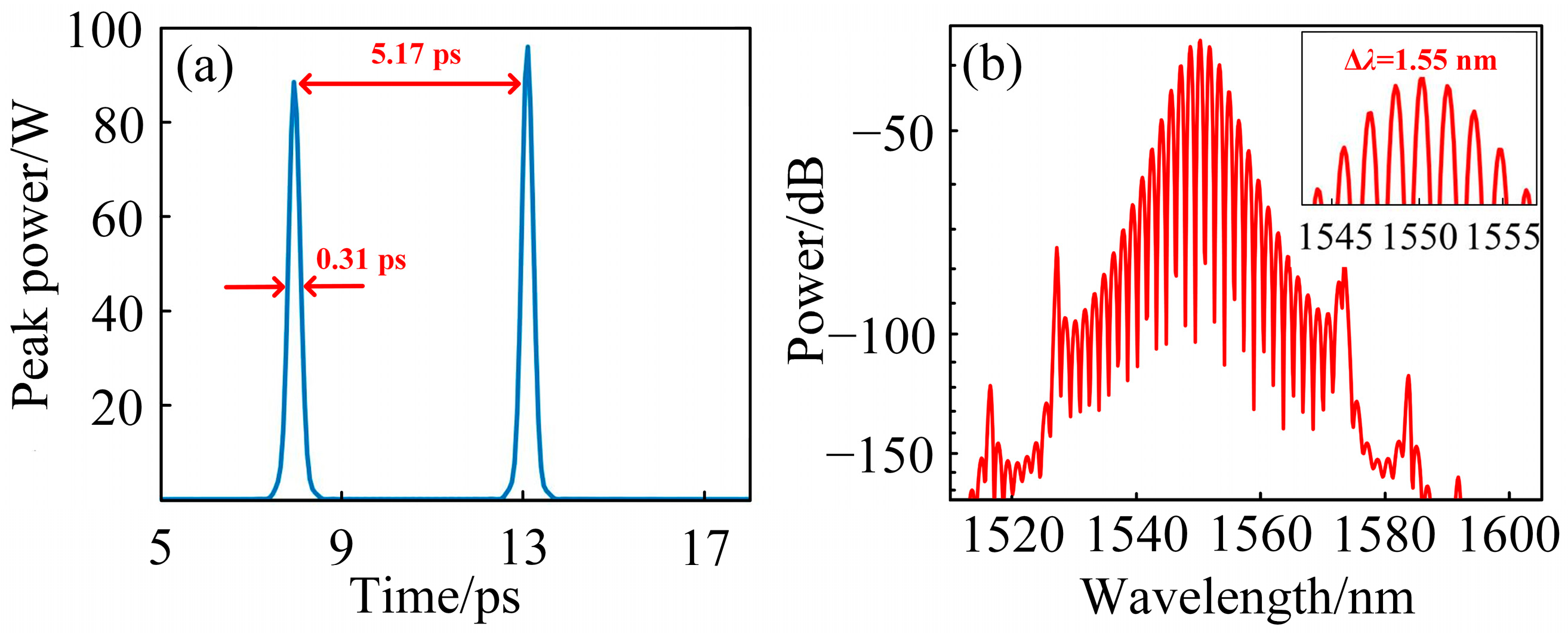
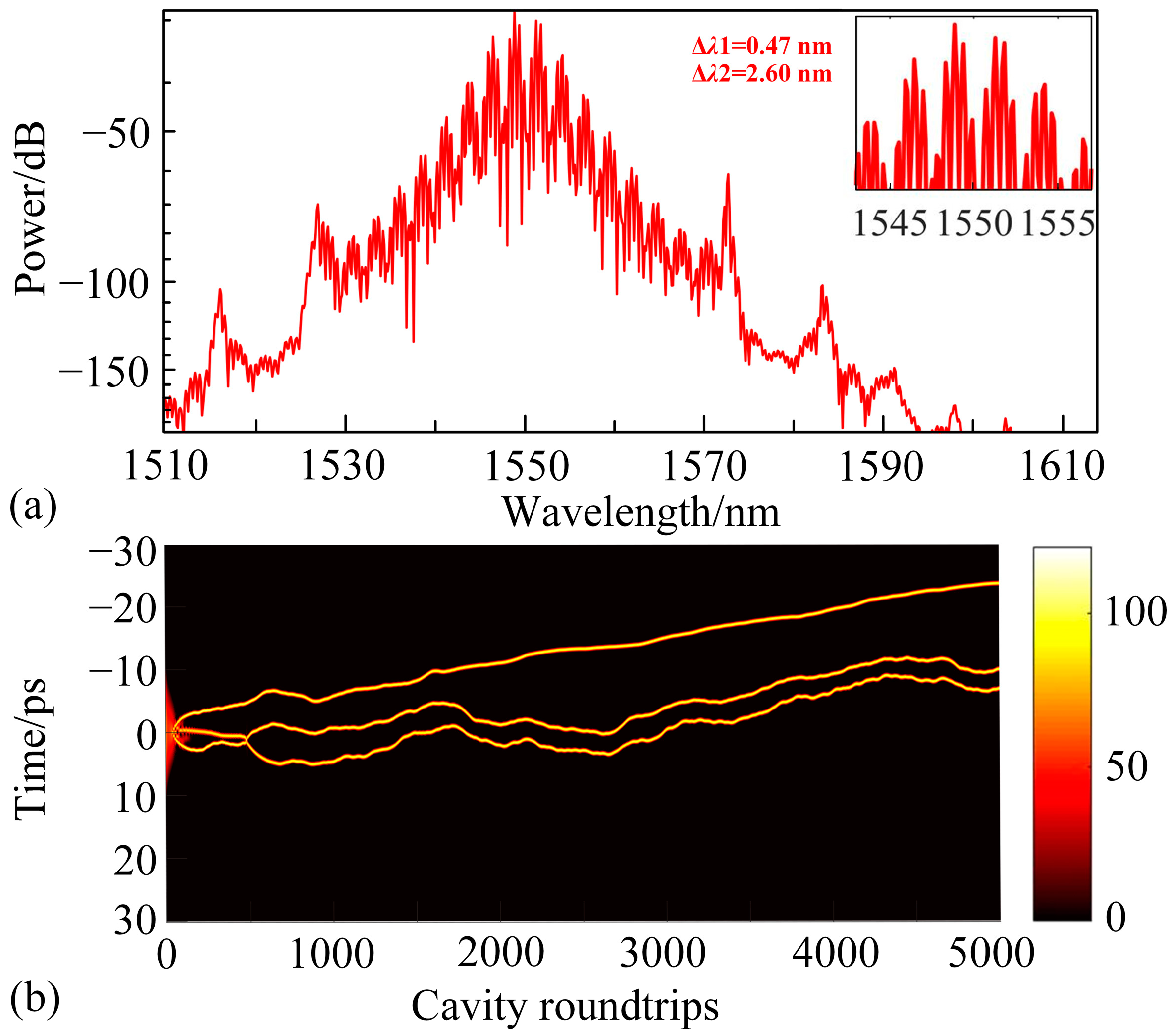
3.3. Double-Bound Solitons
3.4. Triple-Bound Solitons
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wang, X.Z.; Wang, Z.H.; Wang, Y.Y.; Zhang, X.; Song, J.J.; Wei, Z.-Y. A Self-Diffraction Temporal Filter for Contrast Enhancement in Femtosecond Ultra-High Intensity Laser. Chin. Phys. Lett. 2021, 38, 074202. [Google Scholar] [CrossRef]
- Xu, Y.; Xie, H.; Jiang, G.; Miao, L.; Wang, K.; Tang, S.; Yu, X.; Zhang, H.; Bao, Q. Bilayer Bismuth Selenide Nanoplatelets Based Saturable Absorber for Ultra-short Pulse Generation (Invited). Opt. Commun. 2017, 395, 55–60. [Google Scholar] [CrossRef]
- Yang, L.-M.; Wan, P.; Protopopov, V.; Liu, J. 2 μm Femtosecond Fiber Laser at Low Repetition Rate and High Pulse Energy. Opt. Express 2012, 20, 5683. [Google Scholar] [CrossRef] [PubMed]
- Yanik, M.F.; Cinar, H.; Cinar, H.N.; Chisholm, A.D.; Jin, Y.; Ben-Yakar, A. Functional Regeneration after Laser Axotomy. Nature 2004, 432, 822. [Google Scholar] [CrossRef] [PubMed]
- Liu, X.M.; Popa, D.; Akhmediev, N. Revealing the Transition Dynamics from Q Switching to Mode Locking in a Soliton Laser. Phys. Rev. Lett. 2019, 123, 093901. [Google Scholar] [CrossRef] [PubMed]
- Guo, B.; Guo, X.; Zhou, R.; Ren, Z.; Chen, Q.; Xu, R.; Luo, W. Multi-Pulse Bound Soliton Fiber Laser Based on MoTe2 Saturable Absorber. Nanomaterials 2022, 13, 177. [Google Scholar] [CrossRef]
- Sun, D.; Zhao, Q.; Chu, S.; Cao, C.; Pei, J.; Xu, X.; Ruan, S. Multiple Bound State Soliton Pulses in the All Polarization Maintaining Fiber Laser. Micromachines 2023, 14, 1528. [Google Scholar] [CrossRef] [PubMed]
- Wu, C.H.; Yao, Y.; Yang, Y.; Xu, X.C.; Tian, J.J.; Xu, K. Wavelength-Switchable and Multi-Pulse Bound State Based on a Hybrid Mode-Locked Mechanism. Opt. Express 2022, 30, 10732. [Google Scholar] [CrossRef]
- Li, X.; Xia, K.; Wu, D.; Nie, Q.; Dai, S. Bound states of solitons in a fiber laser with a microfiber-based WS2 saturable absorber. IEEE Photonics Technol. Lett. 2017, 29, 2071–2074. [Google Scholar] [CrossRef]
- Herink, G.; Kurtz, F.; Jalali, B.; Solli, D.R.; Ropers, C. Real-Time Spectral Interferometry Probes the Internal Dynamics of Femtosecond Soliton Molecules. Science 2017, 356, 50–54. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Sun, M.; Liang, Q.; Yang, S.; Li, S.; Ning, Q. Observation of Diverse Structural Bound-State Patterns in a Passively Mode-Locked Fiber Laser. Appl. Phys. Express 2020, 13, 022009. [Google Scholar] [CrossRef]
- Torres-Torres, C.; García-Beltrán, G. Theoretical Models for Describing an Enhancement in Nanoscale Optical Nonlinearities for Applications Design. In Optical Nonlinearities in Nanostructured Systems; Springer Tracts in Modern Physics; Springer International Publishing: Cham, Switzerland, 2022; Volume 287, pp. 33–58. ISBN 978-3-031-10823-5. [Google Scholar]
- Qin, L.; Hang, C.; Malomed, B.A.; Huang, G. Stable High-Dimensional Weak-Light Soliton Molecules and Their Active Control. Laser Photonics Rev. 2022, 16, 2100297. [Google Scholar] [CrossRef]
- Nguyen, N.D. Generation of High-order Multi-bound Solitons and Propagation in Optical Fibers. Opt. Commun. 2009, 282, 2394–2406. [Google Scholar] [CrossRef]
- Du, Y.; Gao, Q.; He, Z.; Li, J.; Zeng, C.; Mao, D.; Zhao, J. Stable Loosely Bounded Asymmetric Soliton Molecules in Fiber Lasers. Phys. Rev. A 2021, 104, 043508. [Google Scholar] [CrossRef]
- Liu, X.M.; Han, X.X.; Yao, X.K. Discrete Bisoliton Fiber Laser. Sci. Rep. 2016, 6, 34414. [Google Scholar] [CrossRef] [PubMed]
- Wang, B.; Han, H.; Yu, L.; Wang, Y.; Dai, C. Generation and Dynamics of Soliton and Soliton Molecules from a VSe2/GO-Based Fiber Laser. Nanophotonics 2021, 11, 129–137. [Google Scholar] [CrossRef] [PubMed]
- Hu, J.; Yang, L.; Chen, L.; Huang, J.; Zhu, H.; Miao, L.; Zhao, C. Nanosecond mid-infrared pulse generation modulated by platinum ditelluride nanosheets. Laser Phys. Lett. 2022, 19, 075107. [Google Scholar] [CrossRef]
- Qiao, J.; Zhu, R.; Ahmed, S.; Fan, R.; Ivan, M.N.A.S.; Liu, G.; Tsang, Y.H.; Feng, S. Passive Mode-Locking and Q-Switching of Ytterbium-Doped Fiber Lasers Using Cr2S3 Saturable Absorbers. Opt. Quantum Electron. 2024, 56, 1146. [Google Scholar] [CrossRef]
- Yang, F.; Sui, Z.; Sun, S.; Chen, S.; Wang, Y.; Fan, W.; Li, S.; Wang, G.; Zhang, W.; Lu, C.; et al. Demonstration of Conventional Soliton, Bound-State Soliton, and Noise-Like Pulse Based on Chromium Sulfide as Saturable Absorber. Nanophotonics 2022, 11, 4937–4945. [Google Scholar] [CrossRef]
- Fan, X.; Chen, Z.; Xu, D.; Zou, L.; Ouyang, F.; Deng, S.; Wang, X.; Zhao, J.; Zhou, Y. Phase-Controlled Synthesis of Large-Area Trigonal 2D Cr2S3 Thin Films via Ultralow Gas-Flow Governed Dynamic Transport. Adv. Funct. Mater. 2024, 34, 2404750. [Google Scholar] [CrossRef]
- Xie, L.; Wang, J.; Li, J.; Li, C.; Zhang, Y.; Zhu, B.; Guo, Y.; Wang, Z.; Zhang, K. An Atomically Thin Air-Stable Narrow-Gap Semiconductor Cr2S3 for Broadband Photodetection with High Responsivity. Adv. Electron. Mater. 2021, 7, 2000962. [Google Scholar] [CrossRef]
- Tang, Y.; Fang, H.; Long, M.; Chen, G.; Zheng, Z.; Zhang, J.; Zhou, W.; Ning, Z.; Zhu, Z.; Feng, Y.; et al. Significant Enhancement of Single-Walled Carbon Nanotube Based Infrared Photodetector Using PbS Quantum Dots. IEEE J. Select. Topics Quantum Electron. 2018, 24, 3801608. [Google Scholar] [CrossRef]
- Huang, Z.; Han, W.; Tang, H.; Ren, L.; Chander, D.S.; Qi, X.; Zhang, H. Photoelectrochemical-Type Sunlight Photodetector Based on MoS2 /Graphene Heterostructure. 2D Mater. 2015, 2, 035011. [Google Scholar] [CrossRef]
- Zhang, B.Y.; Liu, T.; Meng, B.; Li, X.; Liang, G.; Hu, X.; Wang, Q.J. Broadband High Photoresponse from Pure Monolayer Graphene Photodetector. Nat. Commun. 2013, 4, 1811. [Google Scholar] [CrossRef] [PubMed]
- Choi, W.; Cho, M.Y.; Konar, A.; Lee, J.H.; Cha, G.; Hong, S.C.; Kim, S.; Kim, J.; Jena, D.; Joo, J.; et al. High-Detectivity Multilayer MoS2 Phototransistors with Spectral Response from Ultraviolet to Infrared. Adv. Mater. 2012, 24, 5832–5836. [Google Scholar] [CrossRef] [PubMed]
- Xu, Y.; Liu, C.; Guo, C.; Yu, Q.; Guo, W.; Lu, W.; Chen, X.; Wang, L.; Zhang, K. High Performance near Infrared Photodetector Based on In-Plane Black Phosphorus p-n Homojunction. Nano Energy 2020, 70, 104518. [Google Scholar] [CrossRef]
- Liu, J.; Li, Y.; Song, Y.; Ma, Y.; Chen, Q.; Zhu, Z.; Lu, P.; Wang, S. Bi2Te3 Photoconductive Detectors on Si. Appl. Phys. Lett. 2017, 110, 141109. [Google Scholar] [CrossRef]
- Tao, Y.; Wu, X.; Wang, W.; Wang, J. Flexible Photodetector from Ultraviolet to Near Infrared Based on a SnS2 Nanosheet MicroSphere Film. J. Mater. Chem. C 2015, 3, 1347–1353. [Google Scholar] [CrossRef]
- Zheng, Z.; Zhang, T.; Yao, J.; Zhang, Y.; Xu, J.; Yang, G. Flexible, Transparent and Ultra-Broadband Photodetector Based on Large-area WSe2 Film for Wearable Devices. Nanotechnology 2016, 27, 225501. [Google Scholar] [CrossRef] [PubMed]
- Gao, Q.; Jin, Z.; Qu, L.; Shao, Z.; Liu, X.; Zhang, Y.; Fu, Z.; Huang, Y.; Wang, L.; Feng, W. CuO Nanosheets for Use in PhotoeLectrochemical Photodetectors. ACS Appl. Nano Mater. 2023, 6, 784–791. [Google Scholar] [CrossRef]
- Han, X.; Xu, G.; Xing, J.; Song, Y.; Sun, Z.; Rong, D.; Ma, F.; Guo, Z.; Feng, B.; Guo, J.; et al. Response Speed-Tunable Photodetectors Based on Hybrid Ternary FePSe3 Nanoflakes. Adv. Opt. Mater. 2023, 11, 2300317. [Google Scholar] [CrossRef]
- D’yachkov, P.N. Optical Band Gap Energies in Quasi-Metal Carbon Nanotubes. Russ. J. Inorg. Chem. 2018, 63, 55–60. [Google Scholar] [CrossRef]
- Popa, D.; Jiang, Z.; Bonacchini, G.E.; Zhao, Z.; Lombardi, L.; Torrisi, F.; Ott, A.K.; Lidorikis, E.; Ferrari, A.C. A Stable, Power Scaling, Graphene-Mode-Locked All-Fiber Oscillator. Appl. Phys. Lett. 2017, 110, 243102. [Google Scholar] [CrossRef]
- Wang, Y.; Mao, D.; Gan, X.; Han, L.; Ma, C.; Xi, T.; Zhang, Y.; Shang, W.; Hua, S.; Zhao, J. Harmonic Mode Locking of Bound-State Solitons Fiber Laser Based on MoS2 Saturable Absorber. Opt. Express 2015, 23, 205. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.; Jiang, G.; Chen, S.; Guo, Z.; Yu, X.; Zhao, C.; Zhang, H.; Bao, Q.; Wen, S.; Tang, D.; et al. Mechanically Exfoliated Black Phosphorus as a New Saturable Absorber for Both Q-switching and Mode-Locking Laser Operation. Opt. Express 2015, 23, 12823. [Google Scholar] [CrossRef] [PubMed]
- Lin, Y.H.; Lin, S.F.; Chi, Y.C.; Wu, C.L.; Cheng, C.H.; Tseng, W.H.; He, J.H.; Wu, C.I.; Lee, C.K.; Lin, G.R. Using N- and P-Type Bi2Te3 Topological Insulator Nanoparticles to Enable Controlled Femtosecond Mode-Locking of Fiber Lasers. ACS Photonics 2015, 2, 481–490. [Google Scholar] [CrossRef]
- Niu, K.; Sun, R.; Chen, Q.; Man, B.; Zhang, H. Passively Mode-Locked Er-Doped Fiber Laser Based on SnS2 Nanosheets as a Saturable Absorber. Photon. Res. 2018, 6, 72. [Google Scholar] [CrossRef]
- Wang, J.; Li, J.; Chen, H.; Zhang, M.; Li, I.L.; Yan, P. Mode-Locked Thulium-Doped Fiber Laser with WSe2 Based Evanescent Field Interaction. In Proceedings of the 2017 16th International Conference on Optical Communications and Networks (ICOCN), Wuzhen, China, 7–10 August 2017; pp. 1–3. [Google Scholar]
- Kong, L.; Chu, H.; Li, Z.; Gao, S.; Pan, Z.; Pan, H.; Zhao, S.; Li, D. The Generation of Noise-like Pulses and Various Solitons with CuO Nanorods as a Broadband Saturable Absorber. J. Alloys Compd. 2024, 984, 173965. [Google Scholar] [CrossRef]
- Wang, Y.; Huang, H.; Li, X.; Ma, K.; Zhao, Y.; Chen, Y.; Feng, J.; Liu, J.; Zheng, C. Controllable Soliton Pairs in Few-Layer FePSe3 Nanosheets-Based Optical-Intensity Modulators. ACS Appl. Nano Mater. 2020, 3, 7713–7719. [Google Scholar] [CrossRef]
- Pawliszewska, M.; Dużyńska, A.; Zdrojek, M.; Sotor, J. Metallic Carbon Nanotube-Based Saturable Absorbers for Holmium-Doped Fiber Lasers. Opt. Express 2019, 27, 11361. [Google Scholar] [CrossRef] [PubMed]
- Agrawal, G.P. Nonlinear Fiber Optics; Springer: Berlin/Heidelberg, Germany, 2000; pp. 195–211. ISBN 978-3-540-66918-0. [Google Scholar]
- Mears, R.J.; Reekie, L.; Jauncey, I.M.; Payne, D.N. Low-Noise Erbium-Doped Fiber Amplifier Operating at 1.54 μm. Electron. Lett. 1987, 23, 1026–1028. [Google Scholar] [CrossRef]
- Zhang, Z.X.; Luo, M.; Liu, J.H.; Yang, Y.T.; Li, T.J.; Liu, M.; Luo, A.P.; Xu, W.C.; Luo, Z.C. Coherence-Controlled Chaotic Soliton Bunch. Nat. Commun. 2024, 15, 6148. [Google Scholar] [CrossRef]
- Li, W.; Lin, R.; Chen, G.; Geng, G.; Xu, P.; Yang, Y.; Wang, X.; Xu, J. Observation of Three Kinds of Bound Solitons in a Black Phosphorus-Based Erbium Fiber Laser. Opt. Fiber Technol. 2024, 82, 103617. [Google Scholar] [CrossRef]
- Nelson, L.E.; Jones, D.J.; Tamura, K.; Haus, H.A.; Ippen, E.P. Ultrashort-Pulse Fiber Ring Lasers. Appl. Phys. B 1997, 65, 277–294. [Google Scholar] [CrossRef]
- Yang, L.; Yao, C.; Wu, Y.; Wang, X.; Ren, G.; Wang, C.; Li, P. Theoretical Study on Multi-Range Pulsewidth Tuning in a Dissipative Soliton Laser Mode-Locked by a Dirac Semimetal. AIP Adv. 2023, 13, 045215. [Google Scholar] [CrossRef]
- Haus, H.A. Mode-Locking of Lasers. IEEE J. Sel. Top. Quantum Electron. 2000, 6, 1173–1185. [Google Scholar] [CrossRef]
- Tang, D.Y.; Zhao, L.M.; Zhao, B. Multipulse Bound Solitons with Fixed Pulse Separations Formed by Direct Soliton Interaction. Appl. Phys. B 2005, 80, 239–242. [Google Scholar] [CrossRef]
- Zeng, J.; Sander, M.Y. Real-Time Transition Dynamics between Multi-Pulsing States in a Mode-Locked Fiber Laser. Opt. Lett. 2020, 45, 5. [Google Scholar] [CrossRef]
- Tang, D.Y.; Zhao, L.M.; Zhao, B.; Liu, A.Q. Mechanism of Multisoliton Formation and Soliton Energy Quantization in Passively Mode-Locked Fiber Lasers. Phys. Rev. A 2005, 72, 043816. [Google Scholar] [CrossRef]
- Duan, X.; Liu, Y.; Huang, Q.; Gao, Z.; Jin, L. Impact of Small-Signal Gain and Saturation Energy on the Mode-Locking States in an YB-Doped Fiber Laser. In Proceedings of the 2023 Asia Communications and Photonics Conference/2023 International Photonics and Optoelectronics Meetings (ACP/POEM), Wuhan, China, 4–7 November 2023; pp. 1–5. [Google Scholar]
- Soto-Crespo, J.M.; Akhmediev, N.; Grelu, P.; Belhache, F. Quantized Separations of Phase-Locked Soliton Pairs in Fiber Lasers. Opt. Lett. 2003, 28, 1757. [Google Scholar] [CrossRef] [PubMed]
- Rohrmann, P.; Hause, A.; Mitschke, F. Two-Soliton and Three-Soliton Molecules in Optical Fibers. Phys. Rev. A 2013, 87, 043834. [Google Scholar] [CrossRef]
- Yang, S.; Zhu, Z.; Qi, Y.; Jin, L.; Li, L.; Lin, X. Internal Motion within Pulsating Pure-Quartic Soliton Molecules in a Fiber Laser. Chaos Solitons Fractals 2023, 172, 113544. [Google Scholar] [CrossRef]
- Zhao, B.; Tang, D.Y.; Shum, P.; Guo, X.; Lu, C.; Tam, H.Y. Bound Twin-Pulse Solitons in a Fiber Ring Laser. Phys. Rev. E 2004, 70, 067602. [Google Scholar] [CrossRef] [PubMed]
- Gan, Y.; Wu, Q.; Yao, Y.; Liu, C.; Fu, Y.; Yang, Y.; Tian, J.; Xu, K. Generation of High-Order Solitons with Order Continuously Adjustable in a Fiber Laser Based on GIMF–SIMF–GIMF Saturable Absorber. Opt. Commun. 2021, 479, 126441. [Google Scholar] [CrossRef]
- Huang, Q.; Jiang, H.; Jin, L.; Gao, Z.; Hu, G.; Duan, X.; Li, L. The Impact of Saturable Absorber Recovery Time on Hybrid Mode-Locked Fiber Lasers with near Zero Net Dispersion. Results Opt. 2023, 13, 100551. [Google Scholar] [CrossRef]
- Liang, H.; Wang, Z.; He, R.; Liu, Y.; Li, H.; Ni, L.; Wang, Z. Evolution of Complex Pulse-Bunches in a Bound-State Soliton Fiber Laser. IEEE Photonics Technol. Lett. 2018, 30, 1475–1478. [Google Scholar] [CrossRef]

| Parameter | Value |
|---|---|
| λ0/nm | 1550 |
| Tmax/ps | 60 |
| M | 210 |
| NL | 0–1 |
| TFWHM/ps | 10 |
| C0 | 0 |
| Fiber Type | β2/ps2/km |
|---|---|
| EDF | 23.495 |
| SMF | −22.86 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, D.; Zhai, R.; Wu, Y.; Liu, M.; Zhao, K.; Yang, Q.; Dong, Y.; Li, X.; Wu, X.; Jia, Z. The Study of Soliton Mode-Locked and Bound States in Erbium-Doped Fiber Lasers Based on Cr2S3 Saturable Absorbers. Materials 2025, 18, 864. https://doi.org/10.3390/ma18040864
Li D, Zhai R, Wu Y, Liu M, Zhao K, Yang Q, Dong Y, Li X, Wu X, Jia Z. The Study of Soliton Mode-Locked and Bound States in Erbium-Doped Fiber Lasers Based on Cr2S3 Saturable Absorbers. Materials. 2025; 18(4):864. https://doi.org/10.3390/ma18040864
Chicago/Turabian StyleLi, Dong, Ruizhan Zhai, Yongjing Wu, Minzhe Liu, Kun Zhao, Qi Yang, Youwei Dong, Xiaoying Li, Xiaoyang Wu, and Zhongqing Jia. 2025. "The Study of Soliton Mode-Locked and Bound States in Erbium-Doped Fiber Lasers Based on Cr2S3 Saturable Absorbers" Materials 18, no. 4: 864. https://doi.org/10.3390/ma18040864
APA StyleLi, D., Zhai, R., Wu, Y., Liu, M., Zhao, K., Yang, Q., Dong, Y., Li, X., Wu, X., & Jia, Z. (2025). The Study of Soliton Mode-Locked and Bound States in Erbium-Doped Fiber Lasers Based on Cr2S3 Saturable Absorbers. Materials, 18(4), 864. https://doi.org/10.3390/ma18040864






