High Sensitivity Design for Silicon-On-Insulator-Based Asymmetric Loop-Terminated Mach–Zehnder Interferometer
Abstract
1. Introduction
2. Sensor Design and Numerical Model
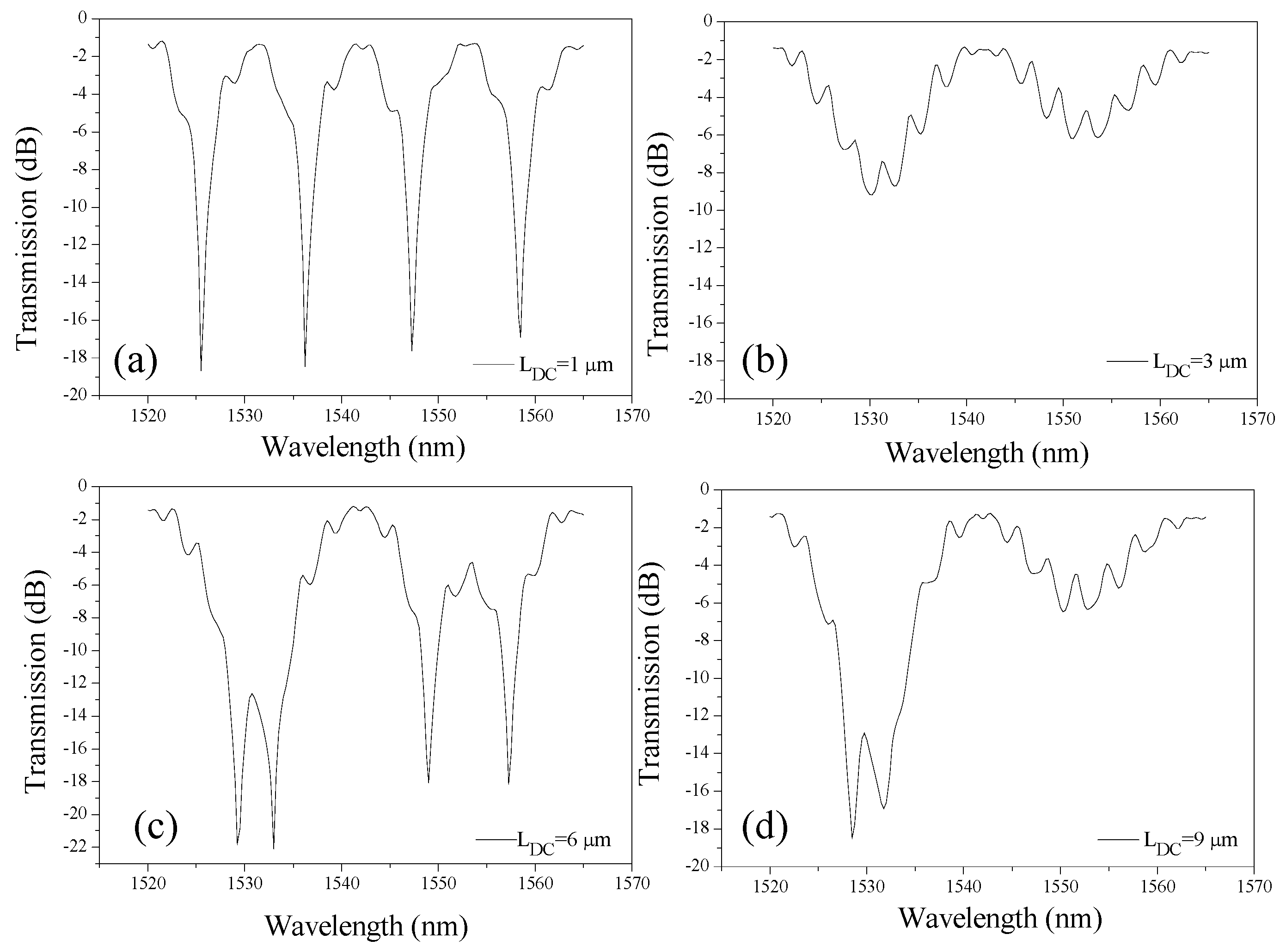
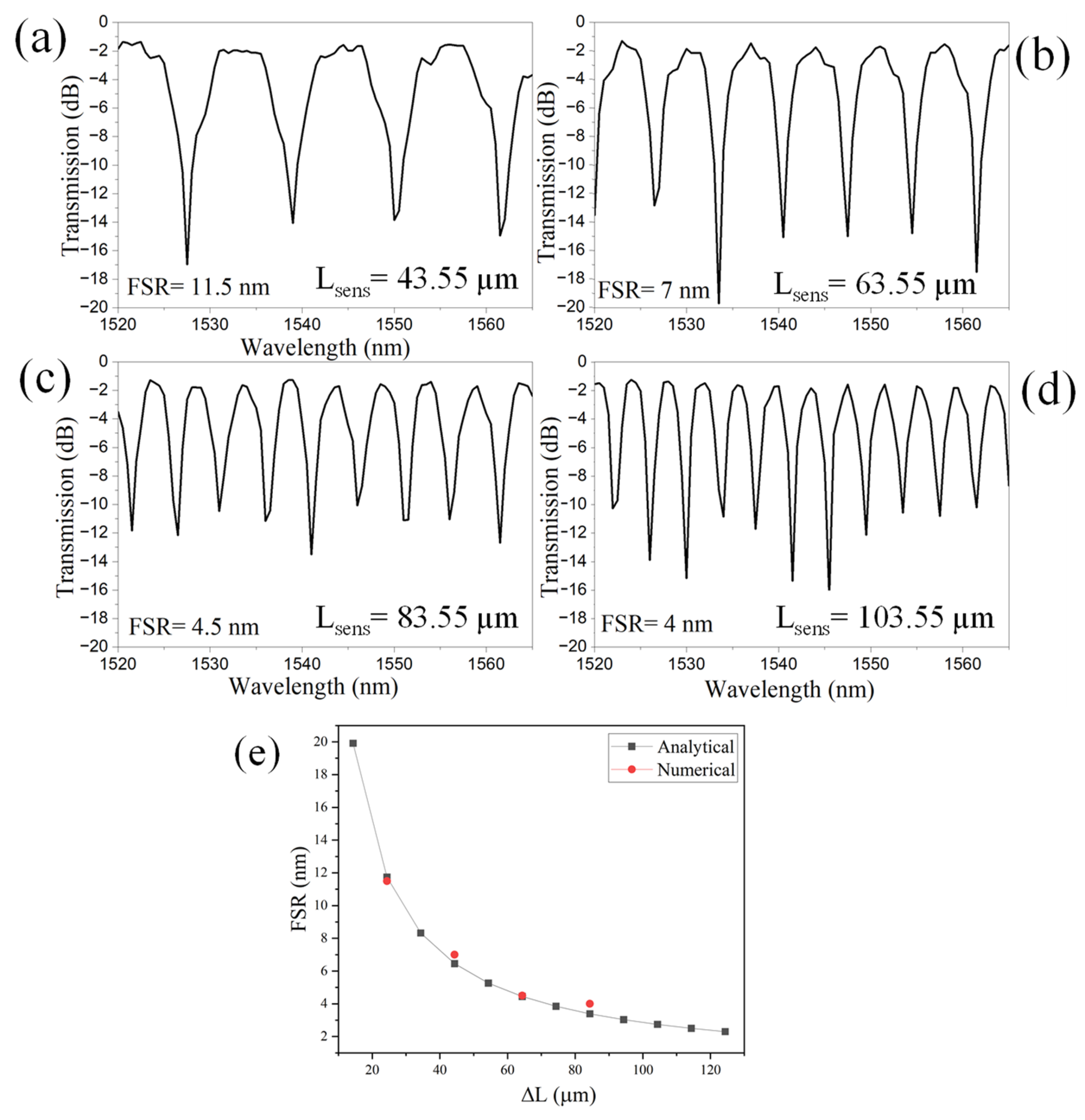
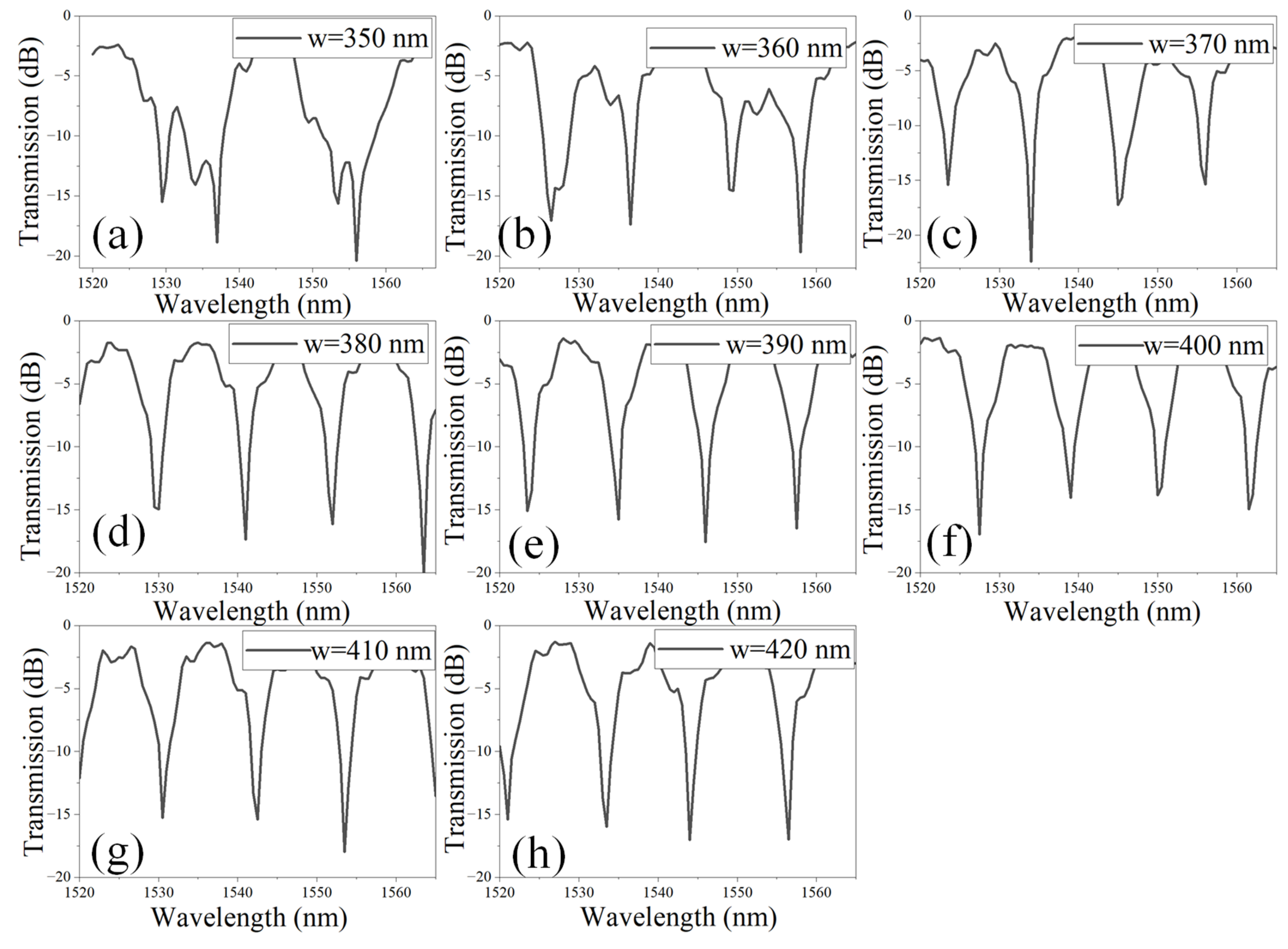
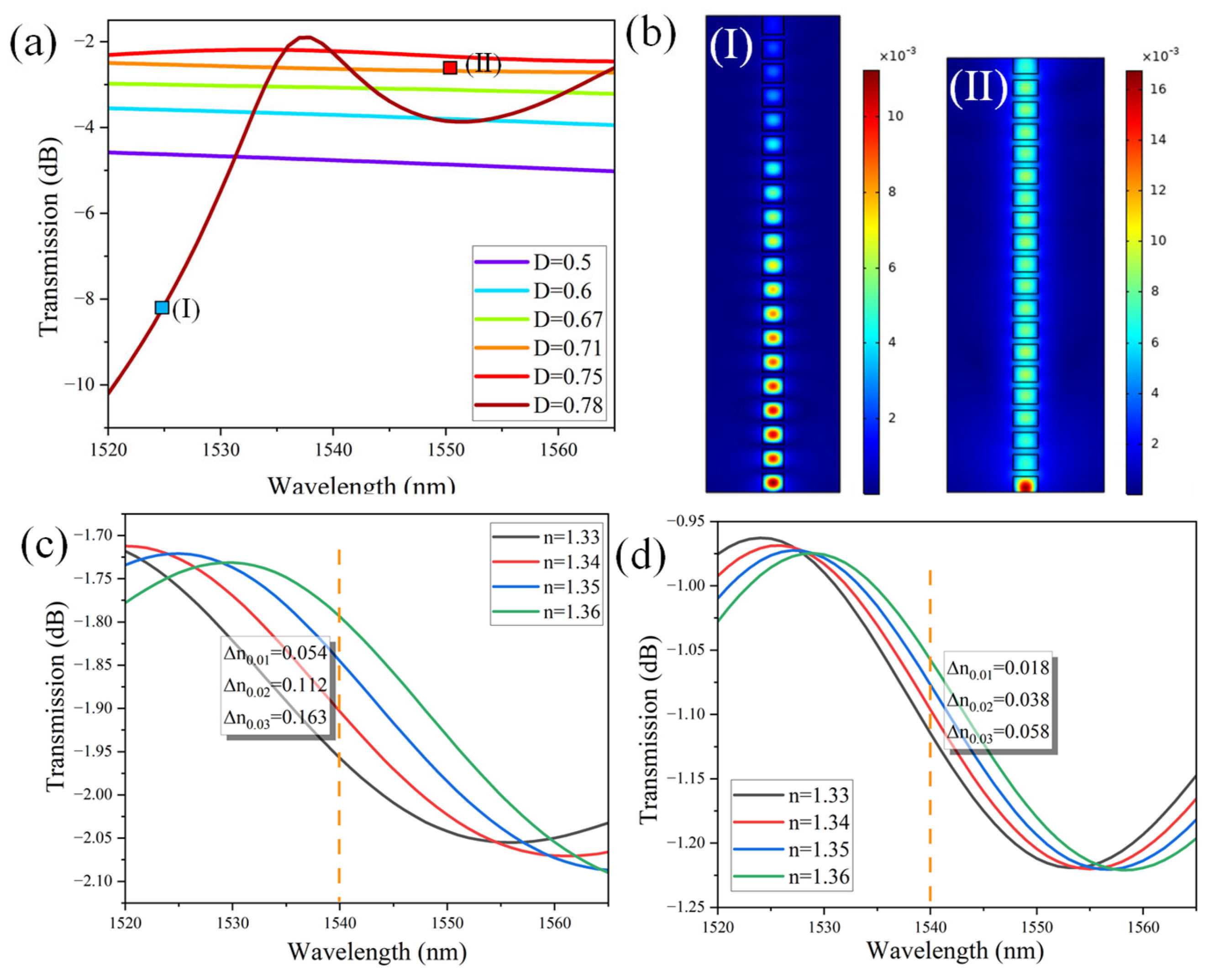
3. Device Optimization
4. RI Sensing Application
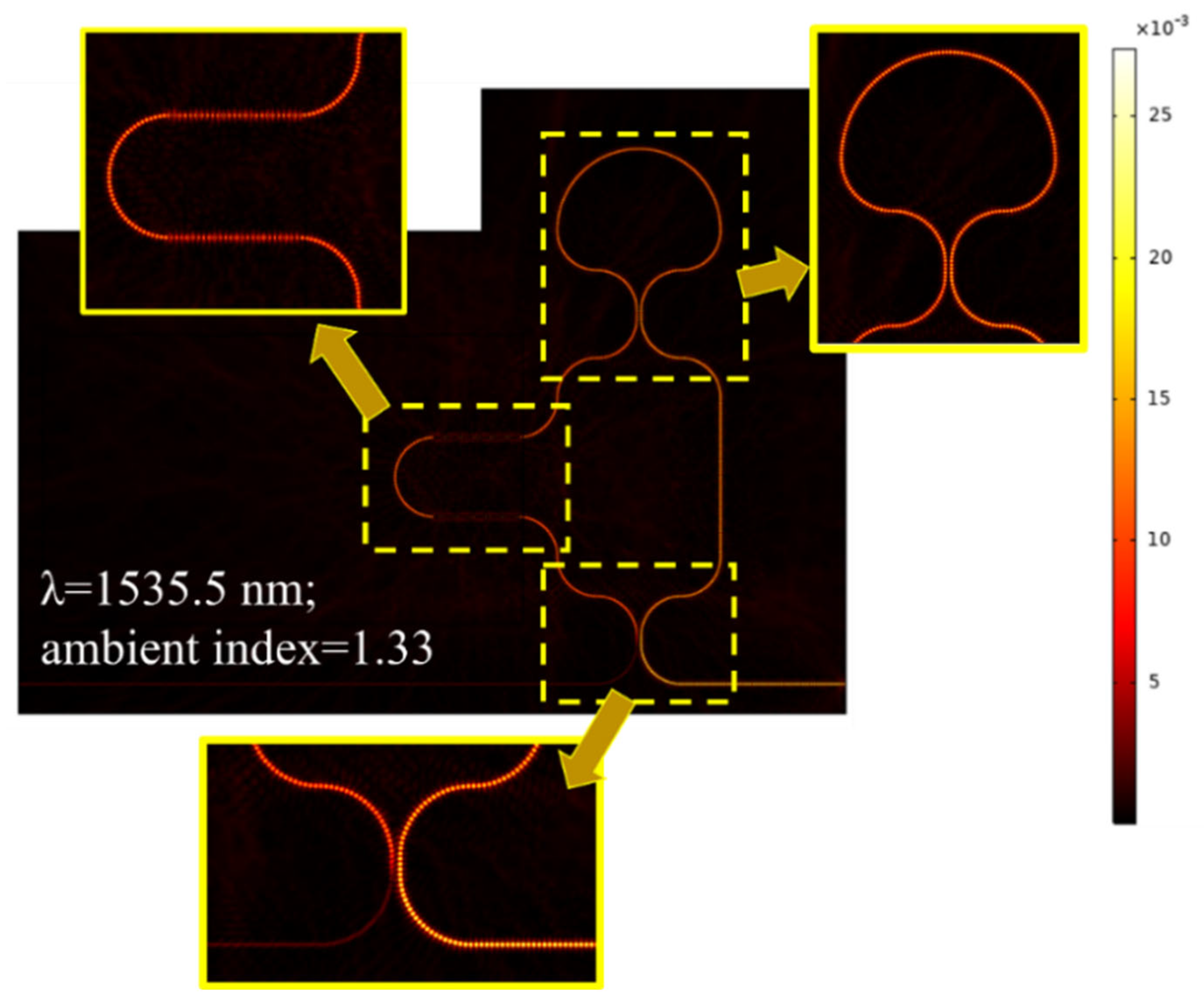
4.1. Design of a-SWG-LT-MZI
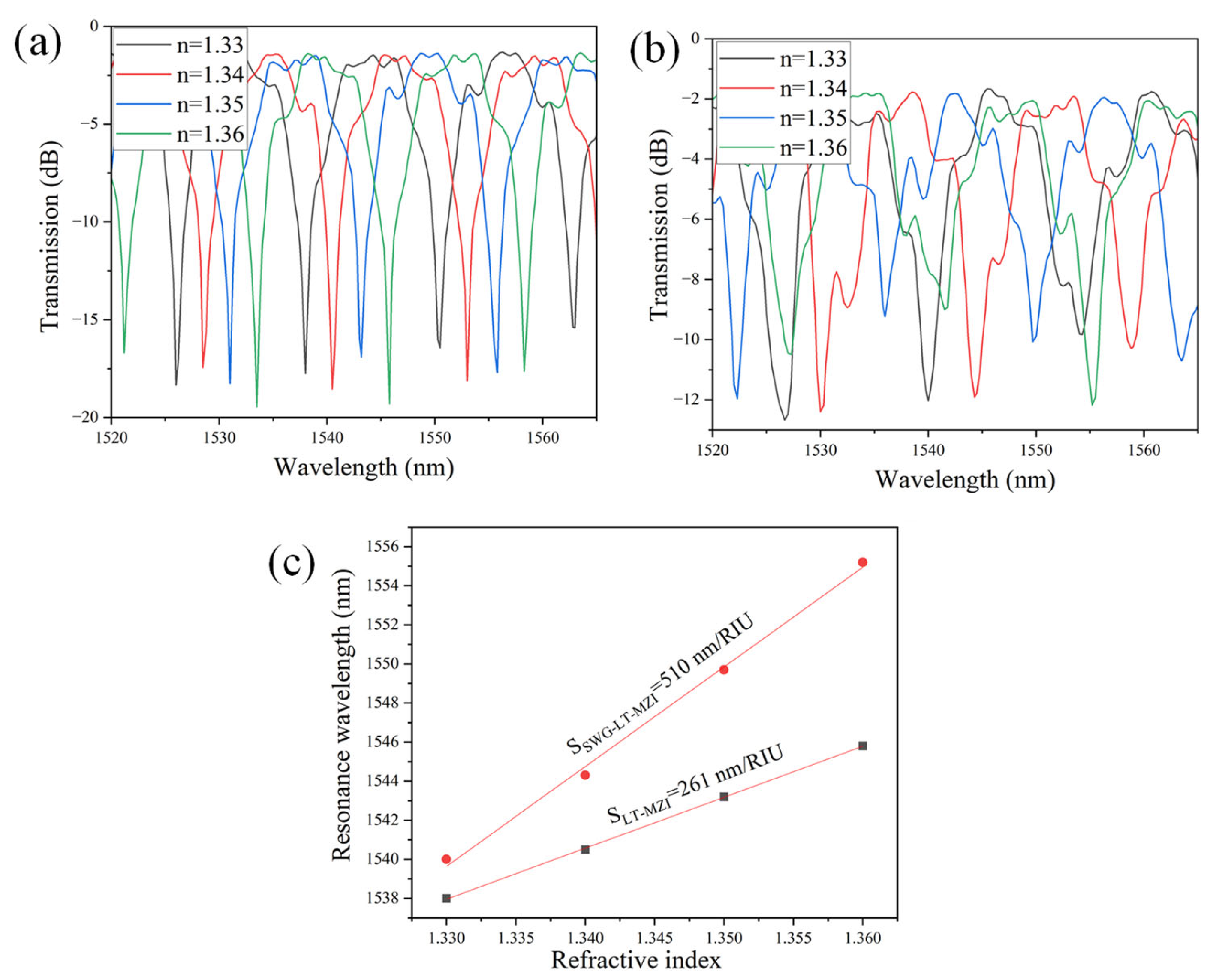
4.2. Sensing Performance of a-LT-MZI and SWG-a-LT-MZI Structures
5. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Levy, U.; Desiatov, B.; Goykhman, I.; Nachmias, T.; Ohayon, A.; Meltzer, S.E. Design, Fabrication, and Characterization of Circular Dammann Gratings Based on Grayscale Lithography. Opt. Lett. 2010, 35, 880–882. [Google Scholar] [CrossRef] [PubMed]
- Li, G.; Li, T.; Liu, Y.; Zheng, Y. A new Mach–Zehnder Interference Temperature Measuring Sensor Based on Silica-Based Chip. Sci. Rep. 2024, 14, 8657. [Google Scholar] [CrossRef] [PubMed]
- Ouyang, B.; Li, Y.; Kruidhof, M.; Horsten, R.; van Dongen, K.W.A.; Caro, J. On-chip silicon Mach–Zehnder Interferometer Sensor for Ultrasound Detection. Opt. Lett. 2019, 44, 1928–1931. [Google Scholar] [CrossRef]
- Zhang, Y.; Zou, J.; He, J.-J. Temperature sensor with enhanced sensitivity based on silicon Mach-Zehnder interferometer with waveguide group index engineering. Opt. Express 2018, 26, 26057–26064. [Google Scholar] [CrossRef] [PubMed]
- Zhao, C.; Xu, L.; Liu, L. Ultrahigh Sensitivity Mach−Zehnder Interferometer Sensor Based on a Weak One-Dimensional Field Confinement Silica Waveguide. Sensors 2021, 21, 6600. [Google Scholar] [CrossRef]
- Ding, Z.; Dai, D.; Shi, Y. Ultra-Sensitive Silicon Temperature Sensor Based on Cascaded Mach–Zehnder Interferometers. Opt. Lett. 2021, 46, 2787–2790. [Google Scholar] [CrossRef]
- Wu, Y.; Zhou, Y.; Pan, J.; Huang, T.; Jin, S. Design of Highly Sensitive Refractive Index Sensor Based on Silicon Photonic Mach–Zehnder Interferometer. Opt. Commun. 2023, 534, 129288. [Google Scholar] [CrossRef]
- Hajshahvaladi, L.; Kaatuzian, H.; Danaie, M. A Very High-Resolution Refractive Index Sensor Based on Hybrid Topology of Photonic Crystal Cavity and Plasmonic Nested Split-Ring Resonator. Photonics Nanostructures Fundam. Appl. 2022, 51, 101042. [Google Scholar] [CrossRef]
- Singh, R.; Priye, V.; Chack, D. Highly Sensitive Refractive Index-Based Sensor for DNA Hybridization Using Subwavelength Grating Waveguide. IETE Tech. Rev. 2022, 39, 1463–1472. [Google Scholar] [CrossRef]
- Douzi, B. Protein–Protein Interactions: Surface Plasmon Resonance. In Bacterial Protein Secretion Systems: Methods and Protocols; Journet, L., Cascales, E., Eds.; Springer: New York, NY, USA, 2017; pp. 257–275. ISBN 978-1-4939-7033-9. [Google Scholar]
- Barrios, C.A. Optical Slot-Waveguide Based Biochemical Sensors. Sensors 2009, 9, 4751–4765. [Google Scholar] [CrossRef]
- Xu, Y.; Bai, P.; Zhou, X.; Akimov, Y.; Png, C.E.; Ang, L.-K.; Knoll, W.; Wu, L. Optical Refractive Index Sensors with Plasmonic and Photonic Structures: Promising and Inconvenient Truth. Adv. Opt. Mater. 2019, 7, 1801433. [Google Scholar] [CrossRef]
- Seyyedmasoumian, S.; Attariabad, A.; Pourziad, A.; Bemani, M. Refractive Index Biosensor Using Metamaterial Perfect Absorber Based on Graphene in Near-Infrared for Disease Diagnosis. IEEE Sens. J. 2022, 22, 14870–14877. [Google Scholar] [CrossRef]
- Soref, R.A.; Leonardis, F.D.; Passaro, V.M.N. Multiple-Sagnac-Loop Mach–Zehnder Interferometer for Wavelength Interleaving, Thermo-Optical Switching and Matched Filteri. J. Light. Technol. 2018, 36, 5254–5262. [Google Scholar] [CrossRef]
- El Shamy, R.S.; Swillam, M.A.; ElRayany, M.M.; Sultan, A.; Li, X. Compact Gas Sensor Using Silicon-on-Insulator Loop-Terminated Mach–Zehnder Interferometer. Photonics 2022, 9, 8. [Google Scholar] [CrossRef]
- Butt, M.A. Loop-Terminated Mach-Zehnder Interferometer Integrated with Functional Polymer for CO2 Gas Sensing. Appl. Sci. 2024, 14, 4714. [Google Scholar] [CrossRef]
- Arianfard, H.; Juodkazis, S.; Moss, D.J.; Wu, J. Sagnac Interference in Integrated Photonics. Appl. Phys. Rev. 2023, 10, 011309. [Google Scholar] [CrossRef]
- El Shamy, R.S.; Afifi, A.E.; Badr, M.M.; Swillam, M.A. Modelling, Characterization, and Applications of Silicon on Insulator Loop Terminated Asymmetric Mach Zehnder Interferometer. Sci. Rep. 2022, 12, 3598. [Google Scholar] [CrossRef]
- Kim, D.-H.; Kang, J.U. Sagnac Loop Interferometer Based on Polarization Maintaining Photonic Crystal Fiber with Reduced Temperature Sensitivity. Opt. Express 2004, 12, 4490–4495. [Google Scholar] [CrossRef]
- Bogdanov, A.L.; Lapointe, J.; Schmid, J.H. Electron-Beam Lithography for Photonic Waveguide Fabrication: Measurement of the Effect of Field Stitching Errors on Optical Performance and Evaluation of a New Compensation Method. J. Vac. Sci. Technol. B 2012, 30, 031606. [Google Scholar] [CrossRef]
- Zheng, Y.; Gao, P.; Jiang, L.; Kai, X.; Duan, J. Surface Morphology of Silicon Waveguide after Reactive Ion Etching (RIE). Coatings 2019, 9, 478. [Google Scholar] [CrossRef]
- Han, M.; Li, X.; Zhang, S.; Liu, J.; Feng, Y.; Shang, C.; Han, H. Wavelength Switchable, Free Spectral Range Accurately Control Single-Pass Mach-Zehnder Interferometer Comb Filter. In Proceedings of the 2017 16th International Conference on Optical Communications and Networks (ICOCN), Wuzhen, China, 7–10 August 2017; pp. 1–3. [Google Scholar]
- Eftimov, T.; Arapova, A.; Janik, M.; Bock, W.J. Broad range bimodal microcavity in-line Mach-Zehnder Interferometers. Opt. Laser Technol. 2022, 145, 107503. [Google Scholar] [CrossRef]
- Doughan, I.; Oyemakinwa, K.; Ovaskainen, O.; Roussey, M. Strip-Loaded Mach–Zehnder Interferometer for Absolute Refractive Index Sensing. Sci. Rep. 2024, 14, 3064. [Google Scholar] [CrossRef] [PubMed]
- Wu, D.; Zhu, T.; Deng, M.; Duan, D.-W.; Shi, L.-L.; Yao, J.; Rao, Y.-J. Refractive Index Sensing Based on Mach–Zehnder Interferometer Formed by Three Cascaded Single-Mode Fiber Tapers. Appl. Opt. 2011, 50, 1548–1553. [Google Scholar] [CrossRef]
- Awasthi, K.; Malviya, N.; Kumar, A. Silicon Subwavelength Grating Slot Waveguide based Optical Sensor for Label Free Detection of Fluoride Ion in Water. IETE Tech. Rev. 2023, 41, 341–352. [Google Scholar] [CrossRef]
- Sun, Y.; Hu, G.; Cui, Y. Subwavelength Grating Waveguide Racetrack-Based Refractive Index Sensor with Improved Figure of Merit. Appl. Opt. 2020, 59, 10613–10617. [Google Scholar] [CrossRef]
- Kazanskiy, N.L.; Butt, M.A.; Khonina, S.N. Silicon Photonic Devices Realized on Refractive Index Engineered Subwavelength Grating Waveguides-A Review. Opt. Laser Technol. 2021, 138, 106863. [Google Scholar] [CrossRef]
- Odeh, M.; Twayana, K.; Sloyan, K.; Villegas, J.E.; Chandran, S.; Dahlem, M.S. Mode Sensitivity Analysis of Subwavelength Grating Slot Waveguides. IEEE Photonics J. 2019, 11, 2700210. [Google Scholar] [CrossRef]
- Ariannejad, M.M.; Akbari, E.; Hanafi, E. Silicon Sub-Wavelength Grating Resonator Structures for Gas Sensor. Superlattices Microstruct. 2020, 142, 106506. [Google Scholar] [CrossRef]
- Bickford, J.R.; Cho, P.S.; Farrell, M.E.; Holthoff, E.L.; Pellegrino, P.M. The Investigation of Subwavelength Grating Waveguides for Photonic Integrated Circuit Based Sensor Applications. IEEE J. Sel. Top. Quantum Electron. 2019, 25, 8200410. [Google Scholar] [CrossRef]
- Wangüemert-Pérez, J.G.; Cheben, P.; Ortega-Moñux, A.; Alonso-Ramos, C.; Pérez-Galacho, D.; Halir, R.; Molina-Fernández, I.; Xu, D.-X.; Schmid, J.H. Evanescent Field Waveguide Sensing with Subwavelength Grating Structures in Silicon-on-Insulator. Opt. Lett. 2014, 39, 4442–4445. [Google Scholar] [CrossRef]
- Kazanskiy, N.L.; Khonina, S.N.; Butt, M.A. Subwavelength Grating Double Slot Waveguide Racetrack Ring Resonator for Refractive Index Sensing Application. Sensors 2020, 20, 3416. [Google Scholar] [CrossRef] [PubMed]
- Kundal, S.; Khandelwal, A. Highly Sensitive Ring Resonator Based Refractive Index Sensor for Label Free Biosensing Applications. In Proceedings of the 2022 International Conference on Numerical Simulation of Optoelectronic Devices (NUSOD), Turin, Italy, 12–16 September 2022; pp. 157–158. [Google Scholar]
- Butt, M.A. Racetrack Ring Resonator-Based on Hybrid Plasmonic Waveguide for Refractive Index Sensing. Micromachines 2024, 15, 610. [Google Scholar] [CrossRef]
- Zhao, C.Y.; Chen, P.Y.; Li, P.Y.; Zhang, C.M. Numerical Analysis of Effective Refractive Index Bio-Sensor Based on Graphene-embedded Slot-Based Dual-Micro-Ring Resonator. Int. J. Mod. Phys. B 2020, 34, 2050145. [Google Scholar] [CrossRef]
- Teng, C.; Zhu, Y.; Yu, F.; Deng, S.; Yuan, L.; Zheng, J.; Cheng, Y. High-Sensitivity Refractive Index Sensor Based on a Cascaded Core-Offset and Macrobending Single-Mode Fiber Interferometer. Front. Mater. 2021, 7, 595437. [Google Scholar] [CrossRef]
- Du, H.; Sun, X.; Hu, Y.; Dong, X.; Zhou, J. High Sensitive Refractive Index Sensor Based on Cladding Etched Photonic Crystal Fiber Mach-Zehnder Interferometer. Photonic Sens. 2019, 9, 126–134. [Google Scholar] [CrossRef]
- Zhao, N.; Wang, Z.; Zhang, Z.; Lin, Q.; Yao, K.; Zhang, F.; Jiao, Y.; Zhao, L.; Tian, B.; Yang, P.; et al. High Sensitivity Optical Fiber Mach–Zehnder Refractive Index Sensor Based on Waist-Enlarged Bitaper. Micromachines 2022, 13, 689. [Google Scholar] [CrossRef]
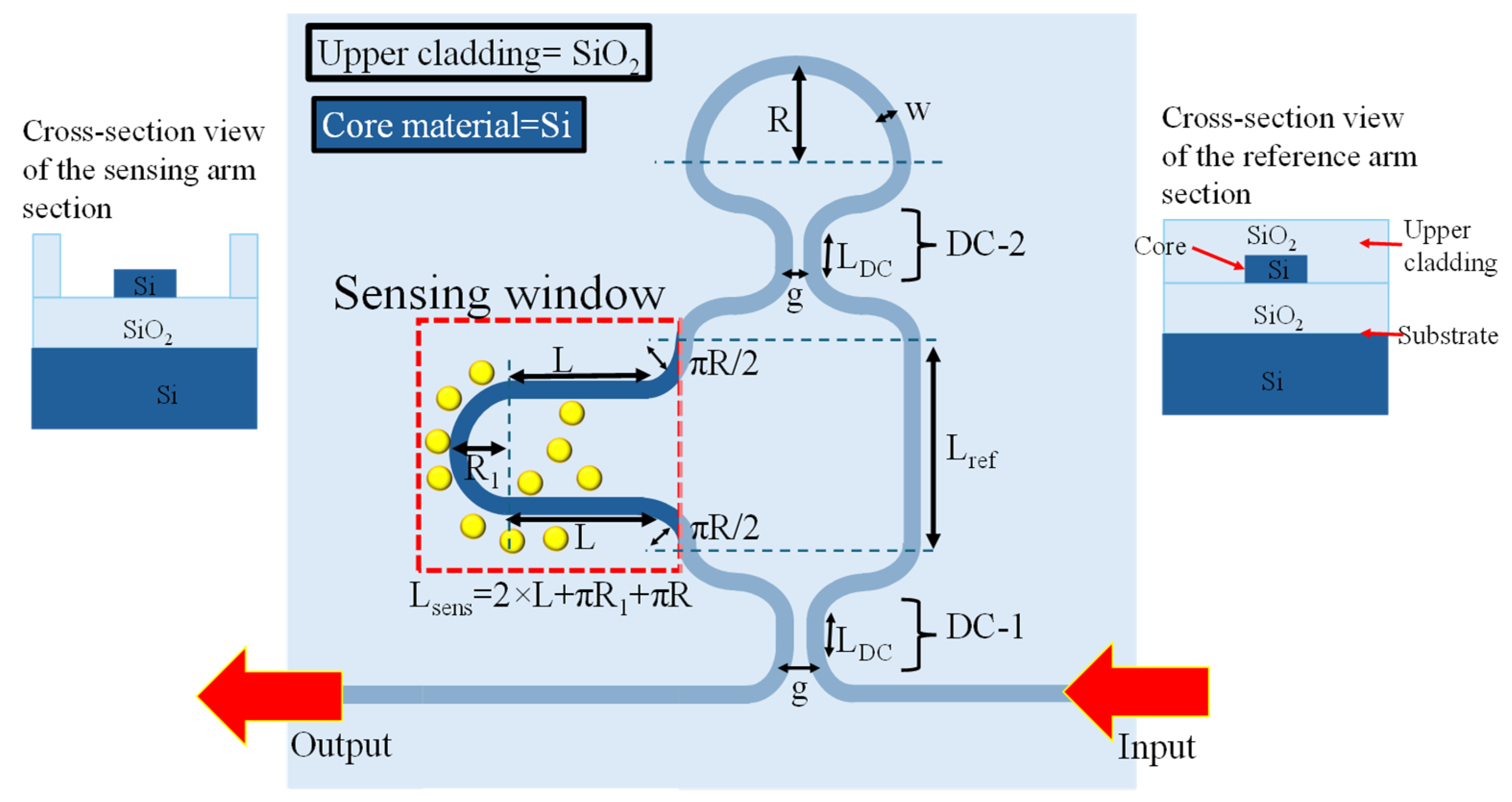



| Parameters | Description | Values |
|---|---|---|
| R | The radius of the reflector | 5 µm (fixed value) |
| R1 | The radius of the loop of the sensing arm | 2.5 µm (fixed) |
| w | Width of WG | 350 nm to 420 nm |
| g | The gap between the WGs | 100 nm to 300 nm |
| LDC | Length of directional coupler (DC-1 and DC-2) | 1 µm to 9 µm |
| Lsens | Length of sensing arm | 2 × L + πR1 + πR. Where L = 10, 20, 30, 40 µm |
| Lsens | Length of sensing arm for L = 10, 20, 30, 40 µm | 43.55, 63.55, 83.55, 103.55 µm |
| Lref | Length of reference arm | 19.2 µm |
| ∆L | Differences in sensing arm and reference arm | 24.35, 44.35, 64.35, 84.35 µm |
| λ | Operational wavelength region | 1520 nm to 1565 nm |
| Design | Application | Sensitivity | References |
|---|---|---|---|
| Ring resonator | RI sensing | 424 nm/RIU | [34] |
| Racetrack ring resonator | RI sensing | 377.1 to 477.7 nm/RIU | [35] |
| Ring resonator | RI sensing | 330 nm/RIU | [36] |
| MZI based on cascaded core-offset and microbending fiber structure | RI sensing | 699.95 nm/RIU | [37] |
| Cladding etched PhC fiber MZI | RI sensing | 211.53 to 359.37 nm/RIU | [38] |
| MZI based on waist-enlarged bitaper | RI sensing | 287.65 nm/RIU | [39] |
| Hollow hybrid plasmonic MZI | RI sensing | 160 nm/RIU | [36] |
| a-LT-MZI | RI sensing | 261 nm/RIU | This work |
| SWG-a-LT-MZI | RI sensing | 510 nm/RIU | This work |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Butt, M.A. High Sensitivity Design for Silicon-On-Insulator-Based Asymmetric Loop-Terminated Mach–Zehnder Interferometer. Materials 2025, 18, 798. https://doi.org/10.3390/ma18040798
Butt MA. High Sensitivity Design for Silicon-On-Insulator-Based Asymmetric Loop-Terminated Mach–Zehnder Interferometer. Materials. 2025; 18(4):798. https://doi.org/10.3390/ma18040798
Chicago/Turabian StyleButt, Muhammad A. 2025. "High Sensitivity Design for Silicon-On-Insulator-Based Asymmetric Loop-Terminated Mach–Zehnder Interferometer" Materials 18, no. 4: 798. https://doi.org/10.3390/ma18040798
APA StyleButt, M. A. (2025). High Sensitivity Design for Silicon-On-Insulator-Based Asymmetric Loop-Terminated Mach–Zehnder Interferometer. Materials, 18(4), 798. https://doi.org/10.3390/ma18040798






