Revisiting the Dependence of Electrical Resistivity on Cu-Rich Precipitates in an Aged Fe-Cu Model Alloy: A Microstructure-Based Prediction Model
Abstract
1. Introduction
2. Materials and Methods
3. Results
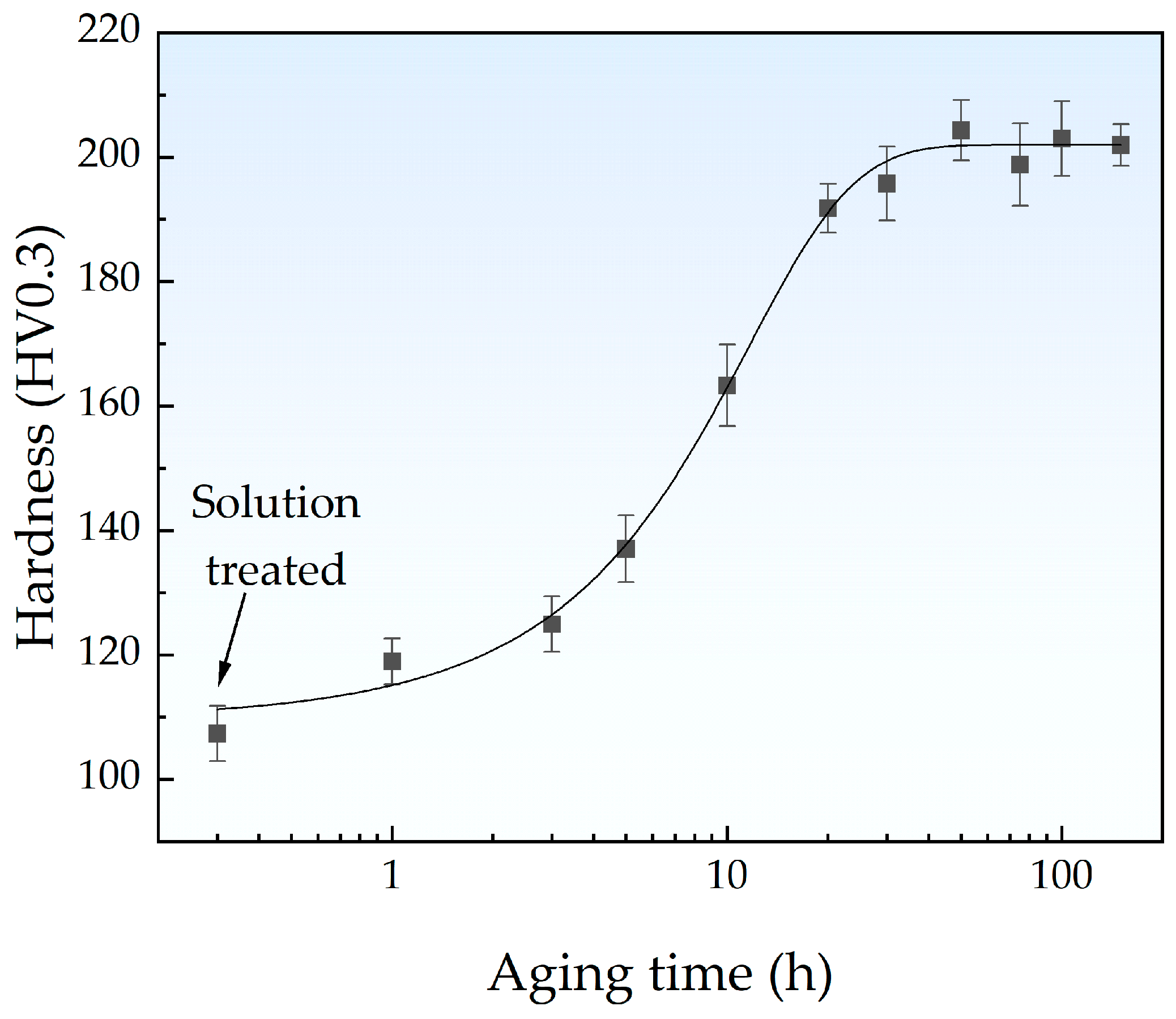
3.1. Hardening Behavior
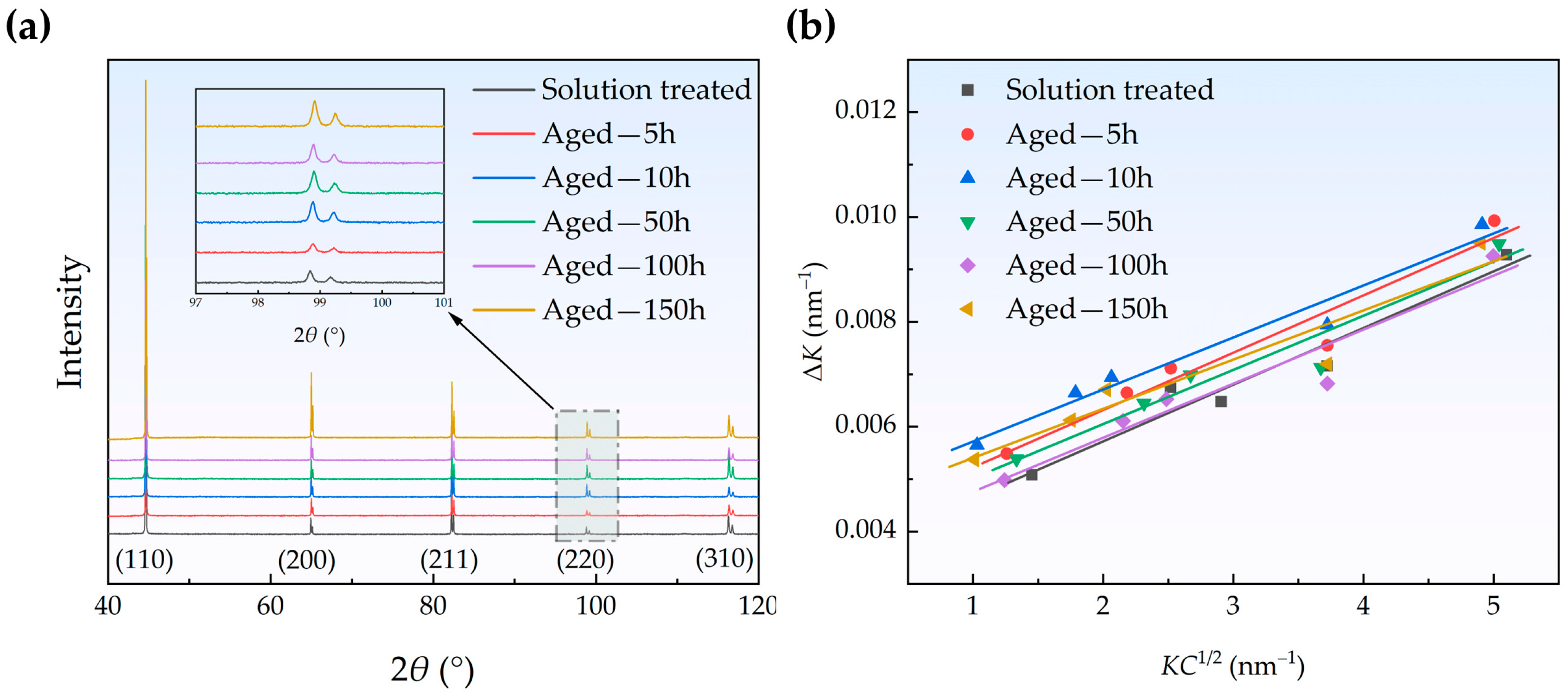
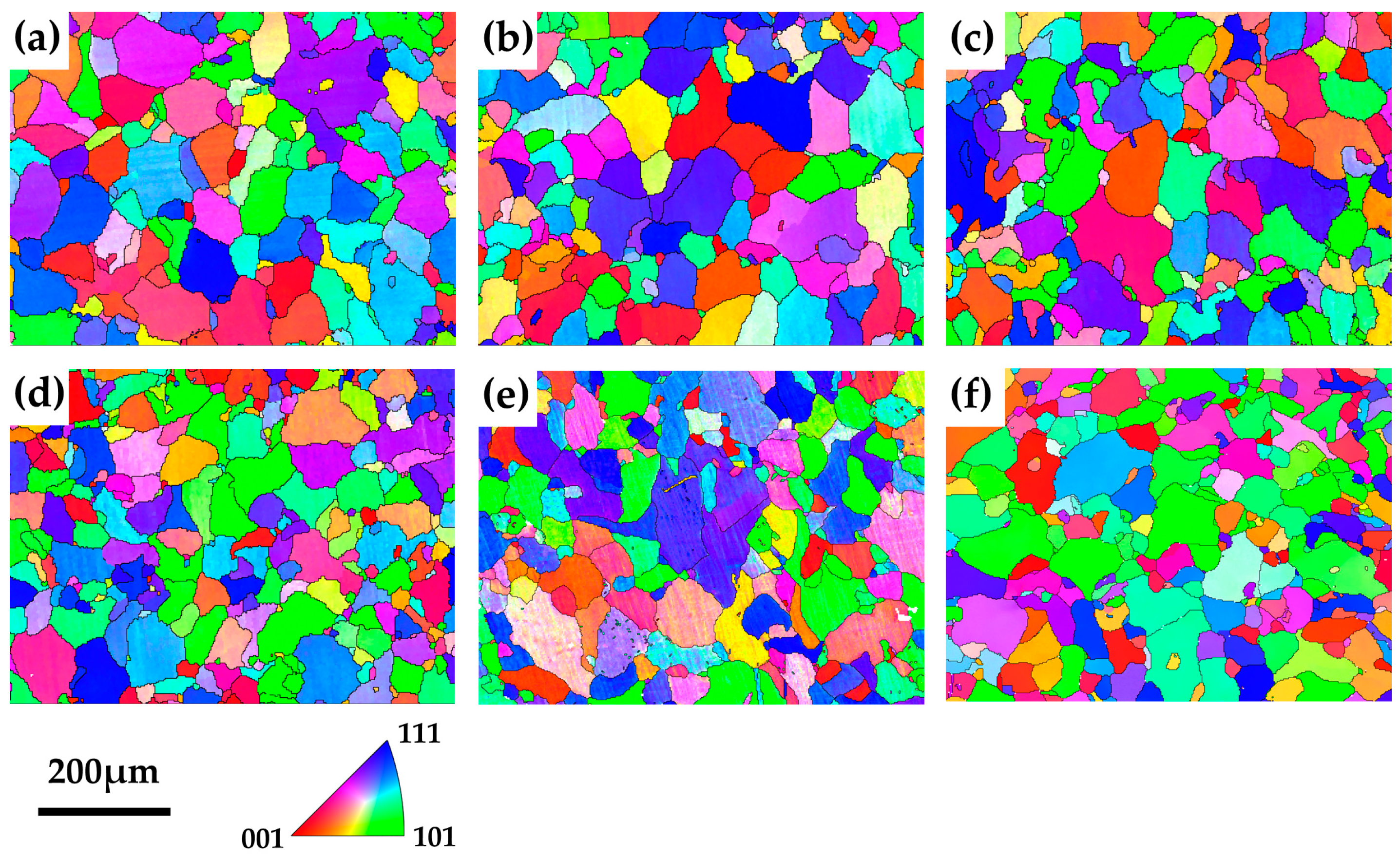
3.2. Evolution of Dislocations and Grains
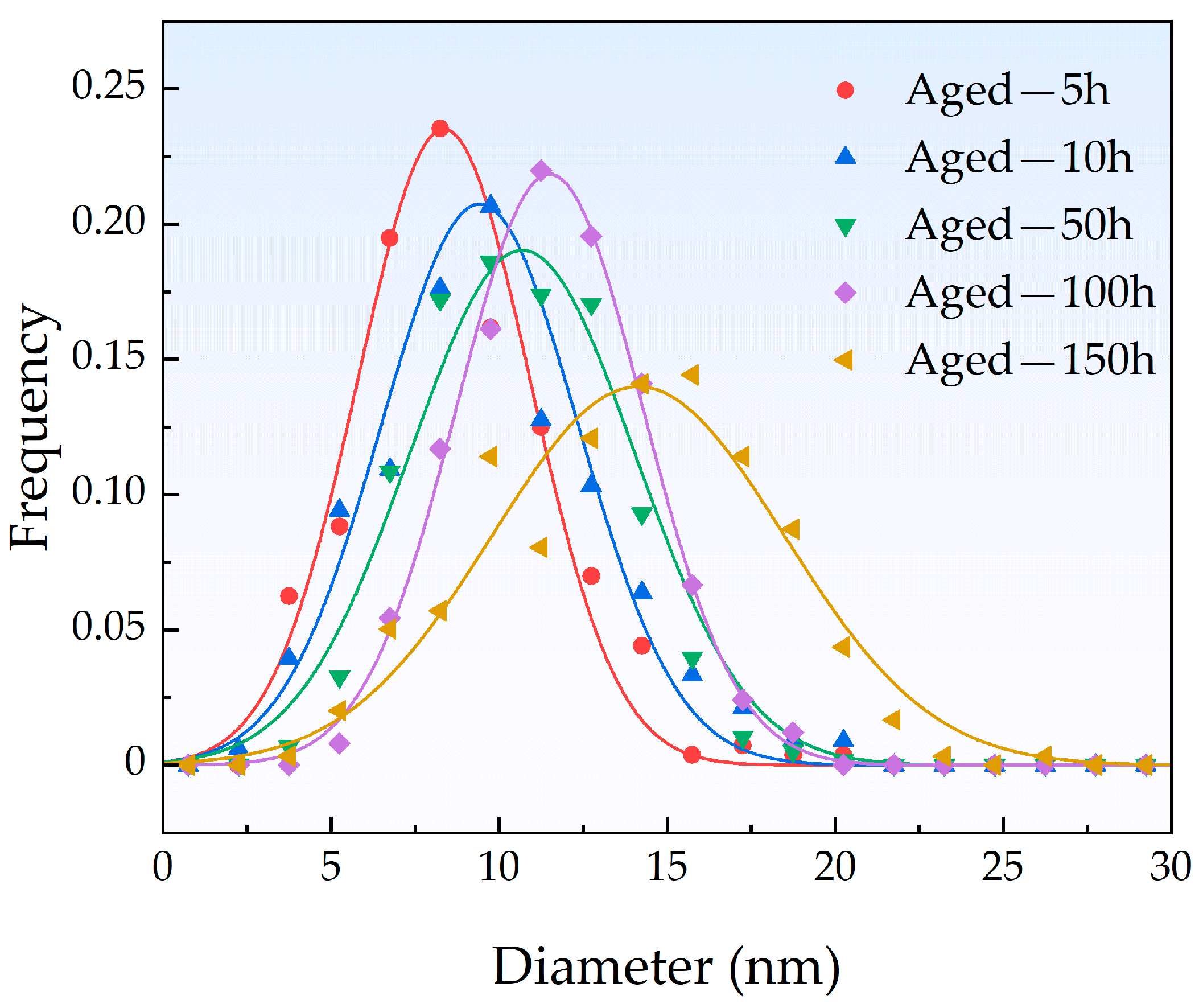
3.3. Observation of Cu-Rich Precipitates
4. Discussion
4.1. Strengthening Mechanism of Cu-Rich Precipitates
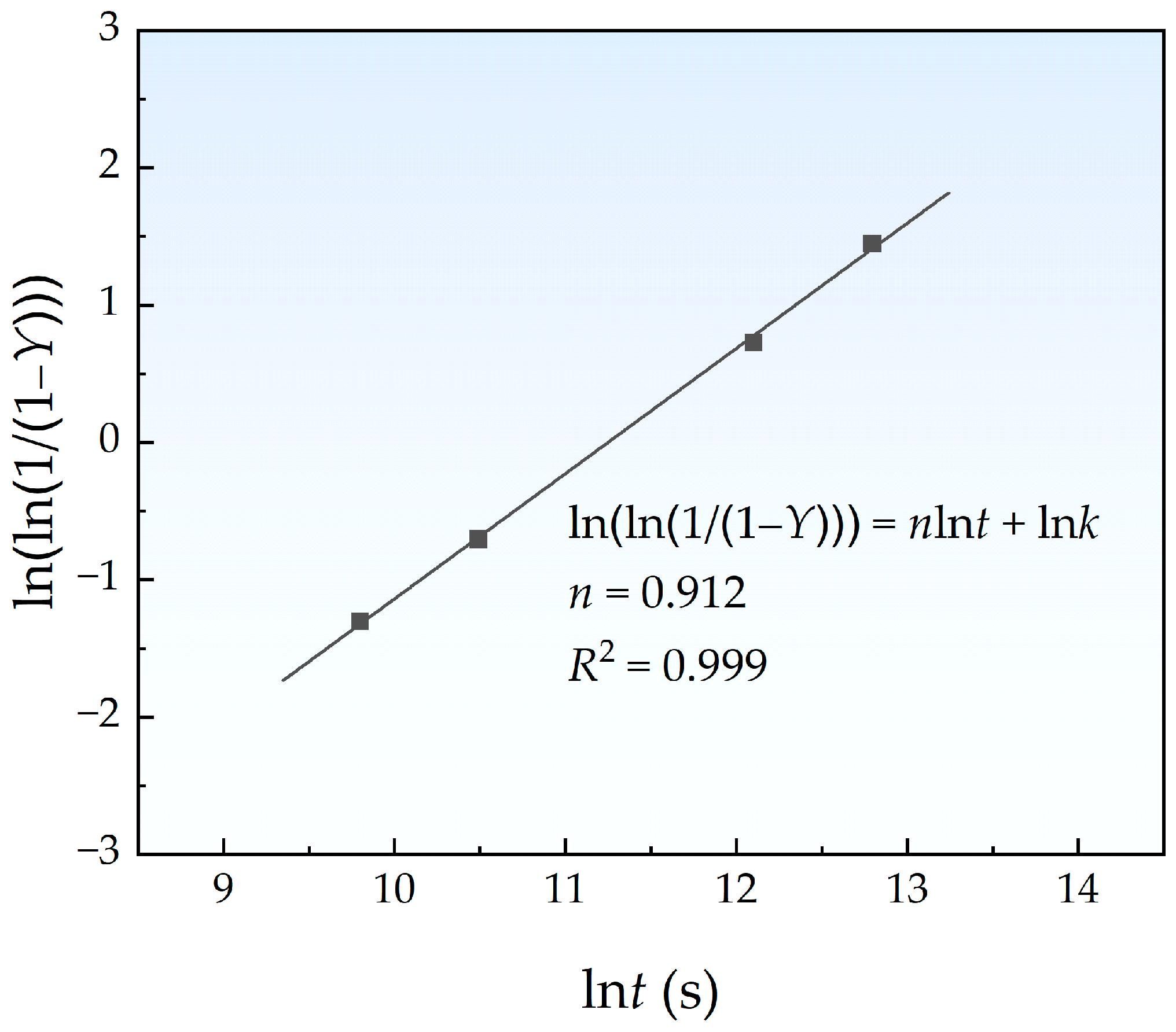
4.2. Kinetics of Cu Precipitation
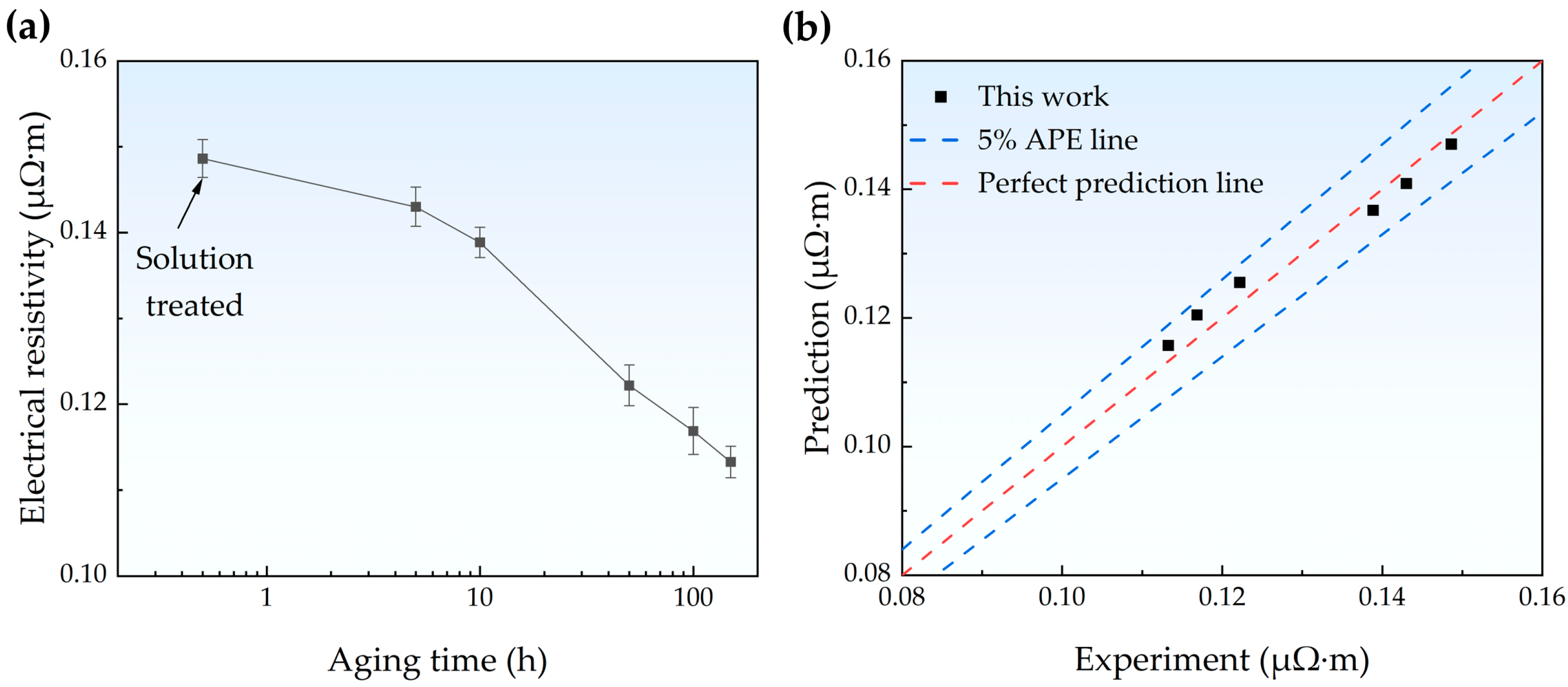
4.3. Electrical Resistivity Prediction Model
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Van Duysen, J.; de Bellefon, G.M. 60th Anniversary of electricity production from light water reactors: Historical review of the contribution of materials science to the safety of the pressure vessel. J. Nucl. Mater. 2017, 484, 209–227. [Google Scholar] [CrossRef]
- Gillemot, F. Review on Steel Enhancement for Nuclear RPVs. Metals 2021, 11, 2008. [Google Scholar] [CrossRef]
- Costanza, G.; Kaciulis, S.; Maddaluno, G.; Montanari, R. HT-XRD analysis of W thick coatings for nuclear fusion technology. Key Eng. Mater. 2014, 605, 31–34. [Google Scholar] [CrossRef]
- Odette, G.R.; Lucas, G.E. Embrittlement of nuclear reactor pressure vessels. JOM 2001, 53, 18–22. [Google Scholar] [CrossRef]
- Odette, G.; Yamamoto, T.; Williams, T.; Nanstad, R.; English, C. On the history and status of reactor pressure vessel steel ductile to brittle transition temperature shift prediction models. J. Nucl. Mater. 2019, 526, 151863. [Google Scholar] [CrossRef]
- Xiao, X. Fundamental mechanisms for irradiation-hardening and embrittlement: A review. Metals 2019, 9, 1132. [Google Scholar] [CrossRef]
- Margolin, B.; Fomenko, V.; Shvetsova, V.; Yurchenko, E. On the link of the embrittlement mechanisms and microcrack nucleation and propagation properties for RPV steels. Part I. Materials, study strategy and deformation properties. Eng. Fract. Mech. 2022, 267, 108400. [Google Scholar] [CrossRef]
- Bergner, F.; Gillemot, F.; Hernández-Mayoral, M.; Serrano, M.; Török, G.; Ulbricht, A.; Altstadt, E. Contributions of Cu-rich clusters, dislocation loops and nanovoids to the irradiation-induced hardening of Cu-bearing low-Ni reactor pressure vessel steels. J. Nucl. Mater. 2015, 461, 37–44. [Google Scholar] [CrossRef]
- Odette, G.R.; Almirall, N.; Wells, P.B.; Yamamoto, T. Precipitation in reactor pressure vessel steels under ion and neutron irradiation: On the role of segregated network dislocations. Acta Mater. 2021, 212, 116922. [Google Scholar] [CrossRef]
- Lê, T.; Barbu, A.; Maury, F. Precipitation kinetics of dilute FeCu and FeCuMn alloys subjected to electron irradiation. Scr. Metall. Mat. 1992, 26, 771–776. [Google Scholar] [CrossRef]
- Soisson, F.; Barbu, A.; Martin, G. Monte Carlo simulations of copper precipitation in dilute iron-copper alloys during thermal ageing and under electron irradiation. Acta Mater. 1996, 44, 3789–3800. [Google Scholar] [CrossRef]
- Matsui, N.H. Quantitative analysis of the dependence of hardening on copper precipitate diameter and density in Fe–Cu alloys. J. Nucl. Mater. 2007, 367, 392–398. [Google Scholar]
- Ishino, S.; Chimi, Y.; Bagiyono; Tobita, T.; Ishikawa, N.; Suzuki, M.; Iwase, A. Radiation enhanced copper clustering processes in Fe-Cu alloys during electron and ion irradiations as measured by electrical resistivity. J. Nucl. Mater. 2003, 323, 354–359. [Google Scholar] [CrossRef]
- Tobita, T.; Nakagawa, S.; Takeuchi, T.; Suzuki, M.; Ishikawa, N.; Chimi, Y.; Saitoh, Y.; Soneda, N.; Nishida, K.; Ishino, S.; et al. Effects of irradiation induced Cu clustering on Vickers hardness and electrical resistivity of Fe–Cu model alloys. J. Nucl. Mater. 2014, 452, 241–247. [Google Scholar] [CrossRef]
- Ahlawat, S.; Sarkar, S.K.; Sen, D.; Biswas, A. Revisiting temporal evolution of Cu-rich precipitates in Fe–Cu alloy: Correlative small angle neutron scattering and atom-probe tomography studies. Microsc. Microanal. 2019, 25, 840–848. [Google Scholar] [CrossRef] [PubMed]
- Zhu, J.; Zhang, T.; Yang, Y.; Liu, C. Phase field study of the copper precipitation in Fe-Cu alloy. Acta Mater. 2019, 166, 560–571. [Google Scholar] [CrossRef]
- Li, N.N.; Feng, L.; Yin, F.S.; Zhao, E.T. Effect of the Cu-rich precipitates on thermal conductivity of RPV model steel. J. Nucl. Sci. Technol. 2019, 56, 953–958. [Google Scholar] [CrossRef]
- Fujii, K.; Fukuya, K. Effects of cold work on solute atom clustering during thermal aging in RPV model alloy. J. Nucl. Sci. Technol. 2021, 58, 527–532. [Google Scholar] [CrossRef]
- Blaszkiewicz, M. The Development of Nondestructive Evaluation (NDE) for Monitoring the Embrittlement in Nuclear Reactor Pressure Vessels. Mater. Sci. Forum 1996, 210, 9–16. [Google Scholar] [CrossRef]
- Robles, K.P.V.; Yee, J.J.; Kee, S.H. Electrical Resistivity Measurements for Nondestructive Evaluation of Chloride-Induced Deterioration of Reinforced Concrete-A Review. Materials 2022, 15, 2725. [Google Scholar] [CrossRef]
- Khudhair, M.; Gucunski, N. Multi-NDE Technology Approach to Improve Interpretation of Corrosion in Concrete Bridge Decks Based on Electrical Resistivity Measurements. Sensors 2023, 23, 8052. [Google Scholar] [CrossRef] [PubMed]
- Norbury, A. The electrical resistivity of dilute metallic solid solutions. Trans. Faraday Soc. 1921, 16, 570–596. [Google Scholar] [CrossRef]
- Bhagat, A.N.; Pabi, S.K.; Ranganathan, S.; Mohanty, O.N. Study on copper precipitation during continuous heating and cooling of HSLA steels using electrical resistivity. Mater. Sci. Technol. 2007, 23, 158–164. [Google Scholar] [CrossRef]
- Jung, J.G.; Jung, M.; Lee, S.M.; Shin, E.; Shin, H.C.; Lee, Y.K. Cu precipitation kinetics during martensite tempering in a medium C steel. J. Alloys Compd. 2013, 553, 299–307. [Google Scholar] [CrossRef]
- Li, Y.; Li, Y.; Deng, S.; Xu, B.; Li, Q.; Shu, G.; Liu, W. Changes in the magnetic and mechanical properties of thermally aged Fe–Cu alloys due to nano-sized precipitates. J. Phys. D Appl. Phys. 2015, 49, 035006. [Google Scholar] [CrossRef]
- Hillel, A.; Rossiter, P. Resistivity mechanisms during clustering in alloys. Philos. Mag. B 1981, 44, 383–388. [Google Scholar] [CrossRef]
- Zijun, W.; Xiaoming, D.; Tianfu, L.; Kai, S.; Xuezhu, T.; Meijuan, L.; Rongdeng, L.; Yuntao, L.; Dongfeng, C. Investigation of Cu-enriched precipitates in thermally aged Fe-Cu and Fe-Cu-Ni model alloys. J. Nucl. Mater. 2022, 562, 153601. [Google Scholar] [CrossRef]
- Xia, S.; Yang, T.; Gao, M.; Hu, X.; Li, Q. Study on the Re-Aging Behavior of Cu-Rich Precipitates in a FeCu Alloy under Electropulsing. Materials 2024, 17, 1287. [Google Scholar] [CrossRef] [PubMed]
- Wu, H.; Li, Q.L.; Xu, B.; Liu, H.L.; Shu, G.G.; Liu, W. Improvement in irradiation resistance of FeCu alloy by pre-deformation through introduction of dense point defect sinks. Rare Met. 2020, 40, 885–896. [Google Scholar] [CrossRef]
- Liu, H.; Wang, X.; Cui, W.; Li, Q.; Xu, B.; Liu, W.; Shu, G. The effect of dislocations on irradiation-induced vacancy-like defects in FeCu alloy and reactor pressure vessel steel. J. Nucl. Mater. 2019, 524, 80–89. [Google Scholar] [CrossRef]
- GB/T 351-2019; Metallic Materials—Resistivity Measurement Method. National Standard of the People’s Republic of China: Beijing, China, 2019.
- ASTM B193-16; Standard Test Method for Resistivity of Electrical Conductor Materials. ASTM: West Conshohocken, PA, USA, 2019.
- Takebayashi, S.; Kunieda, T.; Yoshinaga, N.; Ushioda, K.; Ogata, S. Comparison of the Dislocation Density in Martensitic Steels Evaluated by Some X-ray Diffraction Methods. ISIJ Int. 2010, 50, 875–882. [Google Scholar] [CrossRef]
- Williamson, G.; Hall, W. X-ray line broadening from filed aluminium and wolfram. Acta Metall. 1953, 1, 22–31. [Google Scholar] [CrossRef]
- Ungár, T.; Borbély, A. The effect of dislocation contrast on x-ray line broadening: A new approach to line profile analysis. Appl. Phys. Lett. 1996, 69, 3173–3175. [Google Scholar] [CrossRef]
- Ungár, T.; Dragomir, I.; Revesz, A.; Borbely, A. The contrast factors of dislocations in cubic crystals: The dislocation model of strain anisotropy in practice. J. Appl. Crystallogr. 1999, 32, 992–1002. [Google Scholar] [CrossRef]
- Russell, K.C.; Brown, L. A dispersion strengthening model based on differing elastic moduli applied to the iron-copper system. Acta Metall. 1972, 20, 969–974. [Google Scholar] [CrossRef]
- Wilkens, M. Broadening of X-ray diffraction lines of crystals containing dislocation distributions. Krist. Tech. 1976, 11, 1159–1169. [Google Scholar] [CrossRef]
- Yin, F.; Hanamura, T.; Umezawa, O.; Nagai, K. Phosphorus-induced dislocation structure variation in the warm-rolled ultrafine-grained low-carbon steels. Mater. Sci. Eng. A 2003, 354, 31–39. [Google Scholar] [CrossRef]
- Liu, H.; Li, Q. The characterization of a nanoscale MnNi cluster in thermally aged reactor pressure vessel steels. Mater Res Express 2022, 9, 026531. [Google Scholar] [CrossRef]
- Wang, L.; Zhang, Z.; Ma, E.; Han, X. Transmission electron microscopy observations of dislocation annihilation and storage in nanograins. Appl. Phys. Lett. 2011, 98, 051905. [Google Scholar] [CrossRef]
- Kurzydłowski, K.; Ralph, B.; Chojnacka, A.; Bucki, J. A quantitative description of recrystallization and grain growth in single phase bcc iron. Acta Mater. 1996, 44, 3005–3013. [Google Scholar] [CrossRef]
- Padilha, A.F.; Dutra, J.C.; Randle, V. Interaction between precipitation, normal grain growth, and secondary recrystallisation in austenitic stainless steel containing particles. Mater. Sci. Technol. 1999, 15, 1009–1014. [Google Scholar] [CrossRef]
- Othen, P.; Jenkins, M.; Smith, G. High-resolution electron microscopy studies of the structure of Cu precipitates in α-Fe. Philos. Mag. A 1994, 70, 1–24. [Google Scholar] [CrossRef]
- Monzen, R.; Iguchi, M.; Jenkins, M.L. Structural changes of 9R copper precipitates in an aged Fe-Cu alloy. Philos. Mag. Lett. 2000, 80, 137–148. [Google Scholar] [CrossRef]
- Sun, H.; Li, D.; Diao, Y.; He, Y.; Yan, L.; Pang, X.; Gao, K. Nanoscale Cu particle evolution and its impact on the mechanical properties and strengthening mechanism in precipitation-hardening stainless steel. Mater. Charact. 2022, 188, 111885. [Google Scholar] [CrossRef]
- An, D.; Wang, J.; Zhang, J.; Zhai, X.; Kang, Z.; Fan, W.; Yan, J.; Liu, Y.; Lu, L.; Jia, C.-L.J.E.; et al. Retarding Ostwald ripening through Gibbs adsorption and interfacial complexions leads to high-performance SnTe thermoelectrics. Energy Environ. Sci. 2021, 14, 5469–5479. [Google Scholar] [CrossRef]
- Takeuchi, T.; Kuramoto, A.; Kameda, J.; Toyama, T.; Nagai, Y.; Hasegawa, M.; Ohkubo, T.; Yoshiie, T.; Nishiyama, Y.; Onizawa, K. Effects of chemical composition and dose on microstructure evolution and hardening of neutron-irradiated reactor pressure vessel steels. J. Nucl. Mater. 2010, 402, 93–101. [Google Scholar] [CrossRef]
- Perez, M.; Perrard, F.; Massardier, V.; Kleber, X.; Deschamps, A.; De Monestrol, H.; Pareige, P.; Covarel, G. Low-temperature solubility of copper in iron: Experimental study using thermoelectric power, small angle X-ray scattering and tomographic atom probe. Philos. Mag. 2005, 85, 2197–2210. [Google Scholar] [CrossRef]
- Johnson, W.A.; Mehl, R.F. Reaction kinetics in process of nucleation and growth. Trans. Am. Inst. Min. Metall. Eng. 1939, 135, 416–442. [Google Scholar]
- Barmak, K. A commentary on: “reaction kinetics in processes of nucleation and growth”. Metall. Mater. Trans. A 2010, 41, 2771–2775. [Google Scholar] [CrossRef]
- Kasap, S.O. Principles of Electronic Materials and Devices, 4th ed.; McGraw-Hill: New York, NY, USA, 2018. [Google Scholar]
- Basinski, Z.; Dugdale, J.; Howie, A. The electrical resistivity of dislocations. Philos. Mag. 1963, 8, 1989–1997. [Google Scholar] [CrossRef]
- Karolik, A.S.; Luhvich, A.A. Calculation of electrical resistivity produced by dislocations and grain boundaries in metals. J. Phys. Condens. Matter 1994, 6, 873. [Google Scholar] [CrossRef]
- Braunovic, M.; Haworth, C. Grain-Boundary Contribution to the Electrical Resistivity of Iron. J. Appl. Phys. 1969, 40, 3459–3464. [Google Scholar] [CrossRef]
- Kelekanjeri, V.S.K.G.; Moss, L.K.; Gerhardt, R.A.; Ilavsky, J. Quantification of the coarsening kinetics of γ′ precipitates in Waspaloy microstructures with different prior homogenizing treatments. Acta Mater. 2009, 57, 4658–4670. [Google Scholar] [CrossRef]
- Whelchel, R.L.; Kelekanjeri, V.S.K.G.; Gerhardt, R.A.; Ilavsky, J. Effect of aging treatment on the microstructure and resistivity of a nickel-base superalloy. Metall. Mater. Trans. A 2011, 42, 1362–1372. [Google Scholar] [CrossRef]
- Li, C.; Shu, G.; Liu, Y.; Huang, Y.; Liu, W. Effects of neutron irradiation on resistivity of reactor pressure vessel steel. J. Nucl. Mater. 2018, 499, 446–450. [Google Scholar] [CrossRef]
- Thuinet, L.; Nastar, M.; Martinez, E.; Moladje, G.B.; Legris, A.; Soisson, F. Multiscale modeling of Radiation Induced Segregation in iron based alloys. Comput. Mater. Sci. 2018, 149, 324–335. [Google Scholar] [CrossRef]
- Shimodaira, M.; Toyama, T.; Yoshida, K.; Inoue, K.; Ebisawa, N.; Tomura, K.; Yoshiie, T.; Konstantinović, M.J.; Gérard, R.; Nagai, Y. Contribution of irradiation-induced defects to hardening of a low-copper reactor pressure vessel steel. Acta Mater. 2018, 155, 402–409. [Google Scholar] [CrossRef]



| Element (wt. %) | Fe | Cu | C | Si | S | P |
|---|---|---|---|---|---|---|
| Fe-Cu | Bal. | 1.17 | 0.06 | 0.09 | <0.01 | <0.01 |
| Samples | Dislocation Density (1013 m−2) | Mean Diameter (μm) |
|---|---|---|
| Solution treated | 1.19 | 36.9 |
| Aged—5 h | 1.22 | 39.5 |
| Aged—10 h | 1.00 | 38.2 |
| Aged—50 h | 1.09 | 32.6 |
| Aged—100 h | 1.08 | 35.7 |
| Aged—150 h | 0.90 | 33.1 |
| Aging Time (h) | Mean Radius (nm) | Number Density (1022 m−3) | Volume Fraction (%) |
|---|---|---|---|
| 5 | 4.41 | 1.37 | 0.49 |
| 10 | 4.88 | 1.65 | 0.80 |
| 50 | 5.28 | 2.92 | 1.80 |
| 100 | 5.79 | 2.49 | 2.03 |
| 150 | 6.90 | 1.50 | 2.06 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xia, S.; Gao, M.; Hu, X.; Huang, C.; Liang, S.; Zhang, W.; Li, Q. Revisiting the Dependence of Electrical Resistivity on Cu-Rich Precipitates in an Aged Fe-Cu Model Alloy: A Microstructure-Based Prediction Model. Materials 2025, 18, 752. https://doi.org/10.3390/ma18040752
Xia S, Gao M, Hu X, Huang C, Liang S, Zhang W, Li Q. Revisiting the Dependence of Electrical Resistivity on Cu-Rich Precipitates in an Aged Fe-Cu Model Alloy: A Microstructure-Based Prediction Model. Materials. 2025; 18(4):752. https://doi.org/10.3390/ma18040752
Chicago/Turabian StyleXia, Shengjun, Menglin Gao, Xing Hu, Chunfa Huang, Shuaiheng Liang, Wenlu Zhang, and Qiulin Li. 2025. "Revisiting the Dependence of Electrical Resistivity on Cu-Rich Precipitates in an Aged Fe-Cu Model Alloy: A Microstructure-Based Prediction Model" Materials 18, no. 4: 752. https://doi.org/10.3390/ma18040752
APA StyleXia, S., Gao, M., Hu, X., Huang, C., Liang, S., Zhang, W., & Li, Q. (2025). Revisiting the Dependence of Electrical Resistivity on Cu-Rich Precipitates in an Aged Fe-Cu Model Alloy: A Microstructure-Based Prediction Model. Materials, 18(4), 752. https://doi.org/10.3390/ma18040752







