Dynamics and Formation of Antiferromagnetic Textures in MnBi2Te4 Single Crystal
Abstract
1. Introduction
2. Methodology
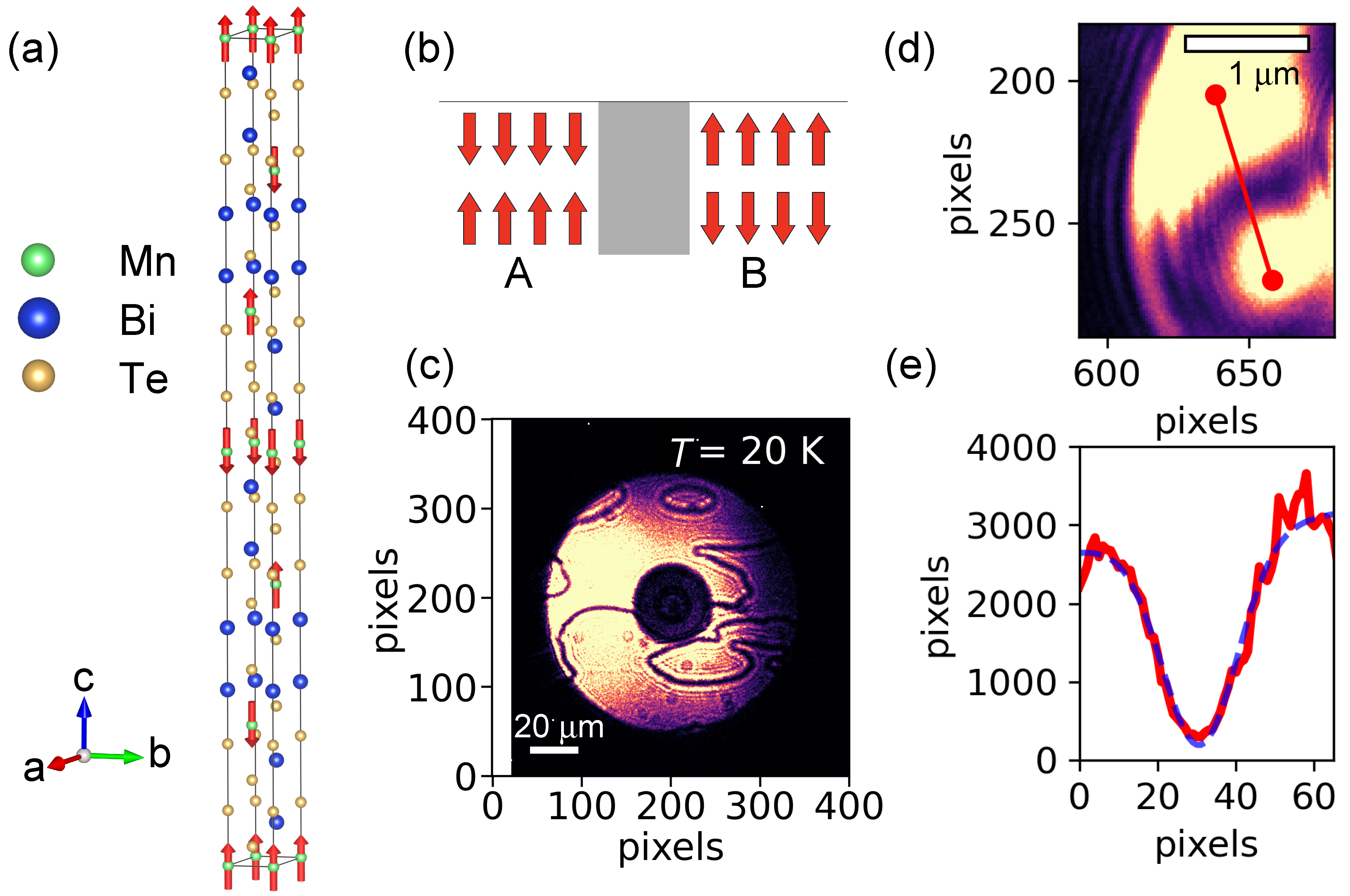
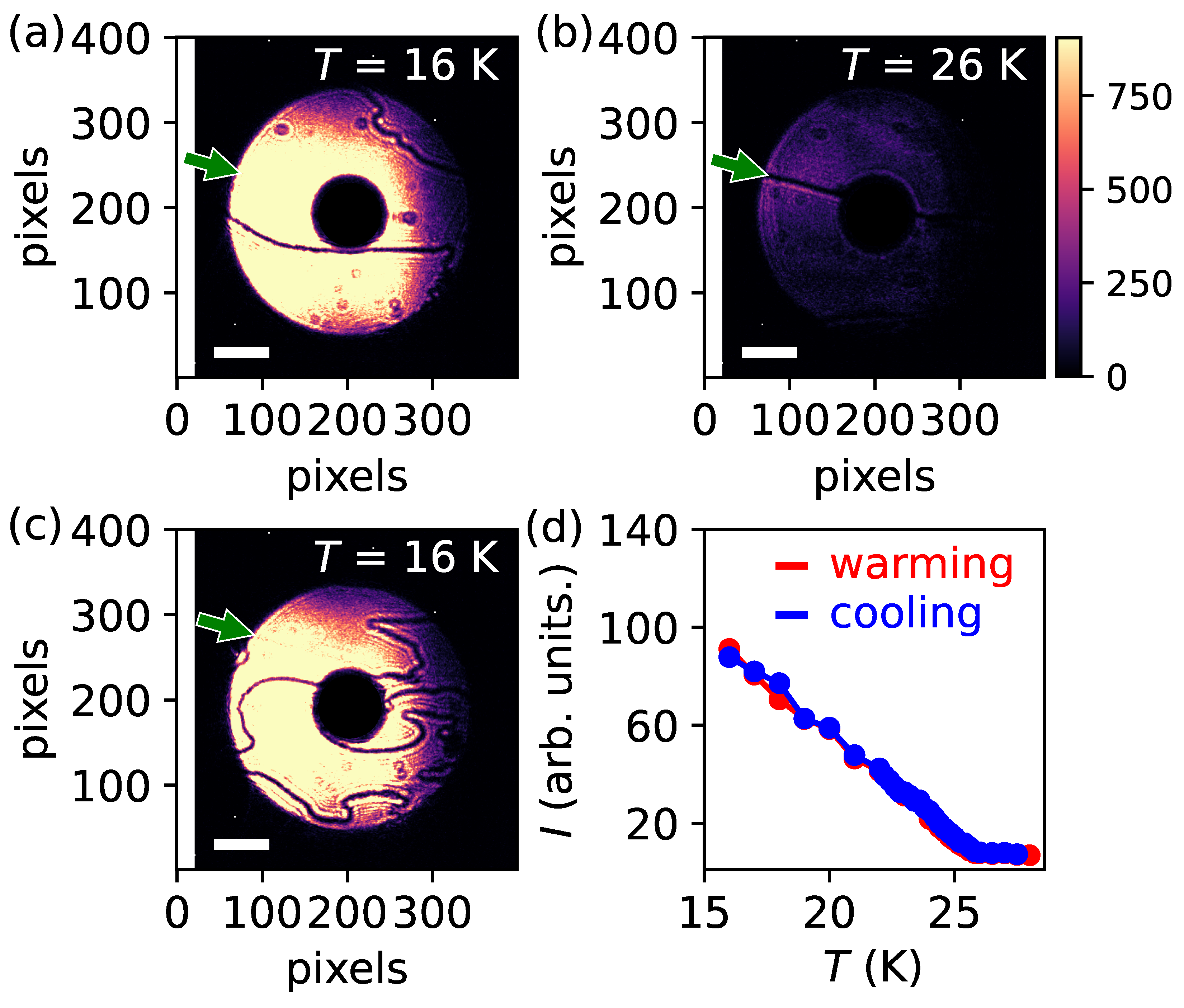
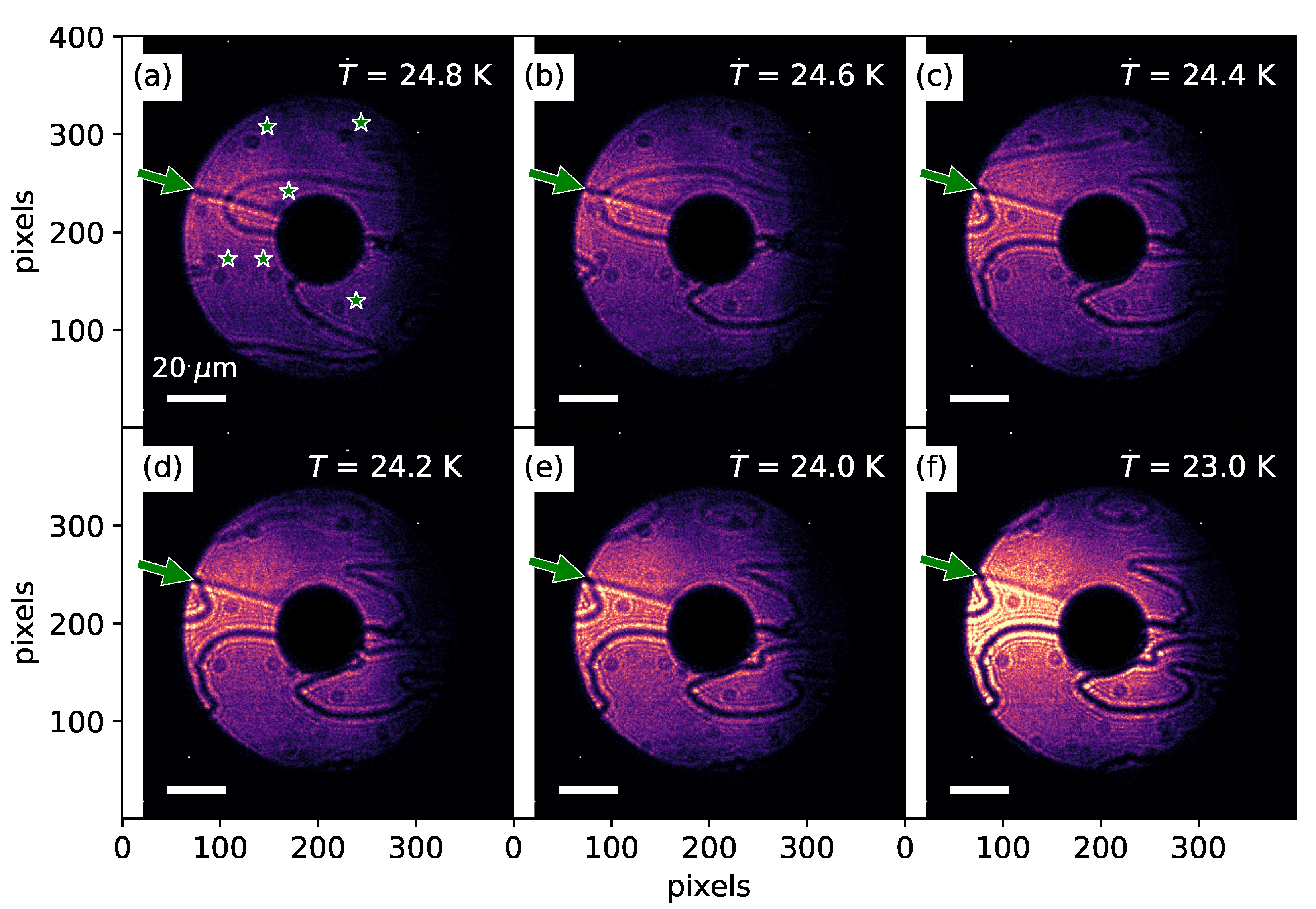
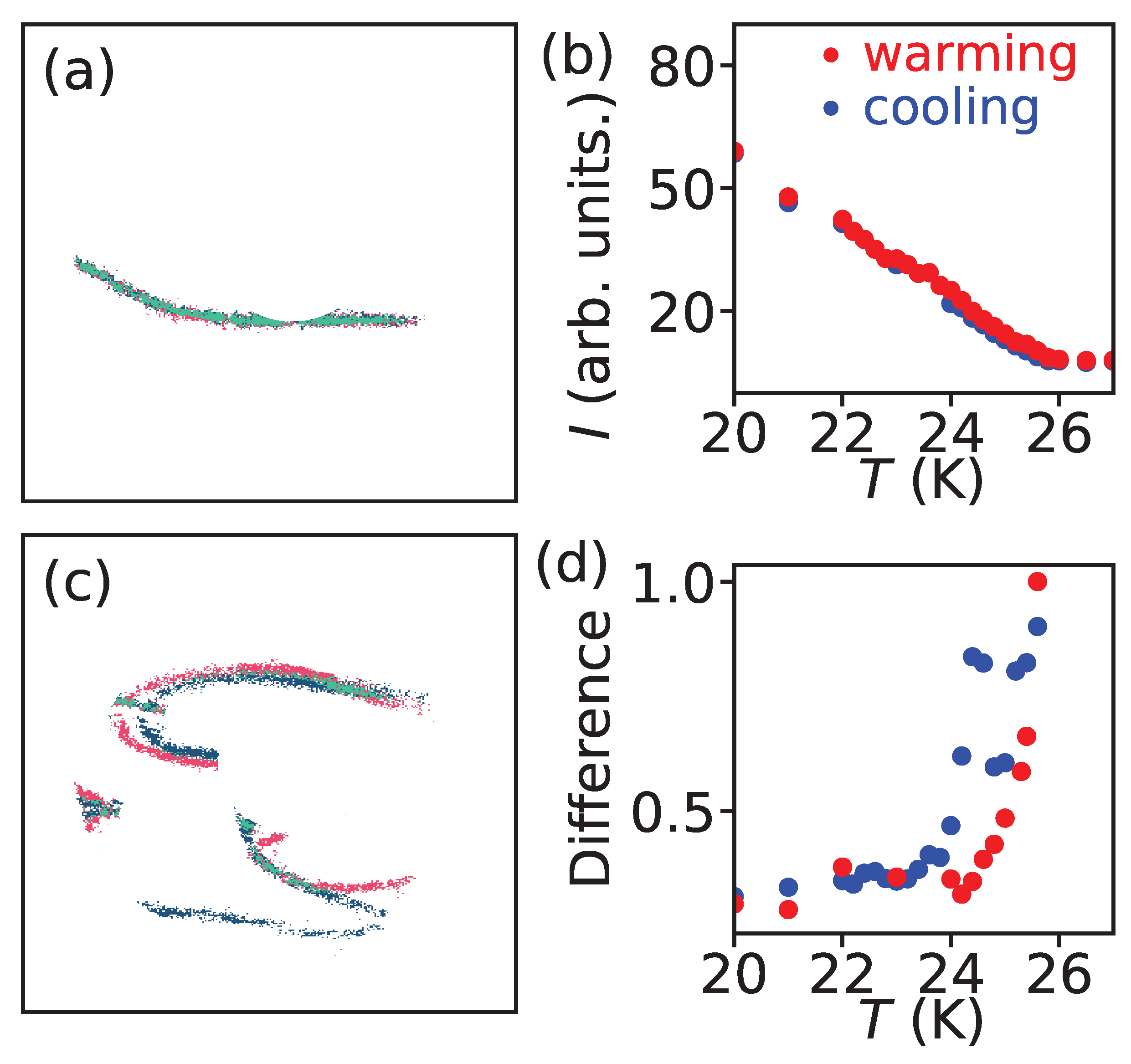
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AFM | Antiferromagnetic |
| DW | Domain wall |
| SL | septuple layer |
| ARPES | Angle-resolved photoemission spectroscopy |
| MFM | Magnetic force microscopy |
| direct-CXI | direct-space and real-time coherent X-ray imaging technique |
| FWHM | full width at a half maximum |
| UHV | Ultra high vacuum |
| FZP | Fresnel zone plate |
References
- Chen, Y.L.; Chu, J.-H.; Analytis, J.G.; Liu, Z.K.; Igarashi, K.; Kuo, H.-H.; Qi, X.L.; Mo, S.K.; Moore, R.G.; Lu, D.H.; et al. Massive dirac fermion on the surface of a magnetically doped topological insulator. Science 2010, 329, 659–662. [Google Scholar] [CrossRef]
- Li, R.; Wang, J.; Qi, X.-L.; Zhang, S.-C. Dynamical axion field in topological magnetic insulators. Nat. Phys. 2010, 6, 284–288. [Google Scholar] [CrossRef]
- Armitage, N.P.; Mele, E.J.; Vishwanath, A. Weyl and dirac semimetals in three-dimensional solids. Rev. Mod. Phys. 2018, 90, 015001. [Google Scholar] [CrossRef]
- Tokura, Y.; Yasuda, K.; Tsukazaki, A. Magnetic topological insulators. Nat. Rev. Phys. 2019, 1, 126–143. [Google Scholar] [CrossRef]
- Mong, R.S.K.; Essin, A.M.; Moore, J.E. Antiferromagnetic topological insulators. Phys. Rev. B 2010, 81, 245209. [Google Scholar] [CrossRef]
- Kreyssig, A.; Kim, M.G.; Kim, J.W.; Pratt, D.K.; Sauerbrei, S.M.; March, S.D.; Tesdall, G.R.; Bud’ko, S.L.; Canfield, P.C.; McQueeney, R.J.; et al. Magnetic order in gdbipt studied by X-ray resonant magnetic scattering. Phys. Rev. B 2011, 84, 220408. [Google Scholar] [CrossRef]
- Khmelevskyi, S. Antiferromagnetic ordering on the frustrated fcc lattice in the intermetallic compound gdptbi. Phys. Rev. B 2012, 86, 104429. [Google Scholar] [CrossRef]
- Miyakoshi, S.; Ohta, Y. Antiferromagnetic topological insulator state in the correlated bernevig-hughes-zhang model. Phys. Rev. B 2013, 87, 195133. [Google Scholar] [CrossRef]
- Zhong, Y.; Wang, Y.-F.; Wang, Y.-Q.; Luo, H.-G. Topological antiferromagnetic spin-density-wave phase in an extended kondo lattice model. Phys. Rev. B 2013, 87, 035128. [Google Scholar] [CrossRef]
- Chang, C.-Z.; Zhang, J.; Feng, X.; Shen, J.; Zhang, Z.; Guo, M.; Li, K.; Ou, Y.; Wei, P.; Wang, L.-L.; et al. Experimental observation of the quantum anomalous hall effect in a magnetic topological insulator. Science 2013, 340, 167–170. [Google Scholar] [CrossRef]
- Varnava, N.; Vanderbilt, D. Surfaces of axion insulators. Phys. Rev. B 2018, 98, 245117. [Google Scholar] [CrossRef]
- Liu, C.; Wang, Y.; Li, H.; Wu, Y.; Li, Y.; Li, J.; He, K.; Xu, Y.; Zhang, J.; Wang, Y. Robust axion insulator and chern insulator phases in a two-dimensional antiferromagnetic topological insulator. Nat. Mater. 2020, 19, 522–527. [Google Scholar] [CrossRef]
- Deng, Y.; Yu, Y.; Shi, M.Z.; Guo, Z.; Xu, Z.; Wang, J.; Chen, X.H.; Zhang, Y. Quantum anomalous hall effect in intrinsic magnetic topological insulator MnBi2Te4. Science 2020, 367, 895–900. [Google Scholar] [CrossRef] [PubMed]
- Šmejkal, L.; Mokrousov, Y.; Yan, B.; MacDonald, A.H. Topological antiferromagnetic spintronics. Nat. Phys. 2018, 14, 242–251. [Google Scholar] [CrossRef]
- Zakharov, Y.V.; Mankov, Y.I. Magnetoresistance of Ferromagnets with Domain Structure; De Gruyter: Berlin, Germany; Boston, MA, USA, 1984; pp. 197–206. [Google Scholar]
- Matsuno, J.; Ogawa, N.; Yasuda, K.; Kagawa, F.; Koshibae, W.; Nagaosa, N.; Tokura, Y.; Kawasaki, M. Interface-driven topological hall effect in srruo3-sriro3 bilayer. Sci. Adv. 2016, 2, e1600304. [Google Scholar] [CrossRef] [PubMed]
- Lang, L.; Qiu, X.; Zhou, S. Anomalous hall-like effect probe of antiferromagnetic domain wall. Sci. Rep. 2018, 8, 329. [Google Scholar] [CrossRef]
- Lee, D.S.; Kim, T.-H.; Park, C.-H.; Chung, C.-Y.; Lim, Y.S.; Seo, W.-S.; Park, H.-H. Crystal structure, properties and nanostructuring of a new layered chalcogenide semiconductor, Bi2MnTe2. CrystEngComm 2013, 15, 5532–5538. [Google Scholar] [CrossRef]
- Zeugner, A.; Nietschke, F.; Wolter, A.U.B.; Gaß, S.; Vidal, R.C.; Peixoto, T.R.F.; Pohl, D.; Damm, C.; Lubk, A.; Hentrich, R.; et al. Chemical aspects of the candidate antiferromagnetic topological insulator MnBi2Te4. Chem. Mater. 2019, 31, 2795–2806. [Google Scholar] [CrossRef]
- Yan, J.-Q.; Zhang, Q.; Heitmann, T.; Huang, Z.; Chen, K.Y.; Cheng, J.-G.; Wu, W.; Vaknin, D.; Sales, B.C.; McQueeney, R.J. Crystal growth and magnetic structure of MnBi2Te4. Phys. Rev. Mater. 2019, 3, 064202. [Google Scholar] [CrossRef]
- Otrokov, M.M.; Klimovskikh, I.I.; Bentmann, H.; Estyunin, D.; Zeugner, A.; Aliev, Z.S.; Gaß, S.; Wolter, A.U.B.; Koroleva, A.V.; Shikin, A.M.; et al. Prediction and observation of an antiferromagnetic topological insulator. Nature 2019, 576, 416–422. [Google Scholar] [CrossRef]
- Gong, Y.; Guo, J.; Li, J.; Zhu, K.; Liao, M.; Liu, X.; Zhang, Q.; Gu, L.; Tang, L.; Feng, X.; et al. Experimental realization of an intrinsic magnetic topological insulator. Chin. Phys. Lett. 2019, 36, 076801. [Google Scholar] [CrossRef]
- Lee, S.H.; Zhu, Y.; Wang, Y.; Miao, L.; Pillsbury, T.; Yi, H.; Kempinger, S.; Hu, J.; Heikes, C.A.; Quarterman, P.; et al. Spin scattering and noncollinear spin structure-induced intrinsic anomalous hall effect in antiferromagnetic topological insulator MnBi2Te4. Phys. Rev. Res. 2019, 1, 012011. [Google Scholar] [CrossRef]
- Chen, Y.J.; Xu, L.X.; Li, J.H.; Li, Y.W.; Wang, H.Y.; Zhang, C.F.; Li, H.; Wu, Y.; Liang, A.J.; Chen, C.; et al. Topological electronic structure and its temperature evolution in antiferromagnetic topological insulator MnBi2Te4. Phys. Rev. X 2019, 9, 041040. [Google Scholar] [CrossRef]
- Li, H.; Gao, S.-Y.; Duan, S.-F.; Xu, Y.-F.; Zhu, K.-J.; Tian, S.-J.; Gao, J.-C.; Fan, W.-H.; Rao, Z.-C.; Huang, J.-R.; et al. Dirac surface states in intrinsic magnetic topological insulators EuSn2As2 and MnBi2nTe3n+1. Phys. Rev. X 2019, 9, 041039. [Google Scholar] [CrossRef]
- Shikin, A.M.; Estyunin, D.A.; Zaitsev, N.L.; Glazkova, D.; Klimovskikh, I.I.; Filnov, S.O.; Rybkin, A.G.; Schwier, E.F.; Kumar, S.; Kimura, A.; et al. Sample-dependent dirac-point gap in MnBi2Te4 and its response to applied surface charge: A combined photoemission and ab initio study. Phys. Rev. B 2021, 104, 115168. [Google Scholar] [CrossRef]
- Nevola, D.; Li, H.X.; Yan, J.-Q.; Moore, R.G.; Lee, H.-N.; Miao, H.; Johnson, P.D. Coexistence of surface ferromagnetism and a gapless topological state in MnBi2Te4. Phys. Rev. Lett. 2020, 125, 117205. [Google Scholar] [CrossRef]
- Sass, P.M.; Ge, W.; Yan, J.; Obeysekera, D.; Yang, J.J.; Wu, W. Magnetic imaging of domain walls in the antiferromagnetic topological insulator MnBi2Te4. Nano Lett. 2020, 20, 2609–2614. [Google Scholar] [CrossRef]
- Sass, P.M.; Kim, J.; Vanderbilt, D.; Yan, J.; Wu, W. Robust a-type order and spin-flop transition on the surface of the antiferromagnetic topological insulator MnBi2Te4. Phys. Rev. Lett. 2020, 125, 037201. [Google Scholar] [CrossRef]
- Cheong, S.W.; Fiebig, M.; Wu, W.; Chapon, L.; Kiryukhin, V. Seeing is believing: Visualization of antiferromagnetic domains. npj Quantum Mater. 2020, 5, 3. [Google Scholar] [CrossRef]
- Kim, M.G.; Miao, H.; Gao, B.; Cheong, S.W.; Mazzoli, C.; Barbour, A.; Hu, W.; Wilkins, S.B.; Robinson, I.K.; Dean, M.P.M.; et al. Imaging antiferromagnetic antiphase domain boundaries using magnetic bragg diffraction phase contrast. Nat. Commun. 2018, 9, 5013. [Google Scholar] [CrossRef]
- Kim, M.G.; Barbour, A.; Hu, W.; Wilkins, S.B.; Robinson, I.K.; Dean, M.P.M.; Yang, J.; Won, C.; Cheong, S.-W.; Mazzoli, C.; et al. Real-space observation of fluctuating antiferromagnetic domains. Sci. Adv. 2022, 8, eabj9493. [Google Scholar] [CrossRef] [PubMed]
- Burgard, L.; Neupane, C.; Balodhi, A.; Bista, S.; Butun, S.; Jangid, R.; Barbour, A.; Basit, N.; Agterberg, D.F.; Weinert, M.; et al. Fresnel diffraction imaging of surface nanostructure using coherent resonant X-ray scattering. J. Appl. Phys. 2025, 138, 013902. [Google Scholar] [CrossRef]
- Merz, W.J. Domain formation and domain wall motions in ferroelectric batio3 single crystals. Phys. Rev. 1954, 95, 690–698. [Google Scholar] [CrossRef]
- Wondratschek, H.; Jeitschko, W. Twin domains and antiphase domains. Acta Crystallogr. Sect. A 1976, 32, 664–666. [Google Scholar] [CrossRef]
- Hubert, A.; Schäfer, R. Magnetic Domains: The Analysis of Magnetic Microstructures; Springer: Berlin/Heidelberg, Germany, 1998. [Google Scholar]
- Fenter, P.; Park, C.; Zhang, Z.; Wang, S. Observation of subnanometre-high surface topography with X-ray reflection phase-contrast microscopy. Nat. Phys. 2006, 2, 700–704. [Google Scholar] [CrossRef]
- Gaunt, P. Ferromagnetic domain wall pinning by a random array of inhomogeneities. Philos. Mag. B 1983, 48, 261–276. [Google Scholar] [CrossRef]
- Kläui, M.; Ehrke, H.; Rüdiger, U.; Kasama, T.; Dunin-Borkowski, R.E.; Backes, D.; Heyderman, L.J.; Vaz, C.A.F.; Bland, J.A.C.; Faini, G.; et al. Direct observation of domain-wall pinning at nanoscale constrictions. Appl. Phys. Lett. 2005, 87, 102509. [Google Scholar] [CrossRef]
- Tanigawa, H.; Koyama, T.; Bartkowiak, M.; Kasai, S.; Kobayashi, K.; Ono, T.; Nakatani, Y. Dynamical pinning of a domain wall in a magnetic nanowire induced by walker breakdown. Phys. Rev. Lett. 2008, 101, 207203. [Google Scholar] [CrossRef]
- Bedau, D.; Kläui, M.; Hua, M.T.; Krzyk, S.; Rüdiger, U.; Faini, G.; Vila, L. Quantitative determination of the nonlinear pinning potential for a magnetic domain wall. Phys. Rev. Lett. 2008, 101, 256602. [Google Scholar] [CrossRef]
- Tanner, B.K. Antiferromagnetic domains. Contemp. Phys. 1979, 20, 187–210. [Google Scholar] [CrossRef]
- Jungwirth, T.; Marti, X.; Wadley, P.; Wunderlich, J. Antiferromagnetic spintronics. Nat. Nanotechnol. 2016, 11, 231–241. [Google Scholar] [CrossRef]
- Ashcroft, N.W.; Mermin, N.D. Solid State Physics, 1st ed.; Brooks Cole: Pacific Grove, CA, USA, 1976. [Google Scholar]
- Coronado, E.; Tsukerblat, B.S.; Georges, R. Exchange Interactions I: Mechanisms. In Molecular Magnetism: From Molecular Assemblies to the Devices; Coronado, E., Delhaès, P., Gatteschi, D., Miller, J.S., Eds.; NATO ASI Series; Springer: Dordrecht, The Netherlands, 1996; Volume 321, pp. 65–84. [Google Scholar]
- Papanicolaou, N. Antiferromagnetic domain walls. Phys. Rev. B 1995, 51, 15062–15073. [Google Scholar] [CrossRef]
- Soboleva, T.K.; Zhedanov, A.S. Discrete versus continuous antiferromagnetic domain wall. Phys. Lett. A 1996, 223, 470–474. [Google Scholar] [CrossRef]
- Papanicolaou, N.; Gribanov, I. Magnetic anisotropy in the layered magnet CsNiF3. J. Phys. Condens. Matter 1998, 10, L131. [Google Scholar] [CrossRef]
- Hanamura, E.; Tanabe, Y. Ferroelectric and antiferromagnetic domain wall. J. Phys. Soc. Jpn. 2003, 72, 2959–2966. [Google Scholar] [CrossRef]
- Mitsumata, C.; Sakuma, A. Generalized model of antiferromagnetic domain wall. IEEE Trans. Magn. 2011, 47, 3501–3504. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, M.G.; Boney, S.; Burgard, L.; Rutowski, L.; Mazzoli, C. Dynamics and Formation of Antiferromagnetic Textures in MnBi2Te4 Single Crystal. Materials 2025, 18, 5337. https://doi.org/10.3390/ma18235337
Kim MG, Boney S, Burgard L, Rutowski L, Mazzoli C. Dynamics and Formation of Antiferromagnetic Textures in MnBi2Te4 Single Crystal. Materials. 2025; 18(23):5337. https://doi.org/10.3390/ma18235337
Chicago/Turabian StyleKim, Min Gyu, Starr Boney, Luke Burgard, Lillian Rutowski, and Claudio Mazzoli. 2025. "Dynamics and Formation of Antiferromagnetic Textures in MnBi2Te4 Single Crystal" Materials 18, no. 23: 5337. https://doi.org/10.3390/ma18235337
APA StyleKim, M. G., Boney, S., Burgard, L., Rutowski, L., & Mazzoli, C. (2025). Dynamics and Formation of Antiferromagnetic Textures in MnBi2Te4 Single Crystal. Materials, 18(23), 5337. https://doi.org/10.3390/ma18235337





