Improved CNN for Predicting Line Heating Forming Deformation of Complex Hull Curved Plate
Abstract
1. Introduction
2. Numerical Calculation of Line Heating Forming Based on SDB
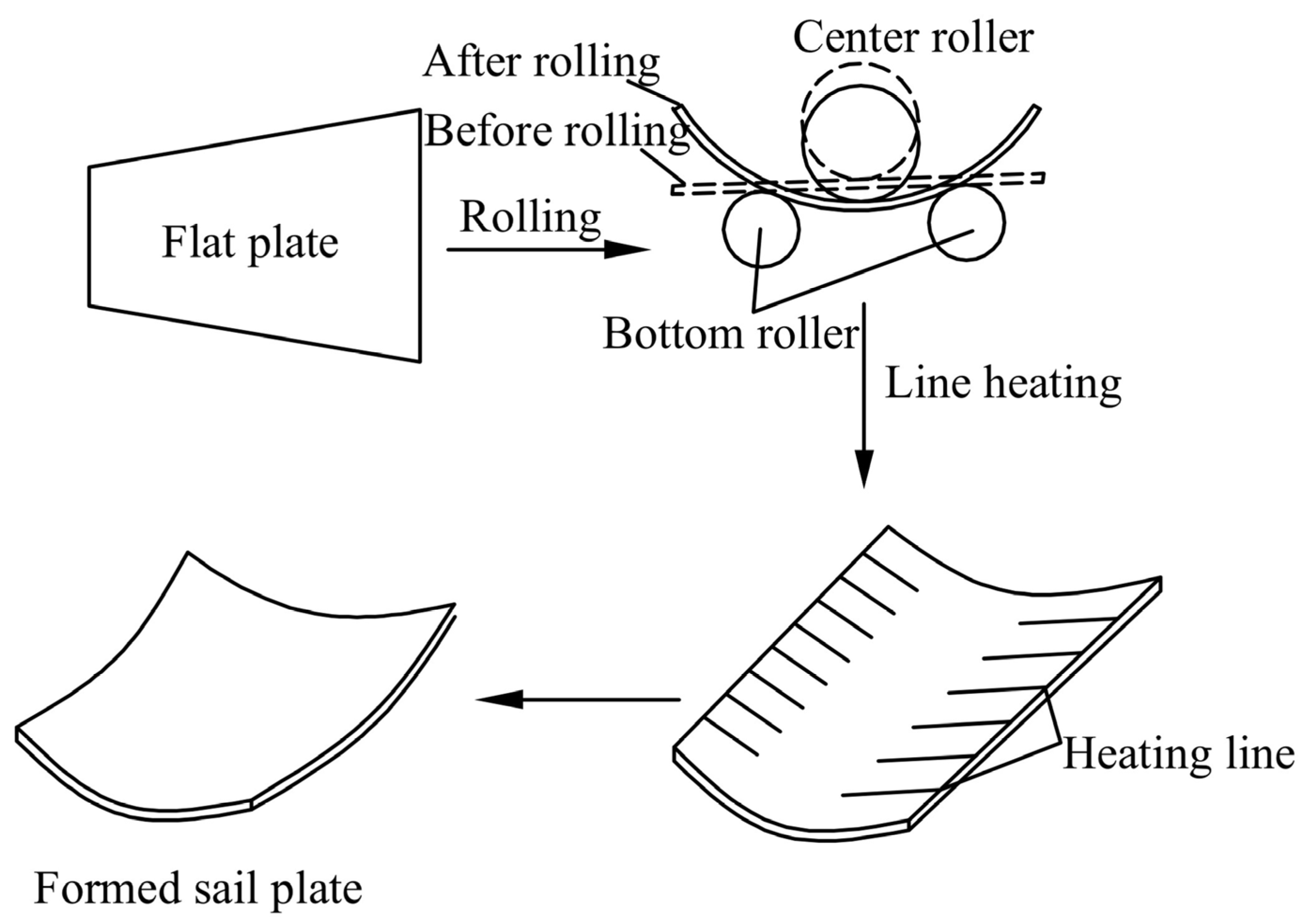
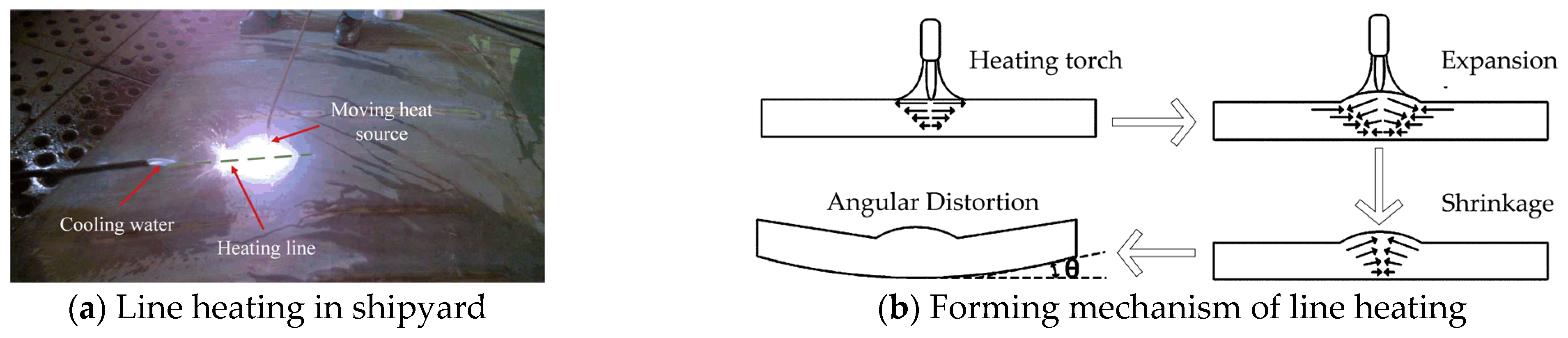
2.1. Line Heating Forming Mechanism of Curved Plate
2.2. Loading Approach of SDB
2.3. Feasibility Verification of Numerical Calculation of SDB
- (1)
- Comparison of numerical results from TEP-FEM with experimental data
- (2)
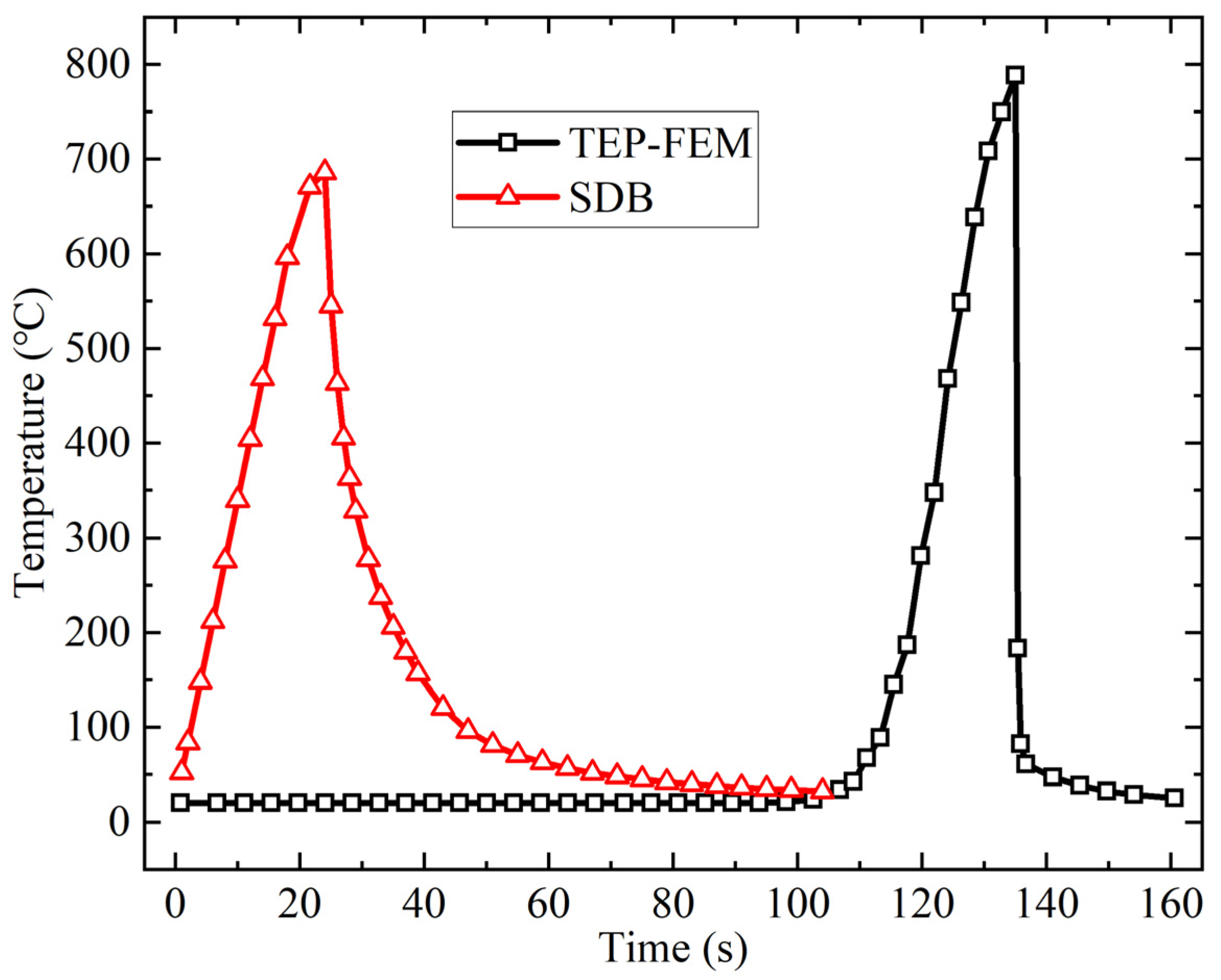
- Temperature results analysis for TEP-FEM and SDB
- (3)
- Deformation results analysis for TEP-FEM and SDB
3. Prediction of Deformation of Line Heating of Curved Plate Based on CNN
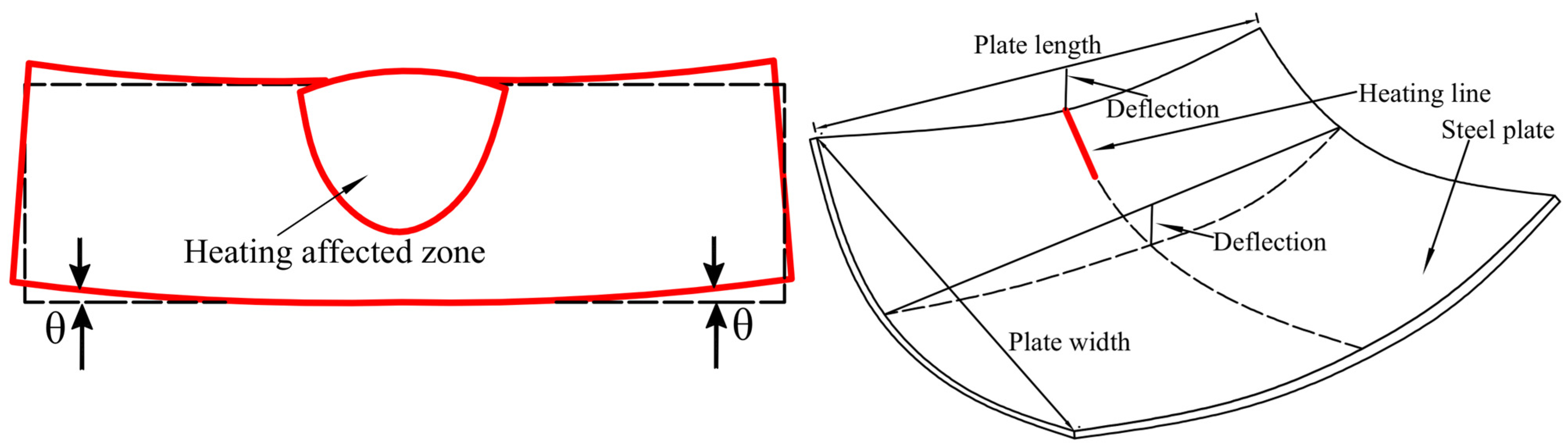
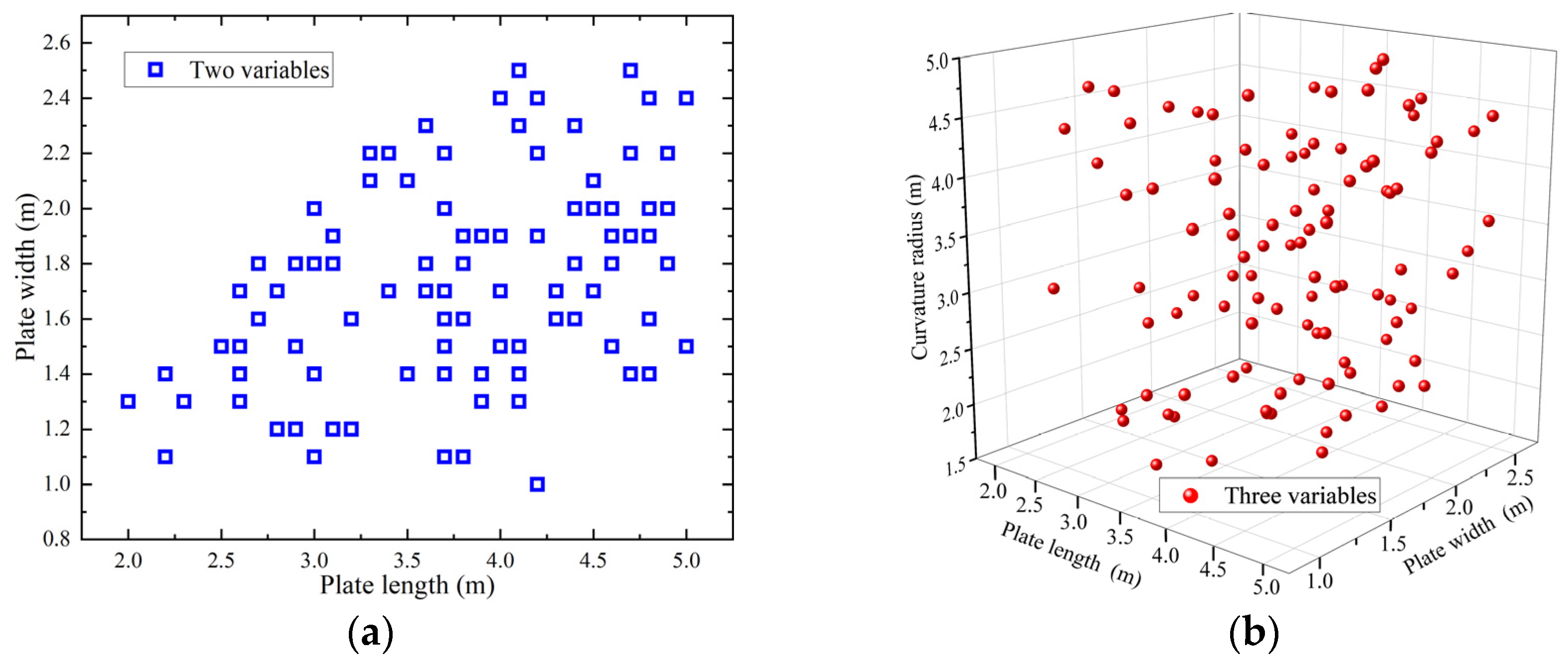
3.1. Sampling and Processing of Samples
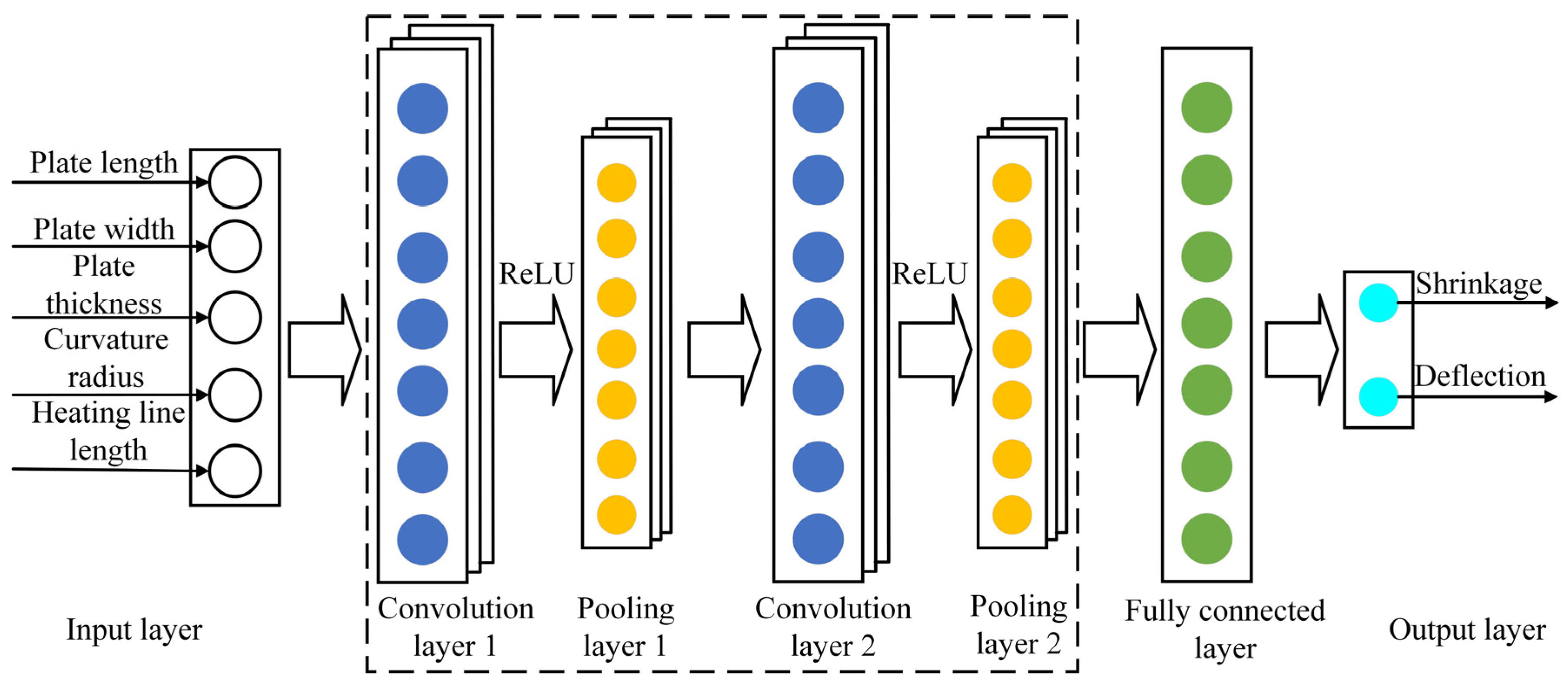
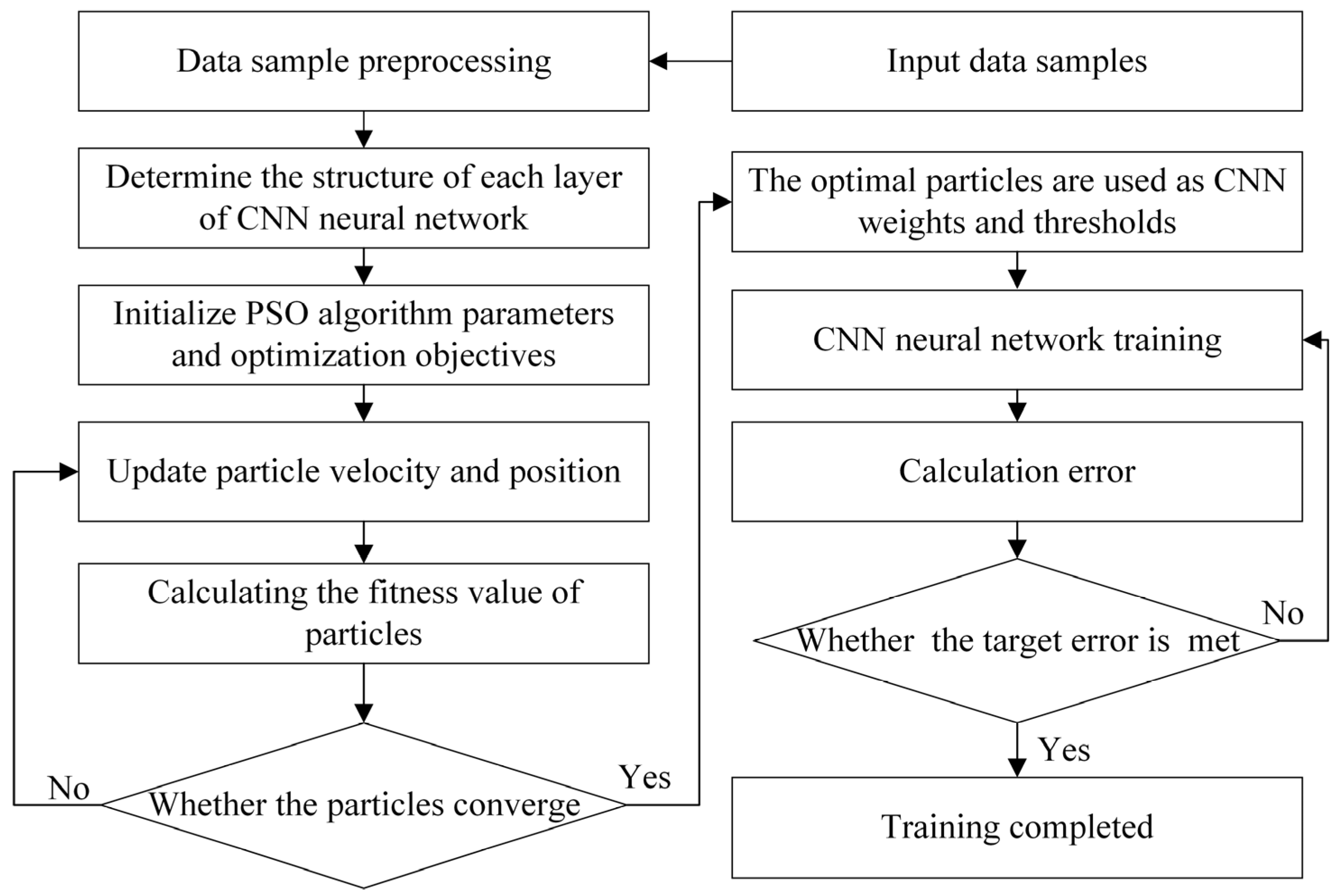
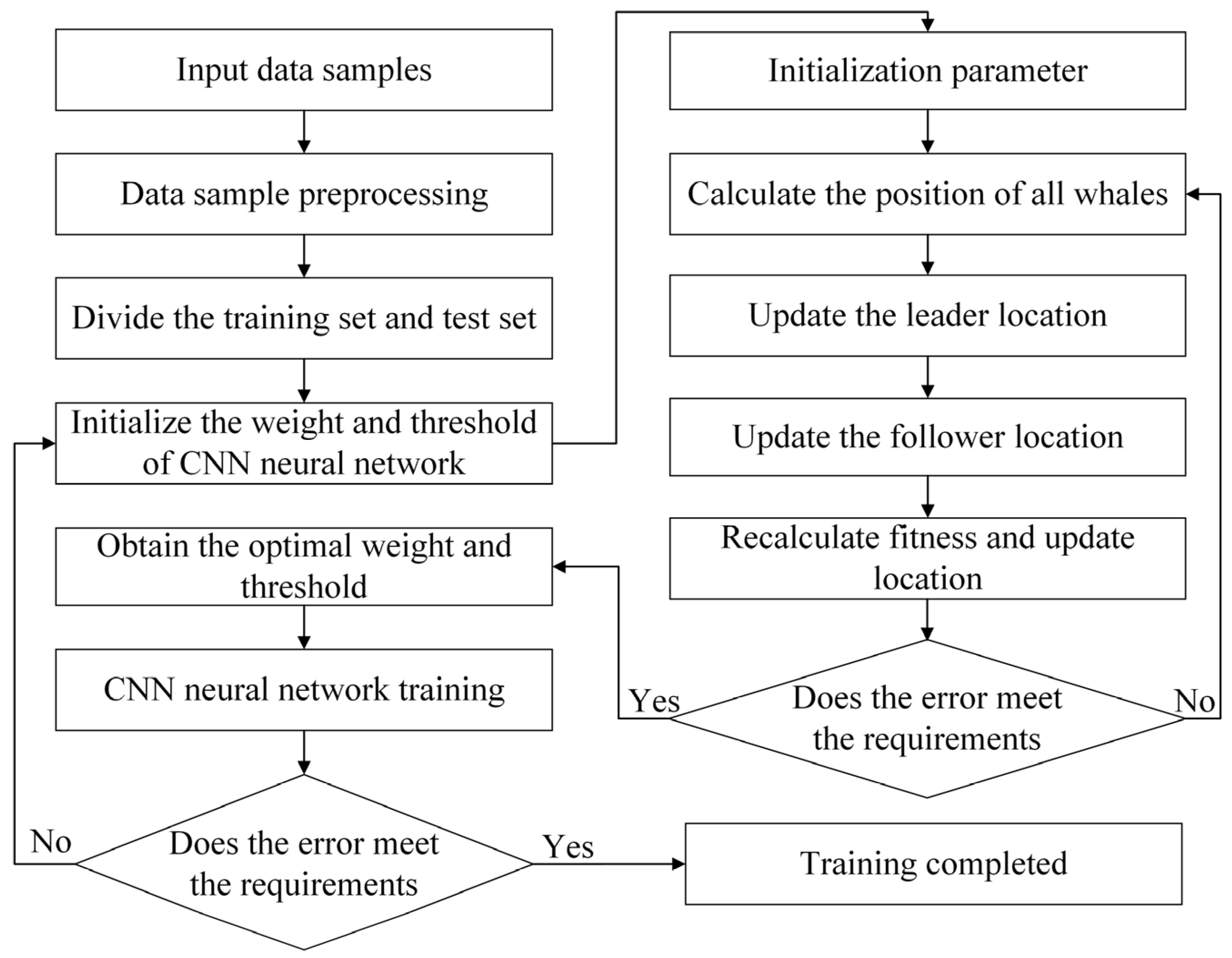
3.2. Intelligent Prediction Model for Deformation of Line Heating of Curved Plate Based on CNN
4. Results and Analysis of Curved Plate Forming Prediction Model
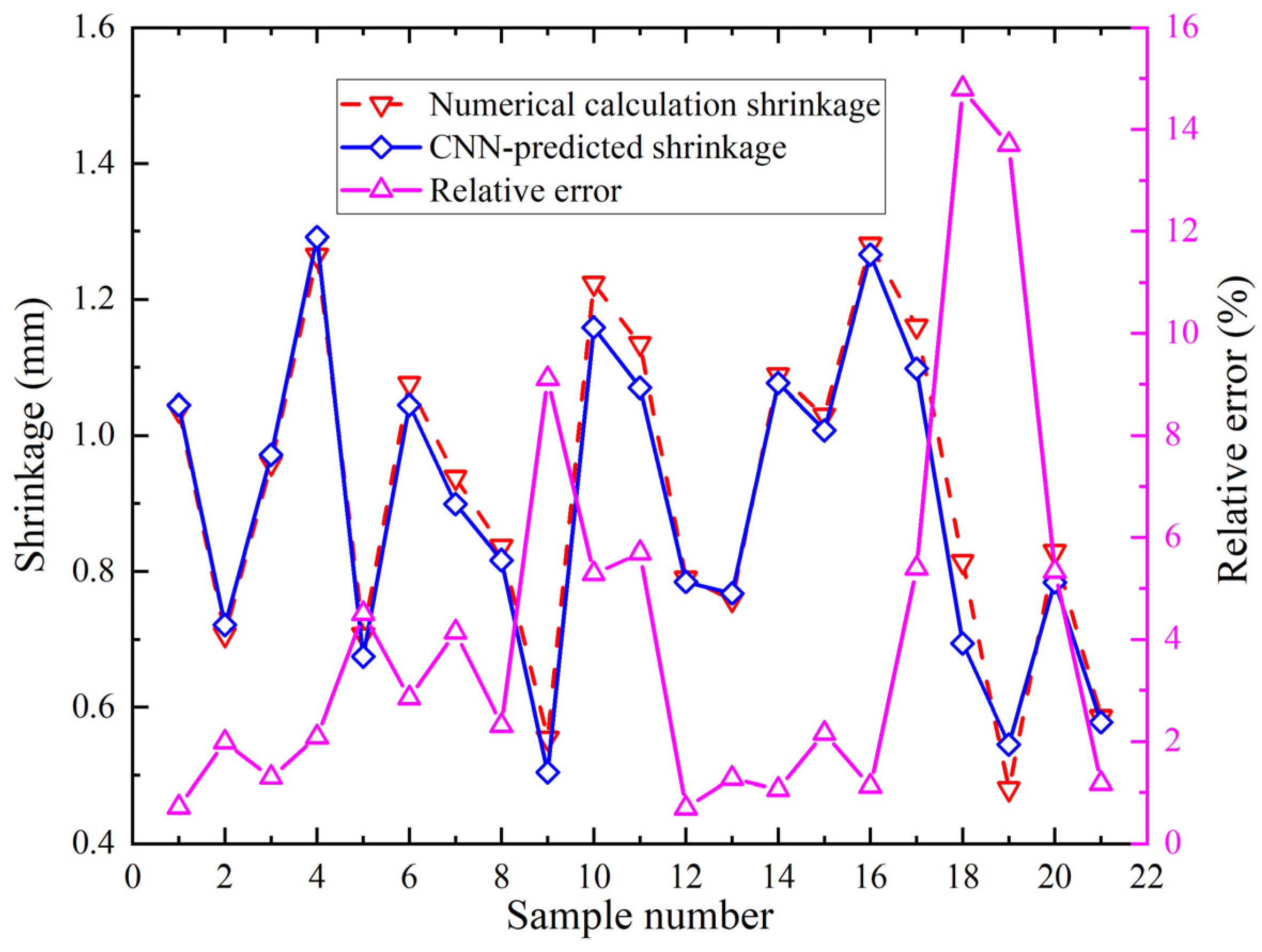
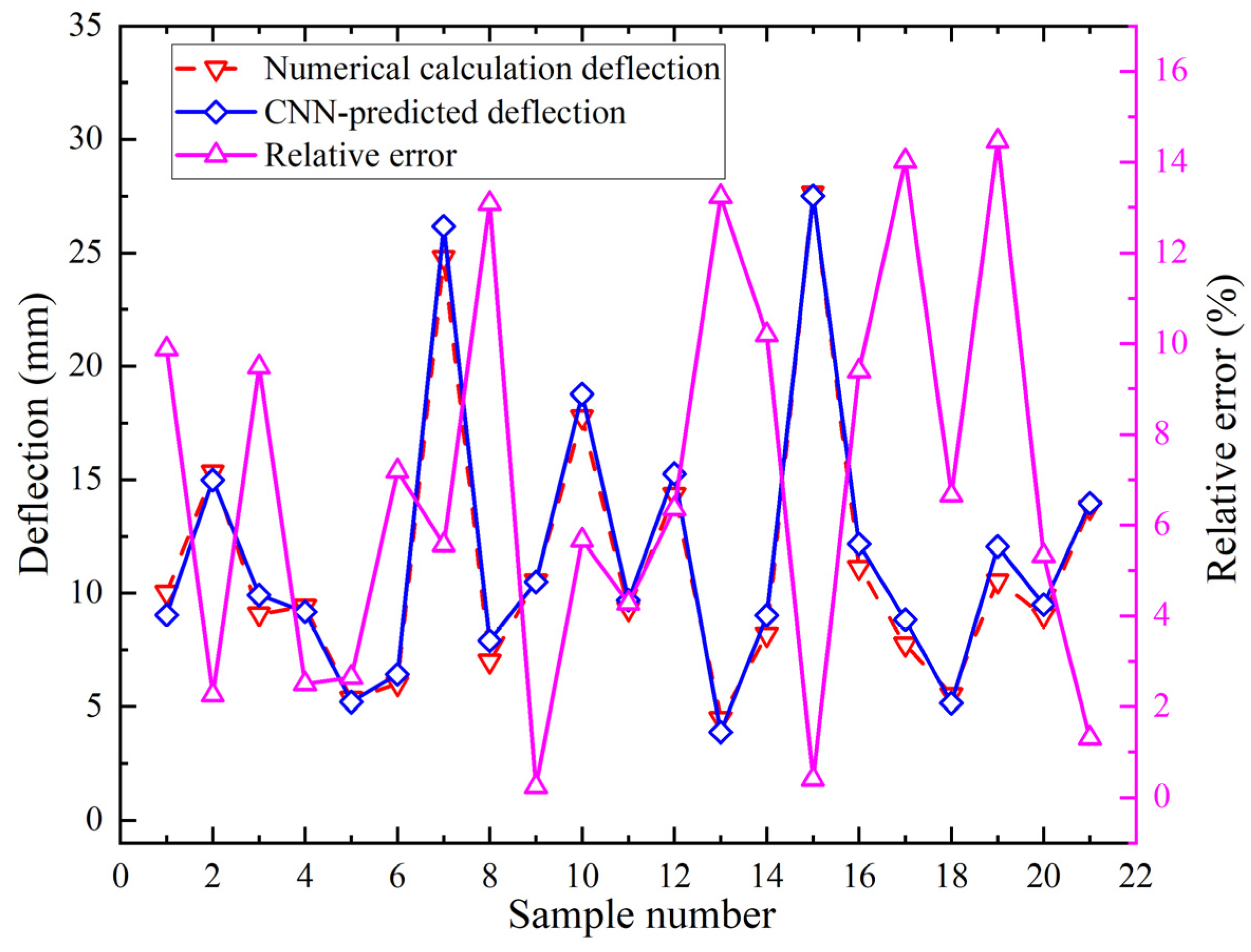
4.1. Analysis of the Results of the Prediction Model
- (1)
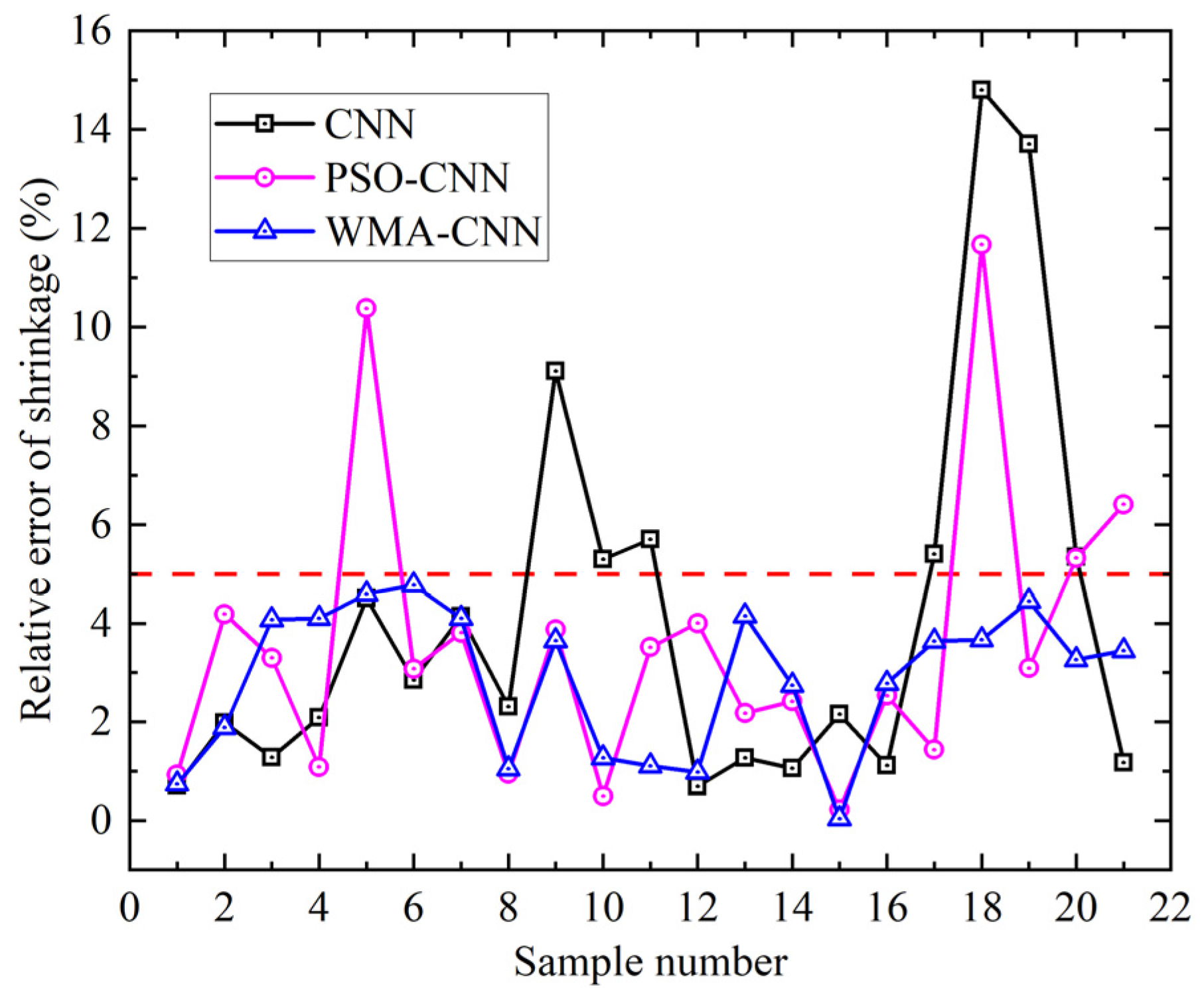
- Accuracy analysis of shrinkage prediction
- (2)
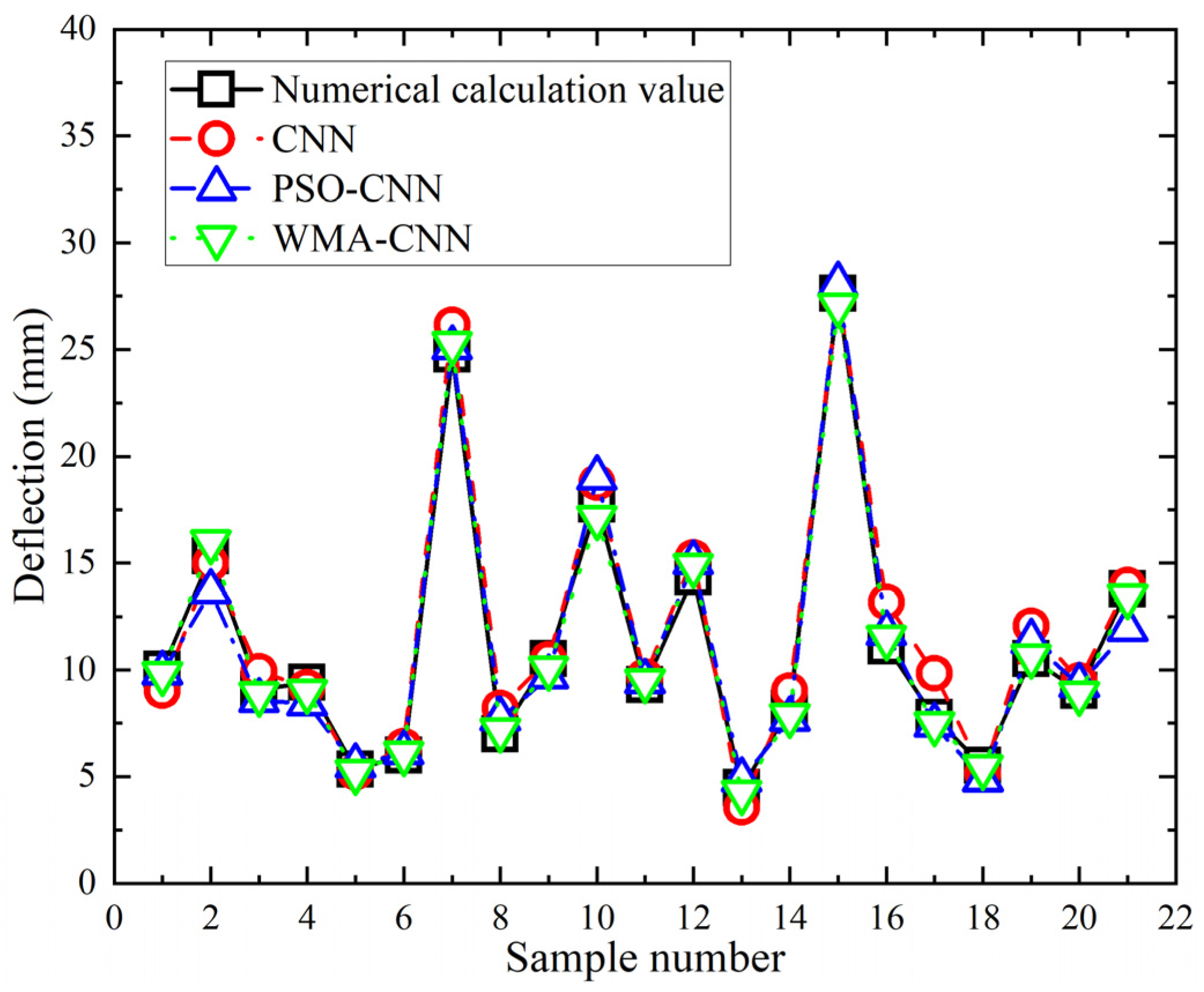
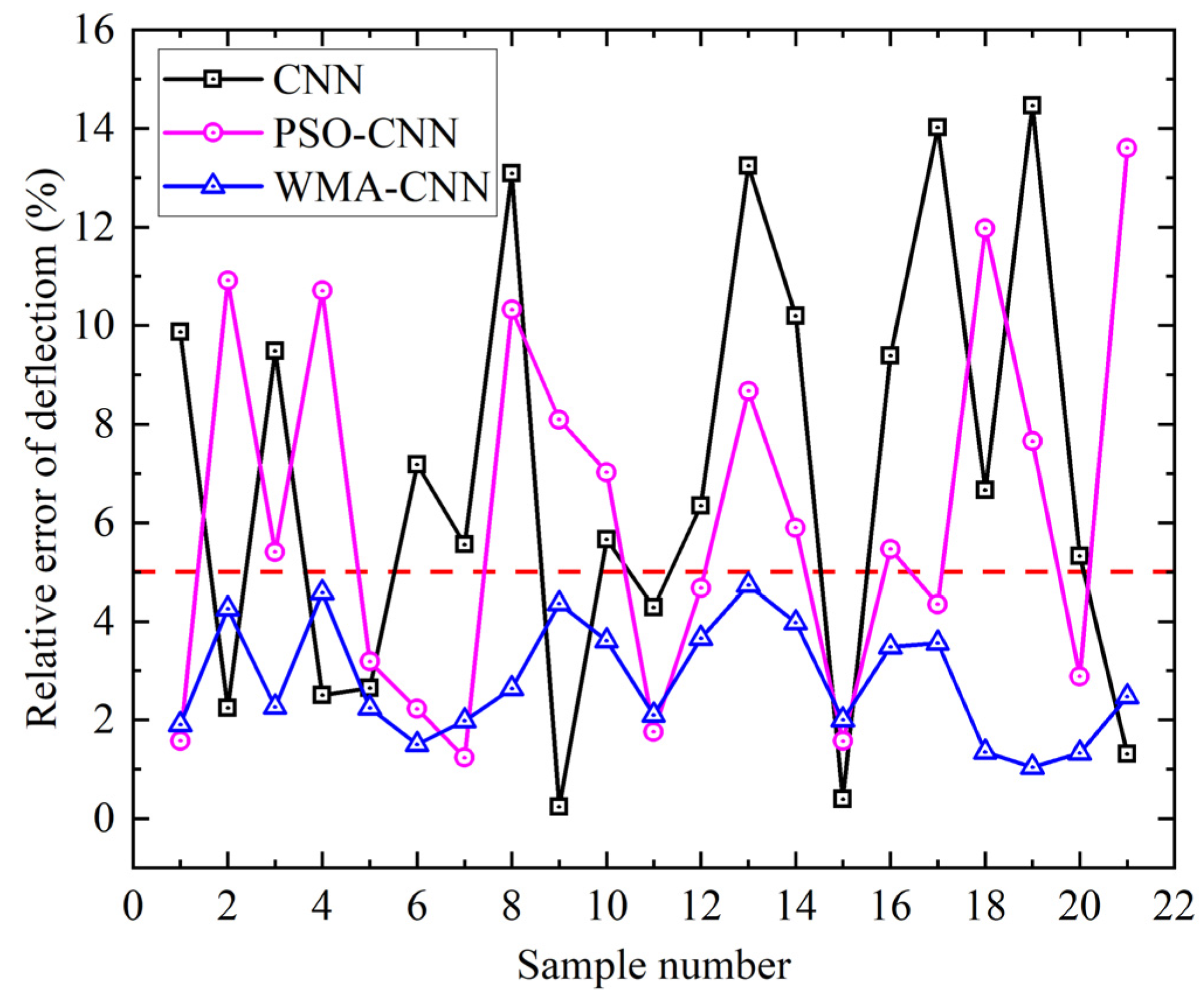
- Accuracy analysis of deflection prediction
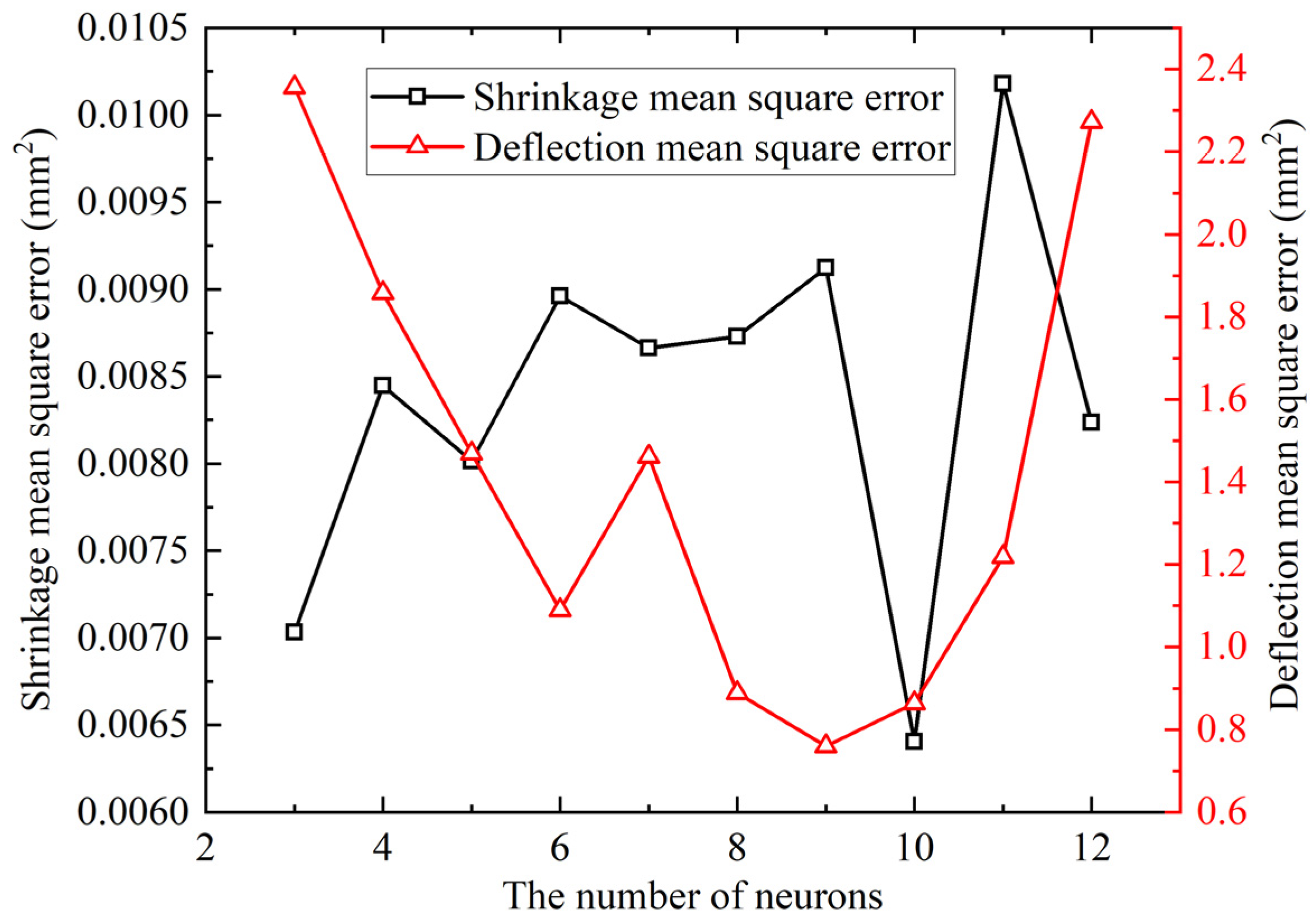
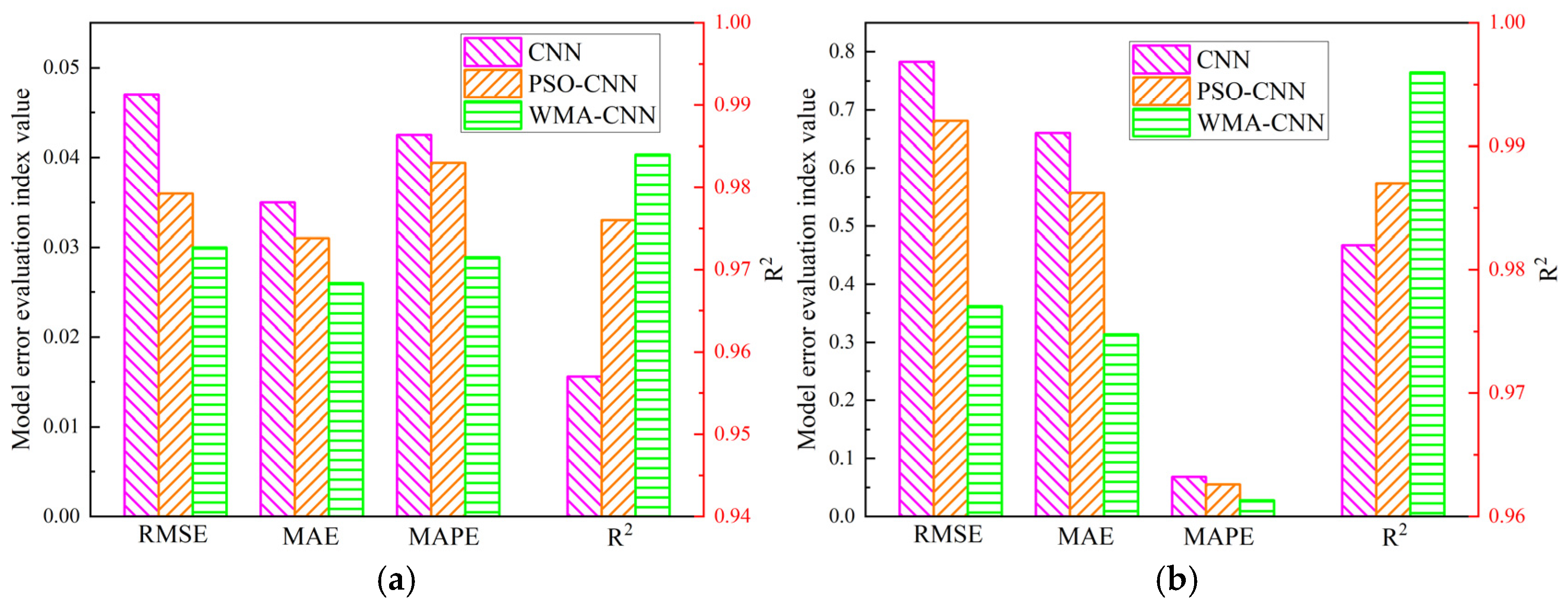
4.2. Analysis of Evaluation Indices for the Prediction Model
4.3. Validation Cases for the WMA-CNN Prediction Model
5. Conclusions
- Numerical calculations from the TEP-FEM and SDB showed closely matched temperature and deformation results. This confirms the applicability of the SDB for line heating forming numerical calculation.
- To realize the fast prediction of curved plate forming, a prediction model of curved plate forming deformation based on CNN was established. The CNN model is optimized by PSO algorithm and WMA algorithm, and the curved plate deformation prediction models by PSO-CNN and WMA-CNN were established. When the WMA-CNN model predicts deformation, the relative error of the sample data is within 5%. It indicates that the prediction accuracy of WMA-CNN model is better than CNN model and PSO-CNN model.
- Among the three models, the WMA-CNN model has the highest prediction accuracy. For shrinkage prediction, the coefficient of determination was the largest (R2 = 0.984). For deflection prediction, the largest coefficient of determination was (R2 = 0.996). Compared to CNN model, for shrinkage prediction, the MAPE of PSO-CNN model and WMA-CNN model were reduced by 7.3% and 32.0%. For deflection prediction, the MAPE of the PSO-CNN model versus the WMA-CNN model was reduced by 19.1% and 59.0%. Therefore, for curved plate deflection prediction, the WMA-CNN model outperforms the CNN model and PSO-CNN model.
- The WMA-CNN model is applied for the validation of five calculation cases. The relative error between the prediction results and the numerical calculation results is within 5%, which is within the acceptable range. It is demonstrated that the WMA-CNN model is suitable for intelligent prediction of curved plate line heating forming. This research provides reference for automated forming of hull curved plate. In the subsequent work, the research findings will be applied to predict the forming parameters of curved plates. Concurrently, the development of automated curved plate forming equipment and a real-time forming control system will be carried out. Finally, the accuracy of the established parameter prediction system will be validated through dedicated curved plate forming experiments, thereby laying a foundation for the practical implementation of intelligent line heating technology.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Chircop, A. The IMO initial strategy for the reduction of GHGs from international shipping: A commentary. Int. J. Mar. Coast. Law 2019, 34, 482–512. [Google Scholar] [CrossRef]
- Wang, S.; Dai, J.; Ji, W. Numerical calculation of high-strength-steel saddle plate forming suitable for light weight construction of ships. Materials 2023, 16, 3848. [Google Scholar] [CrossRef]
- Shen, W.; Yan, R.; Li, S.; Xu, L. Spring-back analysis in the cold-forming process of ship hull plates. Int. J. Adv. Manuf. Technol. 2018, 96, 2341–2354. [Google Scholar] [CrossRef]
- Wei, Z.; Zhao, Y.; Yuan, H.; Chang, L. Equivalent load model for the numerical simulation of integrated induction heating and mechanical rolling forming of curved hull plates. Int. J. Adv. Manuf. Technol. 2024, 130, 3891–3903. [Google Scholar] [CrossRef]
- Tong, L.; Niu, L.; Ren, Z.; Zhao, X. Experimental investigation on fatigue behavior of butt-welded high-strength steel plates. Thin Walled Struct. 2021, 165, 107956. [Google Scholar] [CrossRef]
- Chang, L.; Zhao, Y.; Yuan, H. Effect of plate curvature on heat source distribution in induction line heating for plate forming. Appl. Sci. 2020, 10, 2304. [Google Scholar] [CrossRef]
- Shen, H.; Zhou, W.; Wang, H. Laser forming of doubly curved plates using minimum energy principle and comprehensive strain control. Int. J. Mech. Sci. 2018, 145, 42–52. [Google Scholar] [CrossRef]
- Wang, C.; Kim, Y.; Kim, J. Numerical analysis of thermal deformation in laser beam heating of a steel plate. J. Mech. Sci. Technol. 2017, 31, 2535–2541. [Google Scholar] [CrossRef]
- Wang, S.; Xu, Z.; Zhao, Z.; Wang, J.; Li, R. Numerical calculation of high frequency induction heating for complex hull plate considering deflection. Thin Walled Struct. 2025, 212, 113158. [Google Scholar] [CrossRef]
- Wei, B.; Wei, Y.; Zhang, F. Springback control and plastic deformation of metal plates with large curvature in heat-assisted incremental bending process. Int. J. Adv. Manuf. Technol. 2021, 112, 1483–1500. [Google Scholar] [CrossRef]
- Zhou, H.; Yi, B.; Wang, J.; Zheng, X. Preliminary investigation on plate bending with multiple-line induction heating. J. Mar. Sci. Technol. 2019, 25, 455–466. [Google Scholar] [CrossRef]
- Dong, W.; Bao, L.; Li, W.; Shin, K.; Han, C. Effects of laser forming on the mechanical properties and microstructure of DP980 steel. Materials 2022, 15, 7581. [Google Scholar] [CrossRef]
- Shibahara, M.; Ikushima, K.; Maekawa, M. Approach to automation of line heating by combination of reinforcement learning and finite element method simulation. ASME Open J. Eng. 2022, 1, 011024. [Google Scholar] [CrossRef]
- Zhao, Z.; Yuan, H.; Zhao, Y.; Zeng, F. Processing-scheme design for forming curved ship plate and analysis of calculation cases. J. Mar. Sci. Eng. 2022, 10, 1418. [Google Scholar] [CrossRef]
- Zhou, H.; Wang, Z.; Li, L.; Xu, B. Line heating process parameter forecasting method based on optimization concept. Adv. Mech. Eng. 2022, 14, 16878132221086689. [Google Scholar] [CrossRef]
- Lee, J.; Lee, S. A study on the thermal deformation characteristics of steel plates due to multi-line heating. Int. J. Nav. Archit. Ocean Eng. 2018, 10, 48–59. [Google Scholar] [CrossRef]
- Hai, N.D.X.; Thinh, N.T. Novel method in induction heating for complex steel plate deformation based on artificial neural network. Complexity 2022, 2022, 3531980. [Google Scholar] [CrossRef]
- Song, J.; Lee, J.; Kim, D. Cycle-time estimation for forming curved plates using neural networks. J. Ship Prod. Des. 2022, 38, 129–139. [Google Scholar] [CrossRef]
- Li, L.; Qi, S.; Zhou, H.; Wang, L. Prediction of line heating deformation on sheet metal based on an ISSA–ELM model. Sci. Rep. 2023, 13, 1252. [Google Scholar] [CrossRef]
- Yang, Y.; Nam, H.; Bae, K. Selection of heating lines in the line heating process for steel plates using Faster R−CNN. Int. J. Precis. Eng. Manuf. 2024, 25, 1713–1723. [Google Scholar] [CrossRef]
- Zhang, Z. Research on optimization of steel plate linear heating line planning based on multi-objective PCA-PSO particle swarm optimization. Adv. ML AI 2024, 5, 1–11. [Google Scholar]
- Thinh, N.T.; Bae, K.Y.; Yang, Y. Using a novel CNN model for predicting the induction heating lines to obtain a desired deformed shape of steel plate. Int. J. Precis. Eng. Manuf. 2023, 24, 1781–1791. [Google Scholar] [CrossRef]
- Spathopoulos, S.C.; Stavroulakis, G. Springback prediction in sheet metal forming, based on finite element analysis and artificial neural network approach. Appl. Mech. 2020, 1, 97–110. [Google Scholar] [CrossRef]
- Kim, B.; Son, S.; Ryu, C.; Shin, J.G. Curved hull plate classification for determining forming method using deep learning. J. Ship Prod. Des. 2019, 35, 328–337. [Google Scholar] [CrossRef]
- Wang, S.; Jia, H.; Fu, Y.; Wang, J.; Li, R. Numerical calculation of line heating for hull curved plate based on strain direct boundary. Ocean Eng. 2025, 4, 122816. [Google Scholar] [CrossRef]
- Iordanis, I.; Koukouvinos, C.; Silou, I. On the efficacy of conditioned and progressive Latin hypercube sampling in supervised machine learning. Appl. Numer. Math. 2024, 208, 256–270. [Google Scholar] [CrossRef]
- Wang, J.; Wang, Y.; Tan, Z.K.; Wang, X.; Lei, S.; Wu, P. CNN-POT: Predicting oceanic turbulence phase variations with convolutional neural networks. J. Opt. 2025, 27, 055401. [Google Scholar] [CrossRef]
- Çomak, E.; Gunduz, G. Comparative analysis of performances of an improved particle swarm optimization and a traditional particle swarm optimization for training of neural network architecture space. Acta Polytech. Hung. 2025, 22, 7–30. [Google Scholar] [CrossRef]
- Ghasemi, M.; Deriche, M.; Trojovský, P. An efficient bio-inspired algorithm based on humpback whale migration for constrained engineering optimization. Results Eng. 2025, 25, 104215. [Google Scholar] [CrossRef]

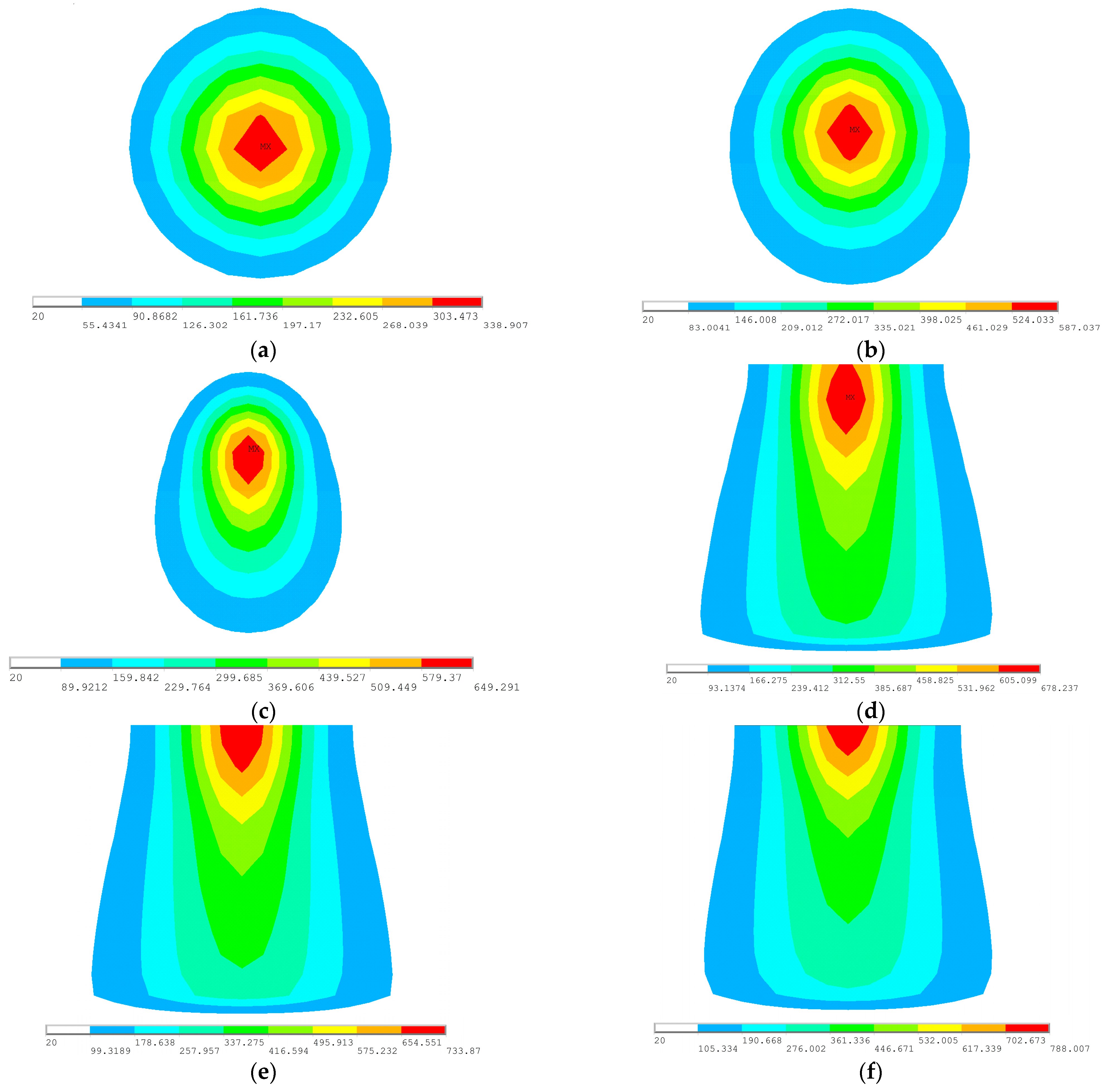




| Position | Temperature 20 mm from the Center (°C) | Temperature 10 mm from the Center (°C) | Center Position Temperature (°C) |
|---|---|---|---|
| First layer | 520.3 | 718.6 | 808.5 |
| Second layer | / | 613.1 | 680.9 |
| Third layer | / | 567.2 | 618.4 |
| Fourth layer | / | / | 583.1 |
| Fifth layer | / | / | / |
| Parameter | Value | Unit |
|---|---|---|
| Plate length | 3 | m |
| Plate width | 1.5 | m |
| Plate thickness | 14 | mm |
| Curvature radius | 5 | m |
| Heating line length | 300 | mm |
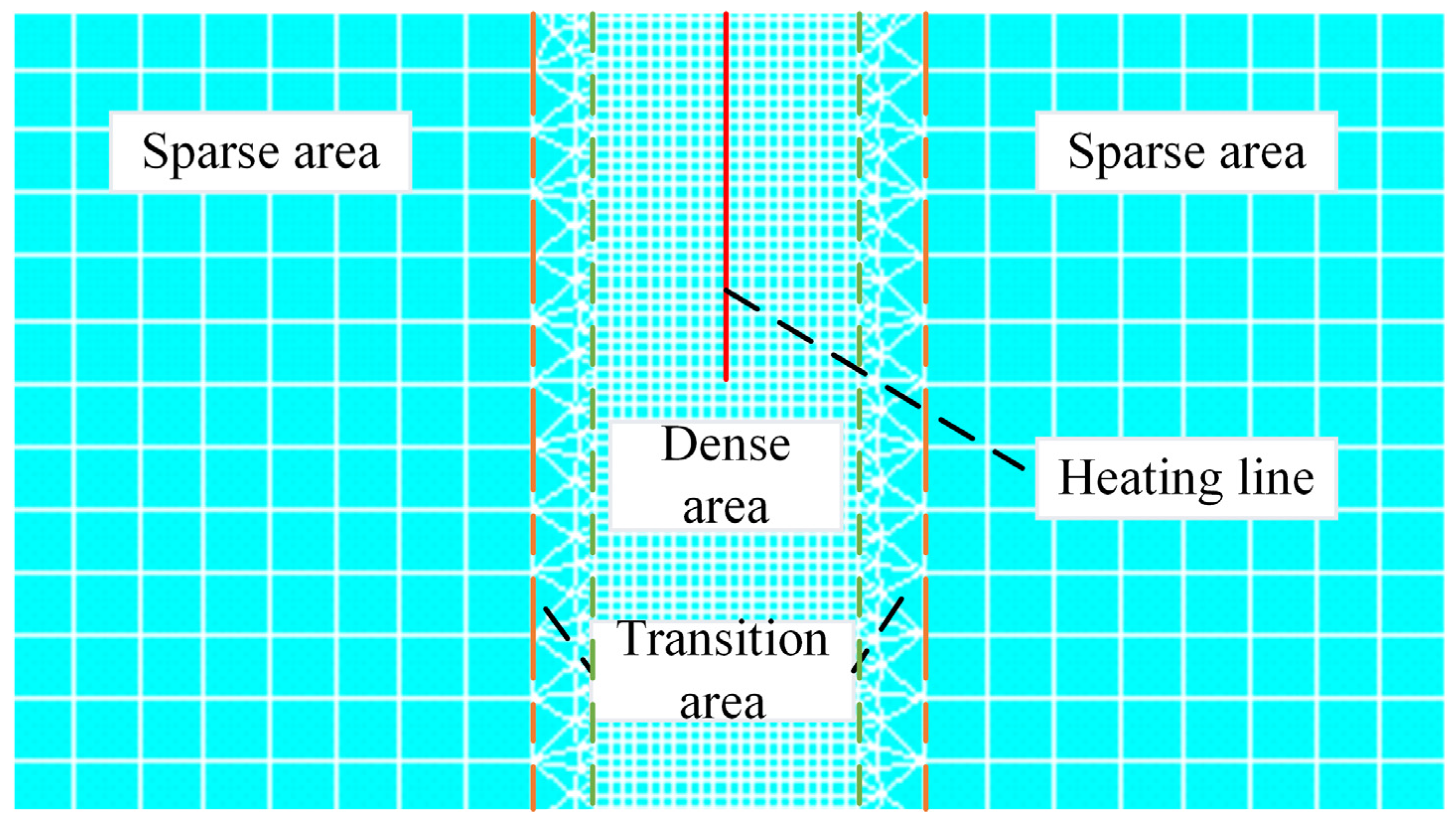
| Mesh Size of Dense Area (mm) | Mesh Size of Transition Area (mm) | Mesh Size of Sparse Area (mm) |
|---|---|---|
| 5 | 10 | 25 |
| 8 | 16 | 40 |
| 10 | 20 | 50 |
| 12 | 24 | 60 |
| 16 | 32 | 80 |
| 18 | 36 | 90 |
| 20 | 40 | 100 |
| 25 | 50 | 125 |
| 28 | 56 | 140 |
| Distance to the Initial Point of Heating Line (mm) | 0 | 75 | 150 | 225 | 300 |
|---|---|---|---|---|---|
| Experimental data (mm) | 0.27 | 0.49 | 0.75 | 1.07 | 1.35 |
| Numerical calculation (mm) | 0.269 | 0.509 | 0.741 | 1.078 | 1.391 |
| Absolute error (mm) | 0.001 | 0.019 | 0.009 | 0.008 | 0.041 |
| Relative error (%) | 0.37 | 3.88 | 1.20 | 0.75 | 3.03 |
| No. | Plate Length (m) | Plate Width (m) | Curvature Radius (m) | Plate Thickness (mm) | Heating Line Length (m) | Shrinkage (mm) | Deflection (mm) |
|---|---|---|---|---|---|---|---|
| 1 | 3.2 | 1.2 | 4 | 12 | 0.3 | 1.18 | 17.76 |
| 2 | 4.8 | 1.6 | 4.3 | 8 | 0.3 | 1.31 | 30.88 |
| 3 | 3.7 | 1.6 | 3 | 24 | 0.3 | 0.91 | 8.65 |
| 4 | 3.6 | 2.3 | 2.8 | 24 | 0.3 | 0.88 | 8.02 |
| 5 | 4.1 | 1.5 | 2.3 | 24 | 0.2 | 0.65 | 11.12 |
| 100 | 4 | 1.9 | 3.7 | 24 | 0.2 | 0.65 | 13.50 |
| 101 | 4.3 | 1.7 | 1.9 | 8 | 0.4 | 1.19 | 13.78 |
| 102 | 5 | 2.6 | 4.4 | 24 | 0.2 | 0.67 | 13.86 |
| No. | Plate Length | Plate Width | Curvature Radius | Plate Thickness | Heating Line Length | Shrinkage | Deflection |
|---|---|---|---|---|---|---|---|
| 1 | 0.400 | 0.125 | 0.706 | 0.200 | 0.500 | 0.833 | 0.332 |
| 2 | 0.933 | 0.375 | 0.794 | 0.000 | 0.500 | 0.988 | 0.660 |
| 3 | 0.567 | 0.375 | 0.412 | 0.800 | 0.500 | 0.512 | 0.104 |
| 4 | 0.533 | 0.813 | 0.353 | 0.800 | 0.500 | 0.476 | 0.089 |
| 5 | 0.700 | 0.313 | 0.206 | 0.800 | 0.000 | 0.202 | 0.166 |
| 100 | 0.667 | 0.563 | 0.618 | 0.800 | 0.000 | 0.202 | 0.226 |
| 101 | 0.767 | 0.438 | 0.088 | 0.000 | 1.000 | 0.845 | 0.233 |
| 102 | 1.000 | 1.000 | 0.824 | 0.800 | 0.000 | 0.226 | 0.235 |
| Variables | Model | MSE (mm2) | RMSE (mm) | MAE (mm) | MAPE | R2 |
|---|---|---|---|---|---|---|
| Shrinkage | CNN | 0.0020 | 0.045 | 0.034 | 0.0425 | 0.963 |
| PSO-CNN | 0.0013 | 0.036 | 0.031 | 0.0394 | 0.976 | |
| WMA-CNN | 0.0009 | 0.030 | 0.026 | 0.0289 | 0.984 | |
| Deflection | CNN | 0.6133 | 0.783 | 0.660 | 0.0686 | 0.982 |
| PSO-CNN | 0.4633 | 0.681 | 0.557 | 0.0555 | 0.987 | |
| WMA-CNN | 0.1312 | 0.362 | 0.314 | 0.0281 | 0.996 |
| Parameters and Indices | Case 1 | Case 2 | Case 3 | Case 4 | Case 5 |
|---|---|---|---|---|---|
| Plate length (m) | 4.4 | 4.6 | 4 | 4.7 | 3.6 |
| Plate width (m) | 2 | 1.9 | 1.7 | 2.5 | 1.7 |
| Plate thickness (mm) | 28 | 8 | 16 | 20 | 20 |
| Curvature radius (m) | 3 | 2.1 | 3.5 | 4.3 | 3.4 |
| Heating line length (m) | 0.4 | 0.4 | 0.2 | 0.2 | 0.3 |
| Calculated shrinkage (mm) | 0.51 | 1.20 | 0.77 | 0.71 | 0.9 |
| Predicted shrinkage (mm) | 0.529 | 1.243 | 0.758 | 0.736 | 0.861 |
| Calculated deflection (mm) | 9.21 | 15.18 | 17.48 | 15.52 | 11.32 |
| Predicted deflection (mm) | 9.463 | 14.589 | 18.250 | 14.936 | 11.110 |
| Absolute error of shrinkage (mm) | −0.019 | −0.043 | 0.012 | −0.026 | 0.039 |
| Relative error of shrinkage | 3.73% | 3.58% | 1.56% | 3.66% | 4.33% |
| Absolute error of deflection (mm) | −0.253 | 0.591 | −0.770 | 0.584 | 0.210 |
| Relative error of deflection | 2.75% | 3.89% | 4.41% | 3.76% | 1.86% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, S.; Jia, H.; Fu, Y.; Wang, J.; Li, R.; Shi, Z. Improved CNN for Predicting Line Heating Forming Deformation of Complex Hull Curved Plate. Materials 2025, 18, 5318. https://doi.org/10.3390/ma18235318
Wang S, Jia H, Fu Y, Wang J, Li R, Shi Z. Improved CNN for Predicting Line Heating Forming Deformation of Complex Hull Curved Plate. Materials. 2025; 18(23):5318. https://doi.org/10.3390/ma18235318
Chicago/Turabian StyleWang, Shun, Haohao Jia, Yuxuan Fu, Ji Wang, Rui Li, and Zhishuo Shi. 2025. "Improved CNN for Predicting Line Heating Forming Deformation of Complex Hull Curved Plate" Materials 18, no. 23: 5318. https://doi.org/10.3390/ma18235318
APA StyleWang, S., Jia, H., Fu, Y., Wang, J., Li, R., & Shi, Z. (2025). Improved CNN for Predicting Line Heating Forming Deformation of Complex Hull Curved Plate. Materials, 18(23), 5318. https://doi.org/10.3390/ma18235318





