Direct Fabrication of Inclined-Sidewall Microgrooves with Shaped Flat-Top Beams
Abstract
1. Introduction
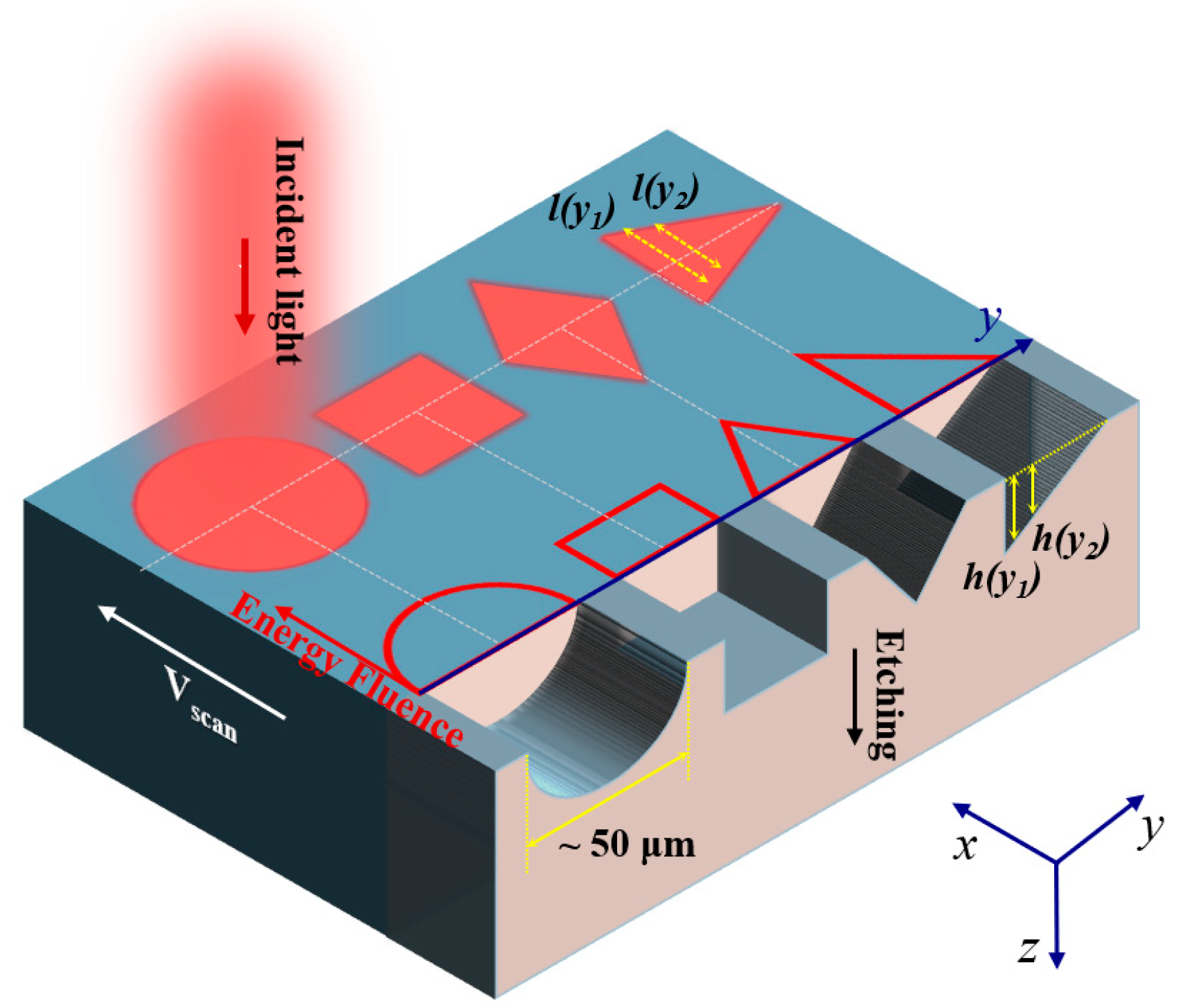
2. Theoretical Model
2.1. Working Principle of Shaped Beam for Microgroove Fabrication
2.2. Optimization of Beam Shaping Phase
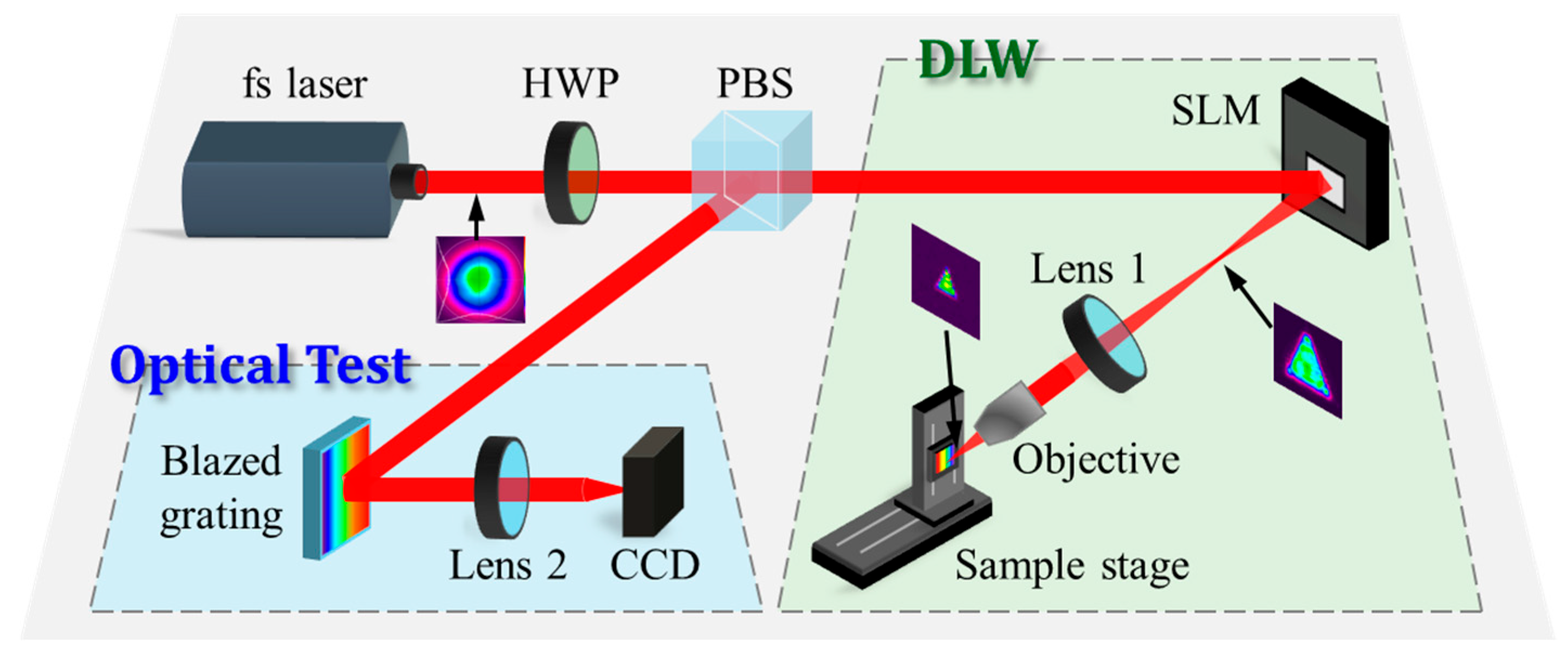
3. Experimental Setup
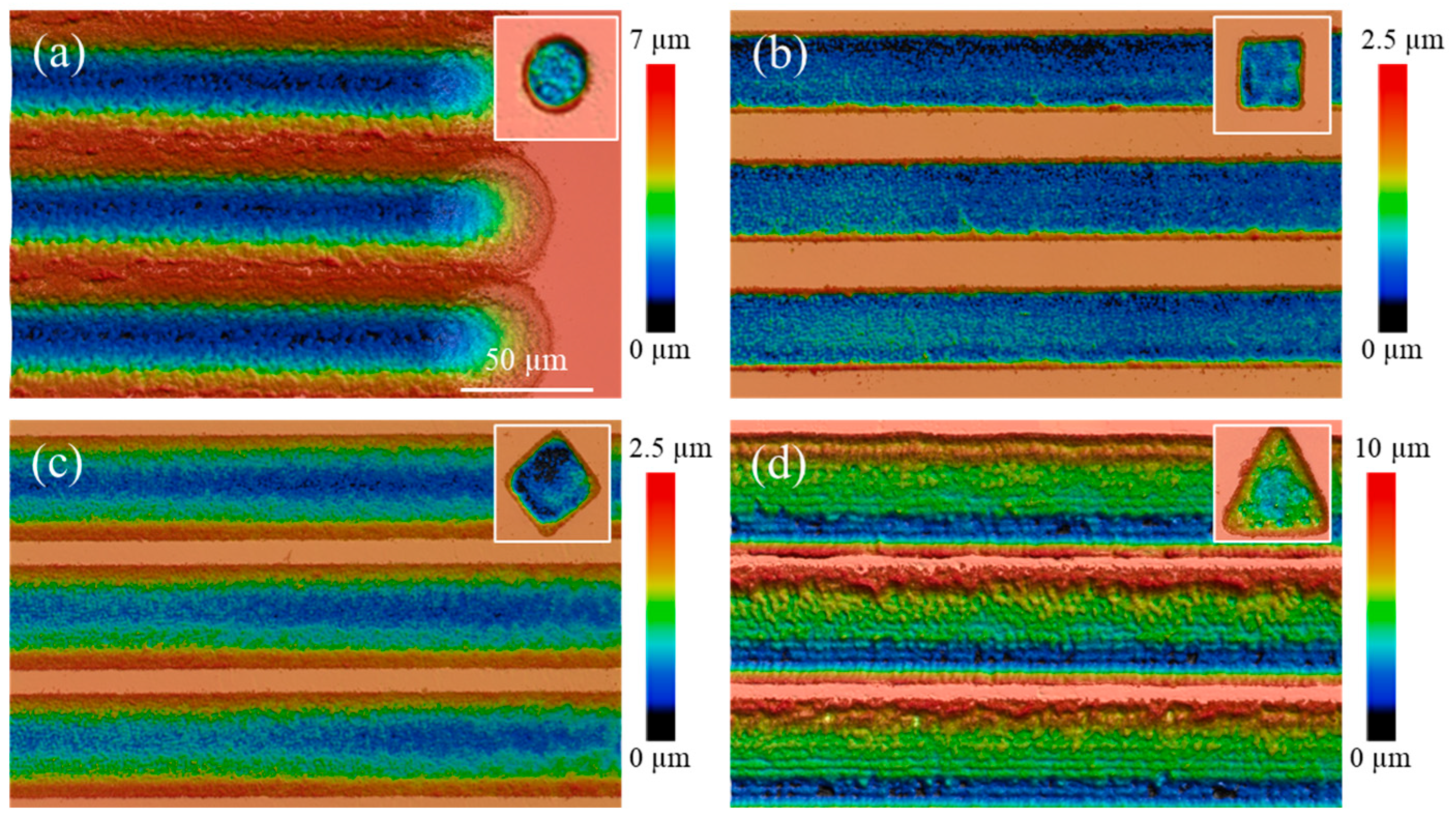
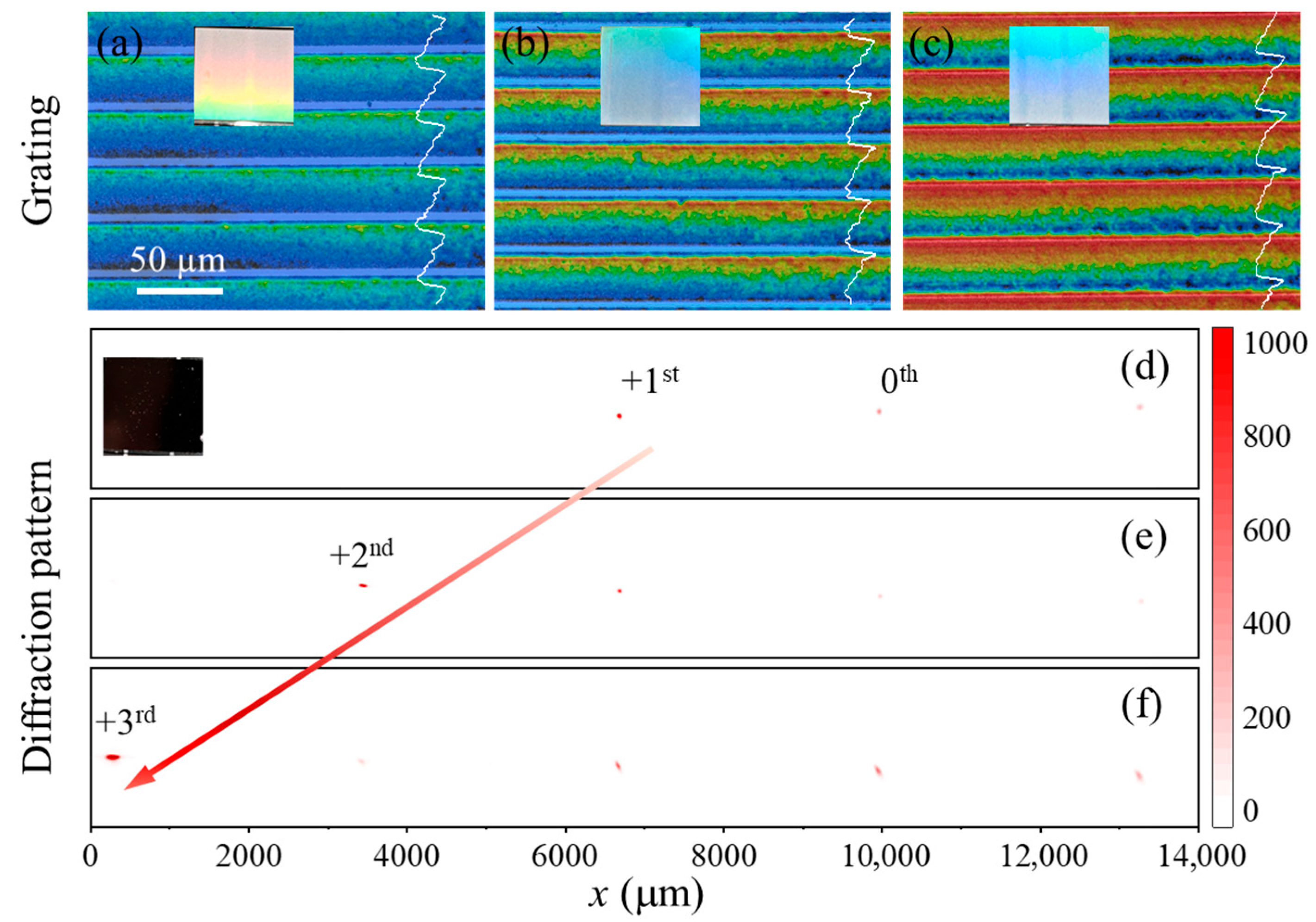
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Luo, H.; Zhang, Y.; Yu, J.; Dong, X.; Zhou, T. Additive, Subtractive and Formative Manufacturing of Glass-Based Functional Micro/Nanostructures: A Comprehensive Review. Mater. Des. 2023, 233, 112285. [Google Scholar] [CrossRef]
- Ma, J.; Zhang, H.; Ye, T.; Wang, S.; Yang, Z.-B.; Jia, Z. New Method of Continuous-Wave Laser Ablation for Processing Microgroove with Variable Cross-Section. Opt. Laser Technol. 2024, 170, 110292. [Google Scholar] [CrossRef]
- Dai, X.; Sun, N.; Nielsen, S.O.; Stogin, B.B.; Wang, J.; Yang, S.; Wong, T.-S. Hydrophilic Directional Slippery Rough Surfaces for Water Harvesting. Sci. Adv. 2018, 4, eaaq0919. [Google Scholar] [CrossRef]
- Li, Q.; Yang, S.; Ying, Y.; Liu, Y.; Wen, R.; Miljkovic, N.; Ma, X. Scalable Photothermal Superhydrophobic Deicing Coating with Mechanochemical-Thermal Robustness. ACS Appl. Mater. Interfaces 2025, 17, 54302–54313. [Google Scholar] [CrossRef]
- Veiko, V.P.; Karlagina, Y.Y.; Egorova, E.E.; Zernitskaya, E.A.; Kuznetsova, D.S.; Elagin, V.V.; Zagaynova, E.V.; Odintsova, G.V. In Vitro Investigation of Laser-Induced Microgrooves on Titanium Surface. J. Phys. Conf. Ser. 2020, 1571, 012010. [Google Scholar] [CrossRef]
- Cong, M.; Wu, X.; Zhu, L.; Gu, G.; Ding, F.; Li, G.; Shi, H. Anisotropic Microtopography Surface of Chitosan Scaffold Regulating Skin Precursor-Derived Schwann Cells towards Repair Phenotype Promotes Neural Regeneration. Regen. Biomater. 2024, 11, rbae005. [Google Scholar] [CrossRef]
- Linklater, D.; Karlagina, Y.; De Sousa, K.M.; Heath, D.E.; Radaev, M.; Chichkov, B.N.; Romanova, G.V.; Veiko, V.P.; Ivanova, E.P. Osteon-Mimetic Laser-Structured Ti-6Al-4V Supports for Guided Stem Cell Growth. Surf. Interfaces 2025, 56, 105503. [Google Scholar] [CrossRef]
- Wang, X.; Ye, C.; Tang, Q.; Yu, H.; Wang, J.; Fu, G.; Ren, K.; Yu, L.; Ji, J. Drop-Shaped Microgrooves Guide Unidirectional Cell Migration for Enhanced Endothelialization. Nat. Commun. 2025, 16, 1928. [Google Scholar] [CrossRef] [PubMed]
- Dai, L.; Jiao, W.; Yao, H.; Liu, X. New-Generation Nanomaterials-Mediated Micro/Nanoscale Thermal Therapy. Magn. Med. 2025, 1, 100006. [Google Scholar] [CrossRef]
- Choi, B.; Oh, J.Y.; Kim, D.; Lee, D.W.; Seo, D. Nano/Microgroove Zirconium-doped Lanthanum Oxide Film with Self-aligned Molecules for Liquid Crystal Device Application. Surf. Interface Anal. 2024, 56, 743–750. [Google Scholar] [CrossRef]
- Lee, D.W.; Kim, T.-H.; Kim, Y.K.; Seo, D.-S. Uniform Molecular Alignment on Ag-Doped Nickel Oxide Films. Nanomaterials 2025, 15, 449. [Google Scholar] [CrossRef]
- Toney, M.F.; Russell, T.P.; Logan, J.A.; Kikuchi, H.; Sands, J.M.; Kumar, S.K. Near-Surface Alignment of Polymers in Rubbed Films. Nature 1995, 374, 709–711. [Google Scholar] [CrossRef]
- Kikuchi, H.; Logan, J.A.; Yoon, D.Y. Study of Local Stress, Morphology, and Liquid-crystal Alignment on Buffed Polyimide Surfaces. J. Appl. Phys. 1996, 79, 6811–6817. [Google Scholar] [CrossRef]
- Lin, G.; Shi, H.; Liu, X.; Wang, Z.; Zhang, H.; Zhang, J. Tool Wear on Machining of Difficult-to-Machine Materials: A Review. Int. J. Adv. Manuf. Technol. 2024, 134, 989–1014. [Google Scholar] [CrossRef]
- Gao, X.; Wang, H.; Zhu, G.; Chang, Z.; Guo, N.; Wang, Z.; Zhu, L. Mechanical and Fatigue Properties of Micro-Groove Structure Formed by Multi-Pass Rolling. J. Braz. Soc. Mech. Sci. Eng. 2022, 44, 164. [Google Scholar] [CrossRef]
- Mahajan, P.; Patil, J.; Mishra, S. Fabrication of Serpentine Micro-Channels Using the Micro-Incremental Forming (μ-ISF) Process: Insights on Microstructure and Texture Evolution. J. Manuf. Process. 2025, 143, 151–159. [Google Scholar] [CrossRef]
- Ullah, N.; Rehan, M.; Farooq, M.U.; Li, H.; Yip, W.S.; To, S.S. A Comprehensive Review of Micro-Milling: Fundamental Mechanics, Challenges, and Future Prospective. Int. J. Adv. Manuf. Technol. 2025, 137, 4309–4351. [Google Scholar] [CrossRef]
- Zhao, L.; Zhang, J.; Zhang, J.; Dai, H.; Hartmaier, A.; Sun, T. Numerical Simulation of Materials-Oriented Ultra-Precision Diamond Cutting: Review and Outlook. Int. J. Extreme Manuf. 2023, 5, 022001. [Google Scholar] [CrossRef]
- Wang, S.; Wang, S.; Zhao, Q. Subsurface Damage in Sapphire Ultra-Precision Grinding. J. Manuf. Process. 2024, 129, 215–237. [Google Scholar] [CrossRef]
- Zhang, H.; Qian, J.; Hong, L. Etching Conditions Effect on Anisotropic Properties of Sapphire. J. Cryst. Growth 2023, 622, 127402. [Google Scholar] [CrossRef]
- Kim, S.; Oh, N.; Lee, M.; Kim, S.; Leesungbok, R.; Lee, S. Surface Microgrooves and Acid Etching on Titanium Substrata Alter Various Cell Behaviors of Cultured Human Gingival Fibroblasts. Clin. Oral Implants Res. 2009, 20, 262–272. [Google Scholar] [CrossRef] [PubMed]
- Shen, T.; Si, J.; Chen, T.; Zhuang, Y.; Hou, X. Fabrication of Microgrooves in PMN-PT Using Femtosecond Laser Irradiation and Acid Etching. Appl. Opt. 2022, 61, 6234. [Google Scholar] [CrossRef]
- Yao, X.; Zhou, T.; Su, X.; Guo, W.; Liu, P.; Yu, Q.; Zhao, B.; Zeng, J. Modeling of Surface Evolution in Plasma Etching for SiC Microgroove Fabrication. Ceram. Int. 2024, 50, 30504–30513. [Google Scholar] [CrossRef]
- Sheng, Y.; Wen, X.; Jia, B.; Gan, Z. Direct Laser Writing on Halide Perovskites: From Mechanisms to Applications. Light Adv. Manuf. 2024, 4, 95–116. [Google Scholar] [CrossRef]
- Yu, K.; Shi, H.; Zhang, P.; Yu, Z.; Yan, H.; Lu, Q. Micro/Nanoengineering of Functionalized Metal Surfaces Based on Short/Ultra-Short-Pulsed Lasers: A Review. J. Mater. Sci. 2024, 59, 1819–1866. [Google Scholar] [CrossRef]
- Yildirim, K.; Nagarajan, B.; Tjahjowidodo, T.; Castagne, S. Review of In-Situ Process Monitoring for Ultra-Short Pulse Laser Micromanufacturing. J. Manuf. Process. 2025, 133, 1126–1159. [Google Scholar] [CrossRef]
- Shin, S. Review of High-Precision Femtosecond Laser Materials Processing for Fabricating Microstructures: Effects of Laser Parameters on Processing Quality, Ablation Efficiency, and Microhole Shape. J. Laser Appl. 2024, 36, 041201. [Google Scholar] [CrossRef]
- Shimotsuma, Y.; Kazansky, P.G.; Qiu, J.; Hirao, K. Self-Organized Nanogratings in Glass Irradiated by Ultrashort Light Pulses. Phys. Rev. Lett. 2003, 91, 247405. [Google Scholar] [CrossRef]
- Pfeifer, M.; Weissmantel, S.; Reisse, G. Direct Laser Fabrication of Blaze Gratings in Fused Silica. Appl. Phys. A 2013, 112, 61–64. [Google Scholar] [CrossRef]
- Qiu, P.; Guo, Y.; Huang, L.; Li, J.; Huang, J.; Wang, M.; Zhang, Z.; Xu, S. Patterned Laser Ablation of Microgrooves with Controllable Cross-Sections. Adv. Mater. Technol. 2023, 8, 2300333. [Google Scholar] [CrossRef]
- Qiu, P.; Li, J.; Yuan, D.; Xin, Z.; Huang, J.; Xu, S. Adaptive Beam-Shaping Enabled High-Precision Patterned Laser Micro-Grooving. Int. J. Extreme Manuf. 2025, 7, 065002. [Google Scholar] [CrossRef]
- Chen, W.; Mao, J.; Chen, K.; Li, X.; Tan, Y.; Li, M.; Zhang, L. Generation of High Uniformity Flat-Top Beams by Reconstructing the Amplitude Distribution at Descending Edges. Opt. Laser Technol. 2025, 186, 112776. [Google Scholar] [CrossRef]
- Sanner, N.; Huot, N.; Audouard, E.; Larat, C.; Huignard, J.-P.; Loiseaux, B. Programmable Focal Spot Shaping of Amplified Femtosecond Laser Pulses. Opt. Lett. 2005, 30, 1479. [Google Scholar] [CrossRef]
- Zhang, H.; Xie, J.; Liu, J.; Wang, Y. Elimination of a Zero-Order Beam Induced by a Pixelated Spatial Light Modulator for Holographic Projection. Appl. Opt. 2009, 48, 5834–5841. [Google Scholar] [CrossRef]
- Chicbkov, B.N.; Momma, C.; Nolte, S. Femtosecond, Picosecond and Nanosecond Laser Ablation of Solids. Appl. Phys. A 1996, 63, 109–115. [Google Scholar] [CrossRef]
- Jee, Y.; Becker, M.F.; Walser, R.M. Laser-Induced Damage on Single-Crystal Metal Surfaces. J. Opt. Soc. Am. B 1988, 5, 648. [Google Scholar] [CrossRef]
- Bulgakov, A.V.; Sládek, J.; Hrabovský, J.; Mirza, I.; Marine, W.; Bulgakova, N.M. Dual-Wavelength Femtosecond Laser-Induced Single-Shot Damage and Ablation of Silicon. Appl. Surf. Sci. 2024, 643, 158626. [Google Scholar] [CrossRef]
- Green, M.A. Self-Consistent Optical Parameters of Intrinsic Silicon at 300K Including Temperature Coefficients. Sol. Energy Mater. Sol. Cells 2008, 92, 1305–1310. [Google Scholar] [CrossRef]
- Pang, H.; Liu, W.; Cao, A.; Deng, Q. Speckle-Reduced Holographic Beam Shaping with Modified Gerchberg–Saxton Algorithm. Opt. Commun. 2019, 433, 44–51. [Google Scholar] [CrossRef]
- Ding, H.; Mao, J.; Chen, W.; Chen, K.; Li, X.; Tan, Y.; Li, M.; Zhang, L. Optimization Algorithm for Flattop Beam Shaping Using Analytically Initial Phase. IEEE Photonics Technol. Lett. 2024, 36, 1285–1288. Available online: https://ieeexplore.ieee.org/document/10594813 (accessed on 4 September 2025). [CrossRef]
- Wang, Y.; Zheng, Y.; Gong, W.; Si, K. Speckle Suppression in Arbitrary Parallel Holographic Illumination by the Spatial Frequency Regaining Method. Opt. Lett. 2023, 48, 4189. [Google Scholar] [CrossRef] [PubMed]


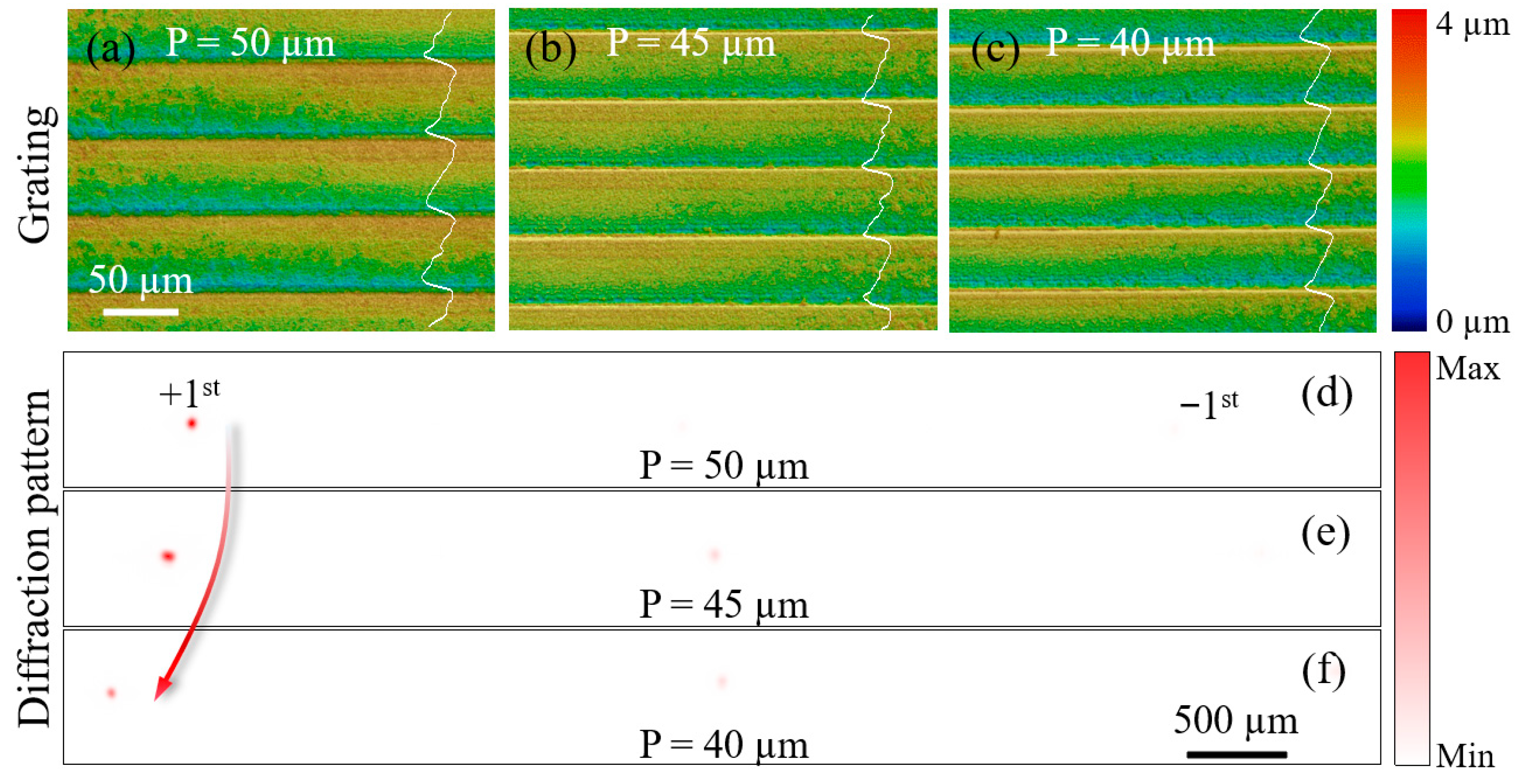
| Period (μm) | Pulse Energy (μJ) | Grating Depth (μm) | Diffraction Angle (°) | Deviation from Theory | |||
|---|---|---|---|---|---|---|---|
| Designed | Measured | Designed | Measured | Designed | Measured | ||
| 50 | 49.9 | 4.48 | 0.52 | 0.56 | 1.18 | 1.22 | 3% |
| 45 | 45.8 | 3.62 | 0.57 | 1.31 | 1.31 | 0% | |
| 40 | 39.2 | 2.94 | 0.55 | 1.47 | 1.5 | 2% | |
| Target Diffraction Order | Diffraction Angle (°) | Scan Speed (mm/s) | Grating Depth (μm) | ||
|---|---|---|---|---|---|
| Designed | Measured | Designed | Measured | ||
| 1 | 1.47 | 1.48 | 6 | 0.52 | 0.53 |
| 2 | 2.95 | 2.95 | 3 | 1.03 | 1.03 |
| 3 | 4.43 | 4.52 | 2 | 1.54 | 1.58 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mao, J.; Chen, W.; Chen, K.; Li, X.; Tan, Y.; Li, M.; Zhang, L. Direct Fabrication of Inclined-Sidewall Microgrooves with Shaped Flat-Top Beams. Materials 2025, 18, 5204. https://doi.org/10.3390/ma18225204
Mao J, Chen W, Chen K, Li X, Tan Y, Li M, Zhang L. Direct Fabrication of Inclined-Sidewall Microgrooves with Shaped Flat-Top Beams. Materials. 2025; 18(22):5204. https://doi.org/10.3390/ma18225204
Chicago/Turabian StyleMao, Jianyong, Wenqiang Chen, Kai Chen, Xun Li, Yu Tan, Ming Li, and Lei Zhang. 2025. "Direct Fabrication of Inclined-Sidewall Microgrooves with Shaped Flat-Top Beams" Materials 18, no. 22: 5204. https://doi.org/10.3390/ma18225204
APA StyleMao, J., Chen, W., Chen, K., Li, X., Tan, Y., Li, M., & Zhang, L. (2025). Direct Fabrication of Inclined-Sidewall Microgrooves with Shaped Flat-Top Beams. Materials, 18(22), 5204. https://doi.org/10.3390/ma18225204







