Fatigue Behavior and Life Prediction of L-PBF Ti64 with Critical Plane Based Small Building Direction Variations Under Non-Proportional and Multiaxial Loading
Abstract
1. Introduction
2. Materials and Experimental Procedures
3. Mechanical Behavior and Fatigue Fracture Mechanism of L-PBF Ti-6Al-4V with Different Building Directions
3.1. Static and Dynamic Mechanical Properties
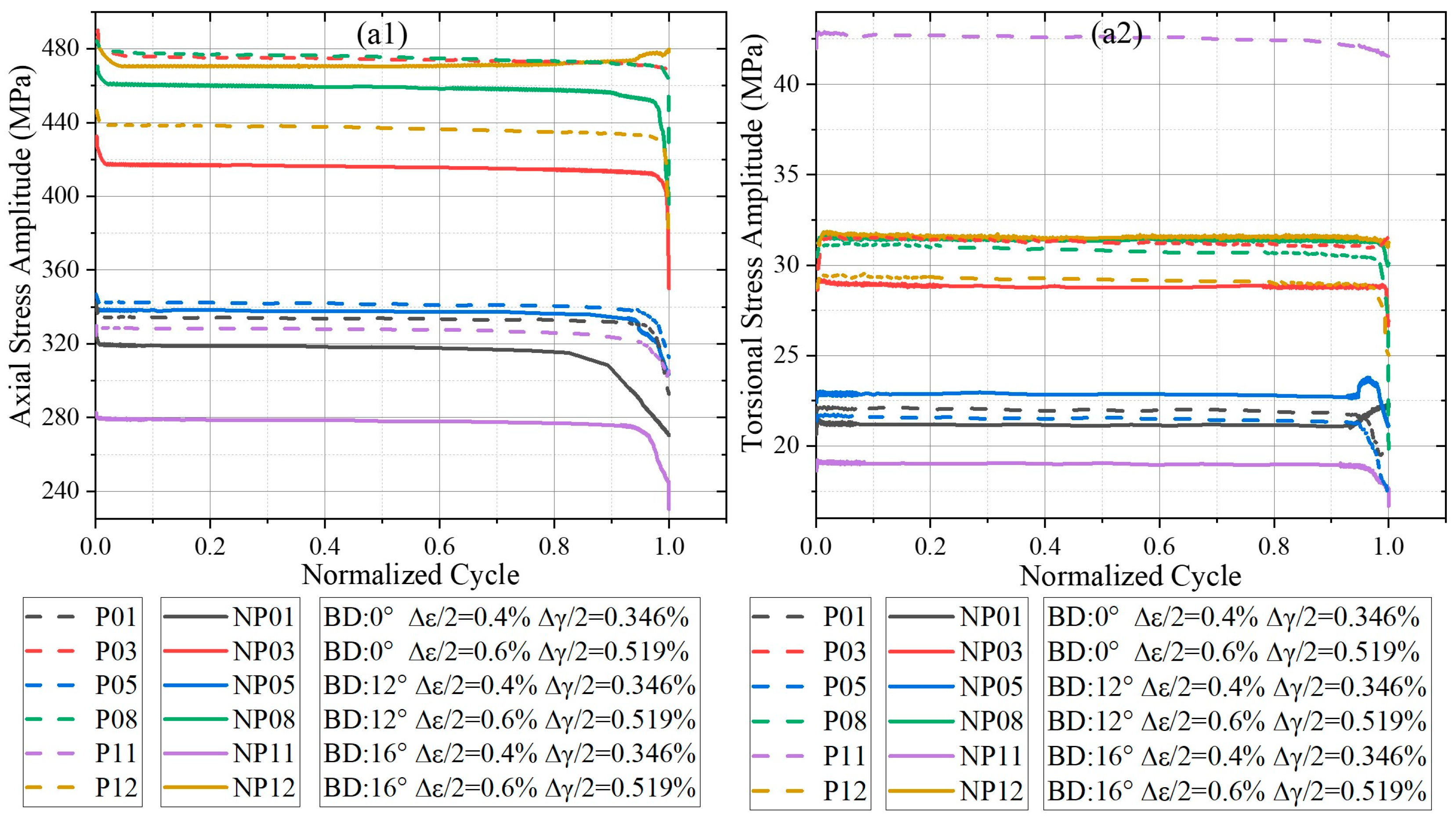
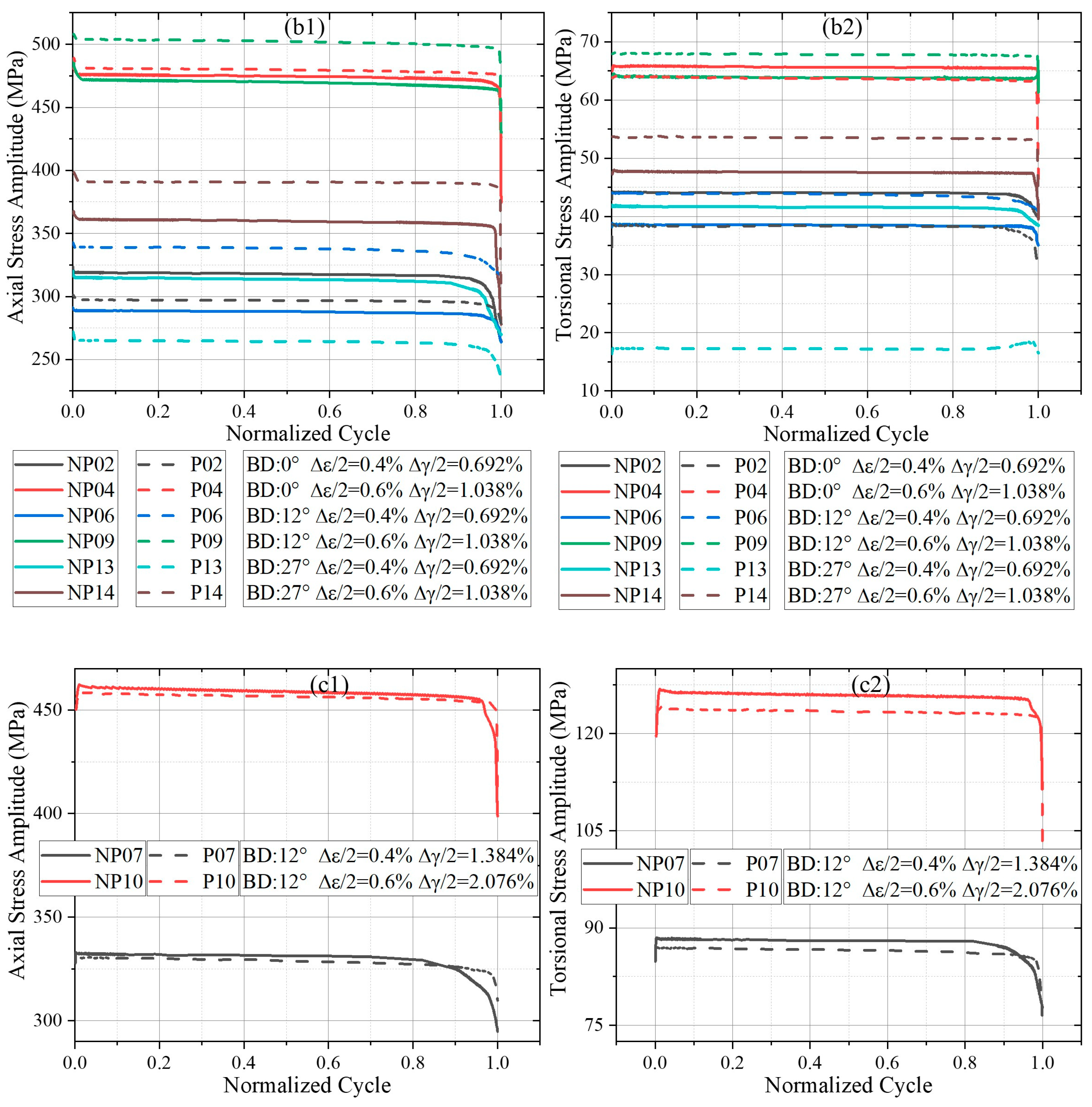
3.2. Cyclic Softening/Hardening Characteristics
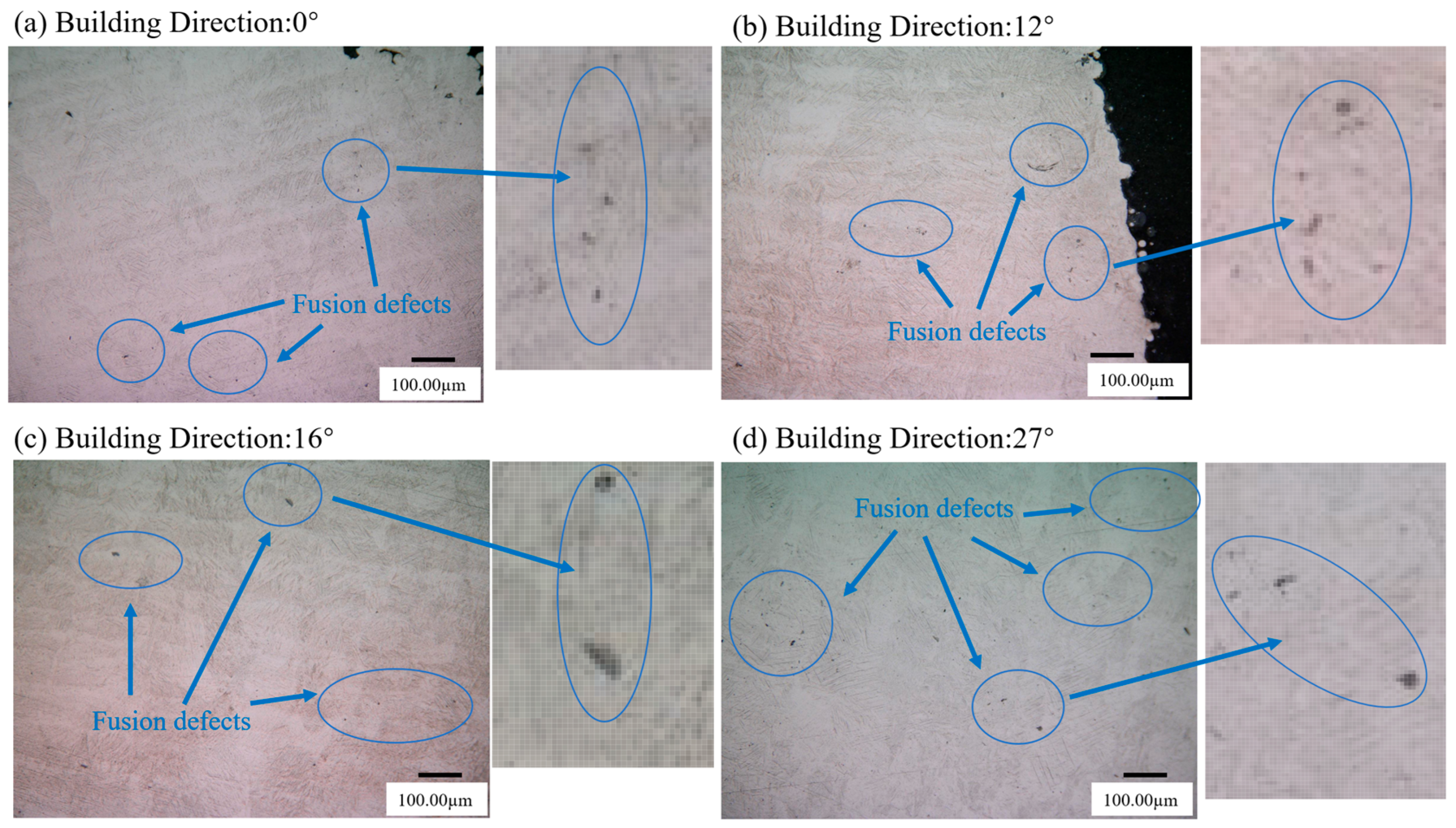
3.3. Fatigue Fracture Mechanism of L-PBF Ti-6Al-4V
4. MLCF Life Prediction of L-PBF Ti-6Al-4V
4.1. Fatigue Life Distribution of L-PBF Ti-6Al-4V
4.2. MLCF Life Prediction Based on Analysis Formula Method
4.2.1. Fatemi–Socie Model
4.2.2. Proposed KBMP Model
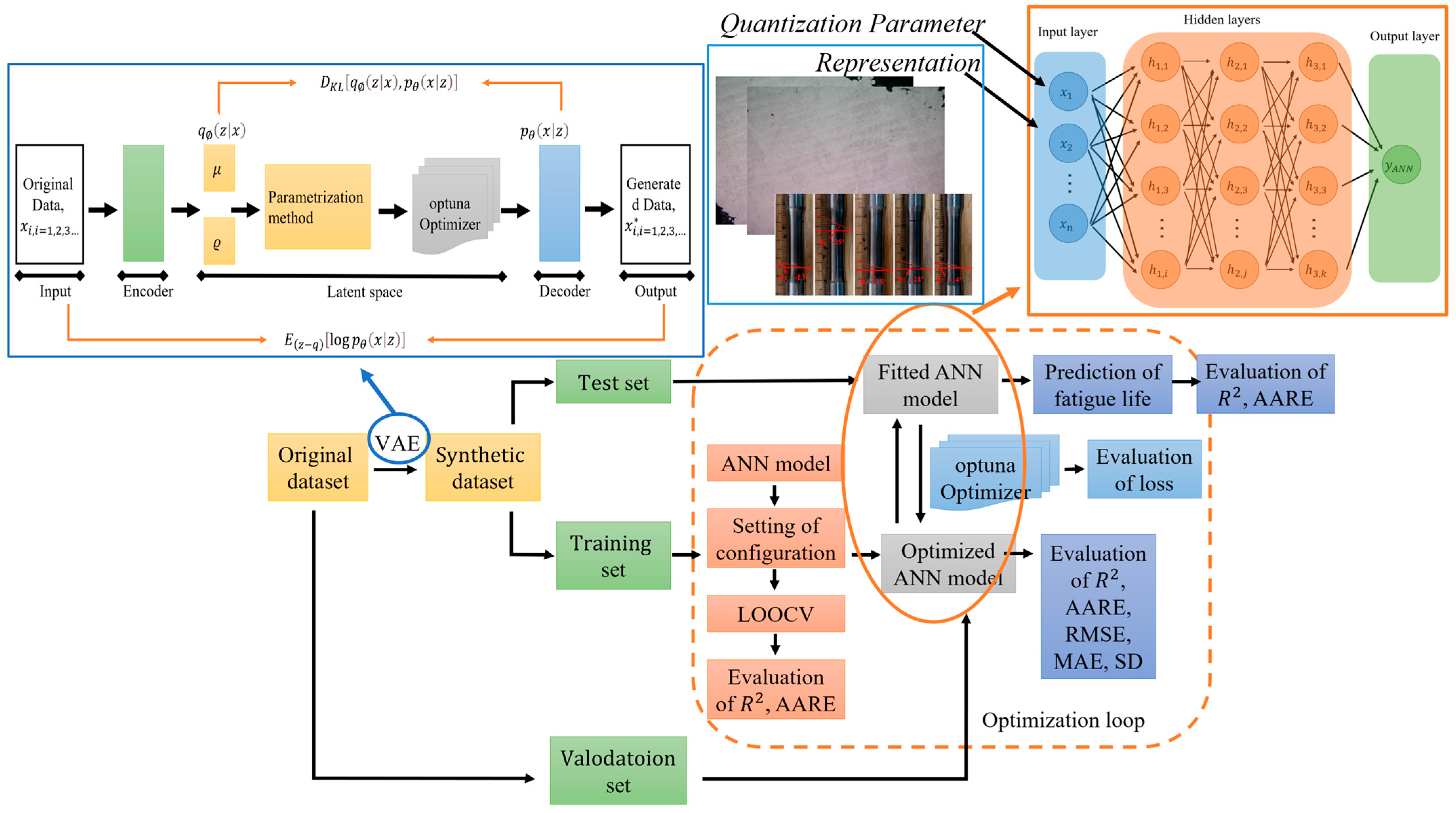
4.3. MLCF Life Prediction Based on Hybrid Physics and Data-Driven Method
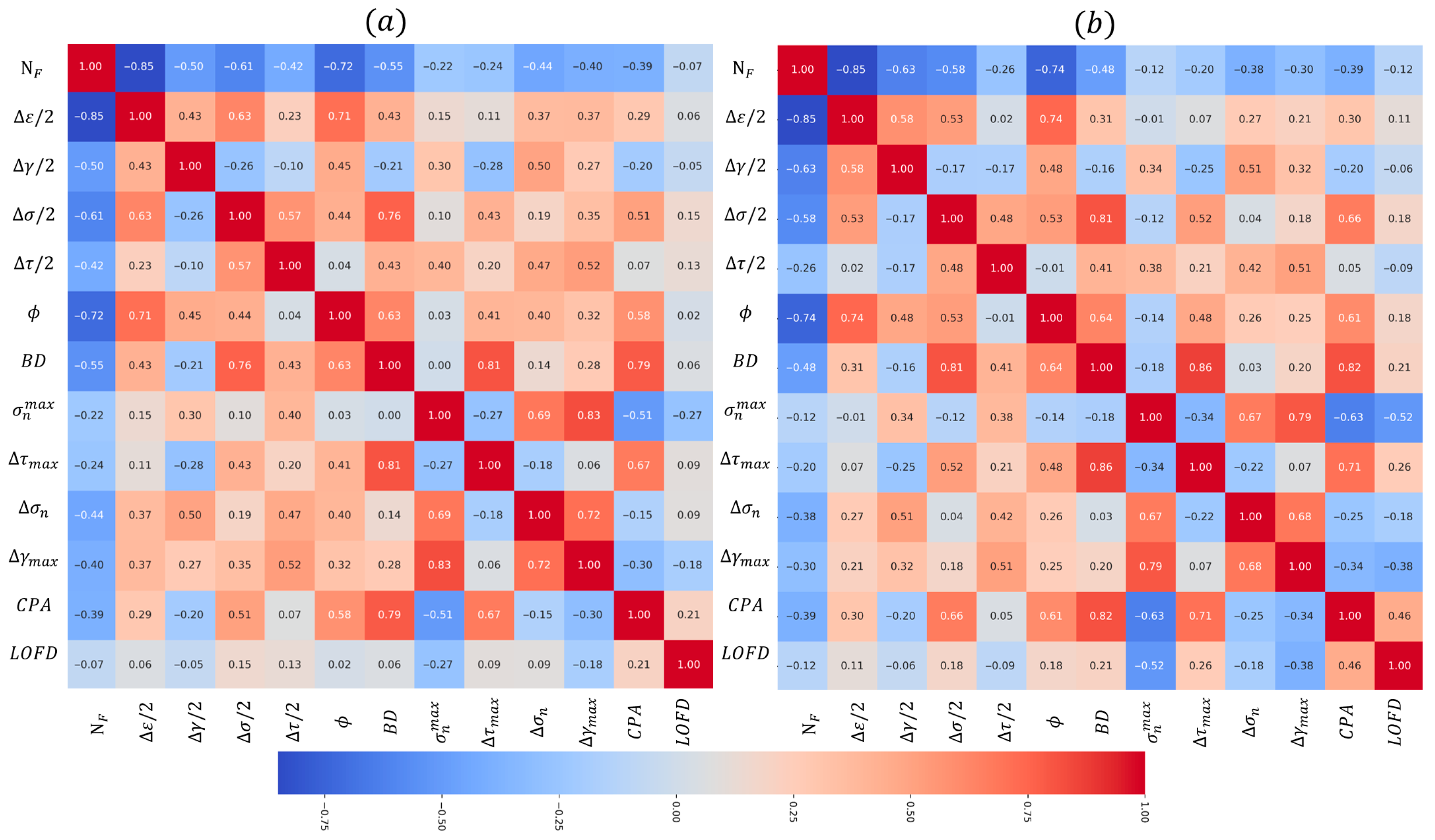
4.3.1. Influencing Parameters on MLCF Life of L-PBF Ti-6Al-4V
| Input Features | Symbol | Example | |
|---|---|---|---|
| Load-based parameters | Axial and torsional strain amplitude (%) | , | (0.4, …, 2.976) |
| Axial and torsional stress amplitude (MPa) | (30, …, 395) | ||
| Phase angle (°) | (0, …, 90) | ||
| Critical plane-based parameters | Maximum shear strain range (%) and Maximum normal stress (MPa) [30] | , | (0.26, …, 378.15) |
| Maximum shear and Normal stress range (MPa) [43] | , | (37.05, …, 703.77) | |
| L-PBF-based parameters | Building Direction (°) | BD | (0, …, 27) |
| Crack Propagation Angle (°) | CPA | (13, …, 29) | |
| Lack-of-Fusion Defects Density (Pixel/Pixel) | LOFD | (1 × 10−4, …, 1 × 10−3) |
4.3.2. Artificial Neural Network with Data Expansion
4.3.3. Hyperparameter Optimization
| λ | Phase Angle | FS/ | KBMP/ | Phase Angle | FS/ | KBMP/ |
|---|---|---|---|---|---|---|
| 0.865 | 0 | −0.057 | 1.30 | 90 | −0.054 | 0.94 |
| 1.73 | −0.065 | 1.36 | −0.069 | 1.73 | ||
| 3.46 | −0.084 | 1.21 | −0.071 | 1.62 | ||
| Data Expansion Model | Latent_dim | 3 | Learning_rate | 5.06 × 10−3 | Batch_size | 28 |
| Hidden_dim1 | Hidden_dim2 | Hidden_dim3 | Learning_rate | Training Time per Epoch | Epoch at Convergence | |
| Model1 | 169 | 128 | 54 | 7.653 × 10−4 | 11 s | 185 |
| Model2 | 442 | 153 | 75 | 3.713 × 10−3 | 24 s | 156 |
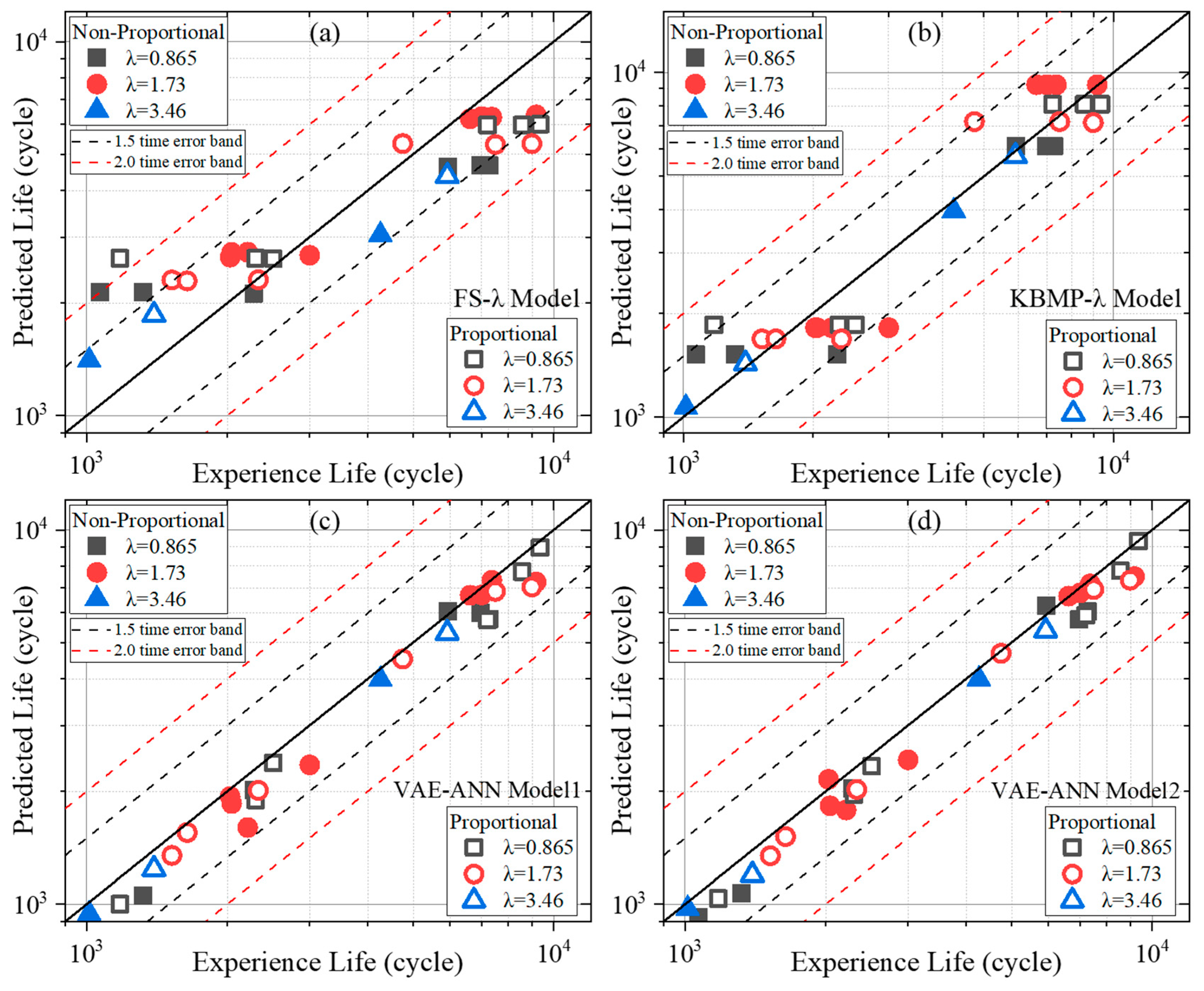
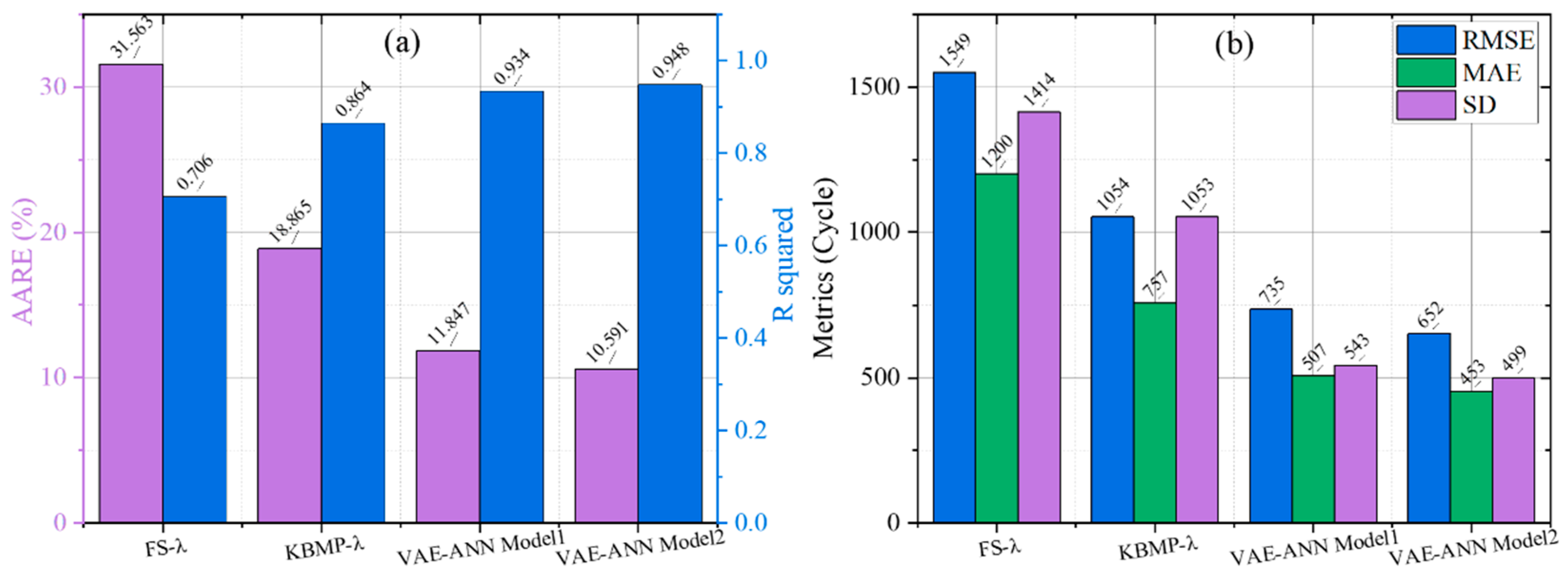
4.4. Comparison of Life Prediction Performance of Different Models
5. Conclusions
- (1)
- L-PBF Ti-6Al-4V exhibits three-stage cyclic softening with occasional initial hardening. Under non-proportional loading, L-PBF Ti-6Al-4V exhibits non-proportional softening, in contrast to the non-proportional hardening typically observed in conventionally manufactured titanium alloys.
- (2)
- Analytical fatigue life prediction models can provide reasonable estimates for L-PBF Ti-6Al-4V within 20% error band. The proposed KBMP model demonstrates superior performance over the traditional FS model.
- (3)
- The hybrid VAE-ANN model, integrating physics-based parameters and macro-micro characterization, predicts MLCF life across different BDs with high accuracy within 10% error band and eliminates the horizontal data point limitations observed in formula-based models.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| AARE | Average Absolute Relative Error |
| AM | Additive Manufacturing |
| ANN | Artificial Neural Network |
| BD | Building Direction |
| CM | Conventional Manufacturing |
| CMA-ES | Covariance Matrix Adaptation Evolution Strategy |
| CPA | Crack Propagation Angle |
| FS | Fatemi–Socie |
| GP | Gaussian Process |
| LCF | Low Cycle Fatigue |
| L-DED | Laser Direct Energy Deposition |
| LOF | Lack-of-Fusion |
| LOFD | Lack-of-Fusion Defects Density |
| L-PBF | Laser Powder Bed Fusion |
| MAE | Mean Absolute Error |
| ML | Machine Learning |
| MLCF | Multiaxial Low-Cycle Fatigue |
| OM | Optical Microscopy |
| PCC | Pearson Correlation Coefficient |
| RMSE | Root Mean Squared Error |
| SD | Standard Deviation |
| SEM | Scanning Electron Microscopy |
| SVM | Support Vector Machine |
| VAE | Variational Autoencoder |
References
- Dong, M.; Zhang, Y.; Zhou, W.; Chen, P.; Zhou, Z.; Kanetaka, H.; Ishimoto, T.; Koizumi, Y.; Nakano, T.; Nomura, N. Laser Additive Manufacturing of a Carbon-Supersaturated β-Ti Alloy for Biomaterial Application. Addit. Manuf. Lett. 2024, 11, 100233. [Google Scholar] [CrossRef]
- Chen, Z.; Dai, J.; Yang, L.; Shen, S.; Li, S.; Xie, Q.; Xu, C. Numerical Simulation of Keyhole-Induced Pores for TA15 in Laser Powder Bed Fusion (L-PBF). Infrared Phys. Technol. 2024, 140, 105408. [Google Scholar] [CrossRef]
- Moeinfar, K.; Khodabakhshi, F.; Kashani-bozorg, S.F.; Mohammadi, M.; Gerlich, A.P. A Review on Metallurgical Aspects of Laser Additive Manufacturing (LAM): Stainless Steels, Nickel Superalloys, and Titanium Alloys. J. Mater. Res. Technol. 2022, 16, 1029–1068. [Google Scholar] [CrossRef]
- Lin, Y.; Shi, W.; Li, J.; Liu, Y.; Liu, S.; Li, J. Evaluation of Mechanical Properties of Ti–6Al–4V BCC Lattice Structure with Different Density Gradient Variations Prepared by L-PBF. Mater. Sci. Eng. A 2023, 872, 144986. [Google Scholar] [CrossRef]
- Chang, L.; Ma, T.; Zhou, B.; Wen, J.; He, X.; Zhou, C. Comprehensive Investigation of Fatigue Behavior and a New Strain-Life Model for CP-Ti under Different Loading Conditions. Int. J. Fatigue 2019, 129, 105220. [Google Scholar] [CrossRef]
- Attar, H.; Bermingham, M.J.; Ehtemam-Haghighi, S.; Dehghan-Manshadi, A.; Kent, D.; Dargusch, M.S. Evaluation of the Mechanical and Wear Properties of Titanium Produced by Three Different Additive Manufacturing Methods for Biomedical Application. Mater. Sci. Eng. A 2019, 760, 339–345. [Google Scholar] [CrossRef]
- Xu, W.; Xiao, S.; Lu, X.; Chen, G.; Liu, C.; Qu, X. Fabrication of Commercial Pure Ti by Selective Laser Melting Using Hydride-Dehydride Titanium Powders Treated by Ball Milling. J. Mater. Sci. Technol. 2019, 35, 322–327. [Google Scholar] [CrossRef]
- Hu, D.; Pan, J.; Mi, D.; Mao, J.; Li, W.; Fu, Y.; Wang, R. Prediction of Anisotropic LCF Behavior for SLM Ti-6Al-4V Considering the Spatial Orientation of Defects. Int. J. Fatigue 2022, 158, 106734. [Google Scholar] [CrossRef]
- Lee, S.; Pegues, J.W.; Shamsaei, N. Fatigue Behavior and Modeling for Additive Manufactured 304L Stainless Steel: The Effect of Surface Roughness. Int. J. Fatigue 2020, 141, 105856. [Google Scholar] [CrossRef]
- Rigon, D.; Coppola, F.; Meneghetti, G. Fracture Mechanics-Based Analysis of the Fatigue Limit of Ti-6Al-4V Alloy Specimens Manufactured by SLM in as-Built Surface Conditions by Means of Areal Measurements. Eng. Fract. Mech. 2024, 295, 109720. [Google Scholar] [CrossRef]
- Nicoletto, G.; Konečná, R.; Frkáň, M.; Riva, E. Surface Roughness and Directional Fatigue Behavior of As-Built EBM and DMLS Ti-6Al-4V. Int. J. Fatigue 2018, 116, 140–148. [Google Scholar] [CrossRef]
- Fatemi, A.; Molaei, R.; Sharifimehr, S.; Phan, N.; Shamsaei, N. Multiaxial Fatigue Behavior of Wrought and Additive Manufactured Ti-6Al-4V Including Surface Finish Effect. Int. J. Fatigue 2017, 100, 347–366. [Google Scholar] [CrossRef]
- Fatemi, A.; Molaei, R.; Sharifimehr, S.; Shamsaei, N.; Phan, N. Torsional Fatigue Behavior of Wrought and Additive Manufactured Ti-6Al-4V by Powder Bed Fusion Including Surface Finish Effect. Int. J. Fatigue 2017, 99, 187–201. [Google Scholar] [CrossRef]
- Kethamukkala, K.; Meng, C.; Chen, J.; Liu, Y. Crack Growth-Based Life Prediction for Additively Manufactured Metallic Materials Considering Surface Roughness. Int. J. Fatigue 2023, 176, 107914. [Google Scholar] [CrossRef]
- Foti, P.; Razavi, N.; Fatemi, A.; Berto, F. Multiaxial Fatigue of Additively Manufactured Metallic Components: A Review of the Failure Mechanisms and Fatigue Life Prediction Methodologies. Prog. Mater. Sci. 2023, 137, 101126. [Google Scholar] [CrossRef]
- Cao, S.; Zhang, H.; Hu, J.; Li, C.; Li, B. Fatigue Life Prediction Model for Shot-Peened Laser Powder Bed Fused 304L Steel Considering Residual Stress Relaxation and Defect Distribution. Eng. Fail. Anal. 2024, 162, 108423. [Google Scholar] [CrossRef]
- Zhou, T.; Sun, X.; Chen, X. A Multiaxial Low-Cycle Fatigue Prediction Method under Irregular Loading by ANN Model with Knowledge-Based Features. Int. J. Fatigue 2023, 176, 107868. [Google Scholar] [CrossRef]
- Horňas, J.; Běhal, J.; Homola, P.; Senck, S.; Holzleitner, M.; Godja, N.; Pásztor, Z.; Hegedüs, B.; Doubrava, R.; Růžek, R.; et al. Modelling Fatigue Life Prediction of Additively Manufactured Ti-6Al-4V Samples Using Machine Learning Approach. Int. J. Fatigue 2023, 169, 107483. [Google Scholar] [CrossRef]
- ASTM F1472-23; Standard Specification for Wrought Titanium-6Aluminum-4Vanadium Alloy for Surgical Implant Applications (UNS R56400). ASTM International: West Conshohocken, PA, USA, 2023.
- ASTM F2924-14; Standard Specification for Additive Manufacturing Titanium-6 Aluminum-4 Vanadium with Powder Bed Fusion. ASTM International: West Conshohocken, PA, USA, 2021.
- Ma, T.-H.; Chang, L.; Guo, S.; Kong, L.-R.; He, X.-H.; Zhou, C.-Y. Comparison of Multiaxial Low Cycle Fatigue Behavior of CP-Ti under Strain-Controlled Mode at Different Multiaxial Strain Ratios. Int. J. Fatigue 2020, 140, 105818. [Google Scholar] [CrossRef]
- Meggiolaro, M.A.; Castro, J.T.P. de A Deviatoric Tensile-Based Critical Plane Model to Predict Peak/Mean Normal Stress Effects in Multiaxial Fatigue. Int. J. Fatigue 2022, 155, 106615. [Google Scholar] [CrossRef]
- Arora, P.; Gupta, S.K.; Samal, M.K.; Chattopadhyay, J. Validating Generality of Recently Developed Critical Plane Model for Fatigue Life Assessments Using Multiaxial Test Database on Seventeen Different Materials. Fatigue Fract. Eng. Mater. Struct. 2020, 43, 1327–1352. [Google Scholar] [CrossRef]
- Xu, Z.; Liu, A.; Wang, X. Fatigue Performance Differences between Rolled and Selective Laser Melted Ti-6Al-4V Alloys. Mater. Charact. 2022, 189, 111963. [Google Scholar] [CrossRef]
- Pertuz-Comas, A.D.; González-Estrada, O.A.; Martínez-Díaz, E.; Villegas-Bermúdez, D.F.; Díaz-Rodríguez, J.G. Strain-Based Fatigue Experimental Study on Ti–6Al–4V Alloy Manufactured by Electron Beam Melting. J. Manuf. Mater. Process. 2023, 7, 25. [Google Scholar] [CrossRef]
- Skelton, R.P.; Maier, H.J.; Christ, H.-J. The Bauschinger Effect, Masing Model and the Ramberg–Osgood Relation for Cyclic Deformation in Metals. Mater. Sci. Eng. A 1997, 238, 377–390. [Google Scholar] [CrossRef]
- Darlington, J.F.; Booker, J.D. Development of a Design Technique for the Identification of Fatigue Initiating Features. Eng. Fail. Anal. 2006, 13, 1134–1152. [Google Scholar] [CrossRef]
- Shamsaei, N.; Fatemi, A. Effect of Microstructure and Hardness on Non-Proportional Cyclic Hardening Coefficient and Predictions. Mater. Sci. Eng. A 2010, 527, 3015–3024. [Google Scholar] [CrossRef]
- Mises, R.V. Mechanik der festen Körper im plastisch- deformablen Zustand. Nachrichten Von Ges. Wiss. Zu Gött. Math.-Phys. Kl. 1913, 1913, 582–592. [Google Scholar]
- Fatemi, A.; Socie, D.F. A Critical Plane Approach to Multiaxial Fatigue Damage Including Out-of-Phase Loading. Fatigue Fract. Eng. Mater. Struct. 1988, 11, 149–165. [Google Scholar] [CrossRef]
- Brown, M.W.; Miller, K.J. A Theory for Fatigue Failure under Multiaxial Stress-Strain Conditions. Proc. Inst. Mech. Eng. 1973, 187, 745–755. [Google Scholar] [CrossRef]
- Ma, T.-H.; Gao, N.; Chang, L.; He, X.-H.; Zhou, C.-Y. Low-Cycle Fatigue Behavior and Life Prediction of CP-Ti under Non-Proportional and Multiaxial Loading. Eng. Fract. Mech. 2021, 254, 107930. [Google Scholar] [CrossRef]
- Kandil, F.A.; Brown, M.W.; Miller, K.J. Biaxial Low-Cycle Fatigue Fracture of 316 Stainless Steel at Elevated Temperature. Mech. Behav. Nucl. Appl. Stainl. Steel Elev. Temp. 1982, 1, 203–209. [Google Scholar]
- Li, J.; Zhang, P.; Lu, L.; Lv, F.; Miao, X.-T.; Chang, L.; Zhou, B.-B.; He, X.-H.; Zhou, C.-Y. Effect of Pre-Strain on Fatigue Crack Growth Behavior for Commercial Pure Titanium at Ambient Temperature. Int. J. Fatigue 2018, 117, 27–38. [Google Scholar] [CrossRef]
- Reza Kashyzadeh, K.; Ghorbani, S. New Neural Network-Based Algorithm for Predicting Fatigue Life of Aluminum Alloys in Terms of Machining Parameters. Eng. Fail. Anal. 2023, 146, 107128. [Google Scholar] [CrossRef]
- Zhao, B.; Song, J.; Xie, L.; Ma, H.; Li, H.; Ren, J.; Sun, W. Multiaxial Fatigue Life Prediction Method Based on the Back-Propagation Neural Network. Int. J. Fatigue 2023, 166, 107274. [Google Scholar] [CrossRef]
- Xu, L.; Zhang, R.; Hao, M.; Xiong, L.; Jiang, Q.; Li, Z.; Wang, Q.; Wang, X. A Data-Driven Low-Cycle Fatigue Life Prediction Model for Nickel-Based Superalloys. Comput. Mater. Sci. 2023, 229, 112434. [Google Scholar] [CrossRef]
- He, G.; Zhao, Y.; Yan, C. Uncertainty Quantification in Multiaxial Fatigue Life Prediction Using Bayesian Neural Networks. Eng. Fract. Mech. 2024, 298, 109961. [Google Scholar] [CrossRef]
- Dang, L.; He, X.; Tang, D.; Li, Y.; Wang, T. A Fatigue Life Prediction Approach for Laser-Directed Energy Deposition Titanium Alloys by Using Support Vector Regression Based on Pore-Induced Failures. Int. J. Fatigue 2022, 159, 106748. [Google Scholar] [CrossRef]
- Chen, D.; Li, Y.; Liu, K.; Li, Y. A Physics-Informed Neural Network Approach to Fatigue Life Prediction Using Small Quantity of Samples. Int. J. Fatigue 2023, 166, 107270. [Google Scholar] [CrossRef]
- Wang, H.; Li, B.; Gong, J.; Xuan, F.-Z. Machine Learning-Based Fatigue Life Prediction of Metal Materials: Perspectives of Physics-Informed and Data-Driven Hybrid Methods. Eng. Fract. Mech. 2023, 284, 109242. [Google Scholar] [CrossRef]
- Ma, T.-H.; Zhang, W.; Chang, L.; Zhao, J.-P.; Zhou, C.-Y. Study of Hybrid Machine Learning Multiaxial Low-Cycle Fatigue Life Prediction Model of CP-Ti. Fatigue Fract. Eng. Mater. Struct. 2025, 48, 2309–2324. [Google Scholar] [CrossRef]
- Ma, T.-H.; Zhou, C.-Y.; Gao, N.; Chang, L.; He, X.-H. Low Cycle Fatigue Behavior of CP-Ti under Multiaxial Load-Controlled Mode at Different Multiaxial Stress Ratios. Int. J. Fatigue 2022, 160, 106868. [Google Scholar] [CrossRef]
- Nowell, D.; Nowell, P.W. A Machine Learning Approach to the Prediction of Fretting Fatigue Life. Tribol. Int. 2020, 141, 105913. [Google Scholar] [CrossRef]
- Durodola, J.F.; Ramachandra, S.; Gerguri, S.; Fellows, N.A. Artificial Neural Network for Random Fatigue Loading Analysis Including the Effect of Mean Stress. Int. J. Fatigue 2018, 111, 321–332. [Google Scholar] [CrossRef]
- Zhou, R.; Xing, Z.; Wang, H.; Piao, Z.; Huang, Y.; Guo, W.; Ma, R. Prediction of Contact Fatigue Life of AT40 Ceramic Coating Based on Neural Network. Anti-Corros. Methods Mater. 2020, 67, 83–100. [Google Scholar] [CrossRef]
- Zhou, C.; Wang, H.; Hou, S.; Han, Y. A Hybrid Physics-Based and Data-Driven Method for Gear Contact Fatigue Life Prediction. Int. J. Fatigue 2023, 175, 107763. [Google Scholar] [CrossRef]
- Li, Z.; Tian, K.; Li, H.; Shi, Y.; Wang, B. A Competitive Variable-Fidelity Surrogate-Assisted CMA-ES Algorithm Using Data Mining Techniques. Aerosp. Sci. Technol. 2021, 119, 107084. [Google Scholar] [CrossRef]


| BD [°] | Strain Amplitude [%] | λ | Phase Angle [°] | Specimen No. | Nf [Cycle] | Phase Angle [°] | Specimen No. | Nf [Cycle] | |
|---|---|---|---|---|---|---|---|---|---|
| Axial | Torsional | ||||||||
| 0 | 0.4 | 0.346 | 0.865 | 90 | NP01 | 7272 | 0 | P01 | 7217 |
| 0 | 0.4 | 0.692 | 1.73 | 90 | NP02 | 7012 | 0 | P02 | 4752 |
| 0 | 0.6 | 0.519 | 0.865 | 90 | NP03 | 2280 | 0 | P03 | 1178 |
| 0 | 0.6 | 1.038 | 1.73 | 90 | NP04 | 2212 | 0 | P04 | 1523 |
| 12 | 0.4 | 0.346 | 0.865 | 90 | NP05 | 6980 | 0 | P05 | 8562 |
| 12 | 0.4 | 0.692 | 1.73 | 90 | NP06 | 6624 | 0 | P06 | 8982 |
| 12 | 0.4 | 1.384 | 3.46 | 90 | NP07 | 4256 | 0 | P07 | 5918 |
| 12 | 0.6 | 0.519 | 0.865 | 90 | NP08 | 1320 | 0 | P08 | 2301 |
| 12 | 0.6 | 1.038 | 1.73 | 90 | NP09 | 2044 | 0 | P09 | 2332 |
| 12 | 0.6 | 2.076 | 3.46 | 90 | NP10 | 1013 | 0 | P10 | 1394 |
| 16 | 0.4 | 0.346 | 0.865 | 90 | NP11 | 5935 | 0 | P11 | 9352 |
| 16 | 0.6 | 0.519 | 0.865 | 90 | NP12 | 1069 | 0 | P12 | 2510 |
| 27 | 0.4 | 0.692 | 1.73 | 90 | NP13 | 7375 | 0 | P13 | 7503 |
| 27 | 0.6 | 1.038 | 1.73 | 90 | NP14 | 2028 | 0 | P14 | 1641 |
| 0 | 0.4 | 0.692 | 1.73 | 90 | NP02-R | 6458 | 0 | P02-R | 5003 |
| 12 | 0.4 | 0.692 | 1.73 | 90 | NP06-R | 6093 | 0 | P06-R | 8164 |
| 12 | 0.6 | 2.076 | 3.46 | 90 | NP10-R | 1169 | 0 | P10-R | 1176 |
| BD [°] | Static Mechanical Properties | Dynamic Mechanical Properties | ||||
|---|---|---|---|---|---|---|
| Tensile Strength/ [MPa] | Yield Strength/ [MPa] | Elastic Modulus [GPa] | R-O Parameter/ | R-O Parameter/ | ||
| 0 | 1266.76 | 1102.18 | 1.150 | 103.93 | 0.188 | 1003.91 |
| 12 | 1257.28 | 1062.41 | 1.184 | 108.01 | 0.176 | 926.50 |
| 16 | 1172.55 | 1000.63 | 1.171 | 108.03 | 0.179 | 971.63 |
| 27 | 1197.34 | 1032.35 | 1.160 | 102.38 | 0.181 | 963.84 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, T.-H.; Wang, Y.-X.; Chang, L.; Zhang, W.; Zhao, J.-P.; Zhou, C.-Y. Fatigue Behavior and Life Prediction of L-PBF Ti64 with Critical Plane Based Small Building Direction Variations Under Non-Proportional and Multiaxial Loading. Materials 2025, 18, 5122. https://doi.org/10.3390/ma18225122
Ma T-H, Wang Y-X, Chang L, Zhang W, Zhao J-P, Zhou C-Y. Fatigue Behavior and Life Prediction of L-PBF Ti64 with Critical Plane Based Small Building Direction Variations Under Non-Proportional and Multiaxial Loading. Materials. 2025; 18(22):5122. https://doi.org/10.3390/ma18225122
Chicago/Turabian StyleMa, Tian-Hao, Yu-Xin Wang, Le Chang, Wei Zhang, Jian-Ping Zhao, and Chang-Yu Zhou. 2025. "Fatigue Behavior and Life Prediction of L-PBF Ti64 with Critical Plane Based Small Building Direction Variations Under Non-Proportional and Multiaxial Loading" Materials 18, no. 22: 5122. https://doi.org/10.3390/ma18225122
APA StyleMa, T.-H., Wang, Y.-X., Chang, L., Zhang, W., Zhao, J.-P., & Zhou, C.-Y. (2025). Fatigue Behavior and Life Prediction of L-PBF Ti64 with Critical Plane Based Small Building Direction Variations Under Non-Proportional and Multiaxial Loading. Materials, 18(22), 5122. https://doi.org/10.3390/ma18225122








