An Artificial Neural Network for Rapid Prediction of the 3D Transient Temperature Fields in Ship Hull Plate Line Heating Forming
Abstract
1. Introduction
2. Methodology
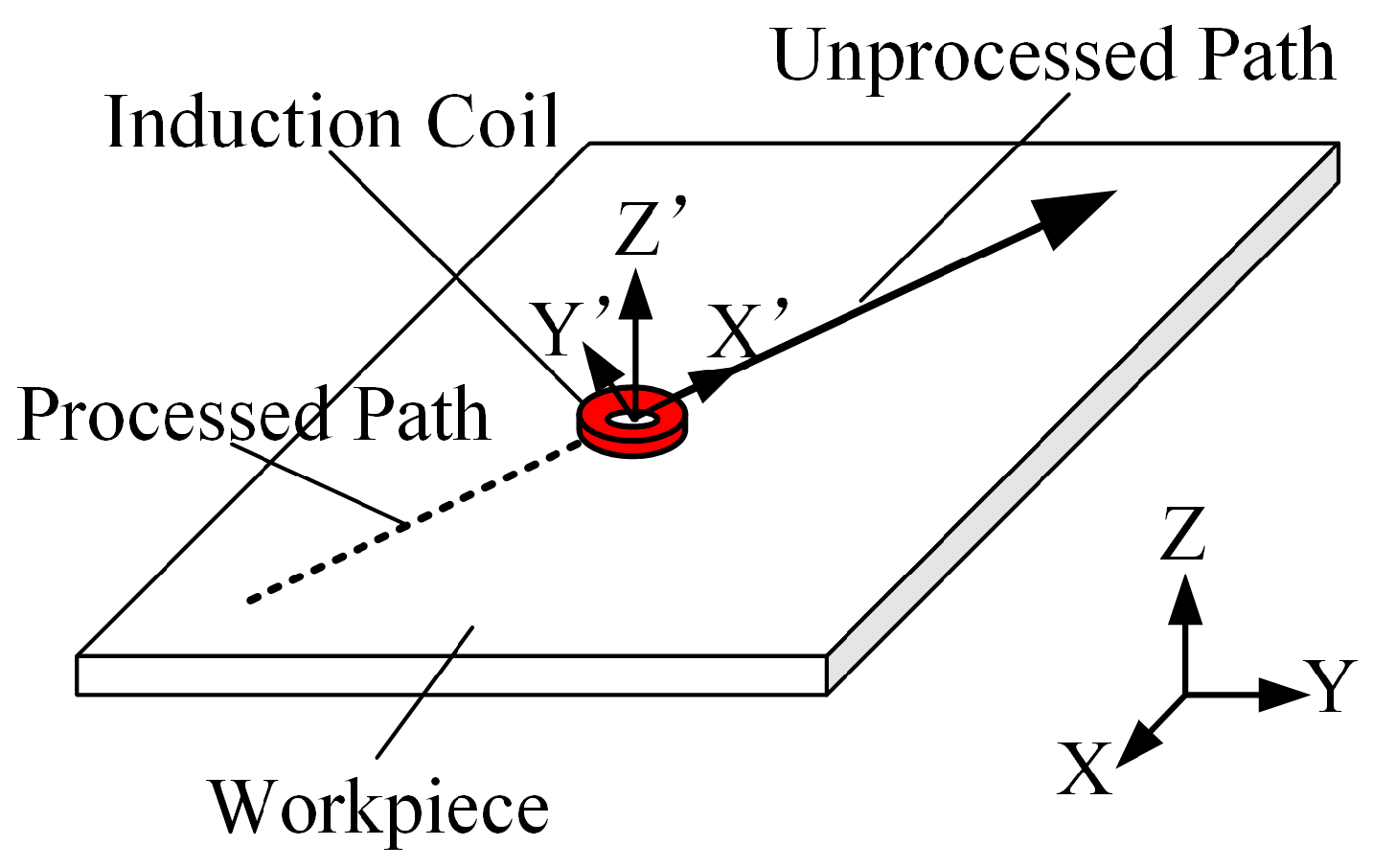
2.1. Governing Equations of Heat Conduction in a Moving Coordinate System
2.2. Definition and Partitioning of the Critical Thermal Region
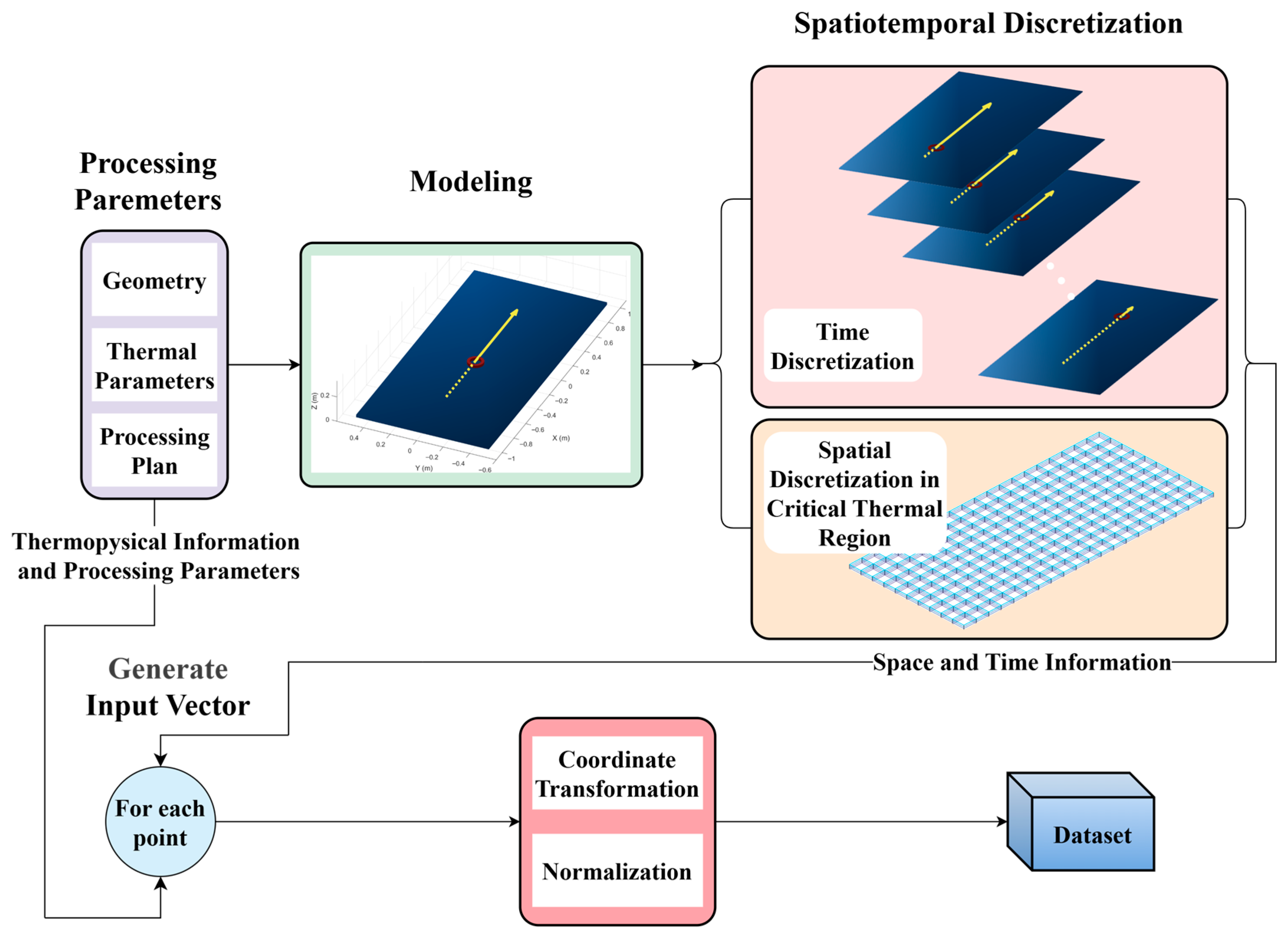
2.3. Data Structure for Training Neural Network
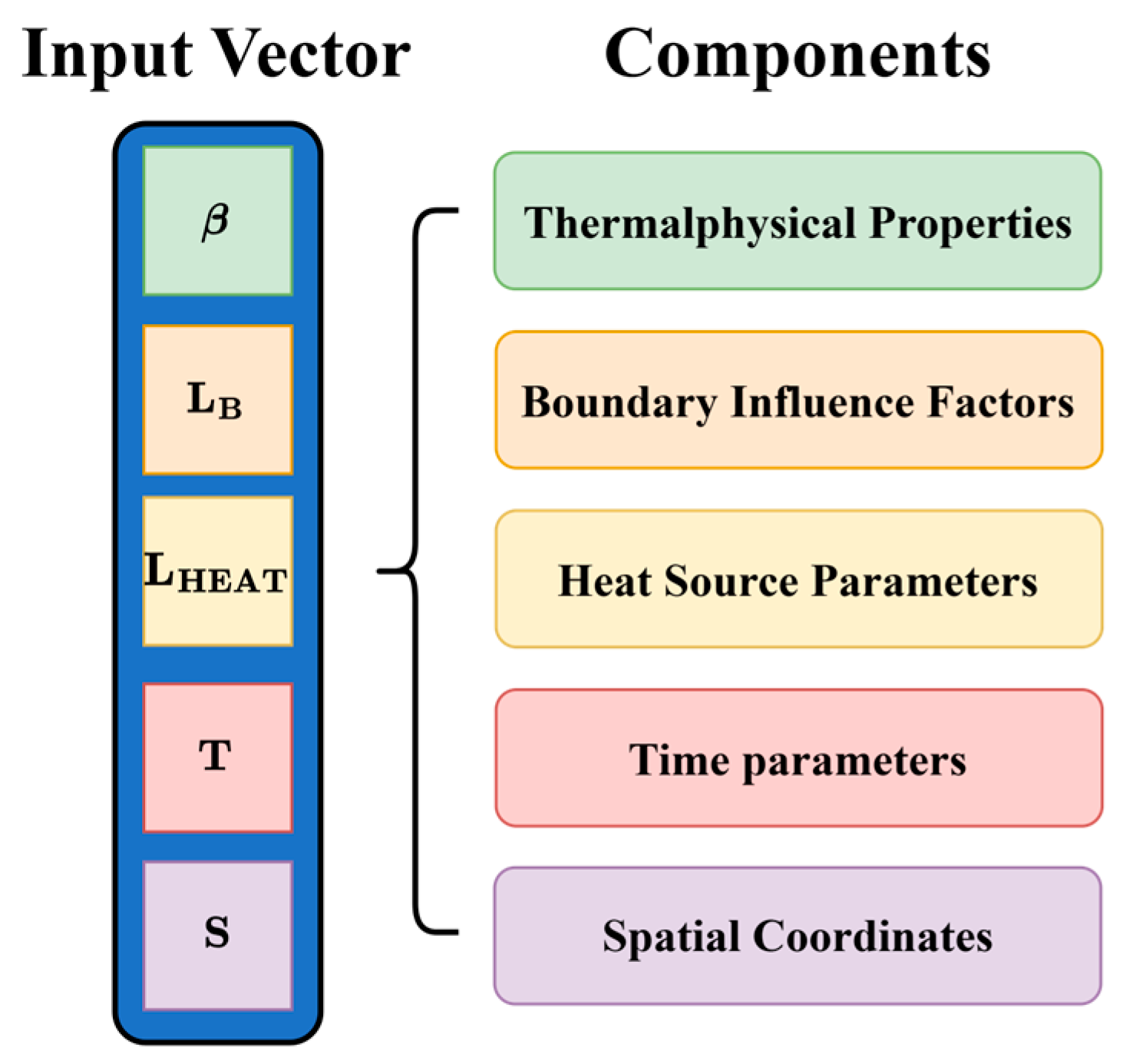
2.3.1. Composition of the Input Vector
2.3.2. Coordinate Transformation and Normalization
- Dimensionless groups are scaled using Equation (11).
- 2.
- Time-related features are normalized via Equation (12).
- 3.
- Length-, velocity-, and temperature-related quantities are normalized according to Equation (13).
2.4. The Architecture of the Neural Network
3. Case Study: Line Heating with Random Processing Paths and Varying Plate Thickness
3.1. Generation of Sample Data
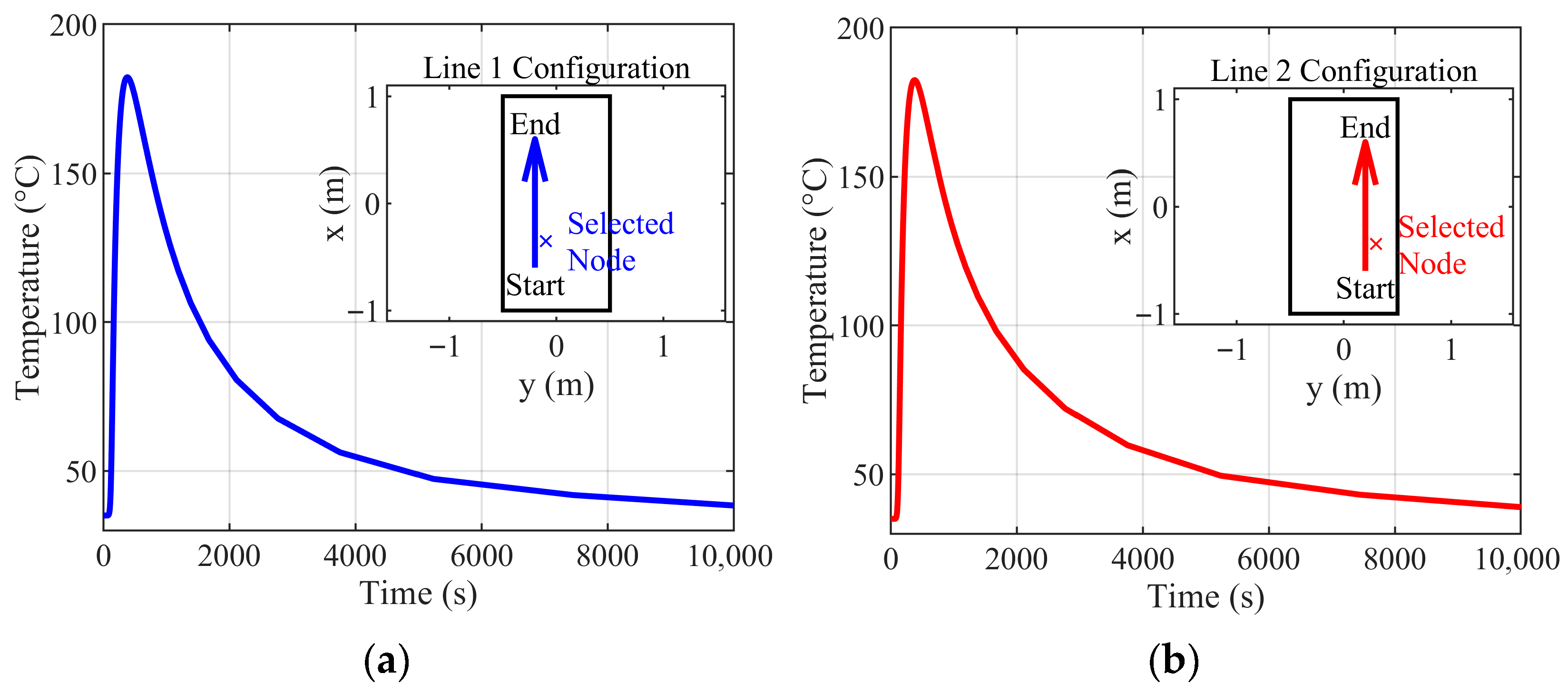
3.2. Selection of Critical Thermal Region Width
3.3. Dataset Generation and Partitioning
- Transient temperature data are jointly filtered by vertical coordinate and time to form whole 2D slices. Further, 5% of these complete slices are assigned to the test set; the remaining 95% are reserved for subsequent partitioning.
- The remaining data are randomly shuffled; 5% are sampled by index as the validation set, and the rest constitute the training set.
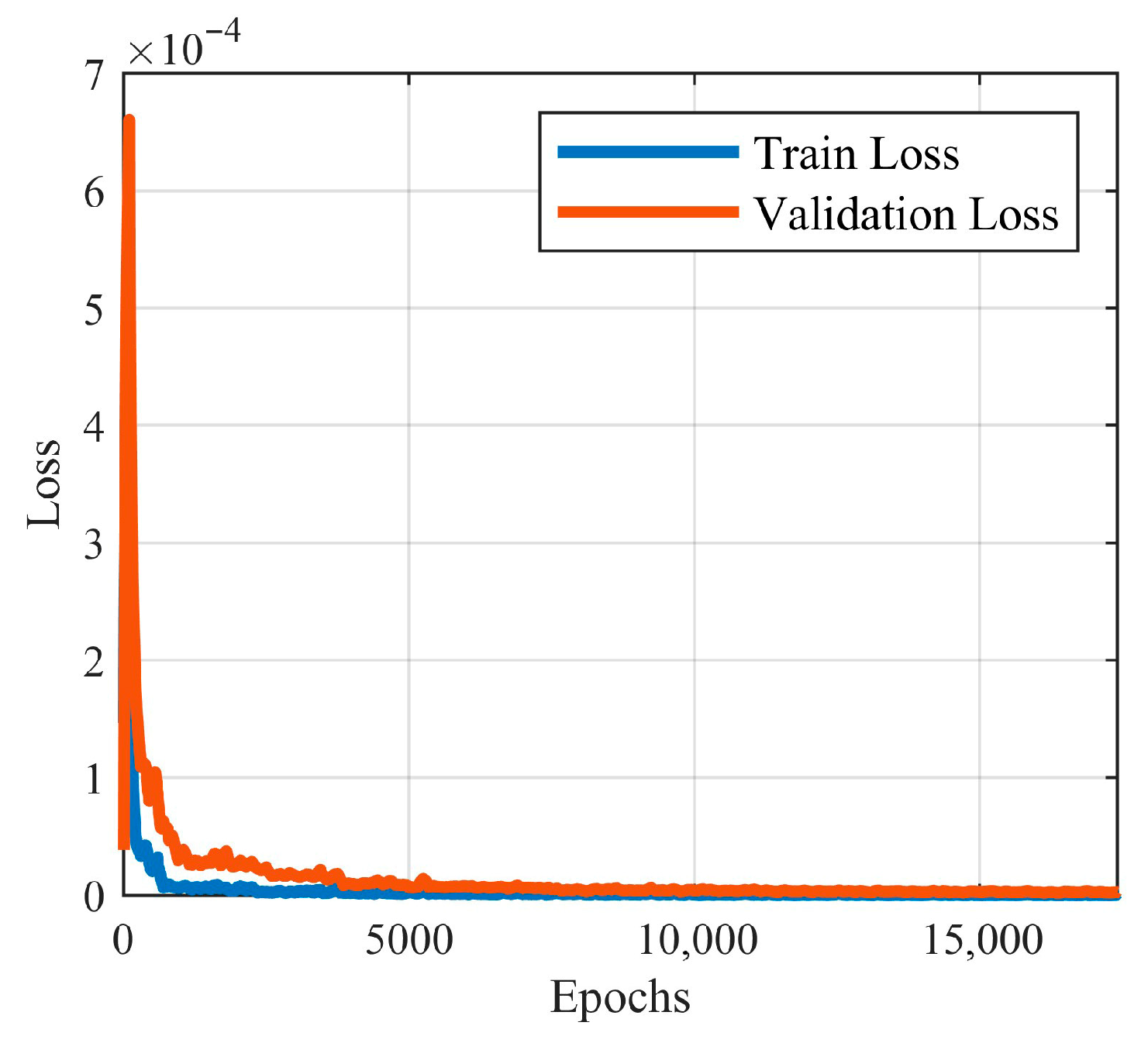
3.4. Optimization of Hyperparameters
4. Experimental Validation Procedure
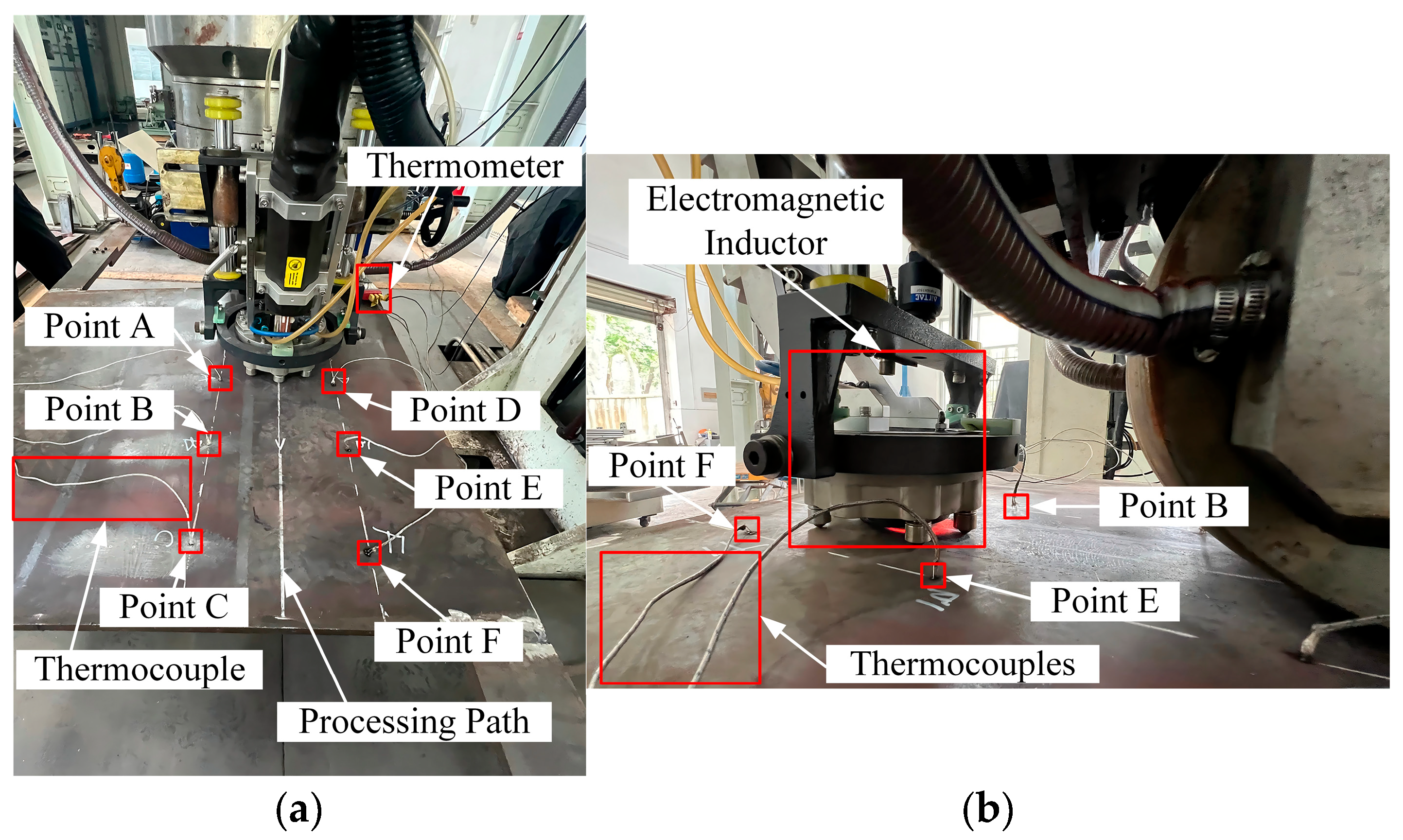
4.1. Experiment 1: Engineering Validation of the Model
4.2. Experiment 2: Adaptability to Different-Sized Plates
5. Results and Discussion
5.1. Metrics
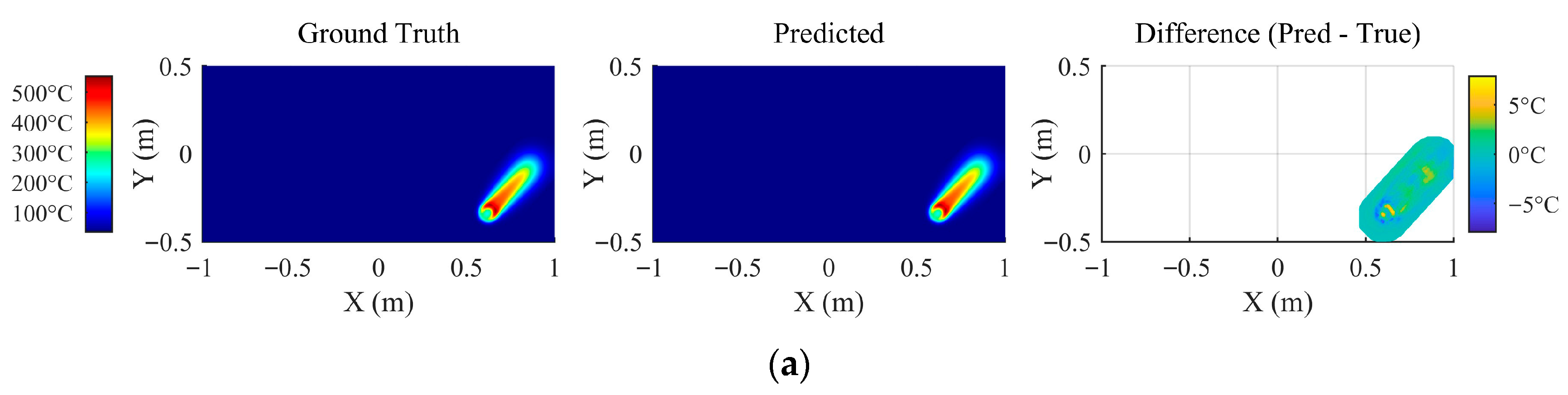
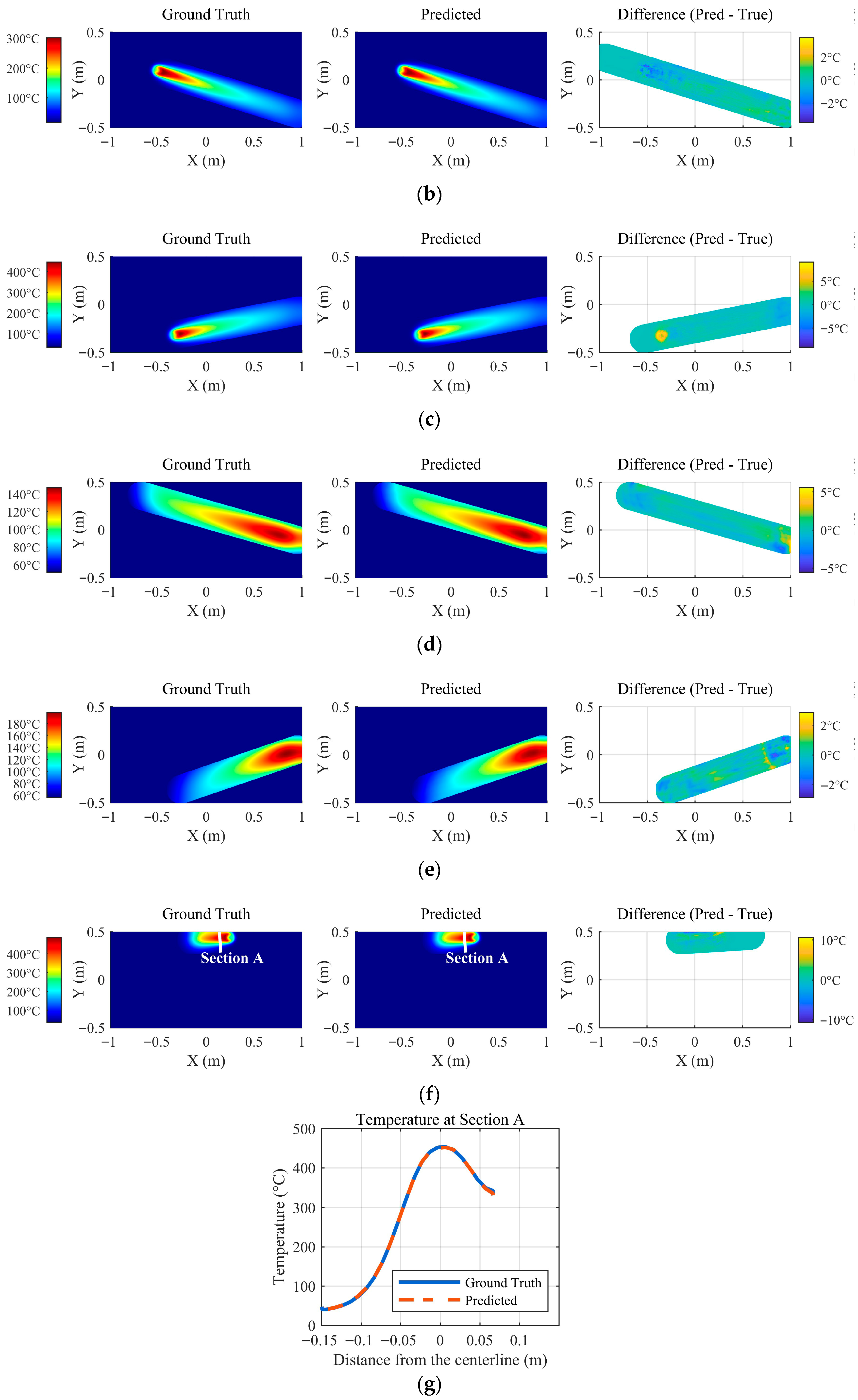
5.2. Results on Test Set
5.2.1. Qualitative Assessment of Temperature Fields
5.2.2. Quantitative Evaluation
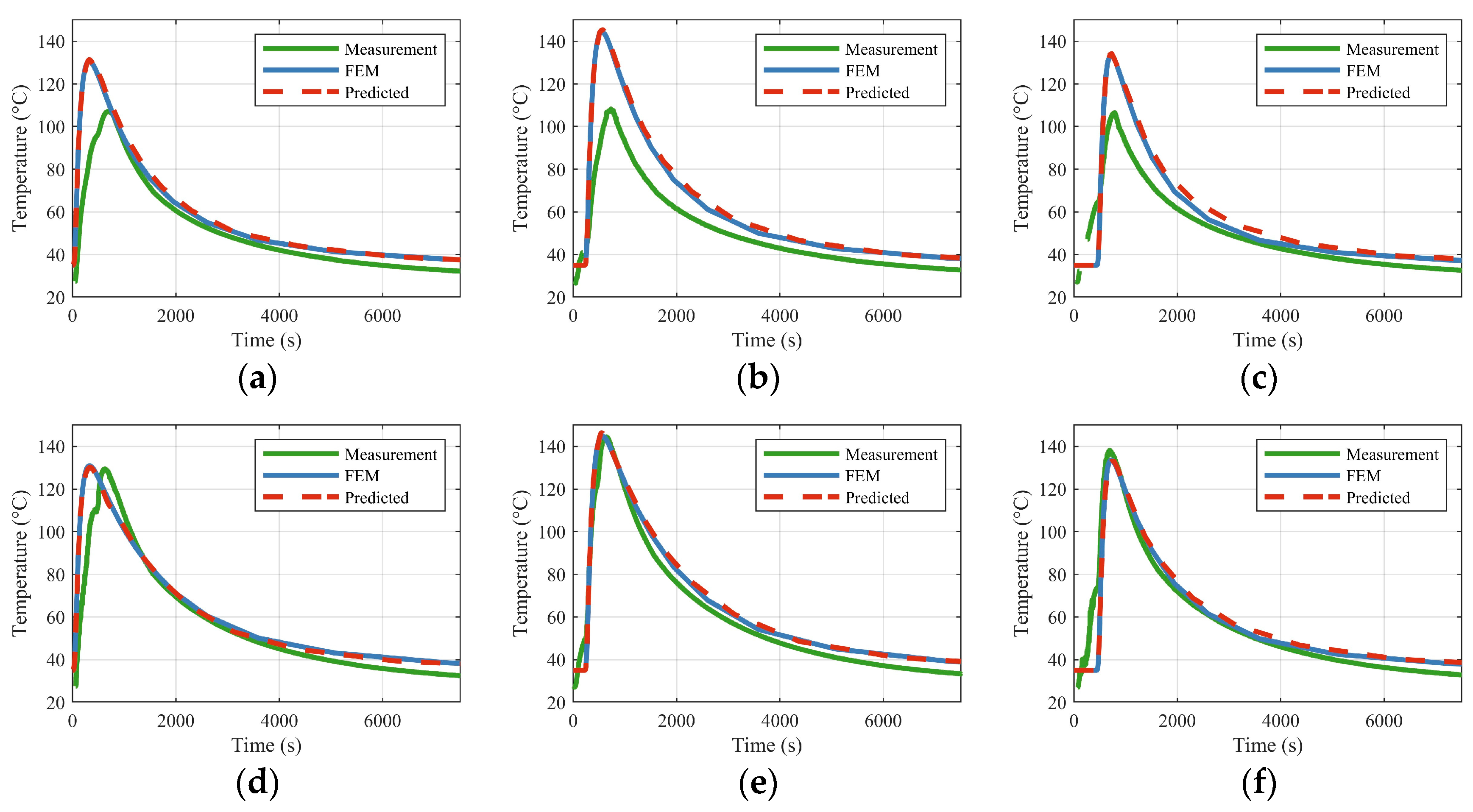
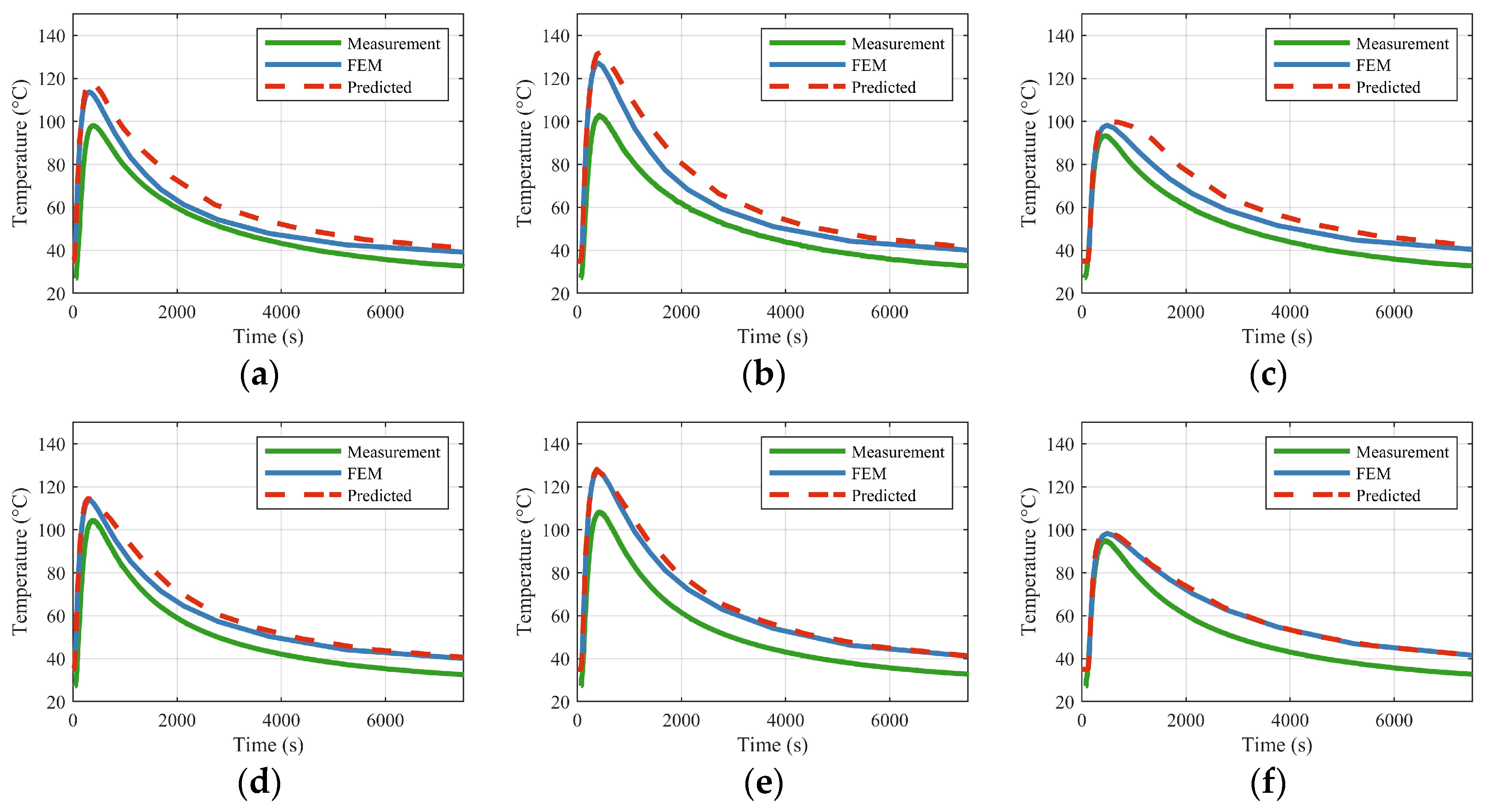
5.3. Comparison with Experimental Data
5.4. Computational Efficiency
6. Conclusions
- This study introduces a unified, data-driven framework that efficiently predicts the whole 3D transient temperature field over a complete line heating cycle. By localizing the predictive domain to a critical thermal region capsule and embedding thermophysical properties, boundary influence factors, and path-aligned coordinates, the method captures key process physics while alleviating the training challenges of large spatiotemporal domains. The resulting model generalizes across plate geometries, thickness, and processing parameters.
- The proposed framework achieves substantial gains in computational efficiency with comparable accuracy to FEM solutions. The model supports versatile inference—returning either full-field results or pointwise queries—and delivers predictions approximately five orders of magnitude faster than FEM under equivalent output conditions, while maintaining high fidelity across standard error metrics.
- Two pure line heating experiments on the IHMRF system verify engineering applicability and cross-size generalization. Notably, the model trained on 2 m × 1 m plates accurately predicts the transient temperature field for a 1 m × 1 m plate without remeshing or resolving, demonstrating strong out-of-sample adaptability.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Seong, W.-J.; Jeon, Y.-C.; Na, S.-J. Ship-Hull Plate Forming of Saddle Shape by Geometrical Approach. J. Mater. Process. Technol. 2013, 213, 1885–1893. [Google Scholar] [CrossRef]
- Liu, Q.; Li, J.; Liu, J.; Lu, B.; Li, H.; Chen, L. Hot Deformation Behavior and Constitutive Modeling of High Strength Low-Carbon Alloyed Steel Manufactured by Wire and Arc Additive Manufacturing. J. Mater. Eng. Perform. 2025, 34, 14084–14096. [Google Scholar] [CrossRef]
- Duan, J.; Farrugia, D.; Slater, C.; Li, Z.; Davis, C. Microstructure Development during Multi-Pass Deformation in a Low Carbon Steel with a Leaner Composition, Finer Grain Size, and Higher Strength. J. Mater. Res. Technol. 2025, 36, 10373–10382. [Google Scholar] [CrossRef]
- Parusov, E.V.; Chuiko, I.M.; Gubenko, S.I.; Oliinyk, E.V.; Parusov, O.V. Influence of Temperature-Deformation Parameters of Thermomechanical Treatment on the Structure and Mechanical Properties of Low-Carbon Alloyed Steel. Mater. Sci. 2025, 61, 42–49. [Google Scholar] [CrossRef]
- Rosenthal, D. The Theory of Moving Sources of Heat and Its Application to Metal Treatments. J. Fluids Eng. 1946, 68, 849–865. [Google Scholar] [CrossRef]
- Wang, Y.; Lu, Y.; Mendez, P.F. Scaling Expressions of Characteristic Values for a Moving Point Heat Source in Steady State on a Semi-Infinite Solid. Int. J. Heat. Mass. Transf. 2019, 135, 1118–1129. [Google Scholar] [CrossRef]
- Ueda, Y.; Murakawa, H.; Rashwan, A.M.; Okumoto, Y.; Kamichika, R. Development of Computer Aided Process Planning System for Plate Bending by Line Heating (Report I): Relation between the Final Form of Plate and the Inherent Strain. J. Ship Prod. 1991, 10, 59–67. [Google Scholar] [CrossRef]
- Ueda, Y.; Murakawa, H.; Rashwan, A.M.; Okumoto, Y.; Kamichika, R. Development of Computer Aided Process Planning System for Plate Bending by Line-Heating (Report II): Practice for Plate Bending in Shipyard Viewed from Aspect of Inherent Strain. J. Ship Prod. 1992, 10, 239. [Google Scholar] [CrossRef]
- Ueda, Y.; Murakawa, H.; Rashwan, A.M.; Neki, I.; Kamichika, R.; Ishiyama, M.; Ogawa, J. Development of Computer Aided Process Planning System for Plate Bending by Line-Heating (Report III): Relation between Heating Condition and Deformation. J. Ship Prod. 1993, 10, 248–257. [Google Scholar] [CrossRef]
- Ueda, Y.; Murakawa, H.; Rashwan, A.M.; Kamichika, R.; Ishiyama, M.; Ogawa, J. Development of Computer Aided Process Planning System for Plate Bending by Line-Heating (Report IV): Decision Making on Heating Conditions, Location and Direction. J. Ship Prod. 1993, 22, 305–313. [Google Scholar]
- Zhu, Y.; Luo, Y. Fully Coupled Magneto-Thermo-Structural Analysis by Morphing Method and Its Application to Induction Heating Process for Plate Bending. Int. J. Appl. Electromagn. Mech. 2018, 56, 573–583. [Google Scholar] [CrossRef]
- Dong, H.; Zhao, Y.; Yuan, H.; Hu, X.; Yang, Z. A Simplified Calculation Method of Heat Source Model for Induction Heating. Materials 2019, 12, 2938. [Google Scholar] [CrossRef]
- Lu, Z.; Qu, J.; Liu, H.; He, C.; Zhang, B.; Chen, Q. Surrogate Modeling for Physical Fields of Heat Transfer Processes Based on Physics-Informed Neural Network. CIESC J. 2021, 72, 1496–1503. [Google Scholar] [CrossRef]
- Zhao, X.; Gong, Z.; Zhang, Y.; Yao, W.; Chen, X. Physics-Informed Convolutional Neural Networks for Temperature Field Prediction of Heat Source Layout without Labeled Data. Eng. Appl. Artif. Intell. 2023, 117, 105516, (In Chinese with English Abstract). [Google Scholar] [CrossRef]
- Chen, Z.; Yang, X.; Chen, N.; Yi, X.; Peng, B. Transient temperature field prediction on anti-icing wing surface based on convolutional temporal networks. Acta Aerodyn. Sin. 2024, 24, 1–11, (In Chinese with English Abstract). [Google Scholar] [CrossRef]
- Liao, S.; Xue, T.; Jeong, J.; Webster, S.; Ehmann, K.; Cao, J. Hybrid Thermal Modeling of Additive Manufacturing Processes Using Physics-Informed Neural Networks for Temperature Prediction and Parameter Identification. Comput. Mech. 2023, 72, 499–512. [Google Scholar] [CrossRef]
- Cao, X.; Duan, C.; Luo, X.; Zheng, S.; Xu, H.; Hao, X.; Zhang, Z. Deep Learning-Based Rapid Prediction of Temperature Field and Intelligent Control of Molten Pool during Directed Energy Deposition Process. Addit. Manuf. 2024, 94, 104501. [Google Scholar] [CrossRef]
- Wei, Z.; Zhao, Y.; Yuan, H.; Chang, L. A Physic-Informed Data-Driven Relational Model of Plastic Strain vs. Process Parameters during Integrated Heating and Mechanical Rolling Forming of Hull Plates. J. Mar. Sci. Eng. 2024, 12, 1710. [Google Scholar] [CrossRef]
- Wei, Z.; Zhao, Y.; Yuan, H.; Chang, L. Equivalent Load Model for the Numerical Simulation of Integrated Induction Heating and Mechanical Rolling Forming of Curved Hull Plates. Int. J. Adv. Manuf. Technol. 2024, 130, 3891–3903. [Google Scholar] [CrossRef]
- International Association of Classification Societies. Shipbuilding and Repair Quality Standard; IACS Recommendation No. 47, Rev. 10; IACS: London, UK, 2025. [Google Scholar]
- Zhang, L.; Reutzel, E.W.; Michaleris, P. Finite Element Modeling Discretization Requirements for the Laser Forming Process. Int. J. Mech. Sci. 2004, 46, 623–637. [Google Scholar] [CrossRef]
- Akiba, T.; Sano, S.; Yanase, T.; Ohta, T.; Koyama, M. Optuna: A Next-Generation Hyperparameter Optimization Framework. In KDD’19: Proceedings of the 25th ACM SIGKDD Conference on Knowledge Discovery and Data Mining, Anchorage, AK, USA, 4–8 August 2019; Association for Computing Machinery: New York, NY, USA, 2019. [Google Scholar]
- Zhao, Y.; Yuan, H.; Tang, G.; Dong, H.; Hu, C.; Yan, J. Automatic Integral Forming Method for Double-Curvature Plate of Ship. U.S. Patent 9,751,123, 5 September 2017. [Google Scholar]
- Zhao, Y.; Wei, Z.; Yuan, H.; Chang, L. An Induction Heating Device. Chinese Patent CN114786285A, 22 July 2022. (In Chinese). [Google Scholar]
- Chen, J.; Zhu, F.; Han, Y.; Xu, Z.; Chen, Q.; Ren, D. Global Temperature Reconstruction of Equipment Based on the Local Temperature Image Using TRe-GAN. Appl. Soft Comput. 2022, 128, 109498. [Google Scholar] [CrossRef]


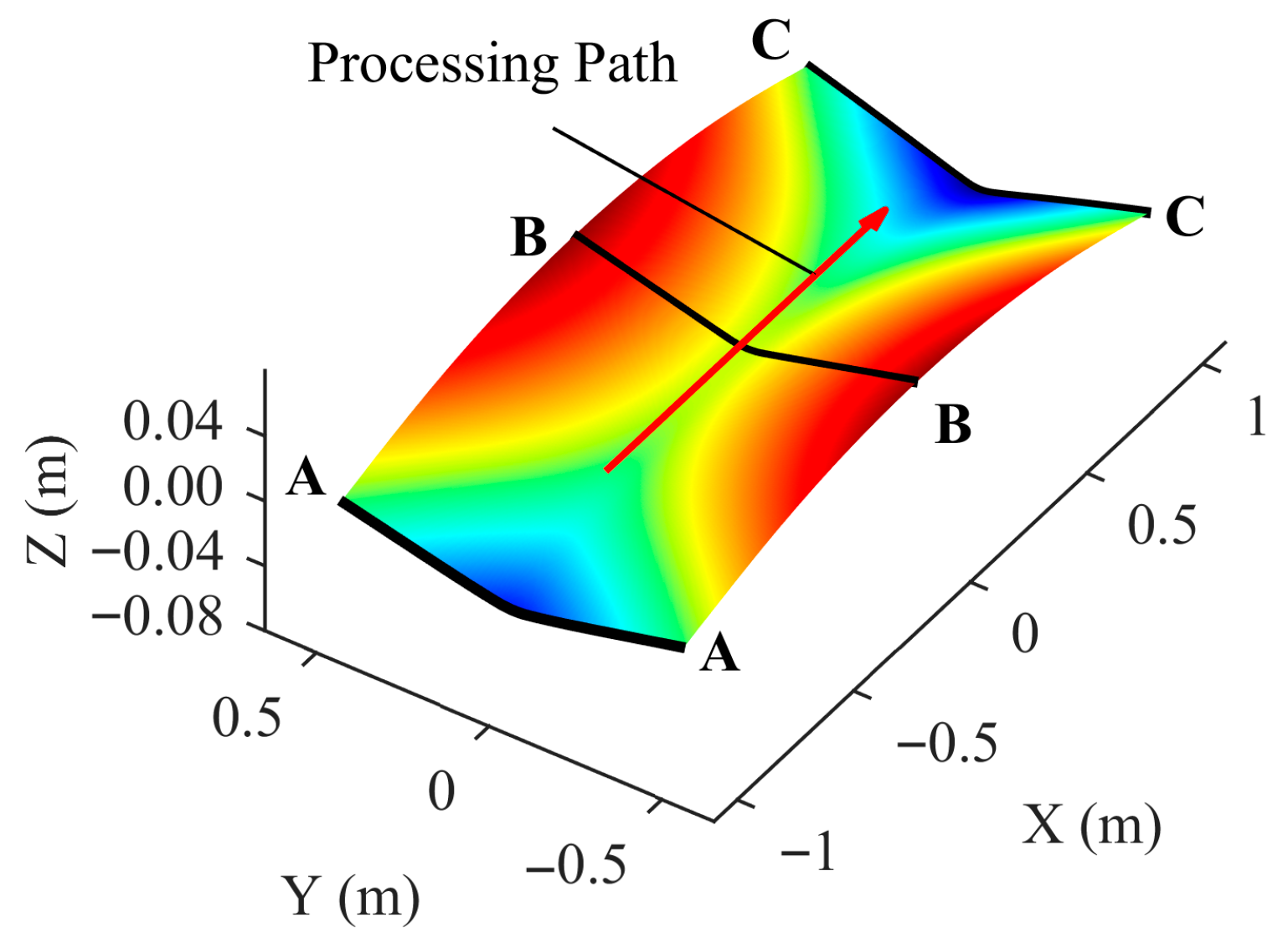

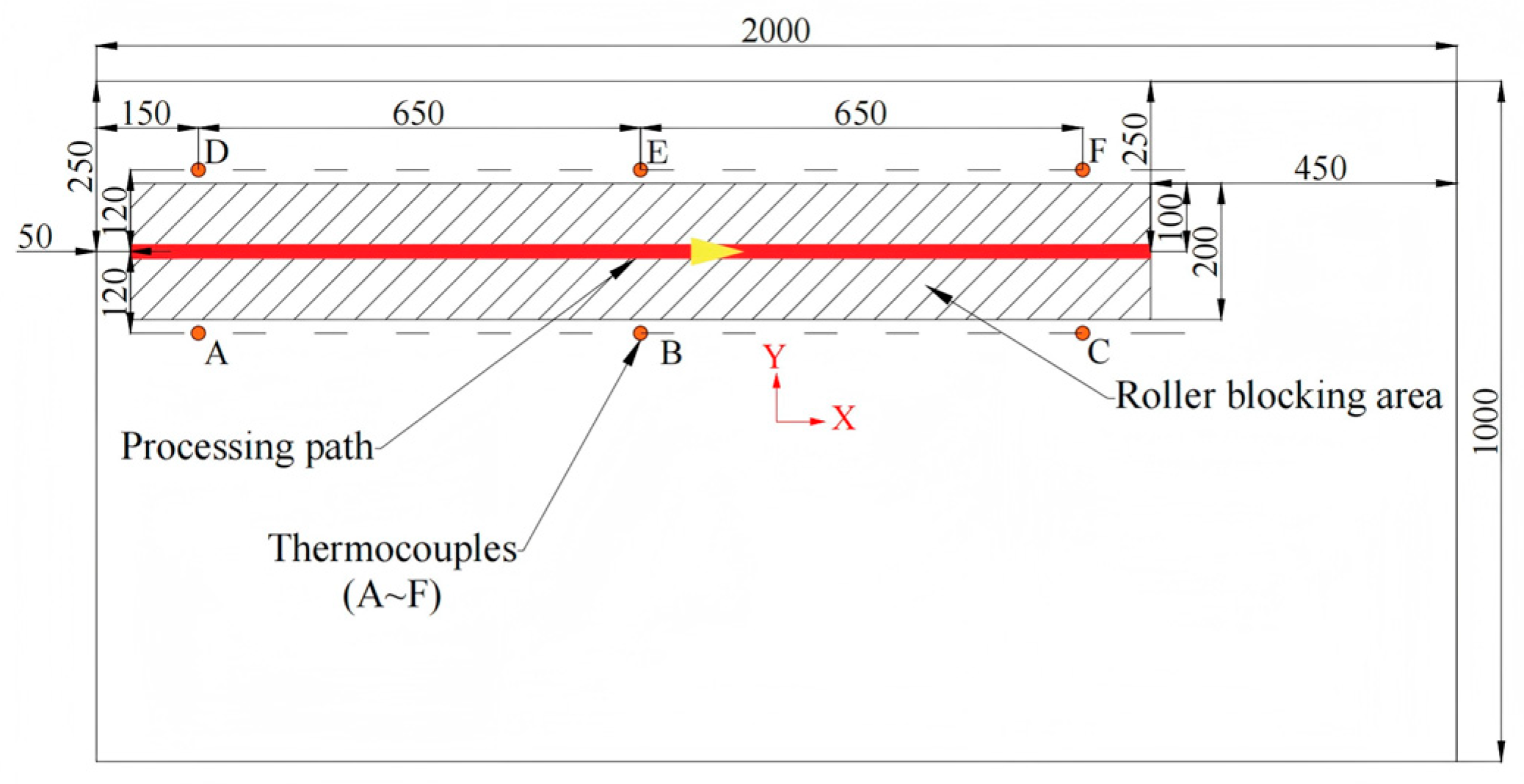
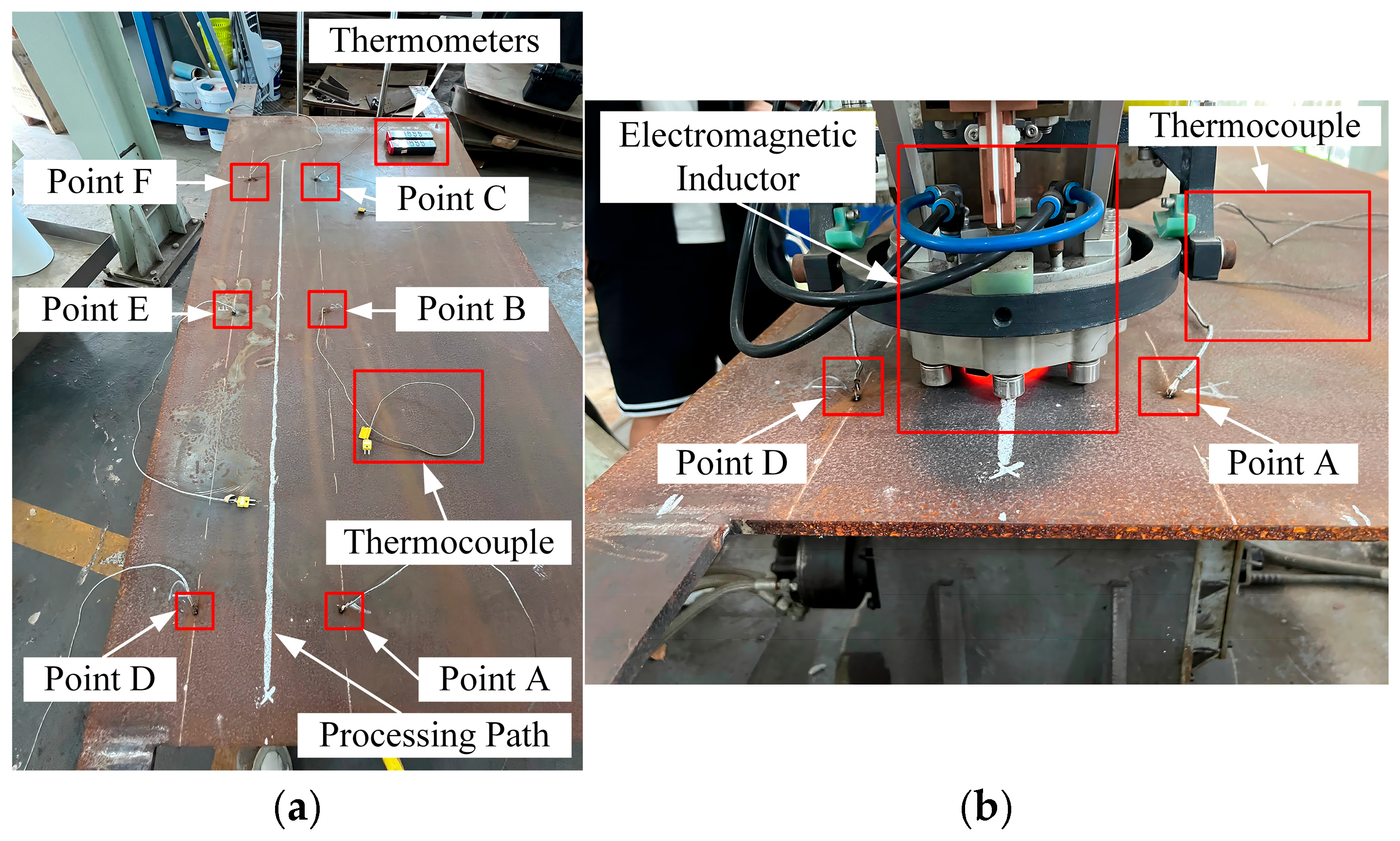
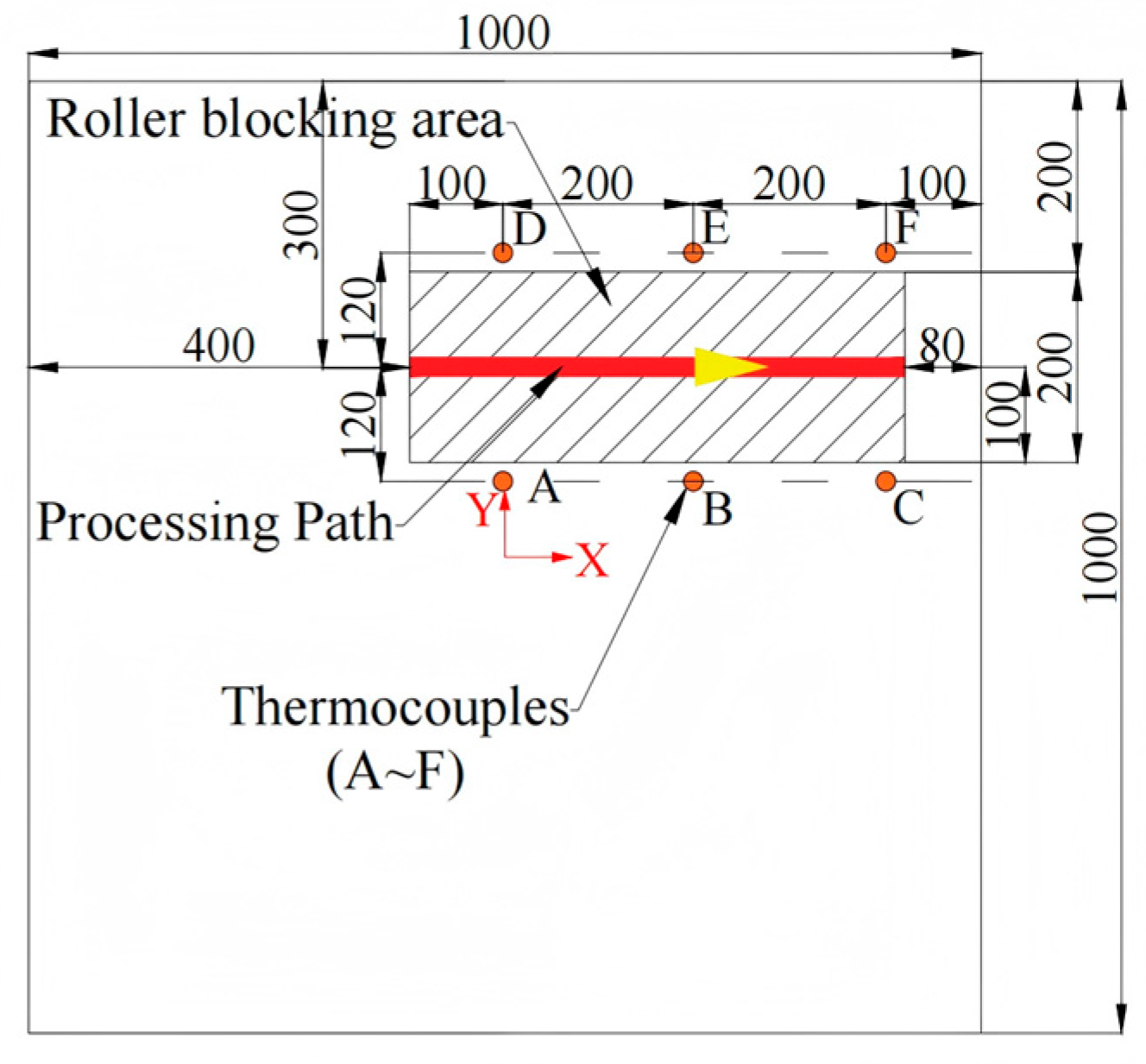
| Maximum Processing Temperature | Heat Source Speed | Plate Thickness | Start/End Coordinates of Processing Path |
|---|---|---|---|
| 400~800 °C | 1 mm/s | 12 mm | Random select from [−1, 1] in x-axis and [−0.5, 0.5] in y-axis |
| 2 mm/s | |||
| 3 mm/s | 16 mm | ||
| 4 mm/s | |||
| 5 mm/s | 20 mm | ||
| 6 mm/s |
| Temperature (°C) | Thermal Conductivity (W∙(mm∙°C)−1) | Specific Heat (KJ∙(kg∙°C)−1) |
|---|---|---|
| 0 | 51.9 × 10−3 | 486 |
| 100 | 51.1 × 10−3 | 486 |
| 200 | 48.6 × 10−3 | 498 |
| 300 | 44.4 × 10−3 | 515 |
| 400 | 42.7 × 10−3 | 536 |
| 500 | 39.4 × 10−3 | 557 |
| 600 | 35.6 × 10−3 | 586 |
| 700 | 31.8 × 10−3 | 619 |
| 800 | 26.0 × 10−3 | 691 |
| 900 | 26.4 × 10−3 | 695 |
| Maximum Absolute Error | Maximum Relative Error | |
|---|---|---|
| 0.25 m | 1.354 mm | 8.08% |
| 0.30 m | 0.693 mm | 6.55% |
| 0.35 m | 0.521 mm | 4.92% |
| 0.40 m | 0.348 mm | 3.28% |
| 0.45 m | 0.250 mm | 2.36% |
| Number of Input Vector | |
|---|---|
| Training Set | 1,692,643,142 |
| Validation Set | 88,875,220 |
| Test Set | 93,402,033 |
| The Number of Hidden Layer | The Number of Nodes per Payer | The Huber Function Threshold | The Learning Rate |
|---|---|---|---|
| 6~10 | 64~256 | 0.1~20 |
| The Number of Hidden Layer | The Number of Neurons per Payer | The Huber Function Threshold | The Learning Rate |
|---|---|---|---|
| 10 | 146 | 0.4965 |
| Parameters | Start Point | End Point | Power | Velocity of Heat Source | Maximum Processing Temperature |
|---|---|---|---|---|---|
| Unit | m | m | W | mm/s | °C |
| Value | (−0.95, 0.25) | (0.55, 0.25) | 26,927 | 3 | 800 |
| Parameters | Start Point | End Point | Power | Velocity of Heat Source | Maximum Processing Temperature |
|---|---|---|---|---|---|
| Unit | m | m | W | mm/s | °C |
| Value | (−0.1, 0.2) | (0.42, 0.2) | 43,233 | 4 | 800 |
| Metrics | MAE | MAPE | RMSE | R2 | MedAE | MMaxE | Error Confidence Interval |
|---|---|---|---|---|---|---|---|
| Unit | °C | % | °C | 1 | °C | °C | °C |
| Value | 0.5994 | 0.4622 | 1.2703 | 0.9950 | 0.2511 | 10.6750 | [−0.2031, −0.0627] |
| Method | FEM | Proposed Framework | Speedup |
|---|---|---|---|
| Experiment 1 | 4381 s | 71.361 ms | 61,392× |
| Experiment 2 | 1047 s | 19.452 ms | 53,824× |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, Z.; Yuan, H.; Wei, Z.; Chang, L.; Zhao, Y.; Liu, J. An Artificial Neural Network for Rapid Prediction of the 3D Transient Temperature Fields in Ship Hull Plate Line Heating Forming. Materials 2025, 18, 5054. https://doi.org/10.3390/ma18215054
Yang Z, Yuan H, Wei Z, Chang L, Zhao Y, Liu J. An Artificial Neural Network for Rapid Prediction of the 3D Transient Temperature Fields in Ship Hull Plate Line Heating Forming. Materials. 2025; 18(21):5054. https://doi.org/10.3390/ma18215054
Chicago/Turabian StyleYang, Zhe, Hua Yuan, Zhenshuai Wei, Lichun Chang, Yao Zhao, and Jiayi Liu. 2025. "An Artificial Neural Network for Rapid Prediction of the 3D Transient Temperature Fields in Ship Hull Plate Line Heating Forming" Materials 18, no. 21: 5054. https://doi.org/10.3390/ma18215054
APA StyleYang, Z., Yuan, H., Wei, Z., Chang, L., Zhao, Y., & Liu, J. (2025). An Artificial Neural Network for Rapid Prediction of the 3D Transient Temperature Fields in Ship Hull Plate Line Heating Forming. Materials, 18(21), 5054. https://doi.org/10.3390/ma18215054






