Design and Optimization of a Hybrid Railcar Structure with Multilayer Composite Panels
Abstract
1. Introduction
2. Methodology
- (1)
- Finite element (FE) model of the car body structure. The process begins with the building of a high-fidelity FE model of the car body shell. This model accurately reproduces the geometry, boundary conditions, and loading scenarios, and serves as the reference framework for subsequent evaluations. Detailed modeling aspects are described in the following section.
- (2)
- Definition of the composite stack. The second step involves defining the multilayer material, hereafter referred to as the stack. Each individual layer, denoted as ply, is characterized by its mechanical properties (elastic modulus, shear modulus, Poisson’s ratio, strength parameters, etc.) and introduced into the FE model through appropriate laminate modeling strategies.
- (3)
- Numerical evaluation under European standard conditions. Once the stack is defined, the FE model is subjected to numerical simulations under the loading conditions prescribed by EN 12663-1:2015. Both static and dynamic performances are assessed for metallic and composite configurations. At this stage, the model provides insights into the global behavior of the structure, including modal properties such as natural frequencies and mode shapes.
- (4)
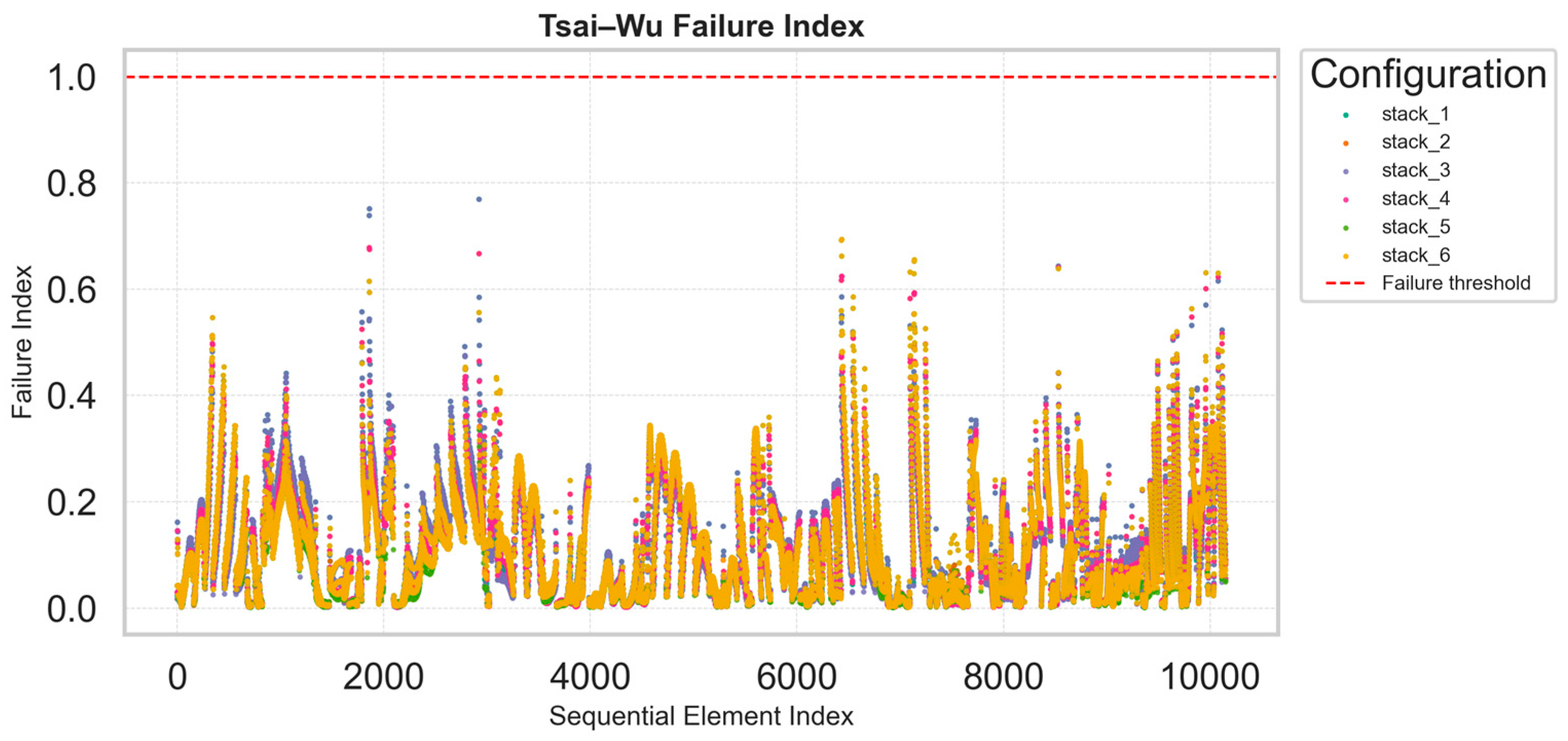
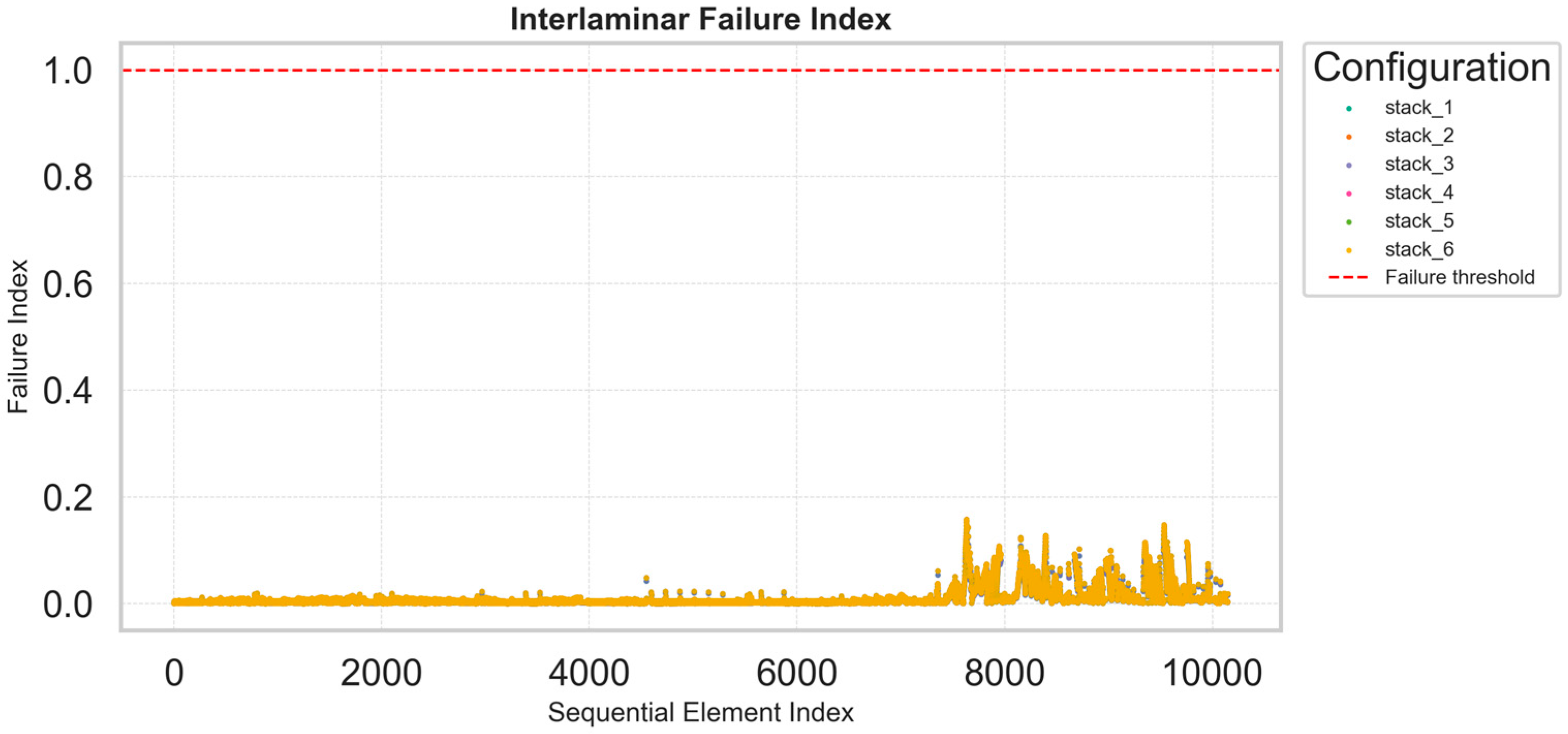
- Optimization Process. The optimization phase is focused on identifying the most efficient stacking sequence for the composite laminate, according to the selected criteria. The procedure evaluates all possible ply arrangements, accounting for n! permutations, where n is the number of distinct plies. Redundancies are avoided by fixing the reference system of the stack, ensuring that no permutation is repeated. If identical plies are present, the number of evaluated configurations is automatically reduced, simplifying the process. The assessment of each configuration is based on Tsai–Wu, interlaminar, and Maximum Stress criteria, as well as on maximum failure index evaluations using percentile-based metrics.
- (5)
- Global comparison of results. After completing the full cycle of n! iterations, a comprehensive comparison of all tested configurations is automatically generated. This final step identifies the optimal stacking sequence that maximizes structural efficiency while guaranteeing compliance with both European standards and design targets.
3. Tram Platform Description
3.1. Structural Materials in Comparison
3.2. FE Model Description and Simulation Settings
4. Results and Discussions
4.1. Performance Indices and Assessment Criteria
4.2. Mass Comparison and Optimization Framework
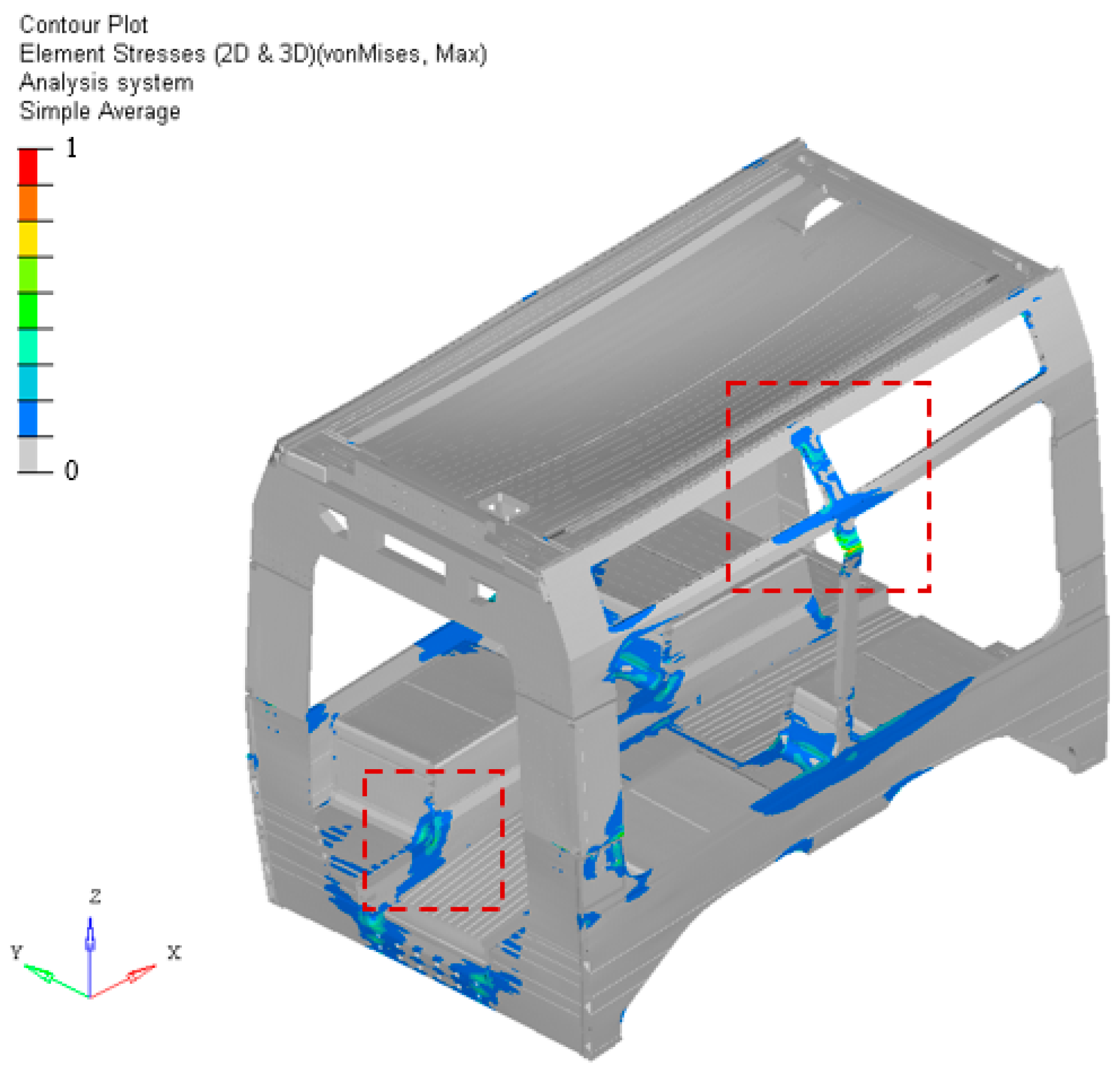
4.3. Tsai–Wu and Interlaminar Failure Index Distributions
4.4. Percentile and Statistical Evaluation of Maximum Failure Index
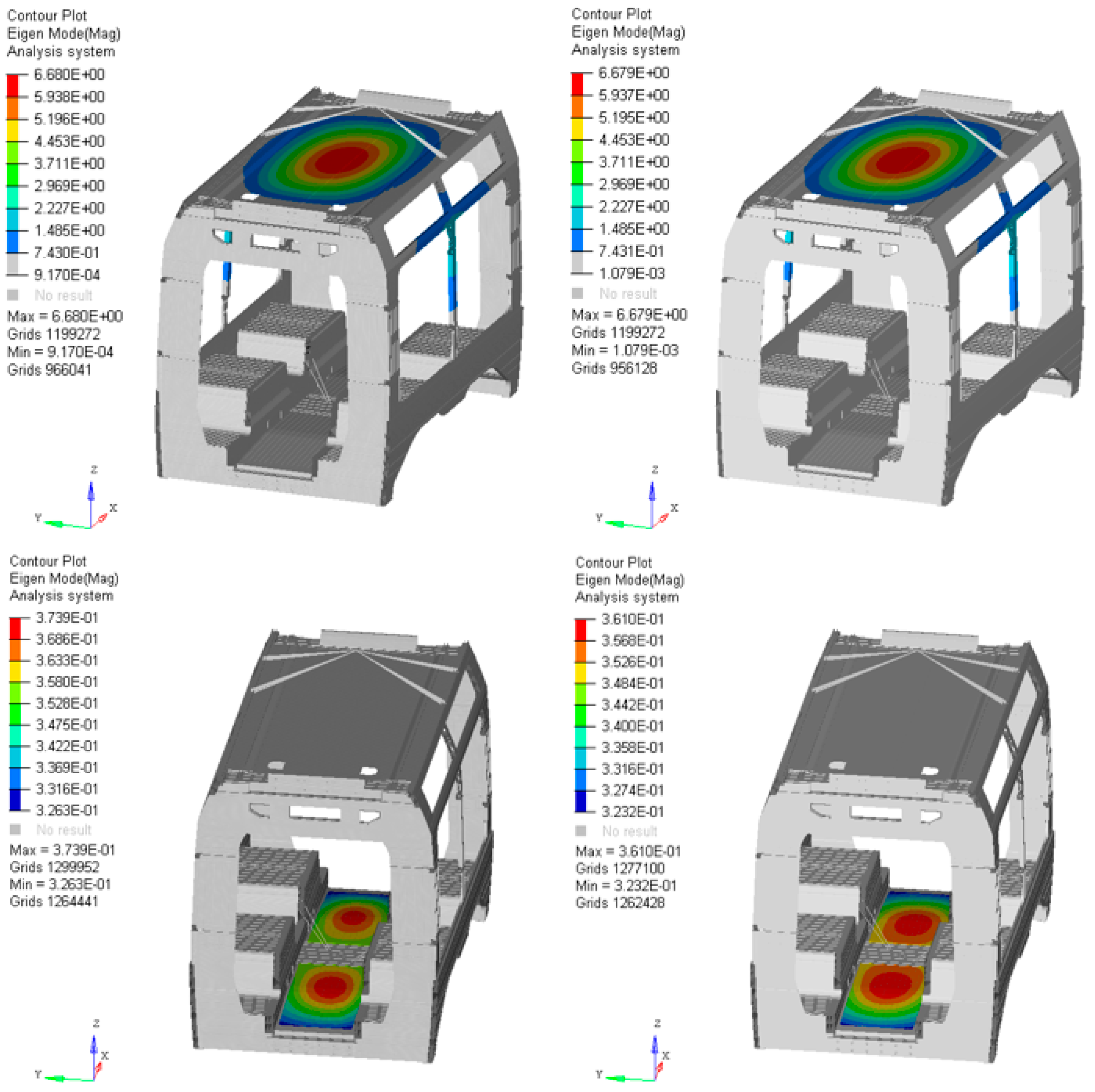
4.5. Stress Distribution and Modal Behavior Assessment
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Dincer, F.; Elbir, T. Estimating national exhaust emissions from railway. Sci. Total Environ. 2007, 374, 127–134. [Google Scholar] [CrossRef]
- Mayer, R.; Poulikakos, L.; Lees, A.; Heutschi, K.; Kalivoda, M.; Soltic, P. Reducing the environmental impact of road and rail vehicles. Environ. Impact Assess. Rev. 2012, 32, 25–32. [Google Scholar] [CrossRef]
- Harte, A.M.; McNamara, J.F.; Roddy, I.D. A multilevel approach to the optimisation of a composite light rail vehicle bodyshell. Compos. Struct. 2004, 63, 447–453. [Google Scholar] [CrossRef]
- Hudson, C.W.; Carruthers, J.J.; Robinson, A.M. Multiple objective optimisation of composite sandwich structures for rail vehicle floor panels. Compos. Struct. 2010, 92, 2077–2082. [Google Scholar] [CrossRef]
- Miao, B.; Luo, Y.; Peng, Q.; Qiu, Y.; Chen, H.; Yang, Z. Multidisciplinary design optimization of lightweight carbody for fatigue assessment. Mater. Des. 2020, 194, 108910. [Google Scholar] [CrossRef]
- Cascino, A.; Meli, E.; Rindi, A. Dynamic size optimization approach to support railway carbody lightweight design process. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2023, 237, 871–881. [Google Scholar] [CrossRef]
- Cascino, A.; Meli, E.; Rindi, A. A strategy for lightweight designing of a railway vehicle car body including composite material and dynamic structural optimization. Rail. Eng. Sci. 2023, 31, 340–350. [Google Scholar] [CrossRef]
- Trzepieciński, T.; Najm, S.M. Current Trends in Metallic Materials for Body Panels and Structural Members Used in the Automotive Industry. Materials 2024, 17, 590. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Chevali, V.S.; Wang, H.; Wang, C.-H. Current status of carbon fibre and carbon fibre composites recycling. Compos. Part B Eng. 2020, 193, 108053. [Google Scholar] [CrossRef]
- Saeedi, A.; Motavalli, M.; Shahverdi, M. Recent advancements in the applications of fiber-reinforced polymer structures in railway industry—A review. Polym. Compos. 2024, 45, 77–97. [Google Scholar] [CrossRef]
- Muhammad, A.; Rahman, M.R.; Baini, R.; Bakri, M.K.B. Advances in Sustainable Polymer Composites; Woodhead Publishing: Cambridge, UK, 2021; Chapter 8. [Google Scholar]
- Arifurrahman, F.; Budiman, B.A.; Aziz, M. On the lightweight structural design for electric road and railway vehicles using fiber reinforced polymer composites—A review. Int. J. Sustain. Transp. 2018, 1, 21–29. [Google Scholar] [CrossRef]
- Jagadeesh, P.; Puttegowda, M.; Oladijo, O.P.; Lai, C.W.; Gorbatyuk, S.; Matykiewicz, D.; Rangappa, S.M.; Siengchin, S. A comprehensive review on polymer composites in railway applications. Polym. Compos. 2022, 43, 1238. [Google Scholar] [CrossRef]
- Alshahrani, H.; Ahmed, A. Enhancing Impact Energy Absorption, Flexural and Crash Performance Properties of Automotive Composite Laminates by Adjusting the Stacking Sequences Layup. Polymers 2021, 13, 3404. [Google Scholar] [CrossRef]
- Ahmed, O.; Aabid, A.; Ali, J.; Hrairi, M.; Yatim, N. Progresses and Challenges of Composite Laminates in Thin-Walled Structures: A Systematic Review. ACS Omega 2023, 8, 30824–30837. [Google Scholar] [CrossRef] [PubMed]
- Azad, M.; Cheon, Y.; Raouf, I.; Khalid, S.; Kim, H. Intelligent Computational Methods for Damage Detection of Laminated Composite Structures for Mobility Applications: A Comprehensive Review. Arch. Comput. Methods Eng. 2024, 32, 441–469. [Google Scholar] [CrossRef]
- Yan, L.; Xu, H. Lightweight composite materials in automotive engineering: State-of-the-art and future trends. Alex. Eng. J. 2025, 118, 1–10. [Google Scholar] [CrossRef]
- Jiang, H.; Ren, Y.; Liu, Z.; Zhang, S.; Lin, Z. Low-velocity impact resistance behaviors of bio-inspired helicoidal composite laminates with non-linear rotation angle based layups. Compos. Struct. 2019, 214, 463–475. [Google Scholar] [CrossRef]
- Riccio, A.; Caprio, F.; Tsai, S.; Russo, A.; Sellitto, A. Optimization of composite aeronautical components by Re-Designing with Double-Double Laminates. Aerosp. Sci. Technol. 2024, 151, 109304. [Google Scholar] [CrossRef]
- Wang, J.; Chang, Z.; Liu, T.; Chen, L. A review of linear and nonlinear vibration analysis of composite laminated structures by computational approaches: 2015–2024. Nonlinear Dyn. 2025, 113, 10839–10859. [Google Scholar] [CrossRef]
- Parveez, B.; Kittur, M.; Badruddin, I.; Kamangar, S.; Hussien, M.; Umarfarooq, M. Scientific Advancements in Composite Materials for Aircraft Applications: A Review. Polymers 2022, 14, 5007. [Google Scholar] [CrossRef]
- Hynes, N.; Vignesh, N.; Jappes, J.; Velu, P.; Barile, C.; Ali, M.; Pruncu, C. Effect of stacking sequence of fibre metal laminates with carbon fibre reinforced composites on mechanical attributes: Numerical simulations and experimental validation. Compos. Sci. Technol. 2022, 221, 109303. [Google Scholar] [CrossRef]
- Redmann, A.; Montoya-Ospina, M.; Karl, R.; Rudolph, N.; Osswald, T. High-force dynamic mechanical analysis of composite sandwich panels for aerospace structures. Compos. Part C Open Access 2021, 5, 100136. [Google Scholar] [CrossRef]
- Shiferaw, H.; Woldemariam, M.; Redda, D.; Ahmed, A. Drop-Weight Impact Analysis of Unidirectional Sisal Fiber –Reinforced Epoxy Resin Composite Material for Automotive Application Based on ASTM D-7136 Standard. J. Eng. 2025, 2025, 5102865. [Google Scholar] [CrossRef]
- Xiao, H.; Sultan, M.; Shahar, F.; Gaff, M.; Hui, D. Recent developments in the mechanical properties of hybrid fiber metal laminates in the automotive industry: A review. Rev. Adv. Mater. Sci. 2023, 62, 20220328. [Google Scholar] [CrossRef]
- Ma’ruf, B.; Ismail, A.; Sari, D.; Sujiatanti, S. Strength analysis of marine biaxial warp-knitted glass fabrics as composite laminations for ship material. Curved Layer. Struct. 2023, 10, 20220209. [Google Scholar] [CrossRef]
- Okuma, S.; Obaseki, M.; Ofuyekpone, D.; Ashibudike, O. A Review Assessment of Fiber-Reinforced Polymers for Maritime Applications. J. Adv. Ind. Technol. Appl. 2023, 4, 17–28. [Google Scholar] [CrossRef]
- Islami, D.; Muzaqih, A.; Adiputra, R.; Prabowo, A.; Firdaus, N.; Ehlers, S.; Braun, M.; Jurkovič, M.; Smaradhana, D.; Carvalho, H. Structural design parameters of laminated composites for marine applications: Milestone study and extended review on current technology and engineering. Results Eng. 2024, 24, 103195. [Google Scholar] [CrossRef]
- Hussnain, S.; Shah, S.; Megat-Yusoff, P.; Hussain, M. Degradation and mechanical performance of fibre-reinforced polymer composites under marine environments: A review of recent advancements. Polym. Degrad. Stab. 2023, 215, 110452. [Google Scholar] [CrossRef]
- Derazkola, H.; Khodabakhshi, F.; Simchi, A. Evaluation of a polymer-steel laminated sheet composite structure produced by friction stir additive manufacturing (FSAM) technology. Polym. Test. 2020, 90, 106690. [Google Scholar] [CrossRef]
- Pradeep, M.; Arivendan, A.; Das, R.; Rajan, M. Effect of stacking sequences on the mechanical properties of high-performance glass fibre epoxy composites for lightweight manufacture applications. Proc. Inst. Mech. Eng. Part E J. Process Mech. Eng. 2025. [Google Scholar] [CrossRef]
- Basaran, M.; Turkmen, H.; Yildiz, M. Sensor-Enhanced Thick Laminated Composite Beams: Manufacturing, Testing, and Numerical Analysis. Sensors 2024, 24, 5366. [Google Scholar] [CrossRef]
- Wang, Q.-A.; Liu, Q.; Ma, Z.-G.; Wang, J.-F.; Ni, Y.-Q.; Ren, W.-X.; Wang, H.-B. Data interpretation and forecasting of SHM heteroscedastic measurements under typhoon conditions enabled by an enhanced Hierarchical sparse Bayesian Learning model with high robustness. Measurement 2024, 230, 114509. [Google Scholar] [CrossRef]
- Cascino, A.; Meli, E.; Rindi, A. Development of a Design Procedure Combining Topological Optimization and a Multibody Environment: Application to a Tram Motor Bogie Frame. Vehicles 2024, 6, 1843–1856. [Google Scholar] [CrossRef]
- Cascino, A.; Meli, E.; Rindi, A. A New Strategy for Railway Bogie Frame Designing Combining Structural–Topological Optimization and Sensitivity Analysis. Vehicles 2024, 6, 651–665. [Google Scholar] [CrossRef]
- Grasso, M.; Gallone, A.; Genovese, A.; Macera, L.; Penta, F.; Pucillo, G.; Strano, S. Composite material design for rail vehicle innovative lightweight components. In Proceedings of the World Congress on Engineering, London, UK, 1–3 July 2015. [Google Scholar]
- Yang, C.; Ying, G.; Guo, W.; Yang, Y.; Xu, P.; Alqahtani, M.S. High-velocity impact behaviour of curved GFRP composites for rail vehicles: Experimental and numerical study. Polym. Test. 2022, 116, 107774. [Google Scholar] [CrossRef]
- Cascino, A.; Meli, E.; Rindi, A. Comparative Analysis and Dynamic Size Optimization of Aluminum and Carbon Fiber Thin-Walled Structures of a Railway Vehicle Car Body. Materials 2025, 18, 1501. [Google Scholar] [CrossRef]
- EN 12663-1:2015; Railway Applications-Structural Requirements of Railway Vehicle Bodies-Part 1: Locomotives and Passenger Rolling Stock (and Alternative Method for Freight Wagons). German Institute for Standardization: Berlin, Germany, 2015.
- UNI EN 1999-1-1:2014; Eurocode 9: Design of Aluminium Structures—Part 1-1: General Rules—General Rules and Rules for Buildings. European Union: Bruxelles, Brussels, 2014.
- UNI EN 15663:2019; Railway Applications-Vehicle Reference Masses. European Union: Bruxelles, Brussels, 2019.
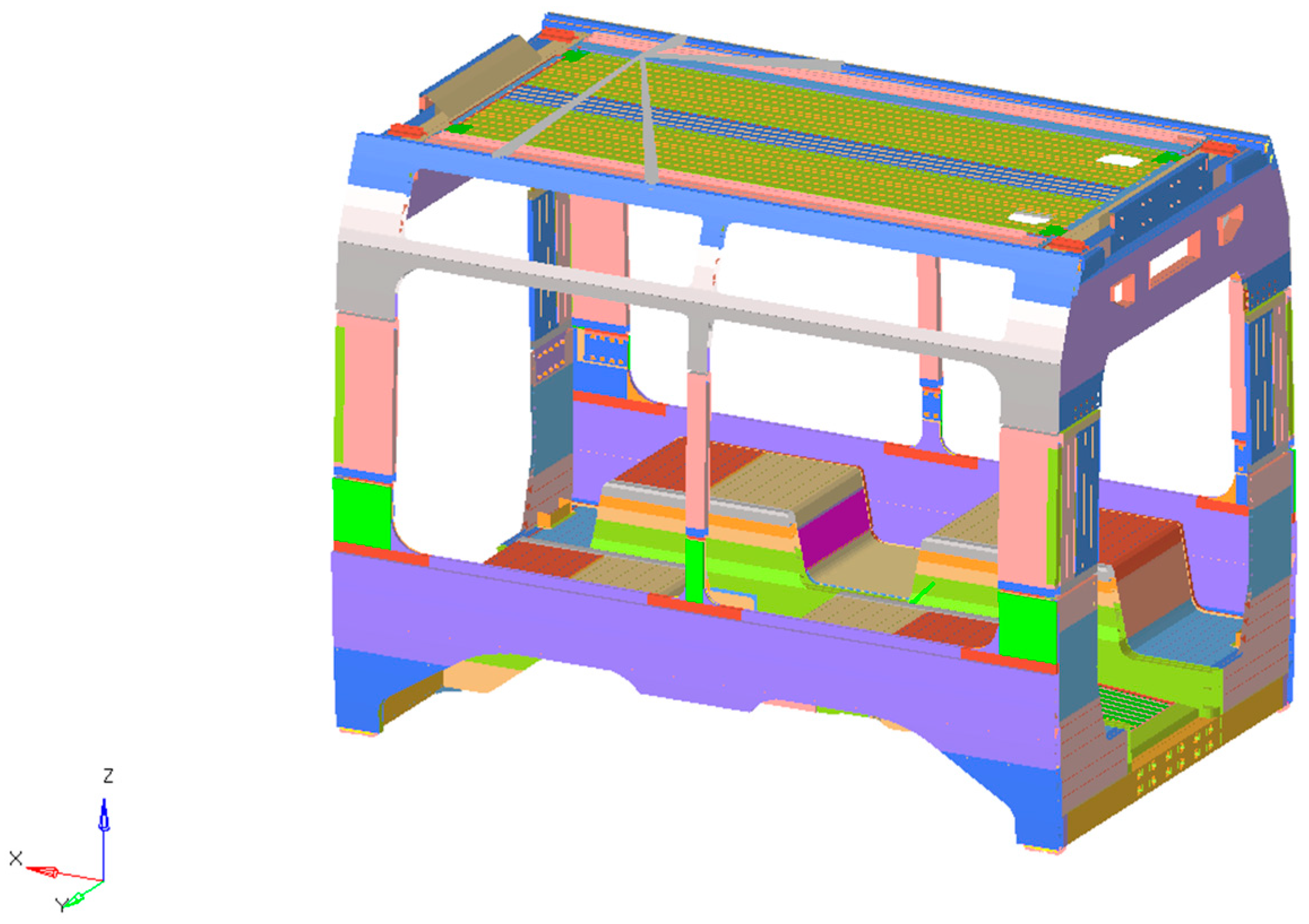
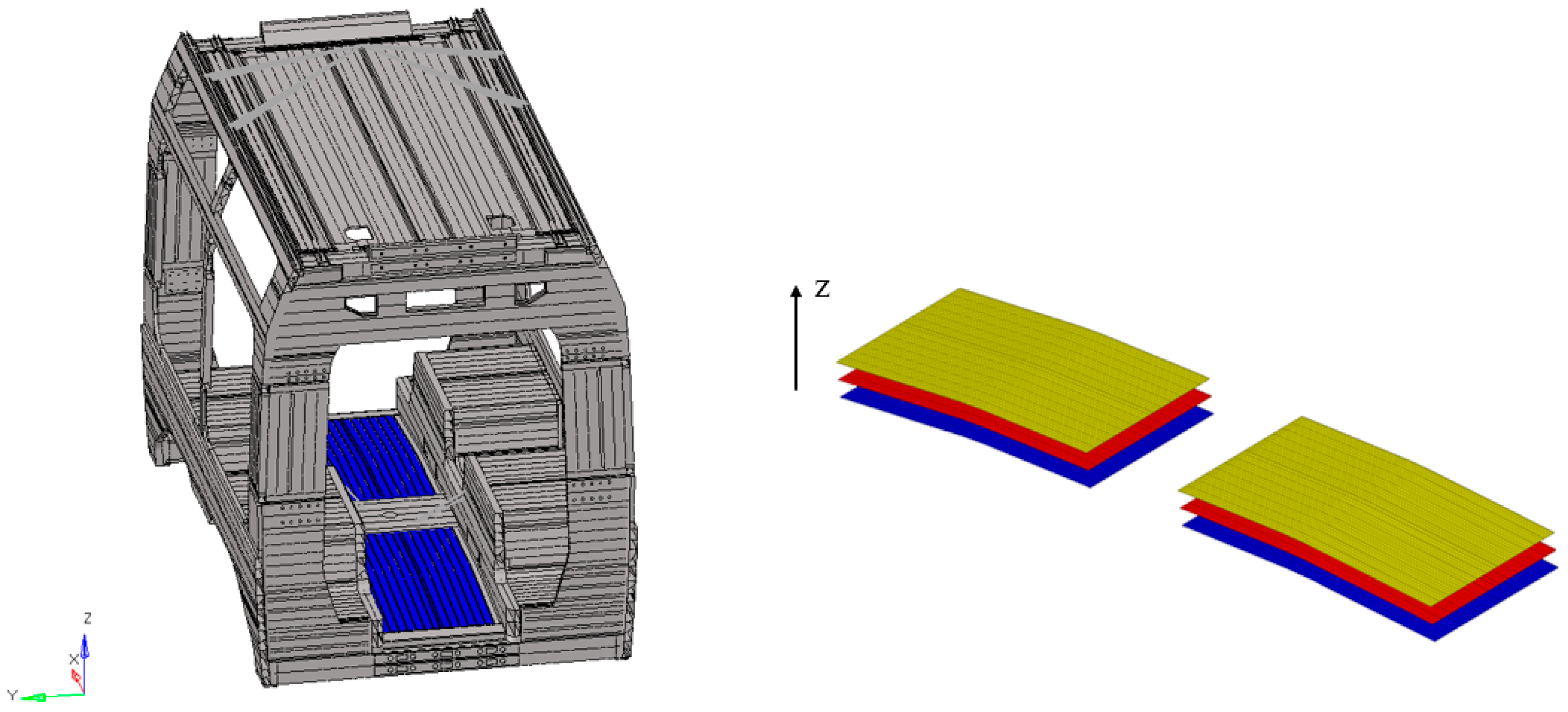

| Material | Density | Young’s Modulus | Proof Strength (0.2%) | Ultimate Tensile Strength | Proof Strength (0.2%) | Ultimate Tensile Strength | Poisson’s Ratio |
|---|---|---|---|---|---|---|---|
| Base Material | Weld Material | ||||||
| [kg/m3] | [N/mm2] | [N/mm2] | [N/mm2] | [-] | |||
| EN AW 6106 T6 | 2700 | 70,000 | 200 | 250 | 95 | 160 | 0.30 |
| Ply | Material | Thickness [mm] | Density [kg/m3] | E1 [GPa] | E2 [GPa] | ν12 [GPa] | G12 [GPa] | G13 [GPa] | G23 [GPa] |
|---|---|---|---|---|---|---|---|---|---|
| 1 | Carbon fiber/Epoxy | 1 | 1590 | 135 | 8.0 | 0.30 | 5.0 | 5.0 | 3.0 |
| 2 | Glass fiber/Epoxy | 1 | 2010 | 40 | 10.0 | 0.25 | 4.5 | 4.5 | 3.5 |
| 3 | Aramid fiber/Epoxy | 1 | 1400 | 25 | 7.5 | 0.35 | 3.0 | 3.0 | 2.0 |
| Ply | Material | Xt [GPa] | Xc [GPa] | Yt [GPa] | Yc [GPa] | S [GPa] | τIL [GPa] |
|---|---|---|---|---|---|---|---|
| 1 | Carbon fiber/Epoxy | 1500 | 800 | 60 | 160 | 80 | 60 |
| 2 | Glass fiber/Epoxy | 400 | 250 | 80 | 150 | 50 | 40 |
| 3 | Aramid fiber/Epoxy | 1200 | 700 | 40 | 140 | 30 | 35 |
| Stack | Sequence (Bottom → Top) |
|---|---|
| stack_1 | Carbon/Glass/Aramid |
| stack_2 | Carbon/Aramid/Glass |
| stack_3 | Glass/Carbon/Aramid |
| stack_4 | Glass/Aramid/Carbon |
| stack_5 | Aramid/Carbon/Glass |
| stack_6 | Aramid/Glass/Carbon |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cascino, A.; Meli, E.; Rindi, A. Design and Optimization of a Hybrid Railcar Structure with Multilayer Composite Panels. Materials 2025, 18, 5013. https://doi.org/10.3390/ma18215013
Cascino A, Meli E, Rindi A. Design and Optimization of a Hybrid Railcar Structure with Multilayer Composite Panels. Materials. 2025; 18(21):5013. https://doi.org/10.3390/ma18215013
Chicago/Turabian StyleCascino, Alessio, Enrico Meli, and Andrea Rindi. 2025. "Design and Optimization of a Hybrid Railcar Structure with Multilayer Composite Panels" Materials 18, no. 21: 5013. https://doi.org/10.3390/ma18215013
APA StyleCascino, A., Meli, E., & Rindi, A. (2025). Design and Optimization of a Hybrid Railcar Structure with Multilayer Composite Panels. Materials, 18(21), 5013. https://doi.org/10.3390/ma18215013








