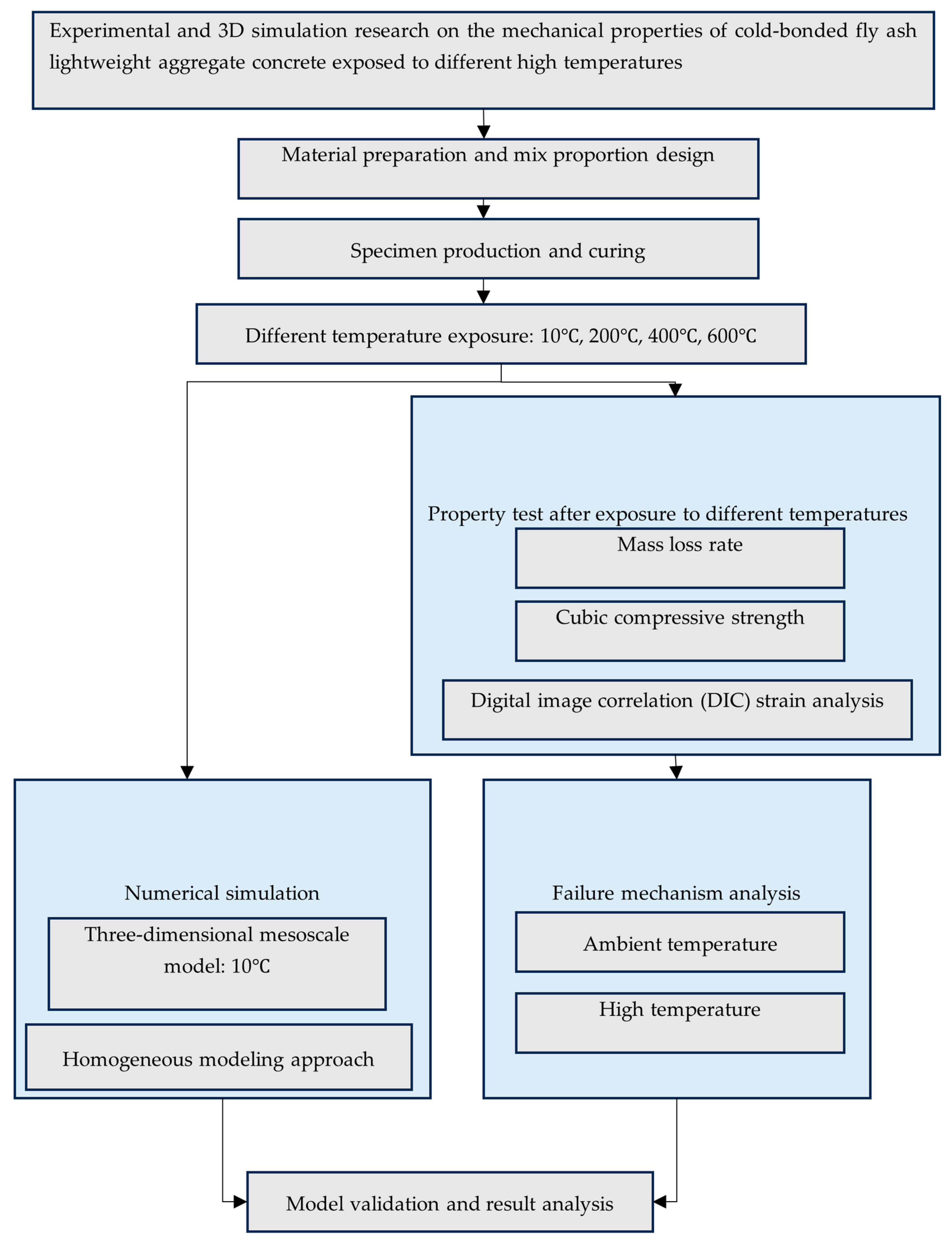
3.4. Destruction Mechanism of LWC-CB Specimen After 10 °C and High Temperature
At 10 °C, the strength of CB aggregates is lower than that of the mortar, and consequently, the strength of the CB aggregates effectively determines the strength of the LWC-CB. Micro-strain in the specimen during compression was observed using DIC equipment.
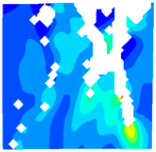
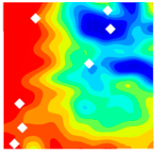
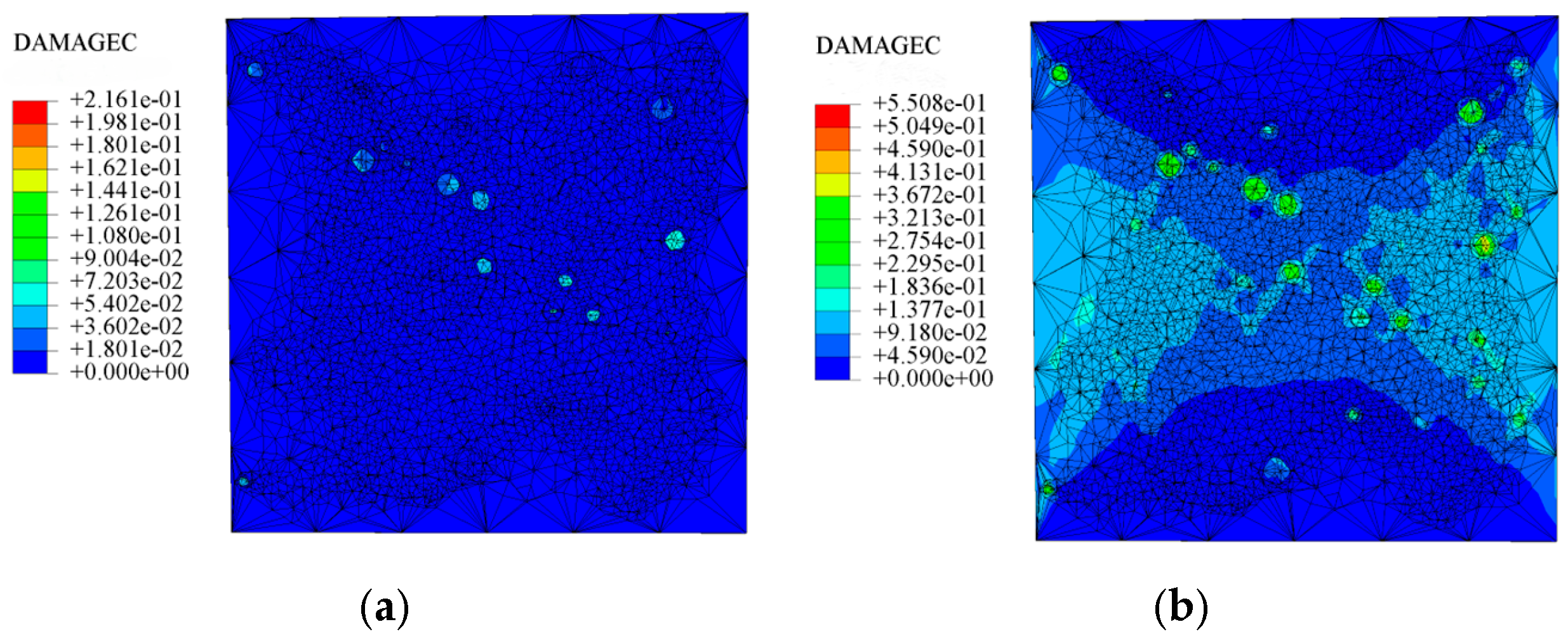
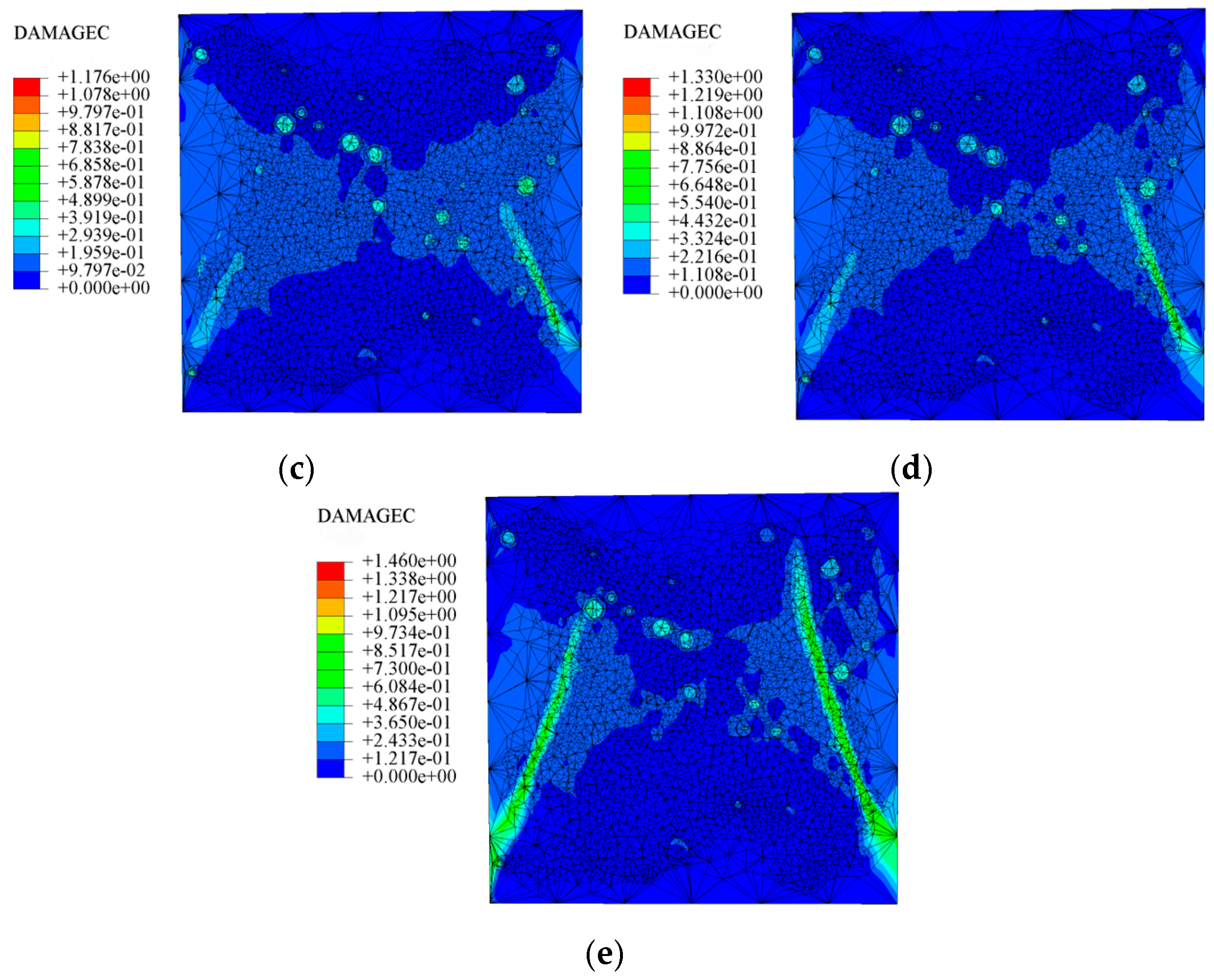
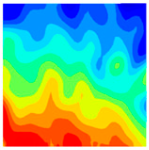
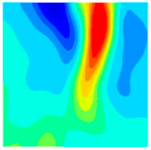
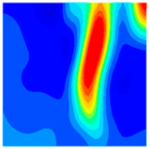
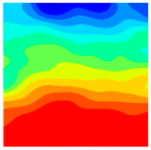
Table 10 below presents the longitudinal (uniaxial compression direction) and transverse (direction perpendicular to uniaxial compression) strain contour plots of 10 °C specimens under different stress levels, obtained via DIC.
Figure 10 illustrates the post-damage morphology of LWC-CB after the 10 °C compression test.
10(a), 10(b), 10(c), 10(d), 10(a′), 10(b′), 10(c′), 10(d′): “10” indicates a temperature of 10 °C. The letters in parentheses (a, b, c, d, a′, b′, c′, d′) identify different test conditions, specimens or test stages. They are used to distinguish strain test results under different conditions at 10 °C.
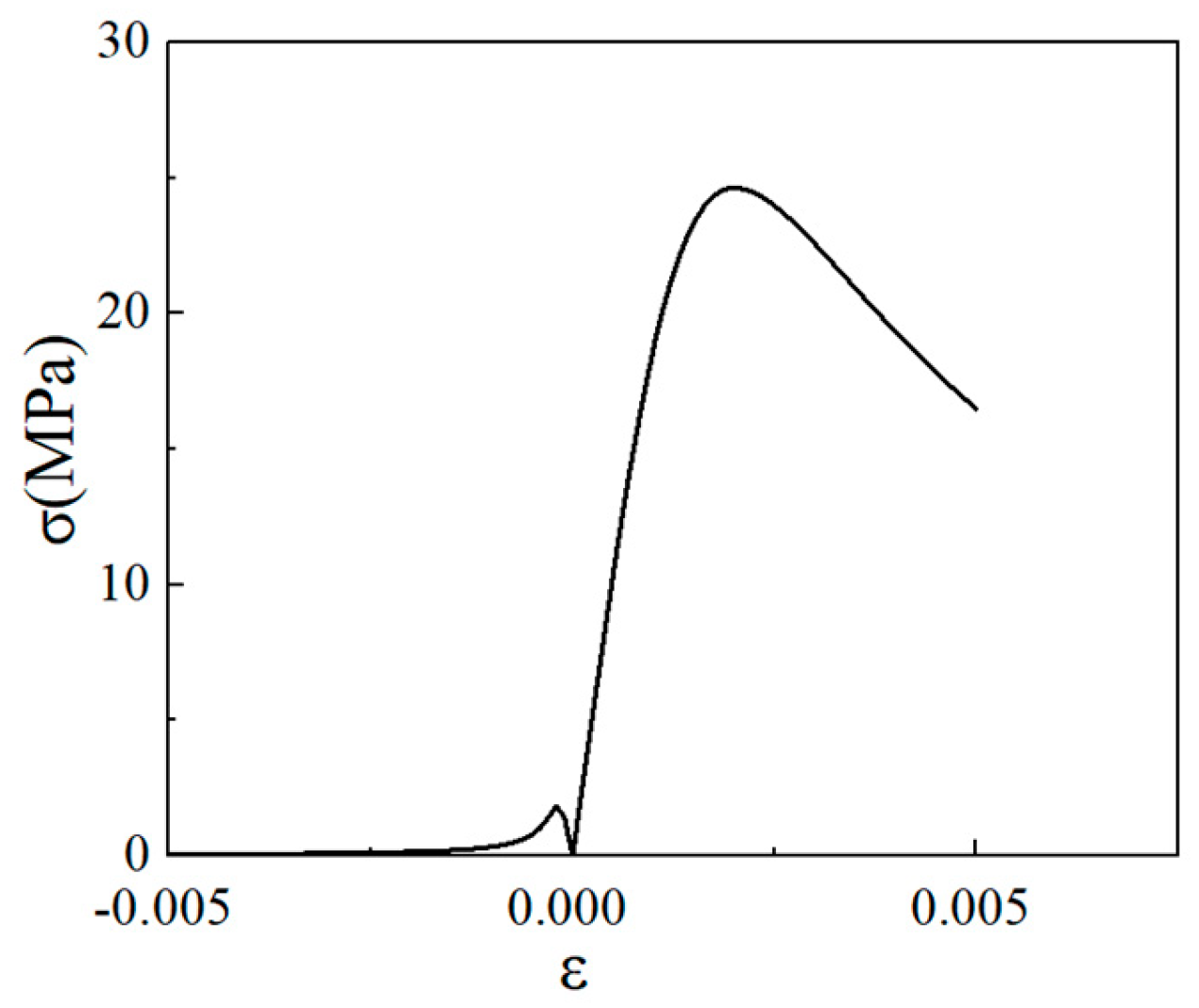
When observing the above figures at 10 °C during the initial loading stage, the transverse strain field ε
x remains relatively stable, with strain values at the top and bottom edges of the specimen being higher than those at the center. They are 267.6 με and −203.1 με, respectively. This is consistent with the findings of studies by Jinna Shi [
26] and Grzegorz Ludwik Golewski [
27]. Meanwhile, stress concentration emerges in specific regions of the top and bottom edges, as depicted in 10(a) within
Table 10. For the longitudinal strain ε
y, the specimen is under compression at this stage, and internal gaps within the specimen are closed by pressure. The specimen gradually compresses, with the maximum compression value appearing at the top and bottom of the specimen. The strains are 367.6 με and −381.8 με. As shown in 10(a′) within
Table 11.
As the load continues to increase to 0.3 fcT, both longitudinal and transverse strains increase. In the transverse strain contour plot, obvious stress concentration appears in specific regions of the top and bottom edges, corresponding to the longitudinal strain contour plot. It concentrates on the lower left corner of the test block, with the maximum values of longitudinal strain and transverse strain being −1360.4 με and 881.0 με, respectively. In the longitudinal strain contour plot, the compression zone of longitudinal stress spreads from the edge regions to the middle. At 0.8 fcT, in the transverse strain field εx, stress concentration zones at the top and bottom edges spread to the center along vulnerable regions. The longitudinal stress compression region not only extends inward but also spreads laterally, with the maximum compression of the longitudinal strain region appearing in the stress concentration zones corresponding to εy.
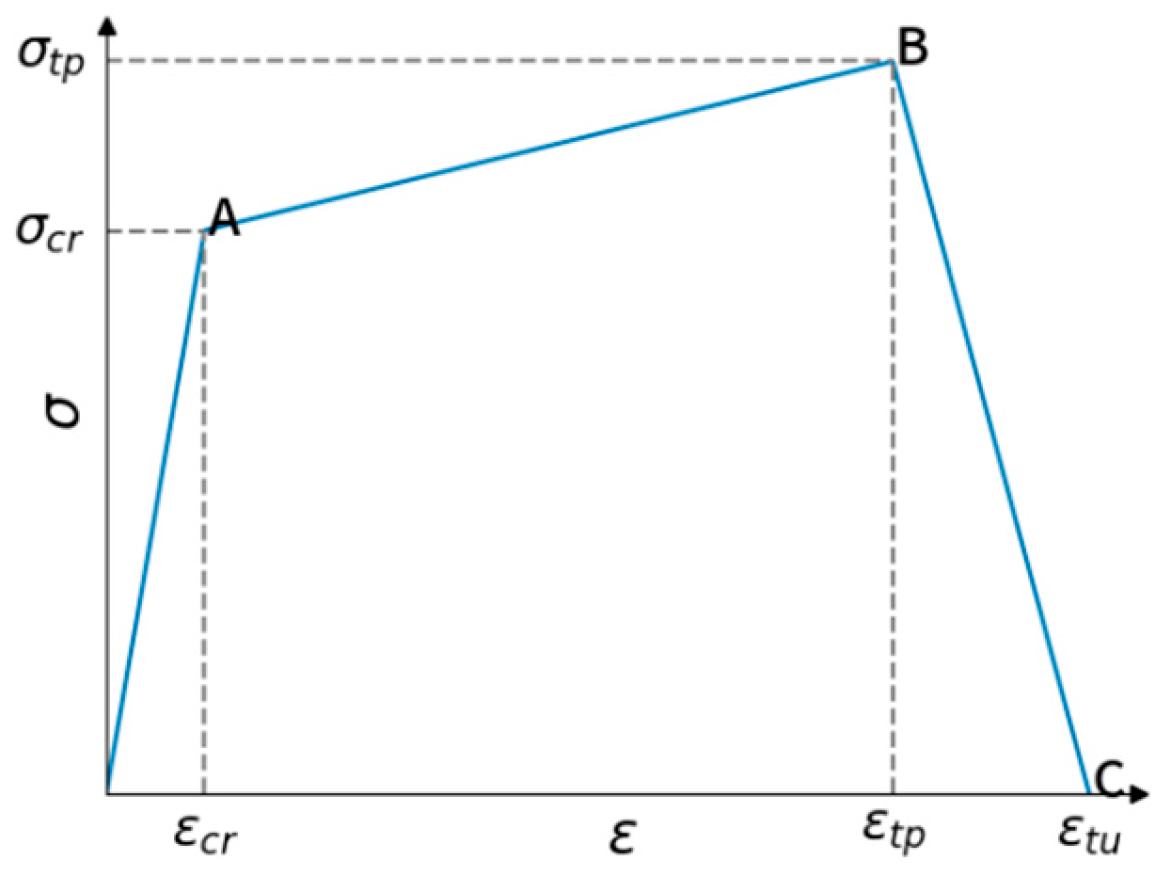
At peak stress
fcT, since the tensile strength of concrete itself is much lower than its compressive strength, with increasing load, transverse deformation occurs due to the Poisson effect. This deformation is constrained by the surrounding concrete, generating transverse tensile stresses. When this tensile stress exceeds the tensile strength of concrete, the specimen develops cracks. As shown in the figures, the transverse strain increases sharply to 7067.3 με, corresponding to a longitudinal strain region of −1920.4 με. The strain concentration zones in the transverse strain contour plot form through-cracks across the specimen as the load increases. The crack initiation process is consistent with that captured by DIC equipment in studies by Jinna Shi [
26] and Grzegorz Ludwik Golewski [
27].
Subsequently, due to excessive deformation, the DIC system was disengaged, and continuous recording was performed using a camera. As the load increased, longitudinal cracks propagated progressively, as shown in
Figure 11a, accompanied by fragment dislodgment. The final damage morphology of the specimen, depicted in
Figure 11b, exhibits a quadrangular cone structure with positive-inversion connection. Observing the test block’s final damage morphology and fragment shedding in
Figure 11c, it is evident that the aggregates were neatly sheared off.
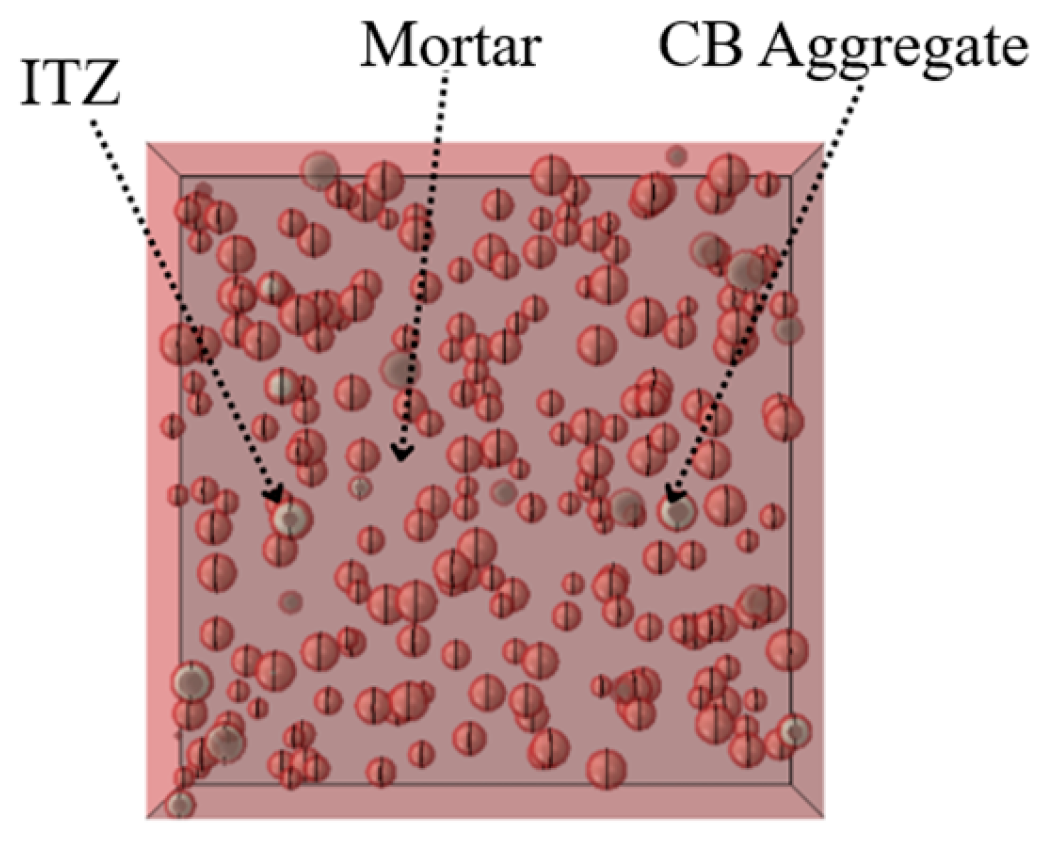
In natural aggregate concrete, the ITZ between coarse aggregates and mortar serves as the weak link, so interfacial damage typically dominates during cube compression tests. At 10 °C, the microstructure of the interface zone is relatively dense. When the temperature reaches 200~300 °C, CH begins to dehydrate, crystal lattices undergo severe distortion, pore channels increase, and numerous interfacial cracks form. These processes severely weaken interfacial bonding, causing a sharp decline in load-bearing capacity. After 400 °C, this degradation gradually intensifies with increasing temperature [
28,
29].
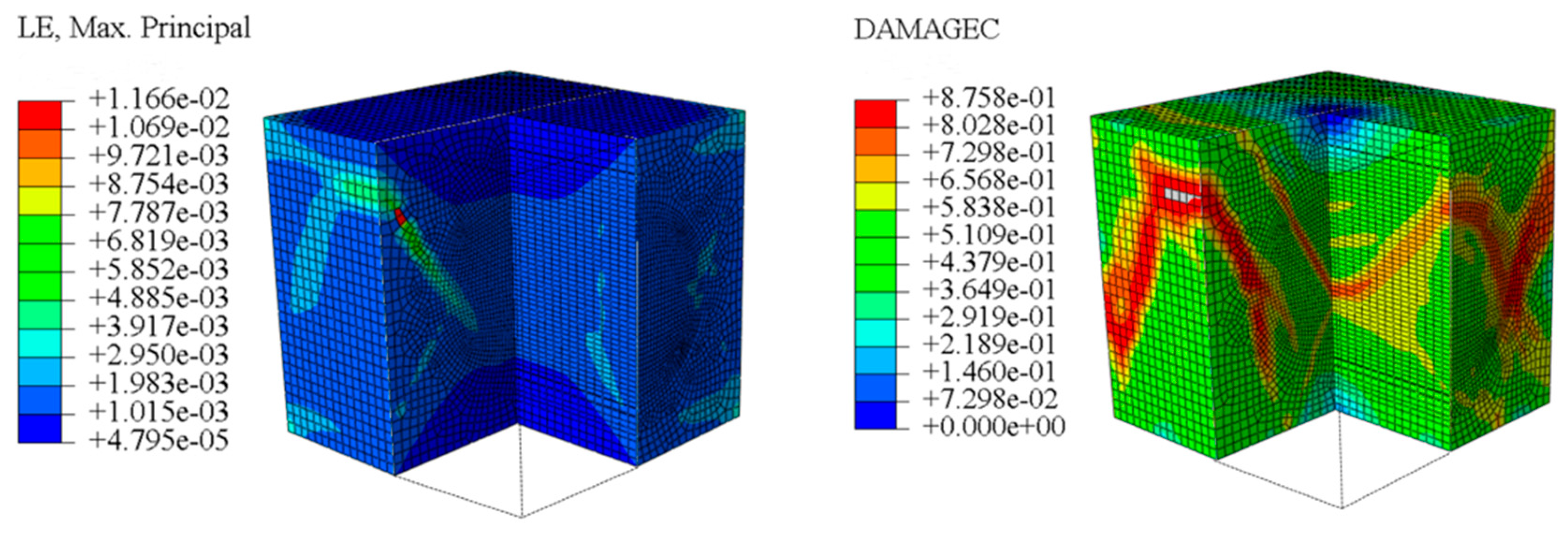
For LWC-CB specimens, the micro-strain during compression was observed using DIC equipment. The longitudinal and transverse strains of the specimens under uniaxial compression at different stress levels after exposure to various high temperatures are presented in
Table 12.
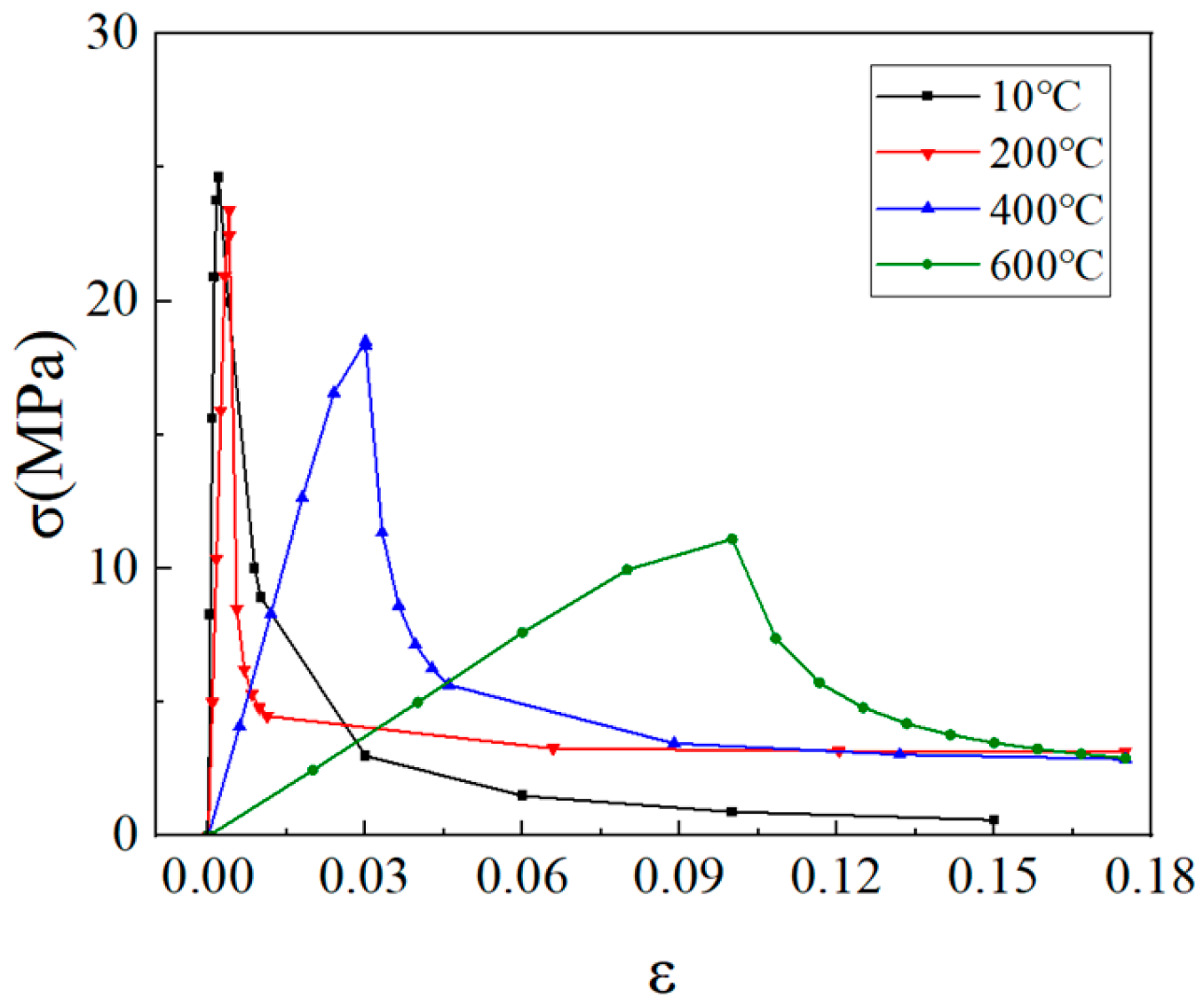
When observing specimens at 200 °C, 400 °C, and 600 °C, partial peeling of the surface occurs after high-temperature loading due to pressure, resulting in white areas in the strain contour plots. This effect becomes more pronounced with increasing temperature. For transverse and longitudinal strain contour plots at 0.3 fcT, 0.8 fcT, and fcT, compared with the 10 °C concrete, the transverse strain contour plots of high-temperature-exposed concrete exhibit stress concentration in edge regions at the initial stage. Moreover, the test blocks exhibit relatively large strain values at the initial loading stage. For instance, under the conditions of 200 °C, 400 °C, and 600 °C, the maximum transverse strain values are generally more than twice those at 10 °C. At the same stress level, the stress concentration area is larger at higher temperatures, with a clear trend of expansion as temperature increases. At 0.3 fcT, 0.8 fcT, and fcT, the maximum transverse strain values under 200 °C, 400 °C, and 600 °C are 5.4 times, 6.1 times, and 9 times those at 10 °C, respectively.
In the longitudinal strain contour plots, longitudinal compression strain propagates rapidly across the entire plane. Although the maximum longitudinal compression strain appears in the region corresponding to the transverse strain concentration area, the range of this maximum strain region expands with increasing stress ratio and temperature. After high-temperature exposure, the specimen becomes loose, with severe damage to particle connections and structural integrity. The internal structure cannot co-load efficiently after loading, leading to delayed force transfer. This results in a mismatch between transverse and longitudinal strain concentration areas, causing premature failure of the transverse strain concentration regions before full propagation.
Jinna Shi [
26] investigated the deformation properties of ordinary concrete after high temperatures. Ordinary concrete also has the following characteristics. First, the higher the temperature, the larger the stress concentration area. It tends to expand as temperature rises. Second, after high-temperature exposure, the test blocks become loose. There is a mismatch between transverse and longitudinal strain concentration areas. However, LWC-CB shows these two characteristics more obviously than ordinary concrete. This also explains why the compressive strength of LWC-CB is lower than that of ordinary concrete after 500 °C.
After the DIC system was disengaged, crack propagation was recorded using a camera, as shown in
Figure 12a,c,e. The final damage morphology of the specimens, depicted in
Figure 12b for each temperature, also exhibits a positive inversion connecting the tetragonal cone. Observing the specimens’ final damage morphology, it is evident that with increasing temperature, CB aggregates are not gradually sheared; instead, internal cracks within the specimens progressively increase, and the mortar structure becomes loose.
For the specimen heated to 200 °C, the CB aggregates in the middle of the damage surface are crushed, while the edge regions of CB aggregates detach and crack from the surrounding mortar, indicating that the bonding strength between CB aggregates and mortar begins to weaken due to high temperature. At 400 °C, CB aggregates are basically no longer crushed, but mortar cracks widen and extend to through-cracks. At this temperature, CH within the mortar starts to dehydrate and decompose, leading to significant reduction in CH quantity, crystal defects, loose structure, pore cracks, and interfacial cracks with CB aggregates, which decreases the bonding strength between CB aggregates and mortar.
As the temperature continues to rise, these structural changes in the mortar gradually intensify, causing continuous strength degradation and severe weakening of interfacial bonding force. Consequently, more interfacial cracking damage occurs between CB aggregates and mortar, as shown in
Figure 12f damage morphology, where most of the mortar is crushed into powder. At this stage, the strength-determining factors of LWC-CB are no longer solely CB aggregates but also depend on mortar strength and interfacial adhesion.















 10(a)
10(a)
 10(b)
10(b)
 10(c)
10(c)
 10(d)
10(d)
 10(a′)
10(a′)
 10(b′)
10(b′)
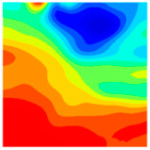 10(c′)
10(c′)
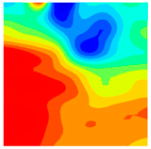 10(d′)
10(d′)