Multi-Parameter Modulation of Dirac Plasmons in Germanene via Doping and Strain: A DFT Insight
Abstract
1. Introduction
2. Methods and Computational Details
- (1)
- (2)
- Evaluation of the full non-interacting response function χ0 via the Hilbert transform:
- (3)
- Construction of the interacting response function χ using the Dyson equation [47]:
- (4)
- Computation of the inverse dielectric function:
- (5)
- Identification of plasmon excitations as peaks in the energy loss spectrum:
3. Results and Discussions
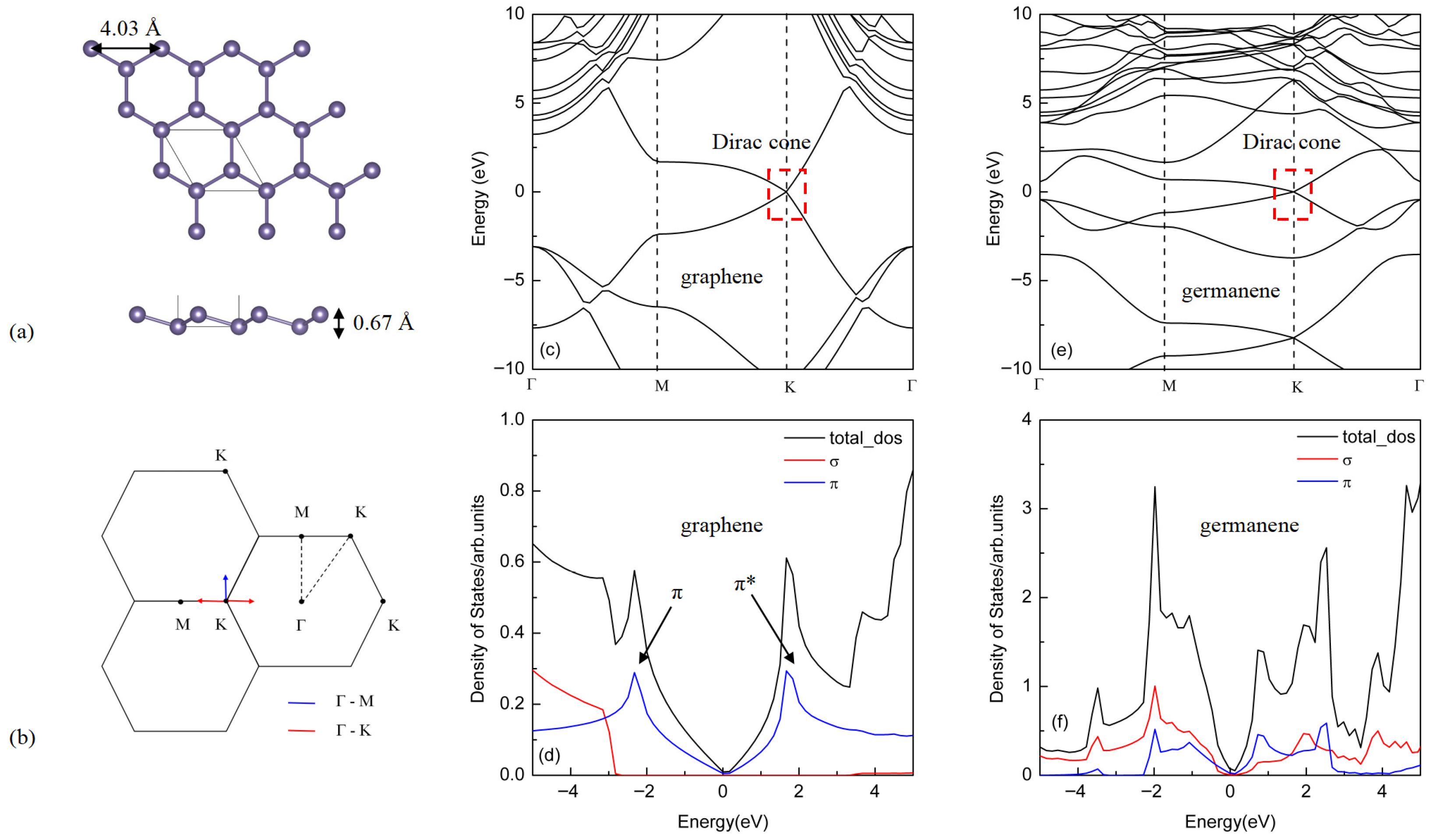
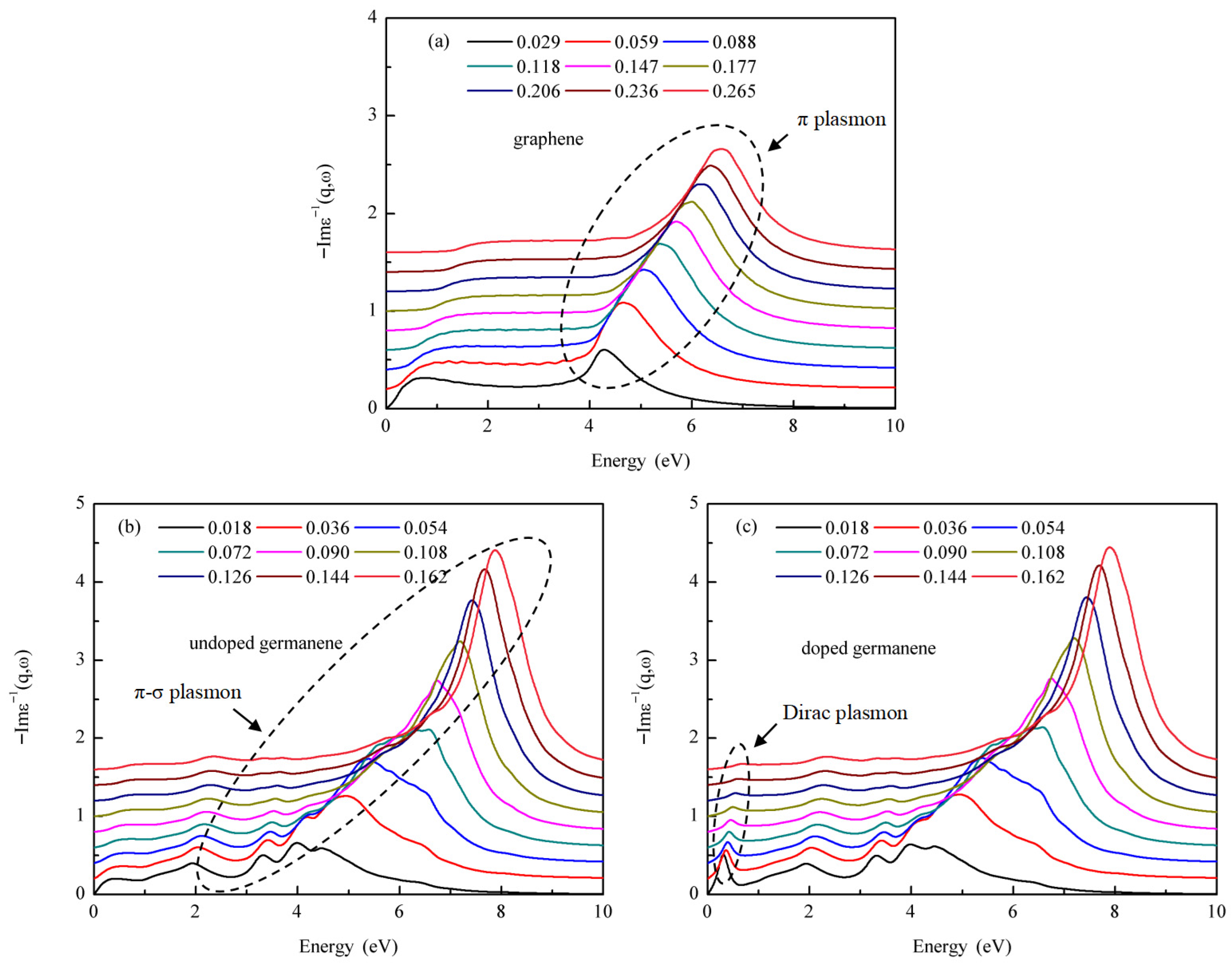
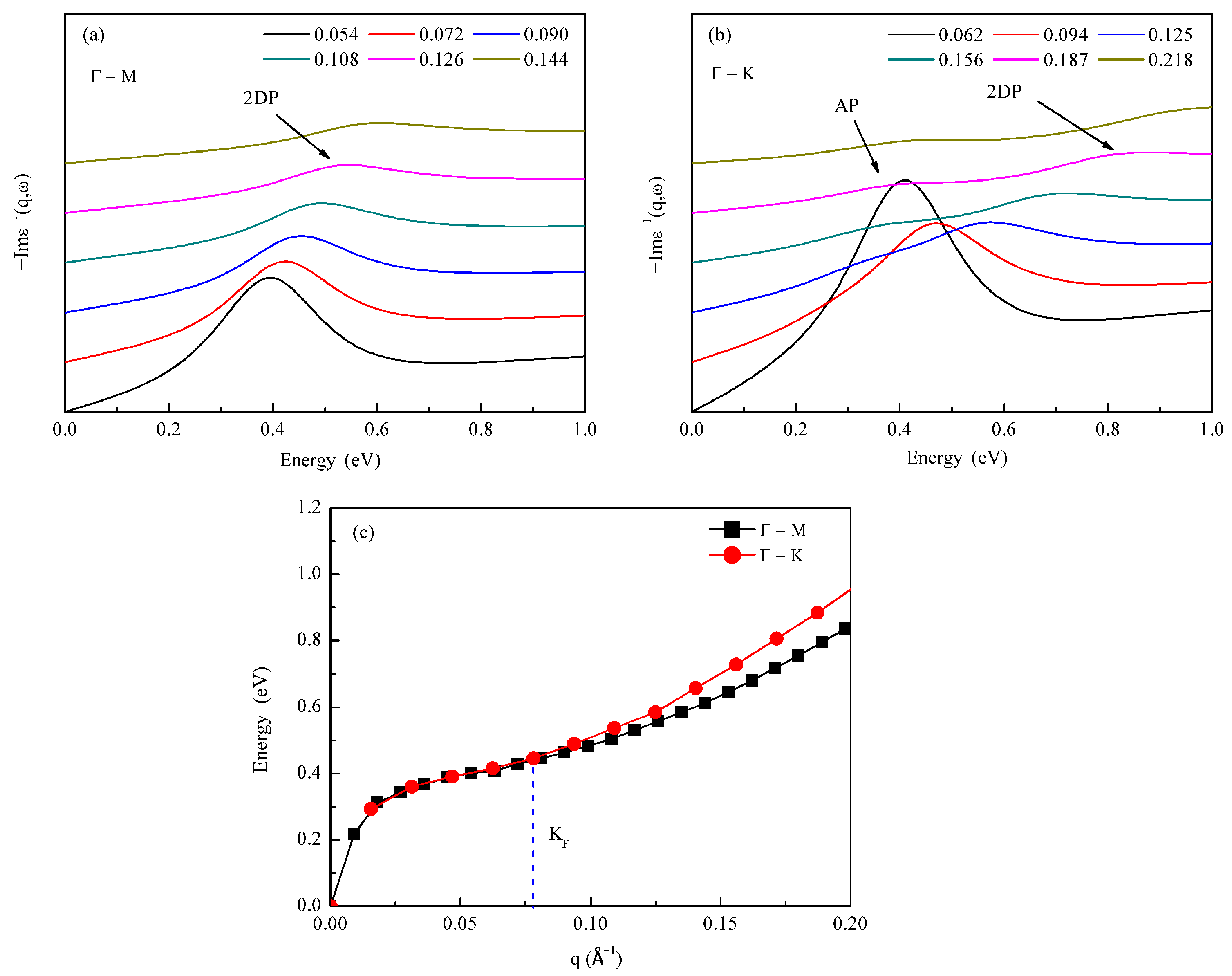
3.1. The Overall Characteristics of Germanene Plasmons
3.2. Carrier Concentration Modulation for Germanene Dirac Plasmons
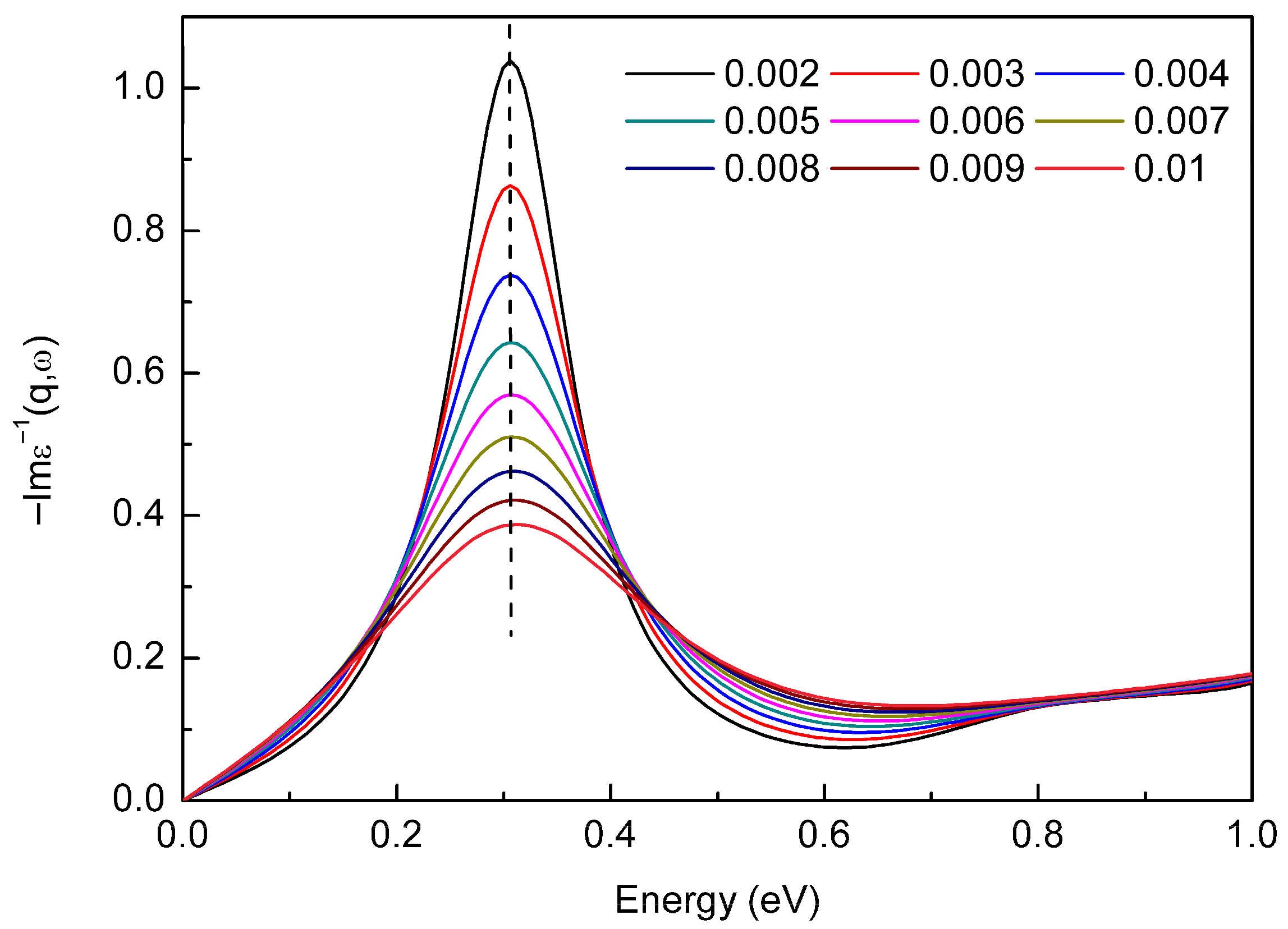
3.3. Biaxial Strain Modulation for Germanene Dirac Plasmons
3.4. Cooperative Modulation of Dirac Plasmon in Germanene by Carrier Concentration and Biaxial Strain
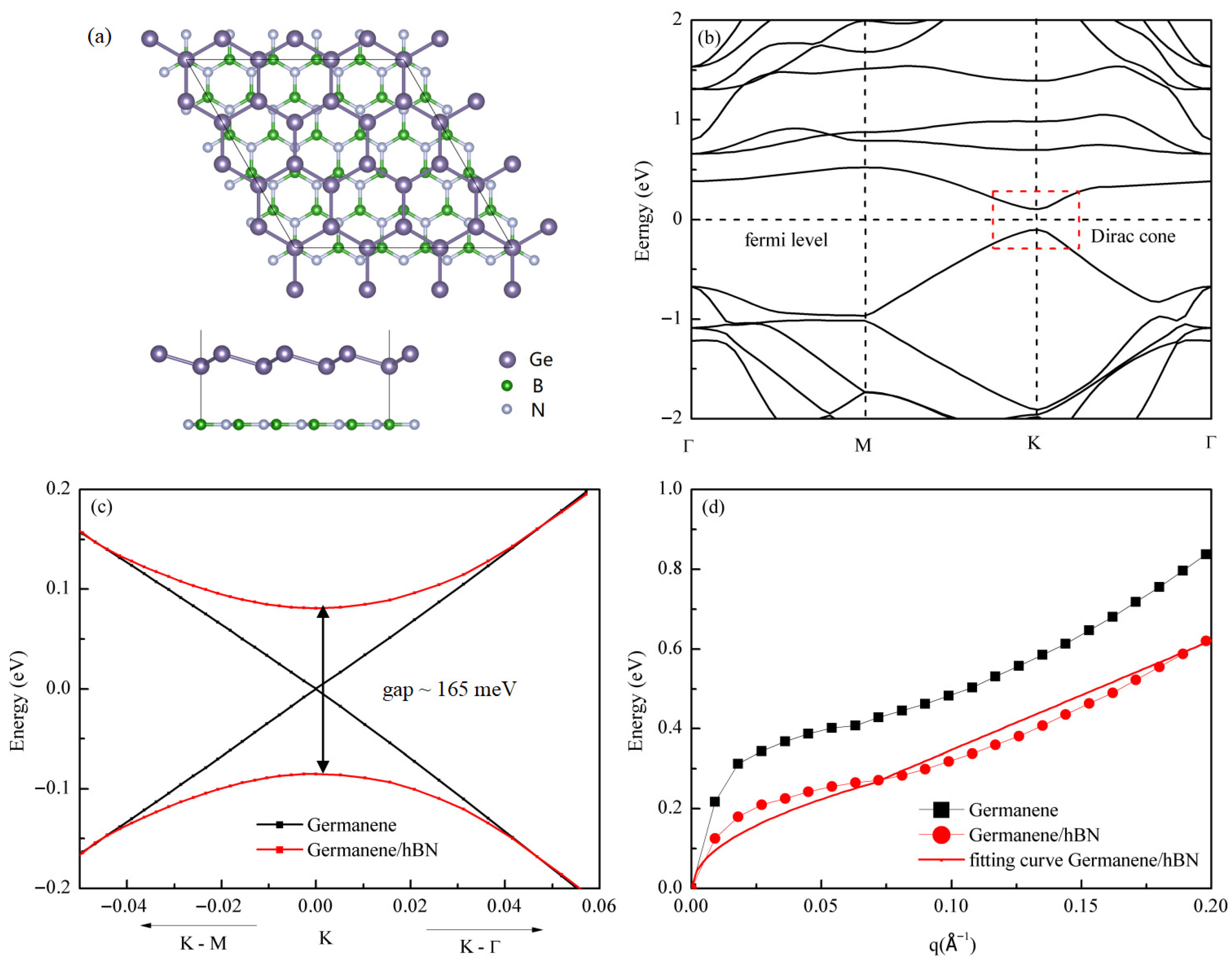
3.5. The Effect of Substrate on Dirac Plasmons in Germanene
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Cahangirov, S.; Topsakal, M.; Aktürk, E.; Şahin, H.; Ciraci, S. Two- and one-dimensional honeycomb structures of silicon and germanium. Phys. Rev. Lett. 2009, 102, 236804. [Google Scholar] [CrossRef]
- Liu, C.C.; Feng, W.; Yao, Y. Quantum spin Hall effect in silicene and two-dimensional germanium. Phys. Rev. Lett. 2011, 107, 076802. [Google Scholar] [CrossRef]
- Liu, C.C.; Jiang, H.; Yao, Y. Low-energy effective Hamiltonian involving spin-orbit coupling in silicene and two-dimensional germanium and tin. Phys. Rev. B 2011, 84, 195430. [Google Scholar]
- Li, L.; Lu, S.Z.; Pan, J.; Qin, Z.; Wang, Y.Q.; Wang, Y.; Cao, G.Y.; Du, S.X.; Gao, H.J. Buckled germanene formation on Pt (111). Adv. Mater. 2014, 26, 4820–4824. [Google Scholar] [CrossRef]
- Dávila, M.E.; Xian, L.; Cahangirov, S.; Rubio, A.; Le Lay, G. Germanene: A novel two-dimensional germanium allotrope akin to graphene and silicene. New J. Phys. 2014, 16, 095002. [Google Scholar] [CrossRef]
- Qin, Z.; Pan, J.; Lu, S.; Shao, Y.; Wang, Y.; Du, S.; Gao, H.J.; Cao, G. Direct evidence of Dirac signature in bilayer germanene islands on Cu (111). Adv. Mater. 2017, 29, 1606046. [Google Scholar] [CrossRef] [PubMed]
- Mu, H.; Liu, Y.; Bongu, S.R.; Bao, X.; Li, L.; Xiao, S.; Zhuang, J.; Liu, C.; Huang, Y.; Dong, Y.; et al. Germanium nanosheets with dirac characteristics as a saturable absorber for ultrafast pulse generation. Adv. Mater. 2021, 33, 2101042. [Google Scholar] [CrossRef] [PubMed]
- Bampoulis, P.; Castenmiller, C.; Klaassen, D.J.; Van Mil, J.; Liu, Y.; Liu, C.C.; Yao, Y.G.; Ezawa, M.; Rudenko, A.; Zandvliet, H.J. Quantum spin Hall states and topological phase transition in germanene. Phys. Rev. Lett. 2023, 130, 196401. [Google Scholar] [CrossRef]
- Xi, Y.; Jing, X.; Xu, Z.; Liu, N.; Liu, Y.; Lin, M.; Yang, M.; Sun, Y.; Zhuang, J.; Xu, X.; et al. Superconductivity in layered van der Waals hydrogenated germanene at high pressure. J. Am. Chem. Soc. 2022, 144, 18887–18895. [Google Scholar] [CrossRef]
- Kumar, V.; Santosh, R.; Sinha, A.; Kumar, J. The structural, electronic, and optical properties of hydrofluorinated germanene (GeH1-xFx): A first-principles study. J. Mol. Model. 2021, 27, 123. [Google Scholar] [CrossRef]
- Liu, S.; Li, X.; Liu, H.; Qiu, G.; Ma, J.; Nie, L.; Meng, Y.; Hu, X.; Ni, H.; Niu, Z.; et al. Super-resolved snapshot hyperspectral imaging of solid-state quantum emitters for high-throughput integrated quantum technologies. Nat. Photon. 2024, 18, 967–974. [Google Scholar] [CrossRef]
- Chen, Y.; Zheng, X.; Zhang, X.; Pan, W.; Wang, Z.; Li, S.; Dong, S.; Liu, F.; He, Q.; Zhou, L.; et al. Efficient meta-couplers squeezing propagating light into on-chip subwavelength devices in a controllable way. Nano Lett. 2023, 23, 3326–3333. [Google Scholar] [CrossRef]
- Ma, J.; Ren, J.; Zhang, J.; Meng, J.; McManus-Barrett, C.; Crozier, K.B.; Sukhorukov, A.A. Quantum imaging using spatially entangled photon pairs from a nonlinear metasurface. eLight 2025, 5, 2. [Google Scholar] [CrossRef]
- Hu, H.; Yu, R.; Teng, H.; Hu, D.; Chen, N.; Qu, Y.; Yang, X.; Chen, X.; Dai, Q. Active control of micrometer plasmon propagation in suspended graphene. Nat. Commun. 2022, 13, 1465. [Google Scholar] [CrossRef] [PubMed]
- Grigorenko, A.N.; Polini, M.; Novoselov, K.S. Graphene plasmonics. Nat. Photon. 2012, 6, 749–758. [Google Scholar] [CrossRef]
- Rodrigo, D.; Limaj, O.; Janner, D.; Etezadi, D.; García de Abajo, F.J.; Pruneri, V.; Altug, H. Mid-infrared plasmonic biosensing with graphene. Science 2015, 349, 165–168. [Google Scholar] [CrossRef] [PubMed]
- Basov, D.N.; Fogler, M.M.; García de Abajo, F.J. Polaritons in van der Waals materials. Science 2016, 354, aag1992. [Google Scholar] [CrossRef]
- Lin, M.F.; Huang, C.S.; Chuu, D.S. Plasmons in graphite and stage-1 graphite intercalation compounds. Phys. Rev. B 1997, 55, 13961. [Google Scholar] [CrossRef]
- Ahuja, R.; Auluck, S.; Wills, J.M.; Alouani, M.; Johansson, B.; Eriksson, O. Optical properties of graphite from first-principles calculations. Phys. Rev. B 1997, 55, 4999. [Google Scholar] [CrossRef]
- Jablan, M.; Buljan, H.; Soljačić, M. Plasmonics in graphene at infrared frequencies. Phys. Rev. B 2009, 80, 245435. [Google Scholar] [CrossRef]
- Eberlein, T.; Bangert, U.; Nair, R.R.; Jones, R.; Gass, M.; Bleloch, A.L.; Briddon, P.R. Plasmon spectroscopy of free-standing graphene films. Phys. Rev. B 2008, 77, 233406. [Google Scholar] [CrossRef]
- Liu, Y.; Willis, R.F.; Emtsev, K.V.; Seyller, T. Plasmon dispersion and damping in electrically isolated two-dimensional charge sheets. Phys. Rev. B 2008, 78, 201403. [Google Scholar] [CrossRef]
- Lu, J.; Loh, K.P.; Huang, H.; Chen, W.; Wee, A.T. Plasmon dispersion on epitaxial graphene studied using high-resolution electron energy-loss spectroscopy. Phys. Rev. B 2009, 80, 113410. [Google Scholar] [CrossRef]
- Liou, S.C.; Shie, C.S.; Chen, C.H.; Breitwieser, R.; Pai, W.W.; Guo, G.Y.; Chu, M.W. π-plasmon dispersion in free-standing graphene by momentum-resolved electron energy-loss spectroscopy. Phys. Rev. B 2015, 91, 045418. [Google Scholar] [CrossRef]
- Guandalini, A.; Senga, R.; Lin, Y.C.; Suenaga, K.; Ferretti, A.; Varsano, D.; Recchia, A.; Barone, P.; Mauri, F.; Pichler, T.; et al. Excitonic effects in energy-loss spectra of freestanding graphene. Nano Lett. 2023, 23, 11835–11841. [Google Scholar] [CrossRef]
- Iurov, A.; Gumbs, G.; Huang, D. Temperature-dependent collective effects for silicene and germanene. J. Phys. Condens. Matter 2017, 29, 135602. [Google Scholar] [CrossRef]
- Shih, P.H.; Chiu, Y.H.; Wu, J.Y.; Shyu, F.L.; Lin, M.F. Coulomb excitations of monolayer germanene. Sci. Rep. 2017, 7, 40600. [Google Scholar] [CrossRef]
- Shih, P.H.; Chiu, C.W.; Wu, J.Y.; Do, T.N.; Lin, M.F. Coulomb scattering rates of excited states in monolayer electron-doped germanene. Phys. Rev. B 2018, 97, 195302. [Google Scholar] [CrossRef]
- Sindona, A.; Vacacela Gomez, C.; Pisarra, M. Dielectric screening versus geometry deformation in two-dimensional allotropes of silicon and germanium. Sci. Rep. 2022, 12, 15107. [Google Scholar] [CrossRef]
- Runge, E.; Gross, E.K. Density-functional theory for time-dependent systems. Phys. Rev. Lett. 1984, 52, 997. [Google Scholar] [CrossRef]
- Gross, E.K.U.; Kohn, W. Local density-functional theory of frequency-dependent linear response. Phys. Rev. Lett. 1985, 55, 2850. [Google Scholar] [CrossRef]
- Chen, M.; Guo, G.C.; He, L. Systematically improvable optimized atomic basis sets for ab initio calculations. J. Phys. Condens. Matter 2010, 22, 445501. [Google Scholar] [CrossRef] [PubMed]
- Li, P.; Liu, X.; Chen, M.; Lin, P.; Ren, X.; Lin, L.; He, L. Large-scale ab initio simulations based on systematically improvable atomic basis. Comput. Mater. Sci. 2016, 112, 503–517. [Google Scholar] [CrossRef]
- Schlipf, M.; Gygi, F. Optimization algorithm for the generation of ONCV pseudopotentials. Comput. Phys. Commun. 2015, 196, 36–44. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865. [Google Scholar] [CrossRef] [PubMed]
- Onida, G.; Reining, L.; Rubio, A. Electronic excitations: Density-functional versus many-body Green’s-function approaches. Rev. Mod. Phys. 2002, 74, 601. [Google Scholar] [CrossRef]
- Silkin, V.M.; Chulkov, E.V.; Echenique, P.M. Band structure versus dynamical exchange-correlation effects in surface plasmon energy and damping: A first-principles calculation. Phys. Rev. Lett. 2004, 93, 176801. [Google Scholar] [CrossRef] [PubMed]
- Yuan, Z.; Gao, S. Linear response approach to collective electronic excitations of solids and surfaces. Comput. Phys. Commun. 2009, 180, 466–473. [Google Scholar] [CrossRef]
- Mowbray, D.J. Theoretical electron energy loss spectroscopy of isolated graphene. Phys. Status Solidi B 2014, 251, 2509–2514. [Google Scholar] [CrossRef]
- Pines, D.; Bohm, D. A collective description of electron interactions: II. Collective vs individual particle aspects of the interactions. Phys. Rev. 1952, 85, 338. [Google Scholar] [CrossRef]
- Bohm, D.; Pines, D. A collective description of electron interactions: III. Coulomb interactions in a degenerate electron gas. Phys. Rev. 1953, 92, 609. [Google Scholar] [CrossRef]
- Wu, Y.; Li, G.; Camden, J.P. Probing nanoparticle plasmons with electron energy loss spectroscopy. Chem. Rev. 2017, 118, 2994–3031. [Google Scholar] [CrossRef]
- Li, P.; Shi, R.; Lin, P.; Ren, X. First-principles calculations of plasmon excitations in graphene, silicene, and germanene. Phys. Rev. B 2023, 107, 035433. [Google Scholar] [CrossRef]
- Li, P.; Hui, N. First-principles calculations and theoretical analysis of π plasmon in graphene and graphite: From 2D to 3D. Vacuum 2025, 240, 114424. [Google Scholar] [CrossRef]
- Adler, S.L. Quantum theory of the dielectric constant in real solids. Phys. Rev. 1962, 126, 413. [Google Scholar] [CrossRef]
- Wiser, N. Dielectric constant with local field effects included. Phys. Rev. 1963, 129, 62. [Google Scholar] [CrossRef]
- Petersilka, M.G.U.J.; Gossmann, U.J.; Gross, E.K.U. Excitation energies from time-dependent density-functional theory. Phys. Rev. Lett. 1996, 76, 1212. [Google Scholar] [CrossRef] [PubMed]
- Rozzi, C.A.; Varsano, D.; Marini, A.; Gross, E.K.; Rubio, A. Exact Coulomb cutoff technique for supercell calculations. Phys. Rev. B 2006, 73, 205119. [Google Scholar] [CrossRef]
- Trivedi, S.; Srivastava, A.; Kurchania, R. Silicene and germanene: A first principle study of electronic structure and effect of hydrogenation-passivation. J. Comput. Theor. Nanosci. 2014, 11, 781–788. [Google Scholar] [CrossRef]
- Pisarra, M.; Sindona, A.; Riccardi, P.; Silkin, V.M.; Pitarke, J.M. Acoustic plasmons in extrinsic free-standing graphene. New J. Phys. 2014, 16, 083003. [Google Scholar] [CrossRef]
- Pines, D. Electron interaction in solids. Can. J. Phys. 1956, 34, 1379–1394. [Google Scholar] [CrossRef]
- Wunsch, B.; Stauber, T.; Sols, F.; Guinea, F. Dynamical polarization of graphene at finite doping. New J. Phys. 2006, 8, 318. [Google Scholar] [CrossRef]
- Hwang, E.H.; Das Sarma, S. Dielectric function, screening, and plasmons in two-dimensional graphene. Phys. Rev. B 2007, 75, 205418. [Google Scholar] [CrossRef]
- Pereira, V.M.; Castro Neto, A.H. Strain engineering of graphene’s electronic structure. Phys. Rev. Lett. 2009, 103, 046801. [Google Scholar] [CrossRef] [PubMed]
- Yan, J.A.; Gao, S.P.; Stein, R.; Coard, G. Tuning the electronic structure of silicene and germanene by biaxial strain and electric field. Phys. Rev. B 2015, 91, 245403. [Google Scholar] [CrossRef]
- Wang, M.; Liu, L.; Liu, C.C.; Yao, Y. van der Waals heterostructures of germanene, stanene, and silicene with hexagonal boron nitride and their topological domain walls. Phys. Rev. B 2016, 93, 155412. [Google Scholar] [CrossRef]
- Grimme, S. Semiempirical GGA-type density functional constructed with a long-range dispersion correction. J. Comput. Chem. 2006, 27, 1787–1799. [Google Scholar] [CrossRef]
- Pisarra, M.; Sindona, A.; Gravina, M.; Silkin, V.M.; Pitarke, J.M. Dielectric screening and plasmon resonances in bilayer graphene. Phys. Rev. B 2016, 93, 035440. [Google Scholar] [CrossRef]
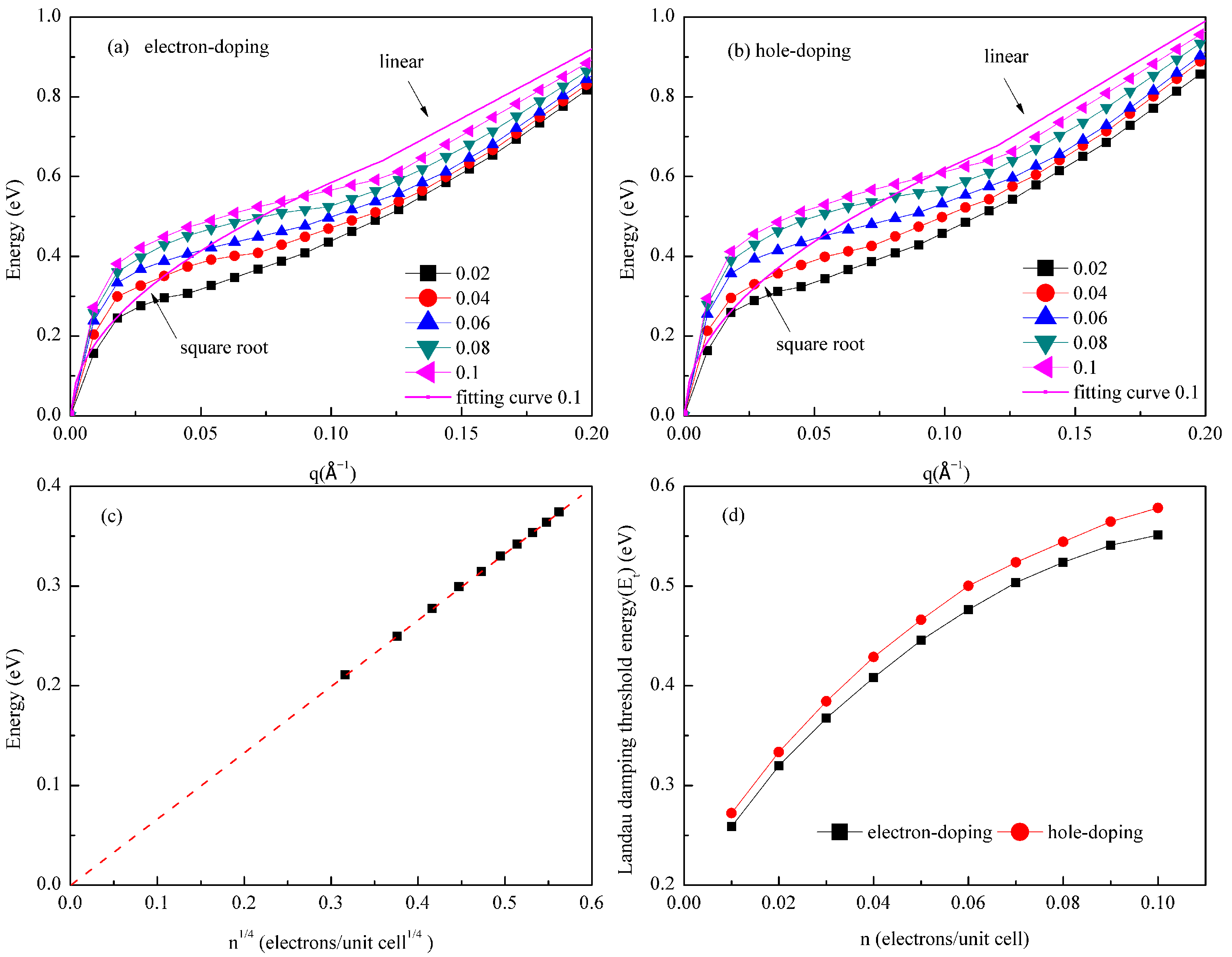
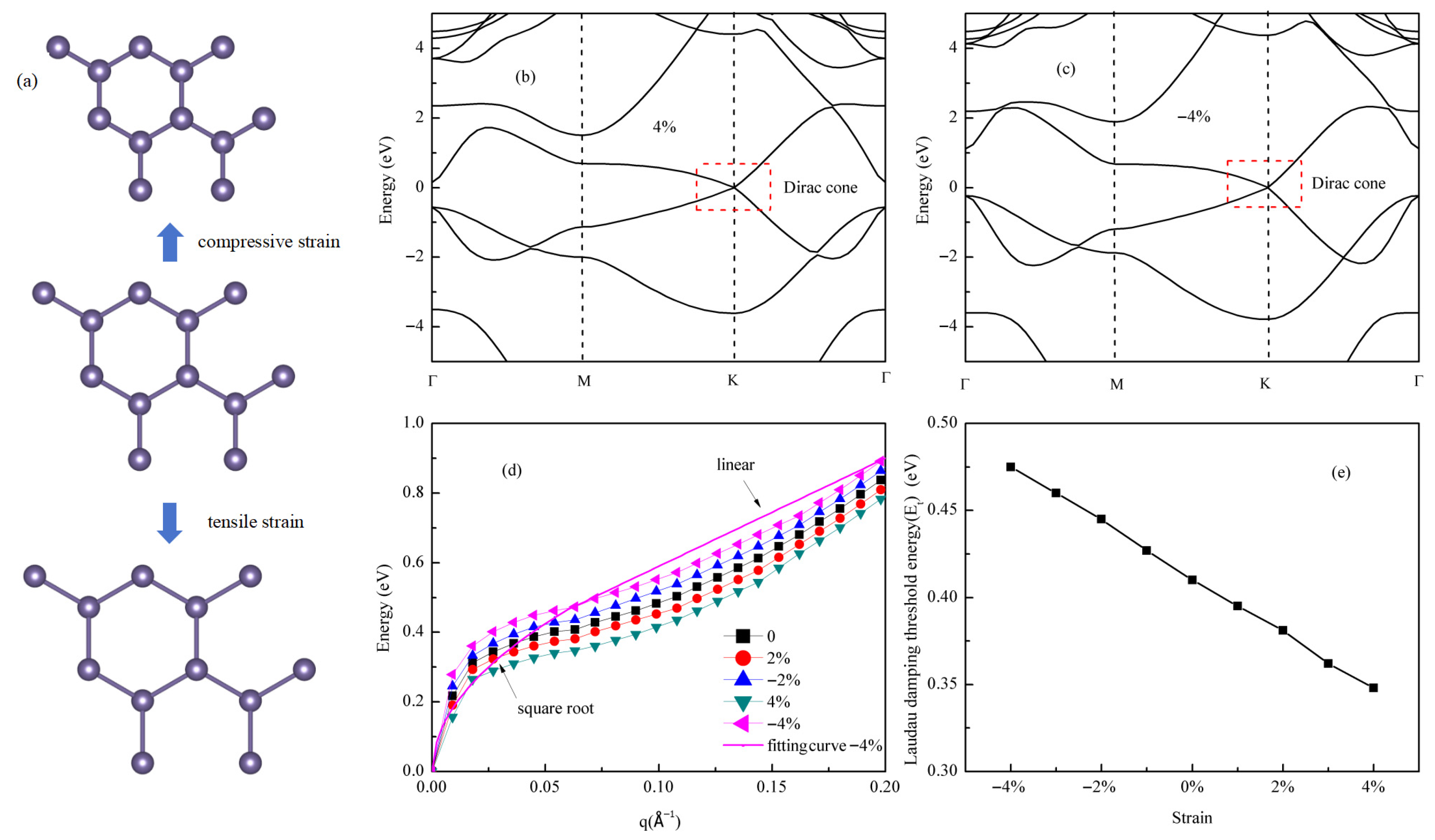
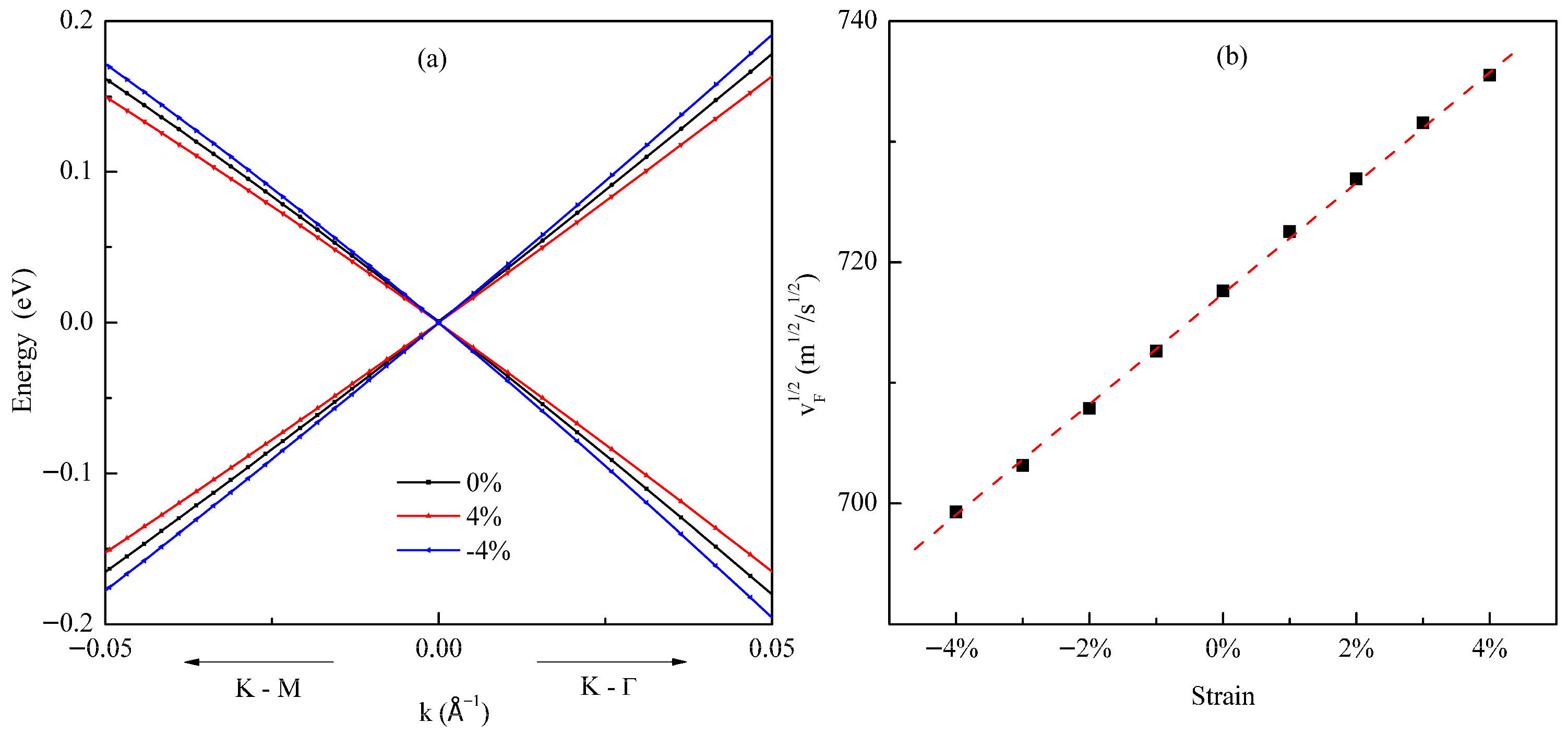
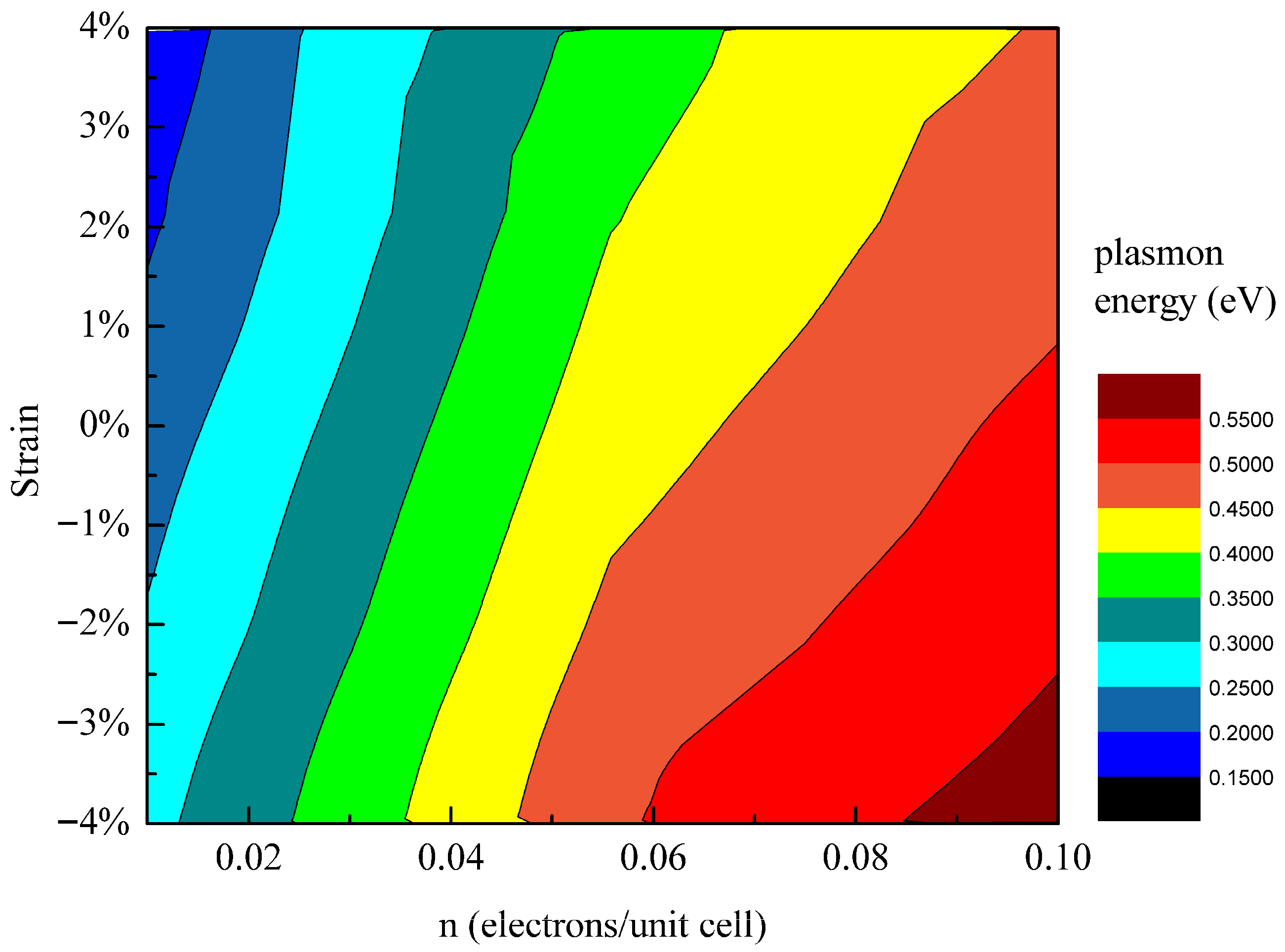
| Strain | −4% | −3% | −2% | −1% | 1% | 2% | 3% | 4% |
|---|---|---|---|---|---|---|---|---|
| Bulking Parameters (Å) | 0.790 | 0.756 | 0.738 | 0.702 | 0.661 | 0.648 | 0.636 | 0.624 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, P.; Han, L.; Zhang, L.; Hui, N. Multi-Parameter Modulation of Dirac Plasmons in Germanene via Doping and Strain: A DFT Insight. Materials 2025, 18, 4824. https://doi.org/10.3390/ma18214824
Li P, Han L, Zhang L, Hui N. Multi-Parameter Modulation of Dirac Plasmons in Germanene via Doping and Strain: A DFT Insight. Materials. 2025; 18(21):4824. https://doi.org/10.3390/ma18214824
Chicago/Turabian StyleLi, Pengfei, Lijun Han, Lin Zhang, and Ningju Hui. 2025. "Multi-Parameter Modulation of Dirac Plasmons in Germanene via Doping and Strain: A DFT Insight" Materials 18, no. 21: 4824. https://doi.org/10.3390/ma18214824
APA StyleLi, P., Han, L., Zhang, L., & Hui, N. (2025). Multi-Parameter Modulation of Dirac Plasmons in Germanene via Doping and Strain: A DFT Insight. Materials, 18(21), 4824. https://doi.org/10.3390/ma18214824





