A Non-Contact Phosphor Thermometry Technique for Determining the Optical Absorptivity of Materials
Abstract
1. Introduction
2. Materials and Methods
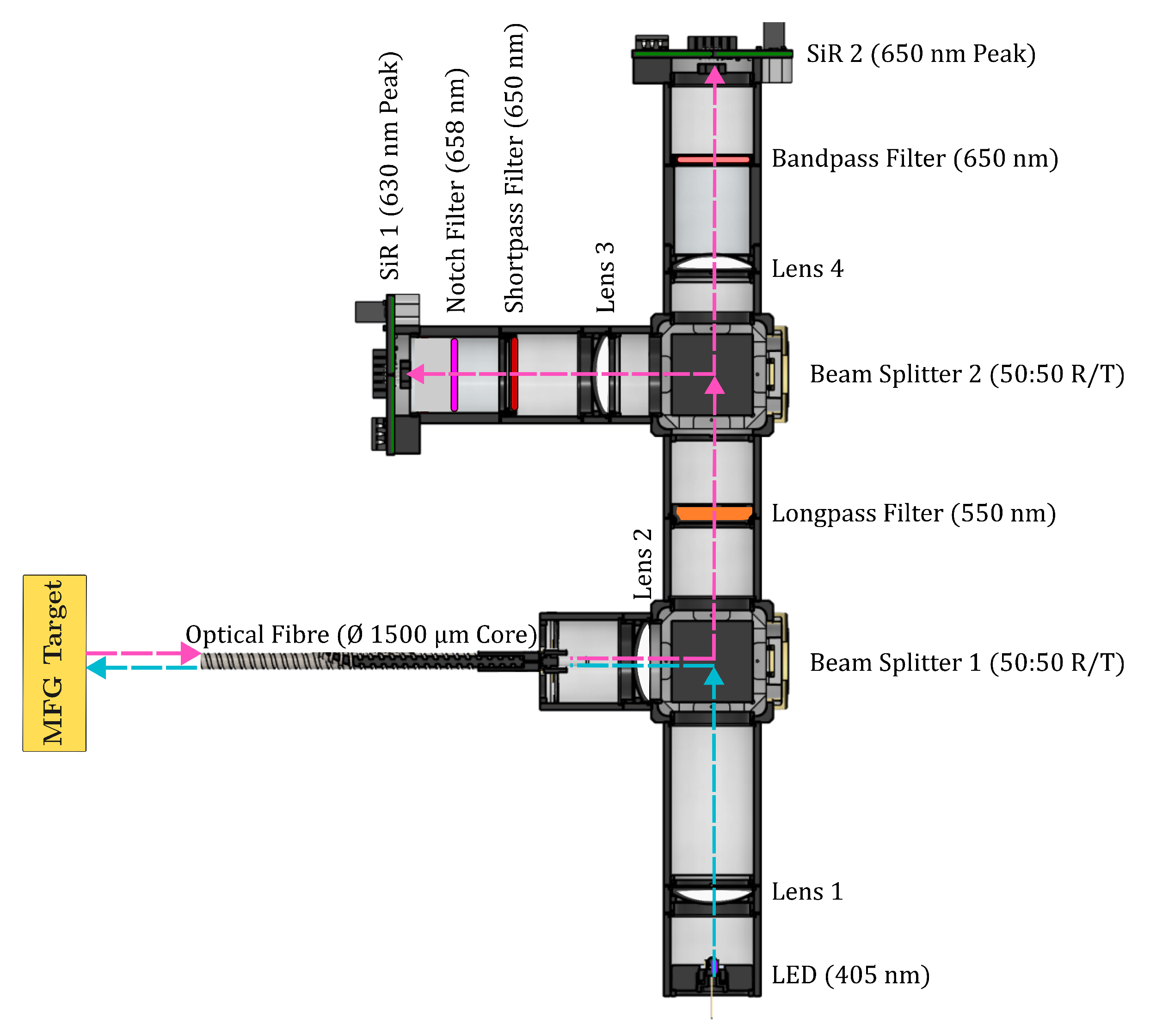
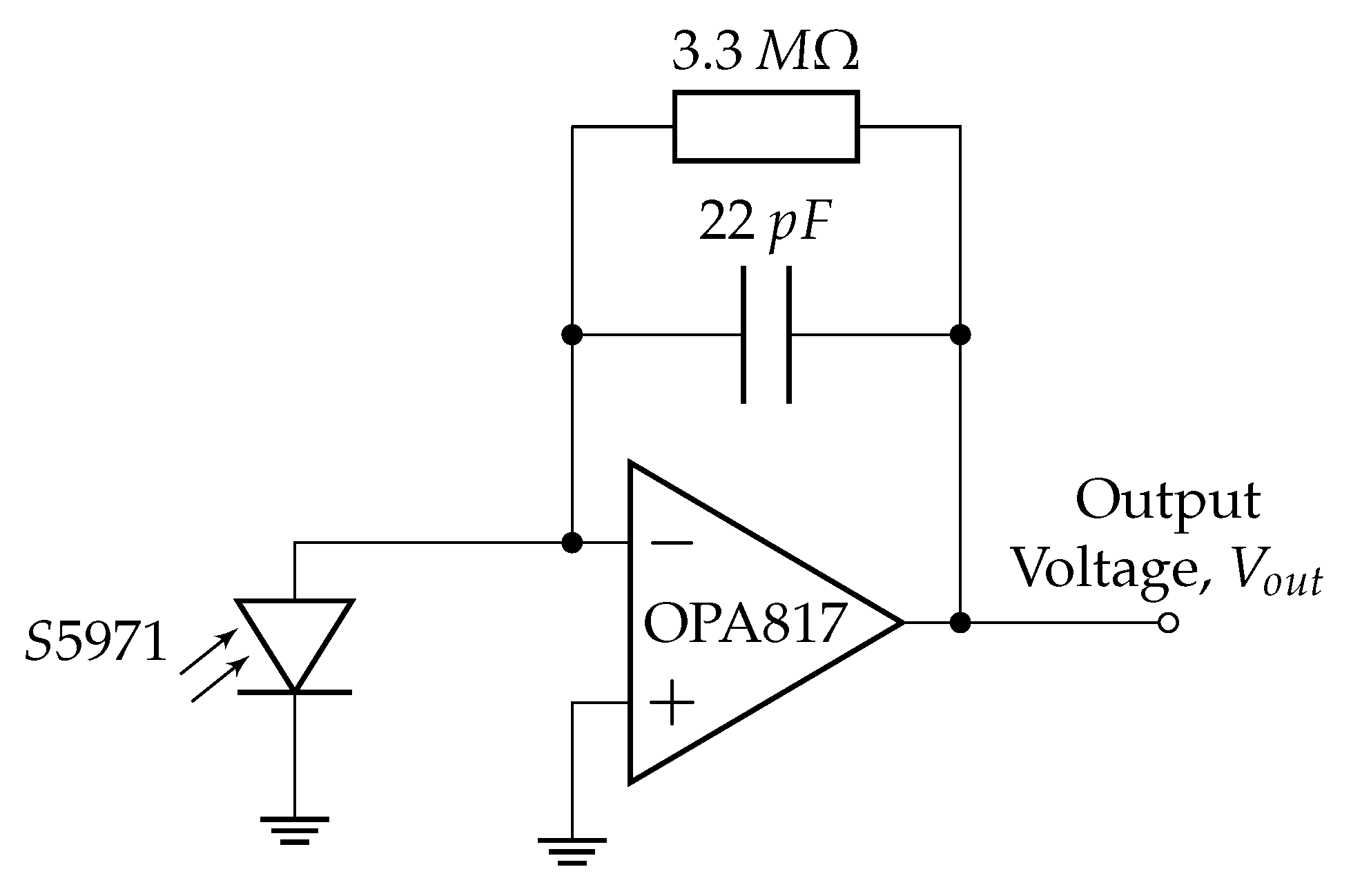
2.1. Instrument Design Overview
- SiR 1 (nm peak): Coupled with a nm shortpass filter (Thorlabs Inc., Newton, NJ, USA) and nm notch filter (Thorlabs Inc., Newton, NJ, USA) to isolate region 1, with a peak intensity at nm, which increases proportionally to increased temperature. The nm filter was used to select the correct region, while the nm notch filter provided a sharp rejection of the neighbouring emissions.
- SiR 2 (nm peak): Coupled with a nm bandpass filter (Thorlabs Inc., Newton, NJ, USA) to isolate region 2, which decreases inversely proportional to increased temperature. The nm bandpass filter was chosen to reject the influence of the spectral broadening; this was observed when using bandpass filters close to a nm peak, causing an increase in the total signal intensity in that region, as opposed to the expected decrease.
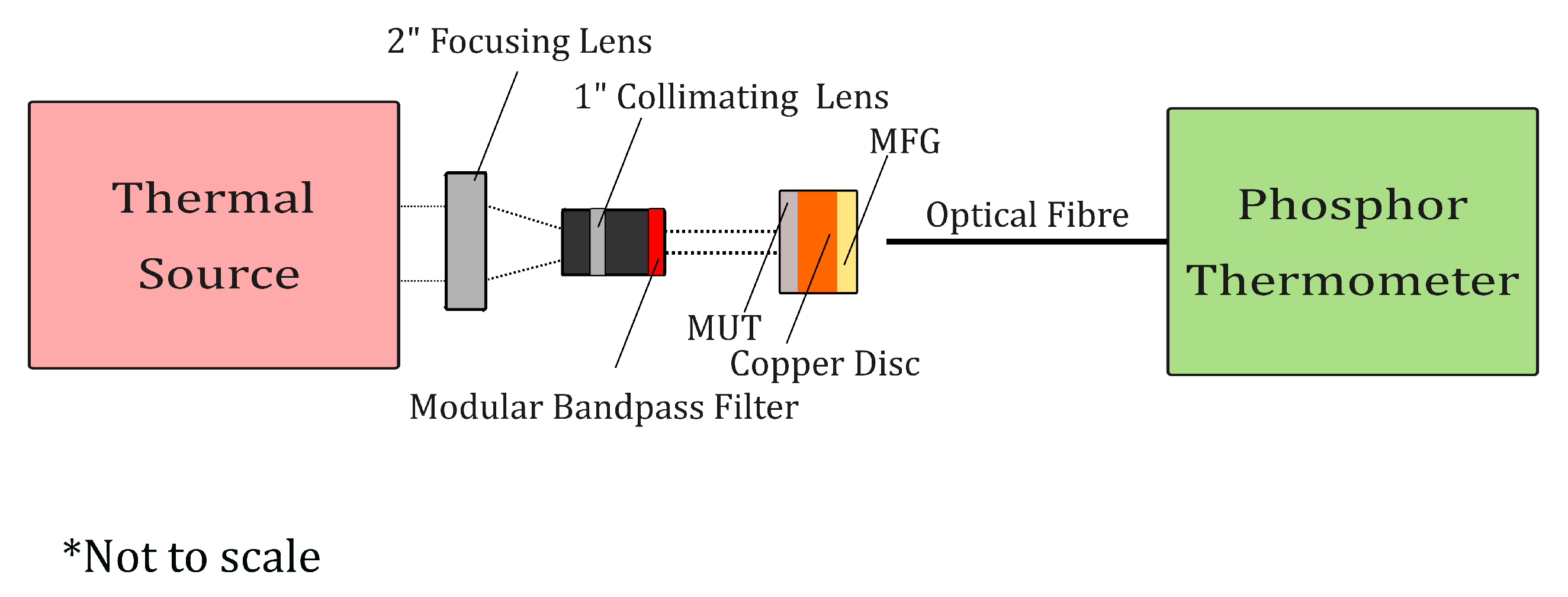
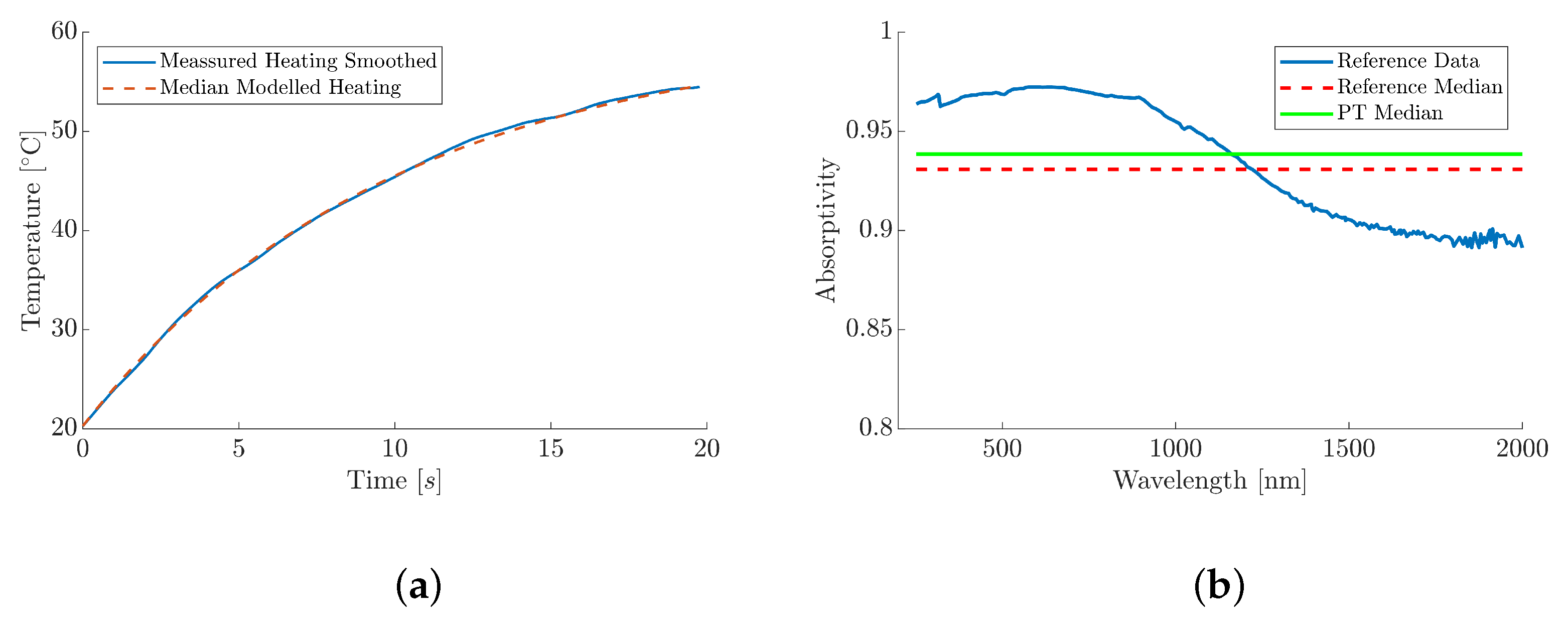
2.2. Absorptivity Measurement Methodology
3. Results and Discussion
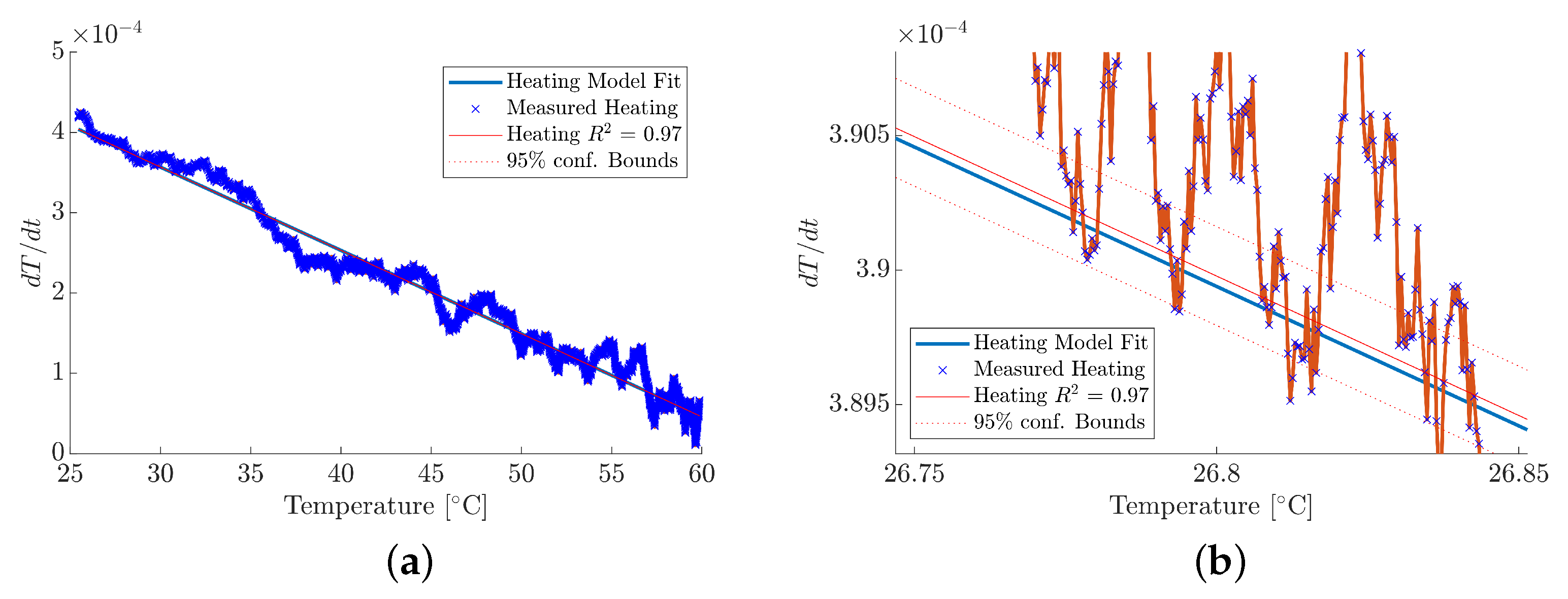
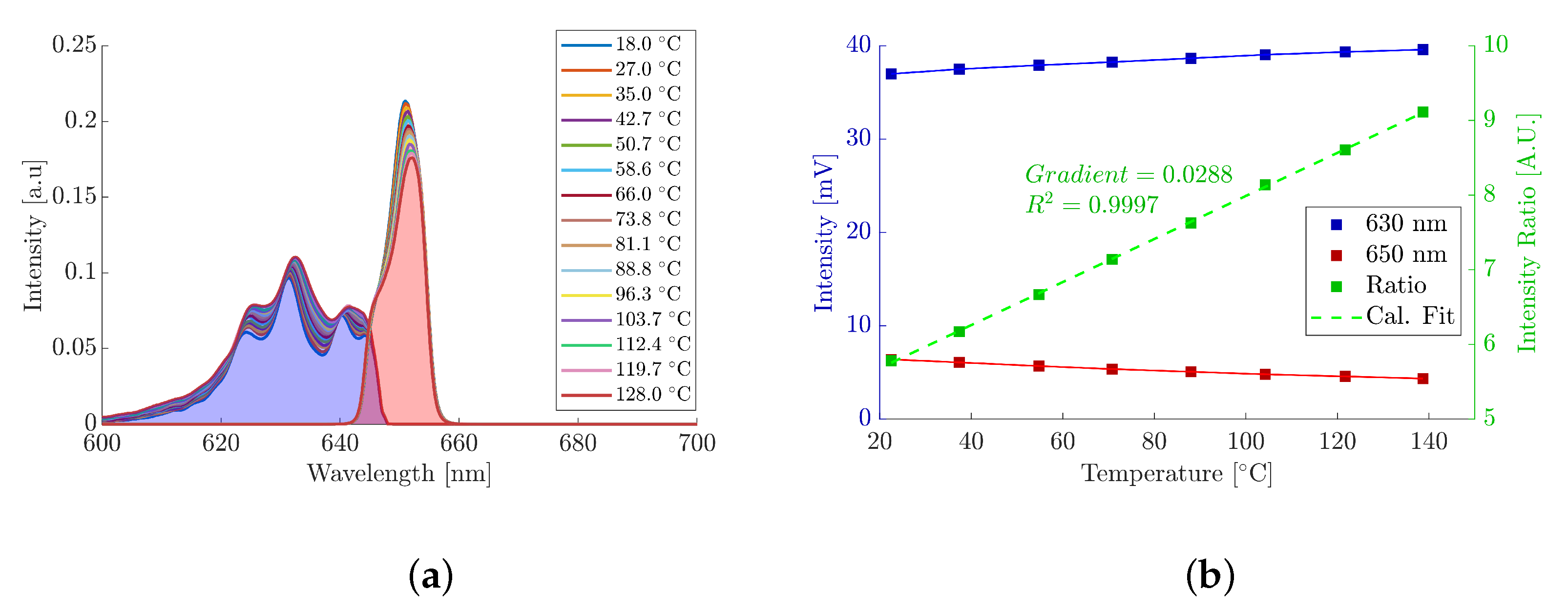
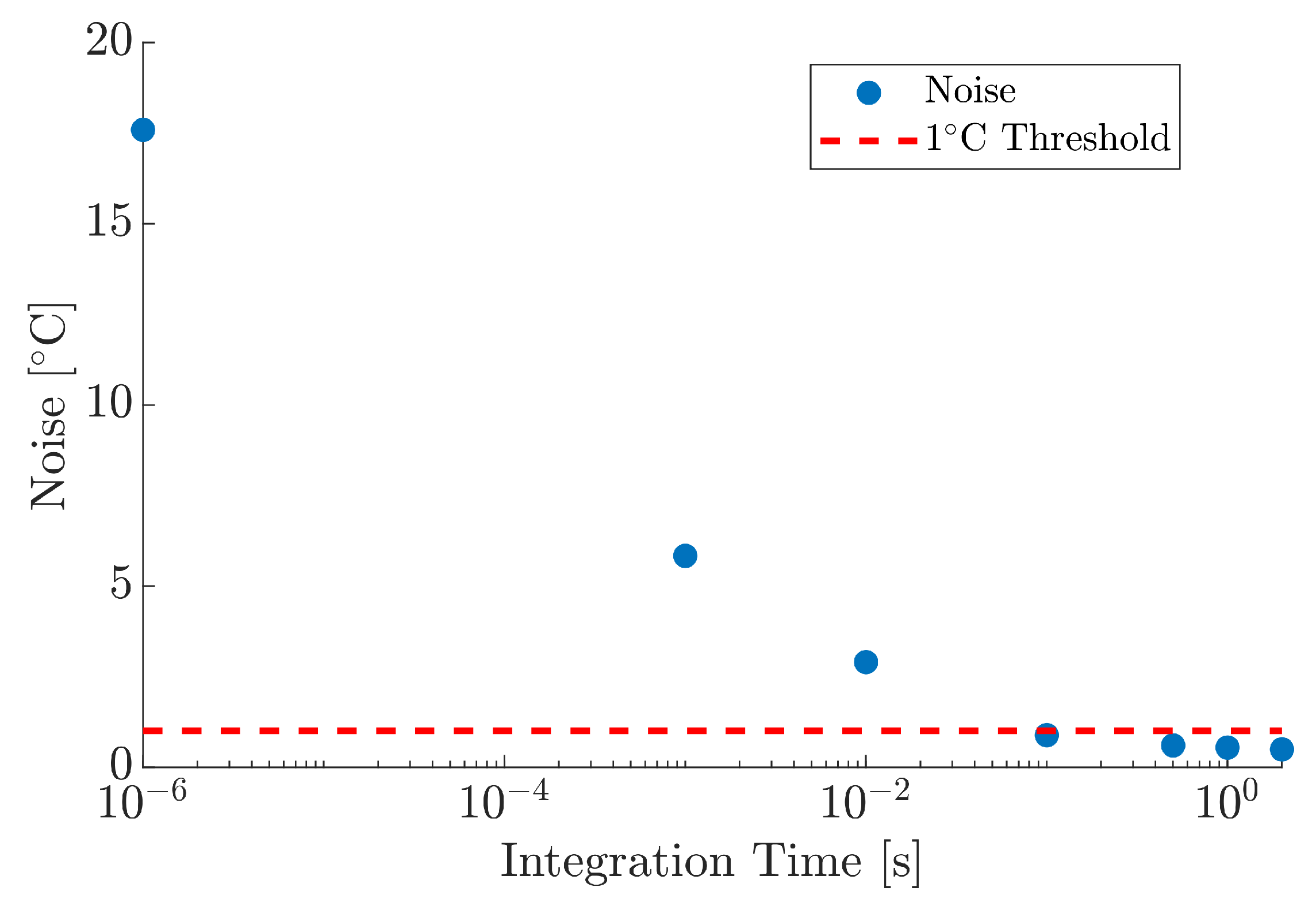
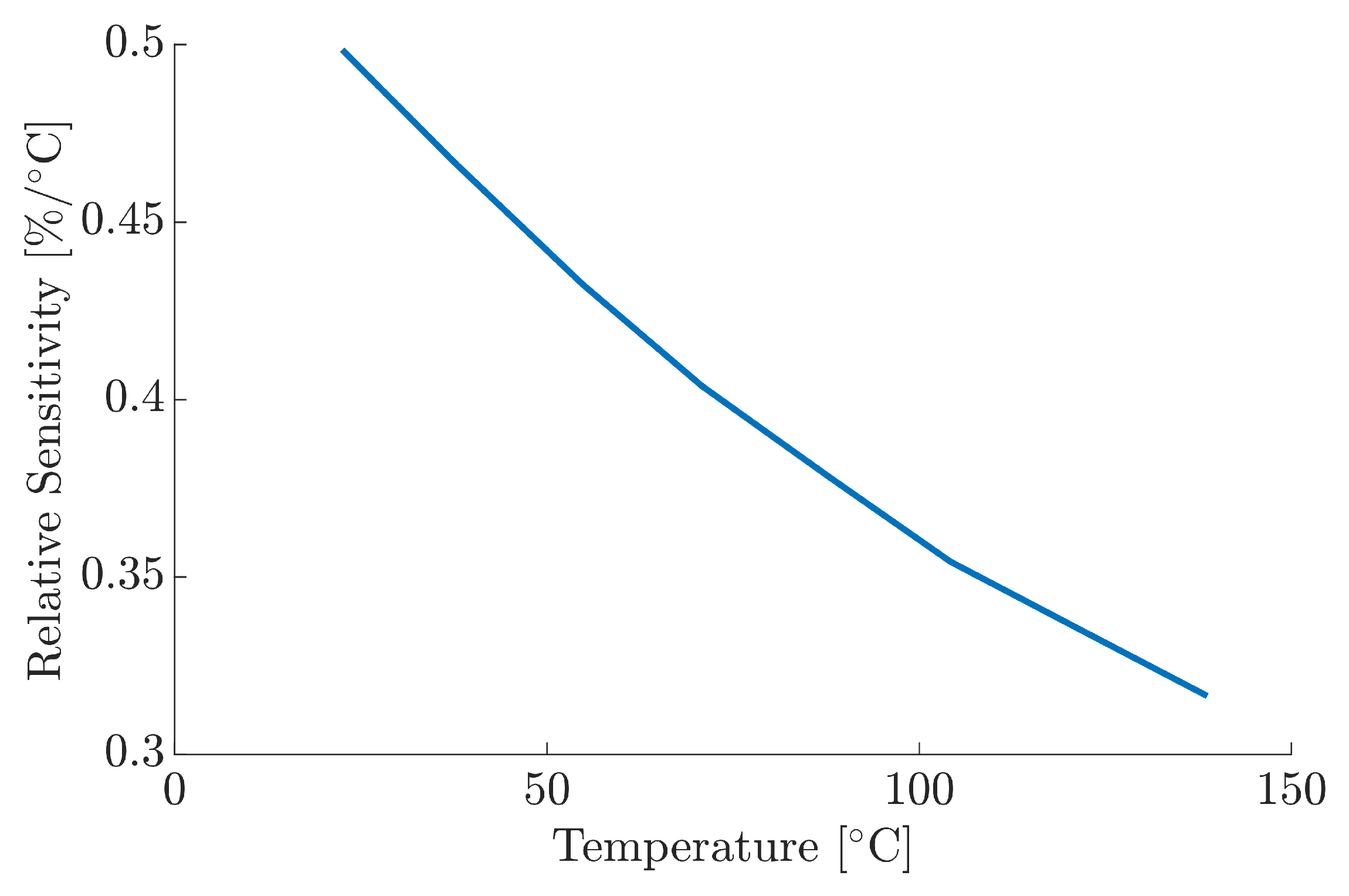
3.1. Instrument Characterisation
3.2. Absorptivity Measurements
3.3. Narrow-Band Absorptivity Measurement
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| EMR | Electromagnetic Radiation |
| FWHM | Full-Width Half-Maximum |
| IR | Infrared |
| IPA | Isopropyl Alcohol |
| IRT | Infrared Radiation Thermometer |
| LED | Light-Emitting Diode |
| LWIR | Long-Wave Infrared |
| MFG | Manganese-activated Magnesium Fluorogermanate |
| MUT | Material Under Test |
| MRI | Magnetic Resonance Imaging |
| NIR | Near-Infrared |
| PD | Photodiode |
| PL | Photoluminecent |
| PT | Phosphor Thermometry |
| RMS | Root Mean Square |
| SiPD | Silicon Photodiode |
| SiR | Silicon Photodiode-based Radiometer |
| SLM | Selective Laser Melting |
| SNR | Signal-to-Noise Ratio |
| SWIR | Short-Wave Infrared |
| TP | Thermographic Phosphor |
| TIA | Transimpedance Amplifier |
| UV | Ultraviolet |
| VIS | Visible |
| VLWIR | Very-Long-Wave Infrared |
Appendix A. Derivation of Heating and Cooling Terms for Mathematical Analysis
Appendix B. Bill of Optical Materials Used in PT Design Setup
| Component | Part Number | Manufacturer |
|---|---|---|
| nm LED | LED405L | Thorlabs Inc. |
| Glass Lens (mm) | LA1131-ML | Thorlabs Inc. |
| 50:50 Beam Spillter | CCM1-BS013/M | Thorlabs Inc. |
| Optical Fibre (µm Core) | M93L01 | Thorlabs Inc. |
| nm Longpass Filter | FELH0550 | Thorlabs Inc. |
| nm Shortpass Filter | FESH0650 | Thorlabs Inc. |
| nm Notch filter | NF658-26 | Thorlabs Inc. |
| nm Bandpass Filter | FBH650-40 | Thorlabs Inc. |
| Silicon Photodiode | S5971 | Hamamatsu Inc. |
| : | EQD25/F-U1 | Phosphor Technology Inc. |
References
- Puthiyaveettil, N.; Rajagopal, P.; Balasubramaniam, K. Influence of Absorptivity of the Material Surface in Crack Detection Using Laser Spot Thermography; Elsevier: Amsterdam, The Netherlands, 2021; Volume 120. [Google Scholar] [CrossRef]
- Brewster, M.Q. Thermal Radiative Transfer and Properties; John Wiley & Sons: Hoboken, NJ, USA, 1992. [Google Scholar]
- Cook, P.S.; Ritchie, D.J. Determining the laser absorptivity of Ti-6Al-4V during laser powder bed fusion by calibrated melt pool simulation. Opt. Laser Technol. 2023, 162, 109247. [Google Scholar] [CrossRef]
- Wallace, N.J.; Jones, M.R.; Crane, N.B. Spectral absorption coefficient of additive manufacturing materials. J. Therm. Sci. Eng. Appl. 2021, 13, 041012. [Google Scholar] [CrossRef]
- Spears, T.G.; Gold, S.A. In-process sensing in selective laser melting (SLM) additive manufacturing. Integr. Mater. Manuf. Innov. 2016, 5, 16–40. [Google Scholar] [CrossRef]
- Zavala-Arredondo, M.; Boone, N.; Willmott, J.; Childs, D.T.; Ivanov, P.; Groom, K.M.; Mumtaz, K. Laser diode area melting for high speed additive manufacturing of metallic components. Mater. Des. 2017, 117, 305–315. [Google Scholar] [CrossRef]
- Siva Prasad, H.; Brueckner, F.; Volpp, J.; Kaplan, A.F. Laser metal deposition of copper on diverse metals using green laser sources. Int. J. Adv. Manuf. Technol. 2020, 107, 1559–1568. [Google Scholar] [CrossRef]
- Trapp, J.; Rubenchik, A.M.; Guss, G.; Matthews, M.J. In situ absorptivity measurements of metallic powders during laser powder-bed fusion additive manufacturing. Appl. Mater. Today 2017, 9, 341–349. [Google Scholar] [CrossRef]
- Rev, T.; Katsir, D.; Králík, T.; Frolec, J. Emissivity of Black Coatings from Ambient to Cryogenic Temperatures: How Spectrally Flat Black Coatings Can Enhance Performance of Space Systems. 2023. Available online: https://tfaws.nasa.gov/wp-content/uploads/TFAWS23-CR-1-Paper.pdf (accessed on 15 February 2025).
- NPL. Accurate Temperature Measurement in Challenging Environments. Available online: https://www.npl.co.uk/products-services/temperature/phosphor-thermometry (accessed on 27 May 2024).
- Santbergen, R.; van Zolingen, R.J.C. The absorption factor of crystalline silicon PV cells: A numerical and experimental study. Sol. Energy Mater. Sol. Cells 2008, 92, 432–444. [Google Scholar] [CrossRef]
- Lee, M.; Kim, G.; Jung, Y.; Pyun, K.R.; Lee, J.; Kim, B.W.; Ko, S.H. Photonic structures in radiative cooling. Light Sci. Appl. 2023, 12, 134. [Google Scholar] [CrossRef]
- Henninger, J.H. Solar Absorptance and Thermal Emittance of Some Common Spacecraft Thermal-Control Coatings; National Aeronautics and Space Adminitration, Scientific and Technical Information Branch: Hampton, VA, USA, 1984. [Google Scholar]
- Zhu, C.; Hobbs, M.J.; Masters, R.C.; Rodenburg, C.; Willmott, J.R. An Accurate Device for Apparent Emissivity Characterization in Controlled Atmospheric Conditions up to 1423 K. IEEE Trans. Instrum. Meas. 2020, 69, 4210–4221. [Google Scholar] [CrossRef]
- Králík, T.; Musilová, V.; Hanzelka, P.; Frolec, J. Method for measurement of emissivity and absorptivity of highly reflective surfaces from 20 K to room temperatures. Metrologia 2016, 53, 743–753. [Google Scholar] [CrossRef]
- Aouali, A.; Chevalier, S.; Sommier, A.; Abisset-Chavanne, E.; Batsale, J.C.; Pradere, C. 3D infrared thermospectroscopic imaging. Sci. Rep. 2020, 10, 22310. [Google Scholar] [CrossRef]
- Jones, H.G.; Serraj, R.; Loveys, B.R.; Xiong, L.; Wheaton, A.; Price, A.H. Thermal infrared imaging of crop canopies for the remote diagnosis and quantification of plant responses to water stress in the field. Funct. Plant Biol. 2009, 36, 978–989. [Google Scholar] [CrossRef] [PubMed]
- Zhu, C.; Hobbs, M.J.; Willmott, J.R. An accurate instrument for emissivity measurements by direct and indirect methods. Meas. Sci. Technol. 2020, 31, 044007. [Google Scholar] [CrossRef]
- Huynh, M. Analyzing Reflectance Data for Various Black Paints and Coatings. In STO-Meeting Proceedings Paper; Science and technology Organisation: Brussels, Belgium, 2019; Available online: https://www.sto.nato.int/document/analyzing-reflectance-data-for-various-black-paints-and-coatings (accessed on 12 April 2024).
- PerkinElmer. LAMBDA 1050+ UV/Vis/NIR Spectrophotometer. Available online: https://www.perkinelmer.com/uk/product/lambda-1050-2d-base-inst-no-sw-l6020055 (accessed on 11 October 2024).
- Corporation, S.O. SOC-100 Hemispherical Directional Reflectometer. Available online: https://surfaceoptics.com/wp-content/uploads/2024/09/SOC-100-HDR-Datasheet.pdf (accessed on 11 October 2024).
- Indhu, R.; Vivek, V.; Loganathan, S.; Bharatish, A.; Soundarapandian, S. Overview of Laser Absorptivity Measurement Techniques for Material Processing. Lasers Manuf. Mater. Process. 2018, 5, 458–481. [Google Scholar] [CrossRef]
- Rubenchik, A.; Wu, S.; Mitchell, S.; Golosker, I.; LeBlanc, M.; Peterson, N. Direct measurements of temperature-dependent laser absorptivity of metal powders. Appl. Opt. 2015, 54, 7230. [Google Scholar] [CrossRef]
- Leonidas, E.; Ayvar-Soberanis, S.; Laalej, H.; Fitzpatrick, S.; Willmott, J.R. A Comparative Review of Thermocouple and Infrared Radiation Temperature Measurement Methods during the Machining of Metals. Sensors 2022, 22, 4693. [Google Scholar] [CrossRef]
- Leonidas, E.; Hobbs, M.J.; Ayvar-Soberanis, S.; Laalej, H.; Fisk, C.; Fitzpatrick, S.; Willmott, J.R. InAsSb Photodiode Fibre Optic Thermometry for High-Speed, near-Ambient Temperature Measurements. Sensors 2023, 23, 9514. [Google Scholar] [CrossRef]
- Aldén, M.; Omrane, A.; Richter, M.; Särner, G. Thermographic phosphors for thermometry: A survey of combustion applications. Prog. Energy Combust. Sci. 2011, 37, 422–461. [Google Scholar] [CrossRef]
- Rosso, L.; Tabandeh, S.; Beltramino, G.; Fernicola, V. Validation of phosphor thermometry for industrial surface temperature measurements. Meas. Sci. Technol. 2019, 31, 034002. [Google Scholar] [CrossRef]
- Heyes, A.L.; Beyrau, F. Recent developments in phosphor thermometry. Meas. Sci. Technol. 2020, 31, 020102. [Google Scholar] [CrossRef]
- Fuhrmann, N.; Kissel, T.; Dreizler, A.; Brübach, J. Gd3Ga5O12:Cr—A phosphor for two-dimensional thermometry in internal combustion engines. Meas. Sci. Technol. 2011, 22, 045301. [Google Scholar] [CrossRef]
- Allison, S.W. A brief history of phosphor thermometry. Meas. Sci. Technol. 2019, 30, 072001. [Google Scholar] [CrossRef]
- Sposito, A.; Heaps, E.; Sutton, G.; Machin, G.; Bernard, R.; Clarke, S. Phosphor thermometry for nuclear decommissioning and waste storage. Nucl. Eng. Des. 2021, 375, 111091. [Google Scholar] [CrossRef]
- Jenkins, T.P.; Hess, C.F.; Allison, S.W.; Eldridge, J.I. Measurements of turbine blade temperature in an operating aero engine using thermographic phosphors. Meas. Sci. Technol. 2020, 31, 044003. [Google Scholar] [CrossRef]
- Vitasek, J.; Jargus, J.; Hejduk, S.; Stratil, T.; Latal, J.; Vasinek, V. Phosphor decay measurement and its influence on communication properties. In Proceedings of the 2017 19th International Conference on Transparent Optical Networks (ICTON), Girona, Spain, 2–6 July 2017. [Google Scholar] [CrossRef]
- Cai, T.; Park, Y.; Mohammadshahi, S.; Kim, K.C. Rise time-based phosphor thermometry using Mg4FGeO6:Mn4+. Meas. Sci. Technol. 2021, 32, 015201. [Google Scholar] [CrossRef]
- Liu, Q.; Wu, M.; Chen, B.; Huang, X.; Liu, M.; Liu, Y.; Su, K.; Min, X.; Mi, R.; Huang, Z. Optical thermometry based on fluorescence intensity ratio of Dy3+-Doped oxysilicate apatite warm white phosphor. Ceram. Int. 2023, 49, 4971–4978. [Google Scholar] [CrossRef]
- Pradhan, S.; Kaur, H.; Jayasimhadri, M. Photoluminescence and thermal sensing properties of Er3+ doped silicate based phosphors for multifunctional optoelectronic device applications. Ceram. Int. 2021, 47, 27694–27701. [Google Scholar] [CrossRef]
- Vu, T.; Bondzior, B.; Stefańska, D.; Dereń, P. An Er3+ doped Ba2 MgWO6 double perovskite: A phosphor for low-temperature thermometry. Dalton Trans. 2022, 51, 8056–8065. [Google Scholar] [CrossRef]
- Balhara, A.; Gupta, S.K.; Patra, G.; Naidu, B.S.; Sudarshan, K. Abnormal anti-thermal quenching of Mn2+ and reverse thermal response of Mn2+/Mn4+ luminescence in garnet phosphor for wide-range temperature sensing. J. Mater. Chem. C 2024, 12, 19671–19680. [Google Scholar] [CrossRef]
- Abou Nada, F.; Knappe, C.; Aldén, M.; Richter, M. Improved measurement precision in decay time-based phosphor thermometry. Appl. Phys. B 2016, 122, 170. [Google Scholar] [CrossRef]
- Fuhrmann, N.; Brübach, J.; Dreizler, A. Phosphor thermometry: A comparison of the luminescence lifetime and the intensity ratio approach. Proc. Combust. Inst. 2013, 34, 3611–3618. [Google Scholar] [CrossRef]
- Technology Phosphor. Thermographic Phosphors. Available online: https://www.phosphor-technology.com/thermographic-phosphors (accessed on 7 August 2023).
- Brites, C.D.; Marin, R.; Suta, M.; Neto, A.N.C.; Ximendes, E.; Jaque, D.; Carlos, L.D. Spotlight on Luminescence Thermometry: Basics, Challenges, and Cutting-Edge Applications. Adv. Mater. 2023, 35, 2302749. [Google Scholar] [CrossRef] [PubMed]
- Yadav, R.; Monika; Rai, S.; Dhoble, S. Recent advances on morphological changes in chemically engineered rare earth doped phosphor materials. Prog. Solid State Chem. 2020, 57, 100267. [Google Scholar] [CrossRef]
- Dramićanin, M.D. Trends in luminescence thermometry. J. Appl. Phys. 2020, 128, 040902. [Google Scholar] [CrossRef]
- Sutton, G.; Greenen, A.; Roebuck, B.; MacHin, G. Imaging phosphor thermometry from T = 20 °C to 450 °C using the time-domain intensity ratio technique. Meas. Sci. Technol. 2019, 30, 044002. [Google Scholar] [CrossRef]
- Liu, S.; Huang, Y.; He, Y.; Zhu, Y.; Wang, Z. Review of Development and Comparison of Surface Thermometry Methods in Combustion Environments: Principles, Current State of the Art, and Applications. Processes 2022, 10, 2528. [Google Scholar] [CrossRef]
- Yáñez-González, Á.; Ruiz-Trejo, E.; Wachem, B.V.; Skinner, S.; Beyrau, F.; Heyes, A. A detailed characterization of BaMgAl10O17:Eu phosphor as a thermal history sensor for harsh environments. Sens. Actuators A Phys. 2015, 234, 339–345. [Google Scholar] [CrossRef]
- ThorLabs. SLS301 Stabilized Tungsten-Halogen Light Source. Available online: https://www.thorlabs.com/drawings/e43549750848f77e-6BB009BF-99DA-1ABC-D6D5E2277313E217/SLS301-Manual.pdf (accessed on 20 September 2024).
- Ronda, C.R.; Justel, T.; Nikol, H. Rare earth phosphors: Fundamentals and applications. J. Alloys Compd. 1998, 275, 669–676. [Google Scholar] [CrossRef]
- Chi, Y.; Chou, P.T. Transition-metal phosphors with cyclometalating ligands: Fundamentals and applications. Chem. Soc. Rev. 2010, 39, 638–655. [Google Scholar] [CrossRef]
- Zhuang, Y.; Katayama, Y.; Ueda, J.; Tanabe, S. A brief review on red to near-infrared persistent luminescence in transition-metal-activated phosphors. Opt. Mater. 2014, 36, 1907–1912. [Google Scholar] [CrossRef]
- Marciniak, L.; Kniec, K.; Elżbieciak-Piecka, K.; Trejgis, K.; Stefanska, J.; Dramićanin, M. Luminescence thermometry with transition metal ions. A review. Coord. Chem. Rev. 2022, 469, 214671. [Google Scholar] [CrossRef]
- Särner, G.; Richter, M.; Aldén, M. Investigations of blue emitting phosphors for thermometry. Meas. Sci. Technol. 2008, 19, 125304. [Google Scholar] [CrossRef]
- Brites, C.D.; Balabhadra, S.; Carlos, L.D. Lanthanide-Based Thermometers: At the Cutting-Edge of Luminescence Thermometry. Adv. Opt. Mater. 2019, 7, 1801239. [Google Scholar] [CrossRef]
- Heyes, A. On the design of phosphors for high-temperature thermometry. J. Lumin. 2009, 129, 2004–2009. [Google Scholar] [CrossRef]
- ThorLabs. Compact Spectrometer—ccs200, Extended Range: 200–1000 nm. Available online: https://www.thorlabs.com/thorproduct.cfm?partnumber=CCS200#ad-image-0 (accessed on 10 July 2023).
- Hamamatsu. Si Photodiode: S5971. Available online: https://www.hamamatsu.com/eu/en/product/optical-sensors/photodiodes/si-photodiodes/S5971.html (accessed on 11 October 2023).
- Components, R. RS PRO Liquid Adhesive. Available online: https://uk.rs-online.com/web/p/adhesives/1863616 (accessed on 15 May 2023).
- BS EN 60584-2:1993; Thermocouples—Tolerances; Technical Report. British Standards Institution: London, UK, 1991.
- Coates, P.; Lowe, D. The Fundamentals of Radiation Thermometers; CRC Press: Boca Raton, FL, USA, 2016. [Google Scholar]
- Palmer, J.M. The measurement of transmission, absorption, emission, and reflection. Handb. Opt. 1995, 2, 25.1–25.12. [Google Scholar]
- Li, E.; Gao, L.; Jiang, X.; Duan, J.; Pu, S.; Wang, J. Analysis of dynamic compression property and energy dissipation of salt rock under three-dimensional pressure. Environ. Earth Sci. 2019, 78, 388. [Google Scholar] [CrossRef]
- Hüfner, S.; Wertheim, G.; Smith, N.; Traum, M. XPS density of states of copper, silver, and nickel. Solid State Commun. 1972, 11, 323–326. [Google Scholar] [CrossRef]
- Xiong, B.; Loss, R.D.; Shields, D.; Pawlik, T.; Hochreiter, R.; Zydney, A.L.; Kumar, M. Polyacrylamide degradation and its implications in environmental systems. NPJ Clean Water 2018, 1, 17. [Google Scholar] [CrossRef]
- CultureHustle. Black 3.0. Available online: https://culturehustle.com/products/black-3-0-the-worlds-blackest-black-acrylic-paint-150ml?_pos=1&_sid=db644fb5f&_ss=r (accessed on 2 December 2024).
- Avian Technologies. Avian-B White Reflectance Coating. Available online: https://aviantechnologies.com/product/avian-b-white-reflectance-coating/ (accessed on 25 January 2025).
- Gchem. Heat Capacities for Some Select Substances. Available online: https://gchem.cm.utexas.edu/data/section2.php?target=heat-capacities.php (accessed on 13 August 2024).
- Yu, S.; Kim, D.K.; Park, C.; Hong, S.M.; Koo, C.M. Thermal conductivity behavior of SiC-Nylon 6,6 and hBN-Nylon 6,6 composites. Res. Chem. Intermed. 2014, 40, 33–40. [Google Scholar] [CrossRef]
- Wojtkowiak, J. Lumped Thermal Capacity Model. In Encyclopedia of Thermal Stresses; Hetnarski, R.B., Ed.; Springer: Dordrecht, The Netherlands, 2014; pp. 2808–2817. [Google Scholar] [CrossRef]
- Çengel, Y.A.; Ghajar, A.J. Heat and Mass Transfer: Fundamentals & Applications, 6th ed.; McGraw Hill: New York, NY, USA, 2020. [Google Scholar]




| Power [W] | Test # | Absorptivity | Median |
|---|---|---|---|
| 1 | 0.9385 | ||
| 7 | 2 | 0.9312 | 0.9385 |
| 3 | 0.9393 |
| MUT | Power | Test # | Absorptivity | Median |
|---|---|---|---|---|
| 1 | 0.0620 | |||
| White | 7 | 2 | 0.0651 | 0.0651 |
| 3 | 0.0747 | |||
| 1 | 0.3609 | |||
| 25:75 | 7 | 2 | 0.3517 | 0.3528 |
| 3 | 0.3528 | |||
| 1 | 0.6509 | |||
| 50:50 | 7 | 2 | 0.6297 | 0.6401 |
| 3 | 0.6401 | |||
| 1 | 0.7662 | |||
| 75:25 | 7 | 2 | 0.7971 | 0.7868 |
| 3 | 0.7868 | |||
| 1 | 0.9385 | |||
| Black | 7 | 2 | 0.9312 | 0.9385 |
| 3 | 0.9393 |
| Filter Wavelength [nm] | Power [W] | Test # | Absorptivity | Median |
|---|---|---|---|---|
| 1 | 0.9755 | |||
| 600–40 | 0.178 | 2 | 0.9598 | 0.9598 |
| 3 | 0.9587 | |||
| 1 | 0.9318 | |||
| 1550–40 | 0.106 | 2 | 0.9172 | 0.9172 |
| 3 | 0.8922 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hutchinson, T.M.F.; Davies, M.; Fisk, C.; Zied, H.; Willmott, J.R.; Hobbs, M.J. A Non-Contact Phosphor Thermometry Technique for Determining the Optical Absorptivity of Materials. Materials 2025, 18, 4806. https://doi.org/10.3390/ma18204806
Hutchinson TMF, Davies M, Fisk C, Zied H, Willmott JR, Hobbs MJ. A Non-Contact Phosphor Thermometry Technique for Determining the Optical Absorptivity of Materials. Materials. 2025; 18(20):4806. https://doi.org/10.3390/ma18204806
Chicago/Turabian StyleHutchinson, Thomas M. F., Matthew Davies, Callum Fisk, Hazem Zied, Jon R. Willmott, and Matthew J. Hobbs. 2025. "A Non-Contact Phosphor Thermometry Technique for Determining the Optical Absorptivity of Materials" Materials 18, no. 20: 4806. https://doi.org/10.3390/ma18204806
APA StyleHutchinson, T. M. F., Davies, M., Fisk, C., Zied, H., Willmott, J. R., & Hobbs, M. J. (2025). A Non-Contact Phosphor Thermometry Technique for Determining the Optical Absorptivity of Materials. Materials, 18(20), 4806. https://doi.org/10.3390/ma18204806






