A Hybrid FE-ML Approach for Critical Buckling Moment Prediction in Dented Pipelines Under Complex Loadings
Abstract
1. Introduction
2. FE Modeling
- The FE analysis only accounts for stable internal pressure and bending moment loads, excluding the effect of temperature variations and cyclic loads.
- The pipeline is modeled as an intact, defect-free structure. Weld seams and other connecting structures are ignored.
- The pipe material is considered as isotropic, homogeneous, and rate-independent.
2.1. General
2.2. Pipeline Material and Buckling Failure Criterion
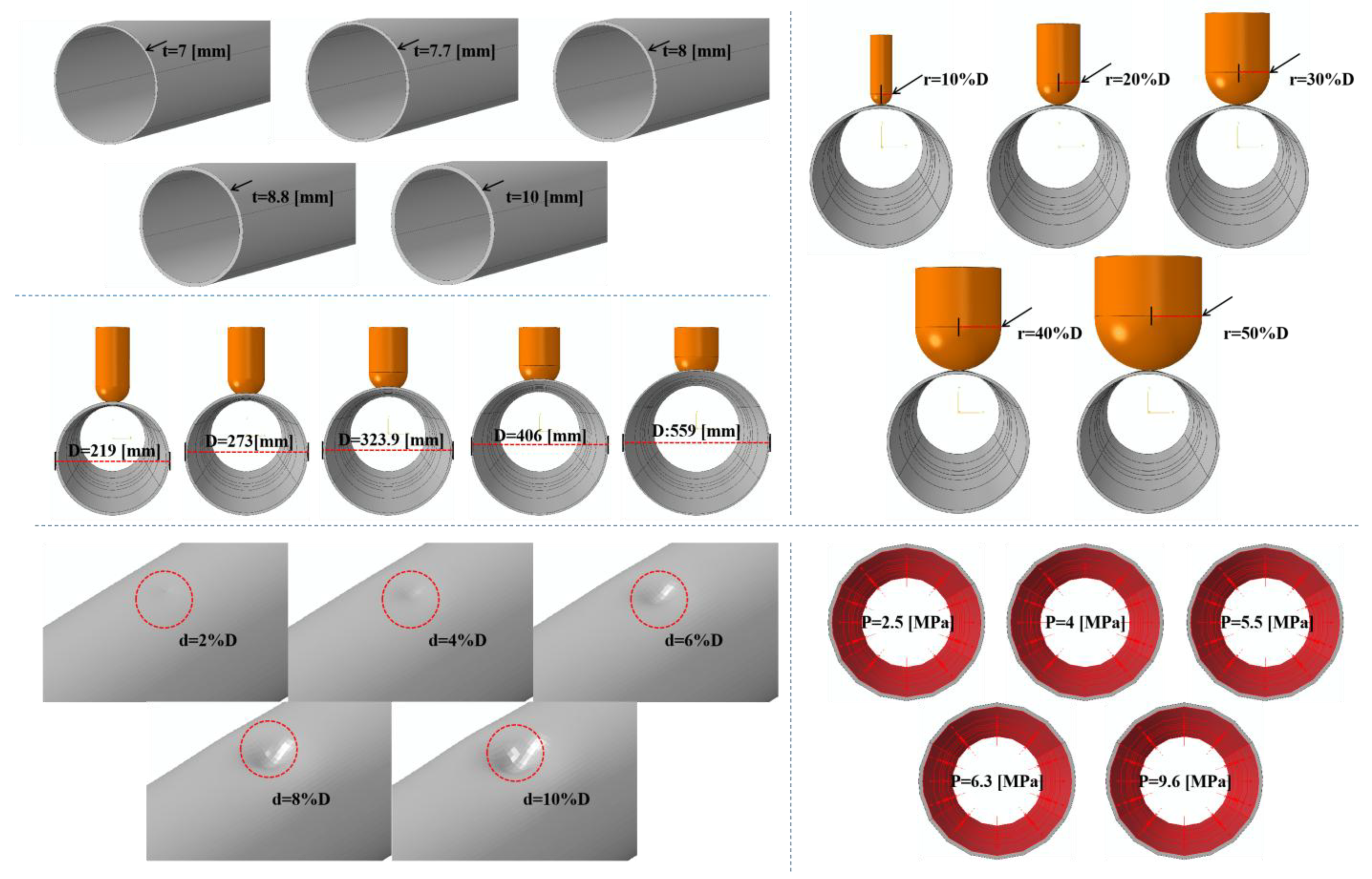
2.3. Parameter Setting
3. FE Results and Discussion
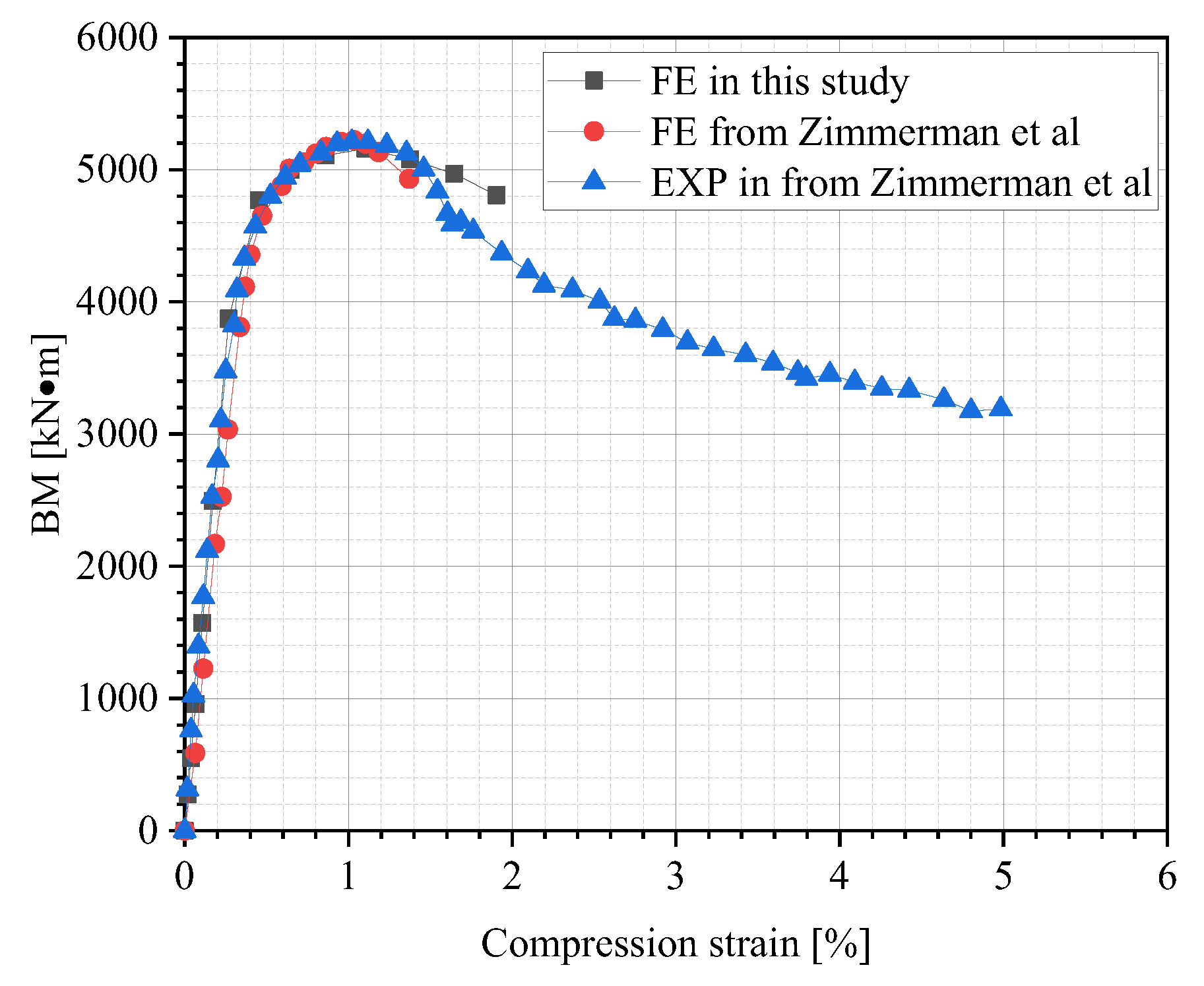
3.1. Model Validation
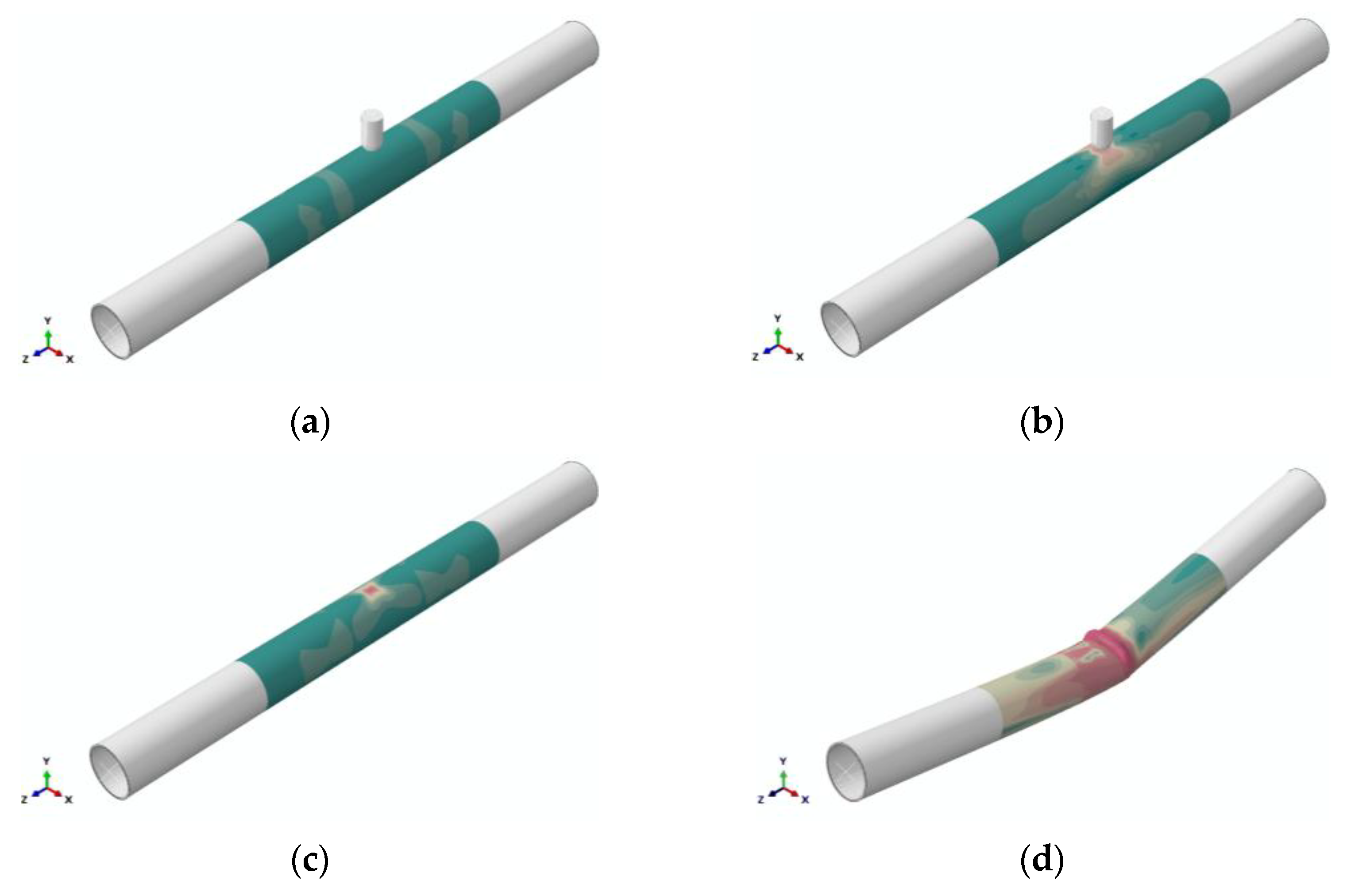
3.1.1. Verification of Pipeline Dent Formation Process
3.1.2. Verification of Pipeline Buckling Process
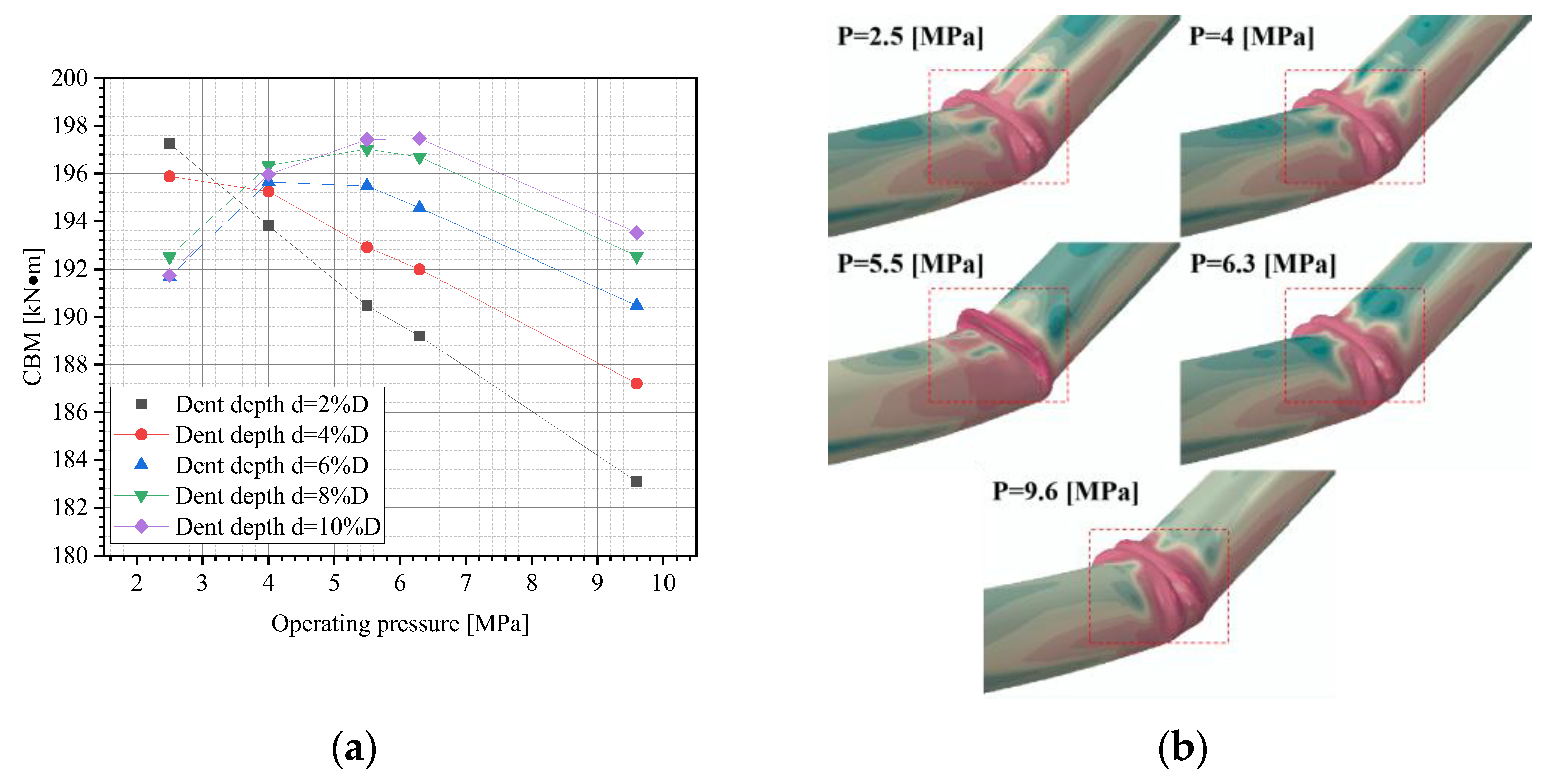
3.2. Effects of Operating Pressure on CBM
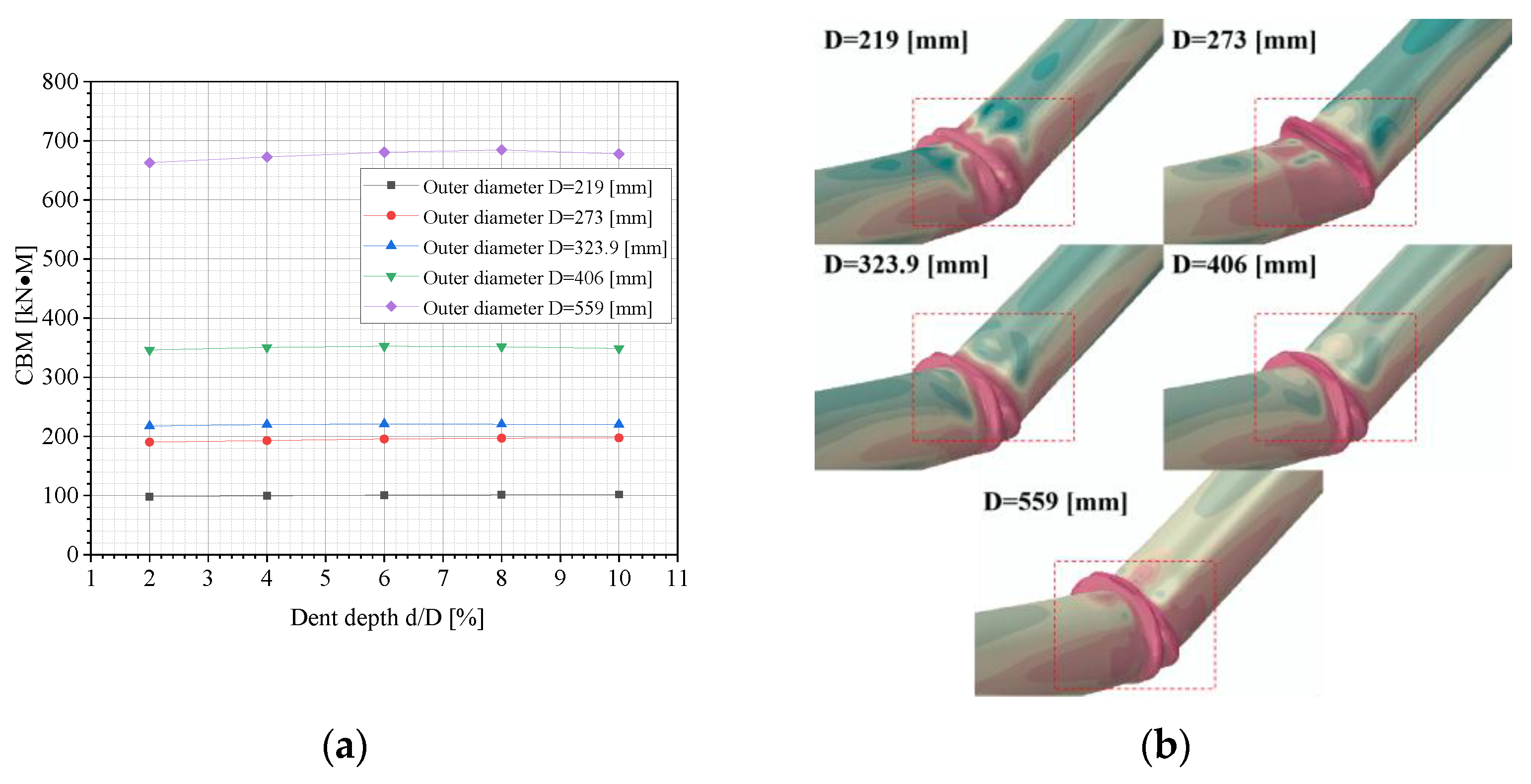
3.3. Effects of the Pipe’s Outer Diameter on CBM
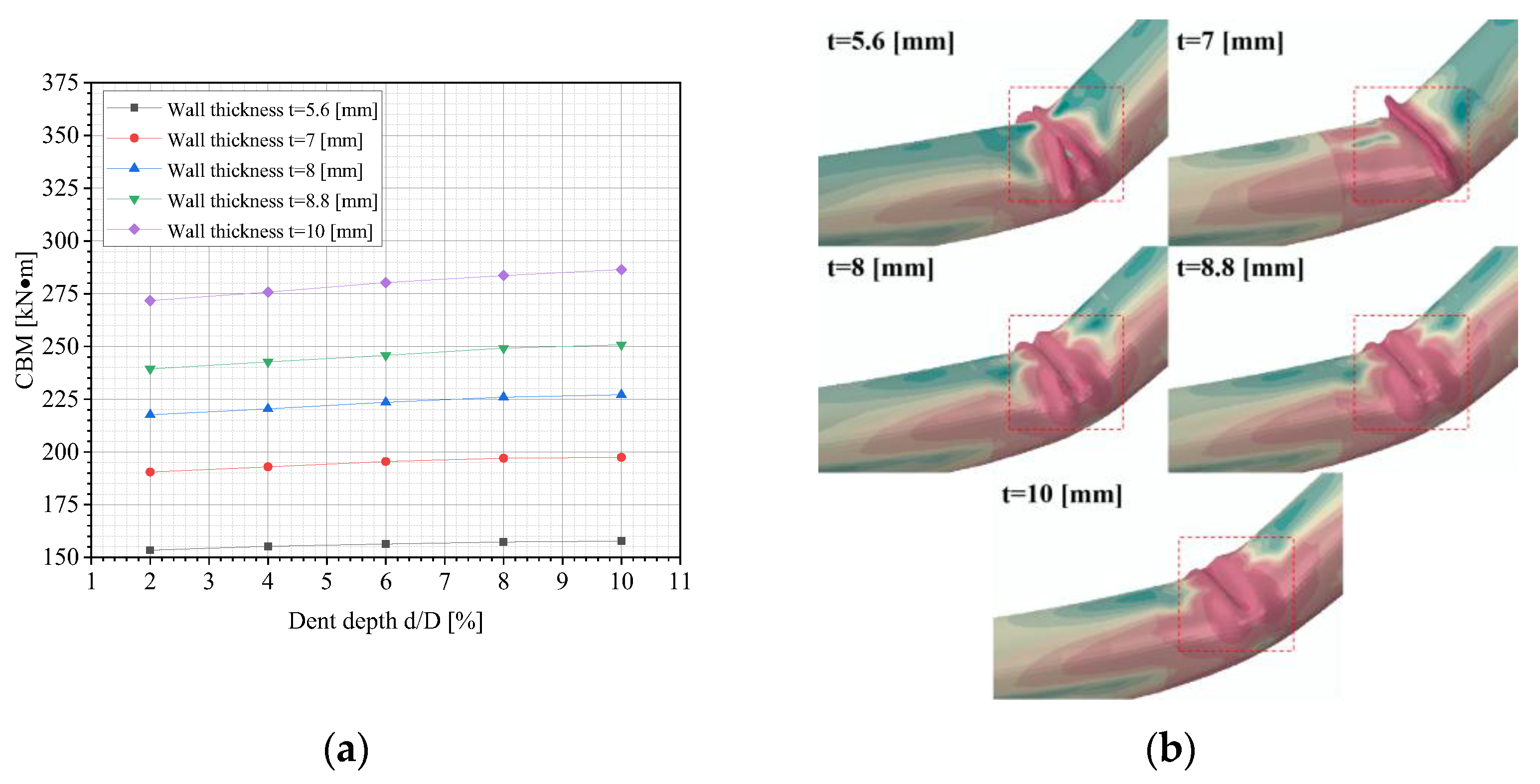
3.4. Effects of the Pipe’s Wall Thickness on CBM
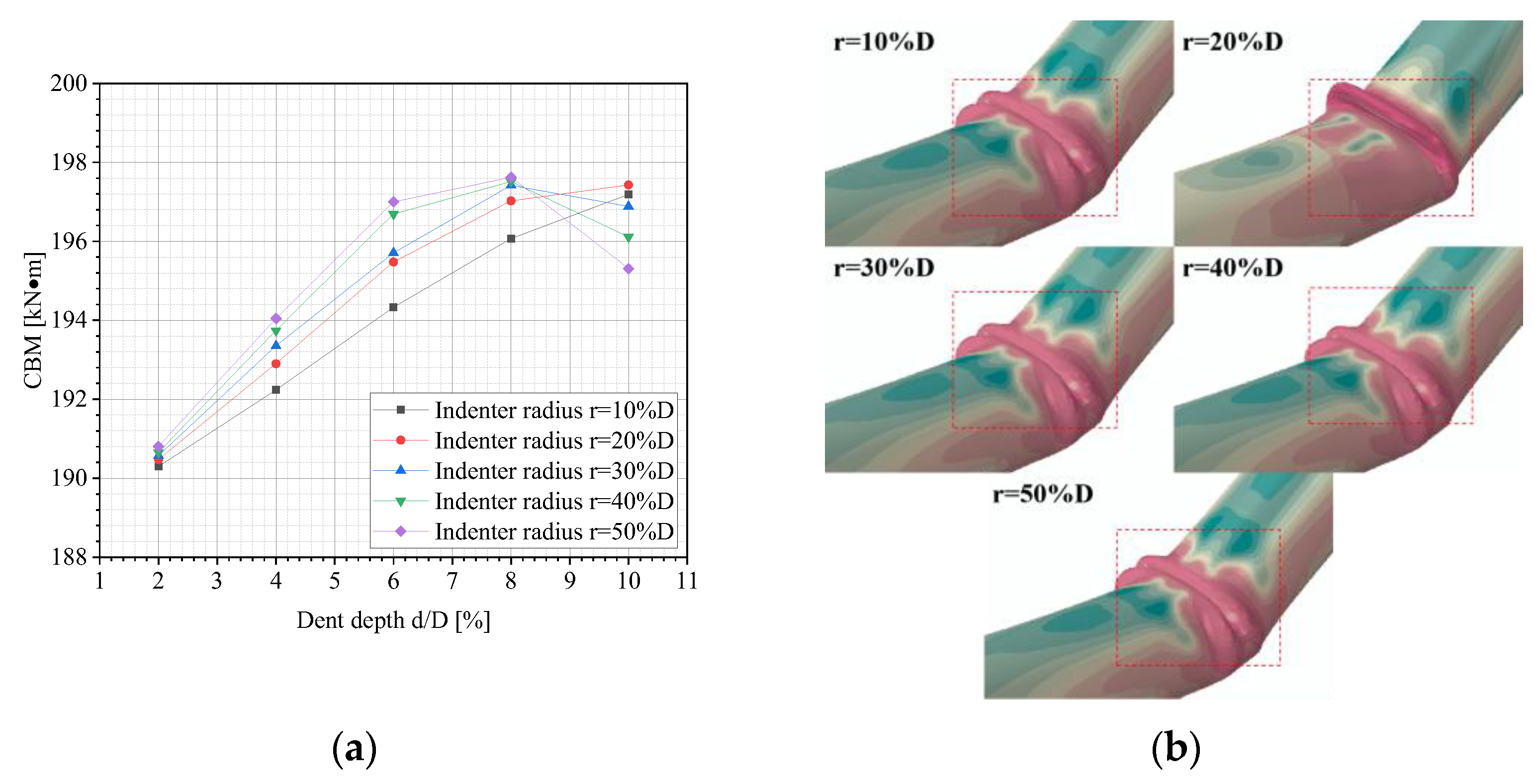
3.5. Effects of Indenter Radius on CBM
4. ML Approach
4.1. Data Collection and Processing
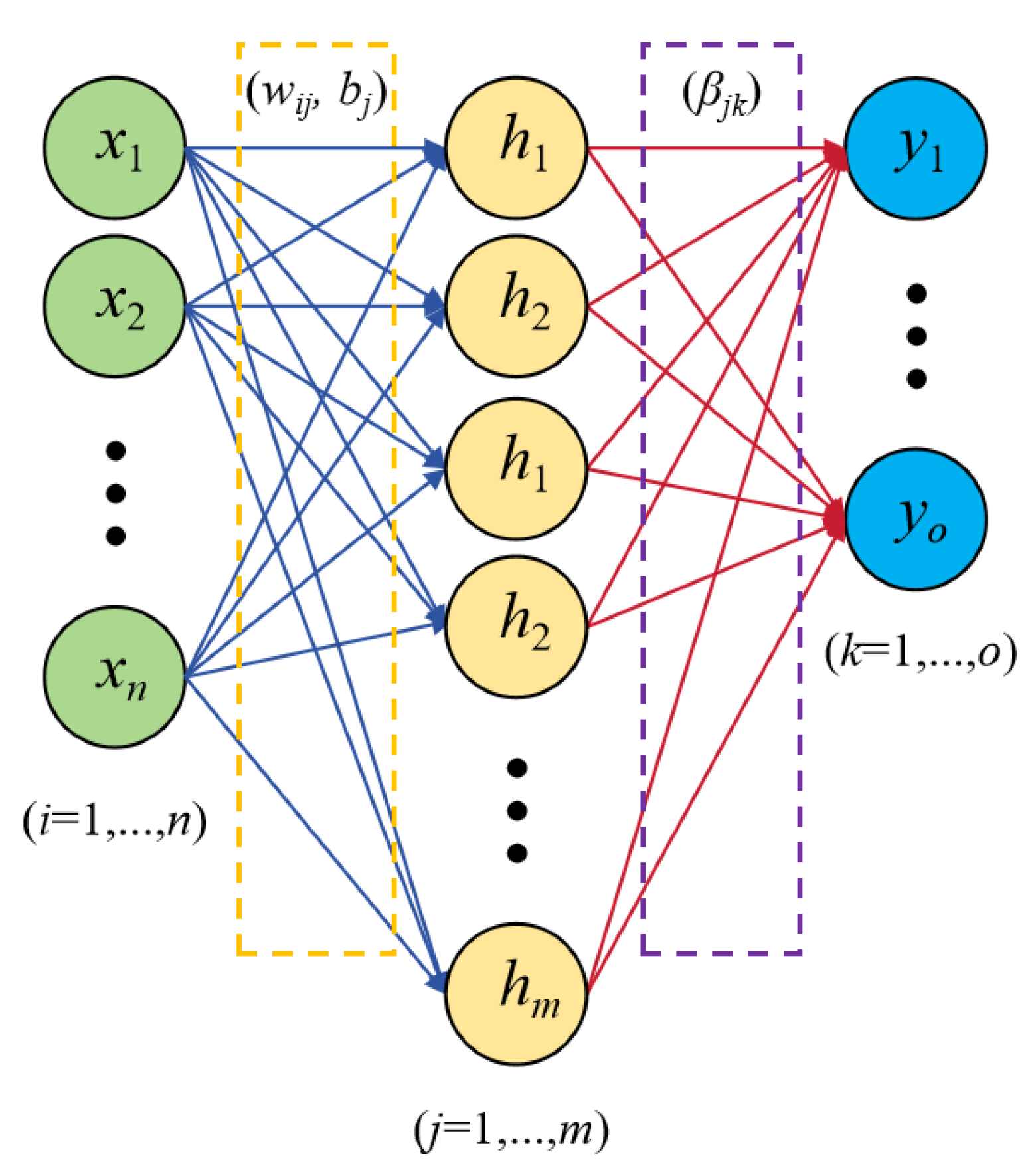
4.2. ML Model Development
4.3. ML Predictions and Discussion
4.3.1. Effects of Training Set Proportion on ML Predictions
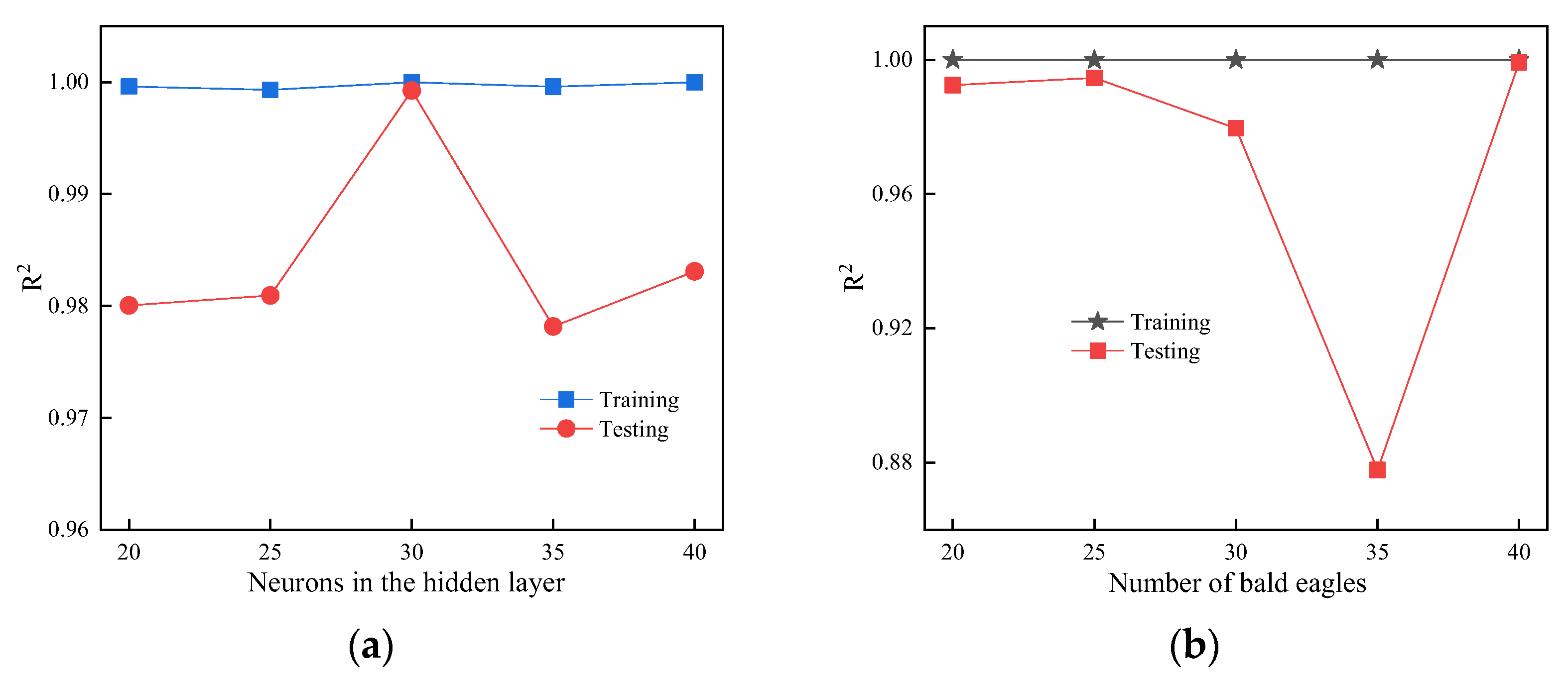
4.3.2. Effects of ELM’s Hidden Neurons and BES’s Population Size on ML Predictions
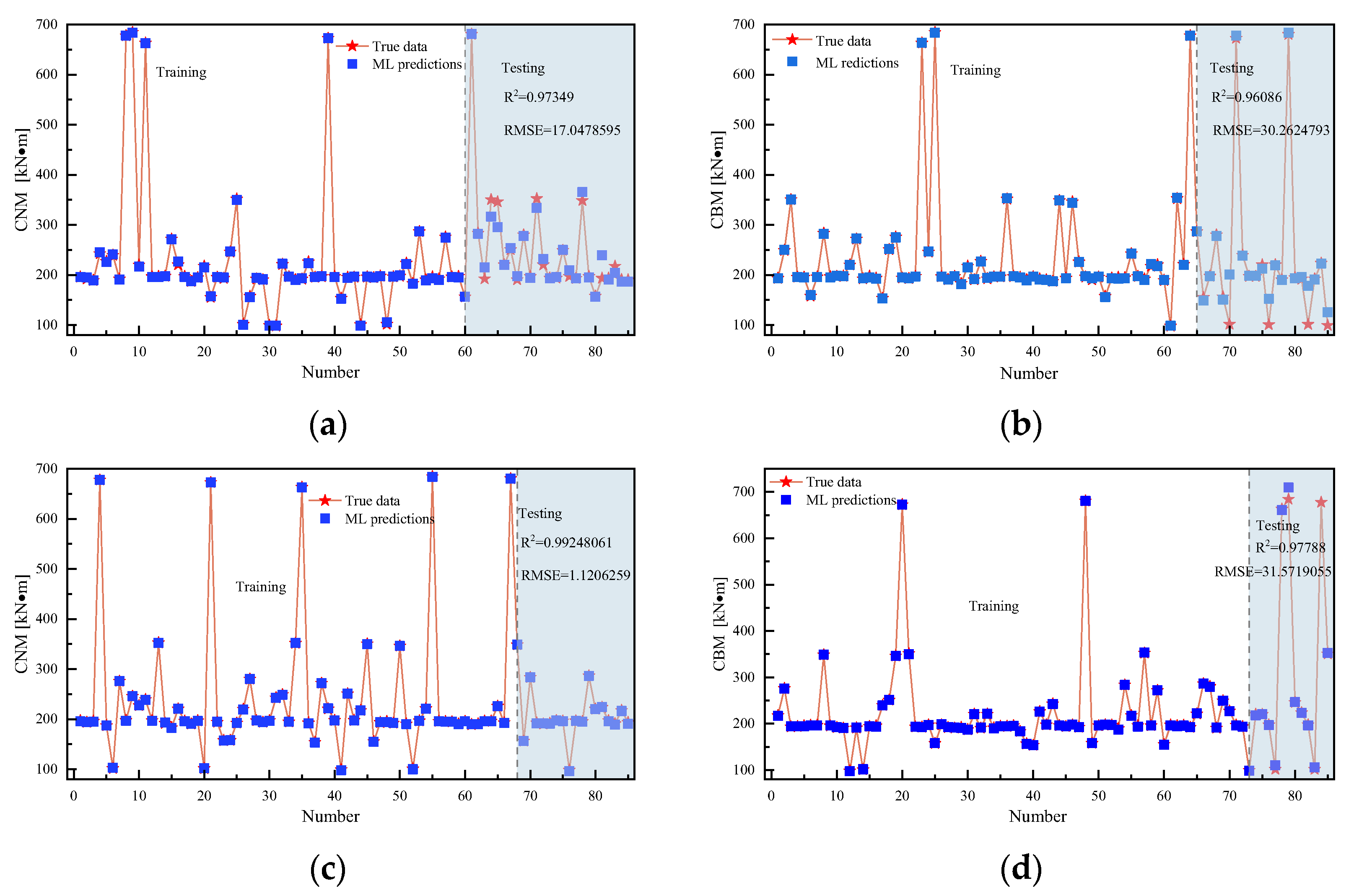
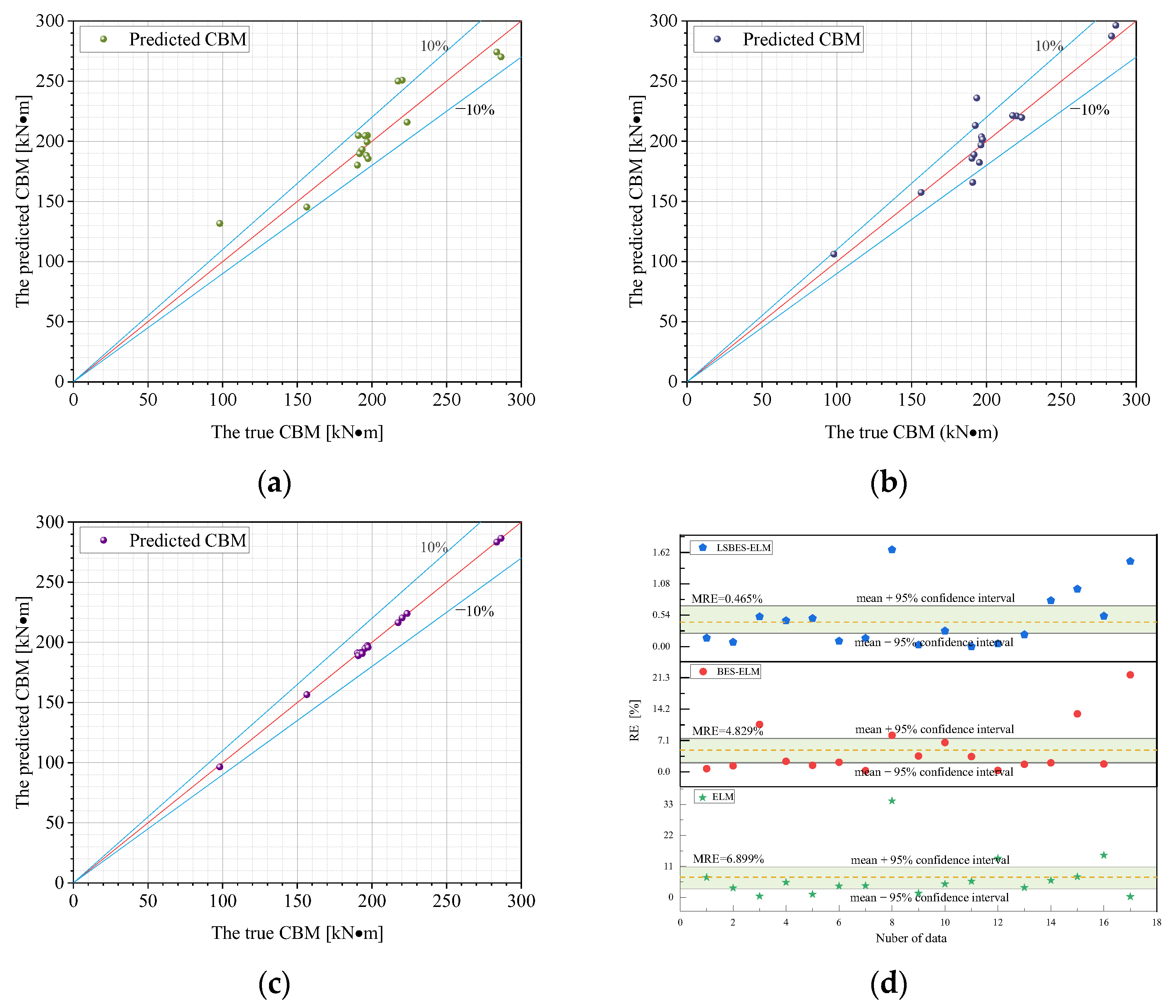
4.3.3. Accuracy Evaluation of ML Predictions
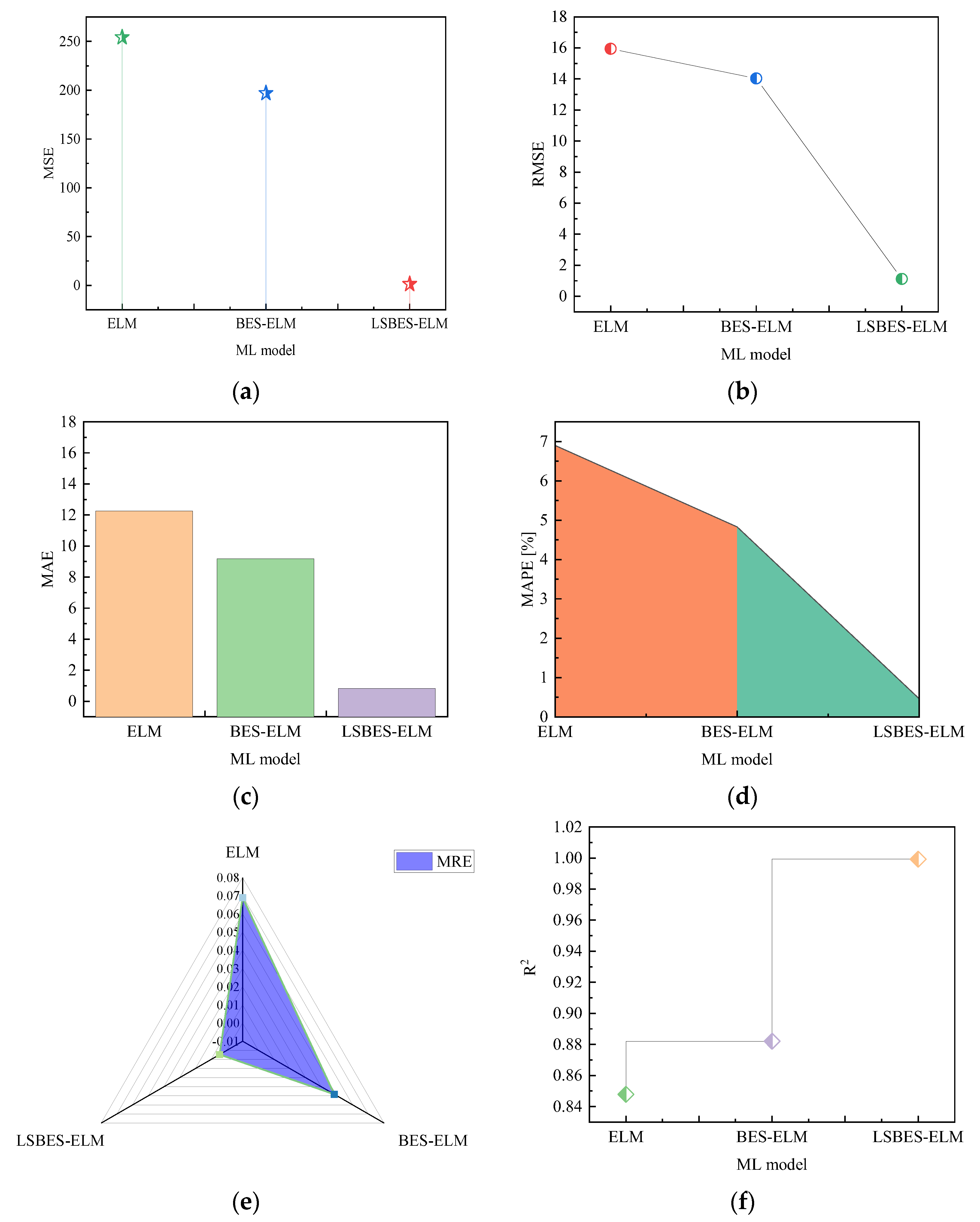
4.3.4. Performance Evaluation of ML Predictions
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| FE | Finite element |
| ML | Machine learning |
| CNM | Critical buckling moment |
| BM | Bending moment |
| ELM | Extreme learning machine |
| BES | Bald eagle search |
| SA | Simulated annealing |
| ILI | Ln-line inspection |
| Plimit | Burst pressure |
| σu | Ultimate tensile strength |
| σy | Yield strength |
| D | Pipe’s wall thickness |
| t | Pipe’s outer diameter |
| F | Axial force, |
| M | Bending moment |
| δ | Corrosion depth |
| W | Corrosion width |
| L | Corrosion length |
| FAD | Failure assessment diagram |
| Buckling strain capacity | |
| Pe | External pressure |
| Pi | Internal pressure |
| d | Dent depth |
| PE | Polyethylene |
| AL | Artificial intelligence |
| C3D8R | 8-node linear brick, reduced integration, hourglass control |
| R-O | Ramberg-Osgood |
| ε | Strain |
| σ | Stress |
| E | Elastic modulus |
| α | Yield offset |
| n | Strain-hardening exponent |
| σtrue | True stress |
| σeng | Engineering stress |
| εtrue | True strain |
| εeng | Engineering strain |
| P | Operating pressure |
| r | Indenter radius |
| RE | Relative error |
| BMtest | Pipe’s maximum bending moment from the test |
| BMFE | Pipe’s maximum bending moment from the numerical simulation |
| x | Variable |
| x′ | Normalized value of variable x |
| xmax | Maximum values of variable x |
| xmin | Minimum values of variable x |
| ymax | Upper limit of the normalization threshold |
| ymin | Lower limit of the normalization threshold |
| SLFNs | Single hidden layer feedforward neural networks |
| FFNNs | Feedforward neural networks |
| BP | Backpropagation |
| H(x) | Hidden layer output |
| hm(x) | Output of the mth neuron in the hidden layer |
| g | Activation function |
| β | Weight of the hidden-to-output layer |
| w | Weight of the input-to-hidden layer |
| b | Hidden layer bias |
| Y | Expected output of the output layer |
| Pi, new | Latest position of the bald eagle swarm |
| Pi | Current position of the bald eagle swarm |
| Pbest | Optimal positional coordinate attained by the bald eagle during iteration |
| α | Position-adaptive control coefficient |
| ρ | Stochastic parameter |
| Pmean | Centroid of the bald eagle swarm’s positional distribution |
| x(i) | Position of the bald eagle in polar coordinates |
| y(i) | Position of the bald eagle in polar coordinates |
| θ(i) | Polar angle of the spiral equation |
| r(i) | Polar diameter of the spiral equation |
| a | Flight trajectory parameter |
| R | Flight trajectory parameter |
| u | Scale parameter of the Lévy distribution |
| φ | Shape parameter of the Lévy distribution |
| v | Random variable |
| δx | Positional offset of the bald eagle relative to its current location |
| δy | Positional offset of the bald eagle relative to its current location |
| c1 | Intensity of motion towards the optimal position |
| c2 | Intensity of motion towards the center |
| p | Probability of accepting a worse solution |
| Enew | Energy of the new solution |
| Eold | Energy of the old solution |
| T | Current temperature |
| MRE | Mean relative error |
| MAPE | Mean absolute percentage error |
| MSE | Mean square error |
| RMSE | Root mean square error |
| MAE | Mean absolute error |
| R2 | Coefficient of determination |
| yi | Prediction results |
| True value | |
| Mean value | |
| n | Number of input variables |
References
- Huang, Y.; Qin, G.; Yang, M.; Nogal, M. Dynamic quantitative assessment of service resilience for long-distance energy pipelines under corrosion. Reliab. Eng. Syst. Safe. 2024, 256, 110792. [Google Scholar] [CrossRef]
- Li, T.; Zhang, H.; Hu, W.; Li, K.; Wang, Y.; Lin, Y. Hydrogen Embrittlement Behavior and Applicability of X52 Steel in Pure Hydrogen Pipelines. Materials 2025, 18, 3417. [Google Scholar] [CrossRef]
- Jing, H.; Zhang, S.; Zhao, D.; Wang, Z.; Liao, J.; Li, Z. Seismic Disaster Risk Assessment of Oil and Gas Pipelines. Appl. Sci. 2025, 15, 9135. [Google Scholar] [CrossRef]
- Fetisov, V.; Ilyushin, Y.V.; Vasiliev, G.G.; Leonovich, I.A.; Müller, J.; Riazi, M.; Mohammadi, A.H. Development of the automated temperature control system of the main gas pipeline. Sci. Rep. 2023, 13, 3092. [Google Scholar] [CrossRef]
- Vishnuvardhan, S.; Murthy, A.R.; Choudhary, A. A review on pipeline failures, defects in pipelines and their assessment and fatigue life prediction methods. Int. J. Hydrogen Energy 2022, 201, 104853. [Google Scholar] [CrossRef]
- An, Z.; Tang, Q.; Huang, Y.; Li, H. Time-dependent analysis of buried high-density polyethylene (PE100) pipelines with a scratch defect subjected to touchdown impact loading of blasting collapsed body. Int. J. Pres. Ves. Pip. 2022, 195, 104605. [Google Scholar] [CrossRef]
- Liu, Z.; Gao, Q.; Zhou, Y.; Pan, R. Research Progress on Major Influencing Factors of Corrosion Behavior of Pipeline Steel in Supercritical CO2 Environment. Materials 2025, 18, 2424. [Google Scholar] [CrossRef] [PubMed]
- Liu, W.; Zhang, P.; Liu, S.; Huang, Y.; Xu, T.; Zhao, M. A comprehensive failure analysis of corroded high-strength steel pipelines under seismic-induced landslide. J. Constr. Steel Res. 2025, 234, 109729. [Google Scholar] [CrossRef]
- Yan, Y.; Zhou, J.; Xie, C.; Yin, S.; Hu, S.; Wang, R. Quantitative Estimation of Pipeline Slope Disaster Risk in China. Int. J. Disaster Risk Sci. 2023, 14, 29–312. [Google Scholar] [CrossRef]
- Huang, Y.; Zhang, P.; Qin, G. Investigation by numerical modeling of the mechano-electrochemical interaction at a dent-corrosion defect on pipelines. Ocean Eng. 2022, 256, 111402. [Google Scholar] [CrossRef]
- Huang, Y.; Qin, G.; Hu, G. Failure pressure prediction by defect assessment and finite element modelling on pipelines containing a dent-corrosion defect. Ocean Eng. 2022, 266, 112875. [Google Scholar] [CrossRef]
- Qin, G.; Zhang, C.; Wang, B.; Wang, Y.; Cheng, Y.F. Investigation by finite element modeling of hydrogen-assisted failure mechanisms in pipelines containing a crack-in-dent defect. Int. J. Hydrogen Energy 2025, 143, 769–779. [Google Scholar] [CrossRef]
- Zhao, J.; Lv, Y.; Cheng, Y.F. Standards and methods for dent assessment and failure prediction of pipelines: A critical review. Petrol. Sci. 2022, 19, 3029–3045. [Google Scholar] [CrossRef]
- Wang, Y.; Li, Y.; Jiao, Y.; Qin, G. Local buckling failure analysis of pipelines containing a dent-corrosion defect under combined internal pressure and bending moment. Thin-Wall. Struct. 2025, 216 Pt C, 113741. [Google Scholar] [CrossRef]
- Zhang, P.; Huang, Y.; Wu, Y. Springback Coefficient Research of API X60 Pipe with Dent Defect. Energies 2018, 11, 3213. [Google Scholar] [CrossRef]
- Liu, S.; Zhang, P.; Tang, Q.; Wu, S.; Huang, Y. A Novel Safety Early Warning Methodology for Pipelines under Landslide Geological Hazard. J. Pipeline Syst. Eng. 2023, 15, 04023050. [Google Scholar] [CrossRef]
- Shuai, Y.; Zhang, X.; Feng, C.; Han, J.; Cheng, Y.F. A novel model for prediction of burst capacity of corroded pipelines subjected to combined loads of bending moment and axial compression. Int. J. Pres. Ves. Pip. 2022, 196, 104621. [Google Scholar] [CrossRef]
- Mondal, B.C.; Dhar, A.S. Burst pressure of corroded pipelines considering combined axial forces and bending moments. Eng. Struct. 2019, 186, 43–51. [Google Scholar] [CrossRef]
- Shuai, Y.; Wang, X.H.; Feng, C.; Zhu, Y.; Wang, C.L.; Sun, T.; Han, J.; Cheng, Y.F. A novel strain-based assessment method of compressive buckling of X80 corroded pipelines subjected to bending moment load. Thin-Wall. Struct. 2021, 167, 108172. [Google Scholar] [CrossRef]
- Shuai, Y.; Wang, X.H.; Cheng, Y.F. Buckling resistance of an X80 steel pipeline at corrosion defect under bending moment. J. Nat. Gas Sci. Eng. 2021, 93, 104016. [Google Scholar] [CrossRef]
- Ma, L.; Zheng, X.; Peng, H.Y.; Yu, J. Analytical ratcheting limits of straight pipeline under internal pressure and reversed bending moments. J. Pipeline Syst. Eng. 2020, 11, 04020018. [Google Scholar] [CrossRef]
- Zhang, Y.; Lie, S.; Zhao, H. Fracture behavior of clad pipeline containing a canoe shape surface crack subjected to large bending moment. Mar. Struct. 2018, 58, 92–108. [Google Scholar] [CrossRef]
- Hou, F.; Jia, L.S.; Chen, Y.F.; Zhang, Q.; Zhong, R.F.; Wang, C.S. Bending failure mode and prediction method of the compressive strain capacity of a submarine pipeline with dent defects. China Ocean Eng. 2024, 38, 636–647. [Google Scholar] [CrossRef]
- Hou, F.; Chen, Y.; Jia, L.; Peng, Z.; Liu, Y.; Liu, R.; Zhong, R.F.; Li, R. A novel model for predicting the ultimate bending moment of subsea pipelines with corrosion-dent coupled defects. Ocean Eng. 2025, 330, 121210. [Google Scholar] [CrossRef]
- Wang, J.; Shuai, Y.; He, R.; Dou, X.; Zhang, P.; Feng, C. Ultimate strain capacity assessment of local buckling of pipelines with kinked dents subjected to bending loads. Thin-Wall. Struct. 2021, 169, 108369. [Google Scholar] [CrossRef]
- Zhu, L.; Li, N.; Jia, B.; Zhang, Y. Fracture Response of X80 Pipe Girth Welds under Combined Internal Pressure and Bending Moment. Materials 2023, 16, 3588. [Google Scholar] [CrossRef]
- Wang, F.; Asce, M.; Dong, D.; Du, Y.J.; Corey, R. Estimating maximum bending moment in high-density polyethylene pipes under traffic loading. J. Pipeline Syst. Eng. 2021, 12, 04021001. [Google Scholar] [CrossRef]
- Sun, M.M.; Fang, H.Y.; Wang, N.N.; Du, X.M.; Zhao, H.S.; Zhai, K.J. Limit state equation and failure pressure prediction model of pipeline with complex loading. Nat. Commun. 2024, 15, 4473. [Google Scholar] [CrossRef]
- Ren, W.; Shuai, J.; Mei, Y. Experiment-Based Reliability Analysis of Girth Welds on Different Grade Steel Pipelines. IEEE T Reliab. 2024, 73, 492–505. [Google Scholar] [CrossRef]
- GB/T 9711; Petroleum and Natural Gas Industries-Steel Pipes for Pipeline Transportation Systems. National Standard of the People’s Republic of China: Beijing, China, 2023.
- Shuai, Y.; Zhou, D.C.; Wang, X.H.; Yin, H.G.; Zhu, S.; Li, J.; Cheng, Y.F. Local buckling failure analysis of high strength pipelines containing a plain dent under bending moment. J. Nat. Gas Sci. Eng. 2020, 77, 103266. [Google Scholar] [CrossRef]
- Zimmerman, T.; Timms, C.; Xie, J.; Asante, J. Buckling Resistance of Large Diameter Spiral Welded Linepipe. In Proceedings of the IPC2004 International Pipeline Conference 2004, Calgary, AB, Canada, 4–8 October 2004. [Google Scholar]
- Yang, L.; Chen, Z.; Cao, G.; Yu, C.; Guo, W. An analytical formula for elastic-plastic instability of large oil storage tanks. Int. J. Pres. Ves. Pip. 2013, 101, 72–80. [Google Scholar] [CrossRef]
- Shen, H.; Wang, Y.; Liu, W.; Liu, S.; Qin, G. Data-driven reliability evolution prediction of underground pipeline under corrosion. Reliab. Eng. Syst. Safe. 2025, 261, 111148. [Google Scholar] [CrossRef]
- Liu, W.; Zhang, P.; Liu, S.; Shen, H.; Huang, Y.; Xu, T.; Wu, S. A hybrid machine learning framework for integrity assessment of buried pipelines subjected to landslide. J. Loss Prevent. Proc. 2025, 98, 105754. [Google Scholar] [CrossRef]
- Wang, J.; Lu, S.; Wang, S.H.; Zhang, Y.D. A review on extreme learning machine. Multimed. Tool. Appl. 2022, 81, 41611–41660. [Google Scholar] [CrossRef]
- Zhou, J.; Zhou, L.; Cai, C.; Zhao, Y. Multi-step ozone concentration prediction model based on improved secondary decomposition and adaptive kernel density estimation. Process Saf. Environ. 2024, 190 Pt B, 386–404. [Google Scholar] [CrossRef]
- Alsattar, H.A.; Zaidan, A.A.; Zaidan, B.B. Novel meta-heuristic bald eagle search optimisation algorithm. Artif. Intell. Rev. 2020, 53, 2237–2264. [Google Scholar] [CrossRef]
- Qin, G.; Xia, A.; Lu, H.; Wang, Y.; Li, R.; Wang, C. A hybrid machine learning model for predicting crater width formed by explosions of natural gas pipelines. J. Loss Prevent. Proc. 2023, 82, 104994. [Google Scholar] [CrossRef]
- Meira, W.H.T.; Magatão, L.; Neves-Jr, F.; Arruda, L.V.R.; Vaqueiro, J.P.; Relvas, S.; Barbosa-Póvoa, A.P. Scheduling of a single-source multiproduct pipeline system by a matheuristic approach: Combining simulated annealing and MILP. Comput. Chem. Eng. 2020, 136, 106784. [Google Scholar] [CrossRef]
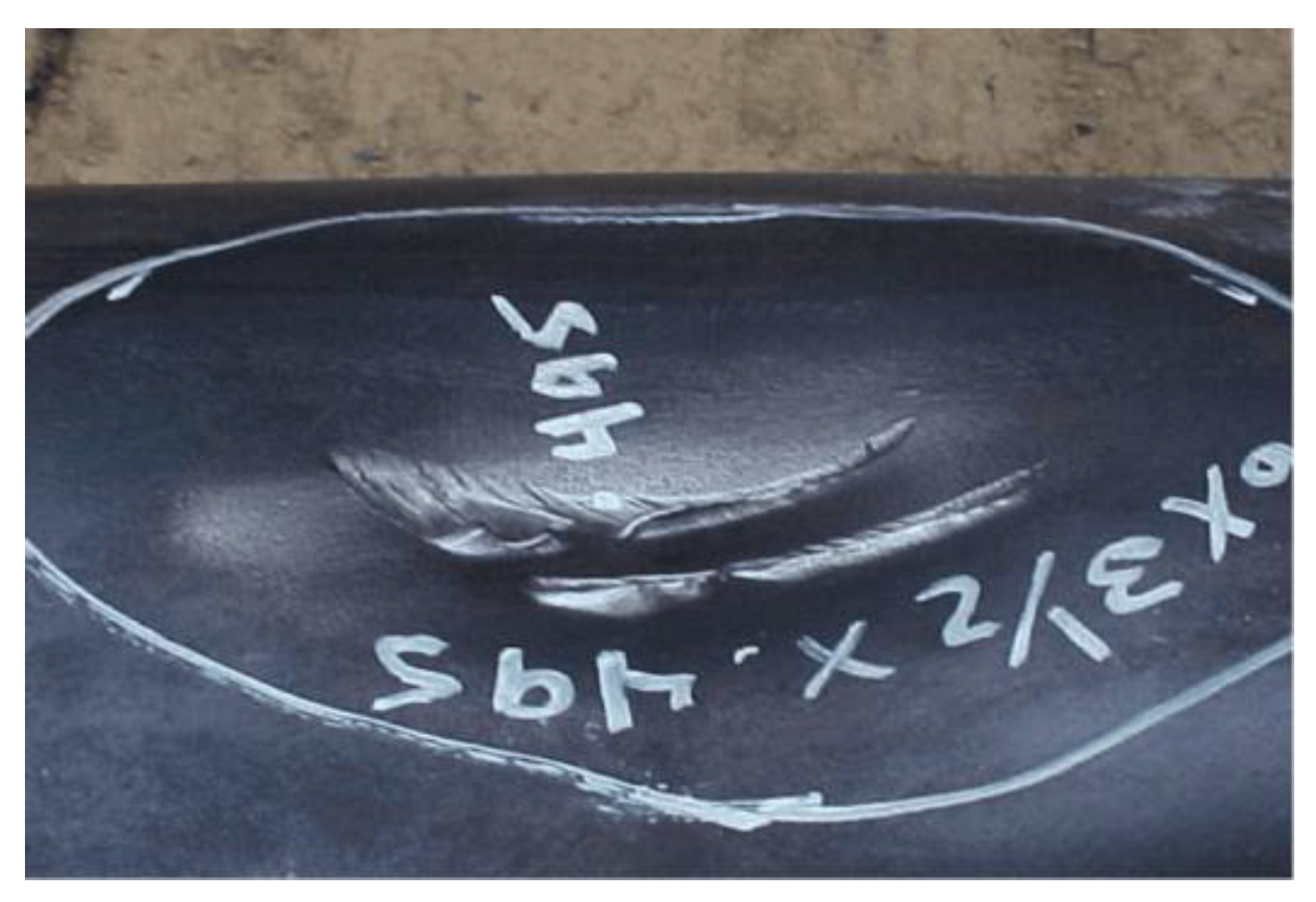


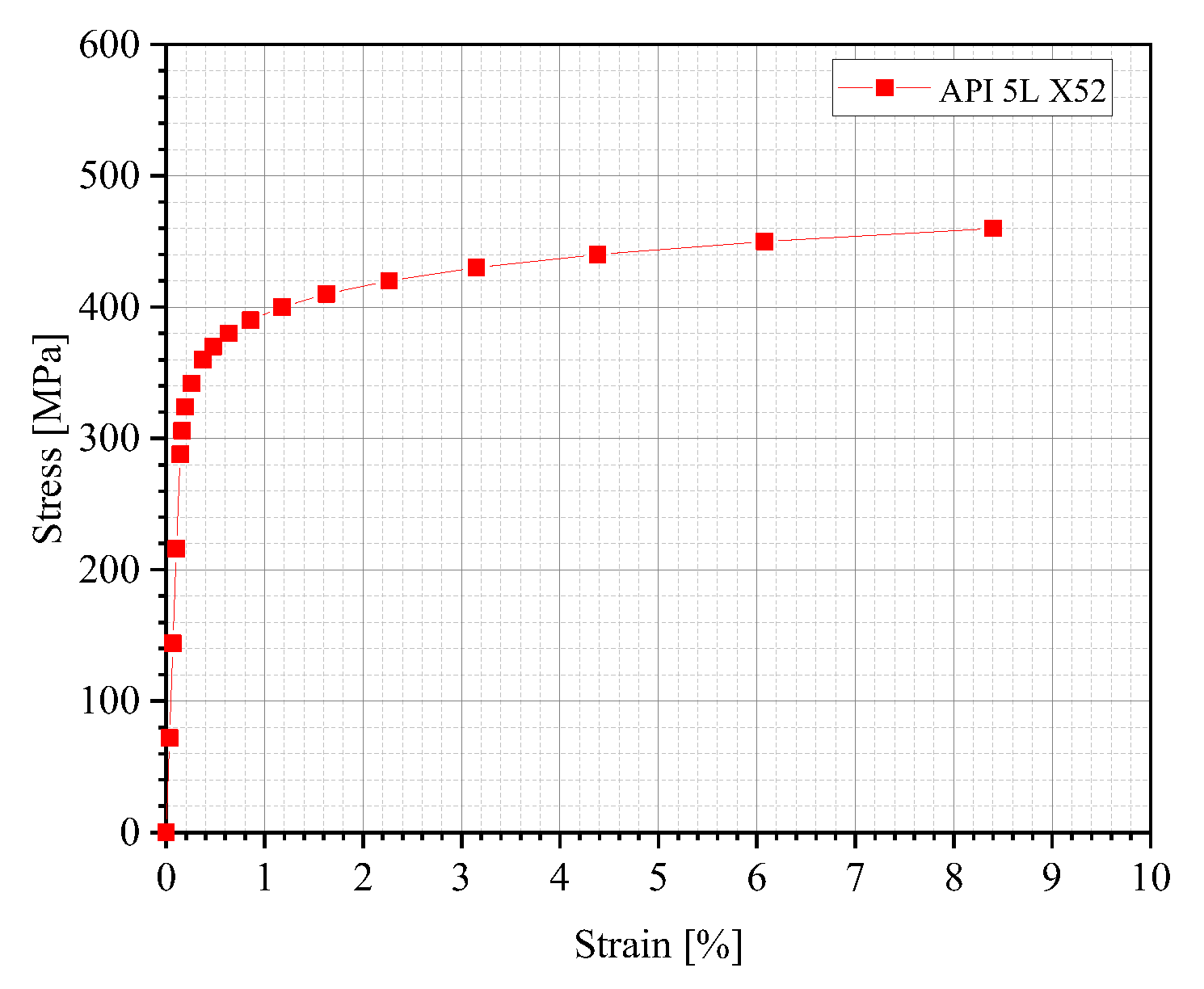




| Young’s Modulus E [GPa] | Poisson’s Ratio | Yield Offset ɑ | Strain-Hardening Exponent n | Yield Strength σy [MPa] | Ultimate Tensile Strength σu [MPa] |
|---|---|---|---|---|---|
| 210 | 0.3 | 1.699 | 14.14 | 360 | 460 |
| Variable | Operating Pressure [MPa] | Pipe Outer Diameter [mm] | Pipe Wall Thickness [mm] | Indenter Radius [mm] | Dent Depth [mm] |
|---|---|---|---|---|---|
| Value | 5.5 | 273 | 7 | 54.6 | 5.46, 10.92, 16.38, 21.84, 27.3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, Y.; Tang, J.; Lin, D.; Sun, M.; Shu, J.; Liu, W.; Hou, X. A Hybrid FE-ML Approach for Critical Buckling Moment Prediction in Dented Pipelines Under Complex Loadings. Materials 2025, 18, 4721. https://doi.org/10.3390/ma18204721
Huang Y, Tang J, Lin D, Sun M, Shu J, Liu W, Hou X. A Hybrid FE-ML Approach for Critical Buckling Moment Prediction in Dented Pipelines Under Complex Loadings. Materials. 2025; 18(20):4721. https://doi.org/10.3390/ma18204721
Chicago/Turabian StyleHuang, Yunfei, Jianrong Tang, Dong Lin, Mingnan Sun, Jie Shu, Wei Liu, and Xiangqin Hou. 2025. "A Hybrid FE-ML Approach for Critical Buckling Moment Prediction in Dented Pipelines Under Complex Loadings" Materials 18, no. 20: 4721. https://doi.org/10.3390/ma18204721
APA StyleHuang, Y., Tang, J., Lin, D., Sun, M., Shu, J., Liu, W., & Hou, X. (2025). A Hybrid FE-ML Approach for Critical Buckling Moment Prediction in Dented Pipelines Under Complex Loadings. Materials, 18(20), 4721. https://doi.org/10.3390/ma18204721






