Equation for Calculation of Critical Current Density Using the Bean’s Model with Self-Consistent Magnetic Units to Prevent Unit Conversion Errors
Abstract
1. Introduction
2. Methods
- –
- When the magnetic moment is in [A m2] and the dimensions in meters, their use in Equation (2) leads to Equation (3) where the current density is directly in
- –
- When the magnetic moment is in [emu] and the dimensions in centimeters, their use in Equation (2) leads to Equation (4) where the current density is in the unpractical . In order to have the current density expressed in more practical units, the conversion can be used, which introduces a multiplicative dimensionless term 10 that transforms the number 2 into 20, and leads to a current density expressed in (Equation (5)). On the contrary, the expression where ΔM is stated to be in emu/cm3 and Jc is resulting in A/cm2 is misleading, because the dimensions on the right and left-hand side of the equation are not coherent and erroneously suggest the need for a further unit conversion.
- –
- Starting from Equation (2) above in this paper, with the use of the SI units system where the magnetic moment μ is expressed in and the dimensions are in meters , the calculation is direct and the critical current density is directly obtained in . Since many magnetometers present their output in emu (although in several models it is possible to choose the units for the output), the same Equation (2) can be used by inserting the magnetic moment μ in emu and the dimensions in centimeters , leading for a certain value (for practical reasons, let us call “Z” this value, simply resulting from the numbers given to the quantities in Equation (2)) in . If the value “Z” in is multiplied by 10, because of the conversion
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Molodyk, A.; Larbalestier, D.C. The Prospects of High-Temperature Superconductors. Science 2023, 380, 1220–1222. [Google Scholar] [CrossRef] [PubMed]
- Marchionini, B.G.; Yamada, Y.; Martini, L.; Ohsaki, H. High-Temperature Superconductivity: A Roadmap for Electric Power Sector Applications, 2015–2030. IEEE Trans. Appl. Supercond. 2017, 27, 1–7. [Google Scholar] [CrossRef]
- Bean, C.P. Magnetization of Hard Superconductors. Phys. Rev. Lett. 1962, 8, 250–253. [Google Scholar] [CrossRef]
- Bean, C.P. Magnetization of High-Field Superconductors. Rev. Mod. Phys. 1964, 36, 31–39. [Google Scholar] [CrossRef]
- Gyorgy, E.M.; Van Dover, R.B.; Jackson, K.A.; Schneemeyer, L.F.; Waszczak, J.V. Anisotropic Critical Currents in Ba2YCu3O7 Analyzed Using an Extended Bean Model. Appl. Phys. Lett. 1989, 55, 283–285. [Google Scholar] [CrossRef]
- Li, M.; Chen, L.; You, W.L.; Ge, J.; Zhang, J. Giant Increase of Critical Current Density and Vortex Pinning in Mn Doped KxFe2-YSe2 Single Crystals. Appl. Phys. Lett. 2014, 105, 192602. [Google Scholar] [CrossRef]
- Haberkorn, N.; Xu, M.; Schmidt, J.; Suárez, S.; Bud’Ko, S.L.; Canfield, P.C. Understanding Vortex Dynamics in CaK(Fe,Ni)4As4 and Ba(Fe,Co)2As2 Single Crystals under the Influence of Random Point Disorder. Supercond. Sci. Technol. 2024, 37, 115003. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, T.; Xu, Z.; Hong, W.; Peng, W.; Lin, Z.R.; Luo, H.; Mu, G. Influences of Quenching Treatment and Cobalt-Doping on the Thermally Activated Flux-Flow Behavior in KCa2(Fe1−xCox)4As4F2. Supercond. Sci. Technol. 2023, 36, 095008. [Google Scholar] [CrossRef]
- Wang, A.; Wu, L.; Ivanovski, V.N.; Warren, J.B.; Tian, J.; Zhu, Y.; Petrovic, C. Critical Current Density and Vortex Pinning in Tetragonal FeS1-XSex (X=0,0.06). Phys. Rev. B 2016, 94, 094506. [Google Scholar] [CrossRef]
- Wang, Y.; Li, M.; Pei, C.; Gao, L.; Bu, K.; Wang, D.; Liu, X.; Yan, L.; Qu, J.; Li, N.; et al. Critical Current Density and Vortex Phase Diagram in the Superconductor Sn0.55In0.45Te. Phys. Rev. B 2022, 106, 054506. [Google Scholar] [CrossRef]
- Eley, S.; Khilstrom, K.; Fotovat, R.; Xiao, Z.L.; Chen, A.; Chen, D.; Leroux, M.; Welp, U.; Kwok, W.K.; Civale, L. Glassy Dynamics in a Heavy Ion Irradiated NbSe2 Crystal. Sci. Rep. 2018, 8, 13162. [Google Scholar] [CrossRef]
- Vlasenko, V.A.; Sadakov, A.V.; Romanova, T.A.; Yu Gavrilkin, S.; Dik, A.V.; Sobolevskiy, O.A.; Massalimov, B.I.; Chareev, D.A.; Vasiliev, A.N.; Maltsev, E.I.; et al. Evolution of Vortex Matter, Phase Diagram, and Upper Critical Field in the FeSe1-XSxsystem. Supercond. Sci. Technol. 2021, 34, 035019. [Google Scholar] [CrossRef]
- Galstyan, E.; Pratap, R.; Majkic, G.; Kochat, M.; Abraimov, D.; Jaroszynski, J.; Selvamanickam, V. In-Field Critical Current and Pinning Mechanisms at 4.2 K of Zr-Added REBCO Coated Conductors. Supercond. Sci. Technol. 2020, 33, 074007. [Google Scholar] [CrossRef]
- Wen, Z.; Jia, T.; Xiao, Y.; Wu, Y.; Li, Y.; Li, S.; Cui, Y.; Zhong, R.; Chen, Y.; Cheng, C.; et al. Flux Dynamics, Anisotropy in Jc and Vortex Phase Diagram of H+-Intercalated FeSe Single Crystal. Chin. J. Phys. 2024, 92, 721–731. [Google Scholar] [CrossRef]
- Narayan, J.; Bhaumik, A.; Sachan, R. High Temperature Superconductivity in Distinct Phases of Amorphous B-Doped Q-Carbon. J. Appl. Phys. 2018, 123, 135304. [Google Scholar] [CrossRef]
- Sun, Y.; Pyon, S.; Tamegai, T.; Kobayashi, R.; Watashige, T.; Kasahara, S.; Matsuda, Y.; Shibauchi, T. Critical Current Density, Vortex Dynamics, and Phase Diagram of Single-Crystal FeSe. Phys. Rev. B Condens. Matter Mater. Phys. 2015, 92, 144509. [Google Scholar] [CrossRef]
- Nakajima, Y.; Tsuchiya, Y.; Taen, T.; Tamegai, T.; Okayasu, S.; Sasase, M. Enhancement of Critical Current Density in Co-Doped BaFe2As2 with Columnar Defects Introduced by Heavy-Ion Irradiation. Phys. Rev. B Condens. Matter Mater. Phys. 2009, 80, 012510. [Google Scholar] [CrossRef]
- Haberkorn, N.; Maiorov, B.; Usov, I.O.; Weigand, M.; Hirata, W.; Miyasaka, S.; Tajima, S.; Chikumoto, N.; Tanabe, K.; Civale, L. Influence of Random Point Defects Introduced by Proton Irradiation on Critical Current Density and Vortex Dynamics of Ba(Fe0.925Co0.075)2As2 Single Crystals. Phys. Rev. B Condens. Matter Mater. Phys. 2012, 85, 014522. [Google Scholar] [CrossRef]
- Lei, H.; Hu, R.; Petrovic, C. Critical Fields, Thermally Activated Transport, and Critical Current Density of β-FeSe Single Crystals. Phys. Rev. B Condens. Matter Mater. Phys. 2011, 84, 014520. [Google Scholar] [CrossRef]
- Plain, J.; Puig, T.; Sandiumenge, F.; Obradors, X.; Rabier, J. Microstructural Influence on Critical Currents and Irreversibility Line in Melt-Textured YBa2Cu3O7-x Reannealed at High Oxygen Pressure. Phys. Rev. B 2002, 65, 104526. [Google Scholar] [CrossRef]
- Pyon, S.; Taya, S.; Kobayashi, Y.; Takahashi, A.; Li, W.; Taen, T.; Wang, T.; Mu, G.; Kitamura, H.; Ichinose, A.; et al. Critical Current Density and Vortex Dynamics in Pristine and Irradiated KCa2Fe4As4F2. Materials 2021, 14, 5283. [Google Scholar] [CrossRef]
- Taen, T.; Tsuchiya, Y.; Nakajima, Y.; Tamegai, T. Critical Current Densities and Vortex Dynamics in FeTexSe1-x Single Crystals. Phys. C 2010, 470, 1106–1108. [Google Scholar] [CrossRef]
- Tao, J.; Deng, Q.; Yang, H.; Wang, Z.; Zhu, X.; Wen, H.H. Magnetization Relaxation, Critical Current Density, and Vortex Dynamics in a Ba0.66 K0.32BiO3+δ Single Crystal. Phys. Rev. B Condens. Matter Mater. Phys. 2015, 91, 214516. [Google Scholar] [CrossRef]
- Yi, X.; Xing, X.; Meng, Y.; Zhou, N.; Wang, C.; Sun, Y.; Shi, Z. Anomalous Second Magnetization Peak in 12442-Type RbCa2Fe4As4F2 Superconductors. Chin. Phys. Lett. 2023, 40, 027401. [Google Scholar] [CrossRef]
- Shahbazi, M.; Wang, X.L.; Choi, K.Y.; Dou, S.X. Flux Pinning Mechanism in BaFe1.9Ni0.1As2 Single Crystals: Evidence for Fluctuation in Mean Free Path Induced Pinning. Appl. Phys. Lett. 2013, 103, 032605. [Google Scholar] [CrossRef]
- Sun, Y.; Taen, T.; Tsuchiya, Y.; Pyon, S.; Shi, Z.; Tamegai, T. Magnetic Relaxation and Collective Vortex Creep in FeTe0.6Se0.4 Single Crystal. Europhys. Lett. 2013, 103, 57013. [Google Scholar] [CrossRef]
- Cheng, W.; Lin, H.; Shen, B.; Wen, H.H. Comparative Study of Vortex Dynamics in CaKFe4As4 and Ba0.6K0.4Fe2As2 Single Crystals. Sci. Bull. 2019, 64, 81–90. [Google Scholar] [CrossRef] [PubMed]
- Ishida, S.; Iyo, A.; Ogino, H.; Eisaki, H.; Takeshita, N.; Kawashima, K.; Yanagisawa, K.; Kobayashi, Y.; Kimoto, K.; Abe, H.; et al. Unique Defect Structure and Advantageous Vortex Pinning Properties in Superconducting CaKFe4As4. npj Quantum Mater. 2019, 4, 27. [Google Scholar] [CrossRef]
- Hossaini, S.J.; Ghorbani, S.R.; Arabi, H.; Wang, X.L.; Lin, C.T. Temperature and Field Dependence of the Flux Pinning Mechanisms in Fe1.06Te0.6Se0.4 Single Crystal. Solid State Commun. 2016, 246, 29–32. [Google Scholar] [CrossRef]
- Eley, S.; Leroux, M.; Rupich, M.W.; Miller, D.J.; Sheng, H.; Niraula, P.M.; Kayani, A.; Welp, U.; Kwok, W.K.; Civale, L. Decoupling and Tuning Competing Effects of Different Types of Defects on Flux Creep in Irradiated YBa2Cu3O7-δ Coated Conductors. Supercond. Sci. Technol. 2017, 30, 015010. [Google Scholar] [CrossRef]
- Ijaduola, A.O.; Wee, S.H.; Goyal, A.; Martin, P.M.; Li, J.; Thompson, J.R.; Christen, D.K. Critical Currents, Magnetic Relaxation and Pinning in NdBa2Cu3O7−δ Films with BaZrO3-Generated Columnar Defects. Supercond Sci. Technol. 2012, 25, 045013. [Google Scholar] [CrossRef]
- Thompson, J.R.; Sinclair, J.W.; Christen, D.K.; Zhang, Y.; Zuev, Y.L.; Cantoni, C.; Chen, Y.; Selvamanickam, V. Field, Temperature, and Angle Dependent Critical Current DensityJc(H,T,θ) in Coated Conductors Obtained via Contact-Free Methods. Supercond. Sci. Technol. 2009, 23, 014002. [Google Scholar] [CrossRef]
- Thompson, J.R.; Sun, Y.R.; Kerchner, H.R.; Christen, D.K.; Sales, B.C.; Chakoumakos, B.C.; Marwick, A.D.; Civale, L.; Thomson, J.O. Enhanced Current Density Jc and Extended Irreversibility in Single-crystal Bi2Sr2Ca1Cu2O8 via Linear Defects from Heavy Ion Irradiation. Appl. Phys. Lett. 1992, 60, 2306–2308. [Google Scholar] [CrossRef]
- Yadav, C.S.; Paulose, P.L. Upper Critical Field, Lower Critical Field and Critical Current Density of FeTe0.60Se0.40 Single Crystals. New J. Phys. 2009, 11, 103046. [Google Scholar] [CrossRef]
- UNITS FOR MAGNETIC PROPERTIES. Available online: https://ieeemagnetics.org/files/ieeemagnetics/2022-04/magnetic_units.pdf (accessed on 2 December 2024).
- Units for Magnetic Properties. Available online: https://www.nist.gov/system/files/documents/pml/electromagnetics/magnetics/magnetic_units.pdf (accessed on 2 December 2024).
- Taen, T.; Ohtake, F.; Pyon, S.; Tamegai, T.; Kitamura, H. Critical Current Density and Vortex Dynamics in Pristine and Proton-Irradiated Ba 0.6 K 0.4 Fe 2 As 2. Supercond. Sci. Technol. 2015, 28, 085003. [Google Scholar] [CrossRef]
- Park, A.; Pyon, S.; Ohara, K.; Ito, N.; Tamegai, T.; Kambara, T.; Yoshida, A.; Ichinose, A. Field-Driven Transition in the Ba1-XKxFe2As2 Superconductor with Splayed Columnar Defects. Phys. Rev. B 2018, 97, 064516. [Google Scholar] [CrossRef]
- Pyon, S.; Kobayashi, Y.; Takahashi, A.; Li, W.; Wang, T.; Mu, G.; Ichinose, A.; Kambara, T.; Yoshida, A.; Tamegai, T. Anisotropic Physical Properties and Large Critical Current Density in KCa2Fe4As4F2 Single Crystal. Phys. Rev. Mater. 2020, 4, 104801. [Google Scholar] [CrossRef]
- Pyon, S.; Takahashi, A.; Veshchunov, I.; Tamegai, T.; Ishida, S.; Iyo, A.; Eisaki, H.; Imai, M.; Abe, H.; Terashima, T.; et al. Large and Significantly Anisotropic Critical Current Density Induced by Planar Defects in CaKFe4As4 Single Crystals. Phys. Rev. B 2019, 99, 104506. [Google Scholar] [CrossRef]
- Wang, J.; Takahashi, A.; Pyon, S.; Yoshida, A.; Kambara, T.; Sun, Y.; Kitano, H.; Tamegai, T. Anisotropic Critical Current Densities in Ba0.6K0.4Fe2As2 with Splayed Columnar Defects. J. Phys. Conf. Ser. 2021, 1975, 012012. [Google Scholar] [CrossRef]
- Talantsev, E.F.; Tallon, J.L. Fundamental Nature of the Self-Field Critical Current in Superconductors. arXiv 2024, arXiv:2409.16758. [Google Scholar] [CrossRef]
- Tarantini, C.; Larbalestier, D.C. Procedures for Proper Validation of Record Critical Current Density Claims. arXiv 2024, arXiv:2410.22195. [Google Scholar] [CrossRef]
- Zhang, Z.; Gao, Z.; Wang, Y.; Meng, J.; Cheng, J.; Wang, Q. The Role of Copper in the Formation of the Nb3Sn Superconducting Phase. Intermetallics 2023, 155, 107848. [Google Scholar] [CrossRef]
- Zheng, B.; Xie, W.; Liu, Y.; Zhu, X.; Ming, X.; Zhang, Y.; Wen, H.H. Optimization of Magnetic Stability in Nb3Sn Materials Near Stoichiometric Composition. IEEE Trans. Appl. Supercond. 2024, 34, 1–10. [Google Scholar] [CrossRef]
- Poole, C.; Farach, H.; Creswick, R.; Prozorov, R. Superconductivity; Academic Press: Cambridge, MA, USA; Elsevier: Amsterdam, The Netherlands, 2007; ISBN 978-0-12-088761-3. [Google Scholar]
- Knoepfel, H.E. Magnetic Fields: A Comprehensive Theoretical Treatise for Practical Use; Wiley-Interscience Publication, John Wiley and Sons Inc.: Hoboken, NJ, USA, 2000; 543p, ISBN -10: 0471322059/-13: 978-0471322054. [Google Scholar]
- Goldfarb, R.B. Electromagnetic Units, the Giorgi System, and the Revised International System of Units. IEEE Magn. Lett. 2018, 9, 1–5. [Google Scholar] [CrossRef]
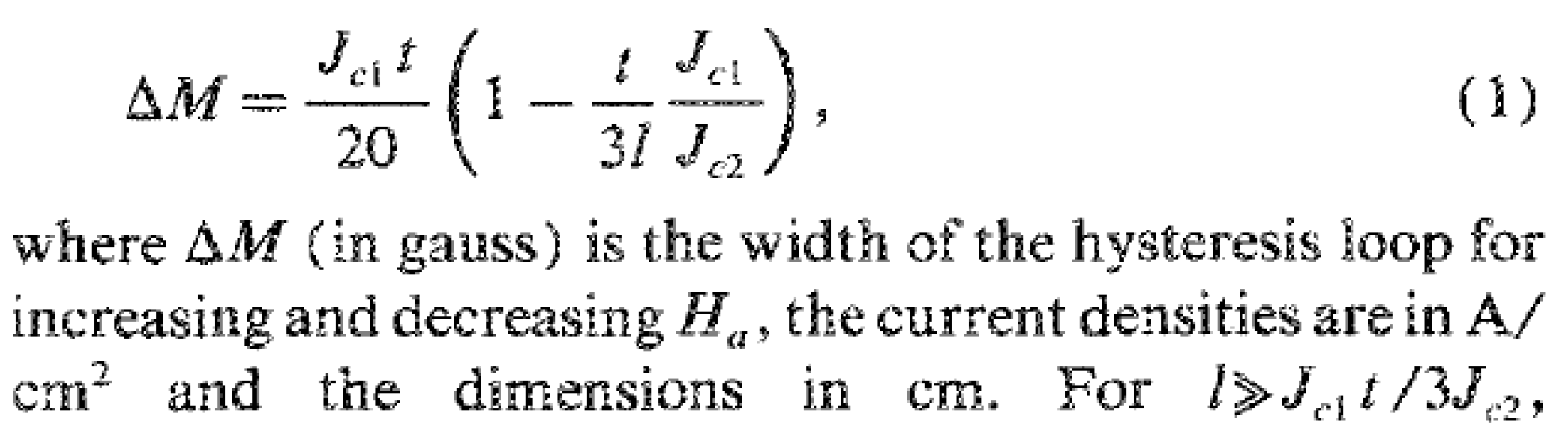
| Equation | M = Magnetization; w = sample’s width; l = sample’s length | ||||
| Case | I | II | III | IV | |
| UNITS FOR | gauss | emu/cm3 | emu/cm3 | emu/mm3 | |
| Sample lengths | cm | cm | cm | mm | |
| A/cm2 | A/cm2 | A/cm2 | A/mm2 | ||
| Pre-factor 20 | dimensionless | dimensionless | A⸱cm2/emu | dimensionless | |
| References | [37,38,39,40,41] | [6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34] | [42,43] | [44,45] | |
| Note | The emu/cm3 has to be converted to gauss, and the corresponding results 12.56 times higher than the correct one. | The emu/cm3 has to be converted to A/cm, and the corresponding results 10 times higher than the correct one. | No unit conversions are applied, and the obtained numerical value for is correct, but the pre-factor 20 is forced to have dimensions, in contrast with the theory. | The equation cannot be applied with the reported units and pre-factor for the considered geometry. The obtained is incorrect. | |
| Quantity | Value in Emu-Cgs | Value in SI System |
|---|---|---|
| Thickness d = 200 nm | ||
| Width w = 4 mm | ||
| Length b = 4 mm | ||
| Volume (wbd) | ||
| Δ(Magnetic moment) = Δ μ |
| Equation | w = sample’s width; b = sample’s length | |||||
| Case | I | II | III | IV | In EMU-CGS | In SI |
| gauss | emu/cm3 | emu/cm3 | emu/mm3 | emu/cm3 | A/m | |
| Sample lengths | cm | cm | cm | mm | cm | m |
| Pre-factor | 20 | 20 | 20 A⸱cm2/emu | 20 | 2 | 2 |
| (A/cm2) | or | |||||
| Correctness of the result | Wrong | Wrong | Correct value but obtained with a wrong pre-factor | Different values, both wrong, depending on the application of the unit conversion | Correct, independently of the used units | Correct, independently of the used units |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Polichetti, M.; Galluzzi, A.; Kumar, R.; Goyal, A. Equation for Calculation of Critical Current Density Using the Bean’s Model with Self-Consistent Magnetic Units to Prevent Unit Conversion Errors. Materials 2025, 18, 269. https://doi.org/10.3390/ma18020269
Polichetti M, Galluzzi A, Kumar R, Goyal A. Equation for Calculation of Critical Current Density Using the Bean’s Model with Self-Consistent Magnetic Units to Prevent Unit Conversion Errors. Materials. 2025; 18(2):269. https://doi.org/10.3390/ma18020269
Chicago/Turabian StylePolichetti, Massimiliano, Armando Galluzzi, Rohit Kumar, and Amit Goyal. 2025. "Equation for Calculation of Critical Current Density Using the Bean’s Model with Self-Consistent Magnetic Units to Prevent Unit Conversion Errors" Materials 18, no. 2: 269. https://doi.org/10.3390/ma18020269
APA StylePolichetti, M., Galluzzi, A., Kumar, R., & Goyal, A. (2025). Equation for Calculation of Critical Current Density Using the Bean’s Model with Self-Consistent Magnetic Units to Prevent Unit Conversion Errors. Materials, 18(2), 269. https://doi.org/10.3390/ma18020269








