Studies of Thermal Conductivity of Graphite Foil-Based Composite Materials
Abstract
1. Introduction
2. Materials and Methods
2.1. Base Materials with High Thermal Conductivity
2.2. Structural and Functional Materials
2.3. Measurements
2.3.1. The Basic Units of the Developed Device
- (1)
- Heating unit consisting of a ceramic heating element and resistance temperature detectors to monitor the input heat flux;
- (2)
- Cooling unit consisting of a Peltier element with a water-cooling system and resistance temperature detectors to monitor the output heat flux;
- (3)
- Central unit including a sample compartment and resistance temperature detectors with a special mechanism for moving them.
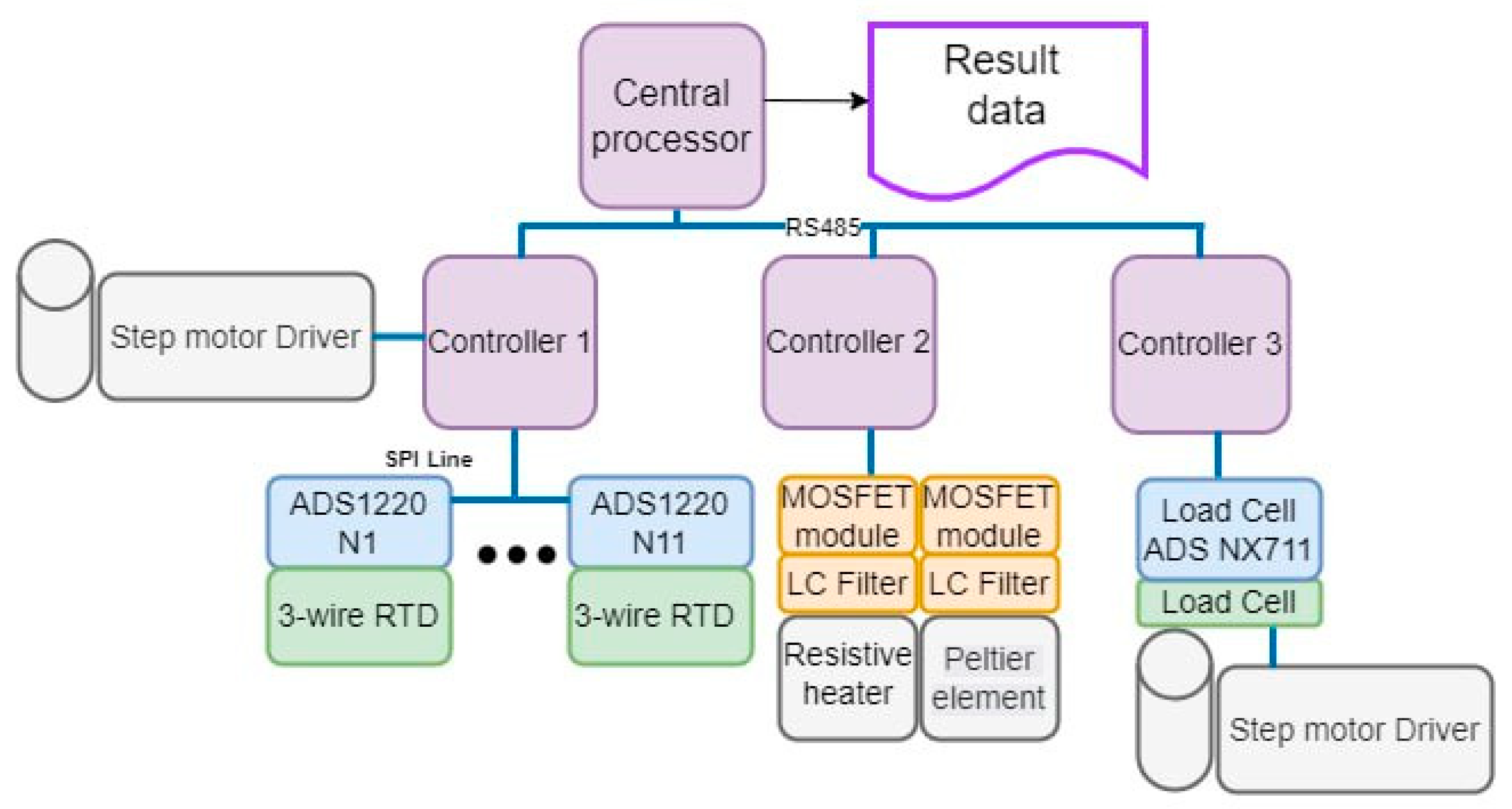
2.3.2. Block Diagram of the Setup Control
- -
- Auxiliary controller 1 is responsible for receiving temperature data on the setup (heating unit, sample, cooling unit), and it also controls the stepper motor which clamps the RTDs;
- -
- Auxiliary controller 2 is responsible for controlling and operating the resistive heater (heating unit) and the Peltier module (cooling unit);
- -
- Auxiliary controller 3 is responsible for clamping the resistive heater after polling the load cell, as well as for controlling its stepper motor.
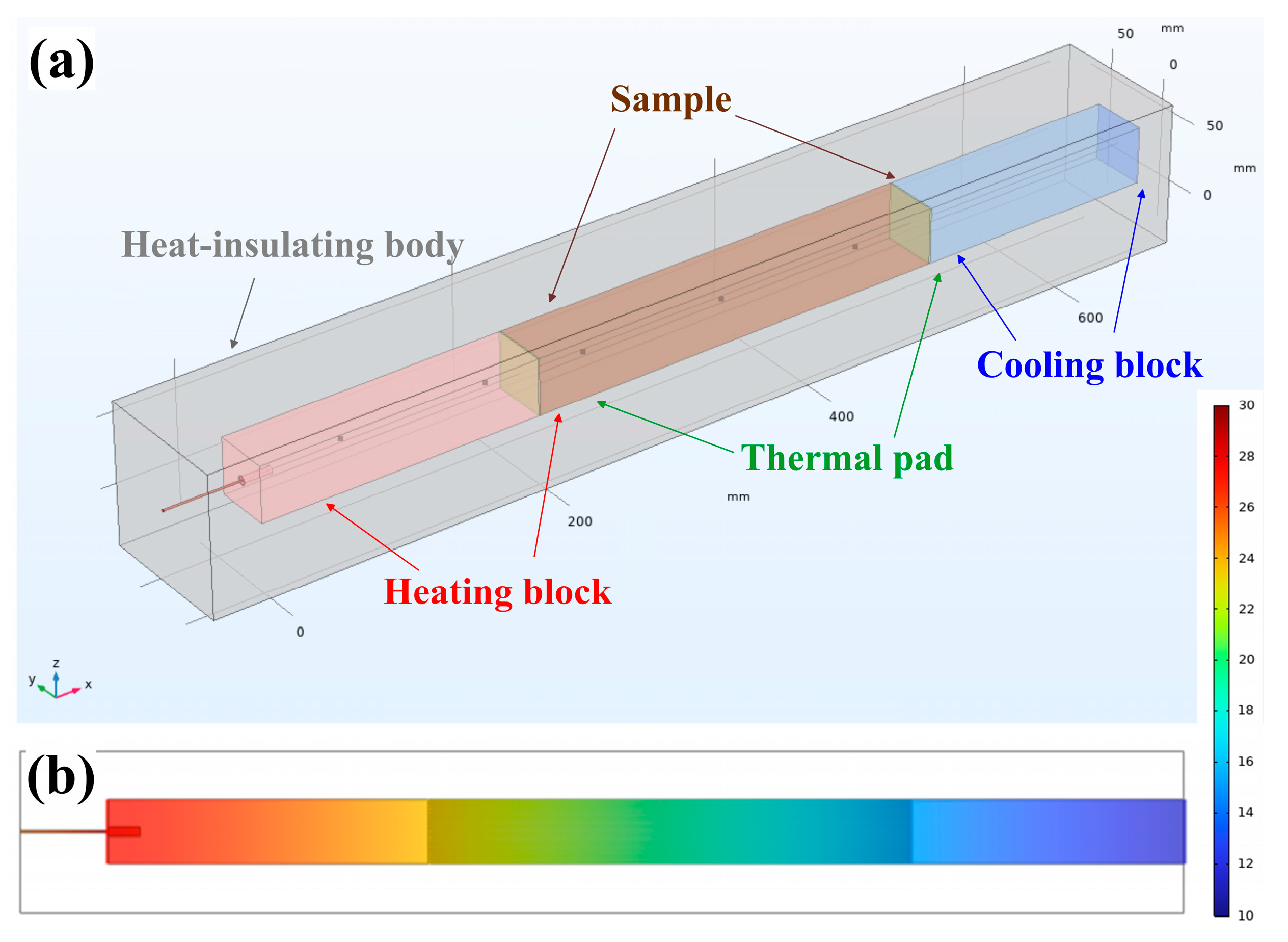
2.4. Modelling Heat Transfer in the Setup
3. Results
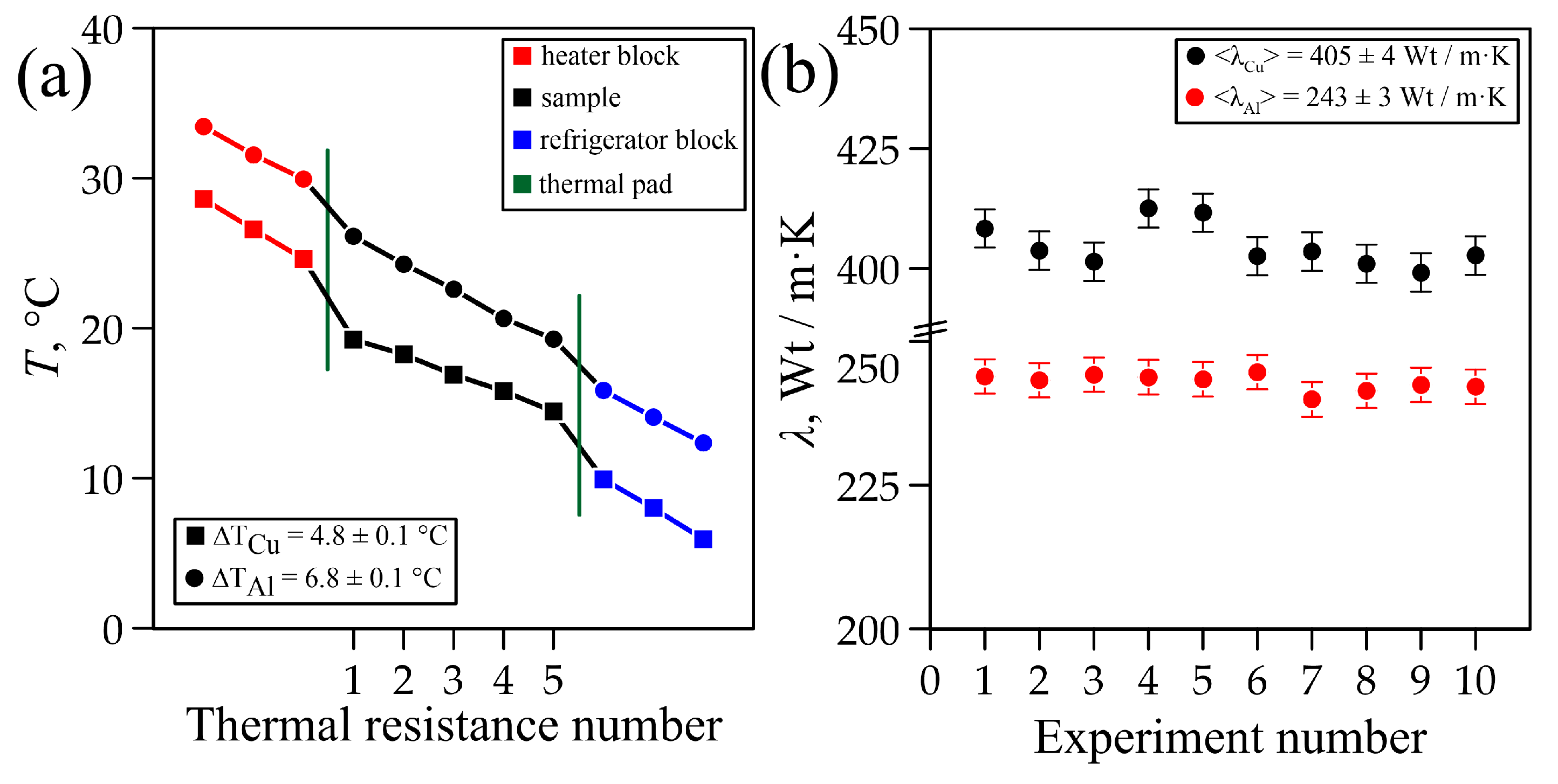
3.1. Study of Thermal Conductivity of Graphite Samples
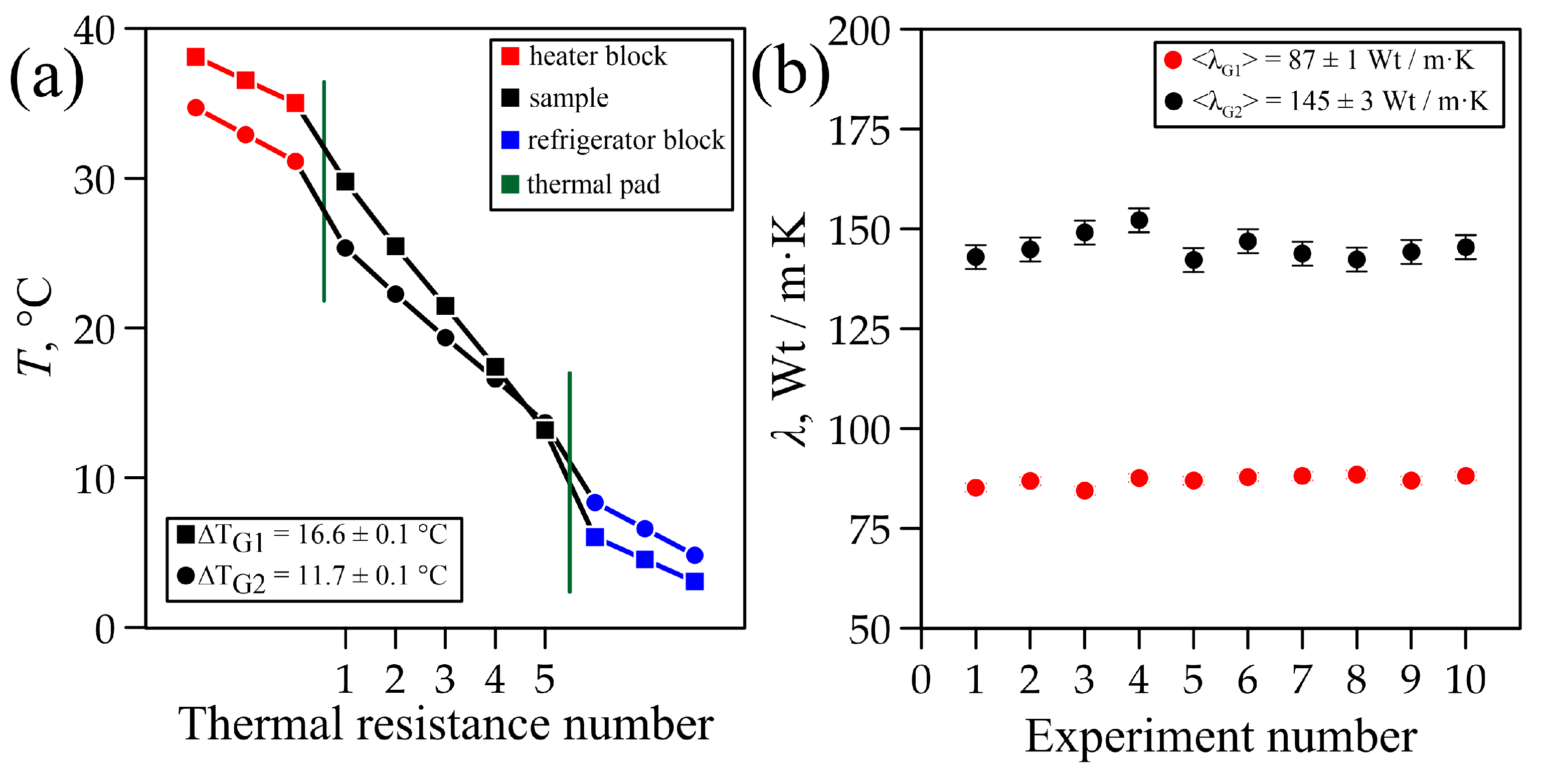
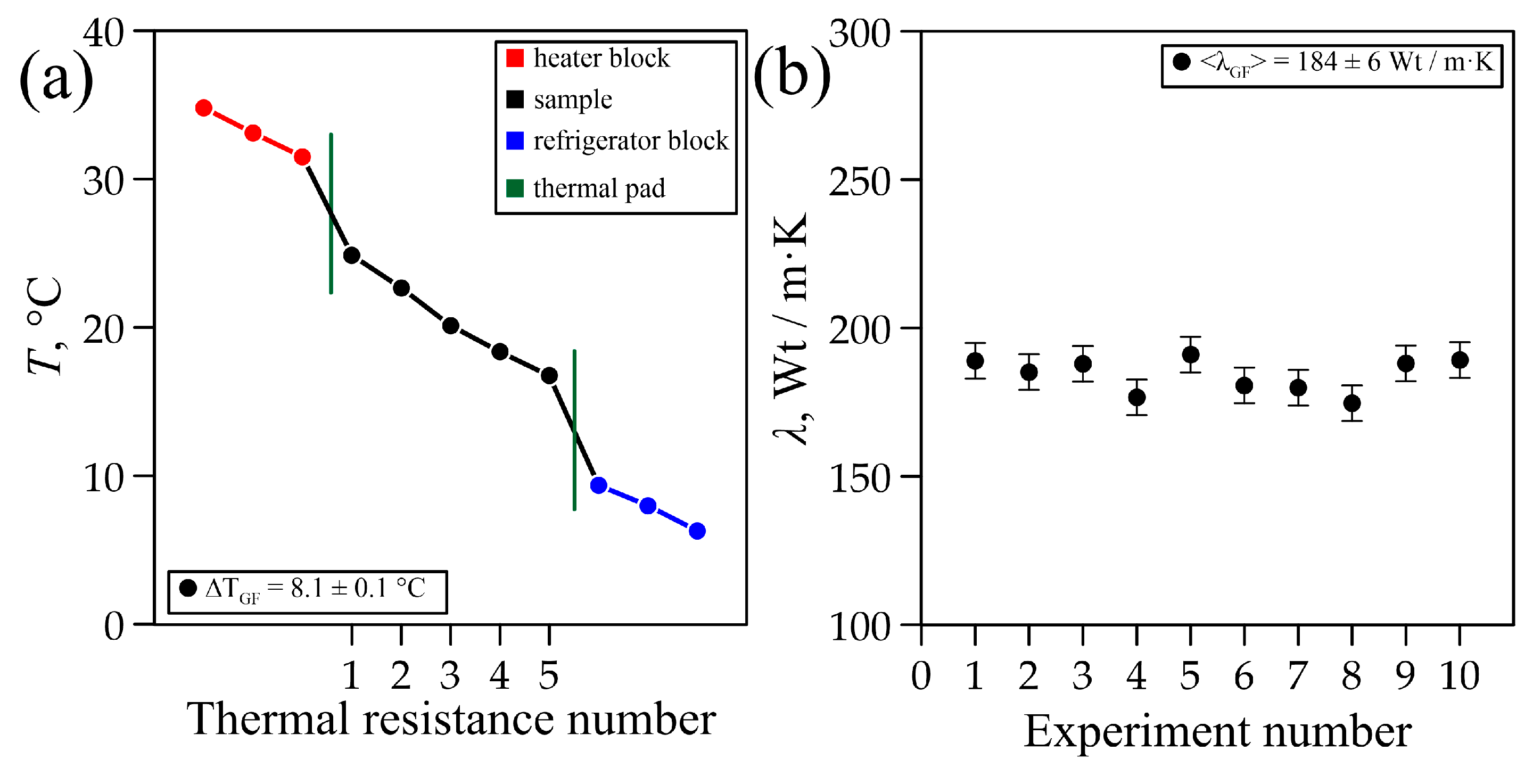
3.2. Study of Thermal Conductivity of Flexible Graphite Foil (GF)
3.3. X-Ray Studies of Graphite Materials
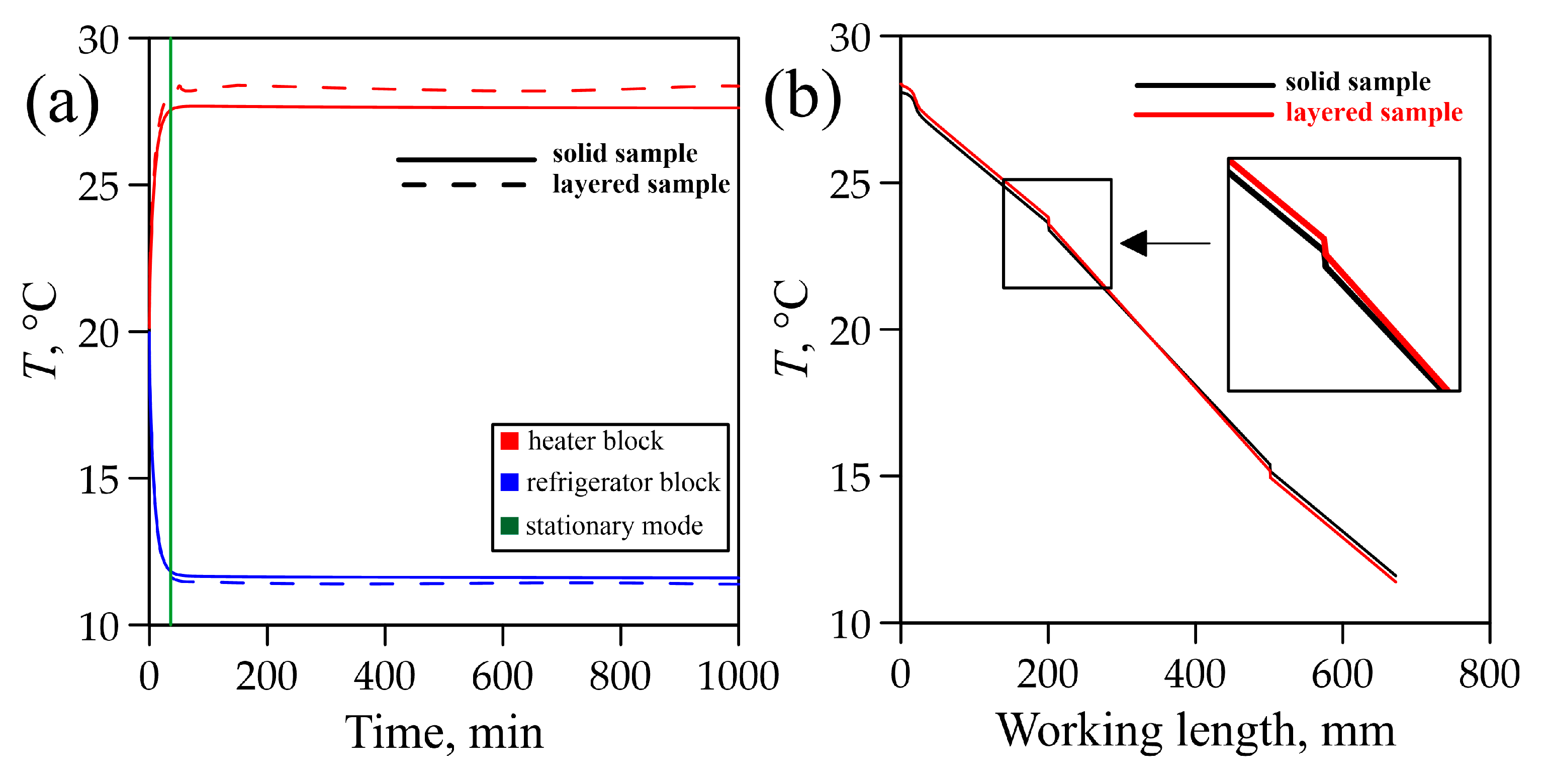
3.4. Modelling of Temperature Fields in Graphite Foil
- (1)
- The time to reach a steady state was the same in both models and was equal to 36 min;
- (2)
- The behavior of the curves describing the temperature distribution in the setup also coincided for the two cases (the difference was about 1%) (Figure 10b).
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhang, A.; Li, Y. Thermal Conductivity of Aluminum Alloys—A Review. Materials 2023, 16, 2972. [Google Scholar] [CrossRef] [PubMed]
- Nováková, I.; Jelínek, M.; Švec, M. Thermal Conductivity of AlSi10MnMg Alloy in Relation to Casting Technology and Heat Treatment Method. Materials 2024, 17, 5329. [Google Scholar] [CrossRef] [PubMed]
- Bieliszczuk, K.; Chmielewski, T.M. Properties of Wedge Wire Bonded Connection Between a Composite Copper Core Aluminum Shell Wire and an 18650 Cylindrical Lithium-Ion Battery Cell. Materials 2024, 17, 5237. [Google Scholar] [CrossRef] [PubMed]
- Pieszka-Łysoń, M.; Rutkowski, P.; Kawalec, M.; Kawalec, D. Determination of Contact Resistance of Thermal Interface Materials Used in Thermal Monitoring Systems of Electric Vehicle Charging Inlets. Materials 2024, 17, 3103. [Google Scholar] [CrossRef]
- Emadi, P.; Andilab, B.; Ravindran, C. Engineering Lightweight Aluminum and Magnesium Alloys for a Sustainable Future. J. Indian Inst. Sci. 2022, 102, 405–420. [Google Scholar] [CrossRef]
- Gan, J.; Huang, Y.; Wen, C.; Du, J. Effect of Sr Modification on Microstructure and Thermal Conductivity of Hypoeutectic Al−Si Alloys. Trans. Nonferr. Met. Soc. China 2020, 30, 2879–2890. [Google Scholar] [CrossRef]
- Chen, Y.; Zhang, Q.; Li, B.; Chen, Z.; Liu, S.; Ma, X.; Tofil, S.; Yao, J. Effect of Laser on the Interface and Thermal Conductivity of Metallized Diamond/Cu Composite Coatings Deposited by Supersonic Laser Deposition. Materials 2024, 17, 5174. [Google Scholar] [CrossRef] [PubMed]
- Arıbuğa, D.; Akkaşoğlu, U.; Çiçek, B.; Balcı-Çağıran, Ö. Enhanced Sinterability, Thermal Conductivity and Dielectric Constant of Glass-Ceramics with PVA and BN Additions. Materials 2022, 15, 1685. [Google Scholar] [CrossRef] [PubMed]
- Wu, D.; Ning, Z.; Zhu, Y.; Yuan, R. Evaluation of Thermal and Mechanical Properties of Bi-In-Sn/WO3 Composites for Efficient Heat Dissipation. Materials 2024, 17, 5315. [Google Scholar] [CrossRef] [PubMed]
- Che, Z.; Li, J.; Wang, Q.; Wang, L.; Zhang, H.; Zhang, Y.; Wang, X.; Wang, J.; Kim, M.J. The Formation of Atomic-Level Interfacial Layer and Its Effect on Thermal Conductivity of W-Coated Diamond Particles Reinforced Al Matrix Composites. Compos. Part A Appl. Sci. Manuf. 2018, 107, 164–170. [Google Scholar] [CrossRef]
- Li, N.; Hao, J.; Zhang, Y.; Wang, W.; Zhao, J.; Wu, H.; Wang, X.; Zhang, H. Thermal Conductivity Stability of Interfacial in Situ Al4C3 Engineered Diamond/Al Composites Subjected to Thermal Cycling. Materials 2022, 15, 6640. [Google Scholar] [CrossRef] [PubMed]
- Molina-Jordá, J.M. Design of Composites for Thermal Management: Aluminum Reinforced with Diamond-Containing Bimodal Particle Mixtures. Compos. Part A Appl. Sci. Manuf. 2015, 70, 45–51. [Google Scholar] [CrossRef]
- Anwajler, B.; Szołomicki, J.; Noszczyk, P.; Baryś, M. The Potential of 3D Printing in Thermal Insulating Composite Materials—Experimental Determination of the Impact of the Geometry on Thermal Resistance. Materials 2024, 17, 1202. [Google Scholar] [CrossRef] [PubMed]
- Pomada, M.; Kieruzel, K.; Ujma, A.; Palutkiewicz, P.; Walasek, T.; Adamus, J. Analysis of Thermal Properties of Materials Used to Insulate External Walls. Materials 2024, 17, 4718. [Google Scholar] [CrossRef]
- Ye, D.; Lv, H.; Zheng, Z.; Luo, L. Preparation and Properties of Flexible Phenolic Silicone Hybrid Aerogels for Thermal Insulation. Molecules 2024, 29, 4942. [Google Scholar] [CrossRef]
- Danaci, H.M.; Akin, N. Thermal Insulation Materials in Architecture: A Comparative Test Study with Aerogel and Rock Wool. Environ. Sci. Pollut. Res. 2022, 29, 72979–72990. [Google Scholar] [CrossRef] [PubMed]
- Zhao, R.; Guo, H.; Yi, X.; Gao, W.; Zhang, H.; Bai, Y.; Wang, T. Research on Thermal Insulation Properties of Plant Fiber Composite Building Material: A Review. Int. J. Thermophys. 2020, 41, 87. [Google Scholar] [CrossRef]
- Khan, M.; Cao, M.; Chu, S.H.; Ali, M. Properties of Hybrid Steel-Basalt Fiber Reinforced Concrete Exposed to Different Surrounding Conditions. Constr. Build. Mater. 2022, 322, 126340. [Google Scholar] [CrossRef]
- Shulyak, V.A.; Morozov, N.S.; Ivanov, A.V.; Gracheva, A.V.; Chebotarev, S.N.; Avdeev, V.V. The Influence of Machining Conditions on the Orientation of Nanocrystallites and Anisotropy of Physical and Mechanical Properties of Flexible Graphite Foils. Nanomaterials 2024, 14, 540. [Google Scholar] [CrossRef]
- Shulyak, V.A.; Morozov, N.S.; Gracheva, A.V.; Gritskevich, M.D.; Chebotarev, S.N.; Avdeev, V.V. Anisotropy of Electrical and Thermal Conductivity in High-Density Graphite Foils. Nanomaterials 2024, 14, 1162. [Google Scholar] [CrossRef] [PubMed]
- Sorokina, N.E.; Redchitz, A.V.; Ionov, S.G.; Avdeev, V.V. Different Exfoliated Graphite as a Base of Sealing Materials. J. Phys. Chem. Solids 2006, 67, 1202–1204. [Google Scholar] [CrossRef]
- Saidaminov, M.I.; Maksimova, N.V.; Zatonskih, P.V.; Komarov, A.D.; Lutfullin, M.A.; Sorokina, N.E.; Avdeev, V.V. Thermal Decomposition of Graphite Nitrate. Carbon 2013, 59, 337–343. [Google Scholar] [CrossRef]
- Cermak, M.; Perez, N.; Collins, M.; Bahrami, M. Material Properties and Structure of Natural Graphite Sheet. Sci. Rep. 2020, 10, 18672. [Google Scholar] [CrossRef] [PubMed]
- Rüdorff, W.; Hofmann, U. Über Graphitsalze. Z. Anorg. Allg. Chem. 1938, 238, 1–50. [Google Scholar] [CrossRef]
- Inagaki, M.; Iwashita, N.; Kouno, E. Potential Change with Intercalation of Sulfuric Acid into Graphite by Chemical Oxidation. Carbon. 1990, 28, 49–55. [Google Scholar] [CrossRef]
- Daumas, N.; Herold, A. Sur Les Relations Entre La Notion de Stade et Les Mécanismes Reactionnels Dans Les Composes d’insertion Du Graphite. Comptes Rendus L’académie Des Sci. Paris 1969, 268, 373–375. [Google Scholar]
- Bonnissel, M.; Luo, L.; Tondeur, D. Compacted Exfoliated Natural Graphite as Heat Conduction Medium. Carbon 2001, 39, 2151–2161. [Google Scholar] [CrossRef]
- Wei, X.H.; Liu, L.; Zhang, J.X.; Shi, J.L.; Guo, Q.G. Mechanical, Electrical, Thermal Performances and Structure Characteristics of Flexible Graphite Sheets. J. Mater. Sci. 2010, 45, 2449–2455. [Google Scholar] [CrossRef]
- Dowell, M.B.; Howard, R.A. Tensile and Compressive Properties of Flexible Graphite Foils. Carbon 1986, 24, 311–323. [Google Scholar] [CrossRef]
- Lee, S.-H.; Seo, S.-D.; Jin, Y.-H.; Shim, H.-W.; Kim, D.-W. A Graphite Foil Electrode Covered with Electrochemically Exfoliated Graphene Nanosheets. Electrochem. Commun. 2010, 12, 1419–1422. [Google Scholar] [CrossRef]
- Nagano, H.; Ohnishi, A.; Nagasaka, Y. Thermophysical Properties of High Thermal Conductivity Graphite Sheet for Spacecraft Thermal Design. In Proceedings of the 34th Thermophysics Conference, Denver, CO, USA, 19–22 June 2000. [Google Scholar]
- Touloukian, Y.S. Thermal Conductivity Metallic Elements and Alloys; IFI/Plenum: New York, NY, USA, 1978. [Google Scholar]
- Balandin, A.A.; Ghosh, S.; Bao, W.; Calizo, I.; Teweldebrhan, D.; Miao, F.; Lau, C.N. Superior Thermal Conductivity of Single-Layer Graphene. Nano Lett. 2008, 8, 902–907. [Google Scholar] [CrossRef] [PubMed]
- Lin, Z.; Karthik, P.; Hada, M.; Nishikawa, T.; Hayashi, Y. Simple Technique of Exfoliation and Dispersion of Multilayer Graphene from Natural Graphite by Ozone-Assisted Sonication. Nanomaterials 2017, 7, 125. [Google Scholar] [CrossRef]
- Holland, M.G.; Klein, C.A.; Straub, W.D. The Lorenz Number of Graphite at Very Low Temperatures. J. Phys. Chem. Solids 1966, 27, 903–906. [Google Scholar] [CrossRef]
- Schmidt, A.J.; Chen, X.; Chen, G. Pulse Accumulation, Radial Heat Conduction, and Anisotropic Thermal Conductivity in Pump-Probe Transient Thermoreflectance. Rev. Sci. Instrum. 2008, 79, 114902. [Google Scholar] [CrossRef]
- Zhao, L.; Tang, J.; Zhou, M.; Shen, K. A Review of the Coefficient of Thermal Expansion and Thermal Conductivity of Graphite. New Carbon Mater. 2022, 37, 544–555. [Google Scholar] [CrossRef]
- Qian, X.; Ding, Z.; Shin, J.; Schmidt, A.J.; Chen, G. Accurate Measurement of In-Plane Thermal Conductivity of Layered Materials without Metal Film Transducer Using Frequency Domain Thermoreflectance. Rev. Sci. Instrum. 2020, 91, 064903. [Google Scholar] [CrossRef]
- Balandin, A.A. Thermal Properties of Graphene and Nanostructured Carbon Materials. Nat. Mater. 2011, 10, 569–581. [Google Scholar] [CrossRef]
- Balandin, A.A. Phononics of Graphene and Related Materials. ACS Nano 2020, 14, 5170–5178. [Google Scholar] [CrossRef] [PubMed]
- Morozov, N.S.; Gubin, V.Y.; Vakhrushin, D.V.; Konstantinov, M.S.; Minushkin, R.A.; Gracheva, A.V.; Chebotarev, S.N.; Avdeev, V.V. Thermal Conductivity Measurement System for Functional and Structural Products. Processes 2024, 12, 2219. [Google Scholar] [CrossRef]
- Powell, R.W.; Ho, C.Y.; Liley, P.E. Thermal Conductivity of Selected Materials; National Bureau of Standards: Gaithersburg, MD, USA, 1966; p. NBS NSRDS 8.
- Pinheiro, P.M.; Junio, J.U.; Gonçalves, L.A.P.; Da Costa, J.Â.P.; Ochoa, A.A.V.; Alves, K.G.B.; Leite, G.D.N.P.; Michima, P.S.A. Modeling and Simulation of the Induction Hardening Process: Evaluation of Gear Deformations and Parameter Optimization. Processes 2024, 12, 1428. [Google Scholar] [CrossRef]
- Vajdi, M.; Sadegh Moghanlou, F.; Sharifianjazi, F.; Shahedi Asl, M.; Shokouhimehr, M. A Review on the Comsol Multiphysics Studies of Heat Transfer in Advanced Ceramics. JCC 2020, 2, 35–44. [Google Scholar] [CrossRef]
- Tamanna, N.; Crouch, R.; Naher, S. Progress in Numerical Simulation of the Laser Cladding Process. Opt. Lasers Eng. 2019, 122, 151–163. [Google Scholar] [CrossRef]
- Peng, Z.; Doroodchi, E.; Moghtaderi, B. Heat Transfer Modelling in Discrete Element Method (DEM)-Based Simulations of Thermal Processes: Theory and Model Development. Prog. Energy Combust. Sci. 2020, 79, 100847. [Google Scholar] [CrossRef]
- Tong, Z.-X.; He, Y.-L.; Tao, W.-Q. A Review of Current Progress in Multiscale Simulations for Fluid Flow and Heat Transfer Problems: The Frameworks, Coupling Techniques and Future Perspectives. Int. J. Heat Mass Transf. 2019, 137, 1263–1289. [Google Scholar] [CrossRef]
- Lau, K.T.; Ahmad, S.; Cheng, C.K.; Khan, S.A.; Eze, C.M.; Zhao, J. Review on Supercritical Fluids Heat Transfer Correlations, Part II: Variants of Correction Factors and Buoyancy-Related Dimensionless Variables. Heat Transf. Eng. 2024, 45, 569–583. [Google Scholar] [CrossRef]
- Sharma, R.; Jadon, V.K.; Singh, B. A Review on the Finite Element Methods for Heat Conduction in Functionally Graded Materials. J. Inst. Eng. India Ser. C 2015, 96, 73–81. [Google Scholar] [CrossRef]
- David Müzel, S.; Bonhin, E.P.; Guimarães, N.M.; Guidi, E.S. Application of the Finite Element Method in the Analysis of Composite Materials: A Review. Polymers 2020, 12, 818. [Google Scholar] [CrossRef] [PubMed]
- Scherrer, P. Bestimmung der Größe und der inneren Struktur von Kolloidteilchen mittels Röntgenstrahlen. Nach. Ges. Wiss. Göttingen 1918, 2, 98–100. [Google Scholar]
- Stokes, A.R.; Wilson, A.J.C. The Diffraction of X Rays by Distorted Crystal Aggregates—I. Proc. Phys. Soc. 1944, 56, 174–181. [Google Scholar] [CrossRef]
- Sheng, L.; Zhang, C.; Wang, L.; Zhou, Q.; Zhang, Z.; Zhang, X.; Zhang, H. Experimental-Numerical Studies on Thermal Conductivity Anisotropy of Lithium-Ion Batteries. J. Energy Storage 2024, 103, 114139. [Google Scholar] [CrossRef]
- Chen, B.; Gong, J.; Zhang, J.; Deng, C.; Gao, X. Rotational Stress-Induced Shish-Kebab Governs the Balance of Enhanced Thermal Conductivity and Mechanical Performance of High-Density Polyethylene (HDPE) / Boron Nitride (BN) Composites via Axial Hot Compression. Mater. Today Commun. 2024, 38, 107911. [Google Scholar] [CrossRef]



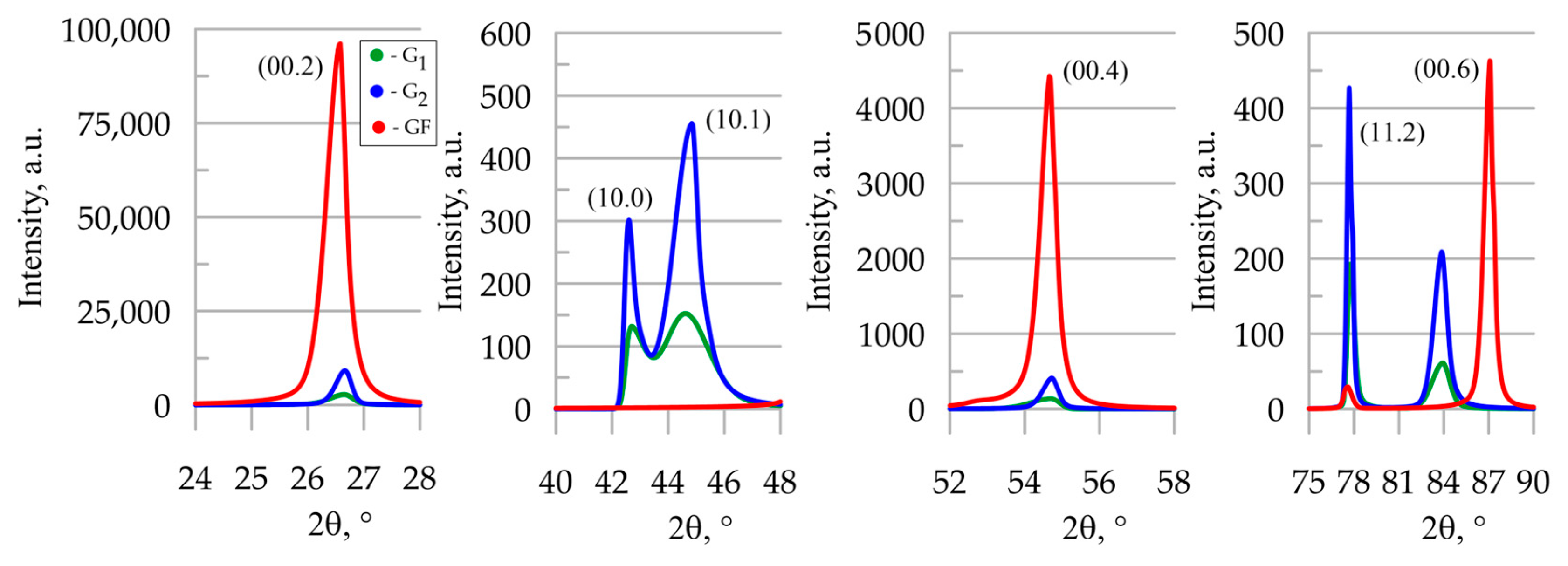
| Sample | , deg. | , deg. | , deg. | , deg. | a, pm | c, pm | Lc, pm | |||
|---|---|---|---|---|---|---|---|---|---|---|
| G1 | 0.175 | 0.066 | 0.944 | 0.491 | 0.780 | 1.860 | 0.410 | 245.2 ± 0.5 | 669.8 ± 1.5 | 13 ± 4 |
| G2 | 0.156 | 0.057 | 0.790 | 0.321 | 0.420 | 1.020 | 0.294 | 245.4 ± 0.4 | 669.4 ± 1.5 | 23 ± 6 |
| GF | - | - | 0.058 | 0.396 | - | - | 0.550 | 246.3 ± 1.9 | 670.8 ± 0.3 | 19 ± 2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shulyak, V.A.; Morozov, N.S.; Minushkin, R.A.; Gubin, V.Y.; Vakhrushin, D.V.; Gracheva, A.V.; Nigmatullin, I.K.; Chebotarev, S.N.; Avdeev, V.V. Studies of Thermal Conductivity of Graphite Foil-Based Composite Materials. Materials 2025, 18, 233. https://doi.org/10.3390/ma18020233
Shulyak VA, Morozov NS, Minushkin RA, Gubin VY, Vakhrushin DV, Gracheva AV, Nigmatullin IK, Chebotarev SN, Avdeev VV. Studies of Thermal Conductivity of Graphite Foil-Based Composite Materials. Materials. 2025; 18(2):233. https://doi.org/10.3390/ma18020233
Chicago/Turabian StyleShulyak, Vladimir A., Nikolai S. Morozov, Roman A. Minushkin, Viktor Yu. Gubin, Dmitriy V. Vakhrushin, Alexandra V. Gracheva, Ildar Kh. Nigmatullin, Sergei N. Chebotarev, and Viktor V. Avdeev. 2025. "Studies of Thermal Conductivity of Graphite Foil-Based Composite Materials" Materials 18, no. 2: 233. https://doi.org/10.3390/ma18020233
APA StyleShulyak, V. A., Morozov, N. S., Minushkin, R. A., Gubin, V. Y., Vakhrushin, D. V., Gracheva, A. V., Nigmatullin, I. K., Chebotarev, S. N., & Avdeev, V. V. (2025). Studies of Thermal Conductivity of Graphite Foil-Based Composite Materials. Materials, 18(2), 233. https://doi.org/10.3390/ma18020233






