Range-Aware Two-Stage Modeling for Feed Ratio Optimization in Fluoroelastomers: Mechanistic Pathways from NMR Structural Features to Macroscopic Properties
Abstract
1. Introduction
2. Materials and Methods
2.1. Dataset and Preprocessing
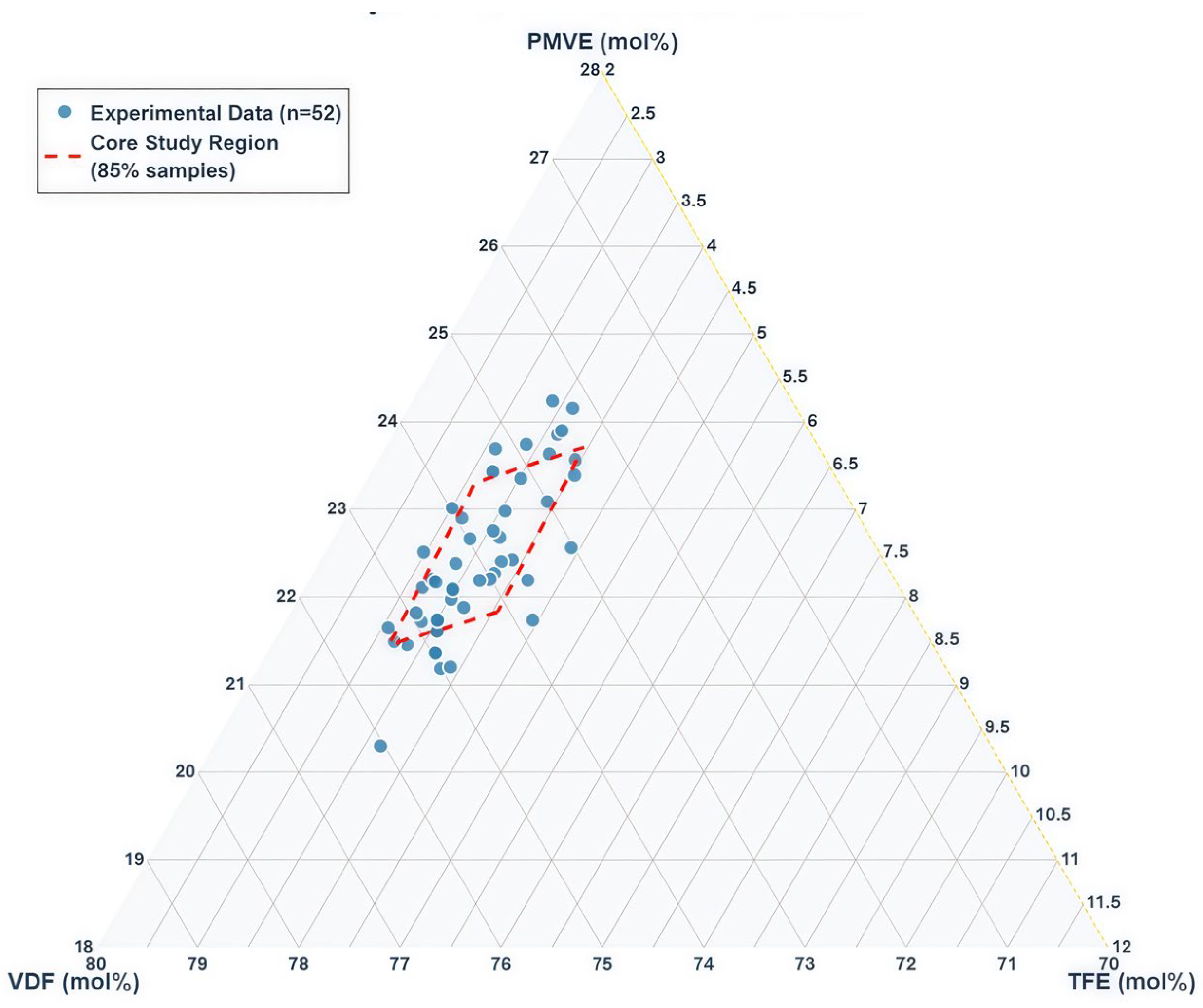
2.1.1. Data Collection
2.1.2. Data Preprocessing
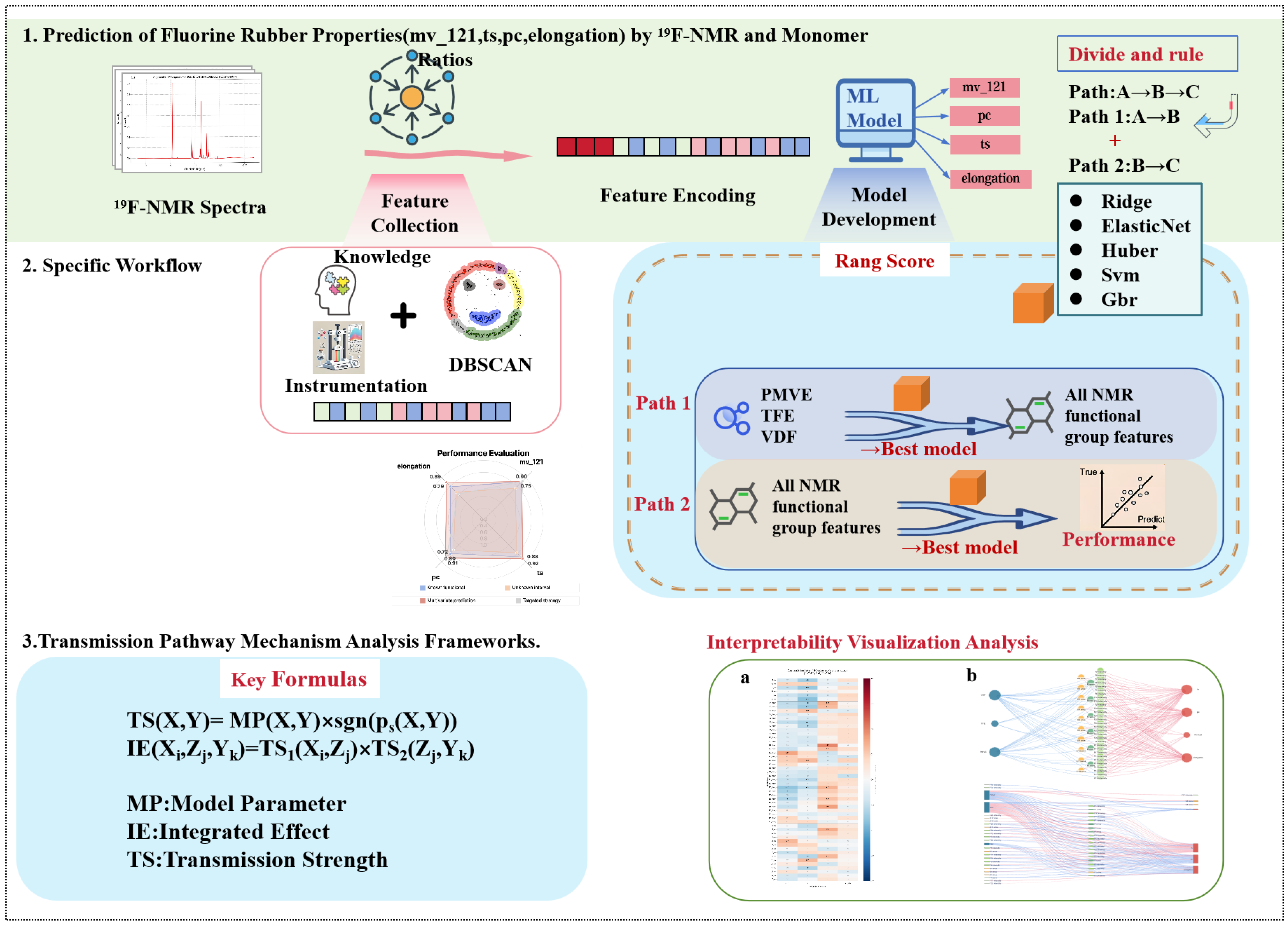
2.2. Range-Aware Feature Engineering
2.2.1. Range Score (RS) Metric
2.2.2. Feature System Construction
2.2.3. Construction of Encoded Feature Matrix
2.3. Two-Stage Modeling Implementation
2.3.1. Modeling Foundation
2.3.2. First Stage Modeling: Feed Ratio → NMR Feature Mapping
2.3.3. Second Stage Modeling: NMR Feature → Property Mapping
2.3.4. Training and Evaluation Strategy
2.3.5. Grouped Comparison Experiments
2.4. Transmission Pathway Analysis Method
2.5. Research Scope and Limitations
3. Results and Discussion
3.1. Two-Stage Modeling Performance Evaluation
3.1.1. First Stage: Ratio → NMR Feature Mapping
3.1.2. Second Stage: NMR Features → Property Mapping
3.2. Model Overall Evaluation Methods
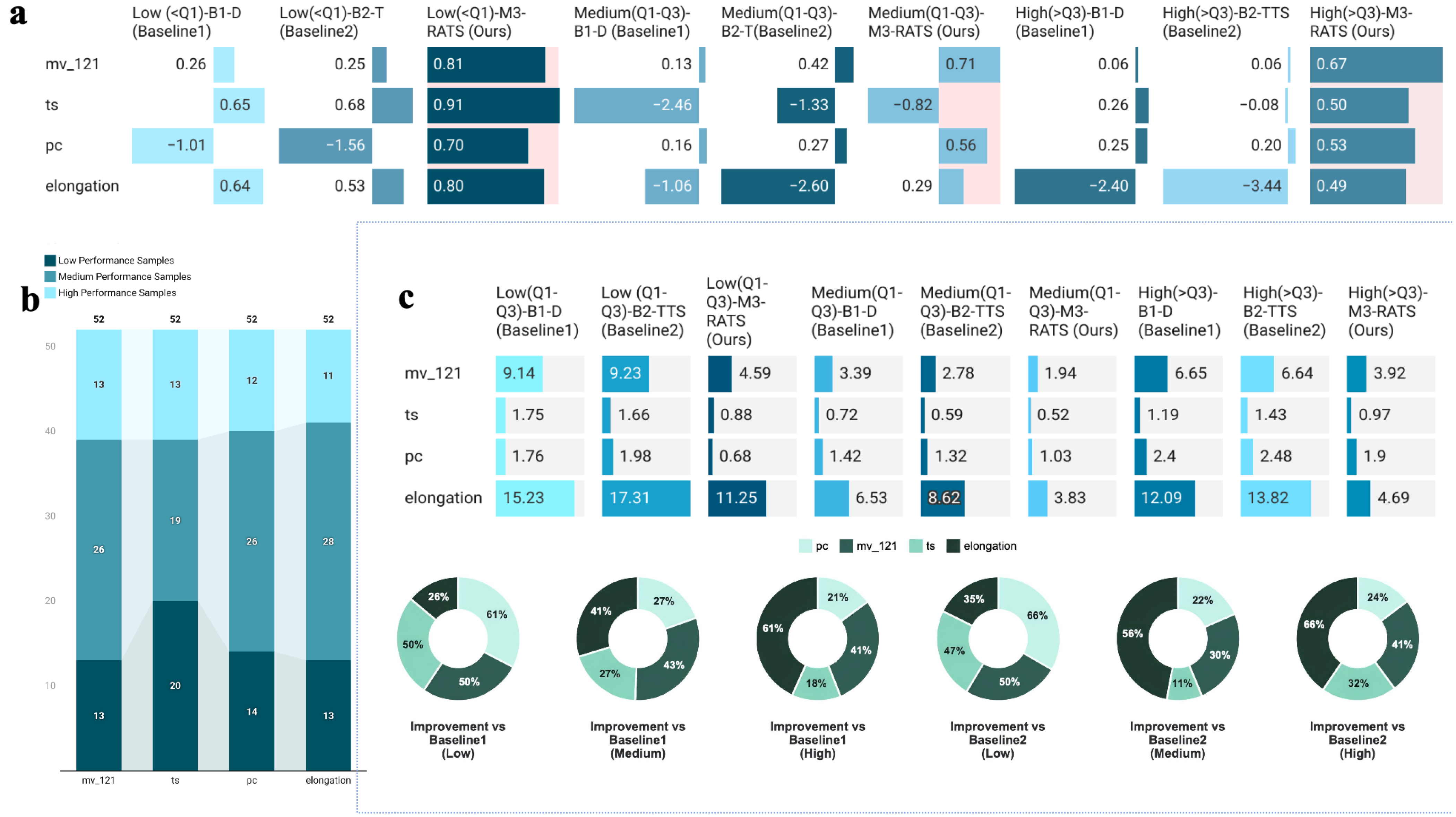
3.2.1. Baseline Comparison Evaluation
3.2.2. Quantile Stratified Performance Analysis
3.2.3. RS Effectiveness
3.3. Analysis of Conductive Pathway Mechanisms
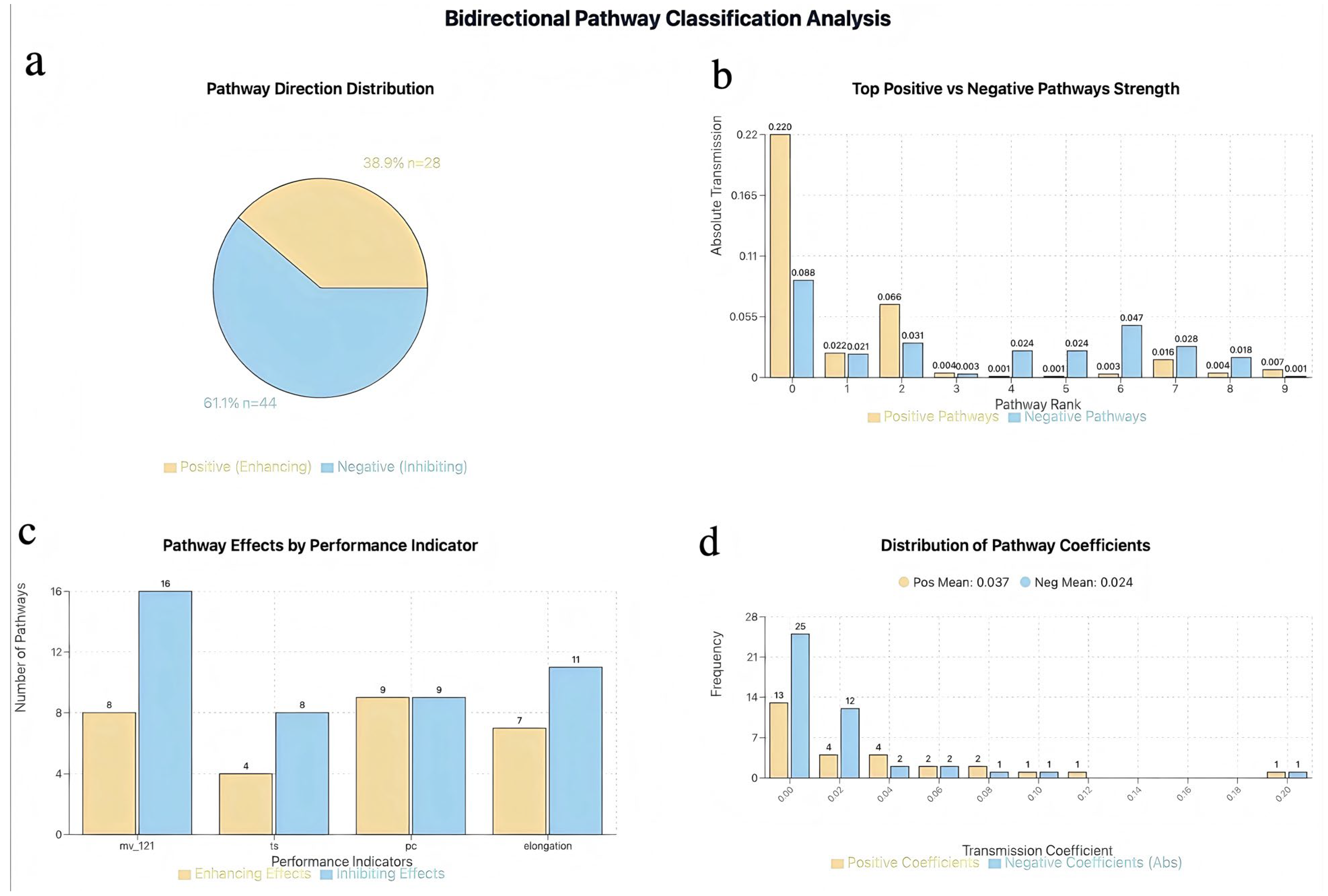
3.3.1. Conductive Pathway Identification Results
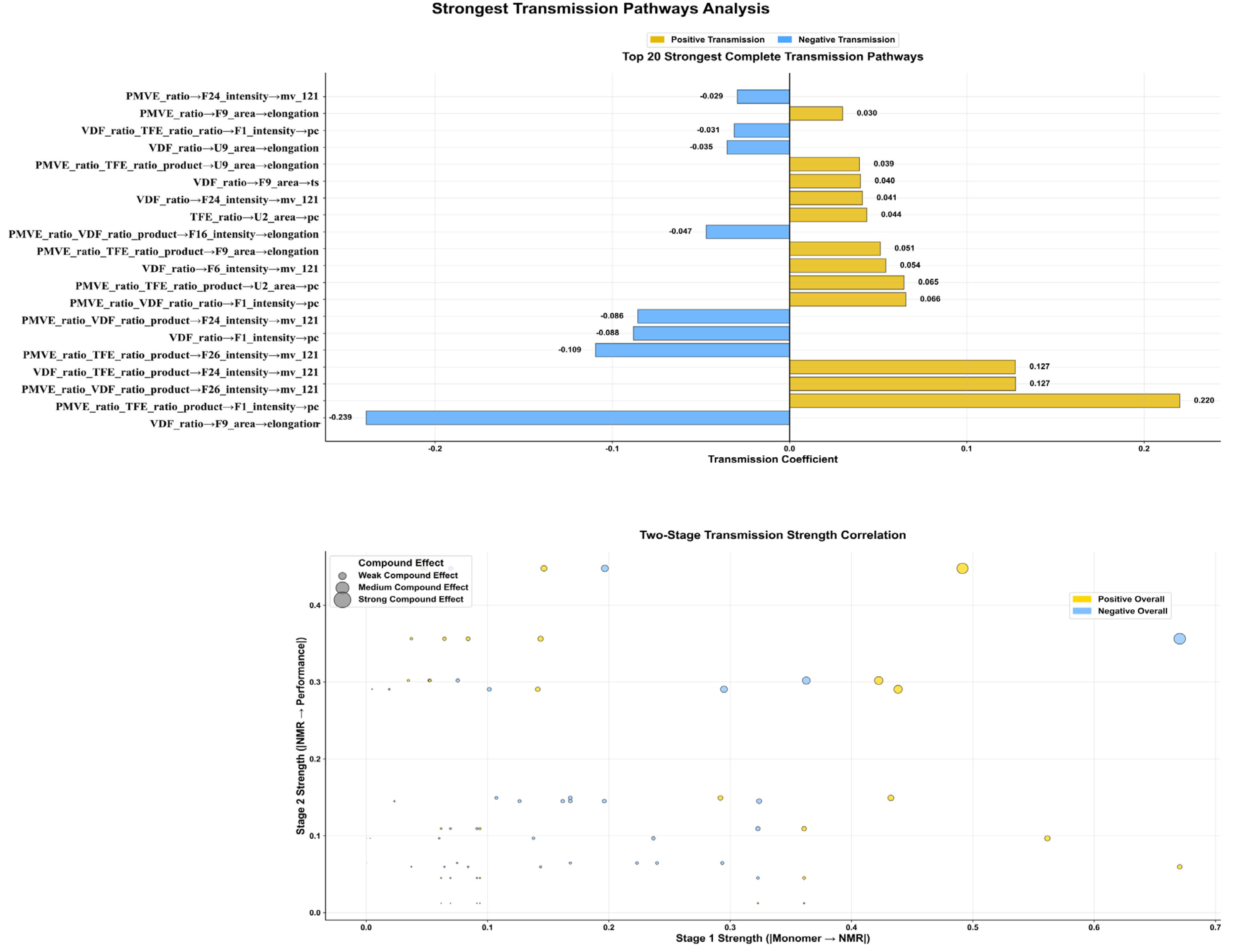
3.3.2. Key Transmission Pathway Identification and Quantitative Analysis
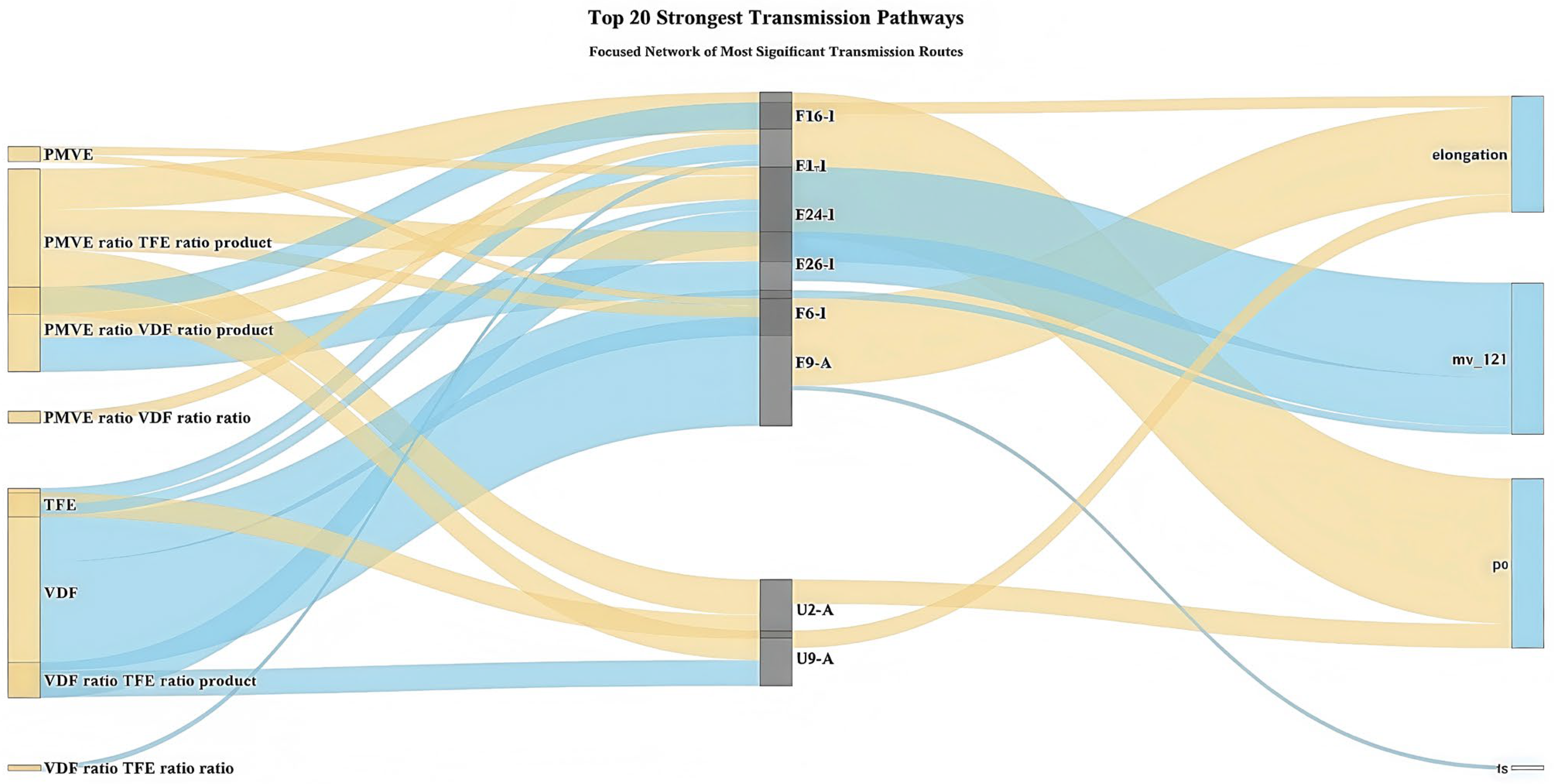
3.3.3. Complete Transmission Network Mechanism Analysis
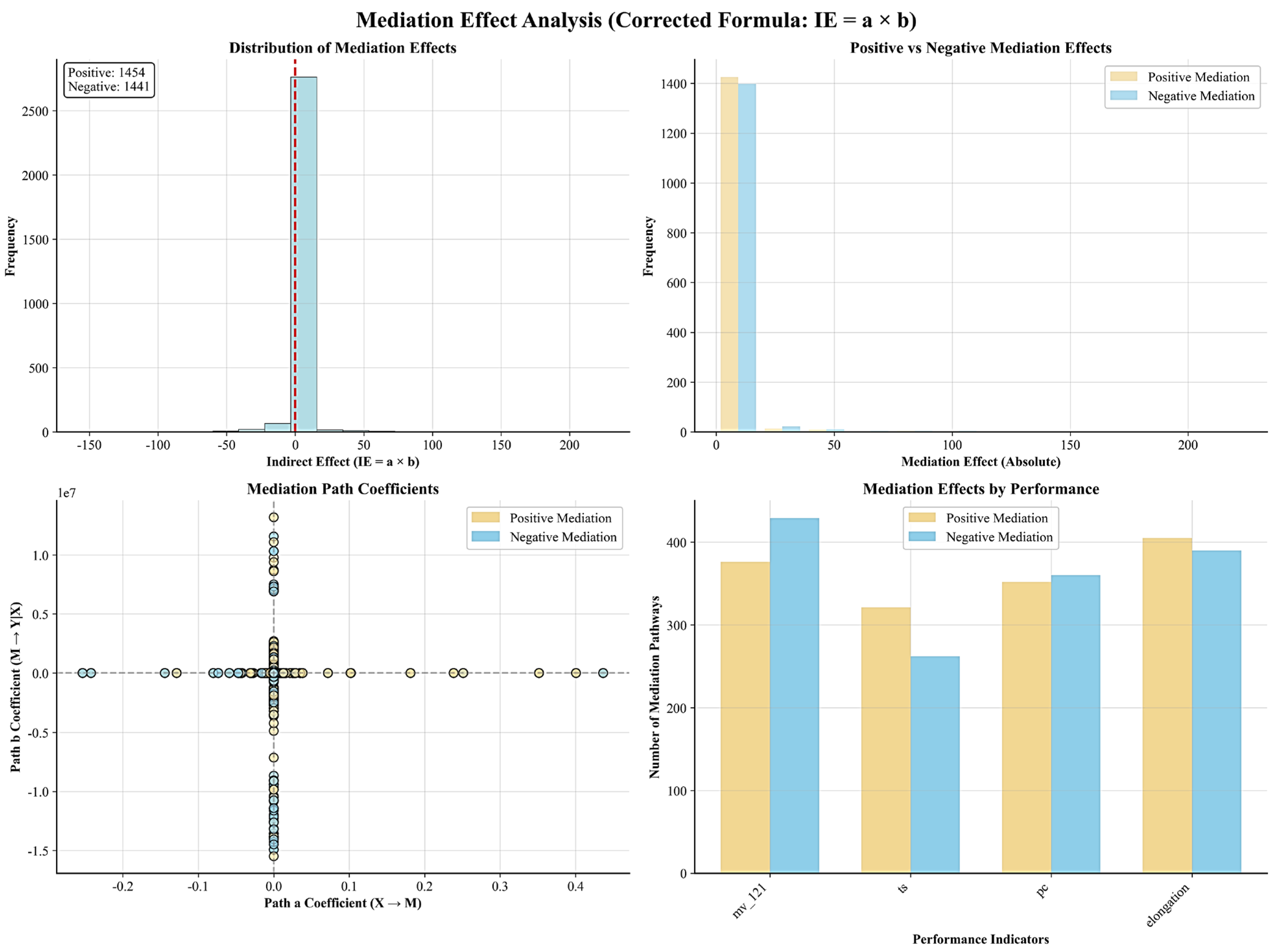
3.3.4. Mediation Effect Validation of Two-Stage Modeling
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ameduri, B.; Boutevin, B.; Kostov, G. Fluoroelastomers: Synthesis, Properties and Applications. Prog. Polym. Sci. 2001, 26, 105–187. [Google Scholar] [CrossRef]
- Moore, A.L. Fluoroelastomers Handbook: The Definitive User’s Guide and Databook; Taylor & Francis: New York, NY, USA, 2006. [Google Scholar]
- Souzy, R.; Ameduri, B. Functional Fluoropolymers for Fuel Cell Membranes. Prog. Polym. Sci. 2005, 30, 644–687. [Google Scholar] [CrossRef]
- Johns, K.; Stead, G. Fluoropolymers 2: Properties; William Andrew: Norwich, NY, USA, 1999. [Google Scholar]
- Yang, H.E.; French, R.; Bruckman, L. (Eds.) Durability and Reliability of Polymers and Other Materials in Photovoltaic Modules; William Andrew: Norwich, NY, USA, 2019. [Google Scholar]
- Logothetis, A.L. Chemistry of Fluorocarbon Elastomers. Prog. Polym. Sci. 1989, 14, 251–296. [Google Scholar] [CrossRef]
- Brennan, N.M.; Evans, A.T.; Fritz, M.K.; Peak, S.A.; von Holst, H.E. Trends in the Regulation of Per- and Polyfluoroalkyl Substances (PFAS): A Scoping Review. Int. J. Environ. Res. Public Health 2021, 18, 10900. [Google Scholar] [CrossRef] [PubMed]
- Bock, A.R.; Laird, B.E. PFAS regulations: Past and present and their impact on fluoropolymers. J. Fluor. Chem. 2022, 280, 111500. [Google Scholar]
- Yuan, C.G.; Hu, C.P.; Xu, X.D.; Zhang, Q.L.; Hu, Q.H. Structure and Properties of VDF/TFE/PMVE Ternary Copolymer. Acta Polym. Sin. 2001, 6, 764–768. [Google Scholar]
- Lu, Y.; Claude, J.; Zhang, Q.; Wang, Q. Microstructures and Dielectric Properties of Ferroelectric Fluoropolymers Synthesized via Reductive Dechlorination of Poly(vinylidene fluoride-co-chlorotrifluoroethylene)s. Macromolecules 2006, 39, 6962–6968. [Google Scholar] [CrossRef]
- Li, B. Preparation of Ter-Polymerized Rubber by Emulsion Polymerization and Effect of feed ratio on Properties of the Product. China Elast. 2012, 22, 1–10. [Google Scholar]
- Puts, G.J.; Crouse, P.; Ameduri, B.M. Polytetrafluoroethylene: Synthesis and Characterization of the Original Extreme Polymer. Chem. Rev. 2019, 119, 1763–1805. [Google Scholar] [CrossRef]
- Yagci, Y.; Jockusch, S.; Turro, N.J. Photoinitiated Polymerization: Advances, Challenges, and Opportunities. Macromolecules 2010, 43, 6245–6260. [Google Scholar] [CrossRef]
- Wang, L.; Li, F.; Su, Z. Effective Thermal Conductivity Behavior of Filled Vulcanized Perfluoromethyl Vinyl Ether Rubber. J. Appl. Polym. Sci. 2008, 108, 2968–2974. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, J.; Li, F. Study on Compatibility of Hydrogenated Nitrile Rubber and Perfluoromethylvinylether (PMVE) Rubber. China Elast. 2007, 17, 5. [Google Scholar]
- Forsythe, J.S.; Hill, D.J.T.; Logothetis, A.L.; Seguchi, T.; Whittaker, A.K. Thermal and Mechanical Properties of Radiation Crosslinked Poly(tetrafluoroethylene-co-perfluoromethyl vinyl ether). Radiat. Phys. Chem. 1998, 53, 657–667. [Google Scholar] [CrossRef]
- Ajroldi, G.; Pianca, M.; Fumagalli, M.; Moggi, G. Fluoroelastomers—Dependence of Relaxation Phenomena on Composition. Polymer 1989, 30, 2180–2187. [Google Scholar] [CrossRef]
- Yagi, T.; Tatemoto, M. A Fluorine-19 NMR Study of the Microstructure of Vinylidene Fluoride–Trifluoroethylene Copolymers. Polym. J. 1979, 11, 429–436. [Google Scholar] [CrossRef]
- Schmiegel, W.W. Crosslinking of elastomeric vinylidene fluoride copolymers with nucleophiles. Die Angew. Makromol. Chem. Appl. Macromol. Chem. Phys. 1979, 76, 39–65. [Google Scholar] [CrossRef]
- da Cunha, F.R.; Davidovich, I.; Talmon, Y.; Ameduri, B. Emulsion copolymerization of vinylidene fluoride (VDF) with perfluoromethyl vinyl ether (PMVE). Polym. Chem. 2020, 11, 2430–2440. [Google Scholar] [CrossRef]
- Boyer, C.; Ameduri, B.; Hung, M.H. Telechelic diiodopoly (VDF-co-PMVE) copolymers by iodine transfer copolymerization of vinylidene fluoride (VDF) with perfluoromethyl vinyl ether (PMVE). Macromolecules 2010, 43, 3652–3663. [Google Scholar] [CrossRef]
- Twum, E.B.; McCord, E.F.; Lyons, D.F.; Rinaldi, P.L. Multidimensional 19F NMR Analyses of Terpolymers from Vinylidene Fluoride (VDF)–Hexafluoropropylene (HFP)–Tetrafluoroethylene (TFE). Macromolecules 2015, 48, 3563–3576. [Google Scholar] [CrossRef]
- Duan, J.; Yang, C.; Kang, H.; Li, L.; Yang, F.; Fang, Q.; Han, W.; Li, D. Structure, Preparation and Properties of Liquid Fluoroelastomers with Different End Groups. RSC Adv. 2022, 12, 3108–3118. [Google Scholar] [CrossRef]
- Ok, S. Characterization and Quantification of Microstructures of a Fluorinated Terpolymer by Both Homonuclear and Heteronuclear Two-Dimensional NMR Spectroscopy. Magn. Reson. Chem. 2015, 53, 130–134. [Google Scholar] [CrossRef]
- Chen, L.; Tran, H.; Batra, R.; Kim, C.; Ramprasad, R. Machine Learning Models for the Lattice Thermal Conductivity Prediction of Inorganic Materials. Comput. Mater. Sci. 2019, 170, 109155. [Google Scholar] [CrossRef]
- Jha, D.; Ward, L.; Paul, A.; Liao, W.K.; Choudhary, A.; Wolverton, C.; Agrawal, A. Elemnet: Deep Learning the Chemistry of Materials from Only Elemental Composition. Sci. Rep. 2018, 8, 17593. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.; Wu, Y.; Lin, Z.; Peng, L.; Chu, Q.; Tang, Y.; Zhang, W. Visual analytics of an interpretable prediction model for the glass transition temperature of fluoroelastomers. Mater. Today Commun. 2024, 40, 110155. [Google Scholar] [CrossRef]
- Sumpter, B.G.; Noid, D.W. On the Use of Computational Neural Networks for the Prediction of Polymer Properties. J. Therm. Anal. 1996, 46, 833–851. [Google Scholar] [CrossRef]
- Kim, C.; Chandrasekaran, A.; Huan, T.D.; Das, D.; Ramprasad, R. Polymer Genome: A Data-Powered Polymer Informatics Platform for Property Predictions. J. Phys. Chem. C 2018, 122, 17575–17585. [Google Scholar] [CrossRef]
- Shmuel, A.; Glickman, O.; Lazebnik, T. Machine and Deep Learning Performance in Out-of-Distribution Regressions. Mach. Learn. Sci. Technol. 2024, 5, 045078. [Google Scholar] [CrossRef]
- Chakravarthi, M.; Sharma, S.; Sahu, A.; Murthy, T.; Arulananth, T.S.; Jain, S. Machine Learning Algorithms for Automated Synthesis of Biocompatible Nanomaterials. In Proceedings of the 2024 International Conference on Intelligent Systems and Advanced Applications (ICISAA), Vellore, India, 28–29 December 2023; pp. 1–6. [Google Scholar]
- Pathak, S.; Quraishi, S.J.; Singh, A.; Singh, M.; Arora, K.; Ather, D. A Comparative Analysis of Machine Learning Models: SVM, Naive Bayes, Random Forest, and LSTM in Predictive Analytics. In Proceedings of the 2023 3rd International Conference on Technological Advancements in Computational Sciences (ICTACS), Tashkent, Uzbekistan, 13–14 December 2023; pp. 790–795. [Google Scholar]
- Iwasaki, Y.; Sawada, R.; Stanev, V.; Ishida, M.; Kirihara, A.; Omori, Y.; Someya, H.; Takeuchi, I.; Saitoh, E.; Shinichi, Y. Materials Development by Interpretable Machine Learning. arXiv 2019, arXiv:1903.02175. [Google Scholar] [CrossRef]
- Silva, A.J.; Cortez, P.; Pilastri, A. Chemical Laboratories 4.0: A Two-Stage Machine Learning System for Predicting the Arrival of Samples. In Proceedings of the 16th IFIP International Conference on Artificial Intelligence Applications and Innovations (AIAI 2020), Neos Marmaras, Greece, 5–7 June 2020; pp. 232–243. [Google Scholar]
- Chen, Q.; Wang, H.; Ji, H.; Ma, X.; Cai, Y. Data-Driven Atmospheric Corrosion Prediction Model for Alloys Based on a Two-Stage Machine Learning Approach. Process Saf. Environ. Prot. 2024, 188, 1093–1105. [Google Scholar] [CrossRef]
- Kieser, M.; Rauch, G.; Pilz, M. Two-Stage Designs with Small Sample Sizes. J. Biopharm. Stat. 2023, 33, 53–59. [Google Scholar] [CrossRef]
- Khasidashvili, Z.; Norman, A.J. Feature Range Analysis. Int. J. Data Sci. Anal. 2021, 11, 195–219. [Google Scholar] [CrossRef]
- Oyamada, M. Accelerating Feature Engineering with Adaptive Partial Aggregation Tree. In Proceedings of the 2018 IEEE International Conference on Big Data (Big Data), Seattle, WA, USA, 10–13 December 2018; pp. 5417–5419. [Google Scholar]
- Kalambet, Y.; Kozmin, Y.; Samokhin, A. Comparison of integration rules in the case of very narrow chromatographic peaks. Chemom. Intell. Lab. Syst. 2018, 179, 22–30. [Google Scholar] [CrossRef]
- Strobl, C.; Boulesteix, A.L.; Zeileis, A.; Hothorn, T. Bias in random forest variable importance measures: Illustrations, sources and a solution. BMC Bioinform. 2007, 8, 25. [Google Scholar] [CrossRef]
- Yu, L.; Liu, H. Efficient feature selection via analysis of relevance and redundancy. J. Mach. Learn. Res. 2004, 5, 1205–1224. [Google Scholar]
- Chen, T.; Guestrin, C. XGBoost: A Scalable Tree Boosting System. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar]
- Otazaghine, B.; Sauguet, L.; Boucher, M.; Ameduri, B. Radical copolymerization of vinylidene fluoride with perfluoroalkylvinyl ethers. Eur. Polym. J. 2005, 41, 1747–1756. [Google Scholar] [CrossRef]

| Chemical Shift Range/Point (ppm) | Corresponding Segment Structure | Feature Type | Calculation |
|---|---|---|---|
| −50.30~−52.10 | -CF(CF3O)CF2- | F1_area | Trapezoidal integration |
| −52.90~−55.30 | -CF(CF3O)CF2- | F2_area | Trapezoidal integration |
| −57.60~−58.90 | -CF(CF3O)CF2- | F3_area | Trapezoidal integration |
| −70.80~−78.10 | -CF(CF3)CF2- | F4_area | Trapezoidal integration |
| 92.50~94.40 | -CH2(CF2)CH2- | F5_area | Trapezoidal integration |
| 108.50~115.10 | -CF2(CF2)CH2- | F6_area | Trapezoidal integration |
| 116.00~120.70 | -CF-CF2(CF2)CF2- | F7_area | Trapezoidal integration |
| 121.10~125.60 | -O-CF-CF2(CF2)CF2- | F8_area | Trapezoidal integration |
| 125.70~128.40 | -CF2(CF2)CF2- | F9_area | Trapezoidal integration |
| −146.59 | -CH2-CF2-CF*-(OCF3)-CF2-CH2- | F1-intensity | Peak height |
| −145.95 | -CF2-CF2-CF*-(OCF3)-CH2-CF2- | F2-intensity | Peak height |
| −128.05 | -Rf-CF2-CF2-CF2*-CF2-Rf- | F4-intensity | Peak height |
| −126.91 | -CF2-CF2-CF2-CF2*-CF2-Rf- | F5-intensity | Peak height |
| −126.80 | -[CF2-CF(OCF3)]-CH2-CF2- | F6-intensity | Peak height |
| −126.32 | -CH2-CF2-CF2-CF2*-CF2-CF2- | F7-intensity | Peak height |
| −124.13 | -CF2-CF2-CF2-CF2*-CF2-CH2-CF2- | F8-intensity | Peak height |
| −123.91 | -CF2-CF2-CF(OCF3)-CF2*-CF2- | F9-intensity | Peak height |
| −123.63 | -CF2-CF(OCF3)-CF2 *-CF2- | F10-intensity | Peak height |
| −123.40 | -CH2-CF2-CF2*-CF2-CF(OCF3)- | F11-intensity | Peak height |
| −122.50 | -[CF2-CF(OCF3)]- | F12-intensity | Peak height |
| −116.97 | -CH2-CF2*-CF(OCF3)-CF2- | F13-intensity | Peak height |
| −115.70 | -(CH2-CF2)-(CF2-CH2)-(CH2-CF2)- | F14-intensity | Peak height |
| −114.80 | -CH2-CF2H- | F15-intensity | Peak height |
| −114.67 | -CF2-CH2-CF2*-CF2-Rf- | F16-intensity | Peak height |
| −113.72 | -(CH2-CF2)-(CF2-CH2)-(CH2-CF2)- | F17-intensity | Peak height |
| −113.48 | -CF2-CH2-CF2*-CF2-CH2- | F18-intensity | Peak height |
| −112.38 | -Rf-CH2-CF2*-CF2-CH2- | F19-intensity | Peak height |
| −111.00 | -(CH2-CF2)-[CF2-CF(OCF3)]- | F20-intensity | Peak height |
| −110.75 | -CH2-CF2-CH2-CF2*-Rf- | F21-intensity | Peak height |
| −110.16 | -Rf-CH2-CF2*-CF2-Rf- | F22-intensity | Peak height |
| −109.00 | -CH2CF2-CF2CH2I- | F23-intensity | Peak height |
| −95.36 | -Rf-CF2-CH2-CF2 *-CH2-Rf- | F24-intensity | Peak height |
| −94.80 | -(CH2-CF2)-(CF2-CH2)-(CH2-CF2)-(CH2-CF2)- | F25-intensity | Peak height |
| −94.21 | -CF2-CH2-CF2 *-CH2-Rf- | F26-intensity | Peak height |
| −92.59 | -CF2-CH2-CF2 *-CH2-CF2- | F27-intensity | Peak height |
| −92.00 | -CF2-CH2-CF2-CH2-CF2- | F28-intensity | Peak height |
| −73.00 | -CF2CF(OCF3)I- | F29-intensity | Peak height |
| −59.00 | -CF(OCF3)CF2I- | F30-intensity | Peak height |
| −53.17 | -CF2-CH2-CF(OCF3 *)-CF2-CF2- | F31-intensity | Peak height |
| −52.00 | -OCF3 | F32-intensity | Peak height |
| −40.00 | -CH2CF2I- | F33-intensity | Peak height |
| Unknown Feature | Chemical Shift (ppm) | Closest Known Feature (ppm) | Δδ (ppm) | Tentative Assignment (Assignment Confidence) |
|---|---|---|---|---|
| U1_area | −125.70 | F9_area (−127.2) | +1.50 | CF2-CF2 variants (Medium) |
| U2_area | −115.80 | F14_intensity (−115.7) | −0.10 | -(CH2-CF2)-(CF2-CH2)- variants (High) |
| U3_area | −115.60 | F14_intensity (−115.7) | −0.10 | Modified -(CH2-CF2)-(CF2-CH2)- (High) |
| U4_area | −115.40 | F14_intensity (−115.7) | +0.30 | -(CH2-CF2)-(CF2-CH2)- environments (High) |
| U5_area | −115.20 | F14_intensity (−115.7) | +0.50 | Similar to F14, different context (Medium) |
| U6_area | −95.52 | F24_intensity (−95.36) | −0.16 | Related to -CF2-CH2-CF2- (High) |
| U7_area | −95.32 | F24_intensity (−95.36) | +0.04 | Similar CH2-CF2 environments (High) |
| U8_area | −95.12 | F25_intensity (−94.8) | −0.32 | Modified -(CH2-CF2)- chains (High) |
| U9_area | −94.92 | F25_intensity (−94.8) | −0.12 | CF2-CH2 chain variants (High) |
| U10_area | −94.72 | F26_intensity (−94.21) | −0.51 | Related to -CF2-CH2-CF2- (Medium) |
| U11_area | −94.52 | F26_intensity (−94.21) | −0.31 | Similar chain structures (High) |
| U12_area | −52.90 | F32_intensity (−52) | −0.90 | OCF3 variants (High) |
| U13_area | −52.70 | F32_intensity (−52) | −0.70 | Modified PMVE-OCF3 (High) |
| U14_area | −52.50 | F32_intensity (−52) | −0.50 | OCF3 in different environments (High) |
| U15_area | −52.30 | F32_intensity (−52) | −0.30 | PMVE-related OCF3 structures (High) |
| Feature Type | Feature Example | Best Model | R2 | RMSE | RMSE% |
|---|---|---|---|---|---|
| KnoArea | F5_area | gbr | 0.93 | 0.11 | 1.50 |
| KnoIntensity | F14_intensity | gbr | 0.96 | 0.11 | 3.60 |
| Unk.Area | U5_area | huber | 0.93 | 0.14 | 2.10 |
| AvgPerformance | - | - | 0.94 | 0.10 | 2.40 |
| Performance Metric |
Two-Stage Best Strategy | RATS R2 |
RATS RMSE |
RS-Direct R2 |
RS-Direct RMSE | Improvement |
|---|---|---|---|---|---|---|
| mv_121 | TargetedStrategy | 0.92 | 3.88 | 0.75 | 5.31 | 0.17 |
| ts | MultivariatePrediction | 0.92 | 0.80 | 0.89 | 1.18 | 0.03 |
| pc | MultivariatePrediction | 0.92 | 1.36 | 0.75 | 5.67 | 0.17 |
| elongation | MultivariatePrediction | 0.86 | 7.75 | 0.68 | 7.16 | 0.18 |
| AvgPerformance | - | 0.90 | 3.45 | 0.76 | 4.83 | 0.14 |
| Performance Metric | B1 R2 | B1 RMSE | B2 R2 | B2 RMSE | RATS R2 | RATS RMSE | RATS vs. B1 | RATS vs. B2 |
|---|---|---|---|---|---|---|---|---|
| mv_121 | 0.79 | 6.14 | 0.80 | 6.01 | 0.92 | 3.88 | 0.13 | 0.12 |
| ts | 0.77 | 1.31 | 0.77 | 1.31 | 0.92 | 0.80 | 0.14 | 0.14 |
| pc | 0.84 | 1.78 | 0.83 | 1.83 | 0.91 | 1.36 | 0.07 | 0.08 |
| elongation | 0.79 | 10.58 | 0.70 | 12.46 | 0.86 | 7.75 | 0.10 | 0.16 |
| AvgPerformance | 0.80 | 4.95 | 0.78 | 5.40 | 0.90 | 3.45 | 0.11 | 0.13 |
| Feature | Range_Score | Range_Rank | Abs_Pearson_corr | Corr_Rank | Proj-Contribution |
|---|---|---|---|---|---|
| F7_area | 1.17 | 1 | 0.01 | 47 | 0.18 |
| U8_area | 1.17 | 2 | 0.13 | 15 | 0.11 |
| F9_area | 1.16 | 3 | 0.15 | 11 | 0.14 |
| F30_intensity | 1.16 | 4 | 0.02 | 44 | 0.10 |
| U15_area | 1.15 | 5 | 0.02 | 45 | 0.08 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.; Wu, Y.; Lin, Z.; Peng, L.; Fu, H. Range-Aware Two-Stage Modeling for Feed Ratio Optimization in Fluoroelastomers: Mechanistic Pathways from NMR Structural Features to Macroscopic Properties. Materials 2025, 18, 4618. https://doi.org/10.3390/ma18194618
Liu Y, Wu Y, Lin Z, Peng L, Fu H. Range-Aware Two-Stage Modeling for Feed Ratio Optimization in Fluoroelastomers: Mechanistic Pathways from NMR Structural Features to Macroscopic Properties. Materials. 2025; 18(19):4618. https://doi.org/10.3390/ma18194618
Chicago/Turabian StyleLiu, Yaxian, Yadong Wu, Zhoujun Lin, Lijuan Peng, and Hongwei Fu. 2025. "Range-Aware Two-Stage Modeling for Feed Ratio Optimization in Fluoroelastomers: Mechanistic Pathways from NMR Structural Features to Macroscopic Properties" Materials 18, no. 19: 4618. https://doi.org/10.3390/ma18194618
APA StyleLiu, Y., Wu, Y., Lin, Z., Peng, L., & Fu, H. (2025). Range-Aware Two-Stage Modeling for Feed Ratio Optimization in Fluoroelastomers: Mechanistic Pathways from NMR Structural Features to Macroscopic Properties. Materials, 18(19), 4618. https://doi.org/10.3390/ma18194618






