Abstract
Rare-earth transition metal-based double perovskite ceramics E2TMO6 (where E = rare-earth metals, T = transition metals, and M = metal) have received impressive attention lately for cryogenic applications as a result of their intrinsic physical features such as multiferroicity, dielectric features, and adjustable magnetic transition temperature. However, determination and enhancement of magnetic transition temperature of E2TMO6 ceramic are subject to experimental procedures and processes with a significant degree of difficulties and cumbersomeness. This work proposes an extreme learning machine (ELM)-based intelligent method of determining magnetic transition temperature of E2TMO6 ceramics with activation function sigmoid (SM) and sine (SE) at varying magnetic field. The outcomes of the SE-ELM and SM-ELM models were compared with genetically optimized support vector regression (GEN-SVR) predictive models using RMSE, CC, and MAE metrics. Using the testing samples of E2TMO6 ceramics, SE-ELM predictive model outperforms GEN-SVR with a superiority of 6.3% (using RMSE metric) and 15.7% (using MAE metric). The SE-ELM predictive model further outperforms the SM-ELM model, with an improvement of 5.3%, using CC computed with training ceramic samples. The simplicity of the employed descriptors, coupled with the outstanding performance of the developed predictive models, would potentially strengthen E2TMO6 ceramics exploration for low-temperature cryogenic applications and circumvent energy challenges in different sectors.
1. Introduction
Magnetocaloric effect–based magnetic materials offer energy-efficient and next-generation systems of refrigeration with significant potential to revolutionize cooling industries and address global energy challenges [1,2,3]. This system of refrigeration is connected with the intrinsic entropy within magnetic materials [4]. Adiabatic conditional inclusion of magnetic fields within magnetic materials orients the magnetic moment domicile in the material and subsequently results in reduction in magnetic entropy [5,6]. Consequently, the system’s effort to keep the total entropy constant leads to an increase in temperature. Removal of magnetic field results in an increase in magnetic entropy with an ultimate decrease in temperature. Magnetic cooling systems utilize the concept of temperature fluctuation due to application/removal of a magnetic field [7,8,9]. This cooling system is thermodynamically efficient and promotes environmental friendliness since it circumvents utilization of ozone-depleting refrigerants [10]. Beyond cooling applications, magnetocaloric effect-based magnetic materials find applications in other cryogenic domains such as magnetic sensors operating at cryogenic temperatures, spin valves, and magnetic memory devices for data storage, among others [11]. The magnetic parameters that significantly influence the candidature of any magnetic materials for cryogenic applications include the magnetocaloric effect, magnetic cooling power, and magnetic transition temperature. Magnetic transition temperature plays a significant role in regulating transition between ferromagnetism to paramagnetism. The absence of magnetocaloric compounds with desired features for cryogenic applications hinders commercialization of the technology [12]. Therefore, discovery of new materials capable of displaying a large magnetocaloric effect and magnetic transition temperature is of significant interest for cryogenic applications. Rare-earth-based compounds have received overwhelming attention lately as novel magnetocaloric materials due to their huge magnetic moments, excellent ferromagnetic interaction, and impressive magnetic properties associated with their localized f-orbital electrons [13,14,15,16]. Super-exchange interactions in rare-earth-based compounds create an avenue for a sharp paramagnetic to ferromagnetic transition. Recent studies utilized computational intelligence approaches to explore the magnetocaloric effect [17] and magnetic cooling power [18] of these compounds for cryogenic applications, while magnetic transition temperature remains unexplored. Magnetic transition temperature is the temperature at which phase transition occurs within the magnetic materials from ferromagnetic to paramagnetic state. This temperature is a critical parameter, as it determines potential applications of magnetocaloric materials for cryogenic applications. Several physical complications are associated with magnetic behavior of double perovskite compounds modeled in this work. In the temperature range near the phase transition, multiple magnetic phases co-exist, and three different magnetic phase transitions were observed and reported in R2NiMnO6 compound [19]. The magnetic phase transitions were attributed to rare-earth ordering, 3d-4d exchange, and 3d metal ordering. Similarly, a paramagnetic state of double perovskite-based compounds has been reported to have a magnetic phase known as Griffiths phase with direct influence on magnetic properties of double perovskite compounds [20]. In order to simplify these associated magnetic phases, only one phase is presently simulated in this work. This work develops computational intelligent methods of determining magnetic transition temperature of E2TMO6 rare-earth transition metal-based double perovskite ceramics.
Over the years, conventional magnetocaloric effect materials have seen extensive investigation. These magnetic materials, including spinel ferrites, europium titanate, manganite, and gadolinium alloys, have demonstrated strong magnetocaloric properties that are important parameters for assessing the cryogenic ability of a material [16,21,22,23,24,25,26]. However, large-scale fabrication and wide adoption have been constrained due to chemical stability, cost-effectiveness, and cryogenic operational temperature, among others. Recently, rare-earth-based oxides have been explored as a new class of material to mitigate these drawbacks. Specifically, double perovskite oxides with the general formula E2TMO6 (where E is a rare-earth metal, T is a transition metal, and M is another metal) present exciting research interest [27]. Besides their elevated MCE and RCP, these ceramics displayed intriguing physical properties that hold potential for cryogenic applications. However, magnetic transition temperature of these ceramics has not been investigated in the literature using computational approaches. These materials are derived from the fundamental ABO3 perovskite structure [28], where a large cation (A-site) is surrounded by twelve oxygen ions, and a smaller cation (B-site) is at the center of six oxygen octahedra [19,29]. In the double perovskite structure, the B-site is occupied by two different cations, T and M, which allows for a vast array of compositional permutations. This structural flexibility is crucial, as altering the ionic radii and electronic configurations of the constituent E, T, and M metals can induce fascinating magnetic behaviors, including spin-phonon coupling and field-induced metamagnetic transitions, which directly influence their magnetic transition temperature [30,31]. The advantage of ionic radii descriptors as compared to other descriptors such as magnetic moment of ions, tolerance factor, and bond angle Mn-O-Mn (which are known to influence magnetic properties of double perovskite compounds) is the simplicity, which promotes pre-laboratory simulation without any experimental procedures with sophisticated equipment. While experimental studies have confirmed their potential, a systematic method for predicting and optimizing the magnetic transition temperature across a vast range of possible alloys remains a point of research interest. This work aims to contribute to this gap by employing intelligent computational models (support vector regression optimized by genetic algorithm and extreme learning machine) to investigate and predict magnetic transition temperature of these perovskites and therefore develop a framework for the rational design of new E2TMO6 with high and tunable magnetic transition temperature.
Support vector regression (SVR) is a class of supervised learning-based intelligent algorithms for addressing regression problems [32,33]. The algorithm employs structural risk principle of minimization for controlling and minimizing training error bounds. The mathematical framework of SVR employs Lagrange multipliers in addressing convex optimization problems and transforms data samples to a space of high dimension where data samples are linearly analyzed [34]. This transformation mechanism allows SVR to conveniently address nonlinear and challenging science as well as engineering problems [35,36,37]. To further control the precision and accuracy of the prediction outcomes of SVR-based predictive models, parameters such as the penalty factor, the parameter associated with nonlinear mapping function called kernel parameter, and epsilon are adjusted in a combinatory manner. Genetic evolutionary algorithm has been employed for this parametric optimization. Genetic algorithm is a population-based search heuristic algorithm for locating optimal solutions in a complex optimization system [38,39]. The algorithm is based on the process of natural selection, inspired by the popular theory of natural evolution. The choice of genetic algorithm in this work is due to the robustness of the algorithm coupled with flexibility as well as absence of premature convergence [40]. The performance of genetically optimized support vector regression (GEN-SVR)-based predictive models was assessed using performance metrics such as the mean absolute error (MAE), correlation coefficient (CC), and root mean square error (RMSR) for training as well as testing E2TMO6 rare-earth transition metal-based double perovskite ceramic samples for magnetic transition temperature prediction.
Extreme learning machine (ELM) is a modified and upgraded version of feedforward neural network characterized by the presence of a single hidden layer with reduced computational complexity [41,42]. It employs empirical principle of minimizing training error range and is known for characteristic fast as well as efficient learning. As compared with the conventional backpropagation learning system, ELM enjoys rapid training speed with simple and excellent generalization [43]. The algorithm utilizes random weights for its input weights, while only output weights are subjected into training processes. Implementation of extreme learning machine algorithm involves the choice of activation function with the number of neurons, initialization of random weights, computation of the output of the hidden layer, computation of output weights, and prediction of the desired material properties [44]. The uniqueness of this algorithm strengthens its applications in science and engineering domains. These unique features are harnessed in this work in determining the magnetic transition temperature of E2TMO6 rare-earth transition metal-based double perovskite ceramics.
The results of modeling indicate that sine function-based ELM (SE-ELM) predictive model outperforms the sigmoid activation function-based ELM (SM-ELM) and genetically optimized SVR (GEN-SVR) predictive models using different performance metrics such as correlation coefficient (CC), mean absolute error (MAE), and root mean square error (RMSE). For the testing samples of E2TMO6 ceramics, SE-ELM outperforms the SM-ELM predictive model with improvements of 26.579% (using CC metric), 53.2679% (using RMSE metric), and 51.5744% (using MAE metric). Similarly, GEN-SVR performs better than the SM-ELM model, with an improvement of 5.3005%, using CC computed with training samples of rare-earth transition metal-based double perovskite ceramics. Using testing samples of rare-earth transition metal-based double perovskite ceramics, the GEN-SVR predictive model performs better than the SM-ELM model, with an improvement of 23.3501% (using CC metric), 50.1124% (using the RMSE metric), and 42.5786% (using MAE metric).
The remaining part of the manuscript is organized as follows: section two describes the mathematical framework of the intelligent algorithm, while section three discusses the computational strategies coupled with a description of E2TMO6 rare-earth transition metal-based double perovskite ceramic samples. The fourth section presents the outcomes of the predictive models and compares the predictions with the measured magnetic transition temperatures. The last section summarizes the findings of the research work.
2. Mathematical Formulation of the Intelligent Algorithms Implemented
The section contains the presentation of mathematical foundation of intelligent algorithms. The algorithms include support vector regression, extreme learning machine, and genetic algorithm.
2.1. Support Vector Regression Mathematical Background
A potent machine learning method for forecasting continuous target variables is support vector regression (SVR) [45,46]. Support vector machines, initially developed for classification problems, form the foundation of SVR. In the context of regression, SVR looks for a function that, while keeping a healthy margin of error, best approximates the connection between the target variable and input descriptors [47]. SVR’s main concept is that the defined descriptors are mapped into a new space with higher dimensions using a nonlinear kernel function. This enables the algorithm to identify intricate associations in the data that conventional linear regression models would overlook. It seeks to create a hyperplane in the feature space that, within a tolerance margin, minimizes the disparity between the measured and predicted magnetic transition temperature.
Modeling nonlinear relationships without explicitly defining the type of nonlinearity is a major benefit of SVR over traditional regression models. SVR can function in a feature space without transformation computation in an explicit manner through kernel utilization, such as the Gaussian and polynomial kernels, which makes it computationally efficient [48,49]. The mathematical foundation of SVR is hereby presented. In order to efficiently model and predict the underlying patterns and dependencies in magnetic transition temperature and descriptors (which include the applied magnetic field, ionic radii of rare-earth metal, transition metal, and other metal for E2TMO6 rare-earth transition metal-based double perovskite ceramics, SVR uses the function given in Equation (1):
Here, γ denotes the SVR model’s projected output (predicted magnetic transition temperature, and d represents the descriptors, which include the applied magnetic field, ionic radii of rare-earth metal, transition metal, and other metal. The essential elements of the model, the weight vector (α), and bias (φ) coefficients are calculated by minimizing the risk function given in Equation (2) [50].
Deviations above the epsilon threshold are penalized by the regularization factor, represented by the symbol s. The Euclidean norm is represented by in Equation (2), while the error threshold is defined by L, as Equation (3) illustrates.
Slack variables δ and δ* must be included, particularly when there is a chance that the error threshold will be surpassed. These variables partially regulate the gap between the defined bounds and the observed values. To address the dual problem, the optimization process was carried out using the procedures outlined in Equation (4) and is constrained by the conditions stated in Equation (5):
where the Lagrange multipliers utilized to solve the optimization are denoted by and . The data points with coefficients which are non-zero are referred to as support vectors. Equation (6) shows the expected values produced by the algorithm using optimization procedures.
The kernel function is essential for transforming the initial nonlinear regression into a linear one in the new space. The mapping function described in Equation (7) captures this transition, and Equation (8) expresses the nonlinear regression model’s final form in the SVR framework [51].
2.2. Genetic Algorithm Theory and Description
Genetic algorithm (GA) is an evolutionary optimization method-based on the fundamental principle of genetics and natural selection [52]. The algorithm addresses the optimization problem through systemic mimicking of evolution theory with key components such as population initiation, fitness function definition, parent selection, crossover, and mutation. In population initialization, probable solutions are initiated and represented as vectors or strings [53,54]. The quality of the individual solutions is subsequently assessed through fitness function computation. The selection procedures follow, in which most fit solutions are selected for reproduction. In the crossover stage, new offspring are created through parent combination, while the mutation stage further alters the solutions through randomization of genetic constituents [55]. Selection, crossover, and mutation procedures are probabilistic with assigned probability values. Figure 1 presents the flowchart of genetic algorithms.
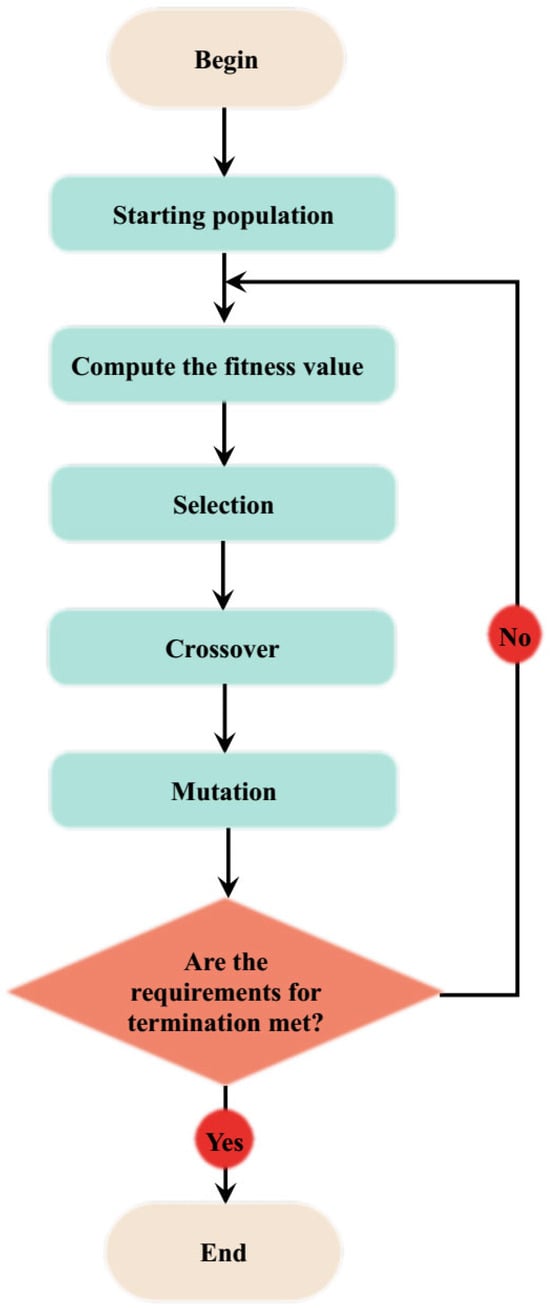
Figure 1.
Computational flowchart of the genetic algorithm (GA).
2.3. Extreme Learning Machine Theory and Description
Extreme learning machine (ELM) is classified as a neural network (feed-forward) with a single hidden layer designed to test and train neural networks without using back-propagation to update their weights [42,56,57]. This method is suggested to shorten a model’s training period, which is caused by repeated parameter adjusting procedures. Therefore, ELM can update the weights without performing a back-propagation phase [58]. Let p, q, and z, respectively, stand for the quantity of input features (which include the applied magnetic field, ionic radii of rare-earth metal, transition metal, and other metal), ELM’s outputs (magnetic transition temperature of E2TMO6 rare-earth transition metal-based double perovskite ceramics), and hidden nodes. Let (, ) with = [, , …, ] ∈ and = [, , …, ] ∈ be the training sample for i = 1, 2, …, P with P is the number of E2TMO6 ceramics. The predicted magnetic transition temperature ( ∈ ) for the input descriptors is represented in Equation (9):
where vector = [, , …, ] ∈ represents the weight vector joining the j output and hidden nodes, and depicts the output of hidden node j, mathematically represented as ) = δ(, , ), where ∈ is the weight vector, represents bias, and δ is the actuation function [59].
The row vector that entails the hidden layer prediction after input vector is represented as G() = [] with matrix form representation shown in Equation (10).
The predicted magnetic transition temperature is shown in Equation (11):
where y = [ , …,] T ∈ . The algorithm aims to determine α, which is the solution objective for the optimization problem shown in Equation (12) [60]:
where D = [d1, d2, …, dP]T ∈ RP×q is the matrix representing the predicted magnetic transition temperature and F is the Frobenius norm. The solution of the given problem is depicted by Equation (13):
where Gτ stands for the Moore–Penrose inverse of G or the pseudo-inverse.
3. Computational Methodology and Approaches
This section contains the acquisition of E2TMO6 rare-earth transition metal-based double perovskite ceramic samples, the computational hybridization of genetic algorithms with support vector regression, and the computational details of ELM-based algorithms.
3.1. E2TMO6 Rare-Earth Transition Metal-Based Double Perovskite Ceramic Samples Acquisition and Description
E2TMO6 rare-earth transition metal-based double perovskite ceramic data samples employed for magnetic transition temperature prediction were extracted from the literature [19,29,61,62,63,64,65,66,67]. The data samples consist of twenty-seven magnetocaloric compounds of E2TMO6, rare-earth transition-metal-based double perovskite ceramics. The descriptors include the applied magnetic field, ionic radii of the rare-earth metal, transition metal, and other incorporated metals. Statistical analysis was conducted on the data sample, and the reports of the analysis are contained in Table 1.

Table 1.
Data sample analysis for all input descriptors and measured magnetic transition temperature.
The computed statistical parameters include the mean values, which entail the overall content of E2TMO6 rare-earth transition metal-based double perovskite ceramic data samples, maximum as well as the minimum values through which data sample ranges are determined. The analysis also contains the standard deviation, which presents the consistency in the employed data samples, as the data were experimentally measured from different experimental conditions. The computed coefficients of correlation explain the nature of the relationship existing between each of the descriptors and the measured magnetic transition temperature. The applied magnetic field, ionic radii of rare-earth metals, and those of transition metals are negatively correlated with the measured magnetic transition temperature, while the ionic radii of the incorporated metals show positive correlation. The coefficients of correlation of all the descriptors are relatively small compared to the incorporated metal descriptor. These observations indicate that ordinary linear models cannot effectively capture the existing relationship between the descriptors and magnetic transition temperature. Hence, choosing nonlinear modeling tools, such as the hybrid SVR and ELM employed, becomes necessary.
3.2. Computational Development of Hybrid Genetic Algorithm and Support Vector Regression
E2TMO6 rare-earth transition metal-based double perovskite ceramics (utilized in developing predictive models through which magnetic transition temperatures are determined and predicted) were randomized and partitioned into training and testing with a 4:1 division ratio. The entire computation was conducted using the computing environment of MATLAB (R2024B). The randomization procedures strengthen even partitioning of the data samples and prevent the likelihood of data disparity in which the model acquires patterns from a part of data samples that cannot be generalized for future prediction. Hybridization of genetic algorithm with support vector regression (GEN-SVR) maximizes regression task performance by combining the advantages of SVR and genetic algorithm. Through this integration, important SVR model parameters like the penalty factor, error epsilon, and kernel parameters are adjusted by utilizing genetic algorithm optimization capabilities. GEN-SVR predictive model has been developed using the following computational procedures:
Step 1: Data partitioning and randomization: The samples were randomized and partitioned. The process of data partitioning involves splitting the dataset into sets for testing and training; 20% of E2TMO6 rare-earth transition metal-based double perovskite ceramic data samples were employed for model validation, while 80% of the E2TMO6 rare-earth transition metal-based double perovskite ceramic samples were utilized for pattern acquisition.
Step 2: Solution space initialization: The search space for the SVR parameters was initiated using a genetic algorithm. A set of hyperparameters to be optimized is represented by each chromosome. The search space has ranges with upper and lower bounds for the kernel parameter, epsilon, and penalty factor. The upper and lower limits of the penalty factor were defined as 10,000 and 10, respectively, while those of epsilon were set at 1.0 and 0.1. For the Gaussian kernel parameter, upper and lower solution spaces were set at 1.0 and 0.1, respectively.
Step 3: Fitness evaluation: The fitness of each of the chromosomes within the solution space was computed through root mean square error determination. The procedures for fitness computation involve the following: (i) selecting nonlinear mapping functions from the pool, which includes Gaussian, polynomial, sigmoid, and other functions; (ii) training E2TMO6 rare-earth transition metal-based double perovskite ceramic samples, together with the chromosome (whose fitness is to be determined), by combining them with the selected mapping function in (i) for magnetic transition temperature determination; (iii) combining the support vectors generated during (ii) with the testing E2TMO6 rare-earth transition metal-based double perovskite ceramic samples to determine the magnetic transition temperature; and (iv) evaluating the performance/fitness of each chromosome using root mean square error (RMSE) between the measured and predicted magnetic transition temperature. The chromosome with the lowest RMSE fits within the solution space.
Step 4: Subsequent generation through genetic operational principles: Selection probability of 0.8 was implemented for selecting parents which produce offspring for the subsequent generations. This ensures that most fit chromosomes within the population migrate to the next generation.
Step 5: Crossover implementation: To produce new offspring with better features, crossover procedures unite segments of specific chromosomes. A crossover probability of 0.9 was employed in order to promote variety and effectively explore the solution space.
Step 6: Mutation operation: In order to preserve diversity without impeding the convergence process, mutation causes random changes to the chromosomes. Mutation probability was set at 0.005.
Step 7: Stopping conditions: The aforementioned six steps were continuously repeated until one of the halting criteria was satisfied. The conditions include reaching a predetermined maximum number of iterations, maintaining the same value of RMSE for 50 consecutive iterations, and obtaining an RMSE value of zero. The computational details are pictorially represented in Figure 2.
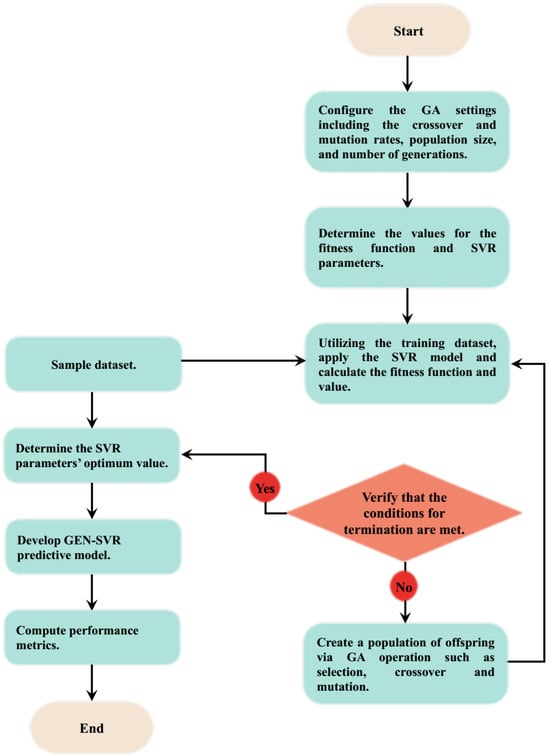
Figure 2.
Computational description of GEN-SVR predictive model for magnetic transition temperature determination.
3.3. Computational Development of ELM-Based Model for Magnetic Transition Temperature Prediction in E2TMO6 System of Ceramics
ELM-based predictive models were developed for predicting magnetic transition temperature of testing E2TMO6 rare-earth transition metal-based double perovskite ceramics. The data samples were subjected to randomization processes and then divided into training and testing with a 4:1 division ratio. The computational procedures are outlined as follows:
Step A: Initialization of ELM parameters and configuration of Mersenne Twister generator: ELM parameters that control the precision of the predictive model were initiated. The parameters include the neuron number and the activation function. Neuron number was optimized using the grid search approach for each selected activation function. Although population-based optimization methods are very efficient for multiple-parameter optimization. Utilization of an evolutionary algorithm for neuron number optimization amounts to a waste of computational resources since only a parameter is to be optimized. The Mersenne Twister generator was initiated and set at a value that was maintained throughout the modeling and simulation stages. Input weights and biases were generated for subsequent use. This process strengthens reproducibility of the model weights.
Step B: Neuron number and activation function selection: The solution space of the neuron number was defined between 1 and 100 for each activation function. The explored activation functions include the radial basis, sine, sigmoid, transig, and triangle basis functions.
Step C: Weights acquisition for future prediction: Training samples of E2TMO6 rare-earth transition metal-based double perovskite ceramics were combined with the outcomes of Steps A and B to compute output weights using the Moore–Penrose generalized inverse matrix.
Step D: Assessment of the generalization and estimation capacity of the developed model: In order to evaluate the developed ELM-based predictive models for future generalization, testing ceramics, biases (outcomes of Step A), output weights (outcomes of Step C), and randomly generated input weights from Step A were all employed. The measurement of generalization capacity was achieved by calculating root mean square error (RMSE) involving the extreme learning machine algorithm’s predictions and the measured magnetic transition temperature. Other performance metrics, such as mean absolute error (MAE) and correlation coefficient (CC), were also computed for the testing and training E2TMO6 rare-earth transition metal-based double perovskite ceramic samples.
Step E: Steps A to D were repeated for using different activation, while the values of the performance metrics were computed and recorded. Activation functions that show better performance include the sine (SE) and sigmoid (SM) functions which give rise to the SE-ELM and SM-ELM predictive models. Figure 3 presents the computational step-by-step procedures of the developed SE-ELM and SM-ELM predictive models.
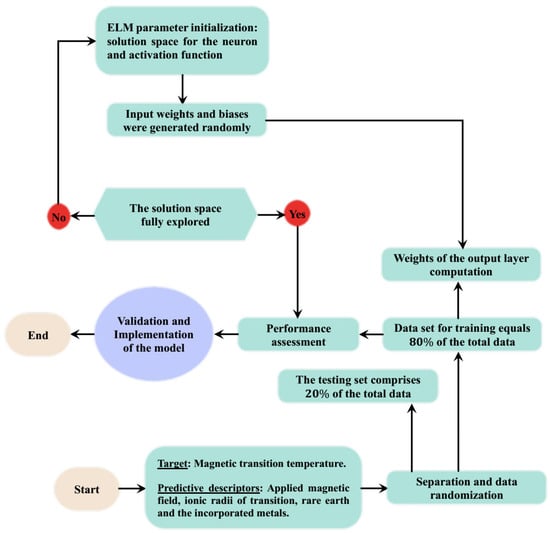
Figure 3.
Computational description of the developed SE-ELM and SM-ELM predictive models.
4. Results and Discussion
In this section, the predictive capacities of the developed SM-ELM, SE-ELM, and GEN-SVR models in determining the magnetic transition temperature of E2TMO6 ceramics are presented. GA convergence at different chromosome sizes is discussed. The future estimated strength of the predictive models is also presented using different metrics.
4.1. Convergence of GEN-SVR Parameters at Different Chromosome Sizes
The exploitation and exploration ability of chromosomes within the genetic algorithm operational principle in optimizing the precision tuning parameters in support vector regression algorithm are shown in Figure 4 over a hundred iterations. Genetic algorithm parameters that influence the model accuracy include the population size, crossover rate, and mutation rate, among others. Larger population size strengthens diversity and enhances the exploration of search space, while small population size may result in premature convergence. Crossover rate helps combine genetic materials of two different parents, which results in offspring production. A high crossover rate enhances the mixing of traits and the exploration of new solutions. Low mutation rate promotes stagnation. Optimum choice of these parameters contributes significantly to the model accuracy. Figure 4a and Figure 4b, respectively, present the convergence of the penalty factor and epsilon, while Figure 4c shows the convergence of the fitness function computed using RMSE between the measured magnetic transition temperature and the estimated values for rare-earth transition metal-based double perovskite ceramics. The genetic algorithm avoids premature convergence through a larger population size, which ranges between 20 and 200 in this case. Crossover and mutation rates were also carefully maintained at probabilities of 0.9 and 0.05, respectively, purposely to avoid potential premature convergence.
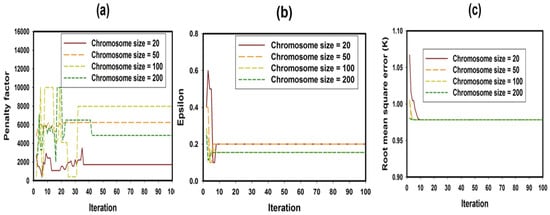
Figure 4.
Parameter convergence in GEN-SVR model for (a) penalty factor, (b) epsilon threshold and (c) model root mean square error.
For the penalty factor convergence presented in Figure 4a, stable convergence was attained after fortieth iteration for all the investigated chromosome sizes. Penalty factor, also known as regularization factor, penalizes data points outside the precision zone. The parameter controls and balances the tradeoff between model complexity and precision. Epsilon convergence shown in Figure 4b describes the user-defined error zone during pattern acquisition. For every investigated chromosome size, stable convergence was attained after tenth iteration. The fitness function, which measures the strength of each individual chromosome, is shown in Figure 4c at different sizes of chromosomes. The convergence of fitness function (determined through root mean square error computation) does not significantly depend on the size of the chromosome and iteration number (since stable convergence appears just before tenth iteration for all the investigated chromosome sizes). Table 2 contains the optimum (global) values for each of the precision tuning parameters in support vector regression algorithm.

Table 2.
Global solutions obtained from genetic algorithm optimization for GEN-SVR model.
4.2. Generalization Strength Comparison Between Developed Models Using Different Metrics
The estimation strength and predictive capacity of magnetic transition temperature predictive models for rare-earth transition metal-based double perovskite ceramics were computed using root mean square error (RMSE), correlation coefficient (CC), and mean absolute error (MAE) for training and testing samples of rare-earth transition metal-based double perovskite ceramics. The comparison is presented in Figure 5 for SE-ELM, SM-ELM and GEN-SVR predictive models. For the CC metric, shown in Figure 5a, using training rare-earth transition metal-based double perovskite ceramics, SE-ELM predictive model has an absolute CC of 100% while the GEN-SVR and SM-ELM models attained CC of 99.95% and 94.66%, respectively. Interestingly, SE-ELM predictive model further shows superior performance over other two predictive models when validated using new data samples through a test set cross-validation system of assessing generalization strength of intelligent models. As shown in Figure 5b, CC of 96.92% was obtained using the SE-ELM model, while the GEN-SVR and SM-ELM predictive models attained 92.84% and 71.16%, respectively. Based on RMSE and MAE, using testing samples of rare-earth transition metal-based double perovskite ceramics—as presented in Figure 5c and Figure 5d, respectively—the SE-ELM model attains RMSE of 0.9165 K compared to 0.9783 K for the GEN-SVR predictive model and 1.9611 K for the SM-ELM model. Similarly, the SE-ELM predictive model attains MAE of 0.7355 K, while the GEN-SVR and SM-ELM models, respectively, attained MAE of 0.8721 K and 1.5189 K.
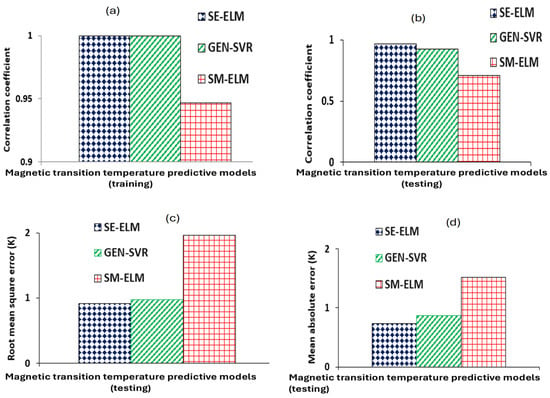
Figure 5.
Generalization strength of the developed models (GEN-SVR, SE-ELM and SM-ELM) using (a) CC for training double perovskite ceramics, (b) CC for testing samples of double perovskite ceramics, (c) RMSE for testing samples of double perovskite ceramics, and (d) MAE for testing samples of double perovskite ceramics.
On the basis of performance superiority, the SE-ELM magnetic transition temperature predictive model performs better than the GEN-SVR predictive model, with an improvement of 0.046% and 4.2125%, using CC metric on training and testing samples of rare-earth transition metal-based double perovskite ceramics, respectively. On the testing samples of rare-earth transition metal-based double perovskite ceramics, the SE-ELM predictive model outperforms the GEN-SVR model with an improvement of 6.3252% (using RMSE metric) and 15.6661% (using MAE metric). The SE-ELM predictive model further outperforms the SM-ELM model, with an improvement of 5.3441% using CC computed with training samples. For the testing samples of rare-earth transition metal-based double perovskite ceramics, SE-ELM outperforms the SM-ELM predictive model, with an improvement of 26.579% (using CC metric), 53.2679% (using RMSE metric), and 51.5744% (using MAE metric). Similarly, GEN-SVR predictive model outperforms the SM-ELM model with superiority of 5.3005% using CC computed with training samples of rare-earth transition metal-based double perovskite ceramics. Using testing samples of rare-earth transition metal-based double perovskite ceramics, the GEN-SVR predictive model performs better than the SM-ELM model by 23.3501% (using CC metric), 50.1124% (using RMSE metric), and 42.5786% (using MAE metric). Table 3 presents the performance measuring parameters and their associated computed metrics. The performance superiorities of each of the predictive model are also contained in the table.

Table 3.
Generalization strength comparison between the developed magnetic transition temperature predictive models.
4.3. Computed Predictions of SE-ELM, GEN-SVR, and SM-ELM Models and Comparison with the Measured Magnetic Transition Temperatures
The predictions of each model are presented in Table 4, along with the absolute difference between the measured and predicted values. The estimates of SE-ELM model agreed excellently well with the measured magnetic transition temperature, except for a few ceramics, where slight deviations were obtained.

Table 4.
Predicted magnetic transition temperature (MTT) of rare-earth transition metal-based double perovskite ceramics and their comparison with the measured values.
Ceramics with little deviation from the measured magnetic transition temperature include Tm2FeCrO6 with measured and predicted magnetic transition temperature of 10.5 K [63] and 10.6 K, respectively, Ho2CoMnO6 with measured and predicted magnetic transition temperature of 8.0 K [29] and 6.8 K, respectively, Gd2FeCoO6 with measured and predicted magnetic transition temperature 4.9 K [67] and 4.3 K, respectively, Dy2ZnMnO6 with measured and predicted magnetic transition temperature 10.4 K [62] and 11.9 K, respectively, and Ho2NiMnO6 with measured and predicted magnetic transition temperature 5.5 K [19] and 5.3 K, respectively. For the SM-ELM predictive model, magnetic transition temperature of many rare-earth transition metal-based double perovskite ceramics were predicted exactly with zero deviation from the measured values. Ceramics with exactly predicted magnetic transition temperature include Ho2CrMnO6 [61], Gd2ZnMnO6 [62], Er2FeCrO6 [63], Gd2FeAlO6 [65], Ho2ZnMnO6 [62], Er2FeCoO6 [67], Er2CrMnO6 [61] and Ho2FeAlO6 [65]. The predicted magnetic transition temperature of the remaining ceramics shows slight deviation. The predicted magnetic transition temperature using GEN-SVR model agree well with the measured values especially with Ho2CrMnO6 [61] ceramic. Other investigated ceramic samples show deviation of 0.2 K except Dy2CuMnO6 [64] with 0.1 K deviation, Er2CrMnO6 [61] with 0.9 K deviation, Ho2ZnMnO6 [62] with 1.6 K deviation, Dy2NiMnO6 [19] with 0.1 K deviation and Ho2NiMnO6 [19] with 0.6 K deviation. The overall mean absolute deviation of the SE-ELM, GEN-SVR and SM-ELM predictive models are 0.1 K, 0.3 K and 0.7 K, respectively. ELM model has demonstrated superior performance over SVR-based model due to different error minimization principle adopted by the algorithms. SVR minimizes training error using structural risk principle while empirical risk principle forms the foundation of ELM-based model. Similarly, sine activation function employed by the SE-ELM model transforms to better predictive strength as compared with sigmoid activation function utilized in the SM-ELM model.
4.4. Dependence of Magnetic Transition Temperature on Applied Magnetic Field Using the SE-ELM Predictive Model
Dependence of magnetic transition temperature on applied magnetic field on rare-earth transition metal-based double perovskite ceramics was investigated using developed SE-ELM predictive model. Understanding this relationship is of great significance in optimizing and tailoring rare-earth transition metal-based double perovskite ceramics for specific applications such as magnetic sensors, magnetic refrigeration, data storage, and spintronics among other cryogenic applications. Through the establishment of dependence of magnetic transition temperature and applied magnetic field, rare-earth transition metal-based double perovskite ceramic can be tailored for designing magnetic sensors that can detect changes in magnetic fields, magnetic memory devices with high stability and storage density, and spintronics devices such as tunnel junctions. Figure 6 presents the magnetic field dependence on magnetic transition temperature using the SE-ELM predictive model for Ho2CuMnO6 (shown in Figure 6a) and Tm2FeCrO6 (shown in Figure 6b).
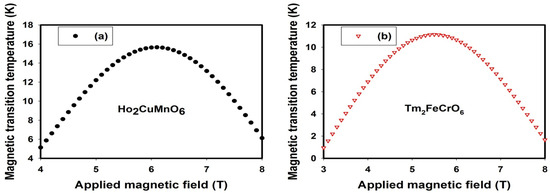
Figure 6.
Dependence of magnetic transition temperature on magnetic field for (a) Ho2CuMnO6 (b) Tm2FeCrO6 rare-earth transition metal-based double perovskite ceramics.
Increase in applied magnetic field results in an increase in magnetic transition temperature due to the alignment of magnetic moment in Ho2CuMnO6 (shown in Figure 6a) and Tm2FeCrO6 (shown in Figure 6b) ceramics. Further increase in applied magnetic field results in a disruption in magnetic interaction and consequently lowers the magnetic transition temperature. The results of modeling and simulation presented in Figure 6a (for Ho2CuMnO6 ceramic) and Figure 6b (for Tm2FeCrO6 ceramic) correspond with the reported experimental values at 5T [63,64]. This investigation employs the weights generated during pattern acquisition in SE-ELM predictive models. Similar observation can be investigated using different samples of rare-earth transition metal-based double perovskite ceramics. The weights associated with the SE-ELM and SM-ELM predictive models are contained in the Appendix A in case of further investigation with newly synthesized or existing on rare-earth transition metal-based double perovskite ceramics.
5. Conclusions
Magnetic transition temperature of E2TMO6 rare-earth transition metal-based double perovskite ceramics is modeled through genetically hybridized support vector regression (GEN-SVR) and extreme learning machine (ELM) intelligent algorithms. The developed predictive models include sine activation function-based ELM (SE-ELM), sigmoid activation function-based ELM (SM-ELM) and GEN-SVR models. The performance of the predictive models was evaluated and assessed using root mean square error (RMSE), correlation coefficient (CC), and mean absolute error (MAE) performance metrics. For the testing samples of double perovskite ceramics, SE-ELM outperforms the SM-ELM predictive model, with an improvement of 26.6% (using CC metric), 53.3% (using RMSE metric), and 51.6% (using MAE metric). SE-ELM predictive model outperforms GEN-SVR model with superiority of 6.3% (using RMSE metric) and 15.7% (using MAE metric). Similarly, the GEN-SVR predictive model performs better than the SM-ELM model with enhancement of 23.4% (using CC metric), 50.1% (using RMSE metric), and 42.6% (using MAE metric). The influence of magnetic field on magnetic transition temperature was investigated for Ho2CuMnO6 and Tm2FeCrO6 ceramics. The developed predictive models are only limited to magnetic transition temperature prediction of E2TMO6 rare-earth transition metal-based double perovskite ceramics. The demonstrated precision of the developed predictive models coupled with the established magnetic field dependence on magnetic transition temperature is crucial in designing E2TMO6 double perovskite ceramics for several cryogenic applications such as magnetic sensors, data storage, spintronics and magnetic refrigeration for addressing global energy crisis.
Funding
This research was funded by the Deanship of Research and Innovation at University of Hafr Al Batin through project number 0169-1446-S.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Acknowledgments
The author is grateful for the continuous support of the University of Hafr Al Batin.
Conflicts of Interest
The author declares no competing interests.
Appendix A

Table A1.
SE-ELM predictive model.
Table A1.
SE-ELM predictive model.
| k | Biases | Output Weight | Magnetic Field Weight | Rare-Earth Weight | Transition Metal Weight | Any Metal Weight |
|---|---|---|---|---|---|---|
| 1 | 0.7225130617 | 1.2427827374 | 0.1148810873 | −0.3055849693 | −0.4482516227 | −0.3552237815 |
| 2 | 0.6849300618 | −1.2434195665 | 0.5617067582 | 0.9311123273 | −0.6659882046 | −0.3743215913 |
| 3 | 0.1373017009 | −0.9468194910 | −0.7209497397 | 0.6701749553 | 0.1015746494 | 0.5451241719 |
| 4 | 0.3599920346 | −0.8540009678 | 0.9754589655 | 0.6552374364 | 0.6345787698 | 0.7214028533 |
| 5 | 0.7907223920 | −1.7162123937 | 0.5423318793 | 0.3483318196 | −0.6136811884 | 0.9418167148 |
| 6 | 0.5750831796 | −0.1828785703 | −0.0829940562 | −0.9131051465 | −0.9170666451 | −0.1276684793 |
| 7 | 0.7662664029 | −0.1886235946 | −0.3753636682 | 0.5743482016 | 0.5065171562 | 0.7923093773 |
| 8 | 0.3746464268 | −2.0139427494 | 0.3628797001 | 0.8929218978 | 0.9170336391 | 0.9389560284 |
| 9 | 0.3788092433 | 1.5966158208 | 0.5453768478 | −0.9265712958 | 0.6234800595 | 0.5056407731 |
| 10 | 0.2536340812 | −2.4636479977 | −0.5706482370 | −0.4988611117 | 0.0145844402 | −0.2040967660 |
| 11 | 0.0851201958 | −1.9694387409 | 0.2371332802 | −0.8610782845 | 0.7489166993 | −0.4903197092 |
| 12 | 0.5709101967 | 0.9993483906 | −0.0777118592 | 0.2285536523 | 0.3535786575 | −0.2811934590 |
| 13 | 0.0961277755 | −0.8102393115 | 0.6526073931 | −0.5661174172 | −0.0803850368 | −0.2983802274 |
| 14 | 0.9619358872 | 0.0098323448 | 0.4677085810 | 0.6354738468 | −0.1657509879 | −0.9582320391 |
| 15 | 0.4707914879 | −0.9885653735 | 0.9540538818 | 0.6839049860 | 0.8879276198 | 0.7799287663 |
| 16 | 0.9907834343 | 0.1539170883 | −0.7996574998 | 0.8301807255 | −0.7243864790 | 0.2819266159 |
| 17 | 0.6678873888 | −1.1401651798 | −0.3234151686 | −0.8743317604 | 0.6950044196 | −0.3578771669 |
| 18 | 0.2376634038 | −2.5425554676 | −0.2767898283 | −0.9726729576 | 0.7707882551 | −0.6746939395 |
| 19 | 0.8323018721 | 1.3888443024 | −0.4830145061 | 0.3207876845 | 0.2593221792 | 0.4063154274 |
| 20 | 0.8194160401 | −0.3749088644 | 0.0116857832 | 0.0526458289 | 0.9834831412 | −0.4806278364 |
| 21 | 0.0971327487 | 2.2993310034 | −0.7055143547 | −0.5006812624 | −0.0324958504 | −0.0889978758 |
| 22 | 0.7127082668 | −0.6617365338 | −0.1490523076 | −0.7719032061 | −0.3058343469 | 0.9576661155 |
| 23 | 0.1340897564 | 1.5865820472 | 0.2140103342 | −0.1862000203 | −0.6480876838 | 0.1971435022 |
| 24 | 0.0908430111 | 0.1061975617 | 0.2004428755 | 0.5649868639 | 0.1986894682 | 0.8913778924 |
| 25 | 0.1763236663 | 1.4488020633 | 0.1456248639 | 0.6091153115 | −0.9922893515 | 0.7853739345 |
| 26 | 0.3369806420 | 0.0170290950 | −0.9517564978 | −0.6518093938 | 0.7986093796 | 0.0718938964 |
| 27 | 0.3993371707 | −1.1988152483 | 0.1083380068 | 0.3303917366 | 0.9758626664 | 0.1973593519 |
| 28 | 0.8156553780 | −1.2920576406 | −0.9893664948 | 0.4878220974 | 0.5938554601 | −0.0111496625 |
| 29 | 0.8616999802 | 0.8958653101 | −0.8782046097 | −0.8199701610 | 0.7457298903 | −0.3736714070 |
| 30 | 0.2959886774 | 1.8906007808 | −0.7107386440 | −0.6714505524 | 0.5855811204 | 0.2868872656 |
| 31 | 0.8027759212 | −0.3547897695 | −0.1767079645 | −0.0553678761 | 0.0374571552 | −0.6203722170 |
| 32 | 0.4577495535 | −1.2054657890 | −0.1451153480 | 0.2015119160 | −0.8250790407 | 0.1787523728 |
| 33 | 0.5550028032 | −0.6662053968 | −0.9912670099 | −0.6222089491 | 0.1131391622 | −0.4404763277 |
| 34 | 0.6299283784 | −0.8174409202 | −0.3841335379 | 0.8541546066 | −0.3748884618 | 0.4725273257 |
| 35 | 0.5235554725 | 0.7602517861 | −0.3363700556 | 0.2798180761 | −0.7516126422 | 0.8595361434 |
| 36 | 0.0424642718 | 1.6497831412 | −0.7371612765 | −0.5793845617 | 0.8957253281 | −0.3219466027 |
| 37 | 0.0915139834 | 0.3941299563 | 0.9751241704 | −0.8004130391 | −0.8693519293 | −0.0690114476 |
| 38 | 0.4281027425 | 0.1463530322 | 0.5421960181 | 0.9561890553 | 0.8029879394 | 0.1257953417 |
| 39 | 0.5275663121 | −1.0685898382 | −0.4911547089 | 0.9272725271 | 0.8448522109 | 0.0587709823 |
| 40 | 0.1603795738 | 0.9283264592 | 0.1849563719 | −0.3475082642 | 0.3965291135 | 0.3069042295 |
| 41 | 0.4305470222 | 0.4131597378 | −0.5995995543 | 0.7244229740 | −0.8321645532 | 0.9202493589 |
| 42 | 0.2068522910 | 0.2696125287 | −0.3370570009 | −0.4464422039 | −0.2413942285 | −0.4854087816 |
| 43 | 0.4290686318 | 1.1591516256 | 0.7986277631 | 0.3216888986 | 0.2778271091 | −0.4802365031 |
| 44 | 0.4770785345 | −0.9223261932 | 0.6241152260 | −0.7863318218 | −0.5401958250 | 0.3819927897 |
| 45 | 0.4159877211 | −0.5150763561 | 0.6444774872 | 0.2565413758 | 0.6034543746 | 0.0052674018 |
| 46 | 0.1784944762 | −0.8020380120 | −0.2233216232 | 0.1447972871 | 0.8271586672 | −0.6615341834 |
| 47 | 0.1457612105 | 0.3408460247 | 0.0216856667 | −0.5782159655 | −0.6303544444 | −0.6247065050 |
| 48 | 0.4023157185 | 1.6104171411 | −0.7846329653 | −0.4301464485 | 0.5429205965 | −0.5299353098 |
| 49 | 0.6686333493 | 0.6502204882 | 0.7275401732 | −0.1850086859 | −0.5542099123 | 0.5078068078 |
| 50 | 0.0332940348 | −0.1509337001 | 0.4192856973 | 0.6203744041 | −0.9066815615 | 0.6009994086 |
| 51 | 0.5225941328 | 1.1298387384 | 0.6785805165 | 0.5402834724 | −0.4368491298 | −0.3836899471 |
| 52 | 0.3953559593 | 0.5474267870 | −0.8001374564 | 0.4103617836 | 0.9035865611 | 0.1532144541 |
| 53 | 0.7039555868 | 0.4711073221 | −0.4430033100 | 0.8014009430 | 0.8652038311 | −0.5053491936 |

Table A2.
SM-ELM predictive models.
Table A2.
SM-ELM predictive models.
| k | Biases | Output Weight | Magnetic Field Weight | Rare-Earth Weight | Transition Metal Weight | Any Metal Weight |
|---|---|---|---|---|---|---|
| 1 | 0.495103 | 28.212456 | −0.479931 | 0.101244 | −0.964970 | 0.929804 |
| 2 | 0.920545 | −10,466,701.398800 | −0.995693 | −0.802332 | −0.937378 | 0.796610 |
| 3 | 0.550515 | −545,220.272782 | 0.414773 | −0.483924 | −0.059765 | −0.484183 |
| 4 | 0.328303 | −1,933,091,513.243830 | 0.992638 | 0.115491 | 0.983123 | −0.207775 |
| 5 | 0.851456 | −1,930,103,987.452320 | −0.472958 | 0.753577 | −0.760417 | 0.475394 |
| 6 | 0.489914 | −1,929,438,129.932470 | 0.641215 | 0.631100 | −0.459157 | 0.917257 |
| 7 | 0.193632 | −1,929,820,803.582070 | −0.191521 | 0.532867 | 0.518408 | 0.609534 |
| 8 | 0.509486 | 10,591.377512 | 0.981898 | −0.650621 | 0.070397 | −0.790181 |
| 9 | 0.482300 | −41,322,937,065.435100 | −0.933548 | −0.107854 | 0.199715 | −0.307776 |
| 10 | 0.927984 | −5,547,088,752.814350 | 0.539871 | 0.902726 | −0.790297 | −0.841089 |
| 11 | 0.923499 | 6.321526 | −0.499757 | −0.480659 | −0.217418 | −0.734662 |
| 12 | 0.236260 | 11,588.533673 | −0.288171 | −0.041518 | 0.221237 | −0.024587 |
| 13 | 0.516165 | 11,397,360.963912 | 0.517438 | 0.783815 | −0.822271 | −0.810507 |
| 14 | 0.862271 | −1,924,164,276.895450 | −0.438467 | 0.981014 | −0.141672 | −0.635907 |
| 15 | 0.903994 | −697,562.494739 | 0.243786 | −0.856419 | 0.403565 | 0.977871 |
| 16 | 0.071308 | −1,929,801,307.588630 | 0.522076 | 0.620839 | −0.272625 | 0.421814 |
| 17 | 0.498830 | −0.000016 | 0.404737 | −0.443972 | −0.184315 | −0.419679 |
| 18 | 0.954388 | −1,929,801,307.589110 | 0.219814 | 0.590575 | 0.496875 | 0.701237 |
| 19 | 0.262015 | −1,929,801,307.589120 | −0.852440 | 0.846436 | −0.187352 | 0.430702 |
| 20 | 0.881432 | −1,408,516.015777 | −0.456174 | 0.606453 | −0.663270 | 0.102670 |
| 21 | 0.990681 | −1,929,801,307.589120 | −0.334289 | 0.504171 | 0.138129 | 0.352268 |
| 22 | 0.003085 | −1,929,801,307.589120 | −0.222435 | 0.446963 | 0.927462 | 0.161070 |
| 23 | 0.546374 | −1,929,801,307.589120 | 0.575198 | 0.573692 | 0.760851 | −0.637897 |
| 24 | 0.213634 | −1,929,801,307.589120 | −0.563331 | −0.285640 | 0.359468 | 0.799460 |
| 25 | 0.174239 | 0.000000 | −0.046091 | −0.827885 | −0.630638 | 0.562965 |
| 26 | 0.641141 | −21,629,467.263229 | 0.053857 | −0.277972 | 0.988591 | −0.321922 |
| 27 | 0.119745 | −35,206,996.791366 | 0.787812 | −0.627138 | 0.788610 | −0.526778 |
| 28 | 0.199852 | −50.706935 | 0.505250 | 0.049929 | −0.671512 | 0.644013 |
| 29 | 0.410902 | 1.502535 | −0.944841 | −0.306882 | −0.806581 | 0.548474 |
| 30 | 0.447623 | 0.819332 | 0.631349 | 0.366138 | −0.584833 | −0.657705 |
| 31 | 0.689286 | 0.000000 | 0.405988 | −0.856346 | 0.352394 | −0.250506 |
| 32 | 0.772646 | −895,325,993.235744 | 0.053254 | 0.007612 | −0.338845 | 0.799921 |
| 33 | 0.209038 | −1,929,801,307.589120 | 0.914569 | 0.790592 | −0.339547 | 0.188207 |
| 34 | 0.595910 | −1,929,801,307.589120 | −0.875421 | 0.703366 | −0.195368 | −0.008984 |
| 35 | 0.738968 | −0.000009 | −0.991784 | −0.960065 | 0.925270 | −0.468429 |
| 36 | 0.590238 | 0.000000 | 0.520370 | −0.603955 | −0.341003 | −0.313557 |
| 37 | 0.950994 | −0.301471 | 0.927915 | −0.438877 | −0.296218 | 0.817231 |
| 38 | 0.108907 | 7,832,794.611025 | 0.643694 | 0.347742 | 0.006215 | −0.802348 |
| 39 | 0.967554 | −1,929,801,307.589120 | 0.062504 | 0.991729 | 0.960567 | 0.426048 |
| 40 | 0.528661 | −1,929,801,307.589120 | −0.827708 | −0.447798 | 0.637542 | 0.932061 |
| 41 | 0.034482 | 45,519,425,253.511100 | 0.392963 | 0.921239 | −0.814654 | −0.048659 |
| 42 | 0.066202 | −149,341.524572 | −0.304685 | −0.002606 | −0.273450 | 0.136545 |
| 43 | 0.041879 | 0.000000 | 0.371048 | 0.190920 | −0.762302 | −0.430662 |
| 44 | 0.302667 | −12.302782 | 0.560988 | 0.232797 | 0.677680 | −0.872136 |
| 45 | 0.340062 | −89,457,091.390429 | 0.492860 | 0.795073 | −0.921520 | 0.157988 |
| 46 | 0.408860 | −1,929,801,307.589120 | 0.431660 | 0.165800 | 0.587793 | 0.419660 |
| 47 | 0.038721 | −7,847,081,357.644930 | 0.215880 | −0.741172 | 0.871389 | 0.568222 |
| 48 | 0.883392 | −1,929,801,307.589120 | 0.609993 | 0.432708 | 0.726688 | 0.079436 |
| 49 | 0.227191 | −55,056,957.589018 | 0.039576 | −0.540297 | 0.901206 | −0.499696 |
| 50 | 0.621551 | 208.011219 | −0.668210 | −0.060474 | 0.980425 | −0.677664 |
| 51 | 0.702999 | −277,631,017,251.814000 | 0.194818 | 0.113756 | 0.268420 | −0.863770 |
| 52 | 0.981236 | −1,929,801,307.589120 | 0.651614 | 0.092626 | 0.152455 | 0.683079 |
References
- Owolabi, T.O. Modeling magnetocaloric effect of doped EuTiO3 perovskite for cooling technology using swarm intelligent based support vector regression computational method. Mater. Today Commun. 2023, 36, 106688. [Google Scholar] [CrossRef]
- Tian, S.; Phan, M.; Yu, S.; Hwi, N. Magnetocaloric effect in a La0.7Ca0.3MnO3 single crystal. Phys. B 2003, 327, 221–224. [Google Scholar] [CrossRef]
- Ayadi, F.; Ammar, S.; Nowak, S.; Cheikhrouhou-Koubaa, W.; Regaieg, Y.; Koubaa, M.; Monnier, J.; Sicard, L. Importance of the synthesis and sintering methods on the properties of manganite ceramics: The example of La0.7Ca0.3MnO3. J. Alloys Compd. 2018, 759, 52–59. [Google Scholar] [CrossRef]
- Li, L.; Yan, M. Recent progresses in exploring the rare earth based intermetallic compounds for cryogenic magnetic refrigeration. J. Alloys Compd. 2020, 823, 153810. [Google Scholar] [CrossRef]
- Ji, R.; Du, Y.; Na, X.; Wang, X.; Li, L. Investigation of the structural and cryogenic magnetic properties in Gd2CrCoO6 oxide. Inorg. Chem. Commun. 2025, 174, 113964. [Google Scholar] [CrossRef]
- Hamad, M.A.; Hemeda, O.M.; Alamri, H.R.; Mohamed, A.M. Extremely relative cooling power of Cu0.35Zn0.65Fe2O4. Phys. Lett. A 2021, 394, 127204. [Google Scholar] [CrossRef]
- Li, L.; Yi, Y.; Su, K.; Qi, Y.; Huo, D.; Pöttgen, R. Magnetic properties and large magnetocaloric effect in Ho2Cu2In and Ho2Au2In compounds. J. Mater. Sci. 2016, 51, 5421–5426. [Google Scholar] [CrossRef]
- Hcini, F.; Hcini, S.; Almoneef, M.M.; Houcine, M.; Alshammari, M.S.; Mallah, A.; Zemni, S.; Lefi, N.; Bouazizi, M.L. Thermal, microstructural, optical, magnetic and magnetocaloric studies for Ni0.5Mn0.5Cr2O4 chromite spinel prepared using sol-gel method. J. Mol. Struct. 2021, 1243, 130769. [Google Scholar] [CrossRef]
- Laouyenne, M.R.; Baazaoui, M.; Mahjoub, S.; Cheikhrouhou-koubaa, W. Enhanced magnetocaloric effect with the high tunability of bismuth in La0.8Na0.2Mn1−xBixO3 (0≤x≤0.06) perovskite manganites. J. Alloy. Compd. 2017, 720, 212–220. [Google Scholar] [CrossRef]
- Thaljaoui, R.; Pękała, M.; Fagnard, J.-F.; Vanderbemden, P. Effect of Ag substitution on structural, magnetic and magnetocaloric properties of Pr0.6Sr0.4–xAgxMnO3 manganites. J. Rare Earths 2017, 35, 875–882. [Google Scholar] [CrossRef]
- Kesarwani, R.; Khanal, S.; Zacek, M.; Veverka, M.; Varade, V.; Dolezal, P.; Horak, L.; Holy, V.; Kalbac, M.; Vejpravova, J. Investigation of temperature-dependent structural and magnetic phase transitions in CrCl3 nanocrystals. J. Alloys Compd. 2025, 1027, 180468. [Google Scholar] [CrossRef]
- Lee, C.G.; Nallathambi, V.; Kang, T.H.; Aota, L.S.; Reichenberger, S.; El-Zoka, A.A.; Choi, P.P.; Gault, B.; Kim, S.H. Magnetocaloric effect of Fe47.5Ni37.5Mn15 bulk and nanoparticles for room temperature magnetic refrigeration. J. Alloys Compd. 2025, 1036, 181743. [Google Scholar] [CrossRef]
- Jaballah, H.; Charbonnier, V.; Bessais, L.; Mliki, N. Investigation of spin reorientation and magnetocaloric behavior in PrCo5−xCux compounds. Mater. Res. Bull. 2023, 165, 112326. [Google Scholar] [CrossRef]
- Jebathew, A.J.; Karunakaran, M.; Arun, K.D.; Valanarasu, S.; Ganesh, V.; Shkir, M.; Alfaify, S.; Kathalingam, A. Physica B: Condensed Matter Effect of novel Nd3+ doping on physical properties of nebulizer spray pyrolysis fabricated ZnS thin films for optoelectronic technology. Phys. B Phys. Condens. Matter. 2019, 572, 109–116. [Google Scholar] [CrossRef]
- Zhou, X.; Zhou, Y.; Zhou, L.; Wei, J.; Wu, J.; Yao, D. Effect of Gd and La doping on the structure, optical and magnetic properties of NiZnCo ferrites. Ceram. Int. 2019, 45, 6236–6242. [Google Scholar] [CrossRef]
- Almessiere, M.A.; Güner, S.; Slimani, Y.; Baykal, A.; Shirsath, S.E.; Korkmaz, A.D.; Badar, R.; Manikandan, A. Investigation on the structural, optical, and magnetic features of Dy3+ and Y3+ co-doped Mn0.5Zn0.5Fe2O4 spinel ferrite nanoparticles. J. Mol. Struct. 2022, 1248, 131412. [Google Scholar] [CrossRef]
- Shamsah, S.M.I. Modeling of Magnetocaloric Effect in A2B′BO6 Transition Metal Double Perovskite-Based Oxides for Cooling Applications Using Random Forest and Hybrid Support Vector Regression Intelligent Methods. J. Mater. Eng. Perform. 2025, 16, 1–12. [Google Scholar] [CrossRef]
- Raffah, B.M.; Owolabi, T.O.; Latif, M.B.; Al-Hadeethi, Y.; Alruqi, A.B.; Jammal, N.H. Modeling refrigeration cooling power of R2TMO6 oxides for green magnetic cooling applications using intelligent learning computational methods. Mater. Today Commun. 2025, 44, 111943. [Google Scholar] [CrossRef]
- Jia, Y.; Wang, Q.; Qi, Y.; Li, L. Multiple magnetic phase transitions and magnetocaloric effect in double perovskites R2NiMnO6 (R = Dy, Ho, and Er). J. Alloys Compd. 2017, 726, 1132–1137. [Google Scholar] [CrossRef]
- Shinde, K.P.; Hwang, C.; Manawan, M.; Choi, Y.; Park, S.; Jo, Y.; Lee, S. Magnetocaloric effect and Griffiths phase analysis in a nanocrystalline Ho2NiMnO6 and Ho2CoMnO6 double perovskite. RSC Adv. 2023, 13, 9099–9108. [Google Scholar] [CrossRef]
- Zhao, J.; Liu, X.; Kan, X.; Liu, C.; Wang, W.; Hu, J.; Lv, Q.; Huang, J.; Shazeda, M. Investigating the structural, magnetic, magnetocaloric and critical behavior. Ceram. Int. 2021, 47, 7906–7917. [Google Scholar] [CrossRef]
- Fortas, N.; Belkahla, A.; Ouyahia, S.; Dhahri, J.; Hlil, E.K.; Taibi, K. Effect of Ni substitution on the structural, magnetic and magnetocaloric properties of Zn0.5−xNixMg0.5Fe2O4 (x = 0, 0.125 and 0.250) ferrites. Solid State Sci. 2020, 101, 106137. [Google Scholar] [CrossRef]
- Sandoval, M.V.; Durán, S.; Prada, A.; Pirovano, C.; Gardoll, O.; Roussel, P.; Gauthier, G.H. Synthesis and preliminary study of NdxAE2−xMnO4±δ (AE: Ca, Sr) for symmetrical SOFC electrodes. Solid State Ion. 2018, 317, 194–200. [Google Scholar] [CrossRef]
- Hamad, M.A.; Alamri, H.R. Room temperature magnetocaloric effect of Ce0.65Mg0.35Co3. J. Mater. Res. Technol. 2022, 17, 2670–2674. [Google Scholar] [CrossRef]
- Zhong, W.; Au, C.-T.; Du, Y.-W. Review of magnetocaloric effect in perovskite-type oxides. Chin. Phys. B 2013, 22, 057501. [Google Scholar] [CrossRef]
- Xie, H.; Su, W.; Lu, H.; Mo, Z.; Wang, D.; Sun, H.; Tian, L.; Gao, X.; Li, Z.; Shen, J. Enhanced low-field magnetocaloric effect in Nb and Al co-substituted EuTiO3 compounds. J. Mater. Sci. Technol. 2022, 118, 128–135. [Google Scholar] [CrossRef]
- Crmno, R.E.; La, R.E.; Jia, Y.; Cheng, Y.; Wang, H.; Zhang, Z.; Li, L. Magnetocaloric properties and critical behavior in double perovskite. Ceram. Int. 2020, 46, 25043–25049. [Google Scholar] [CrossRef]
- Wang, H.; Lu, G.; Tan, W.; Li, J.; Su, K.; Huang, S.; Yang, L.; Wang, H. Giant Negative Temperature Coefficient of Resistance and Magnetotransport in Antiferromagnetic CaMnO3. J. Low Temp. Phys. 2025, 012345678. [Google Scholar] [CrossRef]
- Jia, Y.; Wang, Q.; Wang, P.; Li, L. Structural, magnetic and magnetocaloric properties in R2CoMnO6 (R = Dy, Ho, and Er). Ceram. Int. 2017, 43, 15856–15861. [Google Scholar] [CrossRef]
- Chakraborty, T.; Nhalil, H.; Yadav, R.; Wagh, A.A.; Elizabeth, S. Magnetocaloric properties of R2NiMnO6 (R = Pr, Nd, Tb, Ho and Y) double perovskite family. J. Magn. Magn. Mater. 2017, 428, 59–63. [Google Scholar] [CrossRef]
- Chen, W.; Na, Y.; Chen, F.; Zhang, Y. Cryogenic magnetic and magnetocaloric properties in anhydrous rare-earth sulfate RE2(SO4)3 (RE = Tb, Dy, Ho, Er). Cryogenics 2025, 146, 104012. [Google Scholar] [CrossRef]
- Sabzekar, M.; Hasheminejad, S.M.H. Robust regression using support vector regressions. Chaos Solitons Fractals 2021, 144, 110738. [Google Scholar] [CrossRef]
- Owolabi, T.O.; Akande, K.O.; Olatunji, S.O. Development and validation of surface energies estimator (SEE) using computational intelligence technique. Comput. Mater. Sci. 2015, 101, 143–151. [Google Scholar] [CrossRef]
- Khan, A.; Shamsi, M.H.; Choi, T.S. Correlating dynamical mechanical properties with temperature and clay composition of polymer-clay nanocomposites. Comput. Mater. Sci. 2009, 45, 257–265. [Google Scholar] [CrossRef]
- Tokuyama, H.; Mori, H.; Hamaguchi, R.; Kato, G. Prediction of the lower critical solution temperature of poly(N-isopropylacrylamide-co-methoxy triethyleneglycol acrylate) in aqueous salt solutions using support vector regression. Chem. Eng. Sci. 2021, 231, 116325. [Google Scholar] [CrossRef]
- Chou, J.-S.; Pham, A.-D. Enhanced artificial intelligence for ensemble approach to predicting high performance concrete compressive strength. Constr. Build. Mater. 2013, 49, 554–563. [Google Scholar] [CrossRef]
- Lou, I.; Xie, Z.; Ung, W.K.; Mok, K.M. Integrating Support Vector Regression with Particle Swarm Optimization for numerical modeling for algal blooms of freshwater. Appl. Math. Model. 2015, 39, 5907–5916. [Google Scholar] [CrossRef]
- Owolabi, T.O. Determination of the Velocity of Detonation of Primary Explosives using Genetically Optimized Support Vector Regression. Propellants, Explosives, Pyrotechnics. 2019, 12, 1282–1292. [Google Scholar] [CrossRef]
- Obadawo, B.S.; Oyeneyin, O.E.; Anifowose, M.M.; Fagbohungbe, K.H.; Amoko, J.S. QSAR Evaluation of C-8-Tert-Butyl Substituted as Potent Anti-enterovirus Agents. Sci. Lett. 2020, 8, 28–35. [Google Scholar]
- Katoch, S.; Chauhan, S.S.; Kumar, V. A review on genetic algorithm: Past, present, and future. Multimed. Tools Appl. 2021, 80, 8091–8126. [Google Scholar] [CrossRef]
- Alqahtani, A. Single Hidden Layer Intelligent Approach to Modeling Relative Cooling Power of Rare-Earth-Transition-Metal-Based Refrigerants for Sustainable Magnetic Refrigeration Application. Sustainability 2024, 16, 1542. [Google Scholar] [CrossRef]
- Oyeneyin, O.E.; Obadawo, B.S.; Olanrewaju, A.A.; Owolabi, T.O.; Gbadamosi, F.A.; Ipinloju, N.; Modamori, H.O. Predicting the bioactivity of 2-alkoxycarbonylallyl esters as potential antiproliferative agents against pancreatic cancer (MiaPaCa-2) cell lines: GFA-based QSAR and ELM-based models with molecular docking. J. Genet. Eng. Biotechnol. 2021, 19, 38. [Google Scholar] [CrossRef]
- Liu, X.; Ge, Q.; Chen, X.; Li, J.; Chen, Y. Extreme learning machine for multivariate reservoir characterization. J. Pet. Sci. Eng. 2021, 205, 108869. [Google Scholar] [CrossRef]
- Valipour, A.; Shirgahi, H. Estimation of rip density on intermediate beaches using an extreme learning machine model. Reg. Stud. Mar. Sci. 2022, 52, 102332. [Google Scholar] [CrossRef]
- Parsa, P.; Naderpour, H. Shear strength estimation of reinforced concrete walls using support vector regression improved by Teaching–learning-based optimization, Particle Swarm optimization, and Harris Hawks Optimization algorithms. J. Build. Eng. 2021, 44, 102593. [Google Scholar] [CrossRef]
- Murillo-escobar, J.; Sepulveda-suescun, J.P.; Correa, M.A.; Orrego-metaute, D. Urban Climate Forecasting concentrations of air pollutants using support vector regression improved with particle swarm optimization: Case study in Aburrá Valley, Colombia. Urban Clim. 2019, 29, 100473. [Google Scholar] [CrossRef]
- Chen, R.; Liang, C.Y.; Hong, W.C.; Gu, D.X. Forecasting holiday daily tourist flow based on seasonal support vector regression with adaptive genetic algorithm. Appl. Soft Comput. 2015, 26, 435–443. [Google Scholar] [CrossRef]
- Akinpelu, A.A.; Ali, M.E.; Owolabi, T.O.; Johan, M.R.; Saidur, R.; Olatunji, S.O.; Chowdbury, Z. A support vector regression model for the prediction of total polyaromatic hydrocarbons in soil: An artificial intelligent system for mapping environmental pollution. Neural Comput. Appl. 2020, 32, 14899–14908. [Google Scholar] [CrossRef]
- Dong, Z.; Yang, D.; Reindl, T.; Walsh, W.M. A novel hybrid approach based on self-organizing maps, support vector regression and particle swarm optimization to forecast solar irradiance. Energy 2015, 82, 570–577. [Google Scholar] [CrossRef]
- Akomolafe, O.; Owolabi, T.O.; Rahman, M.A.A.; Kechik, M.M.A.; Yasin, M.N.M.; Souiyah, M. Modeling superconducting critical temperature of 122-iron-based pnictide intermetallic superconductor using a hybrid intelligent computational method. Materials 2021, 14, 4604. [Google Scholar] [CrossRef]
- Hamdi, T.; Ben Ali, J.; Di Costanzo, V.; Fnaiech, F.; Moreau, E.; Ginoux, J.M. Accurate prediction of continuous blood glucose based on support vector regression and differential evolution algorithm. Biocybern. Biomed. Eng. 2018, 38, 362–372. [Google Scholar] [CrossRef]
- Whitley, D. A genetic algorithm tutorial. Statistics and Computing 1994, 4, 65–85. [Google Scholar] [CrossRef]
- Khozani, Z.S.; Bonakdari, H.; Zaji, A.H. Application of a genetic algorithm in predicting the percentage of shear force carried by walls in smooth rectangular channels. Measurement 2016, 87, 87–98. [Google Scholar] [CrossRef]
- Bian, X.Q.; Han, B.; Du, Z.M.; Jaubert, J.N.; Li, M.J. Integrating support vector regression with genetic algorithm for CO2-oil minimum miscibility pressure (MMP) in pure and impure CO2 streams. Fuel 2016, 182, 550–557. [Google Scholar] [CrossRef]
- Wang, Y.; Wei, C. Design optimization of office building envelope based on quantum genetic algorithm for energy conservation. J. Build. Eng. 2021, 35, 102048. [Google Scholar] [CrossRef]
- Yan, C.; Qi, J.; Ma, J.; Tang, H.; Zhang, T.; Li, H. Determination of carbon and sulfur content in coal by laser induced breakdown spectroscopy combined with kernel-based extreme learning machine. Chemom. Intell. Lab. Syst. 2017, 167, 226–231. [Google Scholar] [CrossRef]
- Olatunji, S.O.; Selamat, A.; Raheem, A.A.A. Modeling Permeability Prediction Using Extreme Learning Machines. In Mathematical/Analytical Modelling and Computer Simulation (AMS), 2010 Fourth Asia International Conference; IEEE: Piscataway, NJ, USA, 2010; pp. 29–33. [Google Scholar] [CrossRef]
- Oyeneyin, O.E.; Obadawo, B.S.; Metibemu, D.S.; Owolabi, T.O.; Olanrewaju, A.A.; Orimoloye, S.M.; Ipinloju, N.; Olubosede, O. An Exploration of the Antiproliferative Potential of Chalcones and Dihydropyrazole Derivatives in Prostate Cancer via Androgen Receptor: Combined QSAR, Machine Learning, and Molecular Docking Techniques. Phys. Chem. Res. 2022, 10, 211–223. [Google Scholar] [CrossRef]
- Wang, Y.; Cao, F.; Yuan, Y. A study on effectiveness of extreme learning machine. Neurocomputing 2011, 74, 2483–2490. [Google Scholar] [CrossRef]
- Zhu, Q.-Y.; Qin, A.K.; Suganthan, P.N.; Huang, G.-B. Evolutionary extreme learning machine. Pattern Recognit. 2005, 38, 1759–1763. [Google Scholar] [CrossRef]
- Wu, B.; Guo, D.; Wang, Y.; Zhang, Y. Crystal structure, magnetic properties, and magnetocaloric e ff ect in B-site disordered RE2CrMnO6 (RE = Ho and Er) perovskites. Ceram. Int. 2020, 46, 11988–11993. [Google Scholar] [CrossRef]
- Li, L.; Xu, P.; Ye, S.; Li, Y.; Liu, G.; Huo, D.; Yan, M. Acta Materialia Magnetic properties and excellent cryogenic magnetocaloric performances in B-site ordered RE2ZnMnO6 (RE = Gd, Dy and Ho) perovskites. Acta Mater. 2020, 194, 354–365. [Google Scholar] [CrossRef]
- Dong, Z.; Wang, Z.; Yin, S. Structural, magnetic and cryogenic magneto-caloric properties in RE2FeCrO6 (RE = Er and Tm) compounds. Ceram. Int. 2020, 46, 26632–26636. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, B.; Li, S.; Zhu, J.; Wu, B.; Wang, J.; Ren, Z. Cryogenic magnetic properties and magnetocaloric effects (MCE) in B -site disordered RE2CuMnO6 (RE = Gd, Dy, Ho and Er) double perovskites (DP) compounds. Ceram. Int. 2021, 47, 18205–18212. [Google Scholar] [CrossRef]
- Wu, B.; Zhang, Y.; Guo, D.; Wang, J.; Ren, Z. Structure, magnetic properties and cryogenic magneto-caloric effect (MCE) in RE2FeAlO6 (RE = Gd, Dy, Ho) oxides. Ceram. Int. 2021, 47, 6290–6297. [Google Scholar] [CrossRef]
- Fecoo, H. Nonlinear magnetodielectric and magnetocaloric properties of double. Phys. B Phys. Condens. Matter. 2019, 571, 32–35. [Google Scholar] [CrossRef]
- Dong, Z.; Yin, S. Structural, magnetic and magnetocaloric properties in perovskite RE2FeCoO6 (RE = Er and Gd) compounds. Ceram. Int. 2020, 46, 1099–1103. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).