Gleeble-Simulated Ultra-Fast Cooling Unlocks Strength–Ductility Synergy in Fully Martensitic Ti-6Al-4V
Abstract
1. Introduction
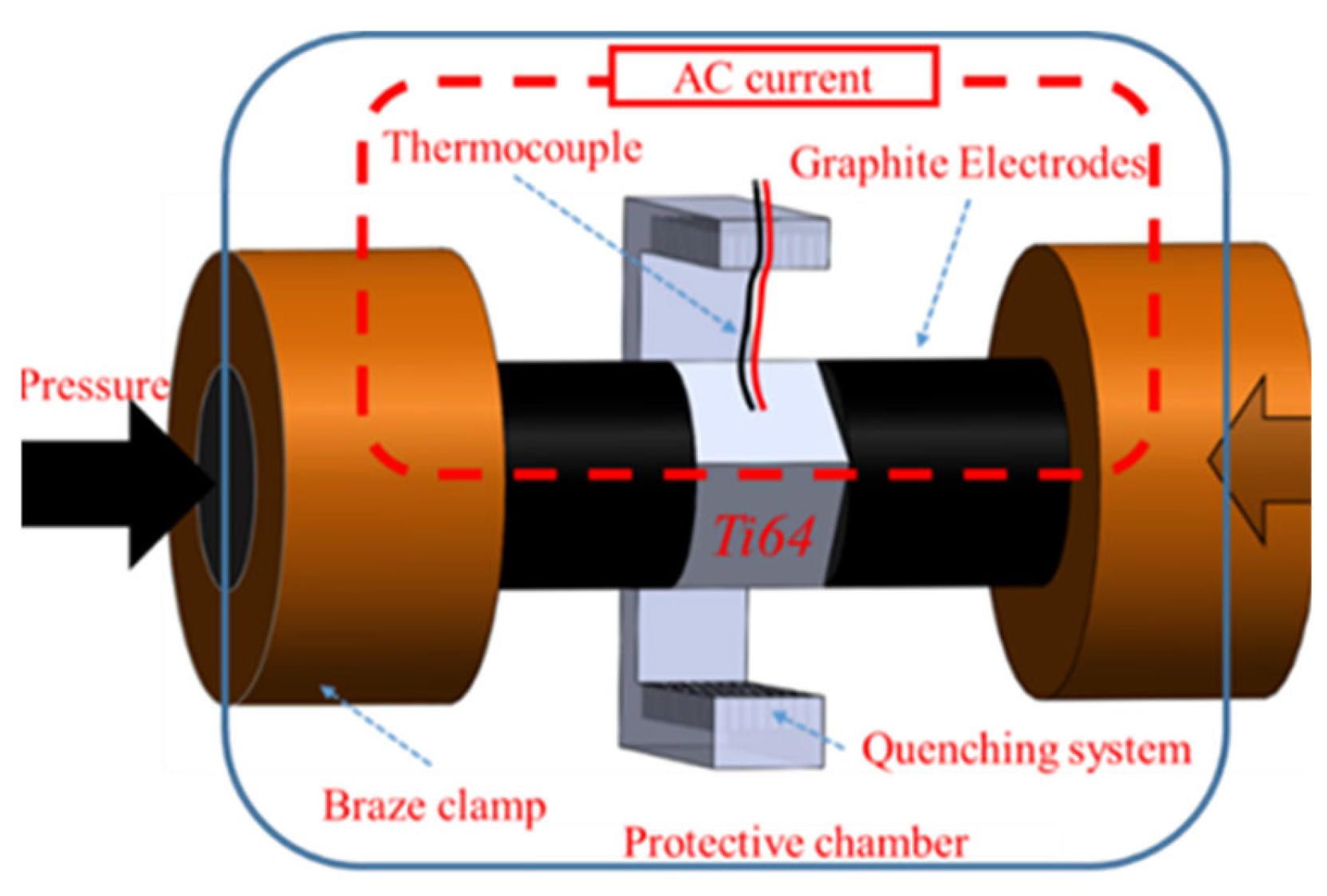
2. Materials and Experimental Procedures
3. Model Descriptions
3.1. FFT Based Elastic-Viscoplastic Self-Consistent Model
3.2. Voce-Type Hardening Law
4. Results
4.1. Experimental Results
4.1.1. Phase and Microstructure Analysis
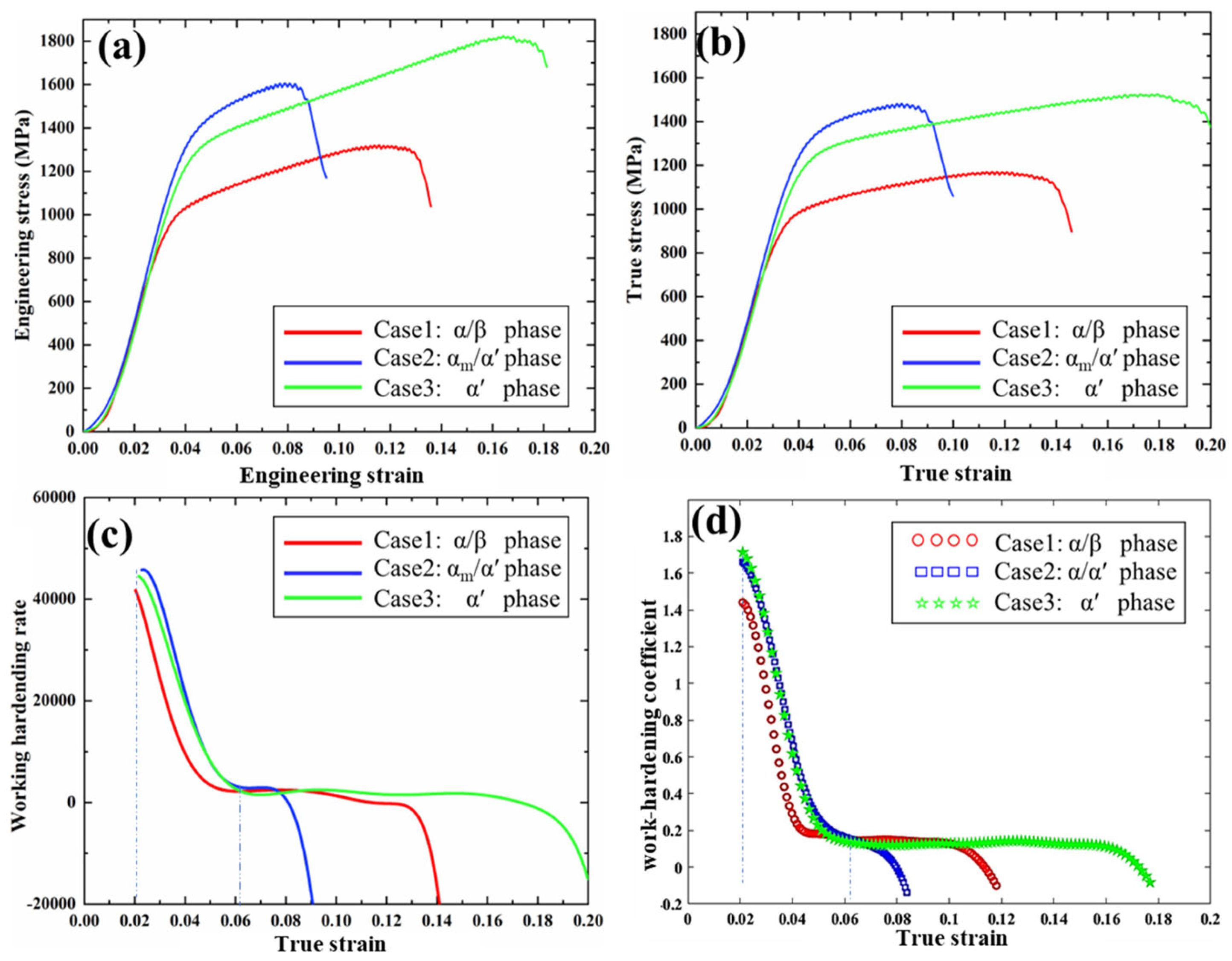
4.1.2. Compression Testing and Work Hardening Behaviors
4.1.3. Fractographic Analyses
4.2. Modeling the Crystal Plasticity of Different Phase Compositions
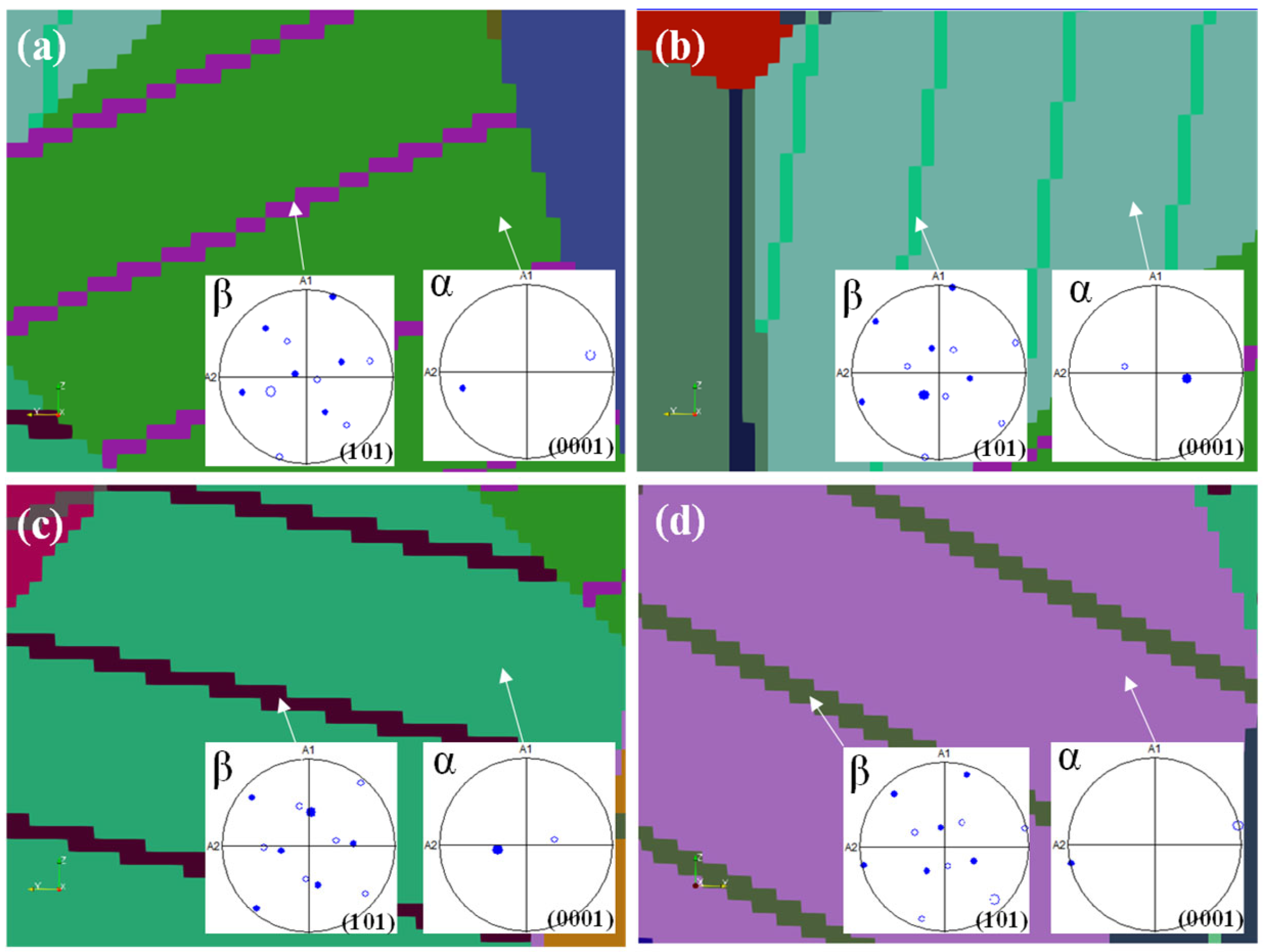
4.2.1. Reconstructed 3D Grain Structures
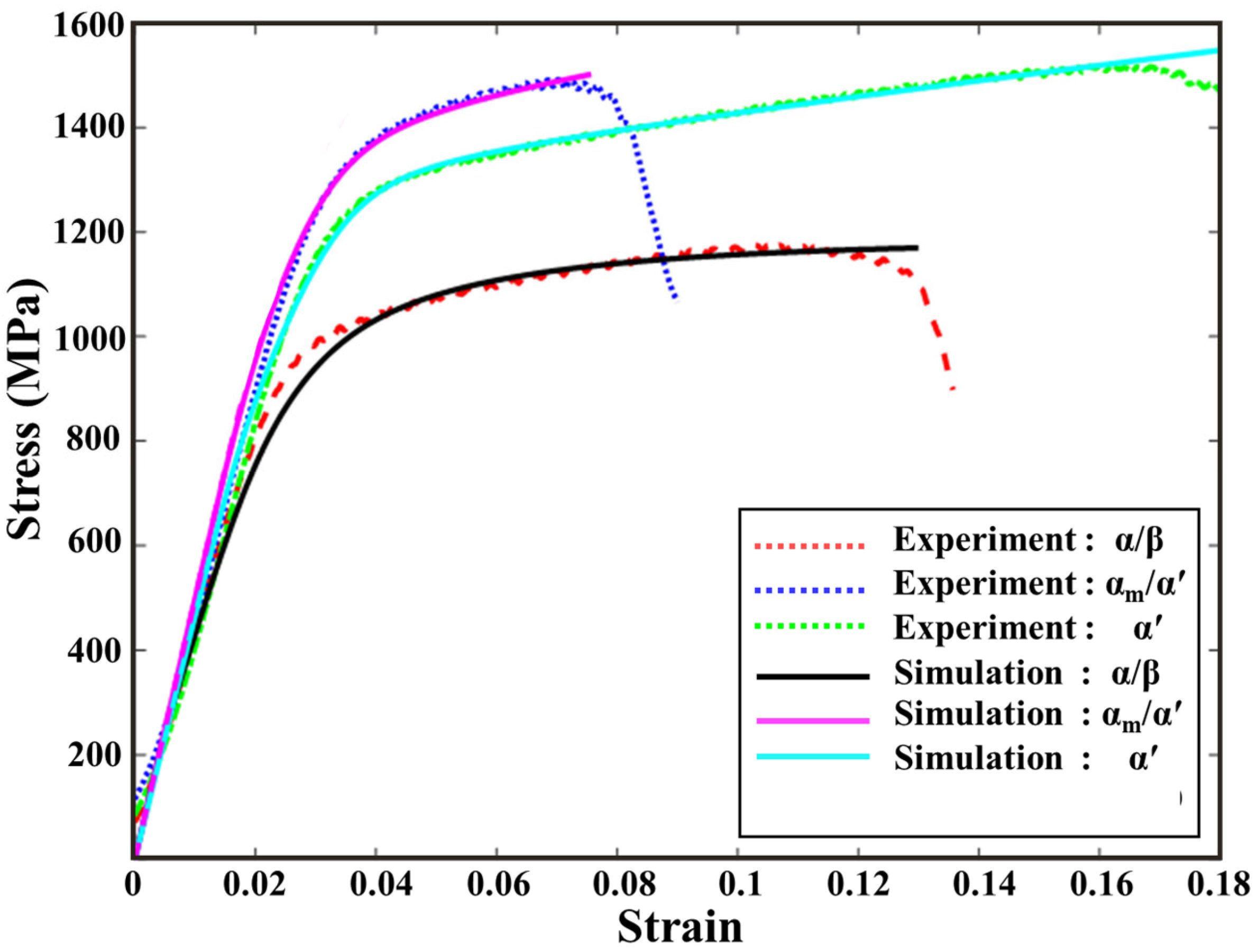
4.2.2. Calibration of Simulation Compression Curves
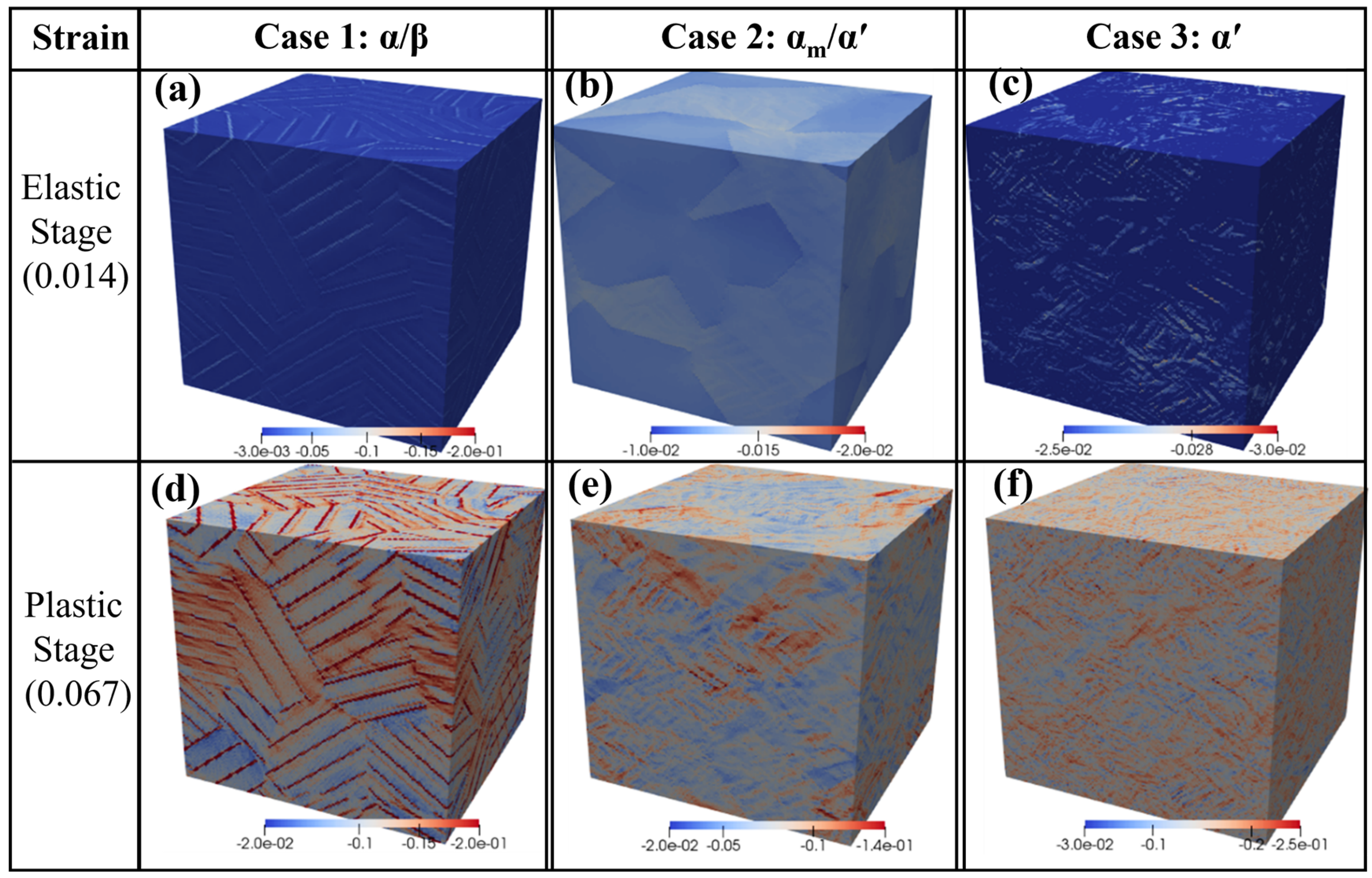
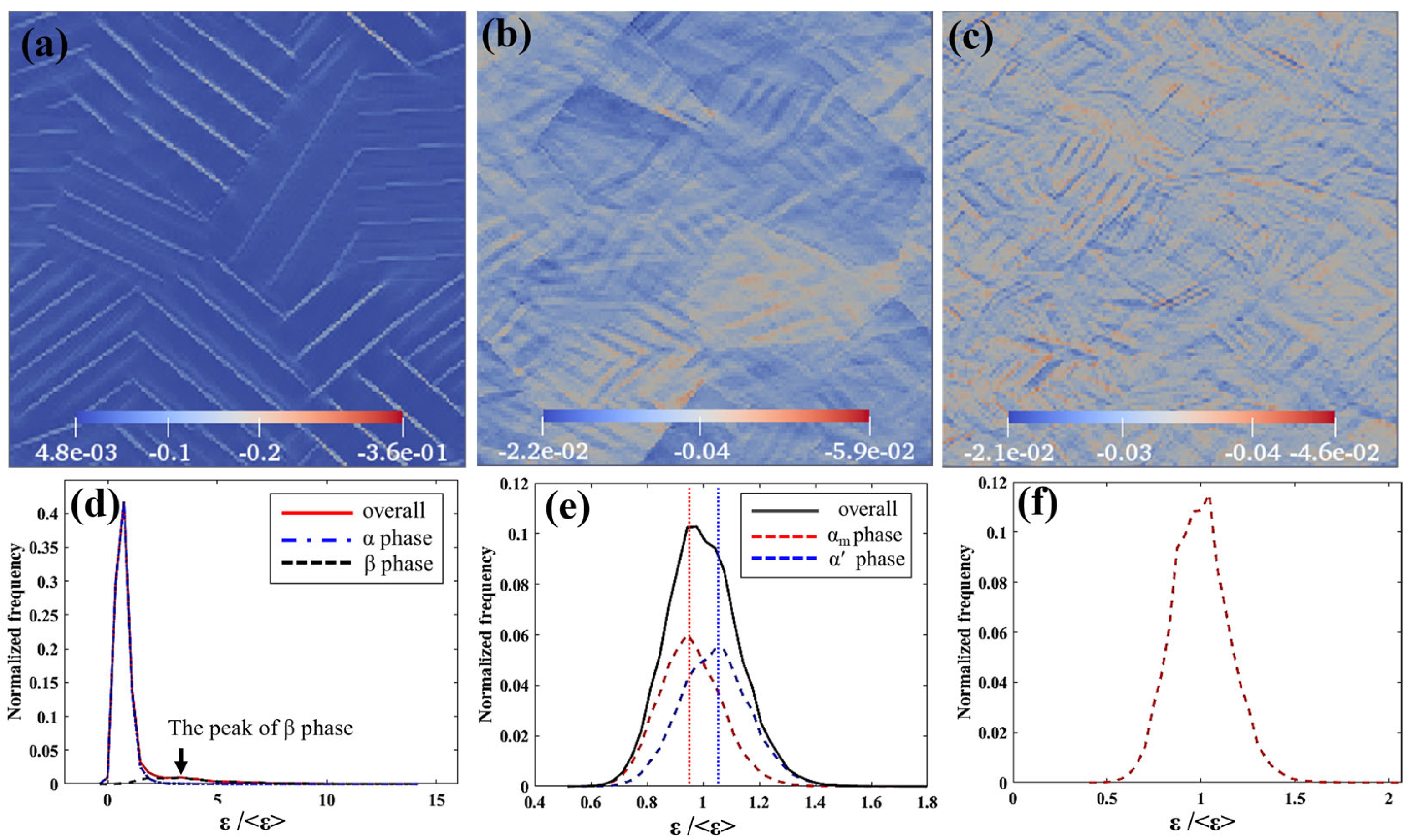
4.2.3. Overall Compressive Strain Field
5. Discussion
5.1. A Quantitative Understanding of the Yield Behaviors for Different Cases
5.2. Potential Mechanisms for the Marked Ductility Improvement in Fully Martensitic Structures
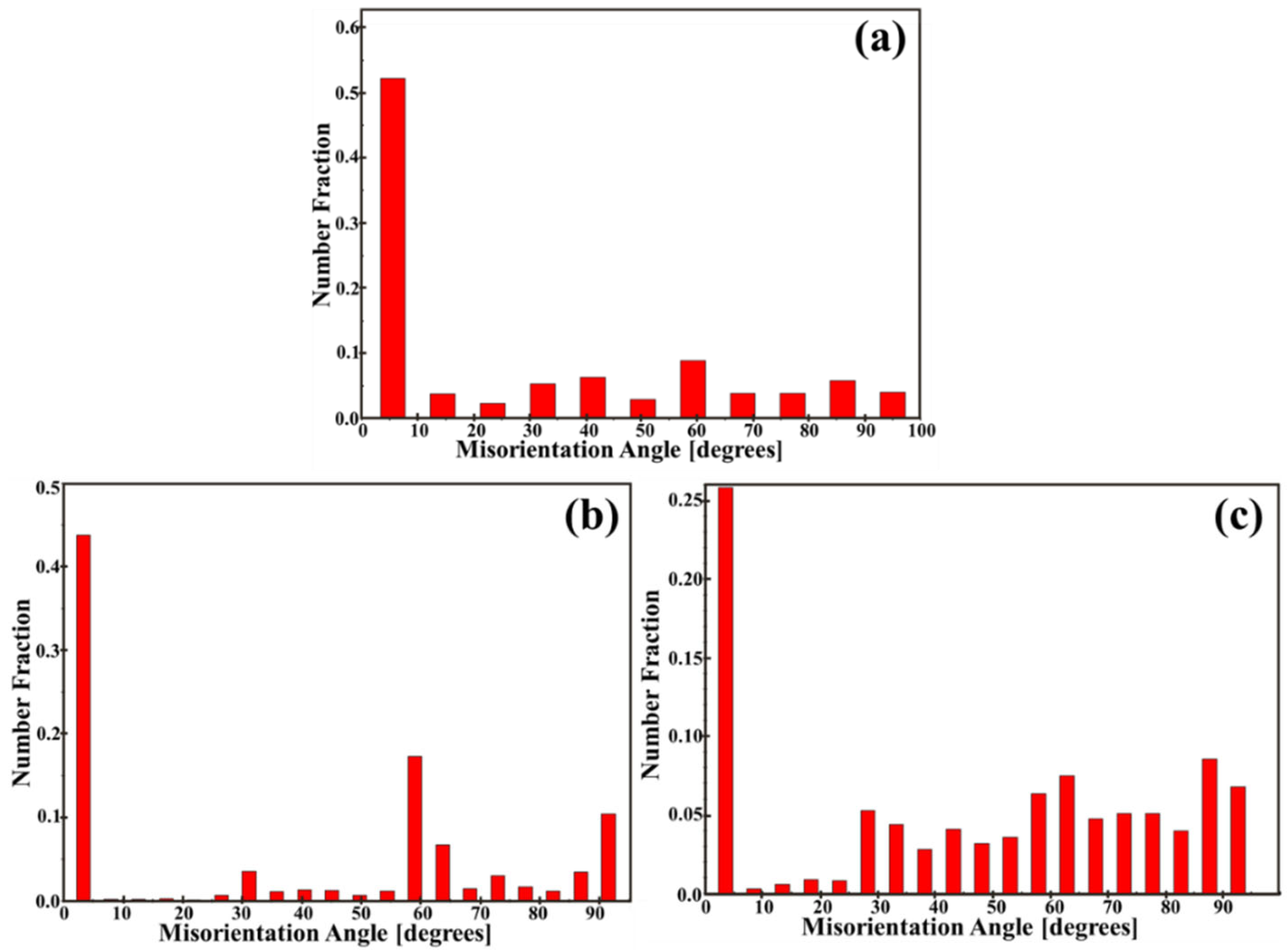
5.2.1. High-Angle Interfaces and Ductility
5.2.2. Stress Triaxiality Factor
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Xiao, Y. Investigations on Microstructure Evolution of Metal Additive Manufacturing by Experiments, Physics-Based and Data-Driven Modeling. Ph.D. Dissertation, University of Michigan, Ann Arbor, MI, USA, 2023. [Google Scholar] [CrossRef]
- Xiao, Y.; Cagle, M.; Mujahid, S.; Liu, P.; Wang, Z.; Yang, W.; Chen, L. A Gleeble-Assisted Study of Phase Evolution of Ti-6Al-4V Induced by Thermal Cycles during Additive Manufacturing. J. Alloys Compd. 2021, 860, 158409. [Google Scholar] [CrossRef]
- Rietema, C.J.; Roehling, J.D.; Smith, W.L.; Bertsch, K.M. Microstructural Control of Additively Manufactured Ti6Al4V via In-Situ Large-Area Laser Annealing. Scr. Mater. 2024, 239, 115823. [Google Scholar] [CrossRef]
- Cui, D.; Zhang, Y.; He, F.; Ma, J.; Zhang, K.; Yang, Z.; Li, J.; Wang, Z.; Kai, J.J.; Wang, J.; et al. Heterogeneous Microstructure of the Bonding Zone and Its Dependence on Preheating in Hybrid Manufactured Ti-6Al-4V. Mater. Res. Lett. 2021, 9, 422–428. [Google Scholar] [CrossRef]
- Wang, C.; Lei, Y.; Li, C. Achieving an Excellent Strength and Ductility Balance in Additive Manufactured Ti-6Al-4V Alloy through Multi-Step High-to-Low-Temperature Heat Treatment. Materials 2023, 16, 6947. [Google Scholar] [CrossRef] [PubMed]
- Bertsch, K.M.; Voisin, T.; Forien, J.B.; Tiferet, E.; Ganor, Y.I.; Chonin, M.; Wang, Y.M.; Matthews, M.J. Critical Differences between Electron Beam Melted and Selective Laser Melted Ti-6Al-4 V. Mater. Des. 2022, 216, 110533. [Google Scholar] [CrossRef]
- Murr, L.E.; Quinones, S.A.; Gaytan, S.M.; Lopez, M.I.; Rodela, A.; Martinez, E.Y.; Hernandez, D.H.; Martinez, E.; Medina, F.; Wicker, R.B. Microstructure and Mechanical Behavior of Ti-6Al-4V Produced by Rapid-Layer Manufacturing, for Biomedical Applications. J. Mech. Behav. Biomed. Mater. 2009, 2, 20–32. [Google Scholar] [CrossRef]
- Thijs, L.; Verhaeghe, F.; Craeghs, T.; Van Humbeeck, J.; Kruth, J.P. A Study of the Microstructural Evolution during Selective Laser Melting of Ti-6Al-4V. Acta Mater. 2010, 58, 3303–3312. [Google Scholar] [CrossRef]
- Ricci, S.; Iannitti, G. Mechanical Behavior of Additive Manufacturing (AM) and Wrought Ti6Al4V with a Martensitic Microstructure. Metals 2024, 14, 1028. [Google Scholar] [CrossRef]
- de Formanoir, C.; Martin, G.; Prima, F.; Allain, S.Y.P.; Dessolier, T.; Sun, F.; Vivès, S.; Hary, B.; Bréchet, Y.; Godet, S. Micromechanical Behavior and Thermal Stability of a Dual-Phase A+α’ Titanium Alloy Produced by Additive Manufacturing. Acta Mater. 2019, 162, 149–162. [Google Scholar] [CrossRef]
- Zafari, A.; Barati, M.R.; Xia, K. Controlling Martensitic Decomposition during Selective Laser Melting to Achieve Best Ductility in High Strength Ti-6Al-4V. Mater. Sci. Eng. A 2019, 744, 445–455. [Google Scholar] [CrossRef]
- Chong, Y.; Bhattacharjee, T.; Yi, J.; Shibata, A.; Tsuji, N. Mechanical Properties of Fully Martensite Microstructure in Ti-6Al-4V Alloy Transformed from Refined Beta Grains Obtained by Rapid Heat Treatment (RHT). Scr. Mater. 2017, 138, 66–70. [Google Scholar] [CrossRef]
- Wang, Z.; Jiang, C.; Liu, P.; Yang, W.; Zhao, Y.; Horstemeyer, M.F.; Chen, L.Q.; Hu, Z.; Chen, L. Uncertainty Quantification and Reduction in Metal Additive Manufacturing. npj Comput. Mater. 2020, 6, 175. [Google Scholar] [CrossRef]
- Xiao, Y.; Wan, Z.; Liu, P.; Wang, Z.; Li, J.; Chen, L. Quantitative Simulations of Grain Nucleation and Growth at Additively Manufactured Bimetallic Interfaces of SS316L and IN625. J. Mater. Process. Technol. 2022, 302, 117506. [Google Scholar] [CrossRef]
- Xiao, Y.; Wang, X.; Yang, W.; Yao, X.X.; Yang, Z.; Lu, Y.; Wang, Z.; Chen, L. Data-Driven Prediction of Future Melt Pool from Built Parts during Metal Additive Manufacturing. Addit. Manuf. 2024, 93, 104438. [Google Scholar] [CrossRef]
- Zhou, H.; Feng, K.; Xiao, Y.; Liu, Y.; Ke, S. Pressure Effects on a Novel W-Mo-Cu Alloy by Large Current Electric Field Sintering: Sintering Behavior, Microstructure and Properties. J. Alloys Compd. 2019, 785, 965–971. [Google Scholar] [CrossRef]
- Zhou, H.; Feng, K.; Liu, Y. Densification, Microstructure, and Properties of W-Mo-Cu Alloys Prepared with Nano-Sized Cu Powders via Large Electric Current Sintering. Adv. Powder Technol. 2022, 33, 103703. [Google Scholar] [CrossRef]
- Feng, K.; Zhou, H.; Xiao, Y.; Liu, Y. Study on the Electric Current Effects on the Microstructure and Properties of W-Mo-Cu Alloy Under the Action of Electric Field. JOM 2023, 75, 780–790. [Google Scholar] [CrossRef]
- Lebensohn, R.A.; Kanjarla, A.K.; Eisenlohr, P. An Elasto-Viscoplastic Formulation Based on Fast Fourier Transforms for the Prediction of Micromechanical Fields in Polycrystalline Materials. Int. J. Plast. 2012, 32, 59–69. [Google Scholar] [CrossRef]
- Chen, L.; Chen, J.; Lebensohn, R.A.; Ji, Y.Z.; Heo, T.W.; Bhattacharyya, S.; Chang, K.; Mathaudhu, S.; Liu, Z.K.; Chen, L.Q. An Integrated Fast Fourier Transform-Based Phase-Field and Crystal Plasticity Approach to Model Recrystallization of Three Dimensional Polycrystals. Comput. Methods Appl. Mech. Eng. 2015, 285, 829–848. [Google Scholar] [CrossRef]
- Ozturk, T.; Rollett, A.D. Effect of Microstructure on the Elasto-Viscoplastic Deformation of Dual Phase Titanium Structures. Comput. Mech. 2018, 61, 55–70. [Google Scholar] [CrossRef]
- Liu, P.W.; Wang, Z.; Xiao, Y.H.; Lebensohn, R.A.; Liu, Y.C.; Horstemeyer, M.F.; Cui, X.Y.; Chen, L. Integration of Phase-Field Model and Crystal Plasticity for the Prediction of Process-Structure-Property Relation of Additively Manufactured Metallic Materials. Int. J. Plast. 2020, 128, 102670. [Google Scholar] [CrossRef]
- Michel, J.C.; Moulinec, H.; Suquet, P. A Computational Method Based on Augmented Lagrangians and Fast Fourier Transforms for Composites with High Contrast. Comput. Model. Eng. Sci. 2000, 1, 79. [Google Scholar] [CrossRef]
- Tome, C.; Canova, G.R.; Kocks, U.F.; Christodoulou, N.; Jonas, J.J. The Relation between Macroscopic and Microscopic Strain Hardening in F.C.C. Polycrystals. Acta Metall. 1984, 32, 1637–1653. [Google Scholar] [CrossRef]
- Lebensohn, R.A.; Tomé, C.N.; Castañeda, P.P. Self-Consistent Modelling of the Mechanical Behaviour of Viscoplastic Polycrystals Incorporating Intragranular Field Fluctuations. Philos. Mag. 2007, 87, 4287–4322. [Google Scholar] [CrossRef]
- Ahmed, T.; Rack, H.J. Phase Transformations during Cooling in A+β Titanium Alloys. Mater. Sci. Eng. A 1998, 243, 206–211. [Google Scholar] [CrossRef]
- Sieniawski, J.; Ziaja, W.; Kubiak, K.; Motyk, M. Microstructure and Mechanical Properties of High Strength Two-Phase Titanium Alloys. In Titanium Alloys-Advances in Properties Control; IntechOpen: London, UK, 2013. [Google Scholar]
- Beladi, H.; Chao, Q.; Rohrer, G.S. Variant Selection and Intervariant Crystallographic Planes Distribution in Martensite in a Ti-6Al-4V Alloy. Acta Mater. 2014, 80, 478–489. [Google Scholar] [CrossRef]
- Tuninetti, V.; Gilles, G.; Milis, O.; Pardoen, T.; Habraken, A.M. Anisotropy and Tension-Compression Asymmetry Modeling of the Room Temperature Plastic Response of Ti-6Al-4V. Int. J. Plast. 2015, 67, 53–68. [Google Scholar] [CrossRef]
- Nagra, J.S.; Brahme, A.; Lévesque, J.; Mishra, R.; Lebensohn, R.A.; Inal, K. A New Micromechanics Based Full Field Numerical Framework to Simulate the Effects of Dynamic Recrystallization on the Formability of HCP Metals. Int. J. Plast. 2019, 125, 210–234. [Google Scholar] [CrossRef]
- Ma, X.; Li, F.; Cao, J.; Li, J.; Sun, Z.; Zhu, G.; Zhou, S. Strain Rate Effects on Tensile Deformation Behaviors of Ti-10V-2Fe-3Al Alloy Undergoing Stress-Induced Martensitic Transformation. Mater. Sci. Eng. A 2018, 710, 1–9. [Google Scholar] [CrossRef]
- Hou, X.; Liu, Z.; Wang, B.; Lv, W.; Liang, X.; Hua, Y. Stress-Strain Curves and Modified Material Constitutive Model for Ti-6Al-4V over Thewide Ranges of Strain Rate and Temperature. Materials 2018, 11, 938. [Google Scholar] [CrossRef]
- Ji, X.; Emura, S.; Min, X.; Tsuchiya, K. Strain-Rate Effect on Work-Hardening Behavior in β-Type Ti-10Mo-1Fe Alloy with TWIP Effect. Mater. Sci. Eng. A 2017, 707, 701–707. [Google Scholar] [CrossRef]
- Zhang, J.; Tan, C.W.; Ren, Y.; Yu, X.D.; Ma, H.L.; Wang, F.C.; Cai, H.N. Adiabatic Shear Fracture in Ti-6Al-4V Alloy. Trans. Nonferrous Met. Soc. China (Engl. Ed.) 2011, 21, 2396–2401. [Google Scholar] [CrossRef]
- Liu, X.; Tan, C.; Zhang, J.; Wang, F.; Cai, H. Correlation of Adiabatic Shearing Behavior with Fracture in Ti-6Al-4V Alloys with Different Microstructures. Int. J. Impact Eng. 2009, 36, 1143–1149. [Google Scholar] [CrossRef]
- Mainprice, D.; Hielscher, R.; Schaeben, H. Calculating Anisotropic Physical Properties from Texture Data Using the MTEX Open-Source Package. Geol. Soc. Spec. Publ. 2011, 360, 175–192. [Google Scholar] [CrossRef]
- Mayeur, J.R.; McDowell, D.L. A Three-Dimensional Crystal Plasticity Model for Duplex Ti-6Al-4V. Int. J. Plast. 2007, 23, 1457–1485. [Google Scholar] [CrossRef]
- Tari, V.; Lebensohn, R.A.; Pokharel, R.; Turner, T.J.; Shade, P.A.; Bernier, J.V.; Rollett, A.D. Validation of Micro-Mechanical FFT-Based Simulations Using High Energy Diffraction Microscopy on Ti-7Al. Acta Mater. 2018, 154, 273–283. [Google Scholar] [CrossRef]
- Zhang, M.; Zhang, J.; McDowell, D.L. Microstructure-Based Crystal Plasticity Modeling of Cyclic Deformation of Ti-6Al-4V. Int. J. Plast. 2007, 23, 1328–1348. [Google Scholar] [CrossRef]
- Yapici, G.G.; Karaman, I.; Luo, Z.P. Mechanical Twinning and Texture Evolution in Severely Deformed Ti-6Al-4V at High Temperatures. Acta Mater. 2006, 54, 3755–3771. [Google Scholar] [CrossRef]
- Prakash, D.G.L.; Ding, R.; Moat, R.J.; Jones, I.; Withers, P.J.; da Fonseca, J.Q.; Preuss, M. Deformation Twinning in Ti-6Al-4V during Low Strain Rate Deformation to Moderate Strains at Room Temperature. Mater. Sci. Eng. A 2010, 527, 5734–5744. [Google Scholar] [CrossRef]
- Huang, T.; Shuai, L.; Wakeel, A.; Wu, G.; Hansen, N.; Huang, X. Strengthening Mechanisms and Hall-Petch Stress of Ultrafine Grained Al-0.3%Cu. Acta Mater. 2018, 156, 369–378. [Google Scholar] [CrossRef]
- Borovikov, V.; Mendelev, M.I.; King, A.H. Effects of Grain Boundary Disorder on Dislocation Emission. Mater. Lett. 2019, 237, 303–305. [Google Scholar] [CrossRef]
- Gao, Q.; Li, R.; Wu, H.; Miao, K.; Wu, H.; Liu, C.; Li, X. Revealing the Superior Post-Necking Elongation in the Fine-Grained Ti-6Al-4V ELI at Cryogenic Temperature. Metals 2024, 14, 600. [Google Scholar] [CrossRef]
- Xie, H.; Zhou, S.; Guan, B.; Ren, Y.; Sun, Z.; Dai, G.; Yang, G. Enhanced Strength-Ductility Synergy in Hybrid Additive Manufactured Ti–6Al–4V via Interlayer Friction Stir Processing Assisted Laser-Directed Energy Deposition. Virtual Phys. Prototyp. 2025, 20, e2499935. [Google Scholar] [CrossRef]
- Qiang, F.; Xin, S.; Tu, X.; Wang, H.; Guo, P.; Hou, H.; Lian, Z.; Zhang, L.; Hou, W. Low-Temperature Superplastic Deformation Mechanism of Ultra-Fine Grain Ti–6Al–4V Alloy by Friction Stir Processing. J. Mater. Res. Technol. 2024, 30, 7413–7419. [Google Scholar] [CrossRef]
- Mirone, G. Role of Stress Triaxiality in Elastoplastic Characterization and Ductile Failure Prediction. Eng. Fract. Mech. 2007, 74, 1203–1221. [Google Scholar] [CrossRef]
- El-Magd, E.; Abouridouane, M. Characterization, Modelling and Simulation of Deformation and Fracture Behaviour of the Light-Weight Wrought Alloys under High Strain Rate Loading. Int. J. Impact Eng. 2006, 32, 741–758. [Google Scholar] [CrossRef]
- Hancock, J.W.; Mackenzie, A.C. On the Mechanisms of Ductile Failure in High-Strength Steels Subjected to Multi-Axial Stress-States. J. Mech. Phys. Solids 1976, 24, 147–160. [Google Scholar] [CrossRef]
- Bouchard, P.O.; Bourgeon, L.; Fayolle, S.; Mocellin, K. An Enhanced Lemaitre Model Formulation for Materials Processing Damage Computation. Int. J. Mater. Form. 2011, 4, 299–315. [Google Scholar] [CrossRef]


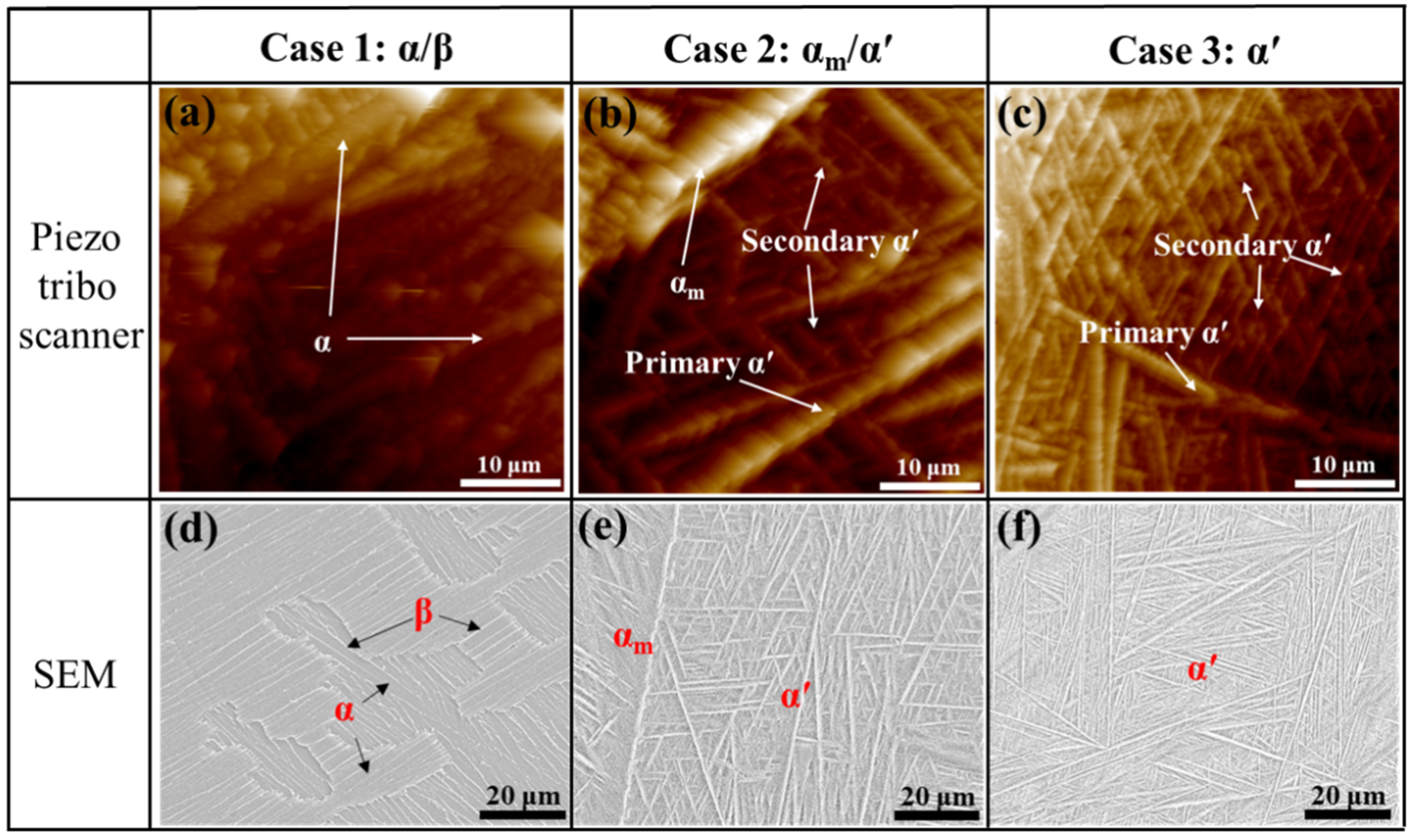


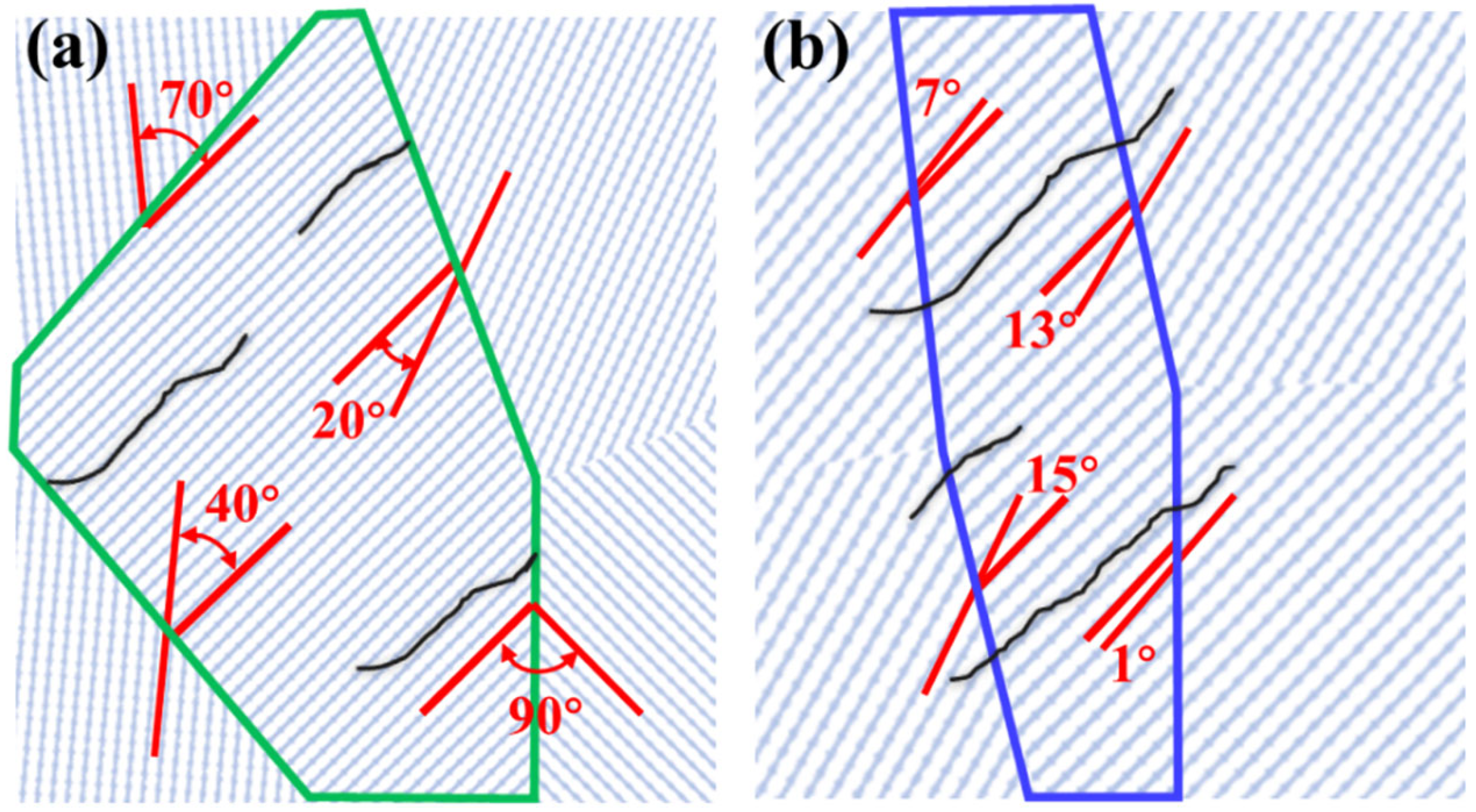
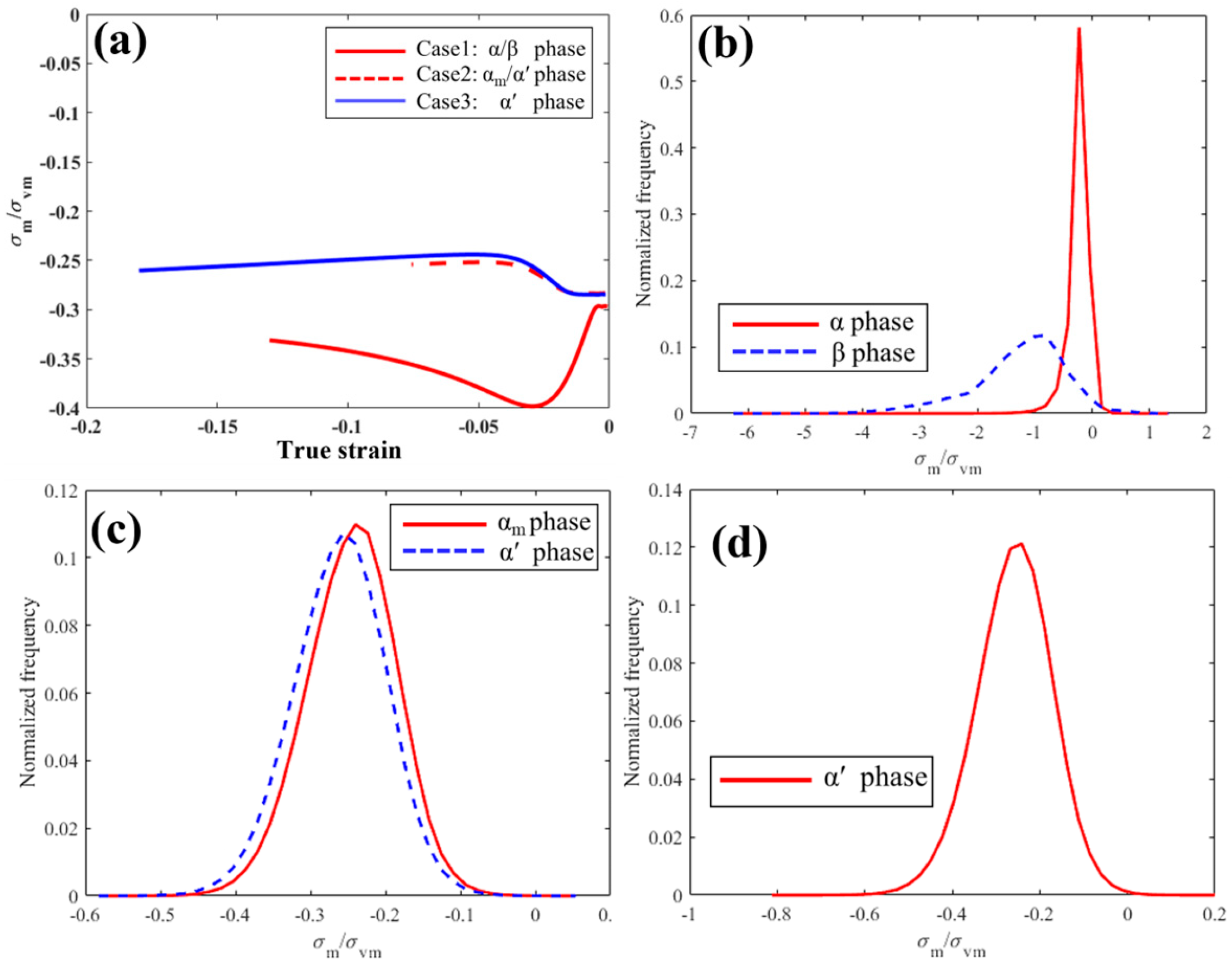
| Sample | Cooling Rate (°C/s) | Phase | Average Thickness (μm) | Average Length (μm) | Average Fraction (%) |
|---|---|---|---|---|---|
| Case 1 | 1 | α | 2.5 ± 1.0 | 325 ± 75 | 87.5 ± 2.5 |
| β | 0.25 ± 0.15 | 325 ± 75 | 12.5 ± 2.5 | ||
| Case 2 | 145 | αm | 8.0 ± 2.0 | 325 ± 75 | 35 ± 5 |
| Primary α′ | 2.5 ± 0.5 | 325 ± 75 | 17.5 ± 2.5 | ||
| Secondary α′ | 4.5 ± 0.5 | 7.5 ± 0.5 | 47.5 ± 2.5 | ||
| Case 3 | 7000 | Primary α′ | 2.5 ± 0.5 | 325 ± 75 | 7.5 ± 2.5 |
| Secondary α′ | 0.6 ± 0.2 | 4.5 ± 1.5 | 92.5 ± 2.5 |
| Specimens | Compositions (Phase) | Cooling Rate (°C/s) | εcy0.2 | εcu | σcy0.2 (MPa) | σcu (MPa) |
|---|---|---|---|---|---|---|
| Case 1 | α/β | 1 | 0.029 | 0.12 | 790.3 | 1160.5 |
| Case 2 | αm/α′ | 145 | 0.039 | 0.08 | 1214.7 | 1478.3 |
| Case 3 | α′ | 7000 | 0.037 | 0.17 | 1074.0 | 1519.2 |
| Elastic Constants (GPa) | C11 | C12 | C13 | C33 | C44 |
|---|---|---|---|---|---|
| β | 114 | 90 | 90 | 114 | 181 |
| α | 123 | 100 | 69 | 145 | 30 |
| α′ | 120 | 100 | 67 | 125 | 30 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xiao, Y.; Zhou, H.; Liu, P.; Chen, L. Gleeble-Simulated Ultra-Fast Cooling Unlocks Strength–Ductility Synergy in Fully Martensitic Ti-6Al-4V. Materials 2025, 18, 4572. https://doi.org/10.3390/ma18194572
Xiao Y, Zhou H, Liu P, Chen L. Gleeble-Simulated Ultra-Fast Cooling Unlocks Strength–Ductility Synergy in Fully Martensitic Ti-6Al-4V. Materials. 2025; 18(19):4572. https://doi.org/10.3390/ma18194572
Chicago/Turabian StyleXiao, Yaohong, Hongling Zhou, Pengwei Liu, and Lei Chen. 2025. "Gleeble-Simulated Ultra-Fast Cooling Unlocks Strength–Ductility Synergy in Fully Martensitic Ti-6Al-4V" Materials 18, no. 19: 4572. https://doi.org/10.3390/ma18194572
APA StyleXiao, Y., Zhou, H., Liu, P., & Chen, L. (2025). Gleeble-Simulated Ultra-Fast Cooling Unlocks Strength–Ductility Synergy in Fully Martensitic Ti-6Al-4V. Materials, 18(19), 4572. https://doi.org/10.3390/ma18194572








