Computational Homogenisation and Identification of Auxetic Structures with Interval Parameters
Abstract
1. Introduction
2. Applied Methods
2.1. Directed Interval Arithmetic
- Opposite of addition:
- Inverse of multiplication:where the set contains all directed intervals with element 0, as follows:Based on the above, directed interval arithmetic implements additional operations, as follows:
- Directed subtraction:
- Directed division:
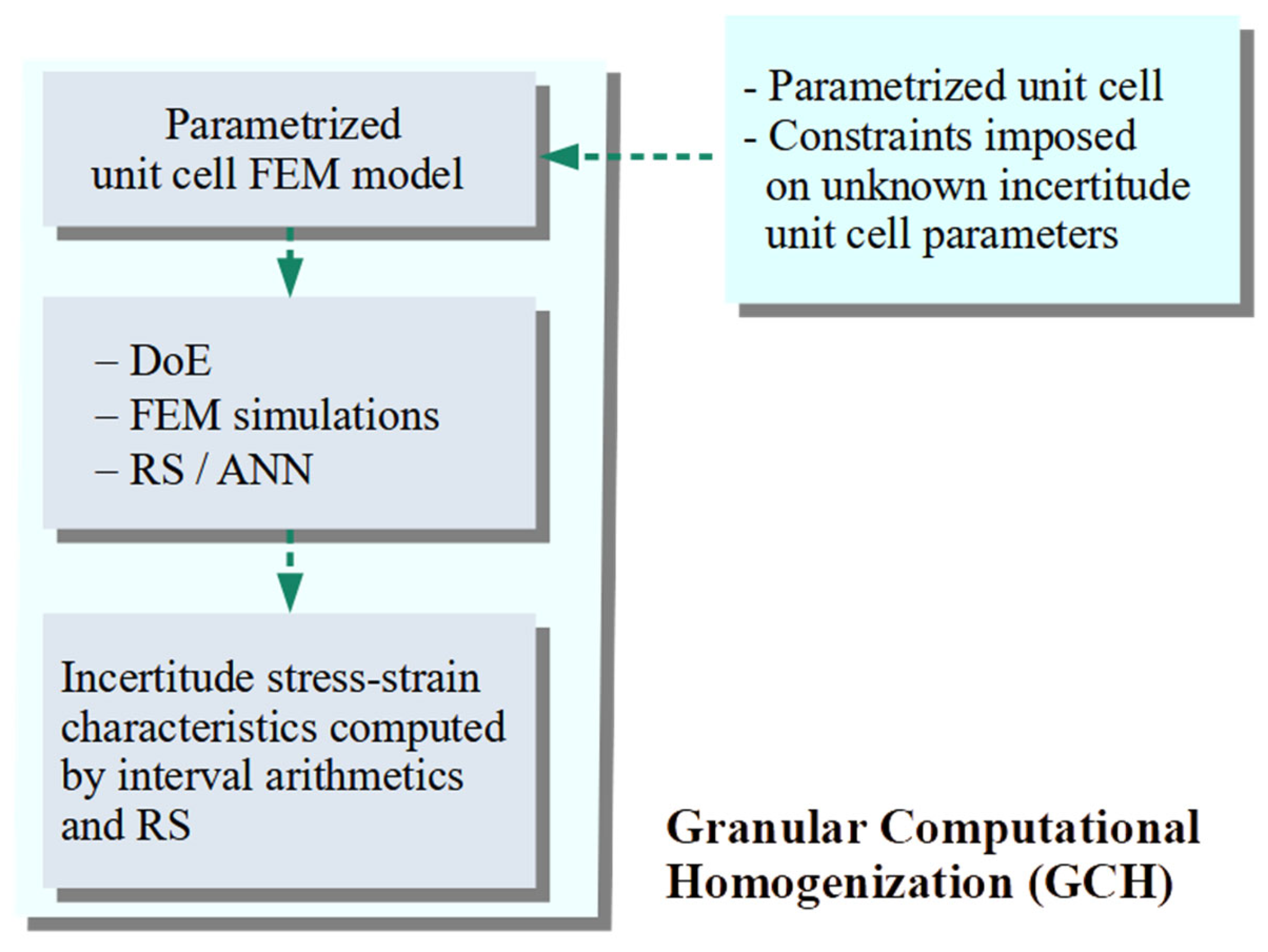
2.2. Computational Interval Homogenisation
- The Hill–Mandel condition, which states that the microscopic average energy density within a unit cell is equal to the macroscopic energy density at the corresponding point in the macrostructure. Typically, volume averages of strains and stresses can be replaced by boundary integrals [69], as follows:where —micro stress tensor, —micro strain tensor, 〈∙〉—average quantity, V—the unit cell volume, Γ—the external boundary of unit cell, ti—traction force component, xj—coordinates, ui—displacement component, nj—unit normal vector to the boundary.
- The boundary conditions that satisfy the Hill–Mandel condition. In the present article, periodic boundary conditions are employed:where , —displacements of the corresponding points at the opposite unit cell boundaries, , —locations of the corresponding points at the opposite unit cell boundaries, , —tractions on the corresponding points at the opposite unit cell boundaries, , —normal vectors at the opposite unit cell boundaries.
- Prescribe the boundary conditions on Γ.
- Solve the nonlinear BVP related to RVE/unit cell by FEM.
- Average the stress in the RVE/unit cell in equilibrium to obtain corresponding , where is a macroscopic stress.
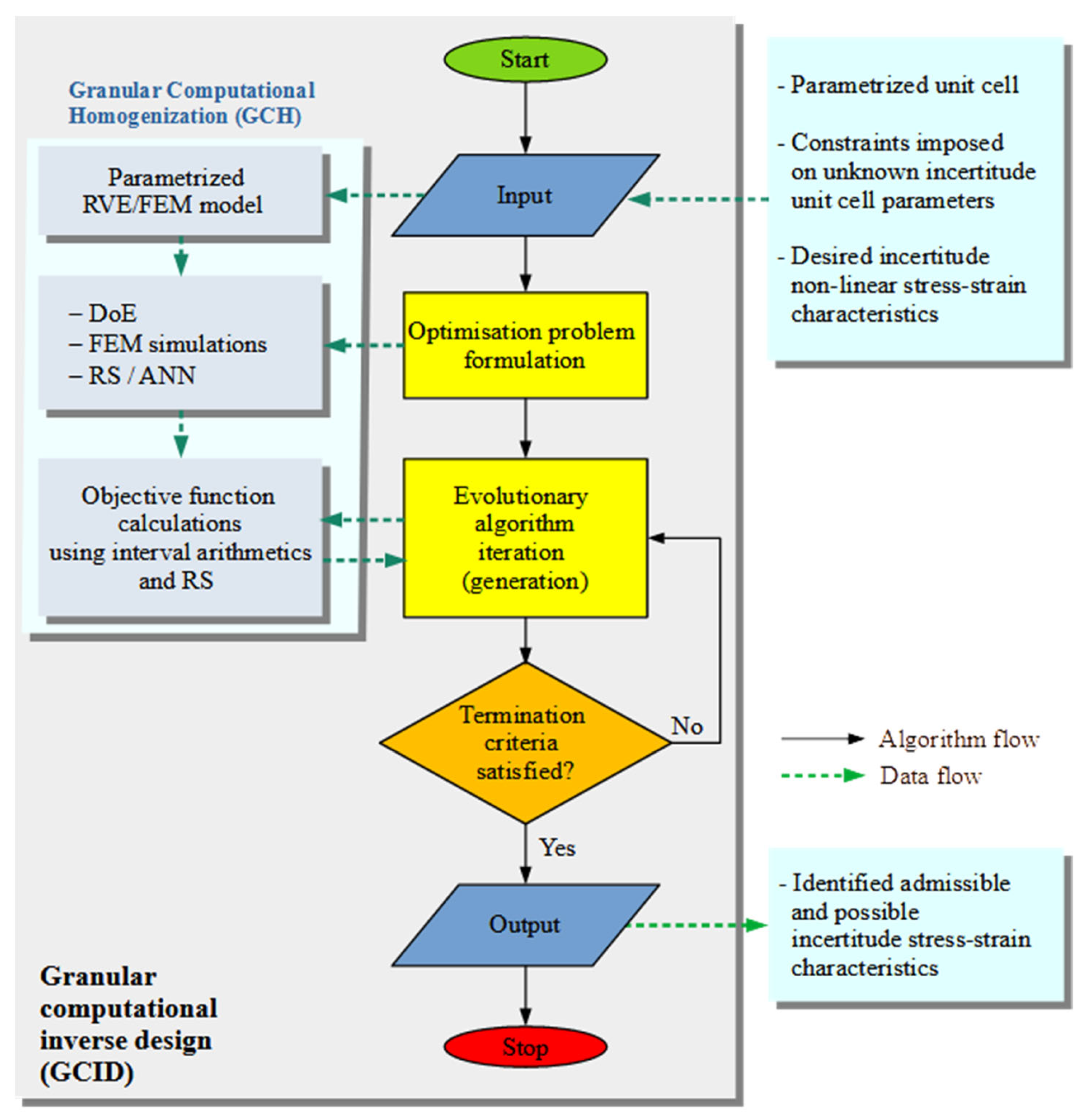
2.3. Computational Interval Identification
3. Numerical Examples
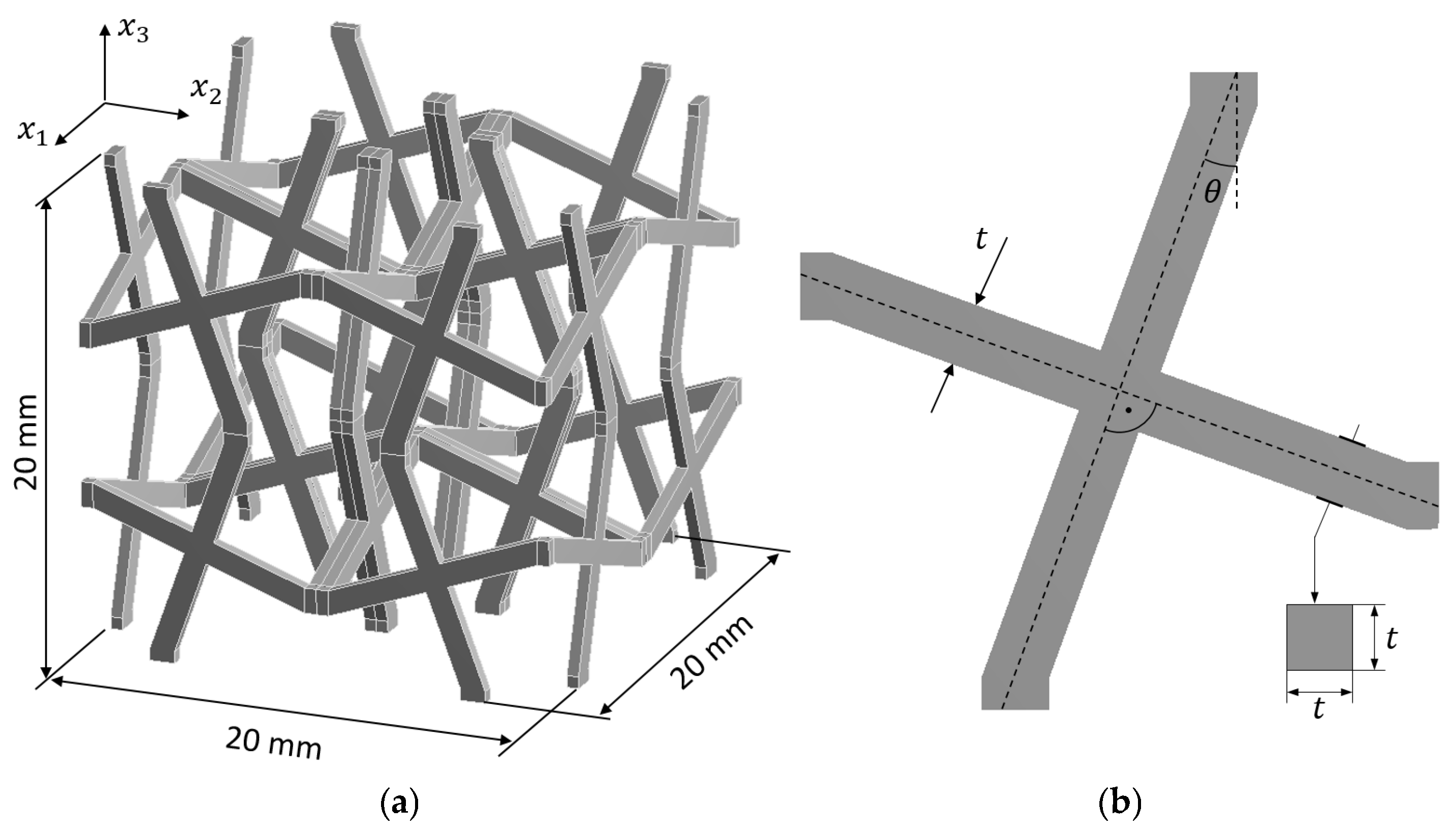
3.1. Computational Interval Homogenisation of Auxetic Structure
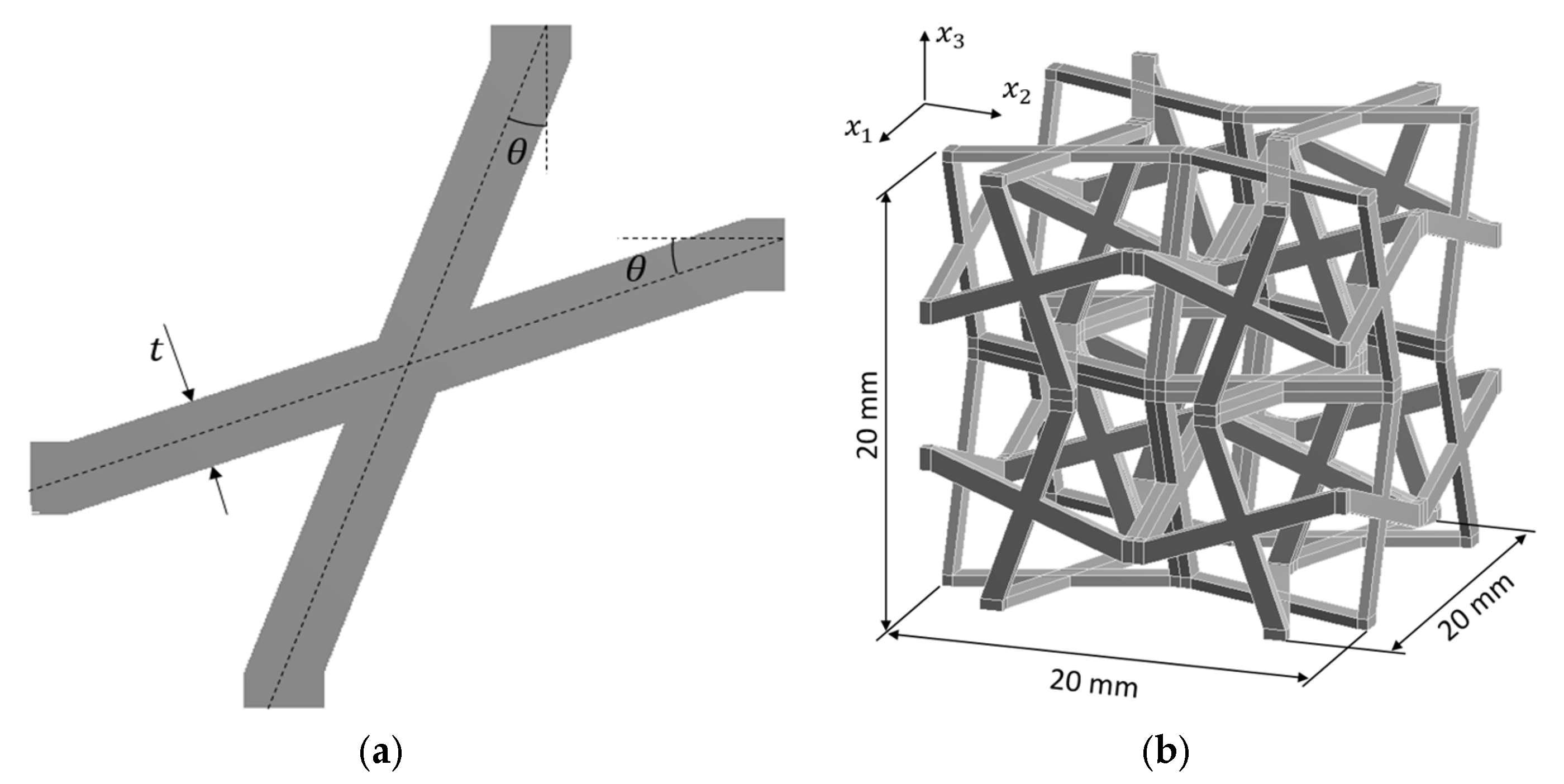
3.1.1. Model Establishment for the Interval Homogenisation
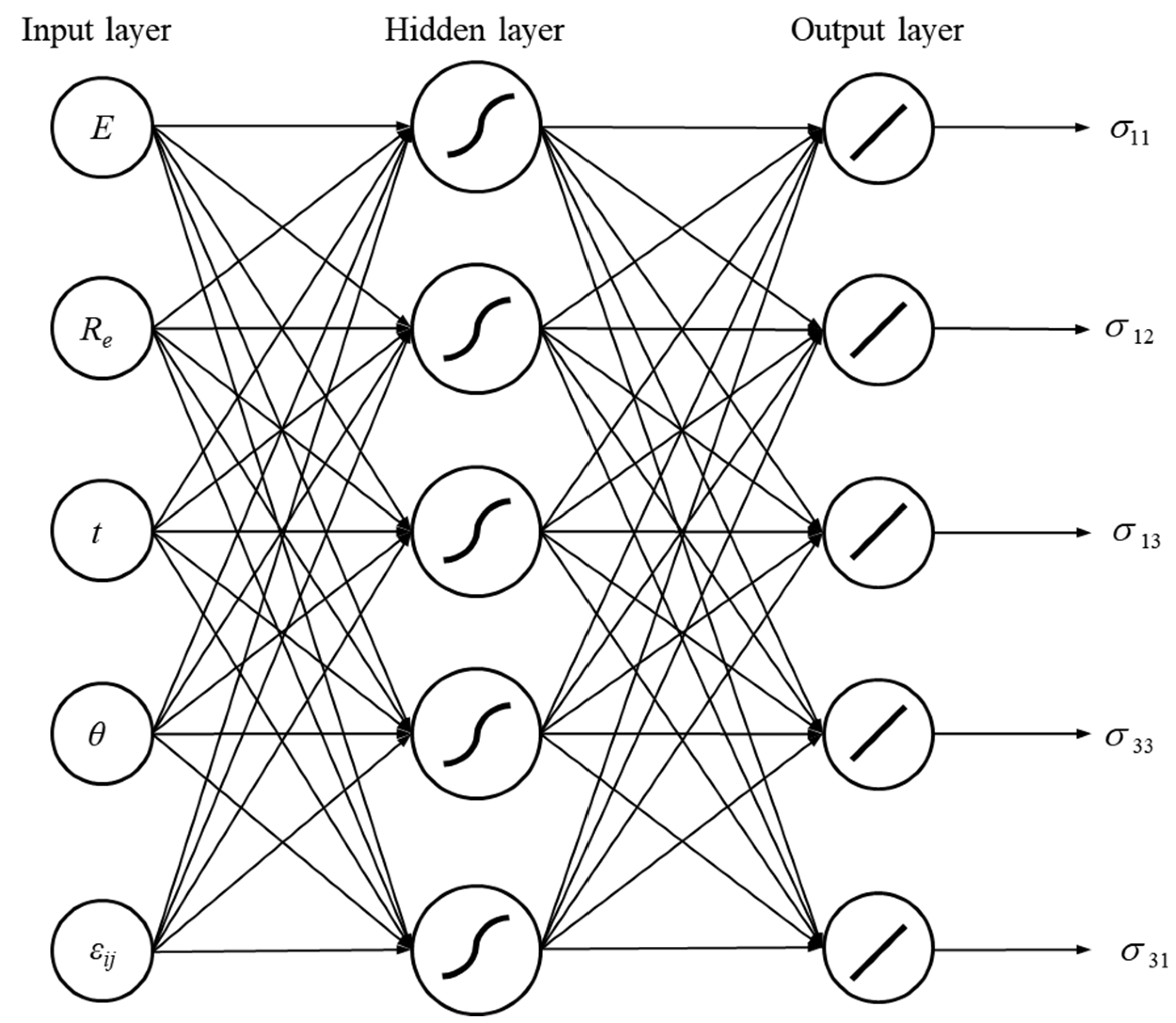
3.1.2. Numerical Results of the Interval Homogenisation
3.2. Computational Interval Identification of Auxetic Structure
3.2.1. Model Establishment for the Interval Identification
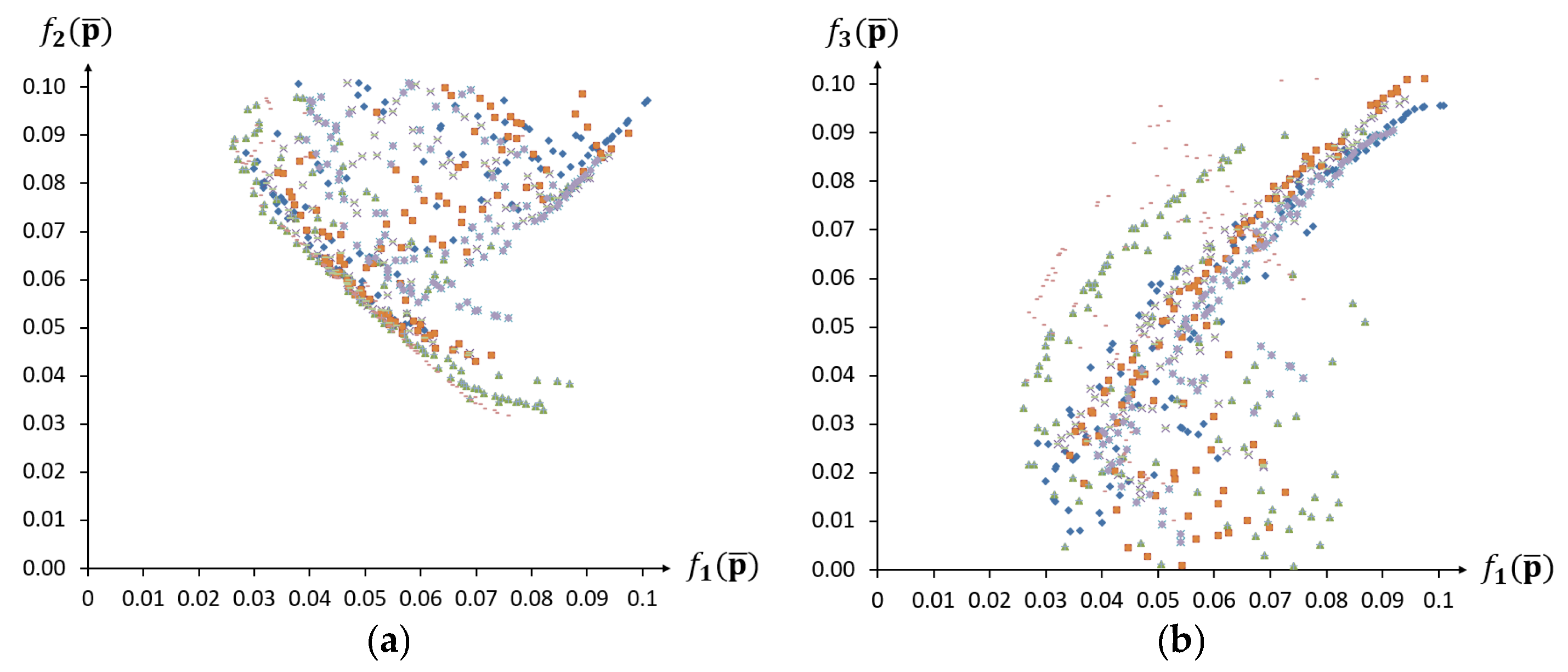
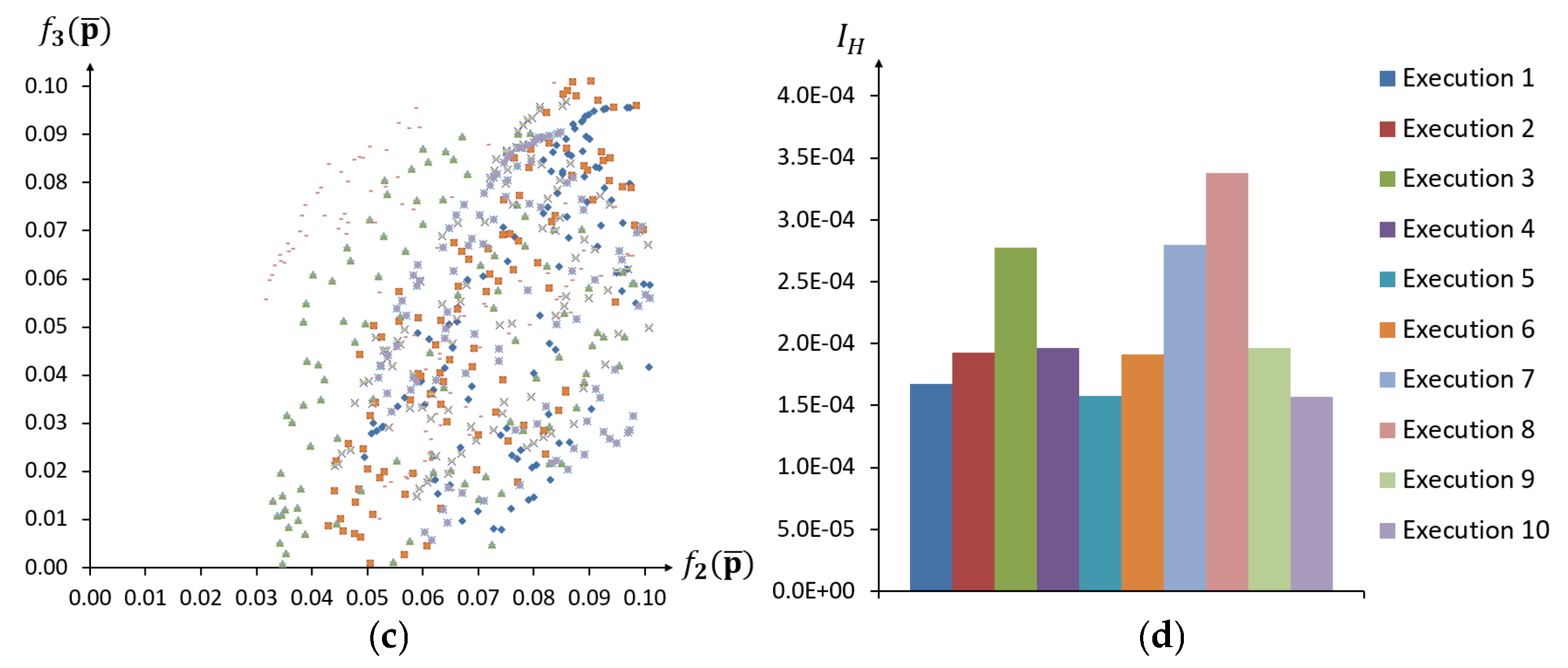
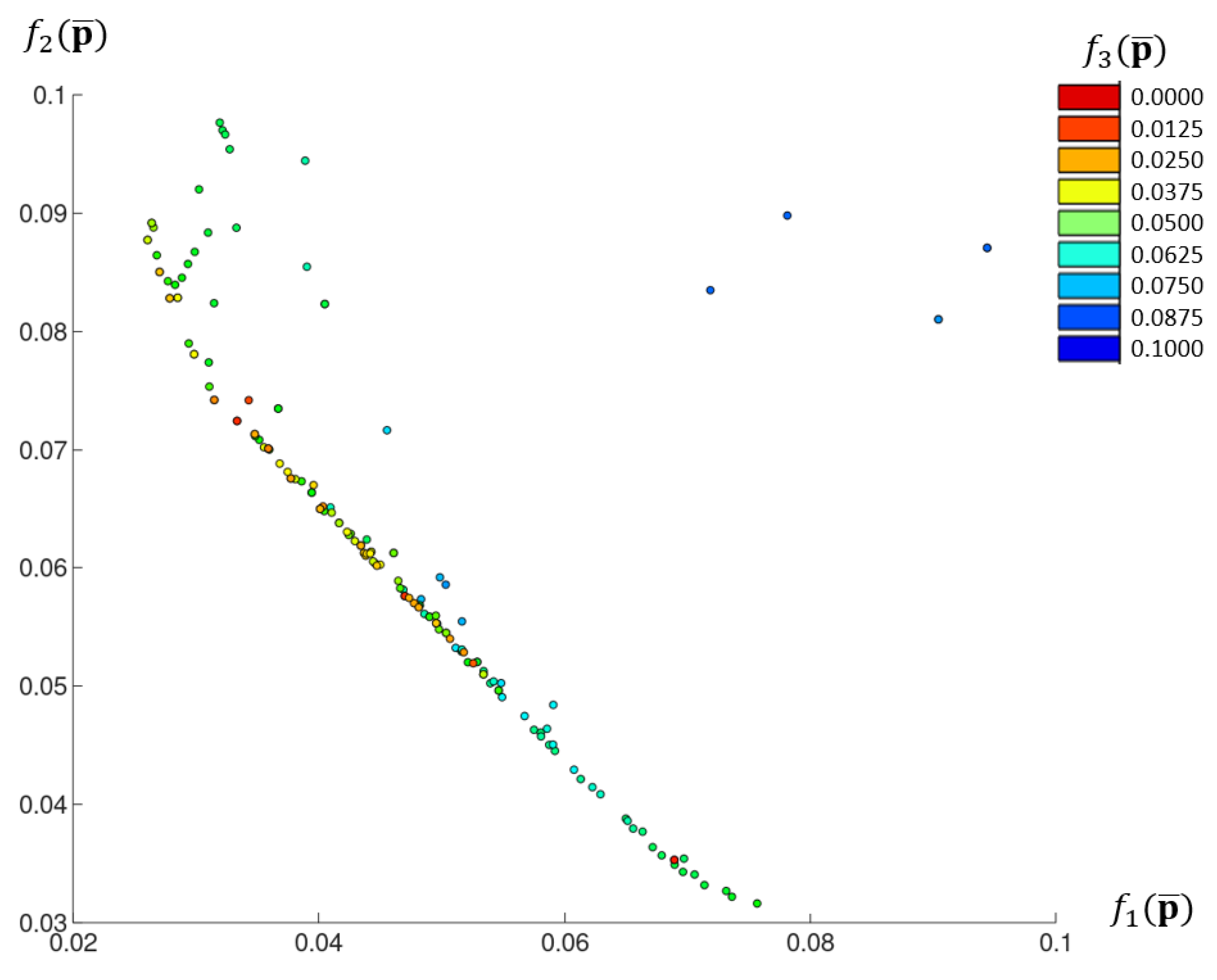
3.2.2. Numerical Results of the Interval Identification
- Number of individuals ni = 200;
- Scatter crossover probability cs = 0.8;
- Number of generations ng = 1000;
- Number of stall generations ns = 50;
- Pareto fraction set Pf = 0.5.
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| ANN | Artificial Neural Network |
| BVP | Boundary value problem |
| DoE | Design of experiment |
| FEM | Finite element method |
| GCID | Granular Computational Inverse Design |
| GCH | Granular Computational Homogenisation |
| RS | Response surface |
References
- Ashby, M.F.; Brechet, Y.J.M. Designing hybrid materials. Acta Mater. 2003, 51, 5801–5821. [Google Scholar] [CrossRef]
- Wojciechowski, K.W. Auxetics and Other Systems with Unusual Characteristics. Phys. Status Solidi B 2022, 259, 2200536. [Google Scholar] [CrossRef]
- Zawistowski, M.; Poteralski, A. Parametric optimization of selected auxetic structures. Multiscale Multidiscip. Model. Exp. Des. 2024, 7, 4777–4789. [Google Scholar] [CrossRef]
- Lu, C.; Hsieh, M.; Huang, Z.; Zhang, C.; Lin, Y.; Shen, Q.; Chen, F.; Zhang, L. Architectural Design and Additive Manufacturing of Mechanical Metamaterials: A Review. Engineering 2022, 17, 44–63. [Google Scholar] [CrossRef]
- Nugroho, W.T.; Dong, Y.; Pramanik, A.; Selvan, M.C.P.; Zhang, Z.; Ramakrishna, S. Additive manufacturing of re-entrant structures: Well-tailored structures, unique properties, modelling approaches and real applications. Addit. Manuf. 2023, 78, 103829. [Google Scholar] [CrossRef]
- Gill, H.S. Mechanical and structure properties of cellular auxetic materials. Mater. Today Proc. 2021, 37, 3320–3323. [Google Scholar] [CrossRef]
- Hou, W.; He, P.; Yang, Y.; Sang, L. Crashworthiness optimization of crash box with 3D-printed lattice structures. Int. J. Mech. Sci. 2023, 247, 108198. [Google Scholar] [CrossRef]
- Zhou, G.; Zhao, W.; Ma, Z.-D.; Wang, C.; Wang, Y. Multi-objective reliability design optimization of a novel side door negative Poisson’s ratio impact beam. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2017, 232, 1196–1205. [Google Scholar] [CrossRef]
- Yong, C.S.; Idapalapati, S.; Lim, C.W.; Goh, K.L. Auxetic Composite Sandwich for Vibration Damping Through Axisymmetric Deformation. J. Compos. Sci. 2025, 9, 162. [Google Scholar] [CrossRef]
- Dong, S.; Hu, H. Sensors Based on Auxetic Materials and Structures: A Review. Materials 2023, 16, 3603. [Google Scholar] [CrossRef]
- Abbaslou, M.; Hashemi, R.; Etemadi, E. Novel hybrid 3D-printed auxetic vascular stent based on re-entrant and meta-trichiral unit cells: Finite element simulation with experimental verifications. Mater. Today Commun. 2023, 35, 105742. [Google Scholar] [CrossRef]
- Amin, F.; Ali, M.N.; Ansari, U.; Mir, M.; Minhas, M.A.; Shahid, W. Auxetic Coronary Stent Endoprosthesis: Fabrication and Structural Analysis. J. Appl. Biomater. Funct. Mater. 2015, 13, 127–135. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.; Yao, X.; Wang, Z.; Ye, J.; Luan, C.; He, Y.; Lin, H.; Fu, J. A flexible porous chiral auxetic tracheal stent with ciliated epithelium. Acta Biomater. 2021, 124, 153–165. [Google Scholar] [CrossRef] [PubMed]
- Ebrahimi, M.S.; Noruzi, M.; Hamzehei, R.; Etemadi, E.; Hashemi, R. Revolutionary auxetic intravascular medical stents for angioplasty applications. Mater. Des. 2023, 235, 112393. [Google Scholar] [CrossRef]
- Kolken, H.M.A.; Janbaz, S.; Leeflang, S.M.A.; Lietaert, K.; Weinans, H.H.; Zadpoor, A.A. Rationally designed meta-implants: A combination of auxetic and conventional meta-biomaterials. Mater. Horiz. 2017, 5, 28–35. [Google Scholar] [CrossRef]
- Lei, M.; Hong, W.; Zhao, Z.; Hamel, C.M.; Chen, M.; Lu, H.; Qi, H.J. 3D Printing of Auxetic Metamaterials with Digitally Reprogrammable Shape. ACS Appl. Mater. Interfaces 2019, 11, 22768–22776. [Google Scholar] [CrossRef]
- Prosperi, G.; Paredes, J.; Aldazabal, J. Integration of correction factors for 3D printing errors in FEM simulations for the precise mechanical analysis of single-layer auxetic scaffolds using a wavy pattern for tissue engineering. Bioprinting 2025, 48, e00401. [Google Scholar] [CrossRef]
- Duncan, O.; Shepherd, T.; Moroney, C.; Foster, L.; Venkatraman, P.D.; Winwood, K.; Allen, T.; Alderson, A. Review of Auxetic Materials for Sports Applications: Expanding Options in Comfort and Protection. Appl. Sci. 2018, 8, 941. [Google Scholar] [CrossRef]
- Urquhart, L.; Tamburrino, F.; Neri, P.; Wodehouse, A.; Fingland, C.; Razionale, A.V. An examination of auxetic componentry for applications in human-centred biomedical product design settings. Int. J. Interact. Des. Manuf. 2023, 18, 5457–5467. [Google Scholar] [CrossRef]
- Foster, L.; Peketi, P.; Allen, T.; Senior, T.; Duncan, O.; Alderson, A. Application of Auxetic Foam in Sports Helmets. Appl. Sci. 2018, 8, 354. [Google Scholar] [CrossRef]
- Cross, T.M.; Hoffer, K.W.; Jones, D.P.; Kirschner, P.B.; Meschter, J.C. Auxetic Structures and Footwear with Soles Having Auxetic Structures. U.S. Patent 9,149,153, 6 October 2015. [Google Scholar]
- Tomažinčič, D.; Klemenc, J. Development of a special self-adaptive auxetic structure for protecting tree trunks from external damage. Trees For. People 2025, 20, 100860. [Google Scholar] [CrossRef]
- Ullah, T.; Hussain, M.; Ali, M.; Umair, M. Impact of auxeticity on mechanical properties of 3D woven auxetic reinforced thermoplastic composites. Polym. Compos. 2022, 44, 897–906. [Google Scholar] [CrossRef]
- Hou, X.; Hu, H.; Silberschmidt, V. A novel concept to develop composite structures with isotropic negative Poisson’s ratio: Effects of random inclusions. Compos. Sci. Technol. 2012, 72, 1848–1854. [Google Scholar] [CrossRef]
- Tsai, S.W.; Hahn, H.T. Introduction to Composite Materials, 2nd ed.; Routledge: Oxfordshire, UK, 2018; ISBN 978-0-203-75014-8. [Google Scholar]
- Bianchi, M.; Scarpa, F.; Smith, C.W. Shape memory behaviour in auxetic foams: Mechanical properties. Acta Mater. 2010, 58, 858–865. [Google Scholar] [CrossRef]
- Zhang, Y.; Yu, H.; Zhu, S.; Wang, J. Fracture mechanics analysis of auxetic chiral materials. Int. J. Mech. Sci. 2025, 295, 110281. [Google Scholar] [CrossRef]
- Dong, H.; Wang, H.; Hazell, P.J.; Sun, N.; Dura, H.B.; Escobedo-Diaz, J.P. Effects of printing parameters on the quasi-static and dynamic compression behaviour of 3D-printed re-entrant auxetic structures. Thin-Walled Struct. 2025, 210, 113000. [Google Scholar] [CrossRef]
- Wurmshuber, M.; Wilmers, J.; Kim, J.; Oh, S.H.; Bargmann, S.; Kiener, D. Lower hardness than strength: The auxetic composite microstructure of limpet tooth. Acta Biomater. 2023, 166, 447–453. [Google Scholar] [CrossRef]
- Pruksawan, S.; Chee, H.L.; Wang, Z.; Luo, P.; Chong, Y.T.; Thitsartarn, W.; Wang, F. Toughened Hydrogels for 3D Printing of Soft Auxetic Structures. Chem.—Asian J. 2022, 17, e202200677. [Google Scholar] [CrossRef]
- McDonald, S.A.; Dedreuil-Monet, G.; Yao, Y.T.; Alderson, A.; Withers, P.J. In situ 3D X-ray microtomography study comparing auxetic and non-auxetic polymeric foams under tension. Phys. Status Solidi B 2010, 248, 45–51. [Google Scholar] [CrossRef]
- Albertini, F.; Dirrenberger, J.; Sollogoub, C.; Molotnikov, A.; Adrien, J.; Maire, E. Hybrid auxetics: Postponing failure with elastomer infiltration of Ti-6Al-4V lattices. Int. J. Mech. Sci. 2025, 306, 110704. [Google Scholar] [CrossRef]
- Geng, X.; Yao, Y.; Huang, H.; Li, Q.; Wang, L.; Fan, Y. Mechanical and biological characteristics of 3D-printed auxetic structure in bone tissue engineering. J. Biomech. 2025, 184, 112685. [Google Scholar] [CrossRef]
- Zohdi, T.I.; Wriggers, P. (Eds.) An Introduction to Computational Micromechanics: Corrected Second Printing; Lecture Notes in Applied and Computational Mechanics; Springer: Berlin/Heidelberg, Germany, 2005; Volume 20, ISBN 978-3-540-77482-2. [Google Scholar]
- Kouznetsova, V.G. Computational Homogenization for the Multi-Scale Analysis of Multi-Phase Materials. Ph.D. Thesis, Technische Universiteit Eindhoven, Eindhoven, The Netherlands, 2002. [Google Scholar]
- Beluch, W.; Hatłas, M.; Ptaszny, J. Granular Computational Homogenisation of Composite Structures with Imprecise Param-eters. Arch. Mech. 2023, 75, 271–300. [Google Scholar] [CrossRef]
- Ogierman, W. A new model for time-efficient analysis of nonlinear composites with arbitrary orientation distribution of fibres. Compos. Struct. 2021, 273, 114310. [Google Scholar] [CrossRef]
- Ptaszny, J. A fast multipole BEM with higher-order elements for 3-D composite materials. Comput. Math. Appl. 2021, 82, 148–160. [Google Scholar] [CrossRef]
- Ptaszny, J.; Hatłas, M. Evaluation of the FMBEM efficiency in the analysis of porous structures. Eng. Comput. 2018, 35, 843–866. [Google Scholar] [CrossRef]
- Ptaszny, J.; Dziatkiewicz, G.; Fedelinski, P. Boundary element method modelling of nanocomposites. Int. J. Multiscale Comput. Eng. 2014, 12, 33–43. [Google Scholar] [CrossRef]
- Sigmund, O. Materials with prescribed constitutive parameters: An inverse homogenization problem. Int. J. Solids Struct. 1994, 31, 2313–2329. [Google Scholar] [CrossRef]
- Trofimov, A.; Abaimov, S.; Sevostianov, I. Inverse homogenization problem: Evaluation of elastic and electrical (thermal) properties of composite constituents. Int. J. Eng. Sci. 2018, 129, 34–46. [Google Scholar] [CrossRef]
- Michalewicz, Z.; Fogel, D.B. How to Solve It: Modern Heuristics, 2nd ed.; rev.extended ed.; Springer: Berlin/Heidelberg, Germany; New York, NY, USA, 2004; ISBN 978-3-540-22494-5. [Google Scholar]
- Burczyński, T.; Kuś, W.; Beluch, W.; Długosz, A.; Poteralski, A.; Szczepanik, M. Intelligent Computing in Optimal Design; Solid Mechanics and Its Applications; Springer International Publishing: Cham, Switzerland, 2020; Volume 261, ISBN 978-3-030-34159-6. [Google Scholar]
- Mesogitis, T.; Skordos, A.; Long, A. Uncertainty in the manufacturing of fibrous thermosetting composites: A review. Compos. Part A Appl. Sci. Manuf. 2014, 57, 67–75. [Google Scholar] [CrossRef]
- Ruediger, P.; Hagen, H. Dealing with uncertainties in manufacturing process simulations. In Applied Mechanics and Materials; Trans Tech Publications Ltd.: Zurich, Switzerland, 2017; Volume 869, pp. 226–233. [Google Scholar]
- Kamiński, M. Homogenization of particulate and fibrous composites with some non-Gaussian material uncertainties. Compos. Struct. 2018, 210, 778–786. [Google Scholar] [CrossRef]
- Bostanabad, R.; Liang, B.; Gao, J.; Liu, W.K.; Cao, J.; Zeng, D.; Su, X.; Xu, H.; Li, Y.; Chen, W. Uncertainty quantification in multiscale simulation of woven fiber composites. Comput. Methods Appl. Mech. Eng. 2018, 338, 506–532. [Google Scholar] [CrossRef]
- Pelz, P.F.; Groche, P.; Pfetsch, M.E.; Schaeffner, M. (Eds.) Mastering Uncertainty in Mechanical Engineering; Springer Tracts in Mechanical Engineering; Springer International Publishing: Cham, Switzerland, 2021; ISBN 978-3-030-78353-2. [Google Scholar]
- Pedrycz, W. Granular Computing: Analysis and Design of Intelligent Systems, 1st ed.; CRC Press: Boca Raton, FL, USA, 2018; ISBN 978-1-315-21673-7. [Google Scholar]
- Möller, B.; Beer, M. Fuzzy Randomness: Uncertainty in Civil Engineering and Computational Mechanics; Springer: Berlin/Heidelberg, Germany, 2004; ISBN 978-3-642-07312-0. [Google Scholar]
- Yao, J. A Ten-Year Review of Granular Computing. In Proceedings of the 2007 IEEE International Conference on Granular Computing (GRC 2007), San Jose, CA, USA, 2–4 November 2007; IEEE: Fremont, CA, USA, 2007; p. 734. [Google Scholar]
- Aliev, R.A.; Guirimov, B.G. Information Granules Problem: An Efficient Solution of Real-Time Fuzzy Regression Analysis. In Information Granulation: Data Mining and Big Data Analysis; Aliev, R.A., Ed.; Studies in Big Data; Springer International Publishing: Cham, Switzerland, 2015; pp. 39–61. ISBN 978-3-319-08253-0. [Google Scholar]
- DeJong, K.A.; De Jong, K. Evolutionary Computation: A Unified Approach; A Bradford Book; MIT Press: Cambridge, MA, USA, 2006; ISBN 978-0-262-52960-0. [Google Scholar]
- Friedman, L.W. Metamodeling. In The Simulation Metamodel; Springer: Boston, MA, USA, 1996; pp. 77–101. ISBN 978-1-4612-8556-4. [Google Scholar]
- Yamanaka, Y.; Matsubara, S.; Hirayama, N.; Moriguchi, S.; Terada, K. Surrogate modeling for the homogenization of elastoplastic composites based on RBF interpolation. Comput. Methods Appl. Mech. Eng. 2023, 415, 116282. [Google Scholar] [CrossRef]
- Fuhg, J.N.; Böhm, C.; Bouklas, N.; Fau, A.; Wriggers, P.; Marino, M. Model-data-driven constitutive responses: Application to a multiscale computational framework. Int. J. Eng. Sci. 2021, 167, 103522. [Google Scholar] [CrossRef]
- Yvonnet, J. Computational Homogenization of Heterogeneous Materials with Finite Elements; Solid Mechanics and Its Applications; Springer International Publishing: Cham, Switzerland, 2019; Volume 258, ISBN 978-3-030-18382-0. [Google Scholar]
- Halmos, P.R. Naive Set Theory; Undergraduate Texts in Mathematics; Springer: New York, NY, USA, 1974; ISBN 978-0-387-90104-6. [Google Scholar]
- Dubois, D.; Prade, H. Operations on fuzzy numbers. Int. J. Syst. Sci. 1978, 9, 613–626. [Google Scholar] [CrossRef]
- Hanss, M. Applied Fuzzy Arithmetic; Springer Heidelberg: Berlin/Heidelberg, Germany, 2005; ISBN 978-3-540-24201-7. [Google Scholar]
- Piasecka-Belkhayat, A. Interval Boundary Element Method for Imprecisely Defined Unsteady Heat Transfer Problems; Monograph; Silesian University of Technology (PŚ): Gliwice, Poland, 2011; Volume 321. [Google Scholar]
- Hansen, E.R. A Generalized Interval Arithmetic. In Proceedings of the International Symposium on Interval Mathematics, Karlsruhe, Germany, 9–11 September 1975; Springer: Berlin/Heidelberg, Germany, 1975; pp. 7–18. [Google Scholar]
- Sendov, B. Some Topics of Segment Analysis. In Interval Mathematics; Academic Press: New York, NY, USA, 1980; pp. 203–222. [Google Scholar]
- Markov, S. On Direct Interval Arithmetic and Its Applications. J. Univers. Comput. Sci. 1995, 1, 514–526. [Google Scholar] [CrossRef]
- Popova, E.D. Multiplication Distributivity of Proper and Improper Intervals. Reliab. Comput. 2001, 7, 129–140. [Google Scholar] [CrossRef]
- Marcov, S. Extended Interval Arithmetic Involving Infinite Intervals. Math. Balk. 1992, 6, 269–304. [Google Scholar]
- Hill, R. Elastic properties of reinforced solids: Some theoretical principles. J. Mech. Phys. Solids 1963, 11, 357–372. [Google Scholar] [CrossRef]
- Yvonnet, J. Nonlinear Computational Homogenization. In Computational Homogenization of Heterogeneous Materials with Finite Elements; Solid Mechanics and Its Applications; Springer International Publishing: Cham, Switzerland, 2019; pp. 161–209. ISBN 978-3-030-18382-0. [Google Scholar]
- Nelson, P.R.; Coffin, M.; Copeland, K.A.F. Response Surface Methods. In Introductory Statistics for Engineering Experimentation; Elsevier: Amsterdam, The Netherlands, 2003; pp. 395–423. ISBN 978-0-12-515423-9. [Google Scholar]
- Rutkowski, L. Computational Intelligence: Methods and Techniques; Springer: Berlin/Heidelberg, Germany, 2008; ISBN 978-3-540-76287-4. [Google Scholar]
- Mikhael, W.B. Levenberg–Marquardt Training. In Artificial Neural Networks: Architectures and Applications; Sundararajan, N., Saratchandran, P., Eds.; CRC Press: Boca Raton, FL, USA, 2013; pp. 253–282. [Google Scholar]
- Johnson, M.; Moore, L.; Ylvisaker, D. Minimax and maximin distance designs. J. Stat. Plan. Inference 1990, 26, 131–148. [Google Scholar] [CrossRef]
- Beluch, W.; Ptaszny, J.; Hatłas, M. Metamodel-Based Inverse Design of a Composite Material with Prescribed Interval Effective Elastic Properties. Acta Mech. Autom. 2025, 19, 268–278. [Google Scholar] [CrossRef]
- MathWorks. Gamultiobj Algorithm—Multiobjective Genetic Algorithm. Available online: https://www.mathworks.com/help/gads/gamultiobj-algorithm.html (accessed on 17 May 2025).
- Brockhoff, D.; Friedrich, T.; Neumann, F. Analyzing Hypervolume Indicator Based Algorithms. In Parallel Problem Solving from Nature—PPSN X; Rudolph, G., Jansen, T., Beume, N., Lucas, S., Poloni, C., Eds.; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2008; Volume 5199, pp. 651–660. ISBN 978-3-540-87699-1. [Google Scholar]
- Lu, Z.; Wang, Q.; Li, X.; Yang, Z. Elastic properties of two novel auxetic 3D cellular structures. Int. J. Solids Struct. 2017, 124, 46–56. [Google Scholar] [CrossRef]
- Dell’Accio, F.; Guessab, A.; Nudo, F. New quadratic and cubic polynomial enrichments of the Crouzeix–Raviart finite element. Comput. Math. Appl. 2024, 170, 204–212. [Google Scholar] [CrossRef]




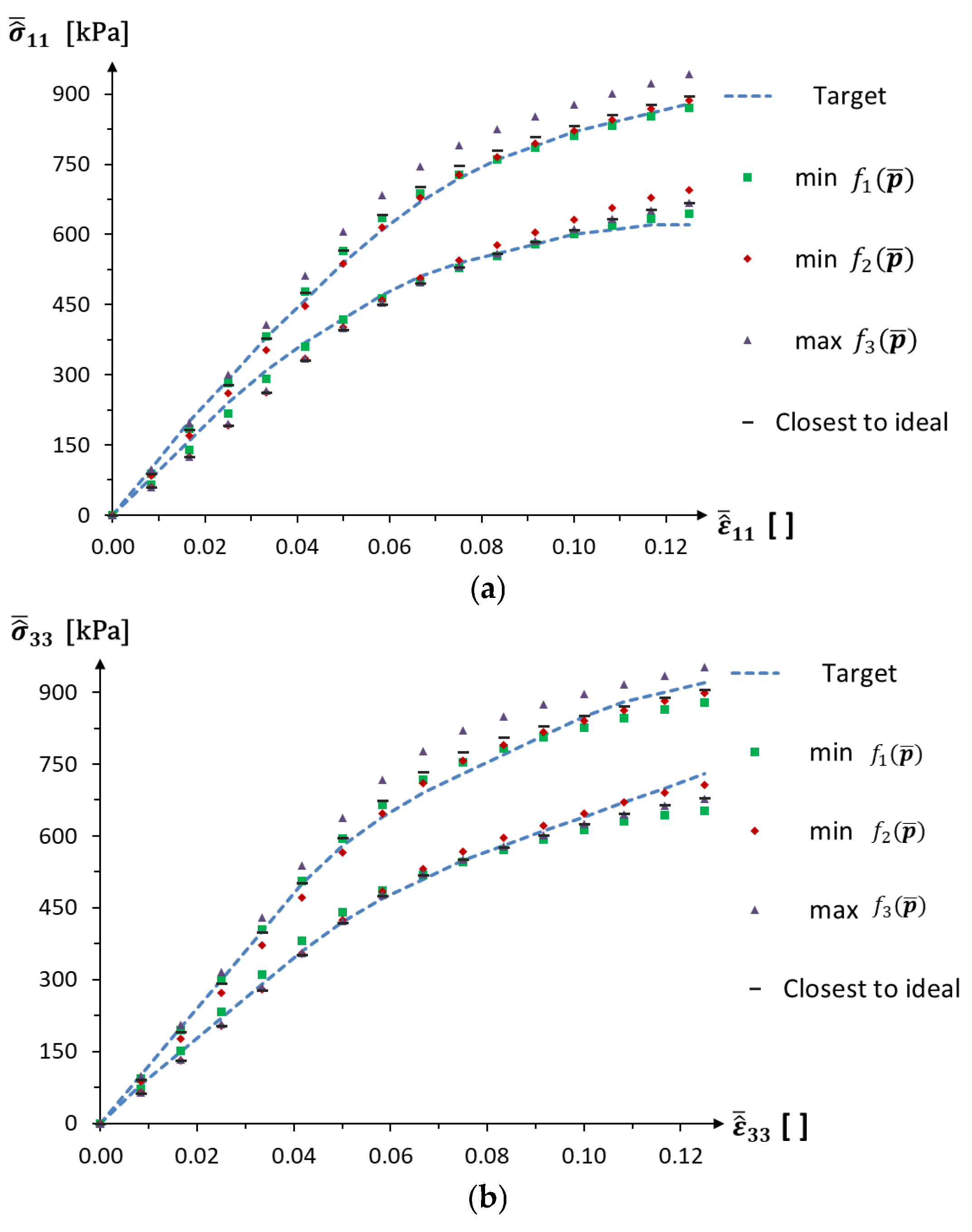
| 0.0083 | 0.0167 | 0.025 | 0.0333 | 0.0417 | 0.050 | 0.0583 | 0.0667 | ||
|---|---|---|---|---|---|---|---|---|---|
| [kPa] | min | 80 | 160 | 240 | 310 | 370 | 420 | 470 | 510 |
| max | 100 | 200 | 290 | 380 | 460 | 540 | 610 | 670 | |
| [kPa] | min | 80 | 150 | 220 | 290 | 360 | 420 | 470 | 510 |
| max | 100 | 200 | 300 | 400 | 500 | 580 | 640 | 690 | |
| 0.075 | 0.0833 | 0.0917 | 0.1000 | 0.1083 | 0.1167 | 0.125 | |||
| [kPa] | min | 540 | 560 | 580 | 600 | 610 | 620 | 620 | |
| max | 720 | 760 | 790 | 820 | 840 | 860 | 880 | ||
| [kPa] | min | 550 | 580 | 610 | 640 | 670 | 700 | 730 | |
| max | 730 | 770 | 810 | 850 | 880 | 900 | 920 |
| Pareto Point | Closest to Ideal | |||
|---|---|---|---|---|
| [mm] | [1.0788, 1.1232] | [1.0238, 1.0822] | [1.0145, 1.1315] | [1.0112, 1.1028] |
| [o] | [22.2422, 22.9978] | [19.9566, 22.1034] | [19.2005, 21.2595] | [19.4915, 21.3485] |
| [MPa] | [745.4873, 875.9127] | [750.6961, 828.3039] | [751.5213, 831.6787] | [751.0145, 832.3855] |
| [MPa] | [26.2683, 33.9317] | [33.3576, 37.2024] | [31.9203, 35.2797] | [32.3513, 35.6487] |
| 2.6072 × 10−2 | 7.5659 × 10−2 | 7.8118 × 10−2 | 5.1137 × 10−2 | |
| 8.7738 × 10−2 | 3.1619 × 10−2 | 8.9809 × 10−2 | 5.3233 × 10−2 | |
| 3.3393 × 10−2 | 5.5613 × 10−2 | 9.9995 × 10−2 | 8.6662 × 10−2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Beluch, W.; Hatłas, M.; Ptaszny, J.; Kloc-Ptaszna, A. Computational Homogenisation and Identification of Auxetic Structures with Interval Parameters. Materials 2025, 18, 4554. https://doi.org/10.3390/ma18194554
Beluch W, Hatłas M, Ptaszny J, Kloc-Ptaszna A. Computational Homogenisation and Identification of Auxetic Structures with Interval Parameters. Materials. 2025; 18(19):4554. https://doi.org/10.3390/ma18194554
Chicago/Turabian StyleBeluch, Witold, Marcin Hatłas, Jacek Ptaszny, and Anna Kloc-Ptaszna. 2025. "Computational Homogenisation and Identification of Auxetic Structures with Interval Parameters" Materials 18, no. 19: 4554. https://doi.org/10.3390/ma18194554
APA StyleBeluch, W., Hatłas, M., Ptaszny, J., & Kloc-Ptaszna, A. (2025). Computational Homogenisation and Identification of Auxetic Structures with Interval Parameters. Materials, 18(19), 4554. https://doi.org/10.3390/ma18194554






