Prediction of Mechanical Properties and Stress–Strain Relation of Closed-Cell Aluminium Foam Under Compression Using Neural Network Models
Abstract
1. Introduction
1.1. Literature Overview
1.2. Previous Research Step
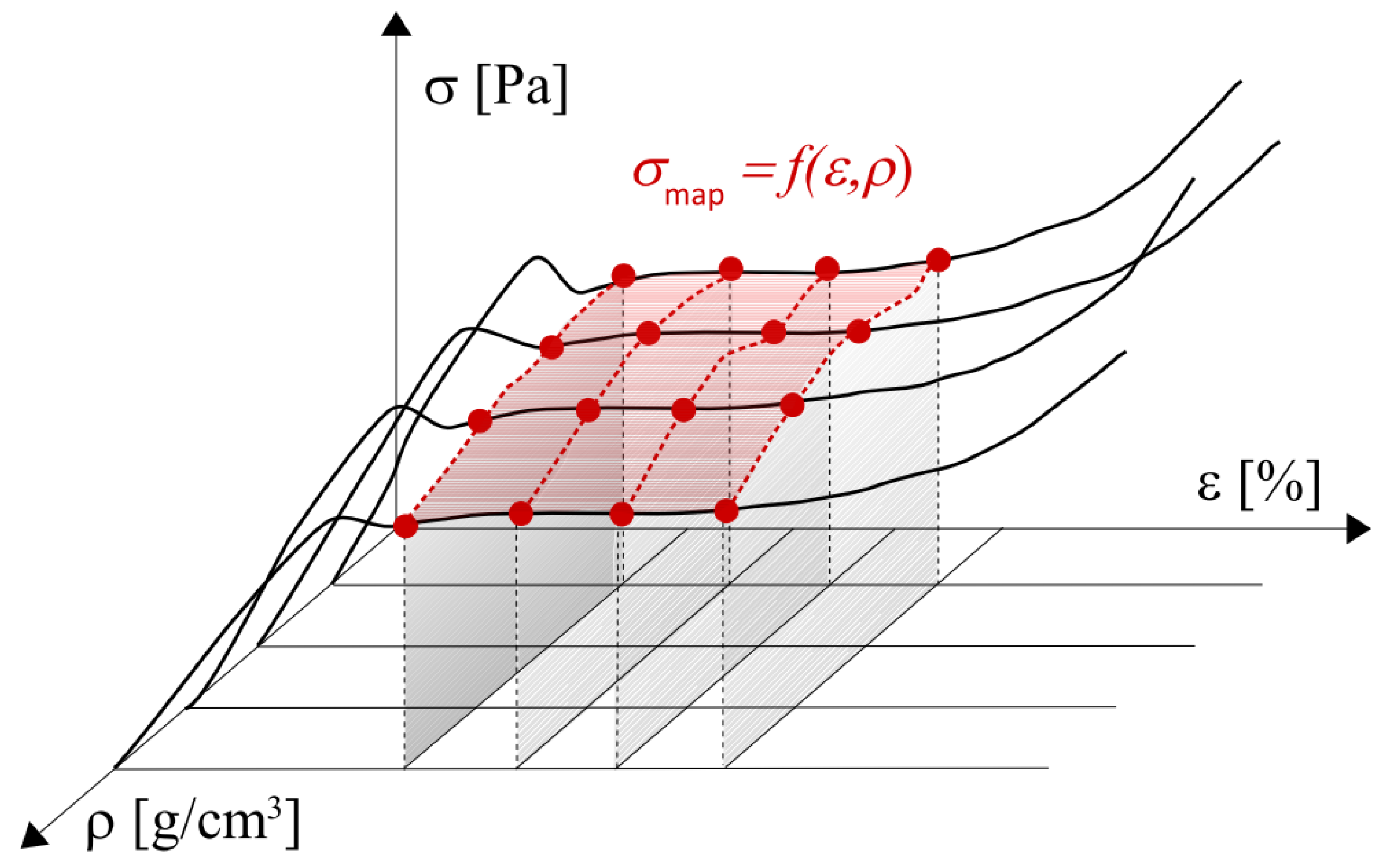
1.3. Aims and Contributions of This Work
- Finding a data-driven stress–strain model of compression of closed-cell aluminium foam for a range of apparent densities. The relationship has an engineering application potential due to its good mapping accuracy (weighted mean absolute relative error ).
- Verification of NNs’ ability to identify mechanical features associated with density (plateau stress), which was not provided directly in the training data.
- Introduction of network quality assessment criteria that were connected with mechanical properties (plateau stress and quasi-static elastic gradient), which enabled the evaluation of networks’ extrapolation capability and finding the best model.
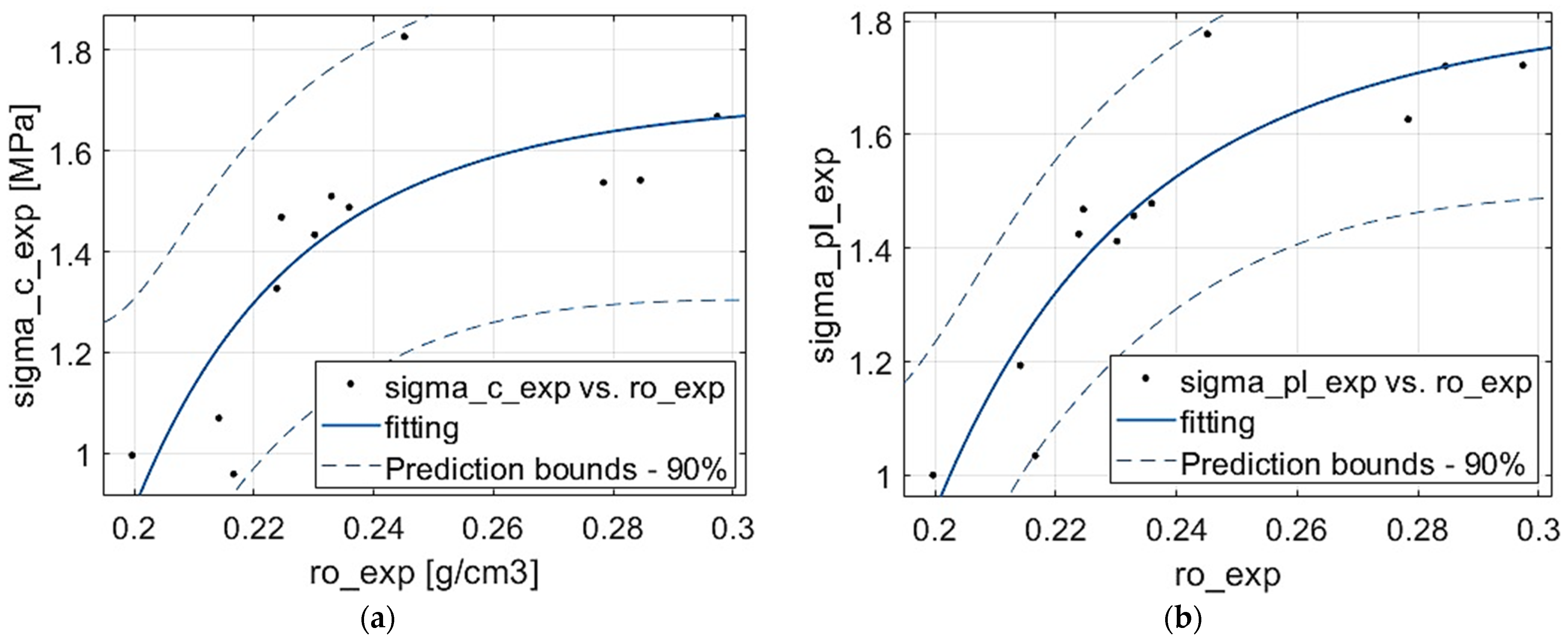
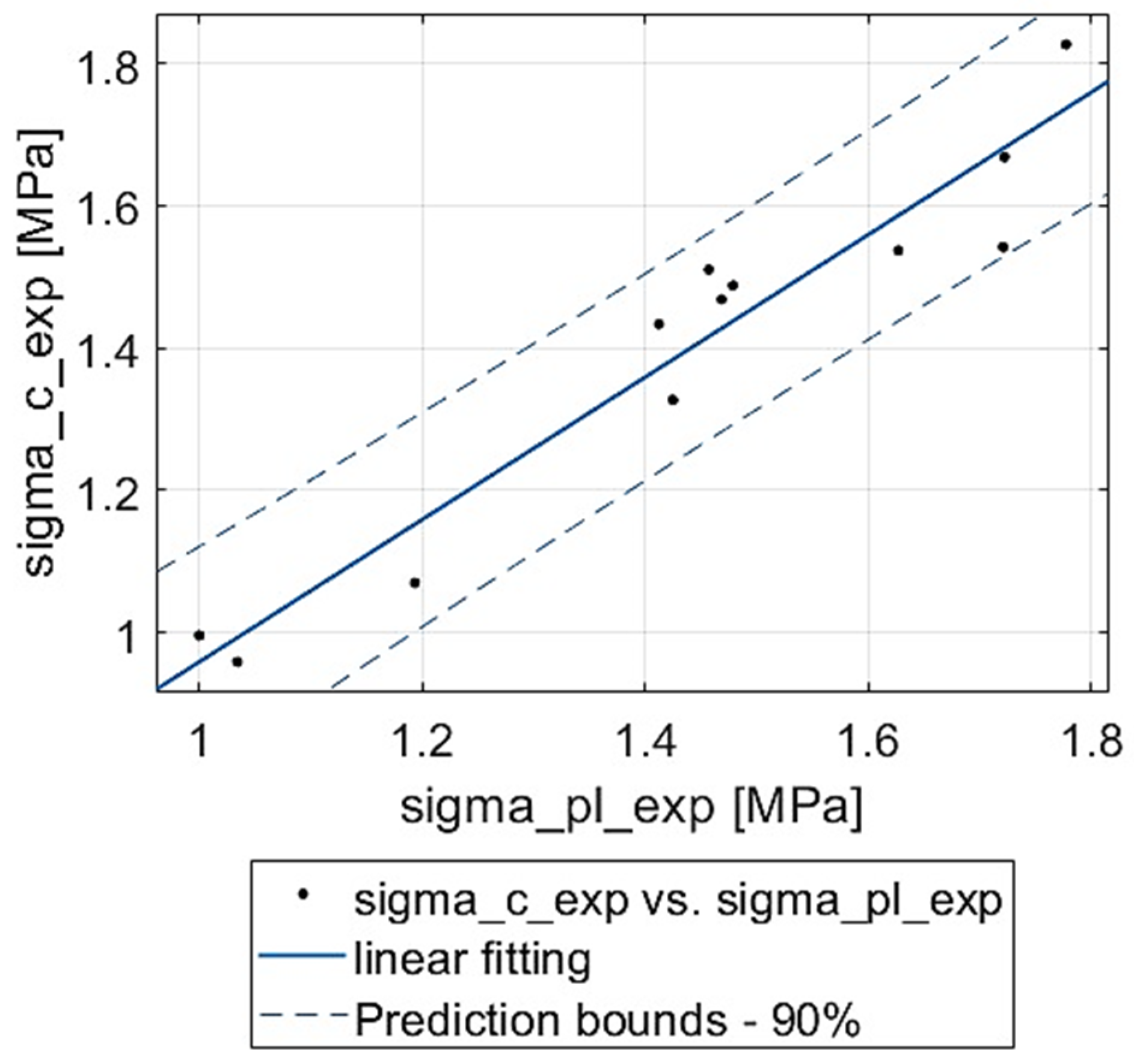
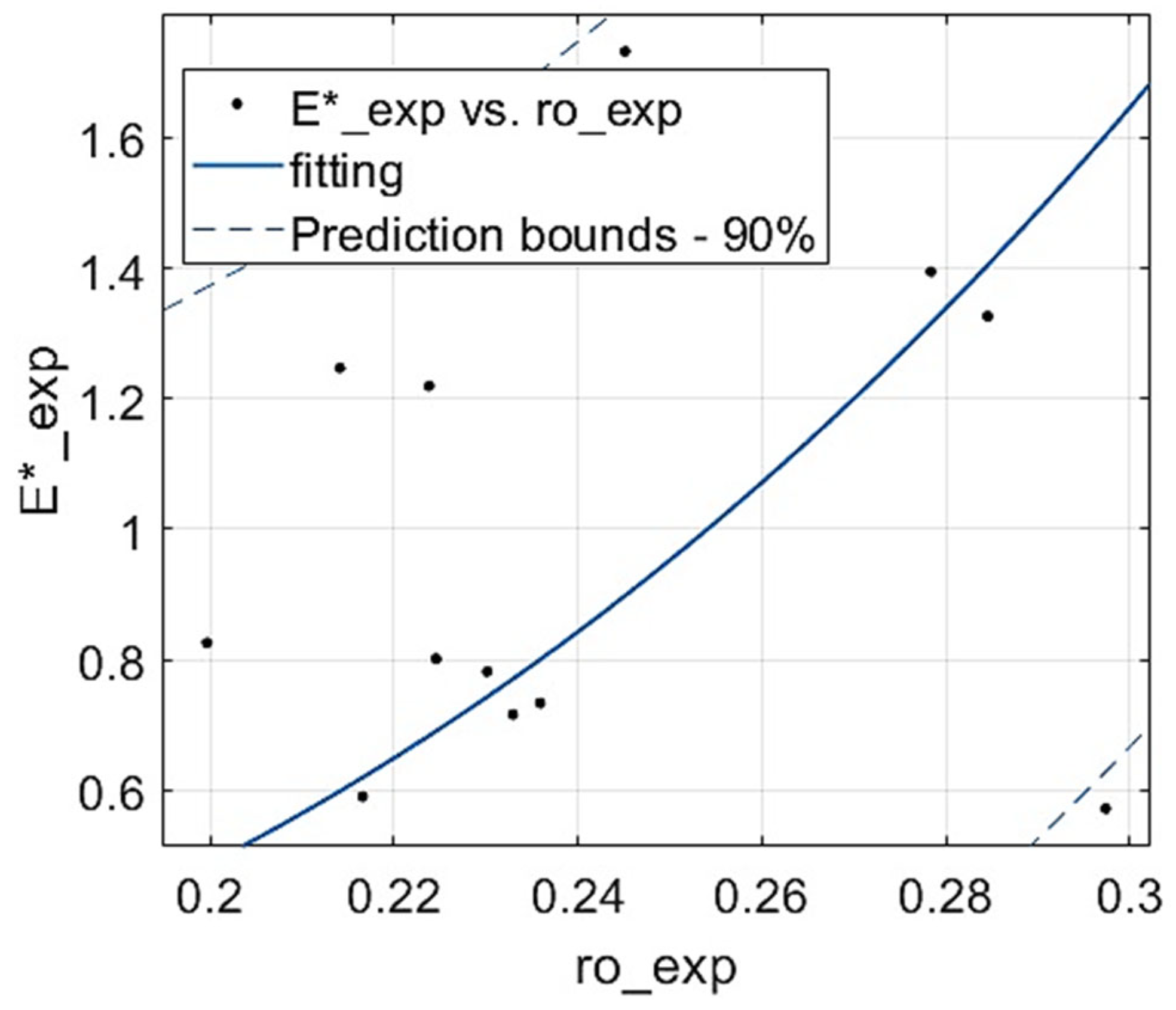
- Finding functions correlating the experimental results of plateau stress with density and compressive strength with plateau stress.
2. Materials and Methods
2.1. Experimental Compression of Closed-Cell Aluminium
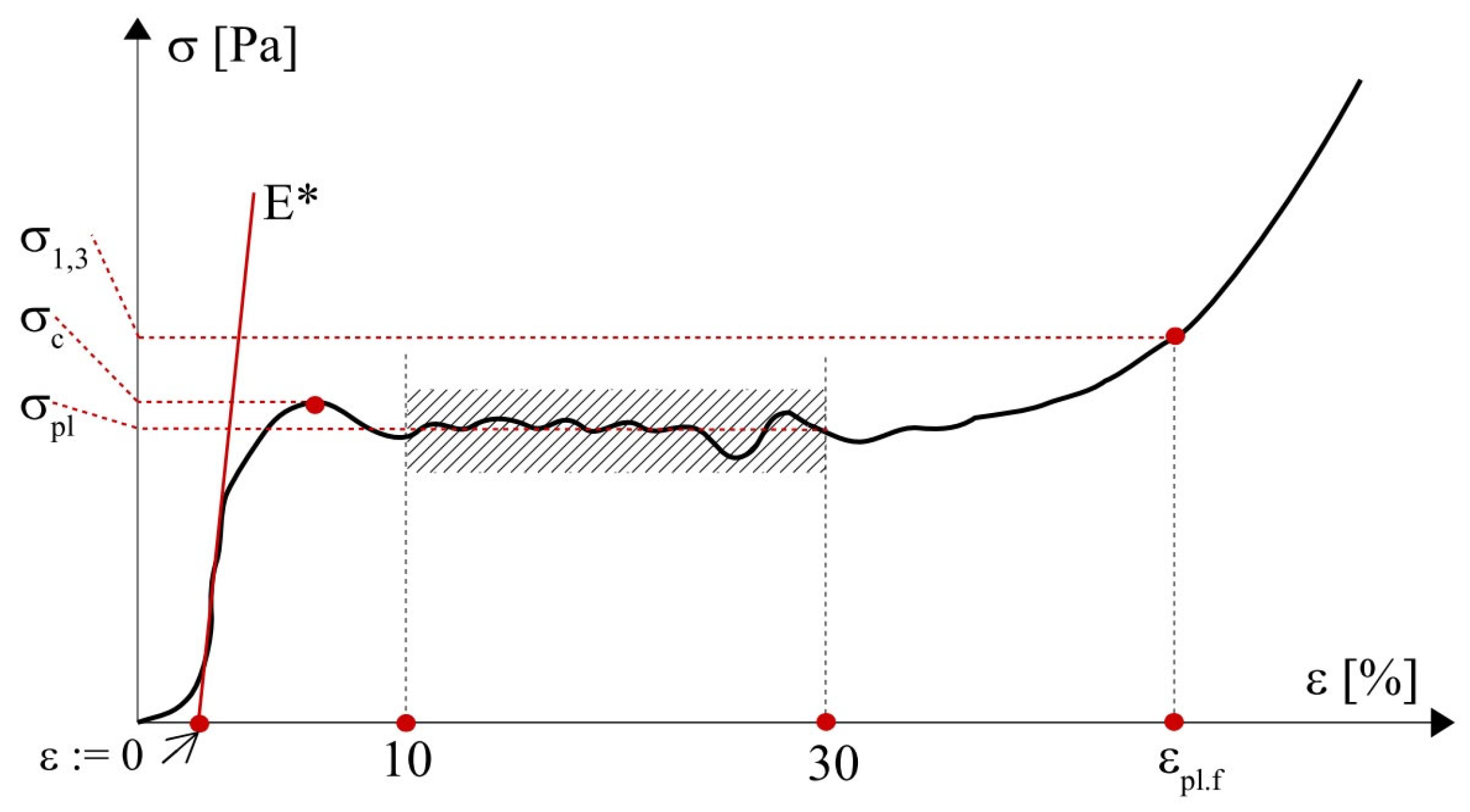
2.2. Determination of Mechanical Properties
- —compressive strength—which should be understood as the stress corresponding to the first local maximum of stresses.
- —plateau stress—calculated as the arithmetic mean of plateau stresses; here assumed for stresses corresponding to strains in the range of 10–30%.
- —auxiliary measure for calculation of plateau end.
- —plateau end strain—strain corresponding to stress . Phenomenologically, it marks the beginning of the densification of the material.
2.3. Neural Network Modelling and Its Quality Assessment
- —mean absolute relative error at the testing stage or respectively at the verification stage,
- —given number of neurons in the hidden layer of the considered network, here ,
- —given number of the training repetition of the considered network, here ,
- —the -th target for the network at the testing stage or respectively at the verification stage,
- —the -th output of the network at the testing stage or respectively at the verification stage,
- —individual data index, should exhaust all data for the given stage,
- —the assumed threshold value for the quality condition at the respective stage.
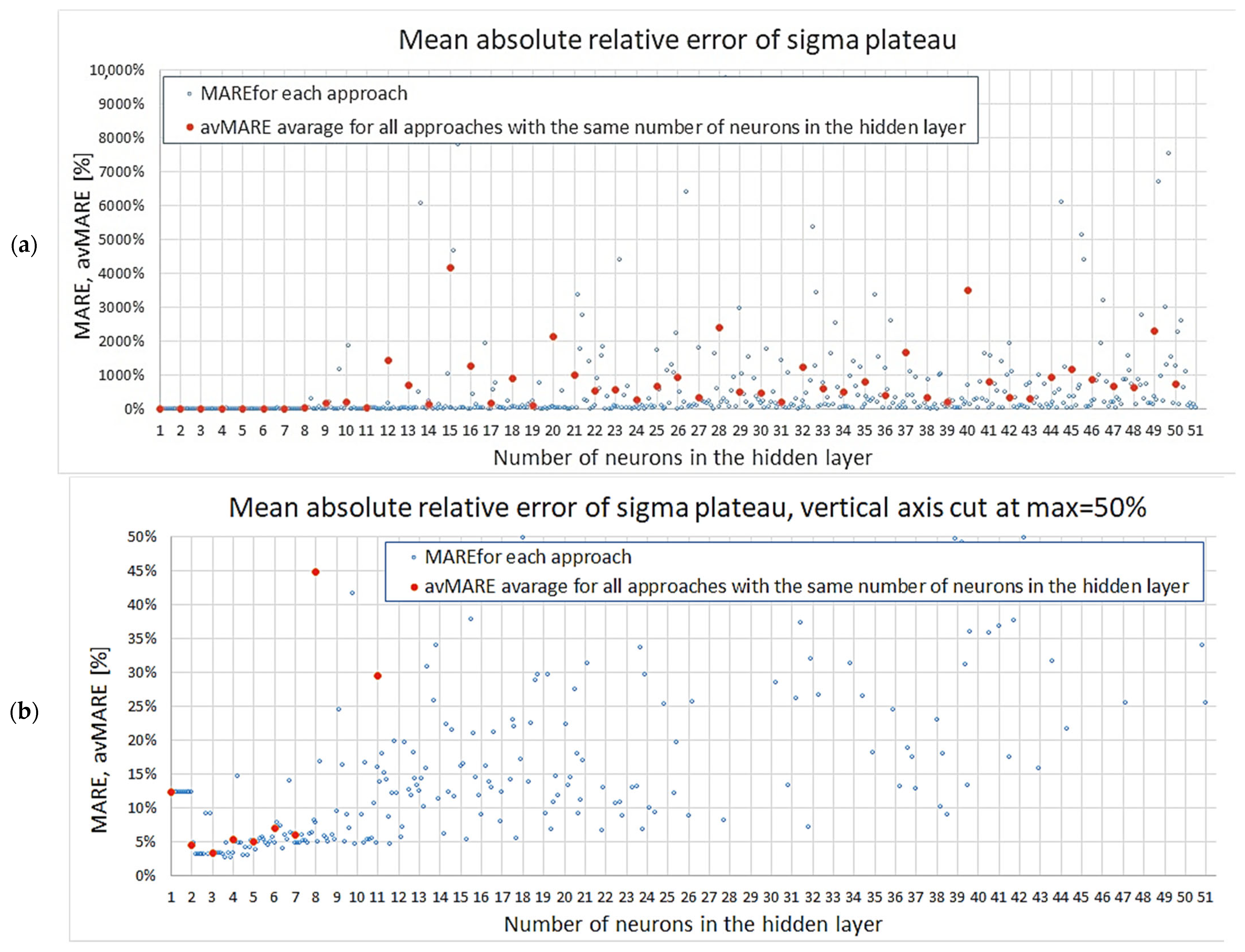
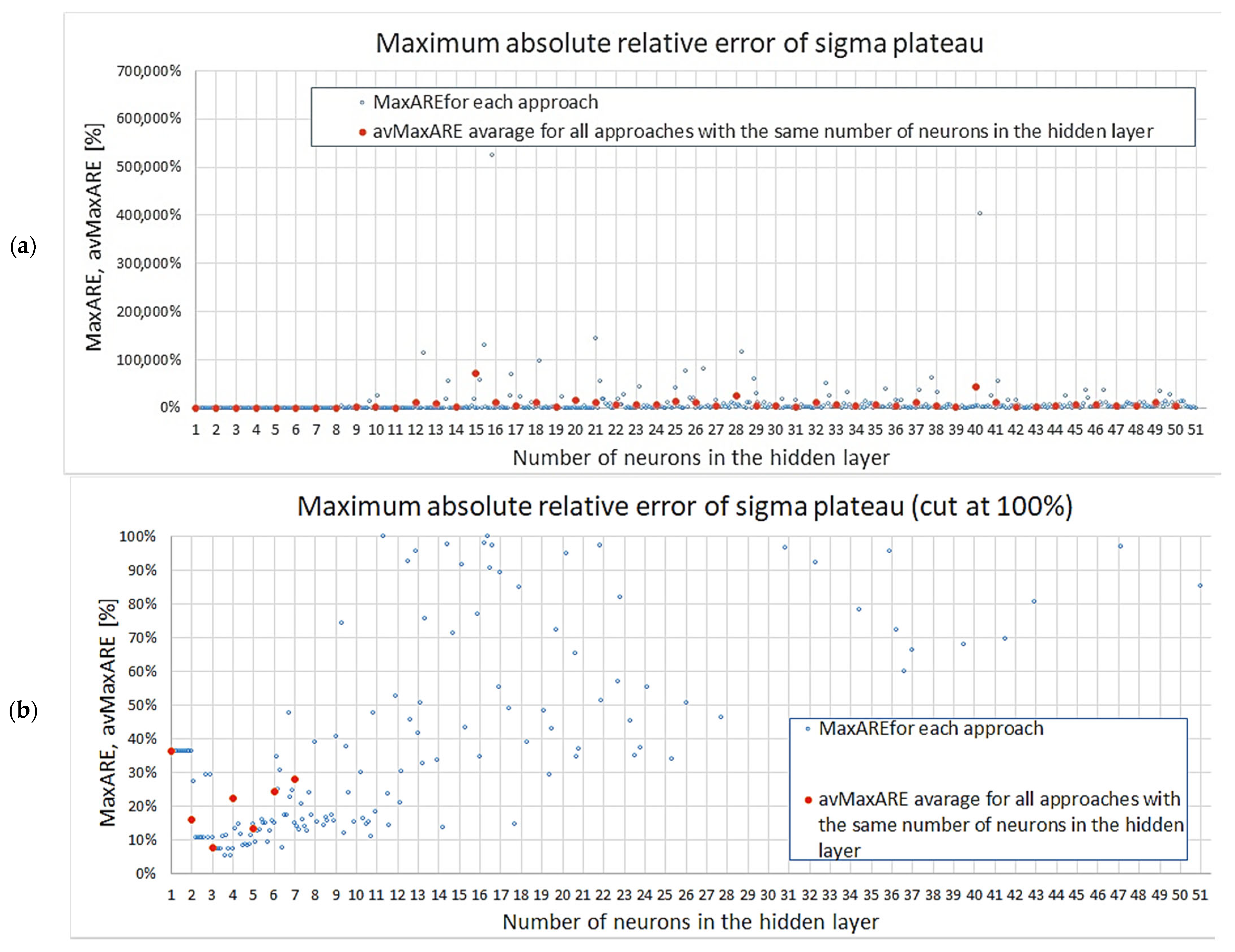
2.4. Mechanical Properties from Neural Network Models
- —mean absolute relative error for the considered property,
- —maximal absolute relative error for the considered property,
- —given number of neurons in the hidden layer of the considered network, here ,
- —given number of the training repetition of the considered network, here ,
- —property value from the experimental fitting relation for the -th apparent density,
- —property value from the considered network mapping relation for the -th apparent density,
- —indicator of the given apparent density value or values, here ,
- , —the assumed threshold values for the quality conditions for the considered property.
2.5. Choice of the Best Networks
- —the weight for the measure at the test stage,
- —the weight for the measure at the verification stage,
- —the weight for the measure for the -th mechanical property,
- —number of considered mechanical properties.
- —the assumed threshold value for the weighted quality condition.
3. Results and Discussion
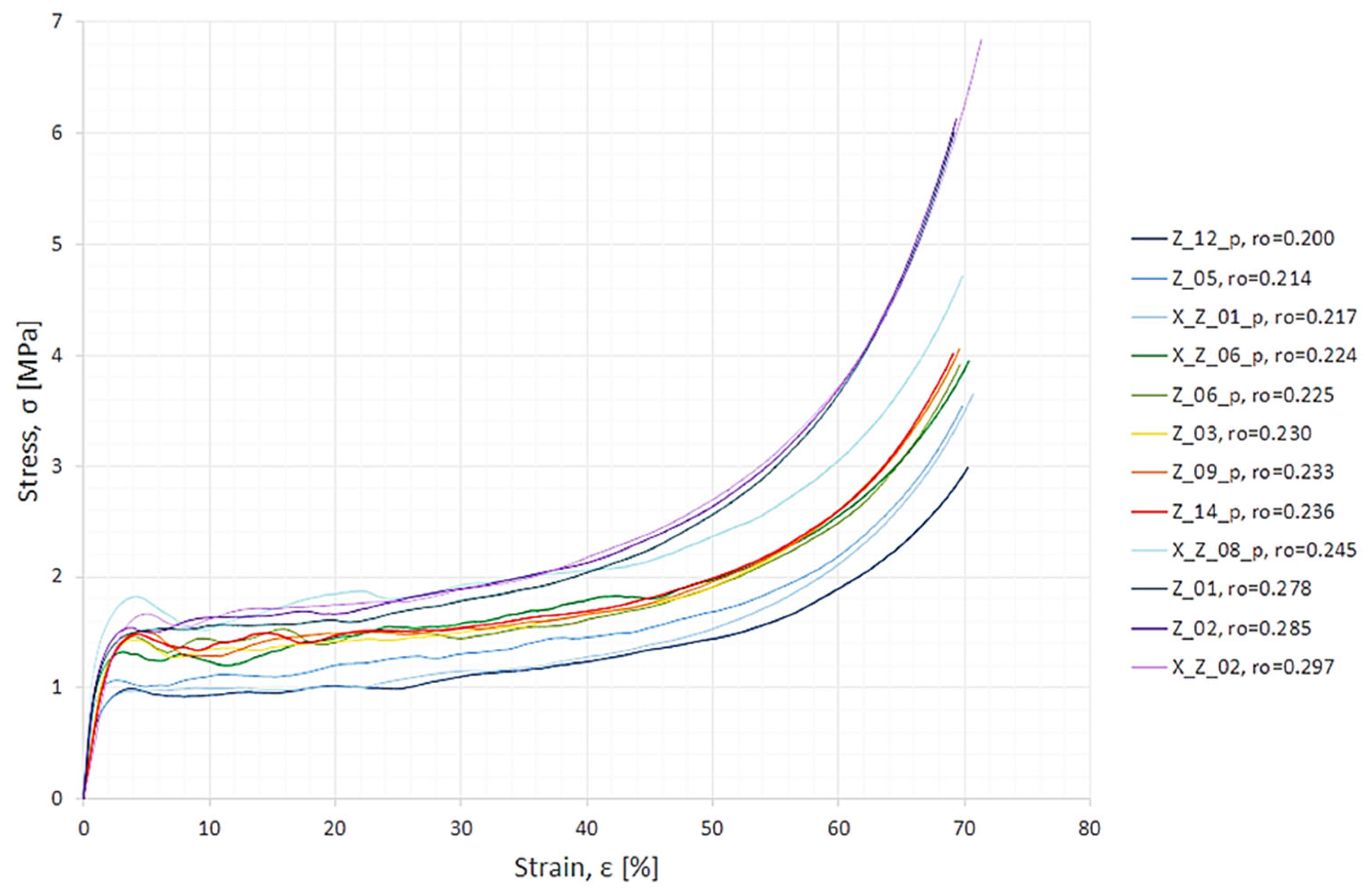
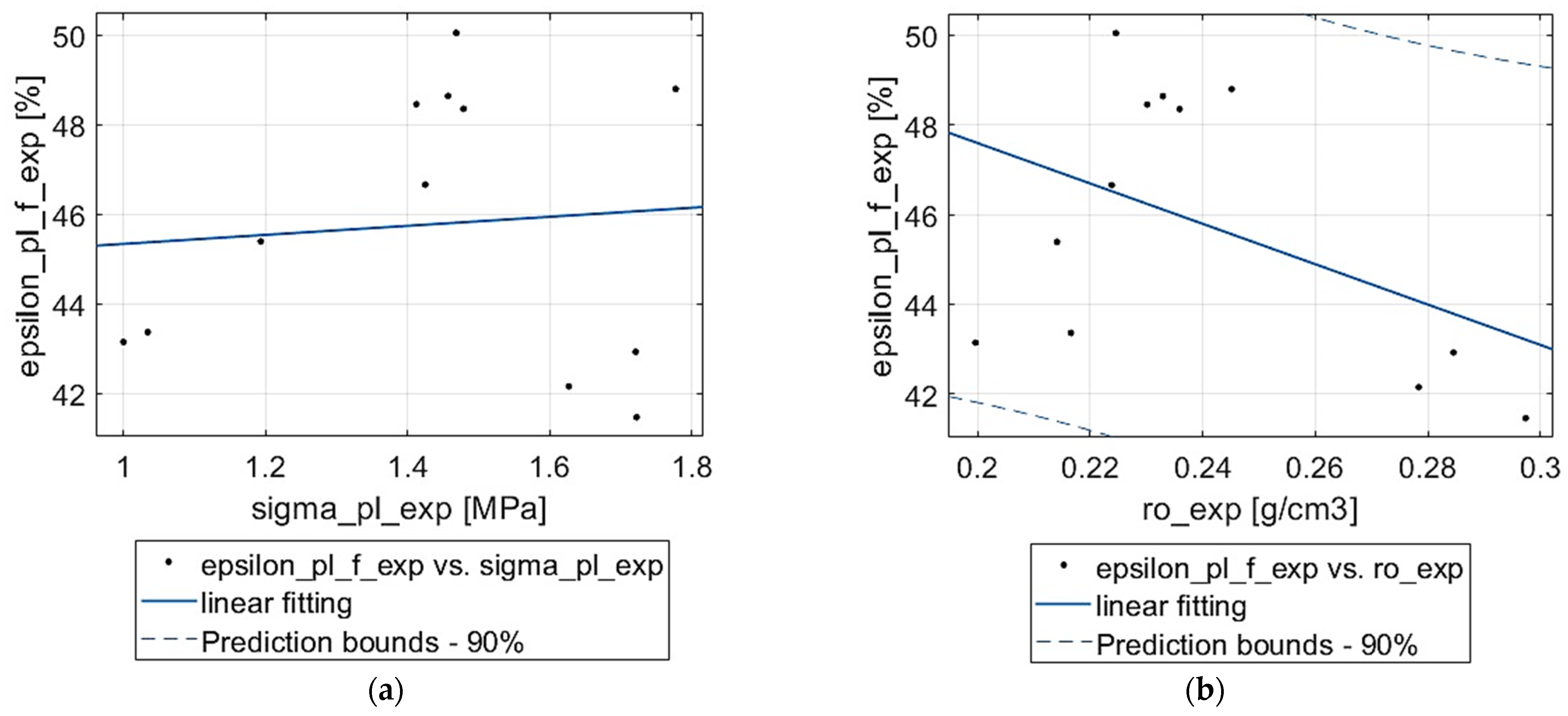
3.1. Mechanical Properties from Experiment
- —plastic yield point of foam,
- —plastic yield point of skeleton material,
- —apparent density of foam,
- —apparent density of skeleton material,
- —constant to be determined experimentally.
- —Young’s modulus of foam,
- —Young’s modulus of skeleton material,
- —apparent density of foam,
- —apparent density of skeleton material,
- —constant to be determined experimentally.
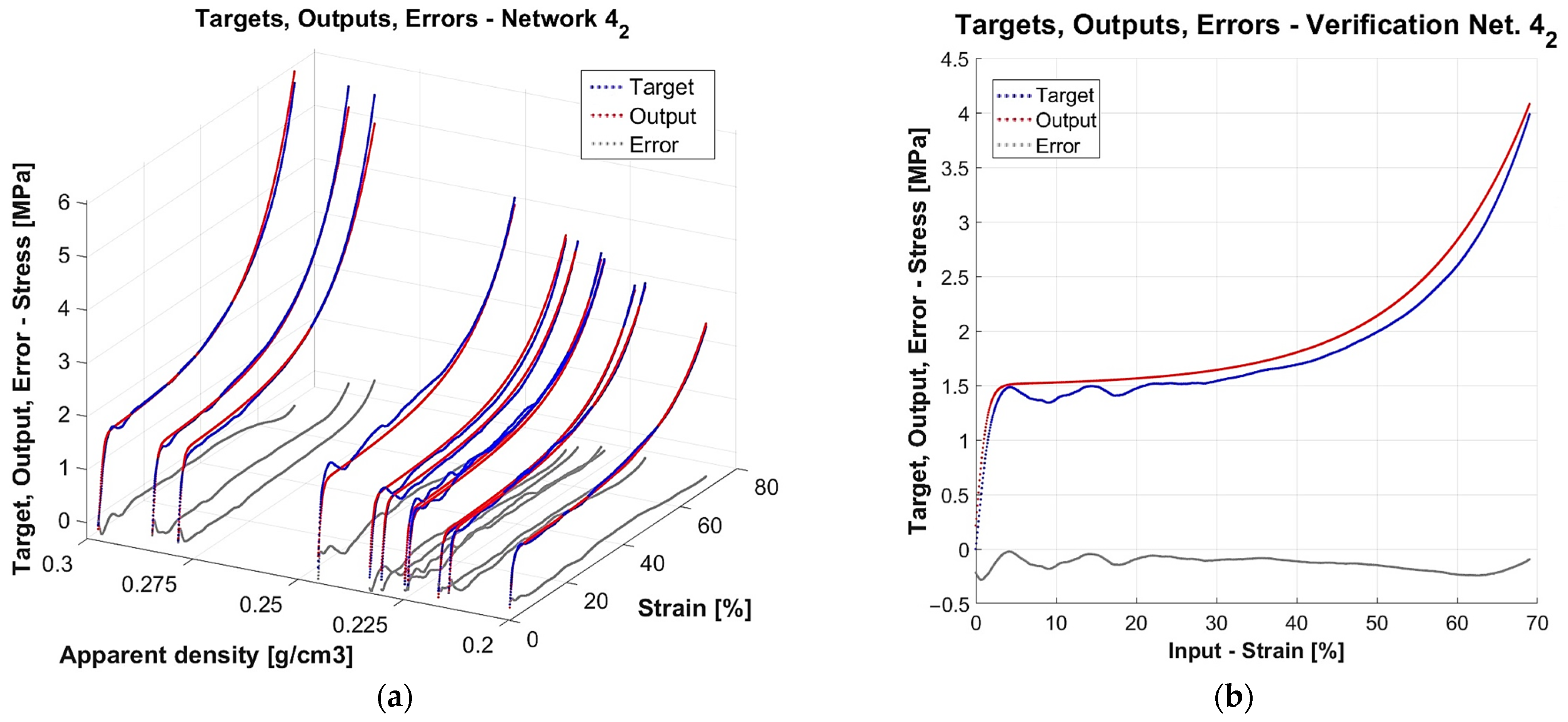
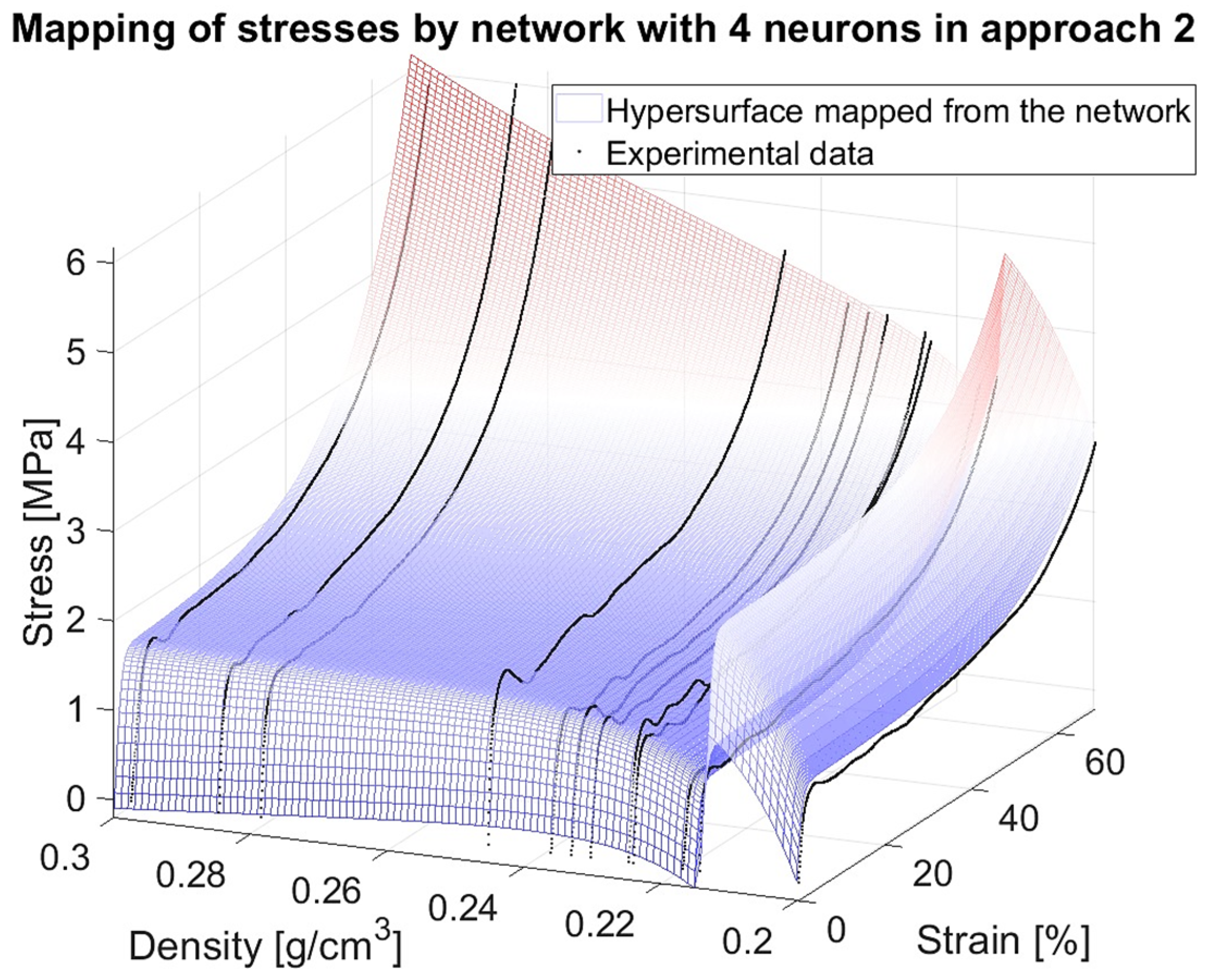
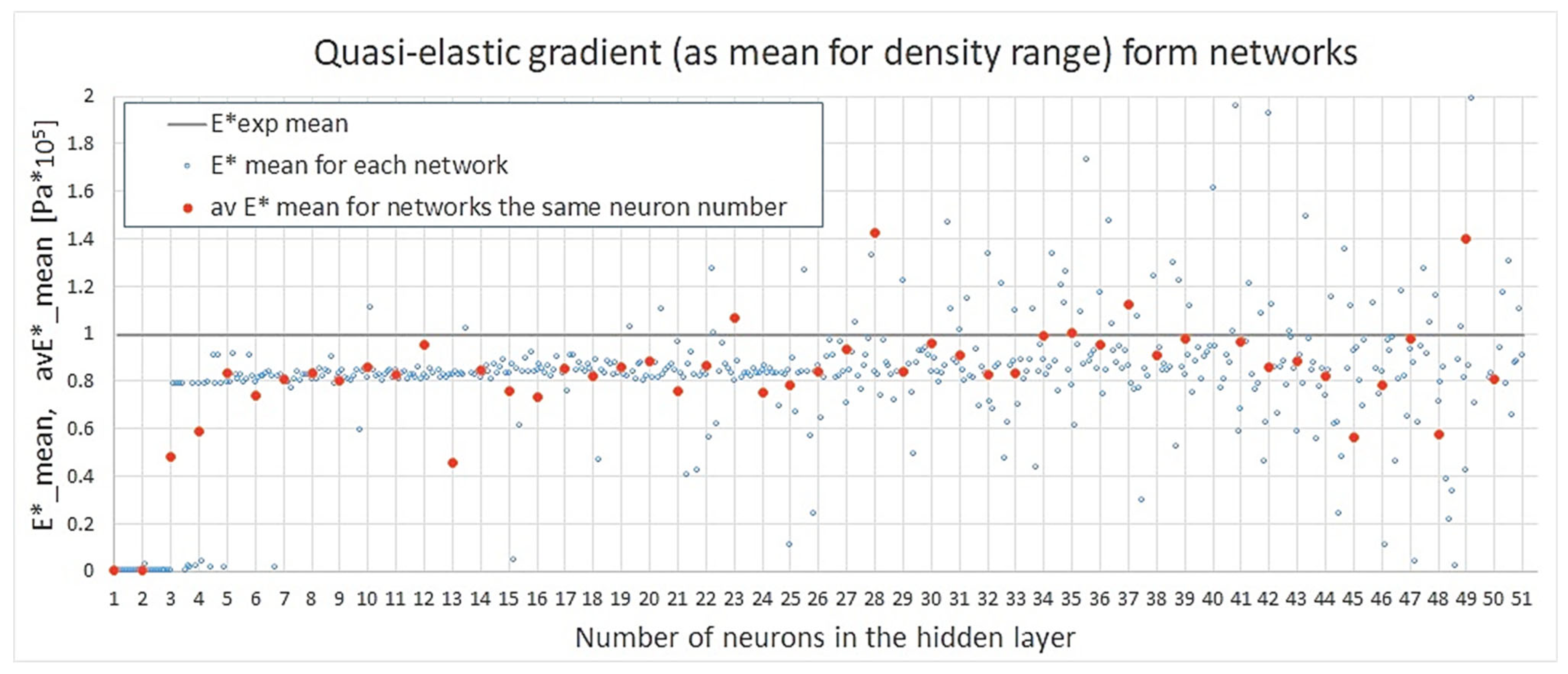
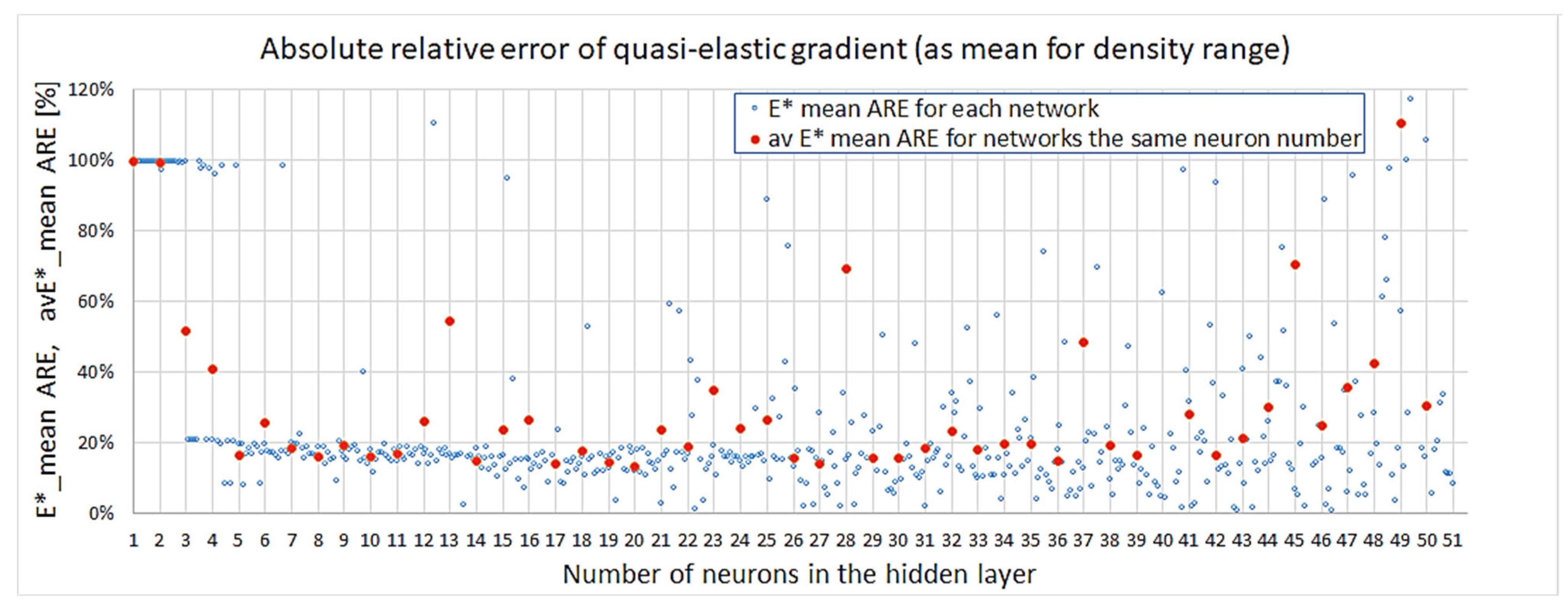
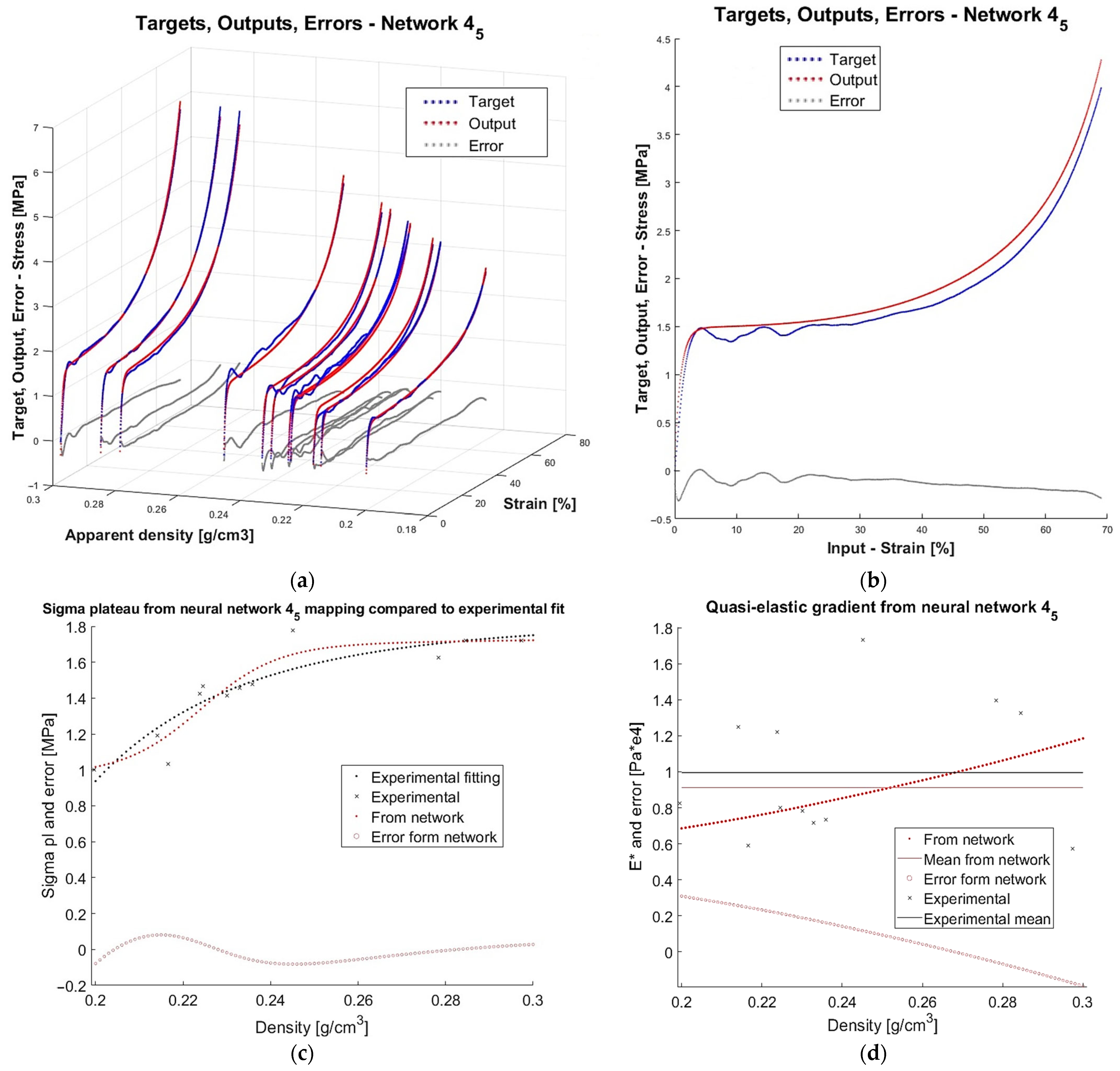
3.2. Results for Mechanical Properties from Neural Network Models
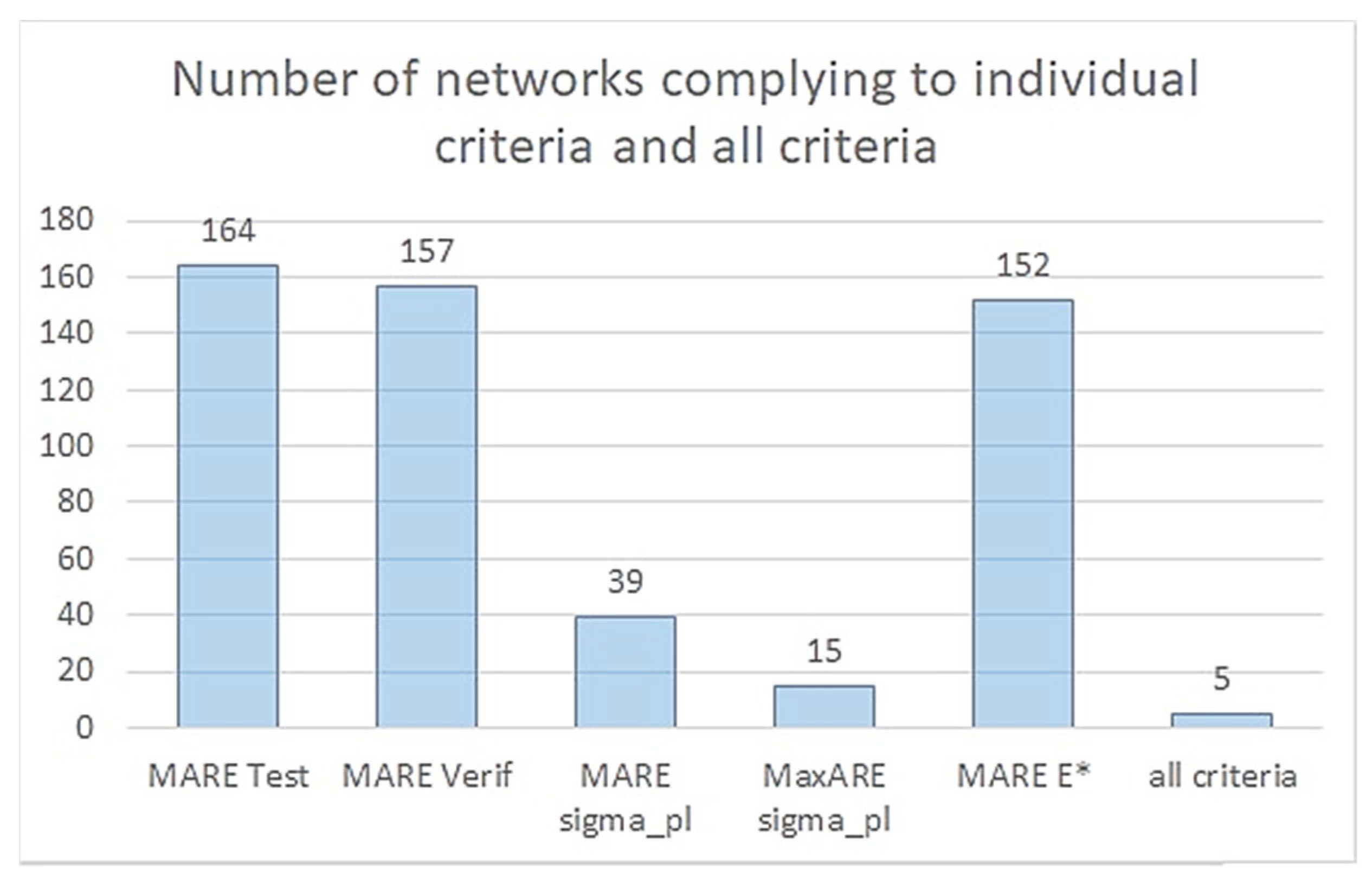
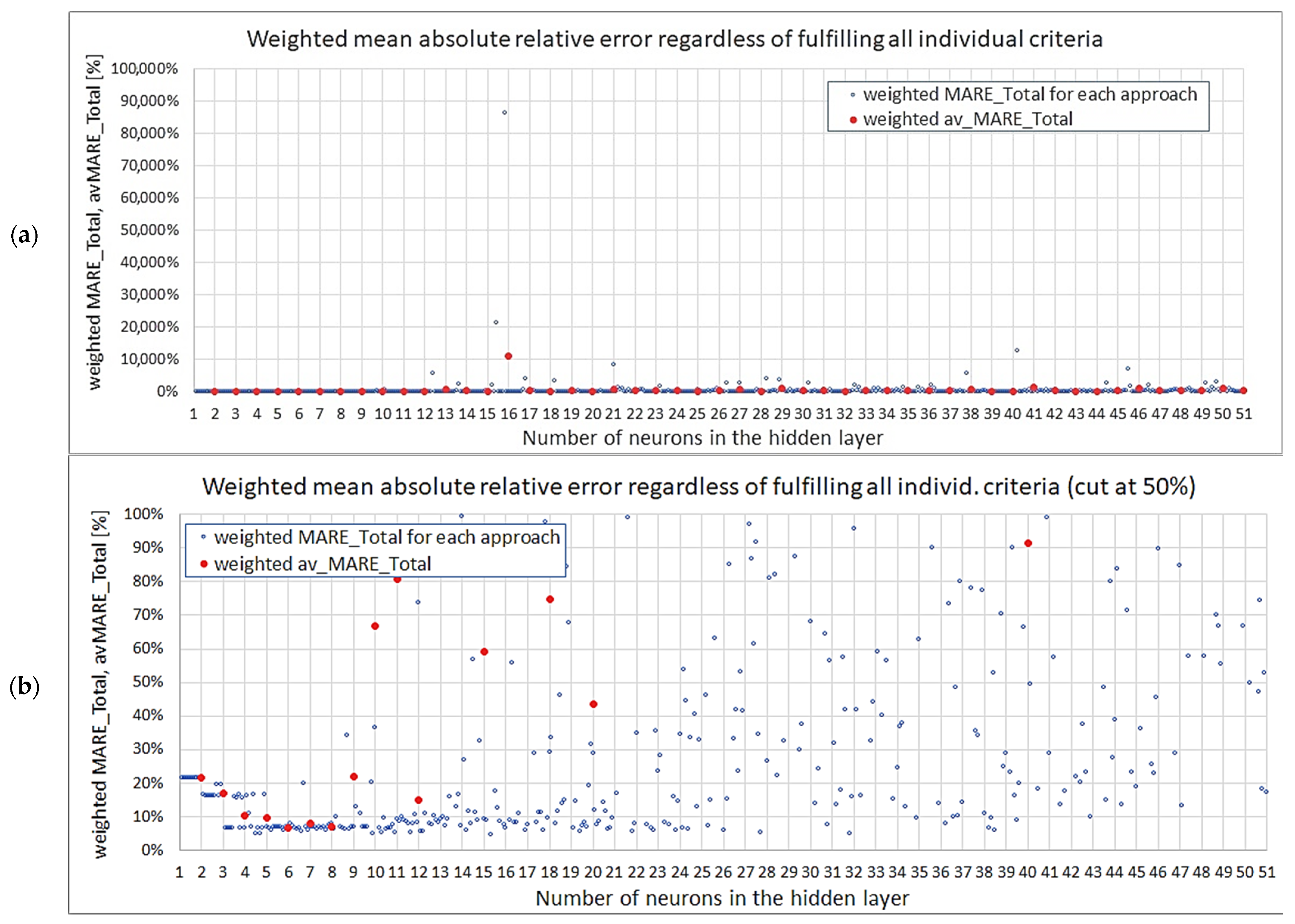
3.3. Choice of the Best Network
4. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AI | Artificial Intelligence |
| ANN(s) | Artificial Neural Network(s) |
| ARE | Absolute Relative Error |
| CNN(s) | Convolutional Neural Network(s) |
| CT | Computed Tomography |
| DIC | Digital Image Correlation |
| DT | Data Tree |
| FEM | Finite Element Method |
| LR | Linear Regression |
| LR | Logistic Regression |
| MARE | Mean Absolute Relative Error |
| ML | Machine Learning |
| NN(s) | Neural Network(s) |
| PR | Polynomial Regression |
| RF | Random Forest |
| RMSE | Root Mean Squared Error |
| RVE(s) | Representative Volume Element(s) |
| SSE | Sum of Square Errors |
| VAE(S) | Variational Autoencoder(s) |
Appendix A
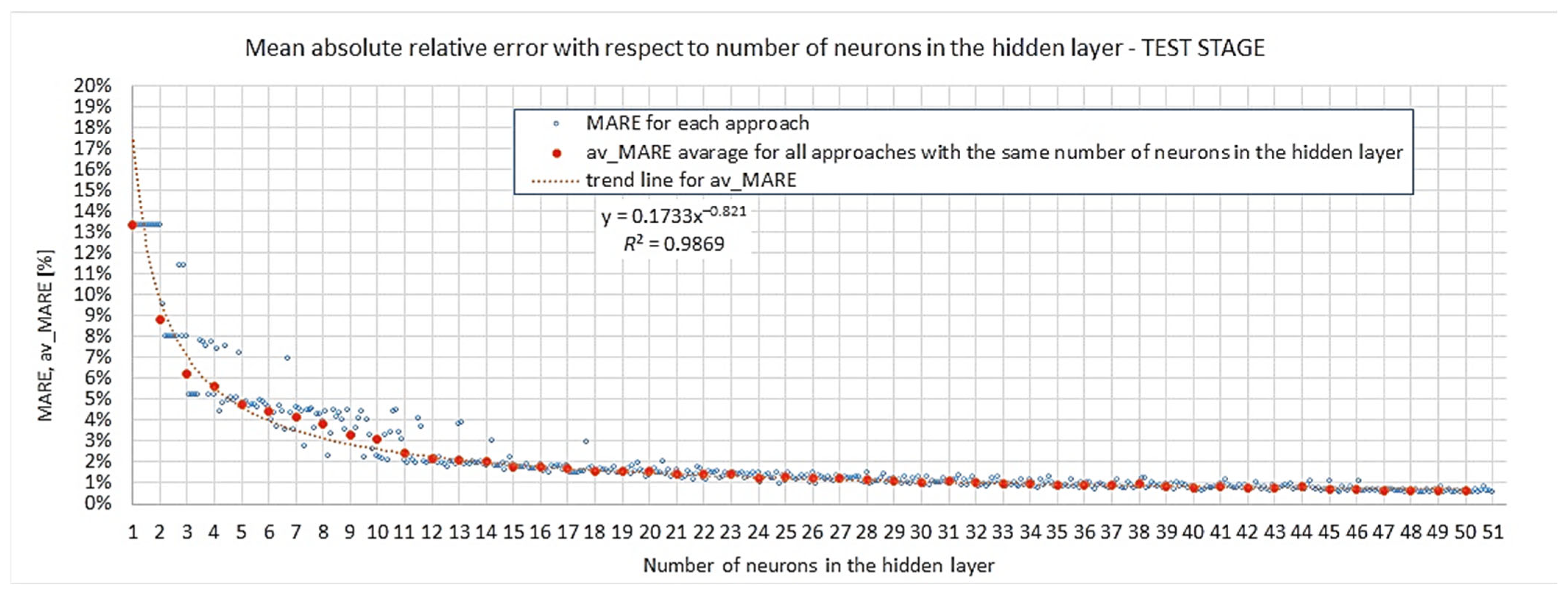
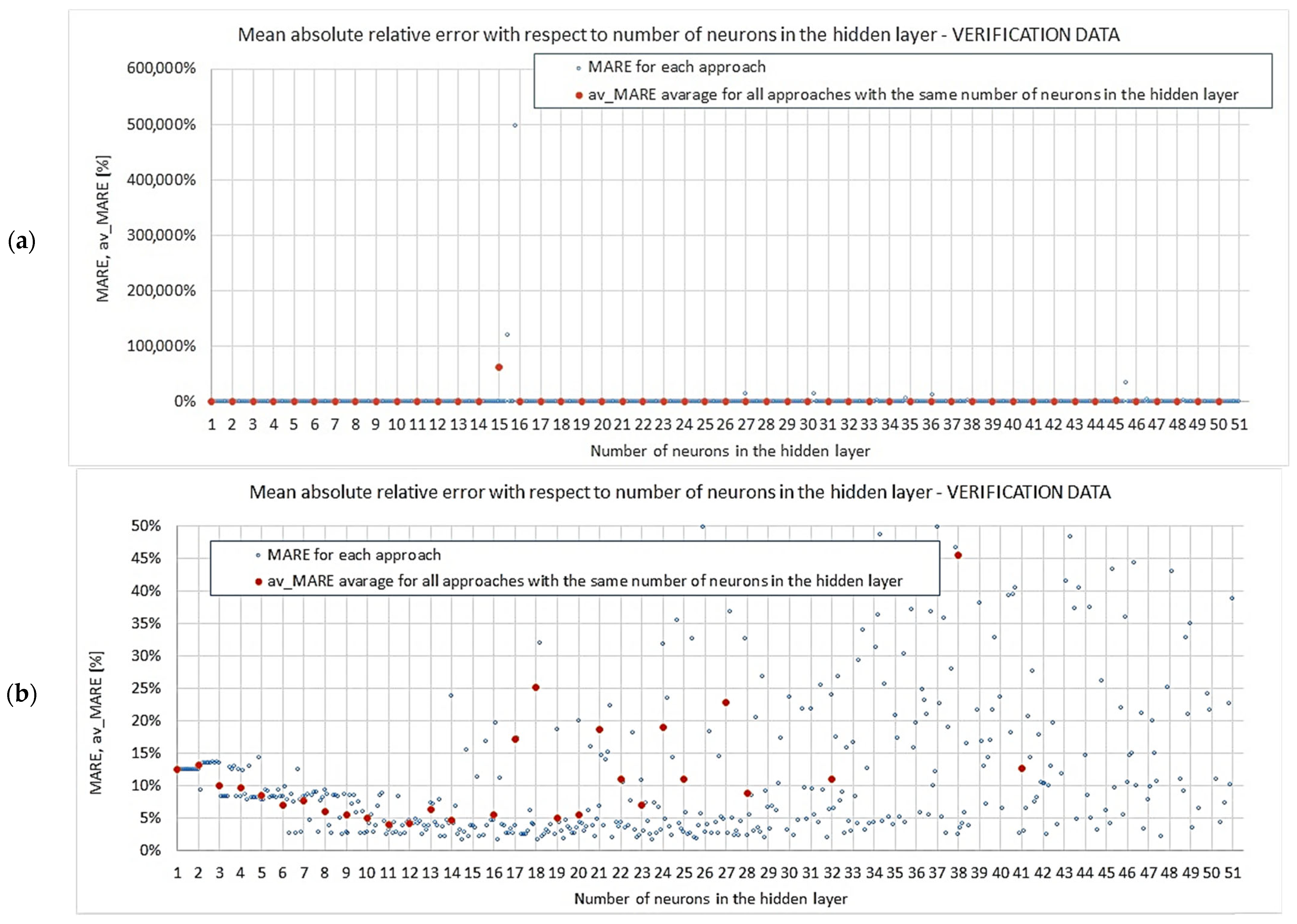
Appendix B
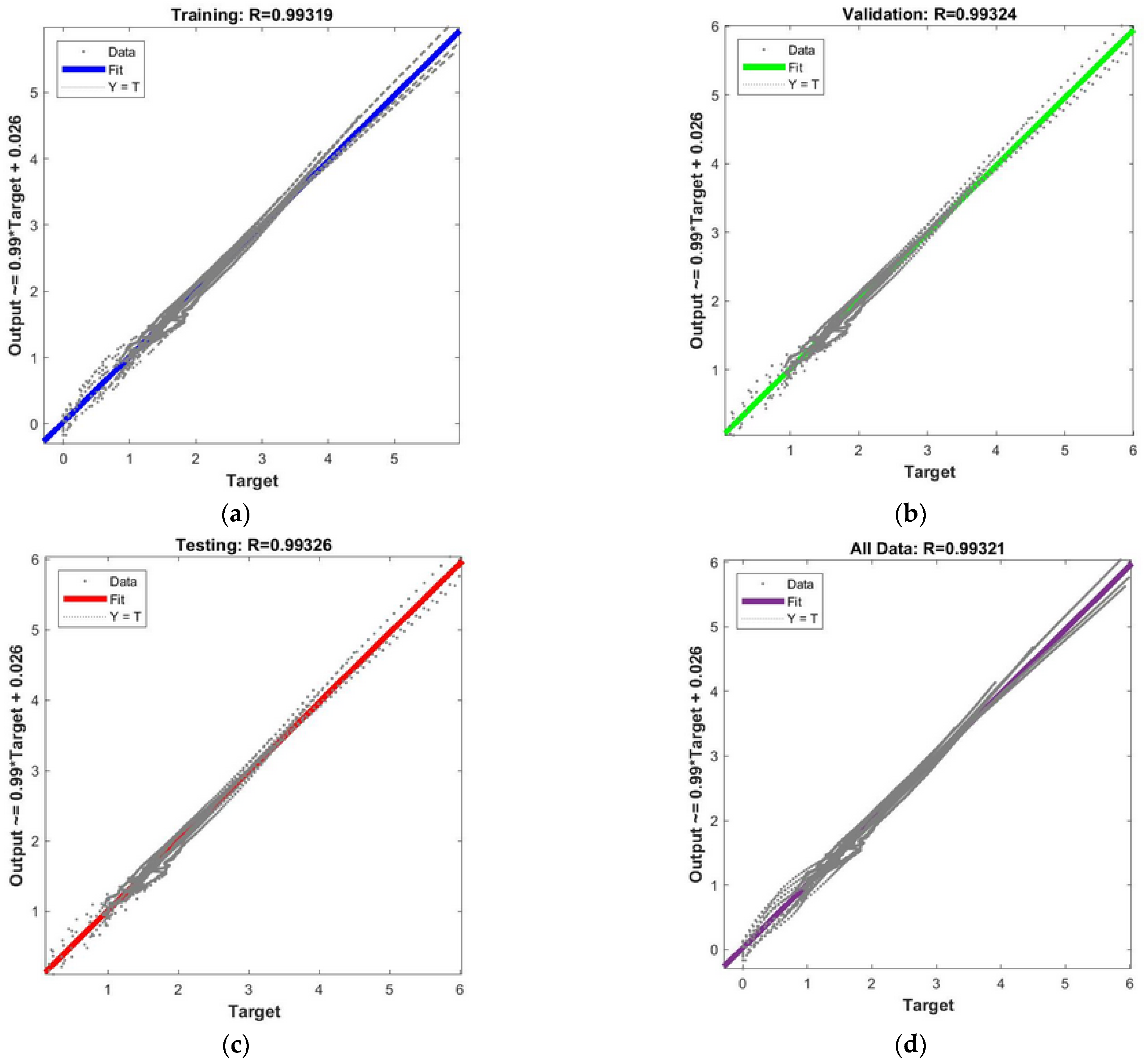
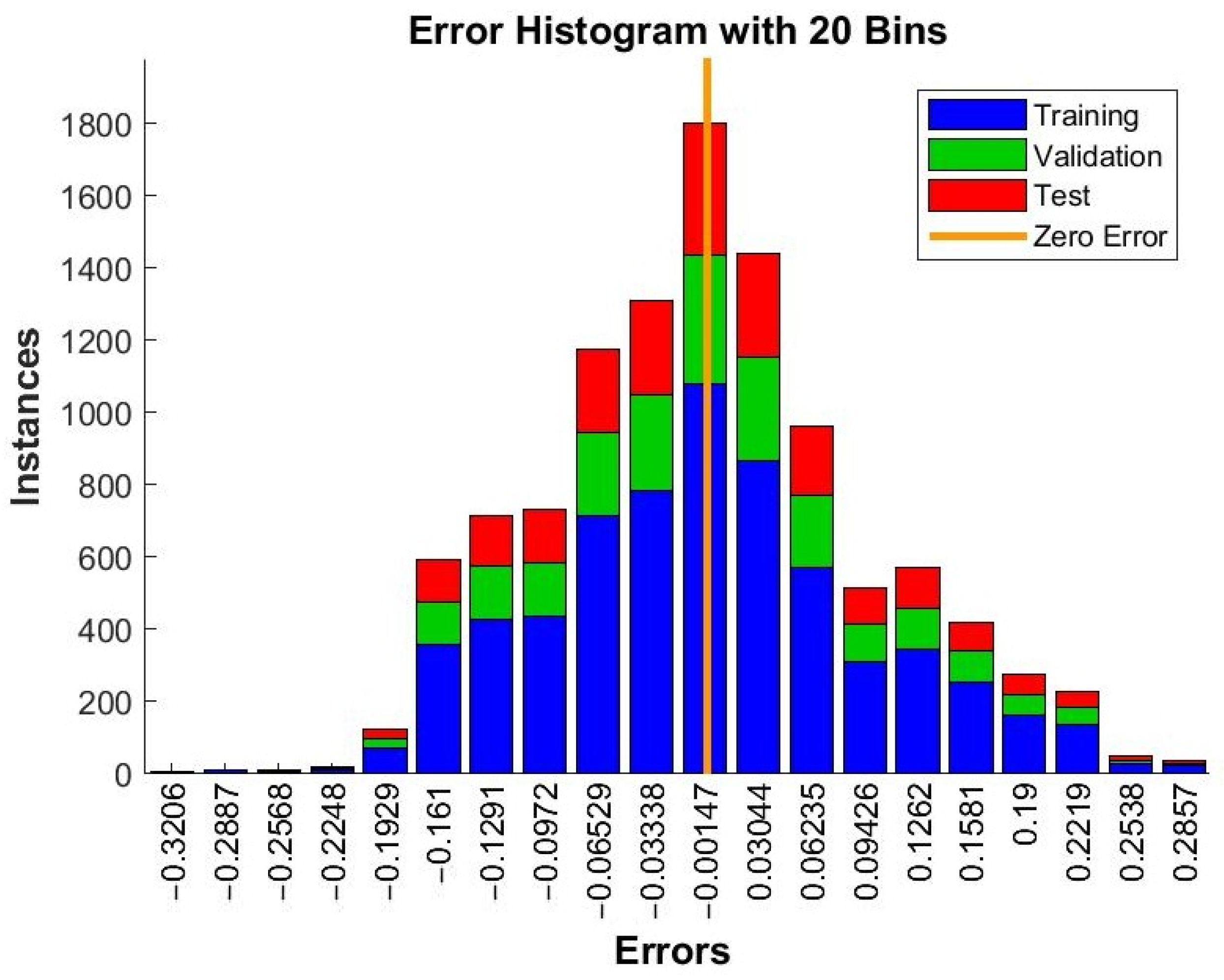
References
- Hamdan, Z.K.; Bakhy, S.H.; Jweeg, M.J. Review of Mechanical Properties, Manufacturing, and Applications of Metal Foams. J. Teknol. 2025, 87, 723–740. [Google Scholar] [CrossRef]
- Fu, W.; Li, Y. Fabrication, Processing, Properties, and Applications of Closed-Cell Aluminum Foams: A Review. Materials 2024, 17, 560. [Google Scholar] [CrossRef]
- Madgule, M.; Sreenivasa, C.G.; Borgaonkar, A.V. Aluminium metal foam production methods, properties and applications- a review. Mater. Today Proc. 2022, 77, 673–679. [Google Scholar] [CrossRef]
- Dineshkumar, J.; Jesudas, T.; Elayaraja, R. Characteristics, applications and processing of aluminium foams—A Review. Mater. Today Proc. 2021, 42, 1773–1776. [Google Scholar] [CrossRef]
- Patel, P.; Bhingole, P.; Makwana, D. Manufacturing, characterization and applications of lightweight metallic foams for structural applications: Review. Mater. Today Proc. 2018, 5, 20391–20402. [Google Scholar] [CrossRef]
- Zhao, B.; Gain, A.K.; Ding, W.; Zhang, L.; Li, X.; Fu, Y. A review on metallic porous materials: Pore formation, mechanical properties, and their applications. Int. J. Adv. Manuf. Technol. 2017, 95, 2641–2659. [Google Scholar] [CrossRef]
- Farhadi, S.; Kafili, D.; Ziadloo, S. Review of Aluminum Foam Applications in Architecture. Eur. J. Eng. Sci. Technol. 2020, 3, 62–70. [Google Scholar] [CrossRef]
- Wang, L.B.; See, K.Y.; Ling, Y.; Koh, W.J. Study of Metal Foams for Architectural Electromagnetic Shielding. J. Mater. Civ. Eng. 2012, 24, 488–493. [Google Scholar] [CrossRef]
- de la Peña, A.; Sato, A.; Latour, M.; Rizzano, G. Conceptual design of anti-seismic devices with metal foam core for CBFs. Procedia Struct. Integr. 2023, 44, 2144–2151. [Google Scholar] [CrossRef]
- Stręk, A.M.; Lasowicz, N.; Kwiecień, A.; Zając, B.; Jankowski, R. Highly Dissipative Materials for Damage Protection against Earthquake-Induced Structural Pounding. Materials 2021, 14, 3231. [Google Scholar] [CrossRef]
- Bisht, A.; Patel, V.K.; Gangil, B. Future of Metal Foam Materials in Automotive Industry. In Automotive Tribology Energy, Environment, and Sustainability; Katiyar, J., Bhattacharya, S., Patel, V., Kumar, V., Eds.; Springer: Singapore, 2019. [Google Scholar] [CrossRef]
- Sharma, S.S.; Yadav, S.; Joshi, A.; Goyal, A.; Khatri, R. Application of metallic foam in vehicle structure: A review. Mater. Today Proc. 2022, 63, 347–353. [Google Scholar] [CrossRef]
- Neu, T.R.; Heim, K.; Seeliger, W.; Kamm, P.H.; García-Moreno, F. Aluminum Foam Sandwiches: A Lighter Future for Car Bodies. JOM 2024, 76, 2619–2630. [Google Scholar] [CrossRef]
- Cocks, F.H. Ultralight reactive metal foams in space—A novel concept. J. Spacecr. Rocket. 1984, 21, 510–512. [Google Scholar] [CrossRef]
- Zhu, L.; Li, N.; Childs, P.R.N. Light-weighting in aerospace component and system design. Propuls. Power Res. 2018, 7, 103–119. [Google Scholar] [CrossRef]
- Wang, S.; Hou, X.; Yin, J.; Xing, Y.; Wang, Z. Comparative Study of the Thermal Enhancement for Spacecraft PCM Thermal Energy Storage Units. Aerospace 2022, 9, 705. [Google Scholar] [CrossRef]
- Lewis, G. Properties of open-cell porous metals and alloys for orthopaedic applications. J. Mater. Sci. Mater. Med. 2013, 24, 2293–2325. [Google Scholar] [CrossRef]
- Rodriguez-Contreras, A.; Punset, M.; Calero, J.A.; Gil, F.J.; Ruperez, E.; Manero, J.M. Powder metallurgy with space holder for porous titanium implants: A review. J. Mater. Sci. Technol. 2021, 76, 129–149. [Google Scholar] [CrossRef]
- Singh, R.; Lee, P.D.; Dashwood, R.J.; Lindley, T.C. Titanium foams for biomedical applications: A review. Mater. Technol. 2013, 25, 127–136. [Google Scholar] [CrossRef]
- Gąsior, G.; Grodzicka, M.; Jędrzejewski, T.; Wiśniewski, M.; Radtke, A. Comparative Study of Porous Iron Foams for Biodegradable Implants: Structural Analysis and In Vitro Assessment. J. Funct. Biomater. 2023, 14, 293. [Google Scholar] [CrossRef]
- Buonomo, B.; Golia, M.R.; Manca, O.; Nardini, S. A review on thermal energy storage with phase change materials enhanced by metal foams. Therm. Sci. Eng. Prog. 2024, 53, 102732. [Google Scholar] [CrossRef]
- Ma, X.; Jing, Z.; Feng, C.; Qiao, M.; Xu, D. Research and development progress of porous foam-based electrodes in advanced electrochemical energy storage devices: A critical review. Renew. Sustain. Energy Rev. 2023, 173, 113111. [Google Scholar] [CrossRef]
- Tan, W.C.; Saw, L.H.; Thiam, H.S.; Xuan, J.; Cai, Z.; Yew, M.C. Overview of porous media/metal foam application in fuel cells and solar power systems. Renew. Sustain. Energy Rev. 2018, 96, 181–197. [Google Scholar] [CrossRef]
- Egorov, V.; O’Dwyer, C. Architected porous metals in electrochemical energy storage. Curr. Opin. Electrochem. 2020, 21, 201–208. [Google Scholar] [CrossRef]
- Ashby, M.F.; Evans, A.; Fleck, N.; Gibson, L.J.; Hutchinson, J.W.; Wadley, H.N. Metal Foams: A Design Guide; Elsevier Science: Burlington, MA, USA, 2000. [Google Scholar]
- Stręk, A. Methodology for Experimental Investigations of Metal Foams and Their Mechanical Properties. Mech. Control. 2012, 31, 90. [Google Scholar] [CrossRef][Green Version]
- DIN 50134:2008-10; Prüfung von Metallischen Werkstoffen—Druckversuch an Metallischen Zellularen Werkstoffen. Beuth Verlag GmbH: Berlin, Germany, 2008.
- ISO 13314:2011; Mechanical Testing of Metals—Ductility Testing—Compression Test for Porous and Cellular Metals. International Organization for Standardization: Geneva, Switzerland, 2011.
- JIS H 7902:2008; Method for Compressive Test of Porous Metals. Japanese Standards Association: Tokyo, Japan, 2008.
- Stręk, A.M. Determination of material characteristics in the quasi-static compression test of cellular metal materials. In Wybrane Problem Geotechniki i Wytrzymałości Materiałów dla Potrzeb Nowoczesnego Budownictwa, 1st ed.; Tatara, T., Pilecka, E., Eds.; Wydawnictwo Politechniki Krakowskiej: Kraków, Poland, 2020. (In Polish) [Google Scholar]
- Kalpakoglou, T.; Yiatros, S. Metal foams: A review for mechanical properties under tensile and shear stress. Front. Mater. 2022, 9, 998673. [Google Scholar] [CrossRef]
- ASTM E8/E8M-24; Standard Test Methods for Tension Testing of Metallic Materials. ASTM International: West Conshohocken, PA, USA, 2024.
- Marx, J.; Rabiei, A. Tensile properties of composite metal foam and composite metal foam core sandwich panels. J. Sandw. Struct. Mater. 2020, 23, 3773–3793. [Google Scholar] [CrossRef]
- ASTM C297/C297M-16(2024); Standard Test Method for Flatwise Tensile Strength of Sandwich Constructions. ASTM International: West Conshohocken, PA, USA, 2024.
- Wang, X.-Z.; Wu, L.-Z.; Wang, S.-X. Tensile and shear properties of aluminium foam. Mater. Technol. 2009, 24, 161–165. [Google Scholar] [CrossRef]
- ASTM C273/C273M-11; Standard Test Method for Shear Properties of Sandwich Core Materials. ASTM International: West Conshohocken, PA, USA, 2011.
- Blazy, J.-S.; Marie-Louise, A.; Forest, S.; Chastel, Y.; Pineau, A.; Awade, A.; Grolleron, C.; Moussy, F. Deformation and fracture of aluminium foams under proportional and non proportional multi-axial loading: Statistical analysis and size effect. Int. J. Mech. Sci. 2004, 46, 217–244. [Google Scholar] [CrossRef]
- Filetin, T. Bending Stiffness of Aluminium Foams. Teh. Znan. knj. 2012, 15, 93–116. [Google Scholar]
- Sato, A.; Latour, M.; D’Aniello, M.; Rizzano, G.; Landolfo, R. Experimental response of full-scale steel-aluminium foam-steel sandwich panels in bending. ce/papers 2023, 6, 452–457. [Google Scholar] [CrossRef]
- Takamatsu, S.; Arai, T.; Sayama, A.; Suzuki, S. Characteristics of Pore Morphology in Aluminum Alloy Foams Fabricated by Semi-Solid Route among Multiple Experimental Runs. Metals 2023, 13, 1654. [Google Scholar] [CrossRef]
- Mauko, A.; Sarıkaya, M.; Güden, M.; Duarte, I.; Borovinšek, M.; Vesenjak, M.; Ren, Z. High strain-rate deformation analysis of open-cell aluminium foam. J. Mater. Res. Technol. 2023, 25, 1208–1221. [Google Scholar] [CrossRef]
- Miedzińska, D.; Niezgoda, T.; Gieleta, R. Numerical and experimental aluminum foam microstructure testing with the use of computed tomography. Comput. Mater. Sci. 2012, 64, 90–95. [Google Scholar] [CrossRef]
- De Giorgi, M.; Giancane, S.; Nobile, R.; Palano, F. Digital Image Correlation technique applied to mechanical characterisation of aluminium foam. EPJ Web Conf. 2010, 6, 31004. [Google Scholar] [CrossRef][Green Version]
- Zlámal, P.; Kytyr, D.; Fíla, T.; Koudelka, P.; Jiroušek, O. Measuring of Elastic Properties of Metal Foam Based on Compression Test and Digital Image Correlation. In Proceedings of the 11th Youth Symposium on Experimental Solid Mechanics, Brasov, Romania, 30 May–2 June 2012. [Google Scholar]
- Sawei, Q.; Xinna, Z.; Qingxian, H.; Renjun, D.; Yan, J.; Yuebo, H. Research Progress on Simulation Modeling of Metal Foams. Rare Met. Mater. Eng. 2015, 44, 2670–2676. [Google Scholar] [CrossRef]
- John, A.; John, M.; Bartela, A. Numerical homogenization of the foamed metal structures. Mechanika 2016, 22, 343–348. [Google Scholar] [CrossRef]
- John, A.; John, M.; Bartela, A. The Foamed Metal Structures in Numerical Testing. Mechanika 2018, 24, 5–10. [Google Scholar] [CrossRef]
- Ćwieka, K.; Skibiński, J. Elastic Properties of Open Cell Metallic Foams—Modeling of Pore Size Variation Effect. Materials 2022, 15, 6818. [Google Scholar] [CrossRef] [PubMed]
- Bleistein, T.; Jung, A.; Diebels, S. A microsphere-based material model for open cell metal foams. Contin. Mech. Thermodyn. 2020, 32, 255–267. [Google Scholar] [CrossRef]
- Michailidis, N.; Stergioudi, F.; Omar, H.; Papadopoulos, D.; Tsipas, D. Experimental and FEM analysis of the material response of porous metals imposed to mechanical loading. Colloids Surf. A Physicochem. Eng. Asp. 2011, 382, 124–131. [Google Scholar] [CrossRef]
- Sawada, M.; Suzuki, S. Prediction of Macroscopic Deformation Bands in Porous Metals with Unidirectional Through-Pores. Adv. Eng. Mater. 2024, 26, 2301001. [Google Scholar] [CrossRef]
- Shan, K.; Zhang, Y.; Lan, Y.; Jiang, K.; Xiao, G.; Li, B. Surface Roughness Prediction of Titanium Alloy during Abrasive Belt Grinding Based on an Improved Radial Basis Function (RBF) Neural Network. Materials 2023, 16, 7224. [Google Scholar] [CrossRef] [PubMed]
- Murugesan, M.; Yu, J.-H.; Chung, W.; Lee, C.-W. Hybrid Artificial Neural Network-Based Models to Investigate Deformation Behavior of AZ31B Magnesium Alloy at Warm Tensile Deformation. Materials 2023, 16, 5308. [Google Scholar] [CrossRef]
- Guo, K.; Yang, Z.; Yu, C.-H.; Buehler, M.J. Artificial intelligence and machine learning in design of mechanical materials. Mater. Horiz. 2021, 8, 1153–1172. [Google Scholar] [CrossRef]
- Badini, S.; Regondi, S.; Pugliese, R. Unleashing the Power of Artificial Intelligence in Materials Design. Materials 2023, 16, 5927. [Google Scholar] [CrossRef] [PubMed]
- Pyzer-Knapp, E.O.; Pitera, J.W.; Staar, P.W.J.; Takeda, S.; Laino, T.; Sanders, D.P.; Sexton, J.; Smith, J.R.; Curioni, A. Accelerating materials discovery using artificial intelligence, high performance computing and robotics. npj Comput. Mater. 2022, 8, 84. [Google Scholar] [CrossRef]
- Sarker, I.H. AI-Based Modeling: Techniques, Applications and Research Issues Towards Automation, Intelligent and Smart Systems. SN Comput. Sci. 2022, 3, 1–20. [Google Scholar] [CrossRef]
- Khanolkar, P.M.; Vrolijk, A.; Olechowski, A. Mapping artificial intelligence-based methods to engineering design stages: A focused literature review. Artif. Intell. Eng. Des. Anal. Manuf. 2023, 37, e25. [Google Scholar] [CrossRef]
- Shalev-Shwartz, S.; Ben-David, S. Understanding Machine Learning: From Theory to Algorithms; Cambridge University Press: Cambridge, UK, 2014; pp. 250–256, 268–282. [Google Scholar]
- Bishop, C.M. Pattern Recognition and Machine Learning; Springer: New York, NY, USA, 2006. [Google Scholar]
- Fukushima, K.; Miyake, S. Neocognitron: A Self-Organizing Neural Network Model for a Mechanism of Visual Pattern Recognition. In Competition and Cooperation in Neural Nets; Springer: Berlin/Heidelberg, Germany, 1982; pp. 267–285. [Google Scholar]
- LeCun, Y.; Haffner, P.; Bottou, L.; Bengio, Y. Object recognition with gradient-based learning. In Shape, Contour and Grouping in Computer Vision; Springer: Berlin/Heidelberg, Germany, 1999; pp. 319–345. [Google Scholar]
- Quinlan, J.R. Induction of decision trees. Mach. Learn. 1986, 1, 81–106. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Kingma, D.P.; Welling, M. Auto-Encoding Variational Bayes. In Proceedings of the 2nd International Conference on Learning Representations, ICLR 2014, Banff, AB, Canada, 14–16 April 2014. [Google Scholar] [CrossRef]
- Cinelli, L.P.; Marins, M.A.; da Silva, E.A.B.; Netto, S.L. Variational Autoencoder. In Variational Methods for Machine Learning with Applications to Deep Networks; Springer: Cham, Switzerland, 2021; pp. 111–149. [Google Scholar] [CrossRef]
- Raj, R.E.; Daniel, B. Prediction of compressive properties of closed-cell aluminum foam using artificial neural network. Comput. Mater. Sci. 2008, 43, 767–773. [Google Scholar] [CrossRef]
- Stręk, A.M.; Dudzik, M.; Kwiecień, A.; Wańczyk, K.; Lipowska, B. Verification of application of ANN modelling for compressive behaviour of metal sponges. Eng. Trans. 2019, 67, 271–288. [Google Scholar]
- Dudzik, M.; Stręk, A.M. ANN Architecture Specifications for Modelling of Open-Cell Aluminum under Compression. Math. Probl. Eng. 2020, 2020, 26. [Google Scholar] [CrossRef]
- Dudzik, M.; Stręk, A.M. ANN Model of stress-strain relationship for aluminium sponge in uniaxial compression. J. Theor. Appl. Mech. 2020, 58, 385–390. [Google Scholar] [CrossRef]
- Stręk, A.M.; Dudzik, M.; Machniewicz, T. Specifications for Modelling of the Phenomenon of Compression of Closed-Cell Aluminium Foams with Neural Networks. Materials 2022, 15, 1262. [Google Scholar] [CrossRef] [PubMed]
- Hangai, Y.; Okada, K.; Tanaka, Y.; Matsuura, T.; Amagai, K.; Suzuki, R.; Nakazawa, N. Classification of Mechanical Properties of Aluminum Foam by Machine Learning. Mater. Trans. 2022, 63, 257–260. [Google Scholar] [CrossRef]
- Hangai, Y.; Ozawa, S.; Okada, K.; Tanaka, Y.; Amagai, K.; Suzuki, R. Machine Learning Estimation of Plateau Stress of Aluminum Foam Using X-ray Computed Tomography Images. Materials 2023, 16, 1894. [Google Scholar] [CrossRef] [PubMed]
- Hangai, Y.; Sakaguchi, Y.; Kitahara, Y.; Takagi, T.; Kenji, O.; Yuuki, T. Plateau stress estimation of aluminum foam by machine learning using X-ray computed tomography images. Int. J. Adv. Manuf. Technol. 2024, 132, 5053–5061. [Google Scholar] [CrossRef]
- Hangai, Y.; Sakaguchi, Y.; Okada, K.; Tanaka, Y. Press-forming of aluminum foam and estimation of its mechanical properties from X-ray CT images using machine learning. Mater. Charact. 2025, 221, 114781. [Google Scholar] [CrossRef]
- Kammbach, T.E.; Kamm, P.H.; Neu, T.R.; García-Moreno, F. Convolutional Neural Network-Based Regression Model for Distribution Data from X-Ray Radiographs of Metallic Foams. Adv. Eng. Mater. 2024, 26, 2401128. [Google Scholar] [CrossRef]
- Zhuang, W.; Wang, E.; Zhang, H. Prediction of compressive mechanical properties of three-dimensional mesoscopic aluminium foam based on deep learning method. Mech. Mater. 2023, 182, 104684. [Google Scholar] [CrossRef]
- Dyckhoff, L.; Huber, N. Data-driven modelling of the multiaxial yield behaviour of nanoporous metals. Int. J. Mech. Sci. 2023, 259, 108601. [Google Scholar] [CrossRef]
- Romero, W.D.; Torres-Bermudez, S.; Valenzuela, B.; Viáfara, C.C.; Meléndez, A.M.; Martínez, F. Geometrical recognition of metallic foam microstructures using a deep learning approach. Mater. Today Commun. 2023, 37, 107407. [Google Scholar] [CrossRef]
- Avalos-Gauna, E.; Zhao, Y.; Palafox, L.; Ortiz-Monasterio-Martínez, P. Porous Metal Properties Analysis: A Machine Learning Approach. JOM 2021, 73, 2039–2049. [Google Scholar] [CrossRef]
- Baiocco, G.; Tagliaferri, V.; Ucciardello, N. Neural Networks Implementation for Analysis and Control of Heat Exchange Process in a Metal Foam Prototypal Device. Procedia CIRP 2017, 62, 518–522. [Google Scholar] [CrossRef]
- Calati, M.; Righetti, G.; Doretti, L.; Zilio, C.; Longo, G.; Hooman, K.; Mancin, S. Water pool boiling in metal foams: From experimental results to a generalized model based on artificial neural network. Int. J. Heat Mass Transf. 2021, 176, 121451. [Google Scholar] [CrossRef]
- E Rodríguez-Sánchez, A.; Plascencia-Mora, H.; Acevedo-Alvarado, M. Neural network-driven interpretability analysis for evaluating compressive stress in polymer foams. J. Cell. Plast. 2024, 60, 237–258. [Google Scholar] [CrossRef]
- Rodríguez-Sánchez, A.E. Modeling Nonlinear Compressive Stress Responses in Closed-Cell Polymer Foams Using Artificial Neural Networks: A Comprehensive Case Study. In Machine Learning in Materials Informatics: Methods and Applications; An, Y., Ed.; American Chemical Society: Washington, DC, USA, 2022; pp. 87–109. [Google Scholar] [CrossRef]
- Rodríguez-Sánchez, A.E.; Plascencia-Mora, H. A machine learning approach to estimate the strain energy absorption in expanded polystyrene foams. J. Cell. Plast. 2021, 58, 399–427. [Google Scholar] [CrossRef]
- Hooshmand, M.J.; Sakib-Uz-Zaman, C.; Khondoker, M.A.H. Machine Learning Algorithms for Predicting Mechanical Stiffness of Lattice Structure-Based Polymer Foam. Materials 2023, 16, 7173. [Google Scholar] [CrossRef]
- Liu, P.; Han, Z.; Wu, W.; Zhao, Y.; Song, Y.; Chai, M. A developed convolutional neural network model for accurately and stably predicting effective thermal conductivity of gradient porous ceramic materials. Int. J. Heat Mass Transf. 2024, 225, 125428. [Google Scholar] [CrossRef]
- Li, L.; Sun, W.; Ayti, A.; Chen, W.; Liu, Z.; Gómez-Zamorano, L.Y. Machine Learning Modeling of Foam Concrete Performance: Predicting Mechanical Strength and Thermal Conductivity from Material Compositions. Appl. Sci. 2025, 15, 7125. [Google Scholar] [CrossRef]
- Nguyen, T.; Kashani, A.; Ngo, T.; Bordas, S. Deep neural network with high-order neuron for the prediction of foamed concrete strength. Comput. Civ. Infrastruct. Eng. 2018, 34, 316–332. [Google Scholar] [CrossRef]
- Settgast, C.; Abendroth, M.; Kuna, M. Constitutive modeling of plastic deformation behavior of open-cell foam structures using neural networks. Mech. Mater. 2019, 131, 1–10. [Google Scholar] [CrossRef]
- Matlab Help Center: Introduction to Least-Squares Fitting. Available online: https://www.mathworks.com/help/curvefit/least-squares-fitting.html (accessed on 31 July 2025).
- Gibson, I.J.; Ashby, M.F. The mechanics of three-dimensional cellular materials. Proc. R. Soc. London. Ser. A Math. Phys. Sci. 1982, 382, 43–59. [Google Scholar] [CrossRef]
- Mathworks Documentation: Mapminmax. Available online: https://www.mathworks.com/help/deeplearning/ref/mapminmax.html (accessed on 21 February 2019).
| Number of Neurons in the Hidden Layer | Approach | ||
|---|---|---|---|
| 4 | 2 | 4.455% | 8.688% |
| 6 | 6 | 3.572% | 2.689% |
| 11 | 4 | 1.959% | 2.976% |
| Sample Name | (Mpa) | (Mpa) | (%) | Pa) | (g/cm3) |
|---|---|---|---|---|---|
| X_Z_02 | 1.668 | 1.722 | 41.465 | 0.571 | 0.297 |
| Z_01 | 1.537 | 1.627 | 42.154 | 1.395 | 0.278 |
| Z_02 | 1.542 | 1.721 | 42.924 | 1.326 | 0.285 |
| Z_03 | 1.434 | 1.412 | 48.451 | 0.782 | 0.230 |
| Z_05 | 1.070 | 1.193 | 45.389 | 1.247 | 0.214 |
| X_Z_01_p | 0.959 | 1.034 | 43.363 | 0.590 | 0.217 |
| X_Z_06_p | 1.327 | 1.425 | 46.655 | 1.220 | 0.224 |
| X_Z_08_p | 1.827 | 1.777 | 48.791 | 1.733 | 0.245 |
| Z_06_p | 1.469 | 1.468 | 50.042 | 0.801 | 0.225 |
| Z_09_p | 1.510 | 1.457 | 48.635 | 0.716 | 0.233 |
| Z_12_p | 0.996 | 1.000 | 43.144 | 0.826 | 0.200 |
| Z_14_p | 1.488 | 1.479 | 48.347 | 0.734 | 0.236 |
| mean | 1.403 | 1.437 | 46.005 | 0.931 | 0.240 |
| median | 1.469 | 1.457 | 46.655 | 0.801 | 0.236 |
| standard deviation | 0.240 | 0.230 | 2.807 | 0.392 | 0.027 |
| coefficient of variation | 17.12% | 16.03% | 6.10% | 42.14% | 11.32% |
| Result of Fitting | Compressive Strength | Plateau Stress |
|---|---|---|
| Function formula * | ||
| Coefficient of determination | ||
| Sum of Square Errors (Mpa2) | ||
| Root Mean Squared Error (Mpa) |
| Result of Fitting | Compressive Strength |
|---|---|
| Function formula | |
| Coefficient of determination | |
| Sum of Square Errors (MPa2) | |
| Root Mean Squared Error (MPa) |
| 4,5 | 4.99% | 8.18% | 2.98% | 8.40% | 8.31% | 4.997% |
| 4,7 | 4.99% | 8.18% | 2.98% | 8.40% | 8.31% | 4.997% |
| 5,1 | 4.85% | 7.91% | 3.93% | 9.36% | 19.67% | 6.422% |
| 5,7 | 4.97% | 8.18% | 4.56% | 9.30% | 18.87% | 6.678% |
| 6,4 | 4.69% | 8.71% | 4.10% | 7.73% | 16.44% | 6.232% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Stręk, A.M.; Dudzik, M.; Machniewicz, T. Prediction of Mechanical Properties and Stress–Strain Relation of Closed-Cell Aluminium Foam Under Compression Using Neural Network Models. Materials 2025, 18, 4492. https://doi.org/10.3390/ma18194492
Stręk AM, Dudzik M, Machniewicz T. Prediction of Mechanical Properties and Stress–Strain Relation of Closed-Cell Aluminium Foam Under Compression Using Neural Network Models. Materials. 2025; 18(19):4492. https://doi.org/10.3390/ma18194492
Chicago/Turabian StyleStręk, Anna M., Marek Dudzik, and Tomasz Machniewicz. 2025. "Prediction of Mechanical Properties and Stress–Strain Relation of Closed-Cell Aluminium Foam Under Compression Using Neural Network Models" Materials 18, no. 19: 4492. https://doi.org/10.3390/ma18194492
APA StyleStręk, A. M., Dudzik, M., & Machniewicz, T. (2025). Prediction of Mechanical Properties and Stress–Strain Relation of Closed-Cell Aluminium Foam Under Compression Using Neural Network Models. Materials, 18(19), 4492. https://doi.org/10.3390/ma18194492






