Uncertainty Quantification of Fatigue Life for Cement-Stabilized Cold Recycled Mixtures Using Probabilistic Programming
Abstract
1. Introduction
2. The Fatigue Test and the Fatigue Life Equation
2.1. Fatigue Laboratory Test
2.2. The Fatigue Life Equation
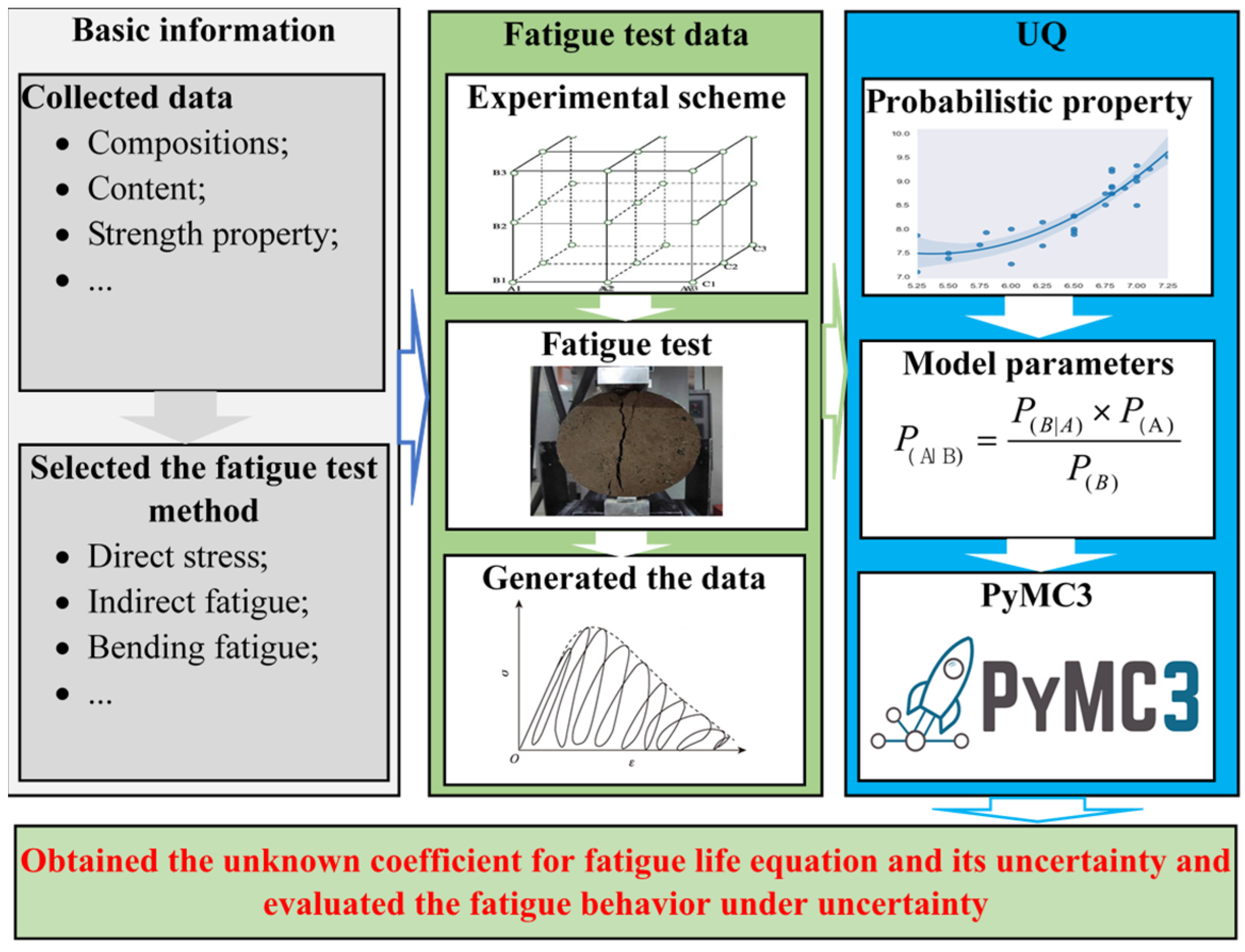
3. Uncertainty Quantification for Fatigue Life Analysis
3.1. Uncertainty Quantification
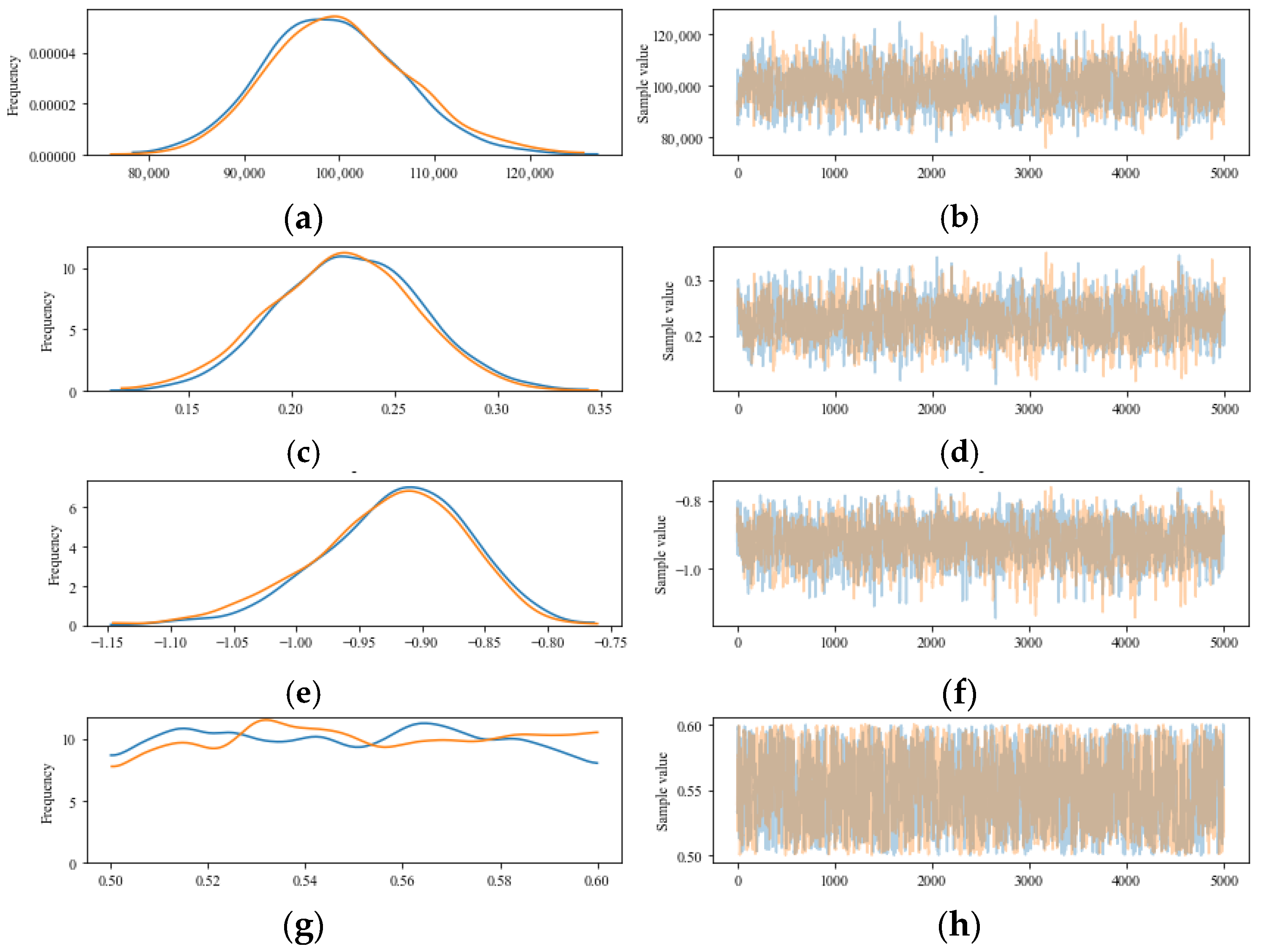
3.2. Uncertainty Quantification of Fatigue Life Using PyMC3
3.3. UQ Procedure
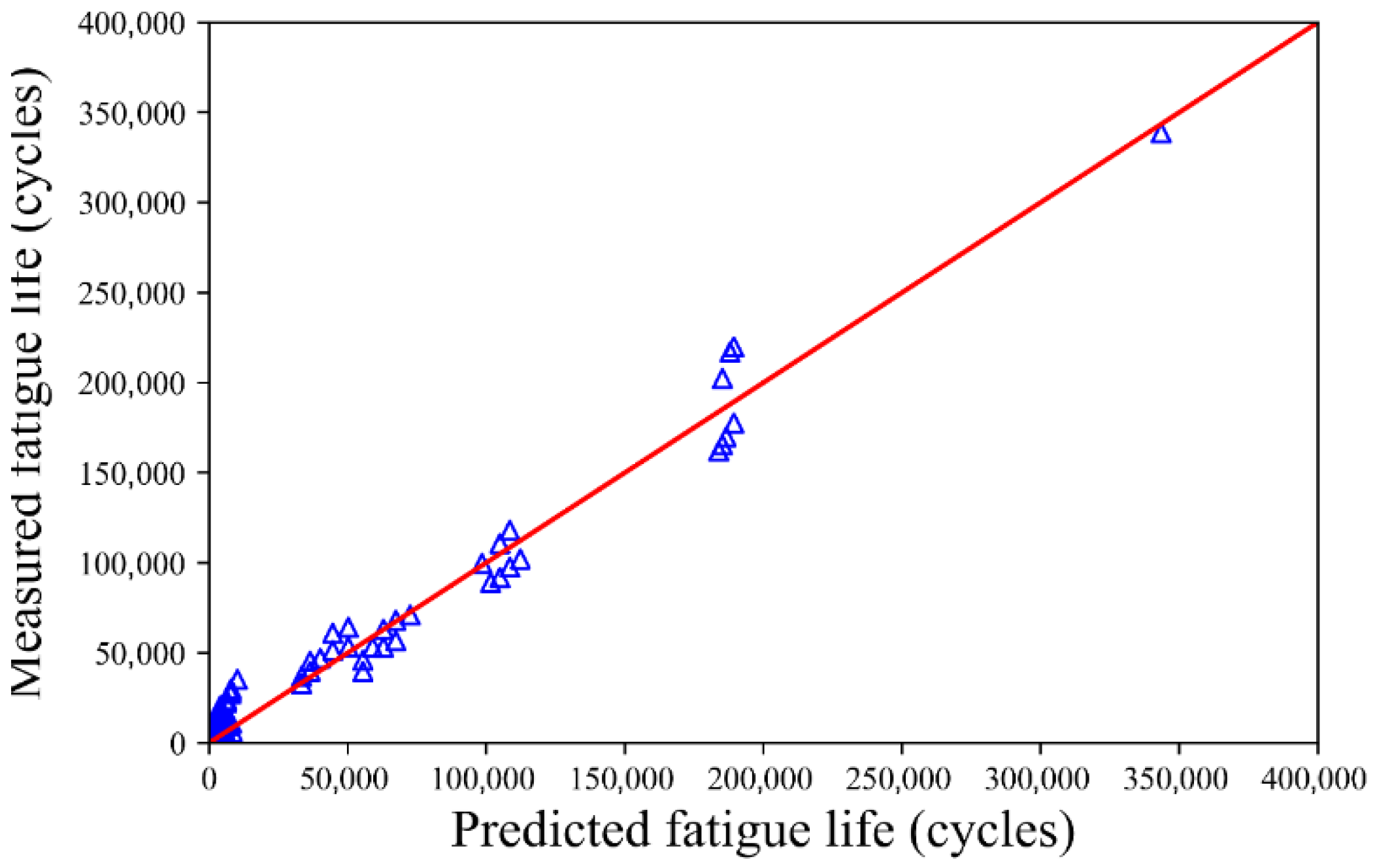
4. Application
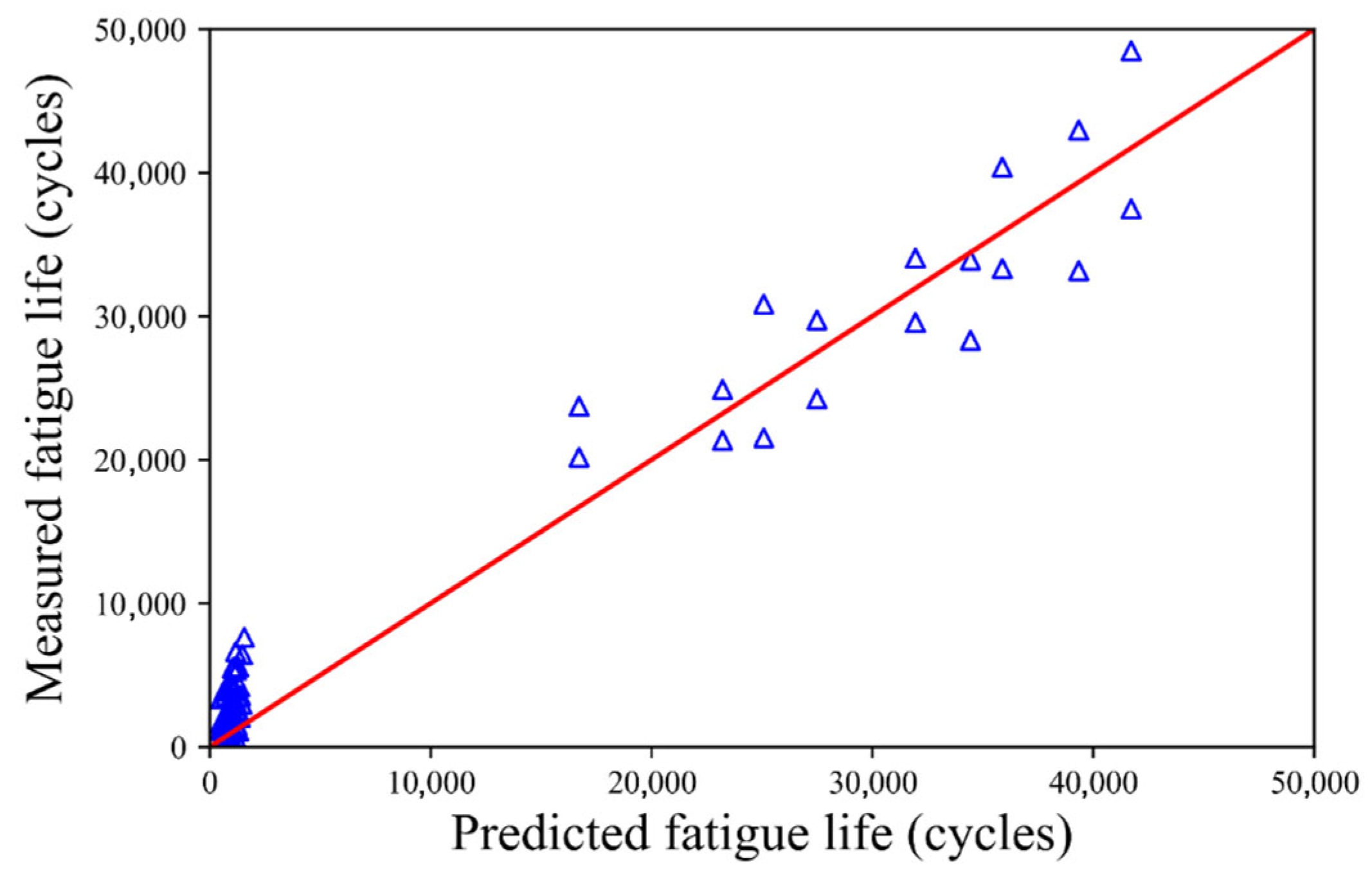
4.1. Indirect Fatigue Test
4.2. Ji and Jiang’s Test
- Because the bond between the natural aggregate (NA) and cement is stronger than the bond between the recycled aggregate (RA) and cement, increasing the amount of the NA can prolong the fatigue life of the CSCRM. In contrast, a higher proportion of RAs—consisting of ARWMs and CRWMs—negatively affects the fatigue life extension of the CSCRM. This study also shows that the RA has a more pronounced effect on the CSCRM′s fatigue life when present in low amounts. Additionally, applying a high level of stress diminishes the impact of a low RA content on the mixture′s fatigue life and decreases the mixture′s fatigue life sensitivity to variations in the low RA content.
- As cement is a binder, an increase in the cement content exhibits a positive correlation with the fatigue life of the CSCRM; however, the sensitivity of the CSCRM′s fatigue life to the cement content is lower than for the RA.
- When the NA content remains constant, the asphalt coating on the surface of ARWMs obstructs water from reaching the aggregate surface, which subsequently influences the interaction between the aggregate and cement, negatively affecting the fatigue life of the CSCRM. In contrast, increasing the amount of the CRWM enhances the fatigue life of the CSCRM.
- The stress level has an inverse impact on fatigue life; however, similar to the RA content, its effect on the fatigue life diminishes as the stress level rises. Under low stress conditions, the RA content and the amount of CRWM in cement-stabilized cold recycled mixtures (CSCRMs) need to be carefully controlled.
5. Conclusions
- The developed method scientifically considered the uncertainty during fatigue testing by combining probabilistic programming, fatigue test data, and an empirical formula. Probabilistic programming was employed to characterize the fatigue behavior and quantify the associated uncertainty during fatigue testing. The developed method provides a scientific, feasible, and helpful way for dealing with the uncertainty regarding the fatigue life of pavement materials.
- The developed method was illustrated and verified based on an empirical formula by two independent CSCRM datasets. PyMC3 is a reliable probabilistic programming package for quantifying uncertainty during the fatigue test.
- The developed method quantified the uncertainty of fatigue life by determining the unknown coefficient of the empirical formula. The empirical formula characterizes the fatigue behavior, and its selection is critical to the developed method. More empirical formulas should be verified and investigated in future studies.
- The developed method was applied to a CSCRM and exhibits excellent performance for the quantification of uncertainty, avoiding complex statistical computations. It should be further applied to other civil materials in future studies.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Main Characteristics of Raw Materials and CSCRMs
| Index | Result | |
|---|---|---|
| CaO content (%) | 66.7 | |
| SiO2 content (%) | 21.9 | |
| Al2O3 content (%) | 6.1 | |
| Fe2O3 content (%) | 4.6 | |
| SO3 content (%) | 2.2 | |
| MgO content (%) | 4.0 | |
| Cl-content (%) | 0.037 | |
| Fineness (%) | 1.1 | |
| Setting time (min) | Initial setting | 196 |
| Final coagulation | 277 | |
| Stability | Le chatelier soundness | Qualified |
| Flexural strength (MPa) | 3-day | 4.8 |
| 28-day | 8.2 | |
| Compressive strength (MPa) | 3-day | 23.9 |
| 28-day | 48.1 | |
| Material Specification | Apparent Density (g·cm−3) | Water Absorption (%) | Needle Sheet Content (%) | Natural Water Content (%) | Crushing Value (%) |
|---|---|---|---|---|---|
| 19~37.5 mm | 2.612 | 1.06 | 10.1 | 0.2 | 11.6 |
| 9.5~19 mm | 2.736 | 1.10 | 10.7 | ||
| 4.75~9.5 mm | 2.719 | 1.29 | 11.2 | ||
| 0~4.75 mm | 2.377 | 1.67 | — |
| Material | Apparent Density (g·cm−3) | Natural Water Content (%) | Water Absorption (%) | Needle Sheet Content (%) | Crushing Value (%) |
|---|---|---|---|---|---|
| ARWM | 2.496 | 4.8 | 7.12 | 4.1 | 13.7 |
| CRWM | 2.404 | 6.1 | 9.81 | 5.5 | 15.9 |
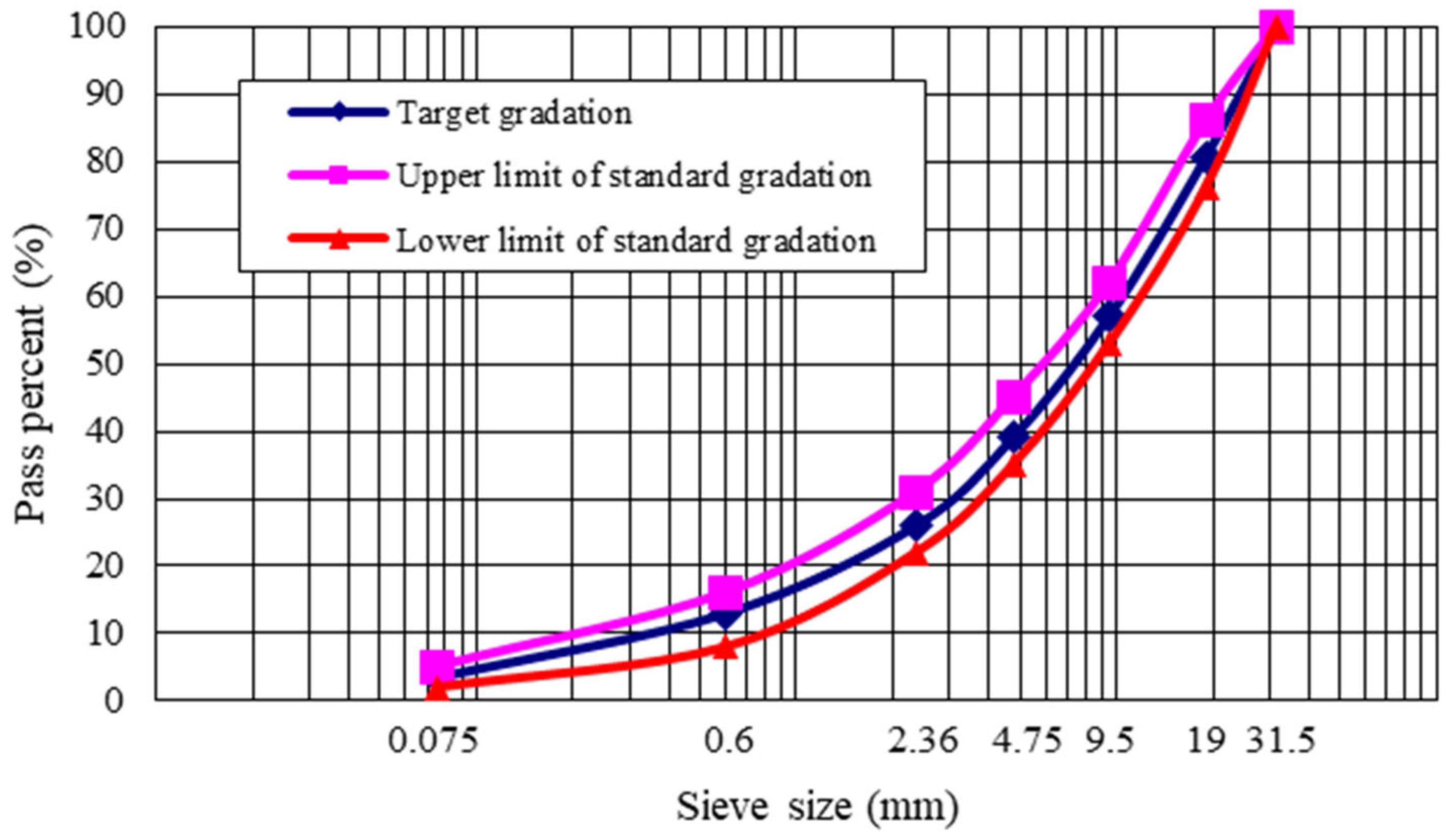
| Cement Content (%) | NA Content (%) | ARWM Content (%) | CRWM Content (%) | OMC (%) | MDD (g·cm−3) | Splitting Strength (MPa) | |
|---|---|---|---|---|---|---|---|
| Mean | Std. | ||||||
| 4 | 100 | 0 | 0 | 4.5 | 2.389 | 1.74 | 0.162 |
| 5 | 100 | 0 | 0 | 4.6 | 2.401 | 2.29 | 0.039 |
| 4 | 75 | 0 | 25 | 4.6 | 2.311 | 1.18 | 0.017 |
| 50 | 0 | 50 | 4.7 | 2.216 | 0.92 | 0.089 | |
| 25 | 0 | 75 | 4.9 | 2.136 | 0.78 | 0.056 | |
| 0 | 0 | 100 | 5.0 | 2.103 | 0.69 | 0.021 | |
| 5 | 75 | 0 | 25 | 4.7 | 2.322 | 1.87 | 0.180 |
| 50 | 0 | 50 | 4.8 | 2.224 | 1.55 | 0.128 | |
| 25 | 0 | 75 | 4.9 | 2.144 | 1.28 | 0.065 | |
| 0 | 0 | 100 | 5.0 | 2.111 | 1.11 | 0.082 | |
| 4 | 75 | 6.25 | 18.75 | 5.0 | 2.317 | 1.21 | 0.022 |
| 50 | 12.5 | 37.5 | 5.3 | 2.243 | 0.95 | 0.083 | |
| 25 | 18.75 | 56.25 | 5.6 | 2.164 | 0.81 | 0.041 | |
| 0 | 25 | 75 | 5.9 | 2.105 | 0.73 | 0.031 | |
| 5 | 75 | 6.25 | 18.75 | 5.1 | 2.332 | 1.90 | 0.099 |
| 50 | 12.5 | 37.5 | 5.4 | 2.258 | 1.60 | 0.043 | |
| 25 | 18.75 | 56.25 | 5.7 | 2.177 | 1.33 | 0.008 | |
| 0 | 25 | 75 | 6.0 | 2.113 | 1.16 | 0.049 | |
| 4 | 75 | 12.5 | 12.5 | 5.3 | 2.328 | 1.23 | 0.059 |
| 50 | 25 | 25 | 5.8 | 2.276 | 0.98 | 0.071 | |
| 25 | 37.5 | 37.5 | 6.4 | 2.210 | 0.84 | 0.063 | |
| 0 | 50 | 50 | 6.9 | 2.105 | 0.77 | 0.048 | |
| 5 | 75 | 12.5 | 12.5 | 5.4 | 2.346 | 1.94 | 0.028 |
| 50 | 25 | 25 | 5.9 | 2.292 | 1.68 | 0.003 | |
| 25 | 37.5 | 37.5 | 6.6 | 2.221 | 1.43 | 0.095 | |
| 0 | 50 | 50 | 6.9 | 2.114 | 1.21 | 0.075 | |
| 4 | 75 | 18.75 | 6.25 | 5.8 | 2.345 | 1.28 | 0.075 |
| 50 | 37.5 | 12.5 | 6.6 | 2.301 | 1.02 | 0.080 | |
| 25 | 56.25 | 18.75 | 7.4 | 2.241 | 0.86 | 0.023 | |
| 0 | 75 | 25 | 8.2 | 2.107 | 0.80 | 0.037 | |
| 5 | 75 | 18.75 | 6.25 | 5.9 | 2.358 | 2.03 | 0.188 |
| 50 | 37.5 | 12.5 | 6.5 | 2.312 | 1.76 | 0.065 | |
| 25 | 56.25 | 18.75 | 7.5 | 2.250 | 1.51 | 0.127 | |
| 0 | 75 | 25 | 8.3 | 2.115 | 1.34 | 0.039 | |
| 4 | 75 | 25 | 0 | 6.7 | 2.358 | 1.35 | 0.047 |
| 50 | 50 | 0 | 7.6 | 2.321 | 1.05 | 0.041 | |
| 25 | 75 | 0 | 8.6 | 2.265 | 0.89 | 0.075 | |
| 0 | 100 | 0 | 9.5 | 2.109 | 0.83 | 0.009 | |
| 5 | 75 | 25 | 0 | 6.6 | 2.368 | 2.15 | 0.029 |
| 50 | 50 | 0 | 7.7 | 2.331 | 1.88 | 0.181 | |
| 25 | 75 | 0 | 8.7 | 2.270 | 1.60 | 0.085 | |
| 0 | 100 | 0 | 9.6 | 2.116 | 1.50 | 0.035 | |
Appendix B. The Results of the Indirect Fatigue Test
| ARWM Content (%) | CRWM Content (%) | NA Content (%) | Cement Content (%) | Fatigue Life Under Different Stress Levels | Correlation Coefficient | |||
|---|---|---|---|---|---|---|---|---|
| 0.5 | 0.6 | 0.7 | 0.8 | |||||
| 0 | 0 | 100 | 4 | 279,492 | 35,196 | 10,986 | 4891 | 0.9553 |
| 5 | 338,716 | 43,938 | 13,691 | 6133 | 0.9564 | |||
| 0 | 100 | 0 | 4 | 32,908 | 6633 | 3187 | 1338 | 0.9666 |
| 0 | 75 | 25 | 39,685 | 7821 | 4537 | 1821 | 0.9539 | |
| 0 | 50 | 50 | 83,347 | 12,881 | 6172 | 2612 | 0.949 | |
| 0 | 25 | 75 | 162,048 | 21,697 | 8001 | 3216 | 0.9593 | |
| 0 | 100 | 0 | 5 | 36,969 | 7481 | 3555 | 1498 | 0.9672 |
| 0 | 75 | 25 | 45,935 | 9101 | 5198 | 2111 | 0.9549 | |
| 0 | 50 | 50 | 99,600 | 15,484 | 7376 | 3089 | 0.9506 | |
| 0 | 25 | 75 | 198,483 | 26,129 | 9811 | 3769 | 0.9607 | |
| 25 | 75 | 0 | 4 | 39,780 | 7710 | 4061 | 1481 | 0.9662 |
| 18.75 | 56.25 | 25 | 45,588 | 8991 | 5088 | 1987 | 0.9579 | |
| 12.5 | 37.5 | 50 | 89,032 | 13,413 | 6603 | 2762 | 0.9463 | |
| 6.25 | 18.75 | 75 | 165,524 | 22,266 | 8399 | 3361 | 0.9588 | |
| 25 | 75 | 0 | 5 | 45,318 | 8766 | 4589 | 1671 | 0.9666 |
| 18.75 | 56.25 | 25 | 53,223 | 9999 | 5943 | 2327 | 0.9501 | |
| 12.5 | 37.5 | 50 | 106,393 | 16,079 | 7719 | 3300 | 0.9466 | |
| 6.25 | 18.75 | 75 | 202,326 | 27,229 | 10,267 | 4176 | 0.9577 | |
| 50 | 50 | 0 | 4 | 46,861 | 8980 | 4585 | 1621 | 0.9691 |
| 37.5 | 37.5 | 25 | 53,164 | 9788 | 5555 | 2211 | 0.9519 | |
| 25 | 25 | 50 | 91,826 | 14,387 | 7461 | 2883 | 0.9509 | |
| 12.5 | 12.5 | 75 | 169,841 | 22,986 | 8829 | 3482 | 0.9593 | |
| 50 | 50 | 0 | 5 | 54,379 | 10,417 | 5318 | 1878 | 0.9692 |
| 37.5 | 37.5 | 25 | 63,132 | 11,581 | 6596 | 2629 | 0.9512 | |
| 25 | 25 | 50 | 110,650 | 17,633 | 9001 | 3474 | 0.9532 | |
| 12.5 | 12.5 | 75 | 208,769 | 28,267 | 10,837 | 4226 | 0.9602 | |
| 75 | 25 | 0 | 4 | 51,413 | 9555 | 5715 | 2092 | 0.953 |
| 56.25 | 18.75 | 25 | 56,707 | 10,339 | 6711 | 2555 | 0.9408 | |
| 37.5 | 12.5 | 50 | 97,516 | 18,011 | 8130 | 3316 | 0.9667 | |
| 18.75 | 6.25 | 75 | 174,718 | 23,461 | 9317 | 3938 | 0.9521 | |
| 75 | 25 | 0 | 5 | 60,861 | 11,316 | 6699 | 2468 | 0.9536 |
| 56.25 | 18.75 | 25 | 68,111 | 12,138 | 8111 | 3071 | 0.9362 | |
| 37.5 | 12.5 | 50 | 117,981 | 19,962 | 9878 | 3939 | 0.957 | |
| 18.75 | 6.25 | 75 | 216,978 | 29,068 | 11,400 | 4799 | 0.9529 | |
| 100 | 0 | 0 | 4 | 53,379 | 9869 | 6496 | 2266 | 0.9455 |
| 75 | 0 | 25 | 58,551 | 10,677 | 7419 | 2779 | 0.9337 | |
| 50 | 0 | 50 | 102,044 | 20,476 | 8596 | 3687 | 0.9718 | |
| 25 | 0 | 75 | 177,584 | 23,976 | 10,007 | 4139 | 0.9513 | |
| 100 | 0 | 0 | 5 | 64,134 | 12,117 | 7991 | 2716 | 0.948 |
| 75 | 0 | 25 | 70,993 | 13,131 | 9099 | 3361 | 0.936 | |
| 50 | 0 | 50 | 125,003 | 21,871 | 10,981 | 4531 | 0.9557 | |
| 25 | 0 | 75 | 219,886 | 30,001 | 12,388 | 5119 | 0.9526 | |
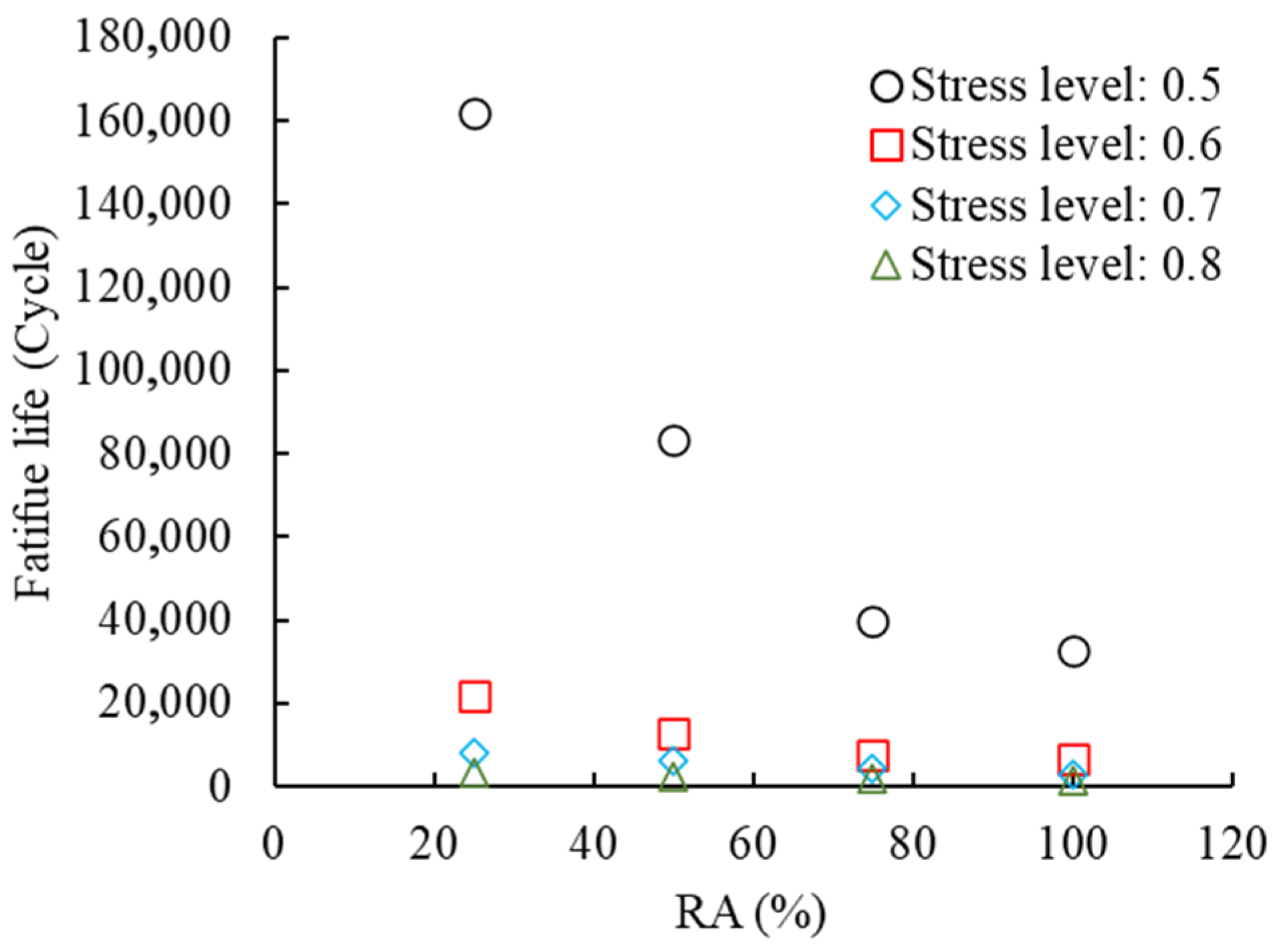
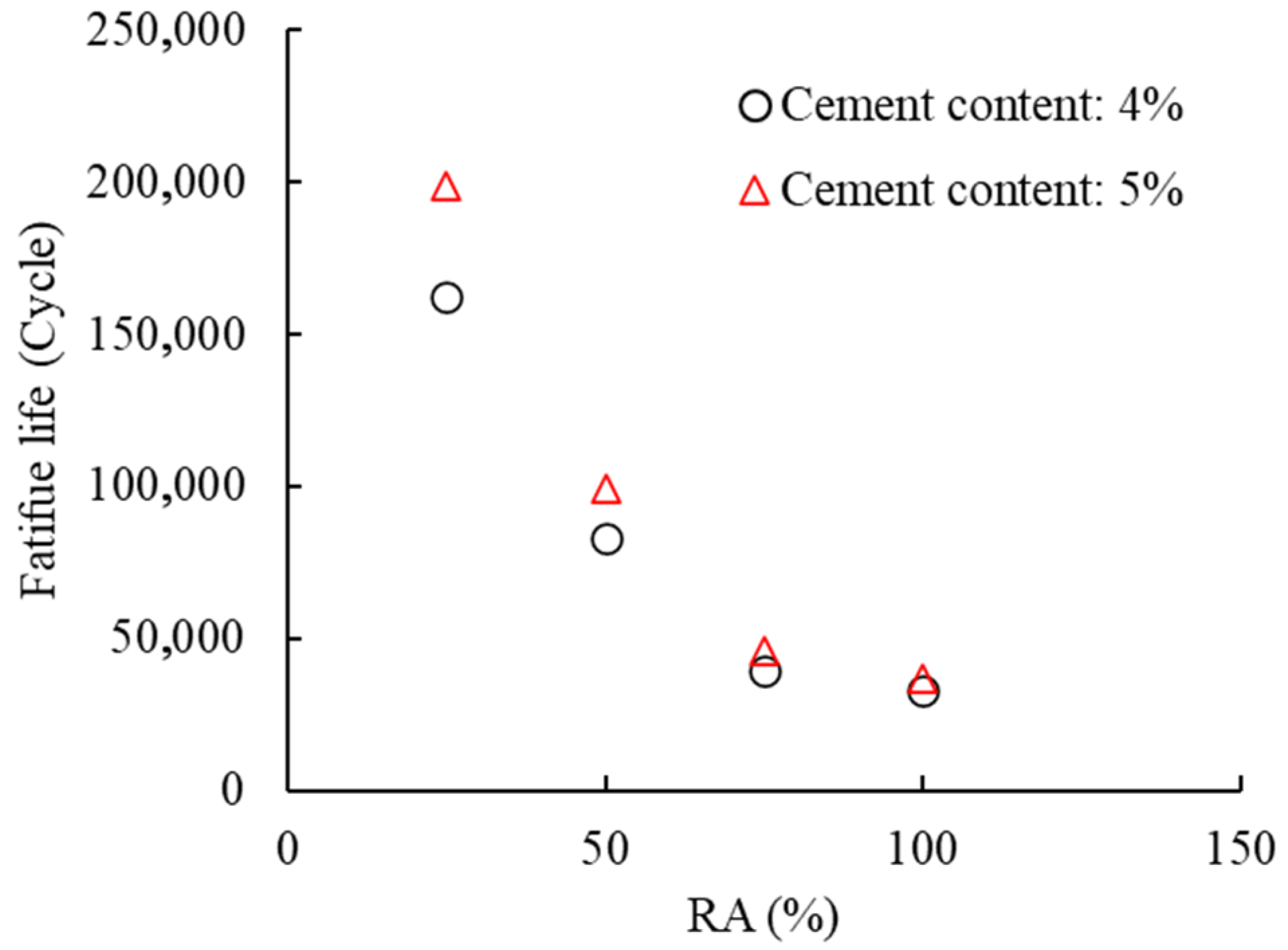
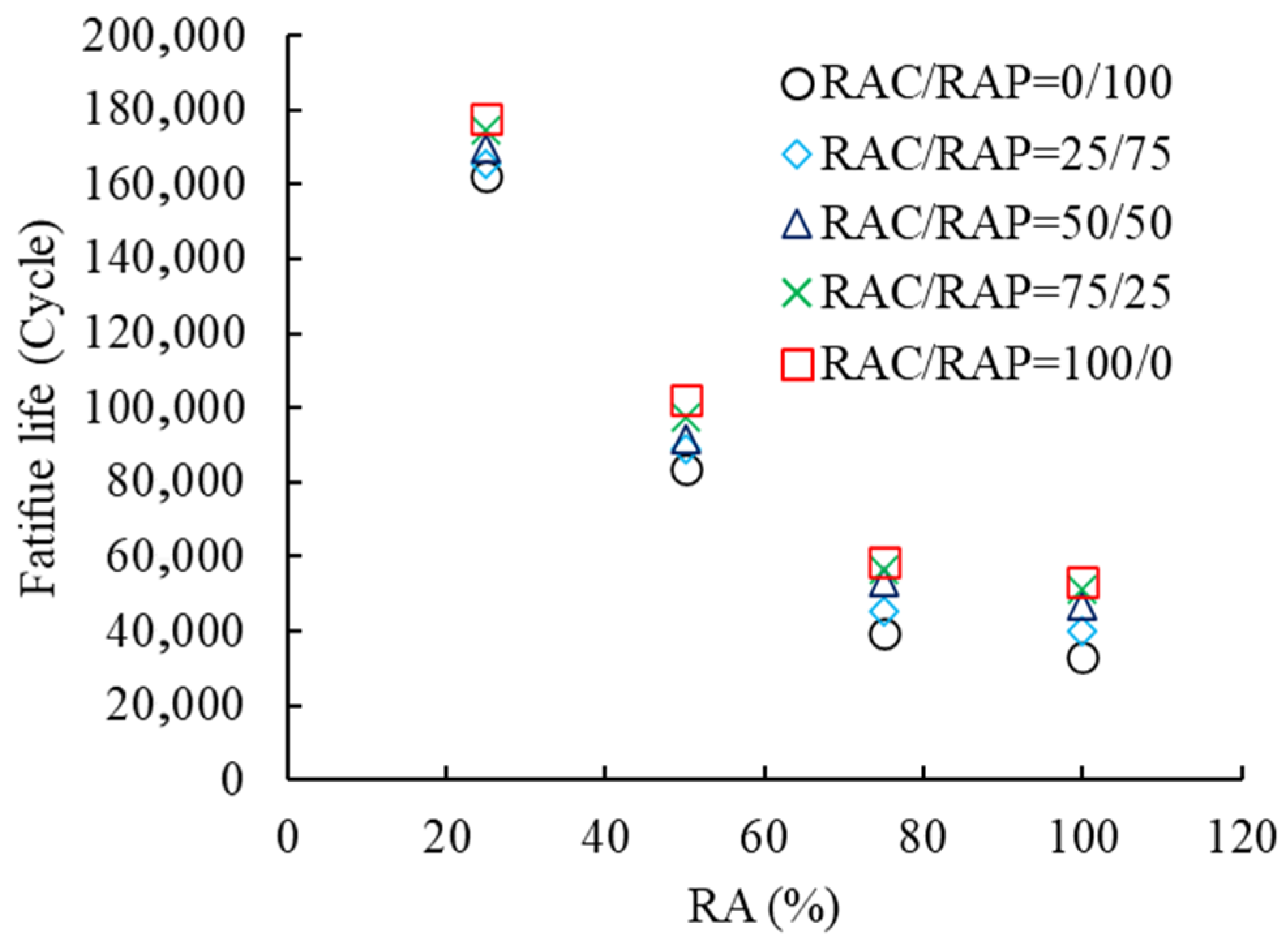
Appendix C. Ji and Jiang’s Test Data
| ARWM Content (%) | CRWM Content (%) | NA Content (%) | Cement Content (%) | Fatigue Life Under Different Stress Levels | Correlation Coefficient | ||||
|---|---|---|---|---|---|---|---|---|---|
| 0.85 | 0.80 | 0.75 | 0.70 | 0.65 | |||||
| 30 | 70 | 0 | 3 | 405 | 1150 | 1635 | 3353 | 20,166 | 0.9334 |
| 24 | 56 | 20 | 605 | 1403 | 1914 | 3536 | 21,517 | 0.9088 | |
| 18 | 42 | 40 | 755 | 1421 | 2238 | 4068 | 28,318 | 0.8976 | |
| 25 | 75 | 0 | 4 | 534 | 1231 | 1919 | 3917 | 23,720 | 0.9312 |
| 18.75 | 56.25 | 25 | 659 | 1383 | 2579 | 4170 | 30,834 | 0.9157 | |
| 6.25 | 18.75 | 75 | 1103 | 2041 | 2956 | 5561 | 33,910 | 0.8975 | |
| 50 | 50 | 0 | 3 | 640 | 1258 | 1929 | 3965 | 21,349 | 0.9266 |
| 40 | 40 | 20 | 988 | 1762 | 2865 | 4585 | 29,555 | 0.8941 | |
| 30 | 30 | 40 | 1147 | 1961 | 2878 | 5554 | 33,166 | 0.8938 | |
| 50 | 50 | 0 | 4 | 724 | 1331 | 2210 | 4628 | 24,892 | 0.9307 |
| 40 | 40 | 20 | 1187 | 2084 | 3293 | 5347 | 34,047 | 0.8903 | |
| 30 | 30 | 40 | 1458 | 2470 | 3550 | 6424 | 42,966 | 0.8745 | |
| 100 | 0 | 0 | 3 | 822 | 1449 | 2324 | 3923 | 24,235 | 0.8988 |
| 80 | 0 | 20 | 1551 | 2033 | 3566 | 5471 | 33,319 | 0.8655 | |
| 60 | 0 | 40 | 1470 | 2474 | 4119 | 6623 | 37,477 | 0.9036 | |
| 100 | 0 | 0 | 4 | 803 | 1231 | 1919 | 3917 | 29,732 | 0.8714 |
| 80 | 0 | 20 | 659 | 1383 | 2579 | 4170 | 40,381 | 0.8947 | |
| 60 | 0 | 40 | 1103 | 2041 | 2956 | 7622 | 48,482 | 0.9082 | |
References
- Ren, J.L.; Li, D.; Xu, Y.S.; Huang, J.D.; Liu, W. Fatigue behaviour of rock asphalt concrete considering moisture, high-temperature, and stress level. Int. J. Pavement Eng. 2022, 23, 4638–4648. [Google Scholar] [CrossRef]
- Decky, M.; Hodasova, K.; Papanova, Z.; Remisova, E. Sustainable adaptive cycle pavements using composite foam concrete at high altitudes in central Europe. Sustainability 2022, 14, 9034. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, J.L.; Ma, T.; Qi, H.N.; Chen, C.L. Predicting asphalt mixture fatigue life via four-point bending tests based on viscoelastic continuum damage mechanics. Case Stud. Constr. Mater. 2023, 19, e02671. [Google Scholar] [CrossRef]
- Azarhoosh, A.R.; Zojaji, Z.; Moghadas, N.F. Nonlinear genetic-base models for prediction of fatigue life of modified asphalt mixtures by precipitated calcium carbonate. Road Mater. Pavement Des. 2020, 21, 850–866. [Google Scholar] [CrossRef]
- Fang, C.Z.; Guo, N.S.; You, Z.P.; Tan, Y.Q. Investigating fatigue life prediction of rubber asphalt mixture based on damage evolution using residual strain analysis approach. Constr. Build. Mater. 2020, 257, 119476. [Google Scholar] [CrossRef]
- Ren, J.L.; Xu, Y.S.; Zhao, Z.D.; Chen, J.C.; Cheng, Y.Y.; Huang, J.D.; Yang, C.X.; Wang, J. Fatigue prediction of semi-flexible composite mixture based on damage evolution. Constr. Build. Mater. 2022, 318, 126004. [Google Scholar] [CrossRef]
- Li, L.M.; Guo, E.; Lin, Y.; He, Z. A Design Method on Durable Asphalt Pavement of Flexible Base on Anti-Rutting Performance and Its Application. Materials 2023, 16, 7122. [Google Scholar] [CrossRef]
- Gajewski, M.; Bankowski, W.; Pronk, A.C. Evaluation of fatigue life of high modulus asphalt concrete with use of three different definitions. Int. J. Pavement Eng. 2020, 21, 1717–1728. [Google Scholar] [CrossRef]
- Fedrigo, W.; Visser, A.T.; Steyn, W.J.; Núñez, W.P. Flexural behaviour of lightly cement stabilised materials: South Africa and Brazil. Road Mater. Pavement Des. 2021, 22, 397–422. [Google Scholar] [CrossRef]
- Seif, M.; Molayem, M. Estimation fatigue life of asphalt mixtures in terms of fatigue life of asphalt binders using the rate of dissipated energy change approach. J. Mater. Civ. Eng. 2022, 34, 04022185. [Google Scholar] [CrossRef]
- Seitllari, A.; Kutay, M.E. Investigation of the fatigue life relationship among different geometry combinations of the 3-point bending cylinder (3PBC) fatigue test for asphalt concrete. Int. J. Pavement Eng. 2023, 24, 2159402. [Google Scholar] [CrossRef]
- Fedrigo, W.; Heller, L.F.; Brito, L.A.T.; Núñez, W.P. Fatigue of cold recycled cement-treated pavement layers: Experimental and modeling study. Sustainability 2023, 15, 7816. [Google Scholar] [CrossRef]
- Ji, X.P.; Jiang, Y.J.; Liu, Y.J. Evaluation of the mechanical behaviors of cement-stabilized cold recycled mixtures produced by vertical vibration compaction method. Mater. Struct. 2015, 49, 2257–2270. [Google Scholar] [CrossRef]
- Zhao, Z.D.; Wang, S.Y.; Ren, J.L.; Wang, Y.; Wang, C.J. Fatigue characteristics and prediction of cement-stabilized cold recycled mixture with road-milling materials considering recycled aggregate composition. Constr. Build. Mater. 2021, 301, 124122. [Google Scholar] [CrossRef]
- Xu, X.Q.; Wan, G.Z.; Kang, F.Y.; Li, S.; Huang, W.; Li, Y.; Li, Q.; Lv, C. Evaluation Method of Fatigue Life for Asphalt Pavement on the Steel Bridge Deck Based on the Inhomogeneous Poisson Stochastic Process. Materials 2024, 17, 780. [Google Scholar] [CrossRef]
- Ingrassia, L.P.; Spadoni, S.; Ferrotti, G.; Virgili, A.; Canestrari, F. Prediction of the Long-Term Performance of an Existing Warm Recycled Motorway Pavement. Materials 2023, 16, 1005. [Google Scholar] [CrossRef]
- Złotowska, M.; Nagórski, R.; Błażejowski, K. Concept of Similarity Method for Prediction of Fatigue Life of Pavement Structures with HiMA Binder in Asphalt Layers. Materials 2021, 14, 480. [Google Scholar] [CrossRef] [PubMed]
- Omrani, M.A.; Babagoli, R.; Hasirchian, M. Predictive modeling of mechanical properties in cold recycled asphalt mixtures enhanced with industrial byproducts. Case Stud. Constr. Mater. 2025, 23, e05202. [Google Scholar] [CrossRef]
- Yang, K.; Cui, H.J.; Liu, P.; Zhu, M.Q.; An, Y.F. Accuracy analysis of fatigue life prediction in asphalt binders under multiple aging conditions based on simplified viscoelastic continuum damage (S-VECD) approach. Constr. Build. Mater. 2024, 435, 136868. [Google Scholar] [CrossRef]
- Han, C.J.; Zhang, J.L.; Tu, Z.J.; Ma, T. PINN-AFP: A novel C-S curve estimation method for asphalt mixtures fatigue prediction based on physics-informed neural network. Constr. Build. Mater. 2024, 415, 135070. [Google Scholar] [CrossRef]
- Holmen, J. Fatigue of concrete by constant and variable amplitude loading. ACI Spec. Publ. 1982, 75, 71–110. [Google Scholar]
- Oh, B.H. Fatigue life distributions of concrete for various stress levels. ACI Mater. J. 1991, 88, 122–128. [Google Scholar] [CrossRef] [PubMed]
- Petryna, Y.; Pfanner, D.; Stangenbery, F.; Kratzig, W. Reliability of reinforced concrete structures under fatigue. Reliab. Eng. Syst. Saf. 2002, 77, 253–261. [Google Scholar] [CrossRef]
- Trisha, S.; Chandra, K. Probabilistic assessment of fatigue crack growth in concrete. Int. J. Fatigue 2008, 30, 2156–2164. [Google Scholar] [CrossRef]
- Yao, J.; Kozin, F.; Wen, Y.; Yang, J.; Schueller, G.; Ditlevsen, O. Stochastic fatigue fracture and damage analysis. Struct. Saf. 1986, 3, 231–267. [Google Scholar] [CrossRef]
- Luo, Z.; Xiao, F.P.; Hu, S.W.; Yang, Y.S. Probabilistic analysis on fatigue life of rubberized asphalt concrete mixtures containing reclaimed asphalt pavement. Constr. Build. Mater. 2013, 41, 401–410. [Google Scholar] [CrossRef]
- Saucedo, L.; Yu, R.; Medeiros, A.; Zhang, X.; Ruiz, G. A probabilistic fatigue model based on the initial distribution to consider frequency effect in plain and fiber reinforced concrete. Int. J. Fatigue 2013, 48, 308–318. [Google Scholar] [CrossRef]
- Ding, Z.D.; Li, J. Modeling of fatigue damage of concrete with stochastic character. In Proceedings of the IALCCE, Tokyo, Japan, 16–19 November 2014. [Google Scholar]
- Liang, J.S.; Ding, Z.D.; Li, J. A probabilistic analyzed method for concrete fatigue life. Probab. Eng. Mech. 2017, 49, 13–21. [Google Scholar] [CrossRef]
- Bressi, S.; Primavera, M.; Santos, J. A comparative life cycle assessment study with uncertainty analysis of cement treated base (CTB) pavement layers containing recycled asphalt pavement (RAP) materials. Resour. Conserv. Recycl. 2022, 180, 106160. [Google Scholar] [CrossRef]
- Das, B.P.; Das, S.; Siddagangaiah, A.K. Probabilistic modeling of fatigue damage in asphalt mixture. Constr. Build. Mater. 2021, 269, 121300. [Google Scholar] [CrossRef]
- Sadek, H.; Masad, H.; Al-Khalid, H.; Sirin, O. Probabilistic analysis of fatigue life for asphalt mixtures using the viscoelastic continuum damage approach. Constr. Build. Mater. 2016, 126, 227–244. [Google Scholar] [CrossRef]
- Assi, A.A.; Sadek, H.; Massarra, C.; Sadeq, M.; Friedland, J.C. Development of an analysis tool for deterministic and probabilistic viscoelastic continuum damage approach. Constr. Build. Mater. 2021, 306, 124853. [Google Scholar] [CrossRef]
- Singh, P.; Swamy, A.K. Probabilistic characterisation of damage characteristic curve of asphalt concrete mixtures. Int. J. Pavement Eng. 2019, 20, 659–668. [Google Scholar] [CrossRef]
- Sadek, H.; Sadeq, M.; Masad, E.; Al-Khalid, H.; Sirin, O. Probabilistic Viscoelastic Continuum Damage Analysis of Fatigue Life of Warm-Mix Asphalt. J. Transp. Eng. Pt. B-Pavements 2019, 145, 04019024. [Google Scholar] [CrossRef]
- Ren, J.L.; Zhang, L.; Zhao, H.B.; Zhao, Z.D.; Wang, S. Determination of the fatigue equation for the cement-stabilized cold recycled mixtures with road construction waste materials based on data-driven. Int. J. Fatigue 2022, 158, 106765. [Google Scholar] [CrossRef]
- Chen, T.; Luan, Y.C.; Ma, T.; Zhu, J.Q.; Huang, X.M.; Ma, S. Mechanical and microstructural characteristics of different interfaces in cold recycled mixture containing cement and asphalt emulsion. J. Clean. Prod. 2020, 258, 120674. [Google Scholar] [CrossRef]
- Li, Z.G.; Hao, P.W.; Liu, H.Y.; Xu, J.Z. Effect of cement on the strength and microcosmic characteristics of cold recycled mixtures using foamed asphalt. J. Clean. Prod. 2019, 30, 956–965. [Google Scholar] [CrossRef]
- Ren, J.L.; Wang, S.Y.; Zang, G.Y. Effects of recycled aggregate composition on the mechanical characteristics and material design of cement stabilized cold recycling mixtures using road milling materials. Constr. Build. Mater. 2020, 244, 118329. [Google Scholar] [CrossRef]
- Khan, Z.; Balunaini, B.; Nguyen, N.; Costa, H. Evaluation of cement-treated recycled concrete aggregates for sustainable pavement base/subbase construction, Constr. Build. Mater. 2024, 449, 138417. [Google Scholar] [CrossRef]
- Hou, Y.Q.; Ji, X.P.; Zou, L.; Liu, S.; Su, X. Performance of cement-stabilised crushed brick aggregates in asphalt pavement base and subbase applications. Road Mater. Pavement Des. 2016, 17, 120–135. [Google Scholar] [CrossRef]
- Xiang, X.L.; Chen, W.L.; Huang, Y.F.; Wang, P.; Wang, G.; Wu, J.L.; Tian, W.Y. Application of recycled concrete aggregates in continuous-graded cement stabilized macadam. Case Stud. Constr. Mater. 2024, 21, e03918. [Google Scholar] [CrossRef]
- Jiang, Y.J.; Liu, H.P.; Xue, J.S. Fatigue performance of vertical vibration compacted cement-stabilized recycled pavement materials. J. Test. Eval. 2018, 46, 20170025. [Google Scholar] [CrossRef]
- Zhang, Y.; Jiang, Y.J.; Li, C.; Bai, C.F.; Zhang, F.X.; Li, J.X.; Guo, M.Y. Prediction of cement-stabilized recycled concrete aggregate properties by CNN-LSTM incorporating attention mechanism. Mater. Today Commun. 2025, 42, 111137. [Google Scholar] [CrossRef]
- Zhao, Y.Y.; Zhao, H.B. Uncertainty quantification based on symbolic regression and probabilistic programming and its application. Mach. Learn. Appl. 2025, 20, 100632. [Google Scholar] [CrossRef]
- Katunin, A.; Wachla, D.; Santos, P.; Reis, P. Fatigue life assessment of hybrid bio-composites based on self-heating temperature. Compos. Struct. 2023, 304, 116456. [Google Scholar] [CrossRef]
- Bassani, M.; Tefa, L.; Coppola, B.; Palmero, P. Alkali-activation of aggregate fines from construction and demolition waste: Valorisation in view of road pavement subbase applications. J. Clean. Prod. 2019, 234, 71–84. [Google Scholar] [CrossRef]
- Ren, J.L.; Zhao, H.B.; Zhang, L.; Zhao, Z.D.; Xu, Y.; Cheng, Y.; Wang, M.; Chen, J.; Wang, J. Design optimization of cement grouting material based on adaptive boosting algorithm and simplicial homology global optimization. J. Build. Eng. 2022, 49, 104049. [Google Scholar] [CrossRef]
- JTG E51-2009; Test Method for Inorganic Binder Stability Materials for Highway Engineering. Ministry of Transport of the People’s Public of China: Beijing, China, 2009.
- Beck, J. Bayesian system identification based on probability logic. Struct. Control. Health Monit. 2010, 17, 825–847. [Google Scholar] [CrossRef]
- Clement, A.; Soize, C.; Yvonnet, J. Uncertainty quantification in computational stochastic multiscale analysis of nonlinear elastic materials. Comput. Methods Appl. Mech. Eng. 2013, 254, 61–82. [Google Scholar] [CrossRef]
- Salvatier, J.; Wiecki, T.; Fonnesbeck, C. Probabilistic programming in Python using PyMC3. PeerJ Comput. Sci. 2016, 2, e55. [Google Scholar] [CrossRef]
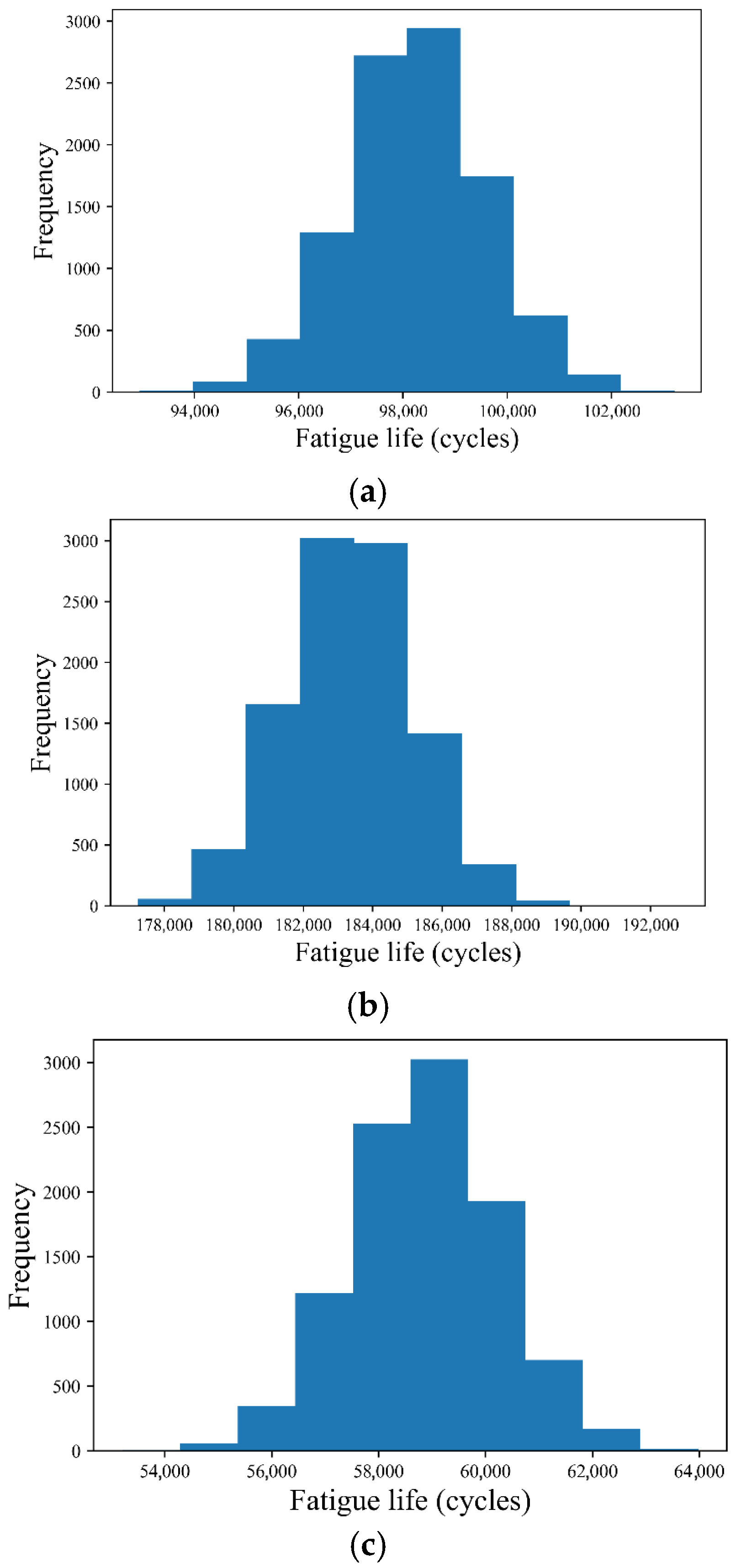
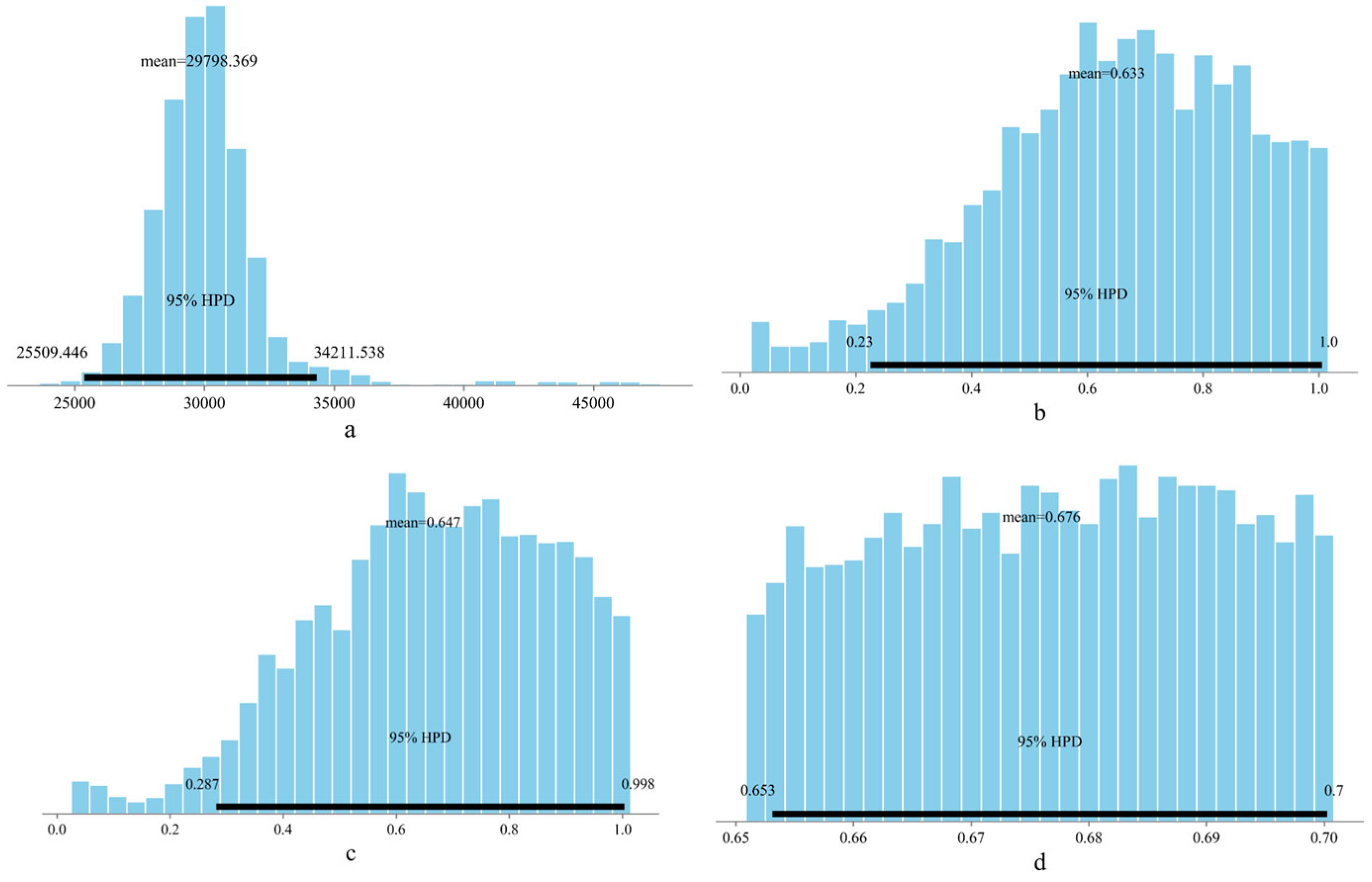
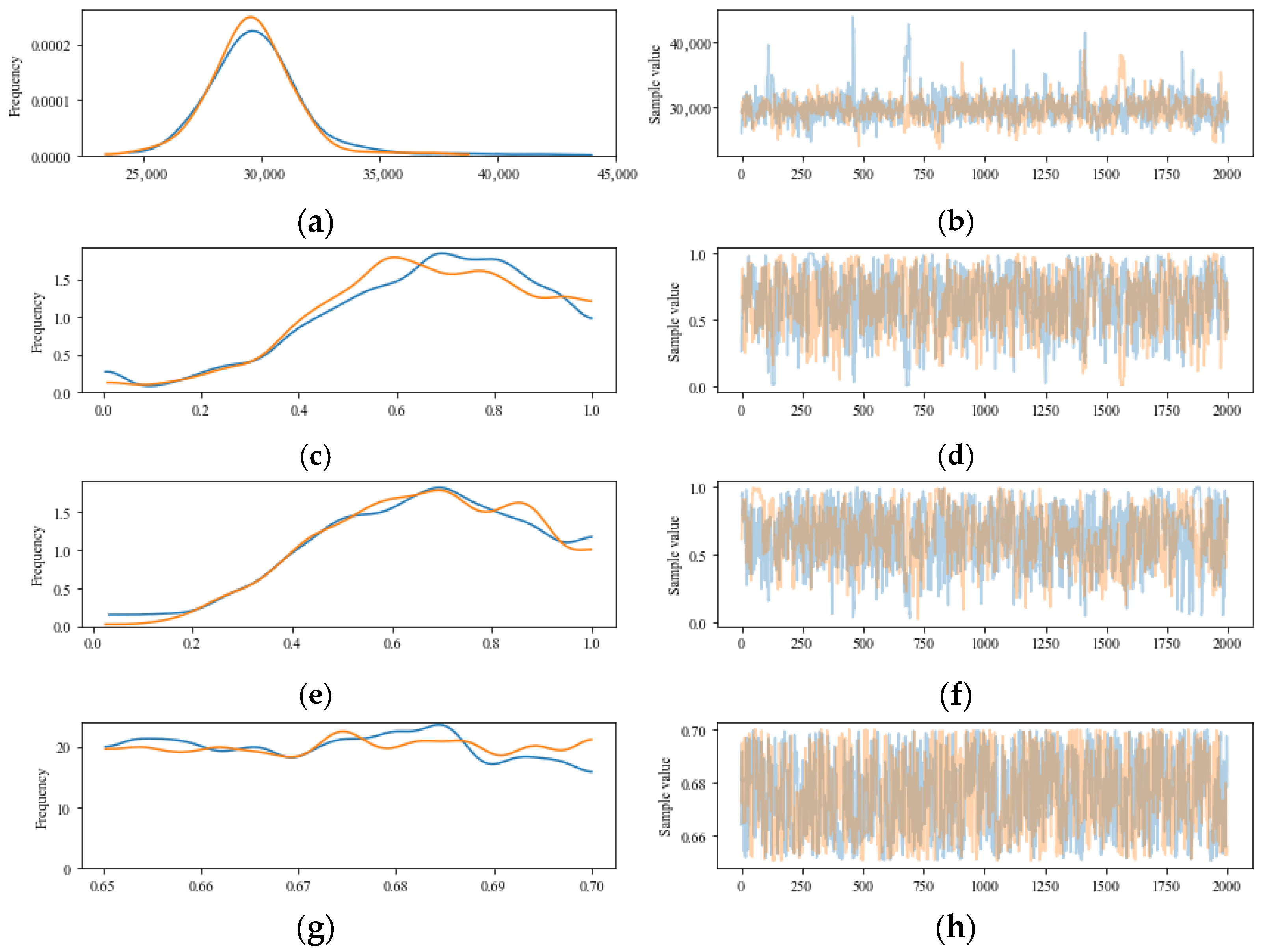
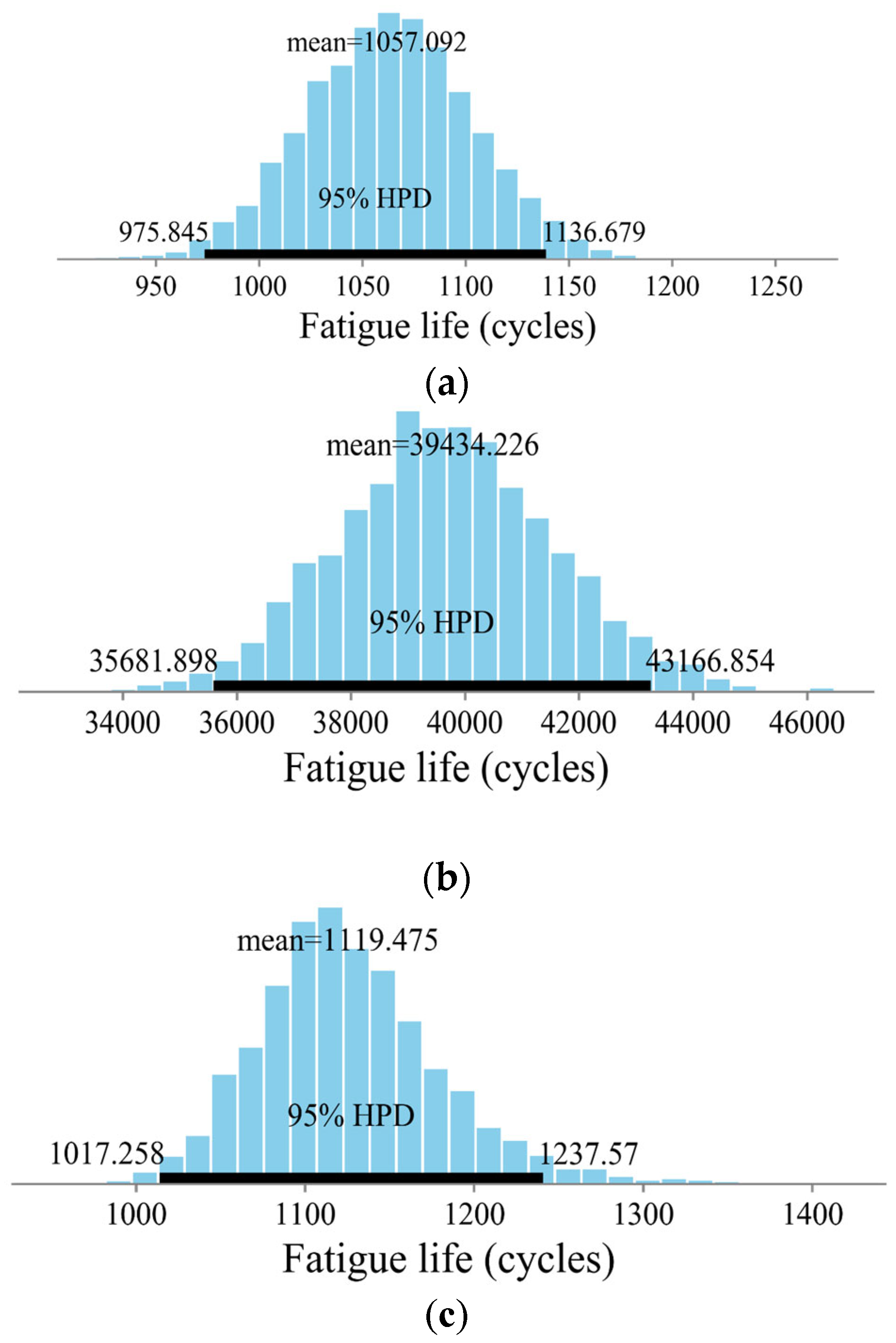
| Unknown Coefficient | UQ | Equation (2) | Relative Error (%) | |
|---|---|---|---|---|
| Mean Value | Standard Deviation | |||
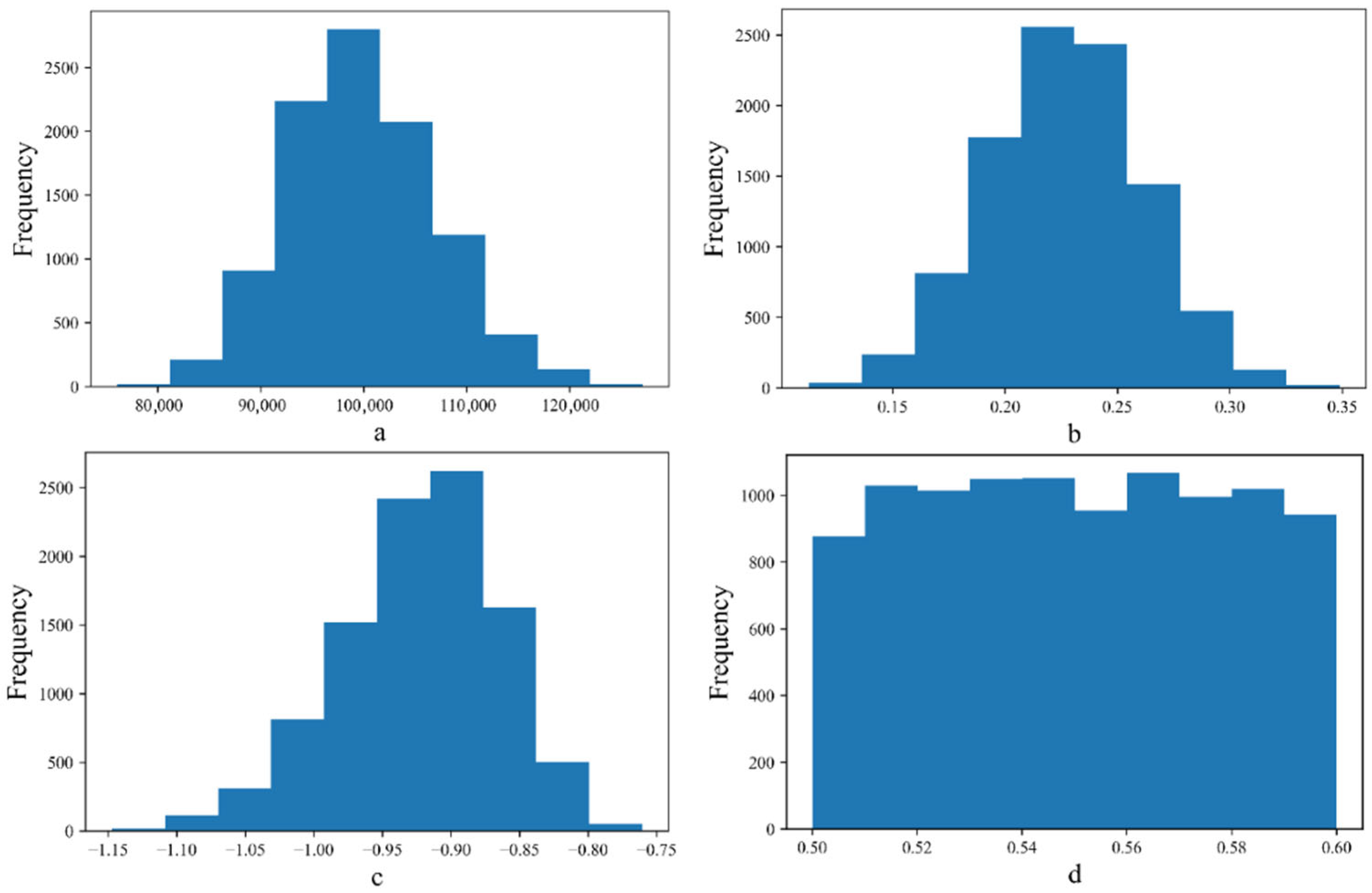
| A | 98,680.28 | 6029.57 | 100,000 | 1.32 |
| B | 0.23 | 0.030 | 0.2 | 15.96 |
| C | −0.91 | 0.046 | −1 | 8.71 |
| D | 0.55 | 0.028 | 0.562 | 1.73 |
| Unknown Coefficient | UQ | Equation (2) | Relative Error (%) | |
|---|---|---|---|---|
| Mean Value | Standard Deviation | |||
| a | 29,798.369 | 2525.195 | 33,207.78 | 10.49 |
| b | 0.633 | 0.2173 | 0.66 | 4.00 |
| c | 0.647 | 0.2136 | 0.66 | 2.64 |
| d | 0.676 | 0.0143 | 0.70 | 3.60 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, H.; Ren, J.; Zhang, L.; Lv, Q.; Zhuang, S.; Zhao, H. Uncertainty Quantification of Fatigue Life for Cement-Stabilized Cold Recycled Mixtures Using Probabilistic Programming. Materials 2025, 18, 4439. https://doi.org/10.3390/ma18194439
Liu H, Ren J, Zhang L, Lv Q, Zhuang S, Zhao H. Uncertainty Quantification of Fatigue Life for Cement-Stabilized Cold Recycled Mixtures Using Probabilistic Programming. Materials. 2025; 18(19):4439. https://doi.org/10.3390/ma18194439
Chicago/Turabian StyleLiu, Hao, Jiaolong Ren, Lin Zhang, Qingyi Lv, Shenghan Zhuang, and Hongbo Zhao. 2025. "Uncertainty Quantification of Fatigue Life for Cement-Stabilized Cold Recycled Mixtures Using Probabilistic Programming" Materials 18, no. 19: 4439. https://doi.org/10.3390/ma18194439
APA StyleLiu, H., Ren, J., Zhang, L., Lv, Q., Zhuang, S., & Zhao, H. (2025). Uncertainty Quantification of Fatigue Life for Cement-Stabilized Cold Recycled Mixtures Using Probabilistic Programming. Materials, 18(19), 4439. https://doi.org/10.3390/ma18194439








