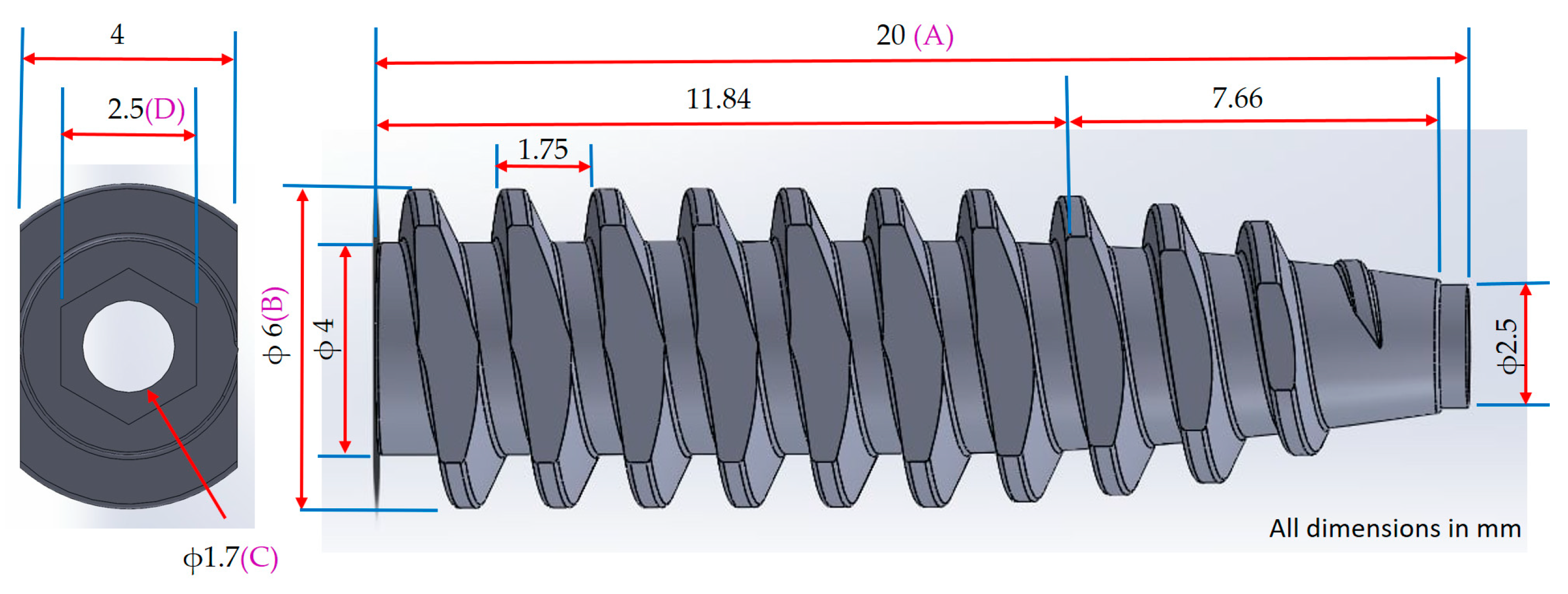
Figure 1.
Dimensional design and shrinkage measurement points of a cannulated bone screw. The figure illustrates the key dimensional parameters of the cannulated bone screw, including total length (A), thread outer diameter (B), bore diameter (C), and hex socket width (D). These labeled positions also serve as reference points for post-molding shrinkage measurements.
Figure 1.
Dimensional design and shrinkage measurement points of a cannulated bone screw. The figure illustrates the key dimensional parameters of the cannulated bone screw, including total length (A), thread outer diameter (B), bore diameter (C), and hex socket width (D). These labeled positions also serve as reference points for post-molding shrinkage measurements.
Figure 2.
Torque and temperature curve of PLA/PCL (80%:20%) with 10 wt% HA during mixing process.
Figure 2.
Torque and temperature curve of PLA/PCL (80%:20%) with 10 wt% HA during mixing process.
Figure 3.
Torque and temperature curve of PLA/PCL (80%:20%) with 3 wt% TiO2 during mixing process.
Figure 3.
Torque and temperature curve of PLA/PCL (80%:20%) with 3 wt% TiO2 during mixing process.
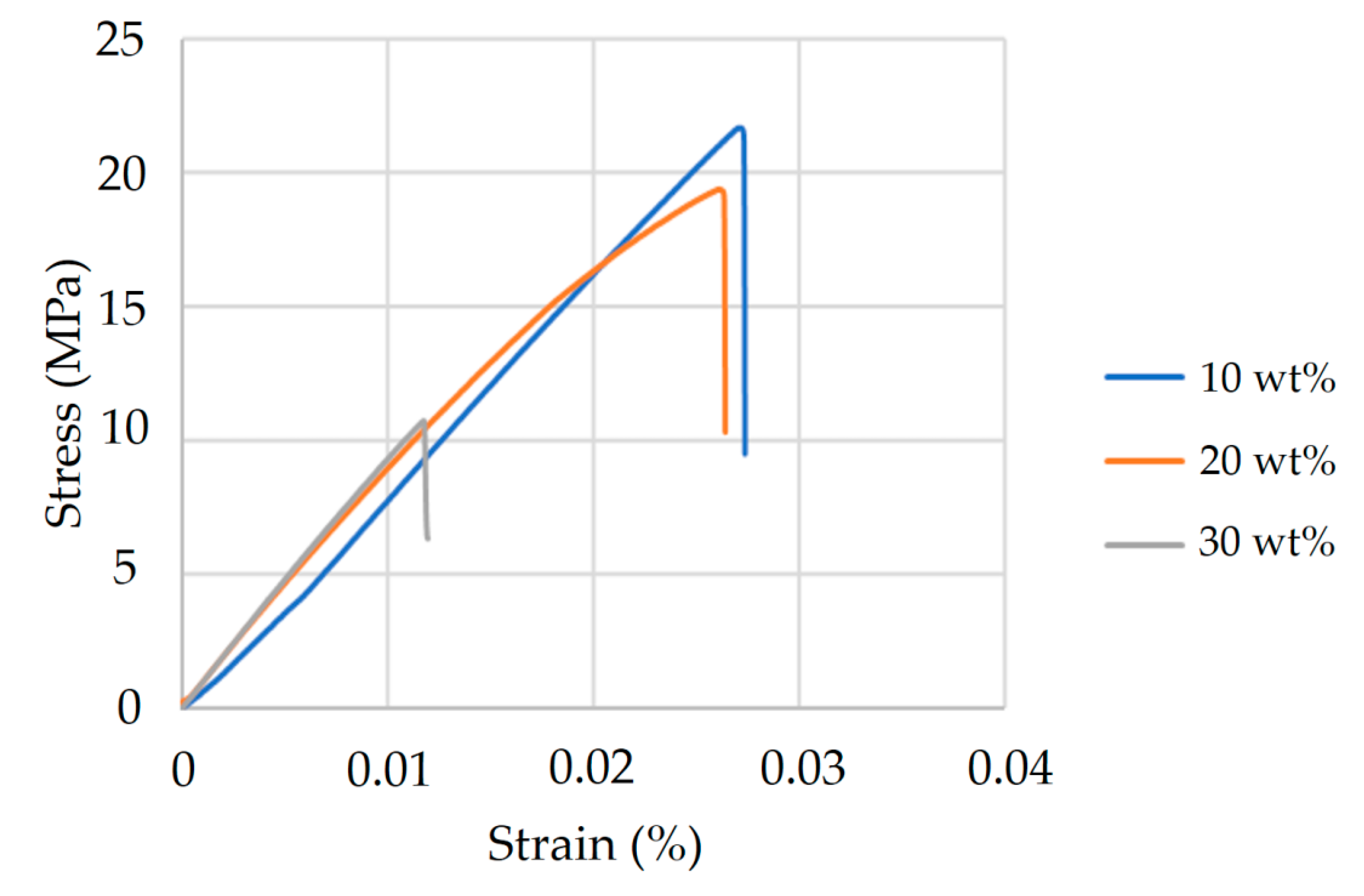
Figure 4.
Tensile strength and elongation of PLA/PCL composites with varying HA content. Specimens containing 10 wt%, 20 wt%, and 30 wt% HA were tested according to ASTM D638 Type V standards. The 10 wt% HA formulation exhibited the highest tensile strength and elongation, suggesting optimal particle dispersion and effective reinforcement. A marked decline in mechanical properties was observed at 30 wt% HA, which may be attributed to reduced matrix continuity and filler overloading.
Figure 4.
Tensile strength and elongation of PLA/PCL composites with varying HA content. Specimens containing 10 wt%, 20 wt%, and 30 wt% HA were tested according to ASTM D638 Type V standards. The 10 wt% HA formulation exhibited the highest tensile strength and elongation, suggesting optimal particle dispersion and effective reinforcement. A marked decline in mechanical properties was observed at 30 wt% HA, which may be attributed to reduced matrix continuity and filler overloading.
Figure 5.
Tensile strength and elongation of PLA/PCL composites with varying TiO2 content. Samples containing 1 wt%, 3 wt%, and 5 wt% TiO2 were evaluated. The 1 wt% group exhibited the highest tensile strength but limited ductility. In contrast, the 3 wt% formulation achieved improved elongation with moderate strength, representing the most favorable balance of toughness and resilience. Both strength and ductility declined notably in the 5 wt% group, possibly due to filler overloading and reduced interfacial compatibility.
Figure 5.
Tensile strength and elongation of PLA/PCL composites with varying TiO2 content. Samples containing 1 wt%, 3 wt%, and 5 wt% TiO2 were evaluated. The 1 wt% group exhibited the highest tensile strength but limited ductility. In contrast, the 3 wt% formulation achieved improved elongation with moderate strength, representing the most favorable balance of toughness and resilience. Both strength and ductility declined notably in the 5 wt% group, possibly due to filler overloading and reduced interfacial compatibility.
Figure 6.
Injection speed–pressure profile simulated via Moldex3D for PLA/PCL blend without additives. Results support the selection of a 40–80 mm/s range for stable injection molding.
Figure 6.
Injection speed–pressure profile simulated via Moldex3D for PLA/PCL blend without additives. Results support the selection of a 40–80 mm/s range for stable injection molding.
Figure 7.
Moldex3D simulation showing gate solidification at 2.635 s during the packing phase. Based on this result, the holding time was conservatively set to 3 s to ensure complete packing and dimensional stability.
Figure 7.
Moldex3D simulation showing gate solidification at 2.635 s during the packing phase. Based on this result, the holding time was conservatively set to 3 s to ensure complete packing and dimensional stability.
Figure 8.
Temperature distribution within the polymer melt inside the cannulated bone screw mold after 10 s of cooling, as simulated using Moldex3D 2020. The maximum and minimum temperatures were 87.131 °C and 85.301 °C, respectively, yielding a cavity temperature difference of 1.83 °C. These results satisfy the cooling uniformity criterion (ΔT < 10 °C) and support the selection of 10 s as the baseline cooling time.
Figure 8.
Temperature distribution within the polymer melt inside the cannulated bone screw mold after 10 s of cooling, as simulated using Moldex3D 2020. The maximum and minimum temperatures were 87.131 °C and 85.301 °C, respectively, yielding a cavity temperature difference of 1.83 °C. These results satisfy the cooling uniformity criterion (ΔT < 10 °C) and support the selection of 10 s as the baseline cooling time.
Figure 9.
Architecture of the BPNN shrinkage predictor. The network consists of three input neurons corresponding to melt temperature, injection speed, and holding speed; a hidden layer with eight neurons; and one output neuron representing the normalized shrinkage rate.
Figure 9.
Architecture of the BPNN shrinkage predictor. The network consists of three input neurons corresponding to melt temperature, injection speed, and holding speed; a hidden layer with eight neurons; and one output neuron representing the normalized shrinkage rate.
Figure 10.
Conceptual overview of the GA–PSO hybrid optimization process, which was adapted from existing variants to suit the specific molding requirements in this study. The flowchart highlights the iterative interaction between BPNN prediction and parameter refinement, enabling an efficient search for optimal shrinkage performance without relying on gradient-based methods.
Figure 10.
Conceptual overview of the GA–PSO hybrid optimization process, which was adapted from existing variants to suit the specific molding requirements in this study. The flowchart highlights the iterative interaction between BPNN prediction and parameter refinement, enabling an efficient search for optimal shrinkage performance without relying on gradient-based methods.
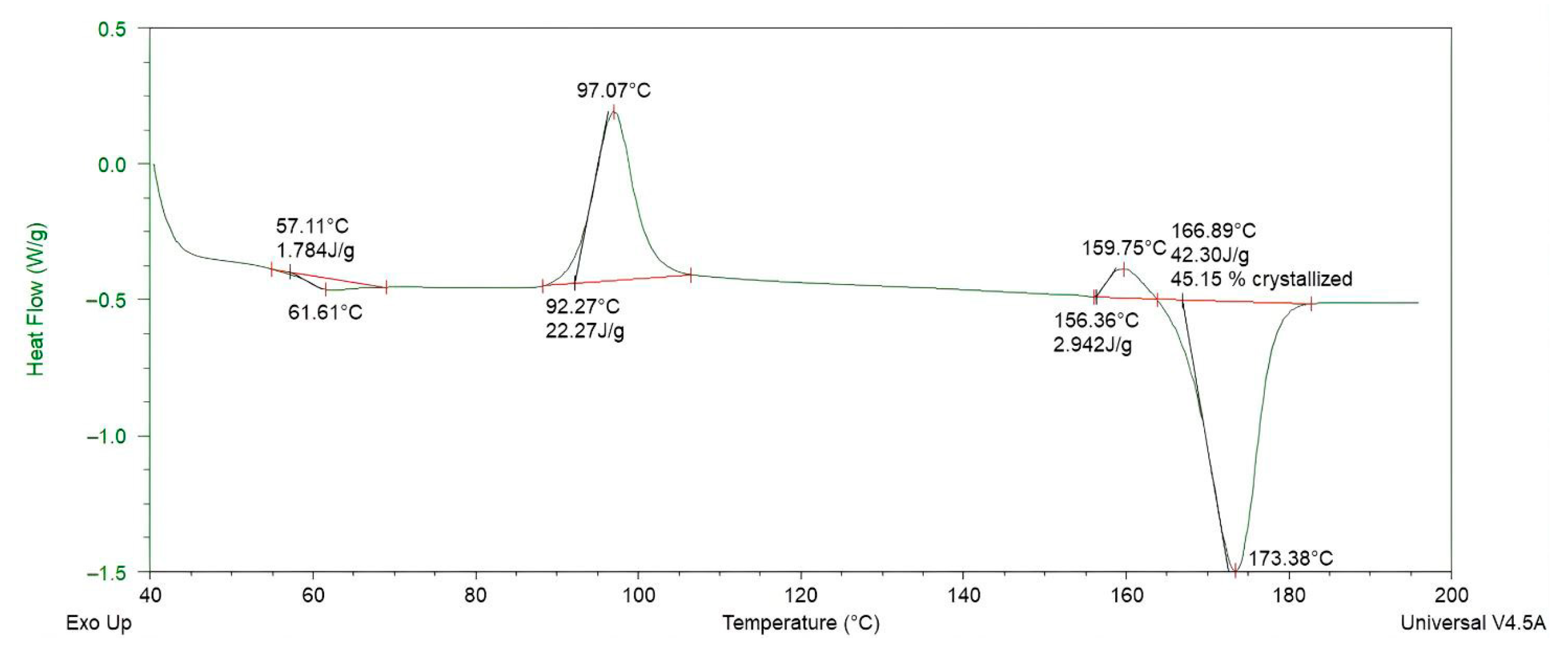
Figure 11.
Differential scanning calorimetry (DSC) thermogram of PLA/PCL (80:20 wt%) blend, showing the melting transition of PLA at 173.38 °C and the thermal behavior of the composite.
Figure 11.
Differential scanning calorimetry (DSC) thermogram of PLA/PCL (80:20 wt%) blend, showing the melting transition of PLA at 173.38 °C and the thermal behavior of the composite.
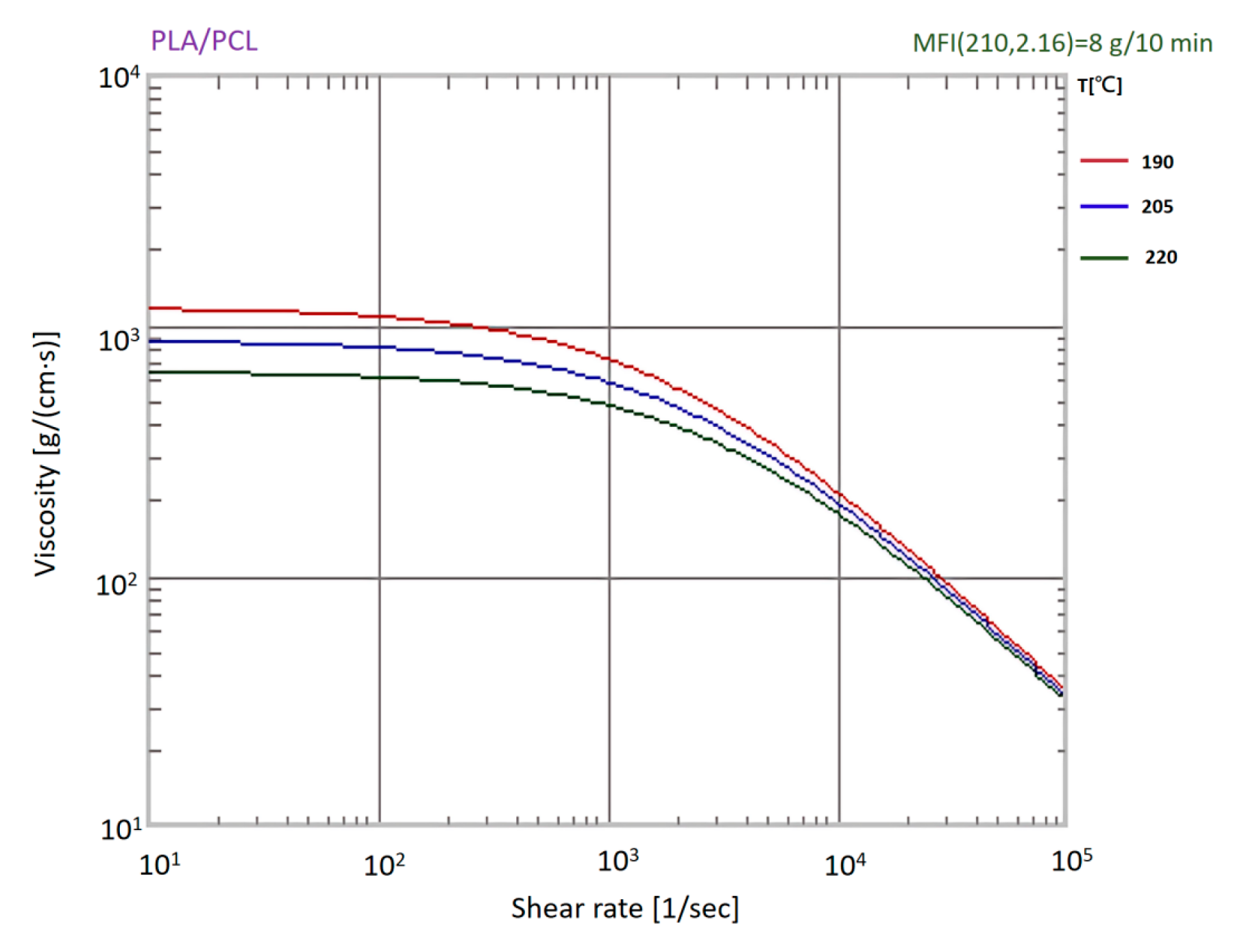
Figure 12.
Shear viscosity profiles of PLA/PCL (80:20 wt%) blend at 190 °C, 205 °C, and 220 °C, showing temperature-dependent shear-thinning behavior.
Figure 12.
Shear viscosity profiles of PLA/PCL (80:20 wt%) blend at 190 °C, 205 °C, and 220 °C, showing temperature-dependent shear-thinning behavior.
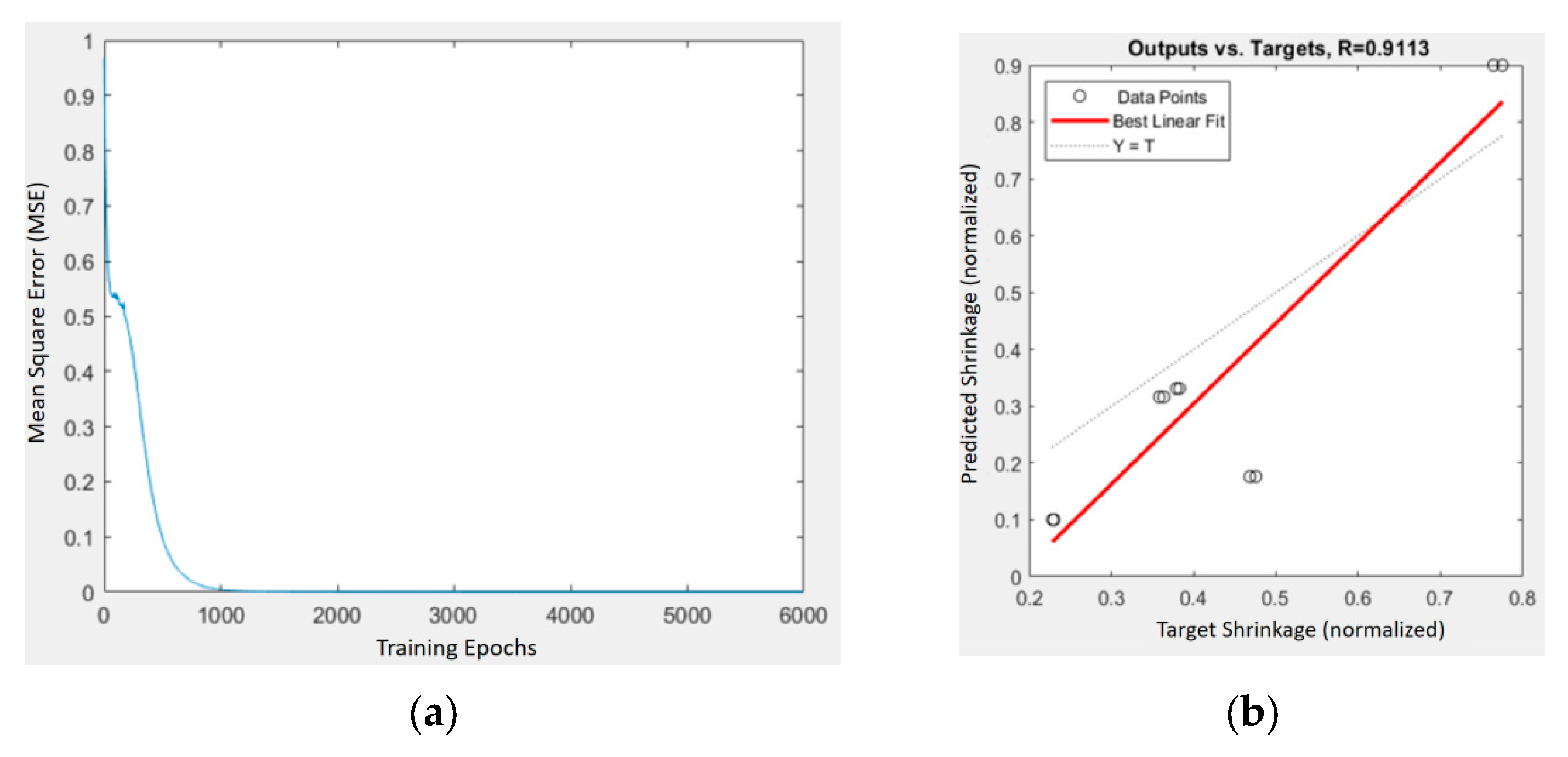
Figure 15.
Training and prediction results of the BPNN model for PLA/PCL/HA composites: (a) MSE vs. iterations; (b) predicted vs. target shrinkage values with regression fit (R = 0.9113).
Figure 15.
Training and prediction results of the BPNN model for PLA/PCL/HA composites: (a) MSE vs. iterations; (b) predicted vs. target shrinkage values with regression fit (R = 0.9113).
Figure 16.
Training and prediction results of the BPNN model for PLA/PCL/TiO2 composites: (a) MSE vs. iterations; (b) predicted vs. target shrinkage values with regression fit (R = 0.94219).
Figure 16.
Training and prediction results of the BPNN model for PLA/PCL/TiO2 composites: (a) MSE vs. iterations; (b) predicted vs. target shrinkage values with regression fit (R = 0.94219).
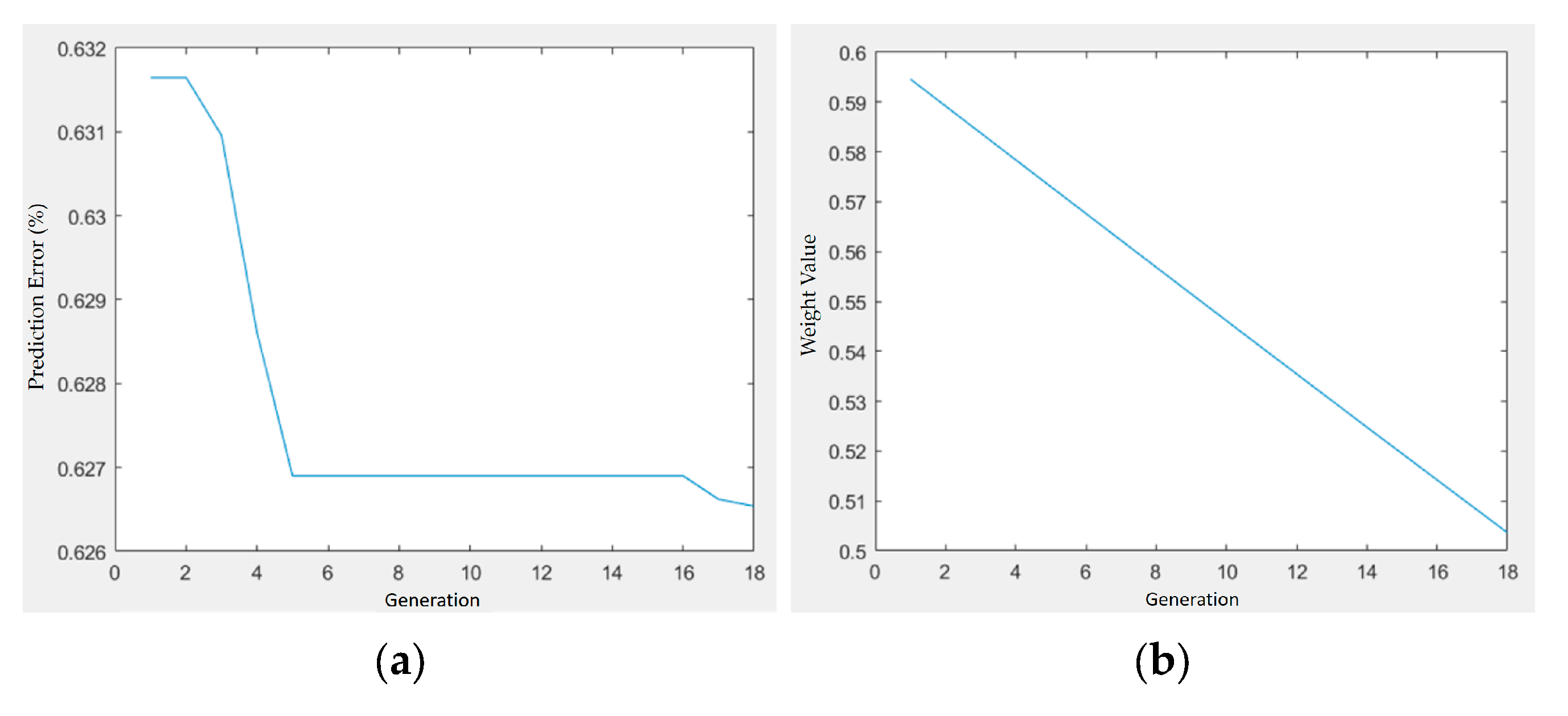
Figure 17.
Optimization trajectory and convergence behavior of GA–PSO for shrinkage minimization in PLA/PCL/HA composites: (a) prediction error vs. generation; (b) weight value vs. generation.
Figure 17.
Optimization trajectory and convergence behavior of GA–PSO for shrinkage minimization in PLA/PCL/HA composites: (a) prediction error vs. generation; (b) weight value vs. generation.
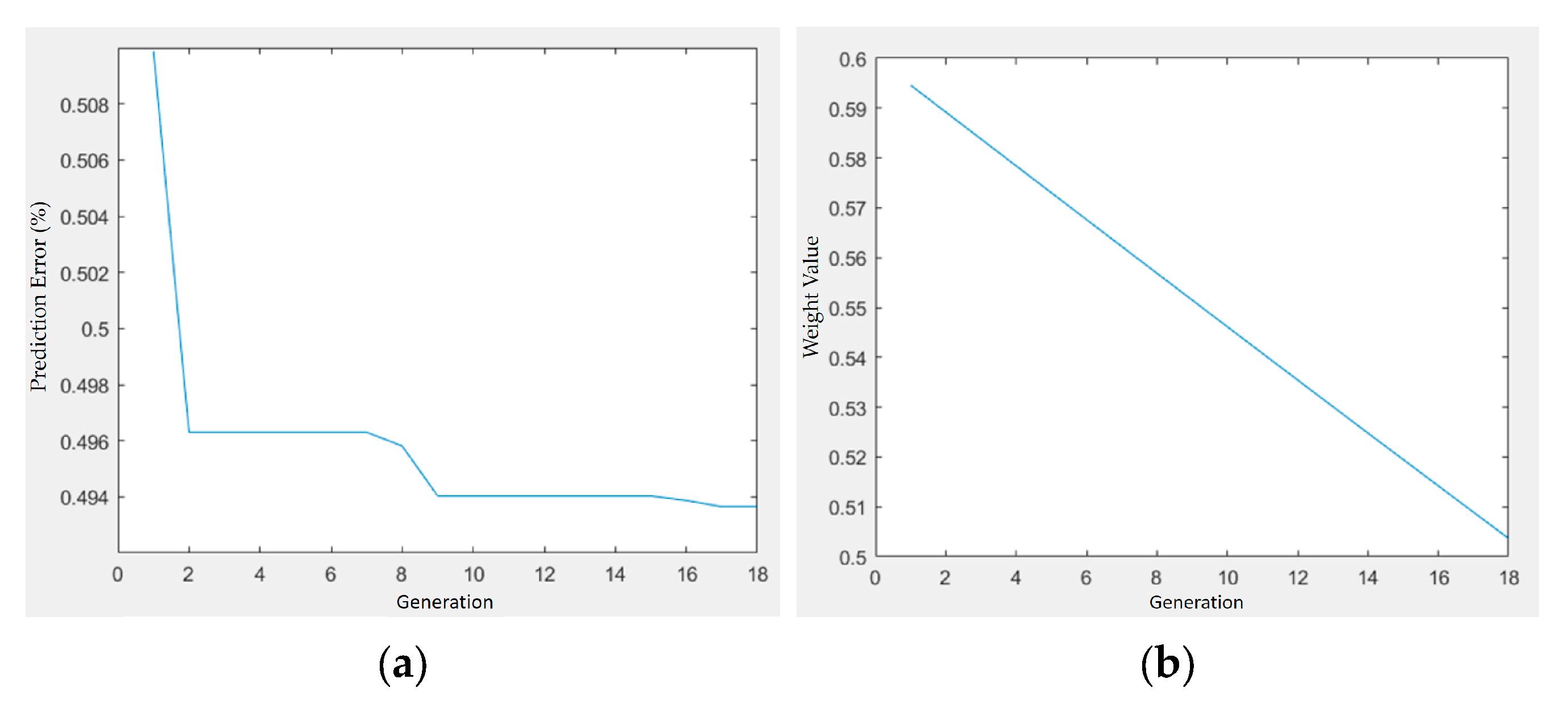
Figure 18.
Optimization trajectory and convergence behavior of GA–PSO for shrinkage minimization in PLA/PCL/TiO2 composites: (a) prediction error vs. generation; (b) weight value vs. generation.
Figure 18.
Optimization trajectory and convergence behavior of GA–PSO for shrinkage minimization in PLA/PCL/TiO2 composites: (a) prediction error vs. generation; (b) weight value vs. generation.
Figure 19.
Molded PLA/PCL/TiO
2 bone screw fabricated under GA–PSO-optimized conditions. The image shows the cannulate bone screw produced using the best parameter combination identified via BPNN-guided GA–PSO optimization. A quantitative comparison of shrinkage performance is provided in
Table 15.
Figure 19.
Molded PLA/PCL/TiO
2 bone screw fabricated under GA–PSO-optimized conditions. The image shows the cannulate bone screw produced using the best parameter combination identified via BPNN-guided GA–PSO optimization. A quantitative comparison of shrinkage performance is provided in
Table 15.
Table 1.
L9 Orthogonal array for injection molding parameters used in bPNN training.
Table 1.
L9 Orthogonal array for injection molding parameters used in bPNN training.
| Level | Melt Temperature (°C) | Injection Speed (mm/s) | Holding Speed (mm/s) |
|---|
| 1 | 190 | 40 | 10 |
| 2 | 200 | 60 | 20 |
| 3 | 210 | 80 | 30 |
Table 2.
Fixed injection molding parameters used in BPNN training.
Table 2.
Fixed injection molding parameters used in BPNN training.
| Parameters | Numerical Value |
|---|
| Mold Temp | 30 °C |
| Cooling Time | 15 s |
| Holding Time | 3 s |
| Back Pressure | 40 bar |
| Screw Speed | 80 rpm |
| Metering Volume | 470 mm3 |
Table 3.
Experimental runs based on L9 orthogonal array for BPNN training. Nine combinations of melt temperature, injection speed, and holding speed were arranged using an L9 orthogonal array to generate uniformly distributed training data and assess the contributions of various factors to product quality.
Table 3.
Experimental runs based on L9 orthogonal array for BPNN training. Nine combinations of melt temperature, injection speed, and holding speed were arranged using an L9 orthogonal array to generate uniformly distributed training data and assess the contributions of various factors to product quality.
| Run | Melt Temperature (°C) | Injection Speed (mm/s) | Holding Speed (mm/s) |
|---|
| 1 | 190 | 40 | 10 |
| 2 | 190 | 60 | 20 |
| 3 | 190 | 80 | 30 |
| 4 | 200 | 40 | 20 |
| 5 | 200 | 60 | 30 |
| 6 | 200 | 80 | 10 |
| 7 | 210 | 40 | 30 |
| 8 | 210 | 60 | 10 |
| 9 | 210 | 80 | 20 |
Table 6.
ANOVA results for shrinkage variation (PLA/PCL/HA).
Table 6.
ANOVA results for shrinkage variation (PLA/PCL/HA).
| Control Factor | Variance (S) | DoF (f) | Mutations (V) | Pure Change (S) | Contribution (ρ)% |
|---|
| A (Melt Temperature) | 25.389 | 2 | 12.695 | 23.764 | 37.70 |
| B (Injection Speed) | 16.458 | 2 | 8.229 | 14.833 | 24.44 |
| C (Holding Speed) | 9.247 | 2 | 4.624 | 7.622 | 13.73 |
| e (Error) | 16.247 | 20 | 0.812 | 0 | 24.13 |
| Total | 67.337 | 26 | | 45.674 | 100 |
Table 7.
Dimensional measurements of PLA/PCL/TiO2 bone screws (unit: mm).
Table 7.
Dimensional measurements of PLA/PCL/TiO2 bone screws (unit: mm).
| Trial | Specimen | Length | Thread Outer Diameter | Bore Diameter | Hex Socket Width |
|---|
| L1 | #1 | 19.647 | 5.92 | 1.673 | 2.449 |
| | #2 | 19.685 | 5.935 | 1.693 | 2.426 |
| | #3 | 19.662 | 5.896 | 1.671 | 2.428 |
| L2 | #1 | 19.479 | 5.883 | 1.68 | 2.363 |
| | #2 | 19.637 | 5.893 | 1.668 | 2.335 |
| | #3 | 19.472 | 5.957 | 1.674 | 2.321 |
| L3 | #1 | 19.71 | 5.885 | 1.66 | 2.431 |
| | #2 | 19.796 | 5.955 | 1.667 | 2.431 |
| | #3 | 19.778 | 5.874 | 1.667 | 2.345 |
| L4 | #1 | 19.763 | 5.891 | 1.675 | 2.282 |
| | #2 | 19.822 | 5.936 | 1.67 | 2.393 |
| | #3 | 19.906 | 5.882 | 1.669 | 2.378 |
| L5 | #1 | 19.725 | 5.863 | 1.652 | 2.331 |
| | #2 | 19.682 | 5.897 | 1.678 | 2.324 |
| | #3 | 19.628 | 5.858 | 1.668 | 2.386 |
| L6 | #1 | 19.969 | 5.934 | 1.653 | 2.443 |
| | #2 | 19.907 | 5.948 | 1.673 | 2.385 |
| | #3 | 19.848 | 5.878 | 1.66 | 2.418 |
| L7 | #1 | 19.945 | 5.853 | 1.659 | 2.422 |
| | #2 | 19.964 | 5.928 | 1.66 | 2.413 |
| | #3 | 19.943 | 5.865 | 1.672 | 2.477 |
| L8 | #1 | 19.943 | 5.936 | 1.67 | 2.449 |
| | #2 | 19.823 | 5.908 | 1.683 | 2.43 |
| | #3 | 19.782 | 5.945 | 1.663 | 2.393 |
| L9 | #1 | 19.727 | 5.856 | 1.686 | 2.383 |
| | #2 | 19.827 | 5.894 | 1.69 | 2.403 |
| | #3 | 19.822 | 5.884 | 1.683 | 2.394 |
Table 8.
Summary of shrinkage rates, standard deviations, shrinkage–variation sums, and S/N ratios for PLA/PCL/TiO2 composite trials.
Table 8.
Summary of shrinkage rates, standard deviations, shrinkage–variation sums, and S/N ratios for PLA/PCL/TiO2 composite trials.
| Run | Total Shrinkage (%) | Total SD(%) | Shrinkage + SD (%) | S/N |
|---|
| L1 | 7.029 | 1.64 | 8.669 | 23.062 |
| L2 | 11.859 | 2.337 | 14.196 | 18.519 |
| L3 | 8.873 | 3.189 | 12.062 | 21.038 |
| L4 | 10.217 | 3.439 | 13.656 | 19.815 |
| L5 | 12.009 | 2.731 | 14.74 | 18.409 |
| L6 | 7.509 | 2.679 | 10.188 | 22.488 |
| L7 | 6.914 | 2.555 | 9.469 | 23.205 |
| L8 | 6.086 | 2.478 | 8.564 | 24.313 |
| L9 | 4.248 | 1.215 | 5.463 | 27.436 |
Table 9.
ANOVA results for shrinkage variation (PLA/PCL/TiO2).
Table 9.
ANOVA results for shrinkage variation (PLA/PCL/TiO2).
| Control Factor | Variance (S) | DoF (f) | Mutations (V) | Pure Change (S) | Contribution (ρ)% |
|---|
| A (Melt Temperature) | 39.853 | 2 | 19.926 | 39.443 | 58.25 |
| B (Injection Speed) | 15.749 | 2 | 7.875 | 15.339 | 23.02 |
| C (Holding Speed) | 8.717 | 2 | 4.359 | 8.307 | 12.74 |
| e (Error) | 4.104 | 20 | 0.2052 | 0 | 6.00 |
| Total | 68.426 | 26 | | 63.089 | 100 |
Table 10.
Setting the parameters of the back-propagation neural network.
Table 10.
Setting the parameters of the back-propagation neural network.
| Input Layer | Three Neurons |
|---|
| Hidden Layer | One layer, eight neurons |
| Learning Rate | 0.01 |
| Normalization range | 0.1~0.9 |
| Activation function | Sigmoid function |
| Convergence Threshold | 10−7 |
| Training maximum epochs | 12,000 |
Table 11.
Verification group parameters. Each group (#1–#5) included three molding parameters—melt temperature, injection speed, and holding speed—for both PLA/PCL/HA and PLA/PCL/TO2 systems.
Table 11.
Verification group parameters. Each group (#1–#5) included three molding parameters—melt temperature, injection speed, and holding speed—for both PLA/PCL/HA and PLA/PCL/TO2 systems.
| | PLA/PCL/HA | PLA/PCL/TO2 |
|---|
| Run | Melt Temp. (°C) | Injection Speed
(mm/s) | Holding Speed
(mm/s) | Melt Temp. (°C) | Injection Speed
(mm/s) | Holding Speed
(mm/s) |
|---|
| #1 | 194 | 80 | 30 | 190 | 63 | 30 |
| #2 | 210 | 53 | 14 | 194 | 40 | 10 |
| #3 | 202 | 60 | 10 | 210 | 74 | 23 |
| #4 | 206 | 40 | 26 | 202 | 80 | 30 |
| #5 | 190 | 46 | 18 | 198 | 51 | 16 |
Table 12.
PLA/PCL/HA back-transfer neural network normalization data.
Table 12.
PLA/PCL/HA back-transfer neural network normalization data.
| | | Melt Temp | Injection Speed | Holding Speed | Shrinkage |
|---|
| Training Group | L1 | 0.100 | 0.100 | 0.100 | 0.730 |
| L2 | 0.100 | 0.500 | 0.500 | 0.900 |
| L3 | 0.100 | 0.900 | 0.900 | 0.785 |
| L4 | 0.500 | 0.100 | 0.500 | 0.871 |
| L5 | 0.500 | 0.500 | 0.900 | 0.352 |
| L6 | 0.500 | 0.900 | 0.100 | 0.100 |
| L7 | 0.900 | 0.100 | 0.900 | 0.656 |
| L8 | 0.900 | 0.500 | 0.100 | 0.818 |
| L9 | 0.900 | 0.900 | 0.500 | 0.521 |
| Test Group | Test 1 | 0.260 | 0.900 | 0.900 | 0.854 |
| Test 2 | 0.900 | 0.367 | 0.260 | 0.534 |
| Test 3 | 0.580 | 0.500 | 0.100 | 0.900 |
| Test 4 | 0.740 | 0.100 | 0.740 | 0.900 |
| Test 5 | 0.100 | 0.233 | 0.420 | 0.100 |
Table 13.
PLA/PCL/TiO2 back-transfer neural network normalization data.
Table 13.
PLA/PCL/TiO2 back-transfer neural network normalization data.
| | | Melt Temp | Injection Speed | Holding Speed | Shrinkage |
|---|
| Training Group | L1 | 0.100 | 0.100 | 0.100 | 0.387 |
| L2 | 0.100 | 0.500 | 0.500 | 0.885 |
| L3 | 0.100 | 0.900 | 0.900 | 0.577 |
| L4 | 0.500 | 0.100 | 0.500 | 0.715 |
| L5 | 0.500 | 0.500 | 0.900 | 0.900 |
| L6 | 0.500 | 0.900 | 0.100 | 0.436 |
| L7 | 0.900 | 0.100 | 0.900 | 0.375 |
| L8 | 0.900 | 0.500 | 0.100 | 0.289 |
| L9 | 0.900 | 0.900 | 0.500 | 0.100 |
| Test Group | Test 1 | 0.100 | 0.557 | 0.900 | 0.100 |
| Test 2 | 0.260 | 0.100 | 0.100 | 0.706 |
| Test 3 | 0.900 | 0.786 | 0.633 | 0.900 |
| Test 4 | 0.580 | 0.900 | 0.900 | 0.827 |
| Test 5 | 0.420 | 0.329 | 0.367 | 0.730 |
Table 14.
GA–PSO-optimized process parameters for PLA/PCL/HA and PLA/PCL/TiO2 formulas used in injection molding trials.
Table 14.
GA–PSO-optimized process parameters for PLA/PCL/HA and PLA/PCL/TiO2 formulas used in injection molding trials.
| | | Melt Temperature | Injection Speed | Holding Speed |
|---|
| HA | Normalized Value | 0.4024 | 0.7472 | 0.2932 |
| Actual Value | 197.56 °C | 72.36 mm/s | 14.83 mm/s |
| TiO2 | Normalized Value | 0.7548 | 0.8362 | 0.6448 |
| Actual Value | 206.37 °C | 76.81 mm/s | 23.62 mm/s |
Table 15.
Dimensional measurements and average shrinkage rates of bone screws fabricated under AI-optimized molding conditions for HA and TiO2 systems. Measurements were obtained for three samples per material system. The dimensional consistency and shrinkage rates reflect the effectiveness of AI-driven process optimization.
Table 15.
Dimensional measurements and average shrinkage rates of bone screws fabricated under AI-optimized molding conditions for HA and TiO2 systems. Measurements were obtained for three samples per material system. The dimensional consistency and shrinkage rates reflect the effectiveness of AI-driven process optimization.
| HA | Length (mm) | Thread Outer Diameter (mm) | Bore Diameter (mm) | Hex Socket Width (mm) | Average Shrinkage (%) |
|---|
| #1 | 19.941 | 5.929 | 1.693 | 2.494 | 2.238 |
| #2 | 19.985 | 5.966 | 1.677 | 2.468 | 3.383 |
| #3 | 19.888 | 5.964 | 1.688 | 2.477 | 2.893 |
| Average | 19.938 | 5.953 | 1.686 | 2.480 | 2.838 |
| TiO2 | Length (mm) | Thread Outer Diameter (mm) | Bore Diameter (mm) | Hex Socket Width (mm) | Average Shrinkage (%) |
| #1 | 19.988 | 5.928 | 1.699 | 2.486 | 1.986 |
| #2 | 19.984 | 5.962 | 1.675 | 2.497 | 2.412 |
| #3 | 19.966 | 5.982 | 1.691 | 2.497 | 1.226 |
| Average | 19.979 | 5.957 | 1.688 | 2.493 | 1.875 |