Optimum Mix Design and Correlation Analysis of Pervious Concrete
Abstract
1. Introduction
2. Materials and Methods
2.1. Raw Materials
2.1.1. Cement
2.1.2. Coarse Aggregate
2.1.3. Fine Aggregate
2.1.4. Viscosity-Modifying Admixture (VMA)
2.1.5. Water-Reducing Agent
2.2. Mix Proportion Design
2.2.1. Single-Factor Mix Proportion Design
2.2.2. Orthogonal Test
2.3. Sample Preparation and Curing
2.4. Characterization of Performance
2.4.1. Compressive Strength Test
2.4.2. Splitting Tensile Strength Test
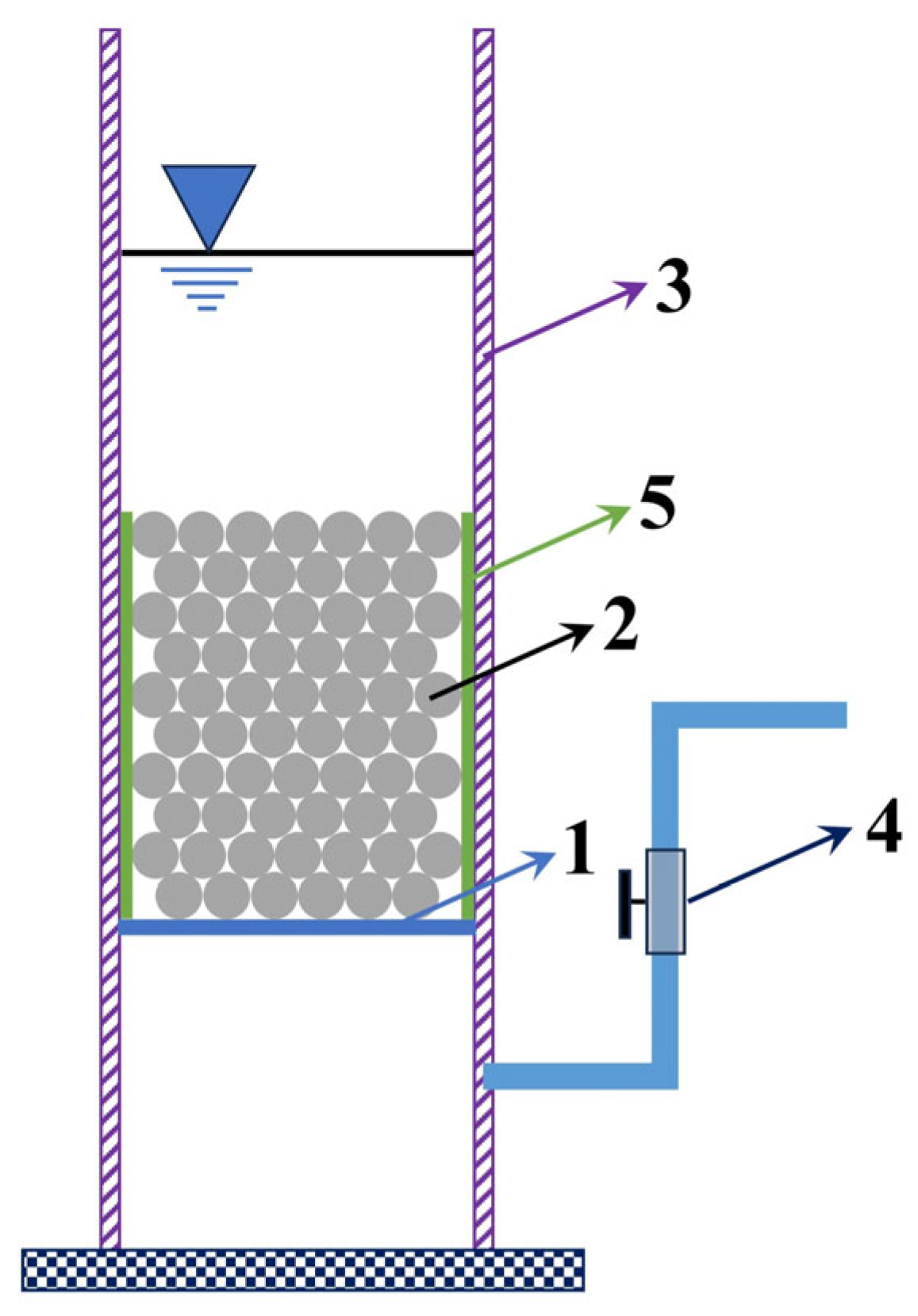
2.4.3. Permeability Testing
3. Results and Discussion
3.1. Single-Factor Analysis
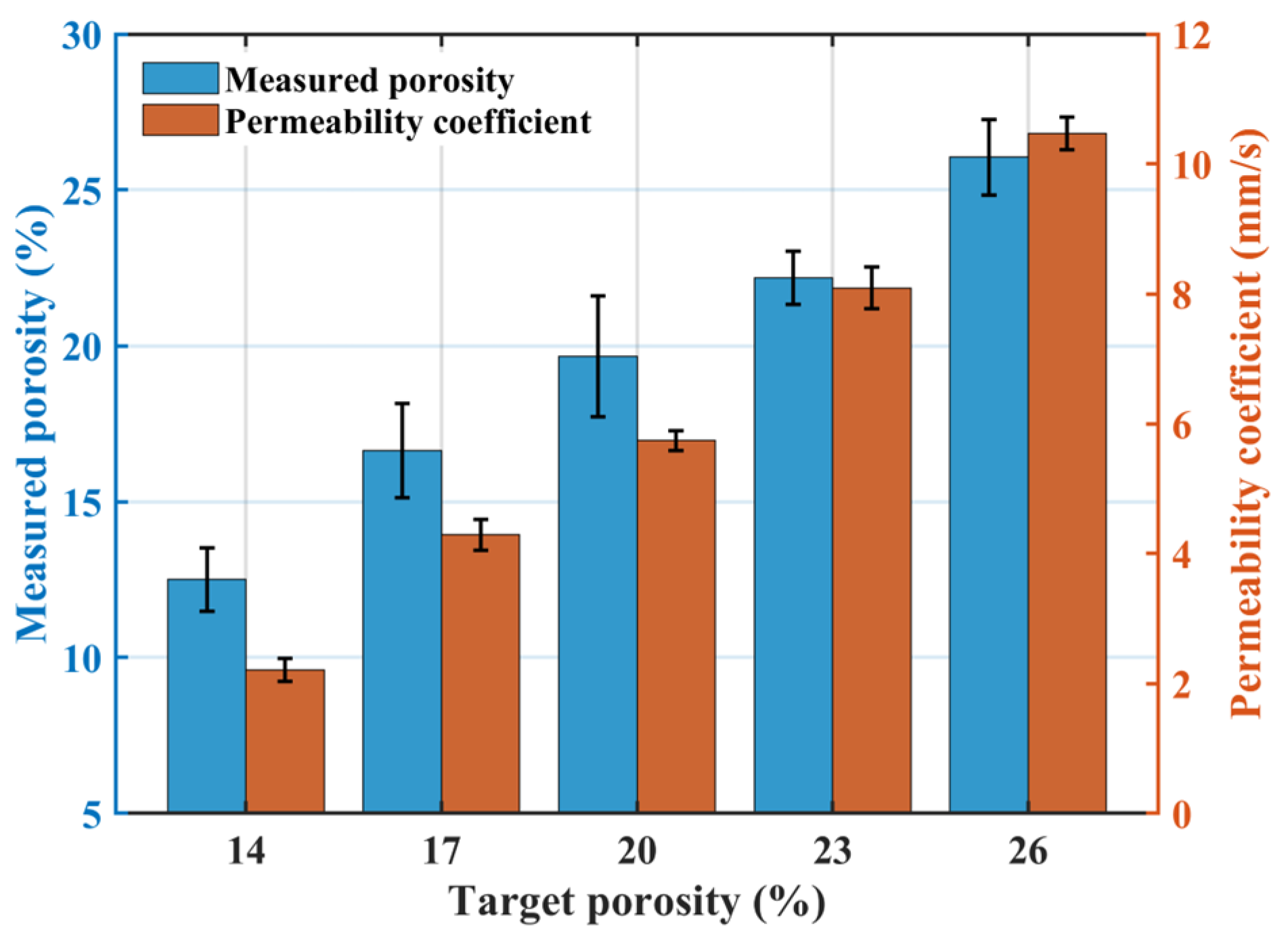
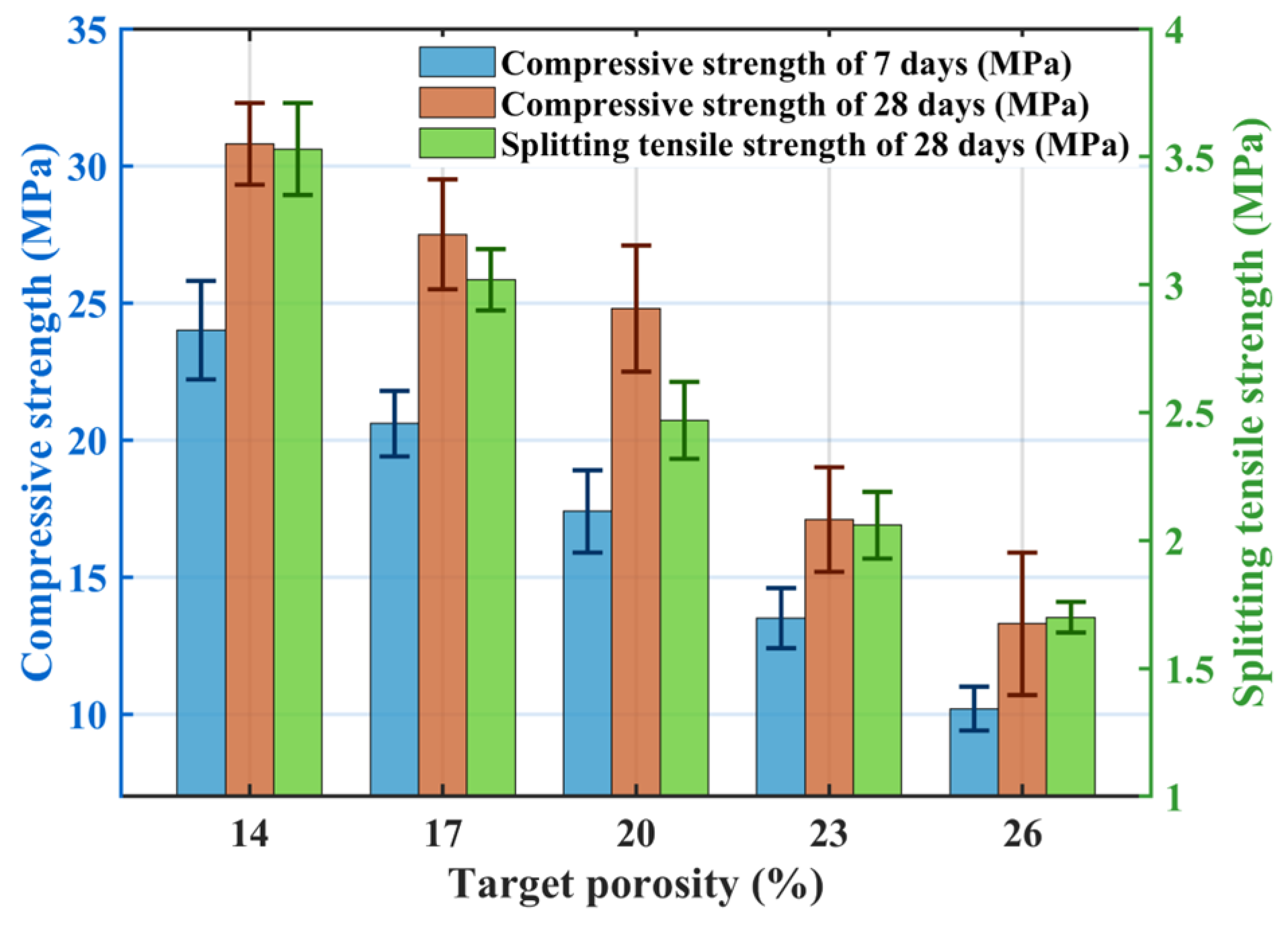
3.1.1. Effect of Target Porosity
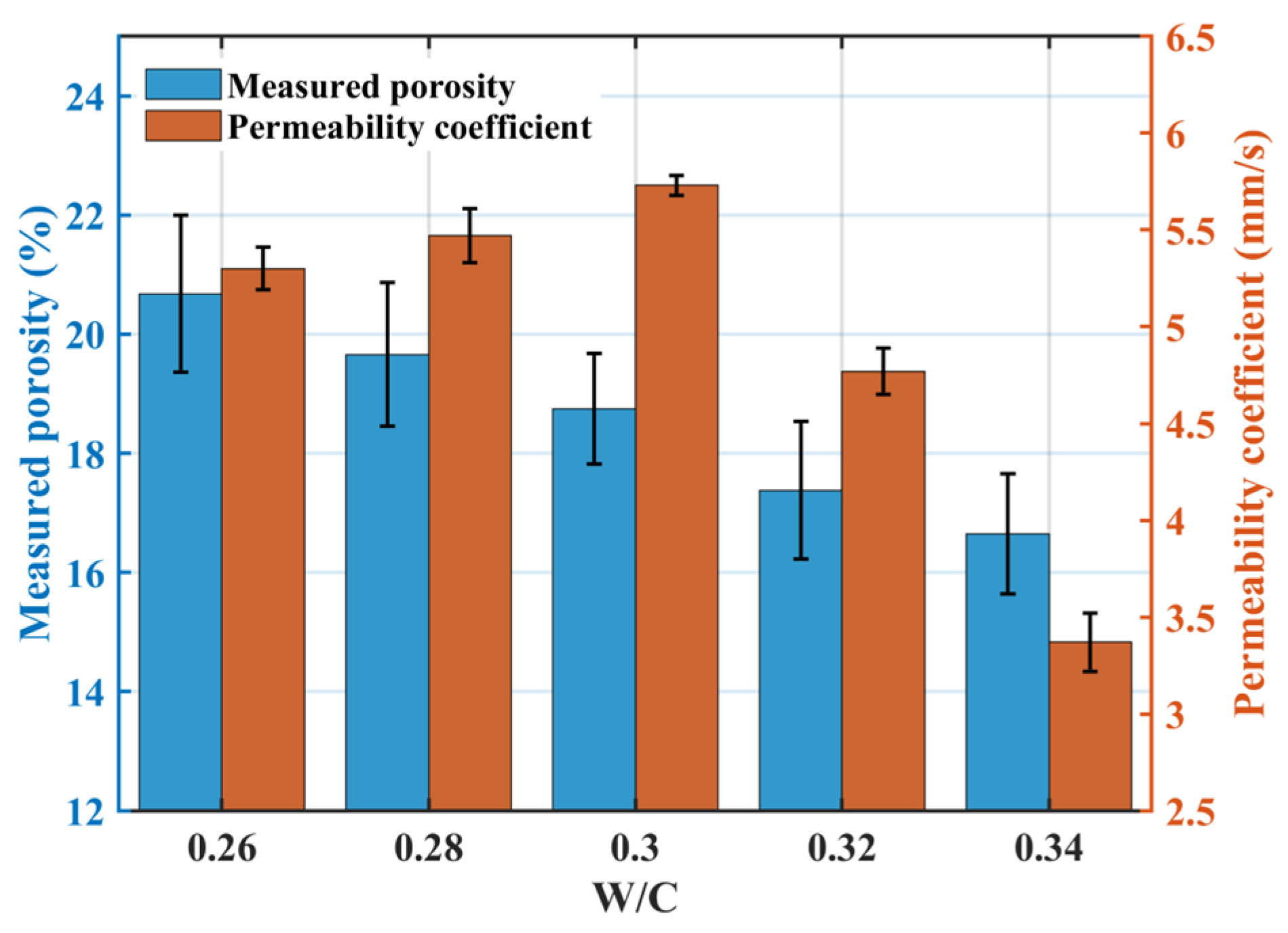
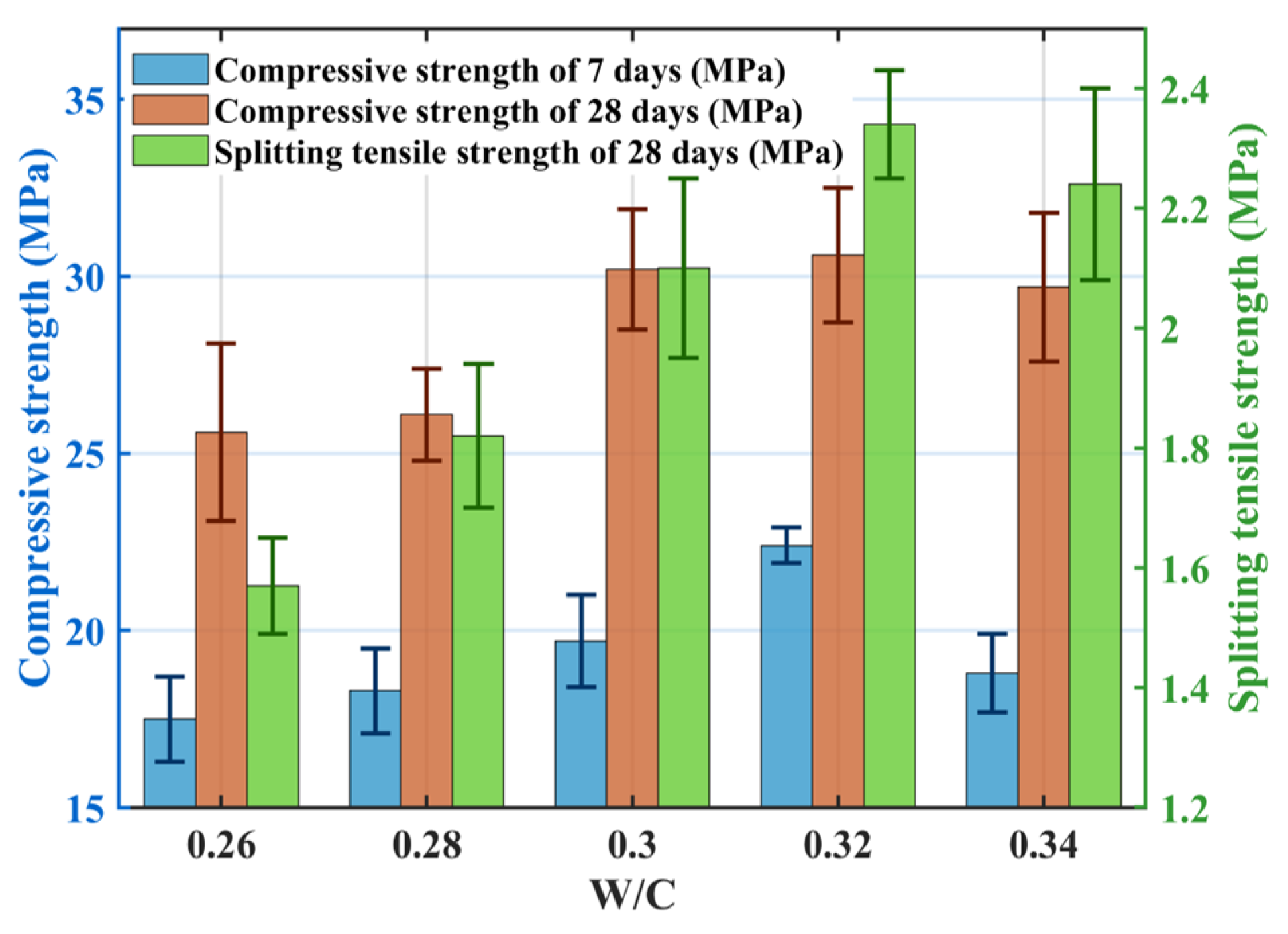
3.1.2. Effect of Water–Cement Ratio
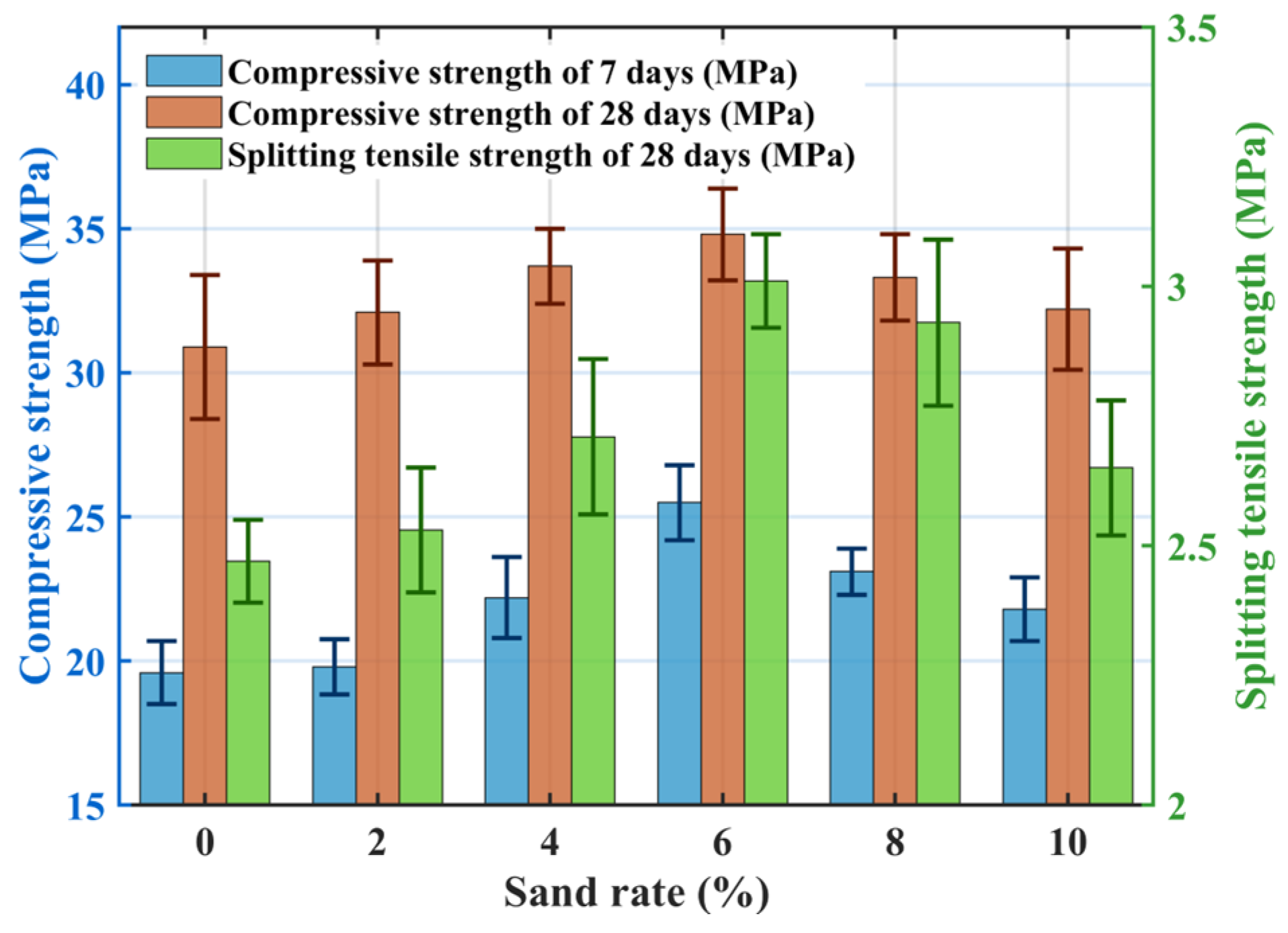
3.1.3. Effect of Sand Rate
3.1.4. Effect of VMA Dosage
3.2. Orthogonal Test Results Analysis and Mix Optimization
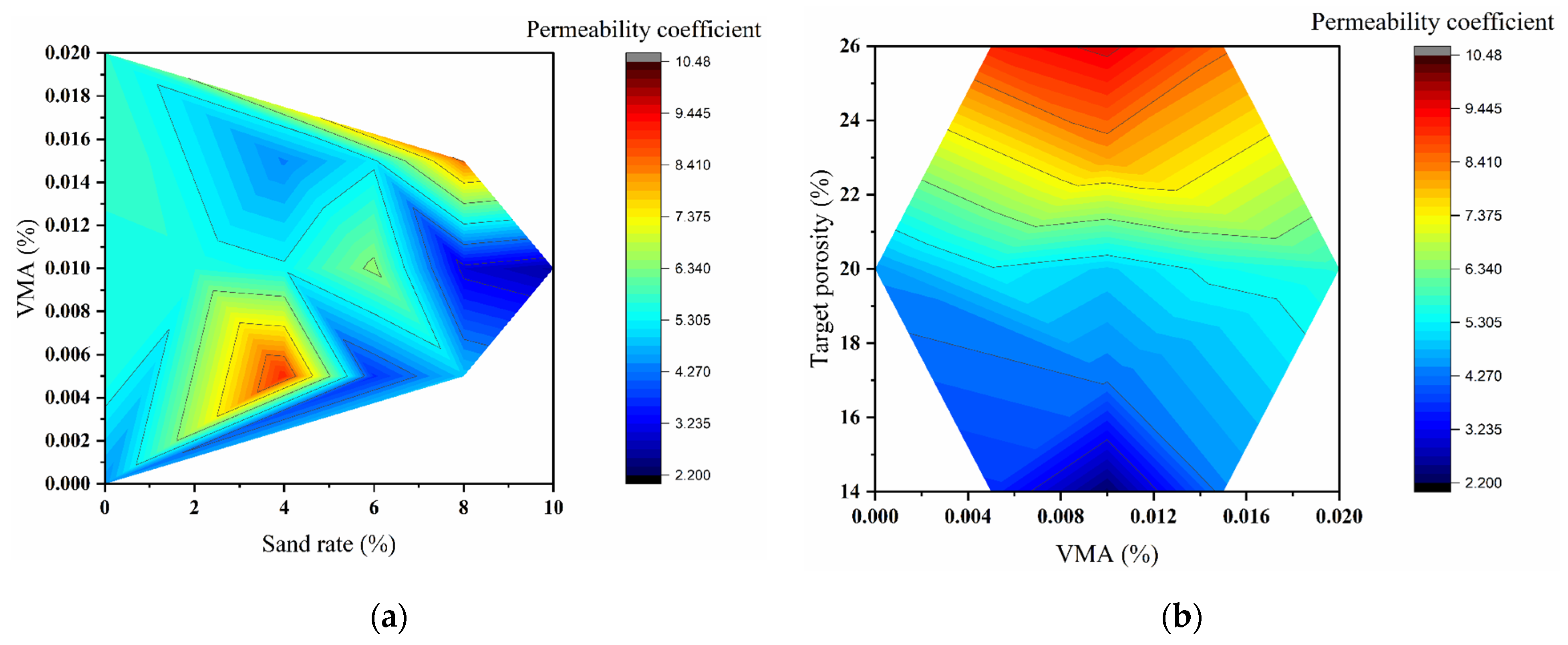
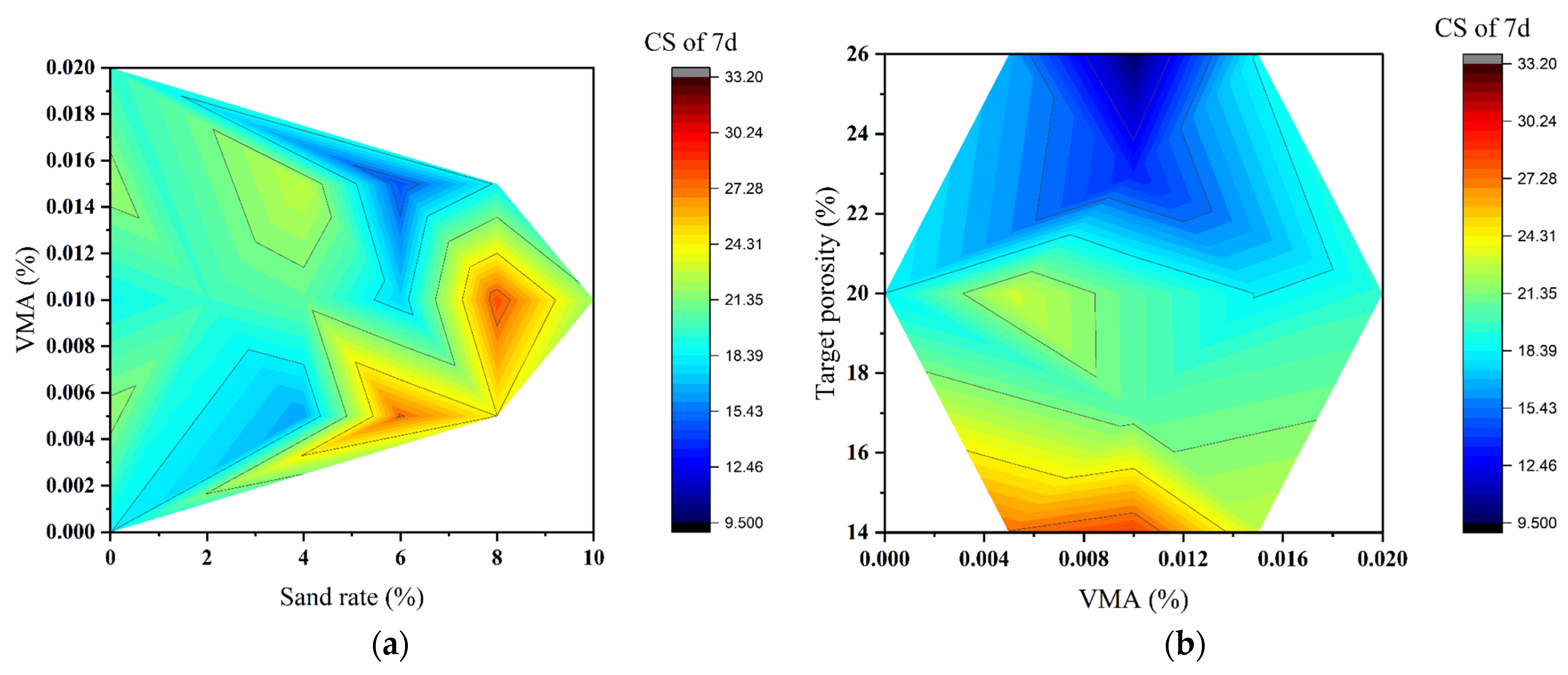
3.2.1. Permeability Coefficient: Range Analysis and Contour Mapping
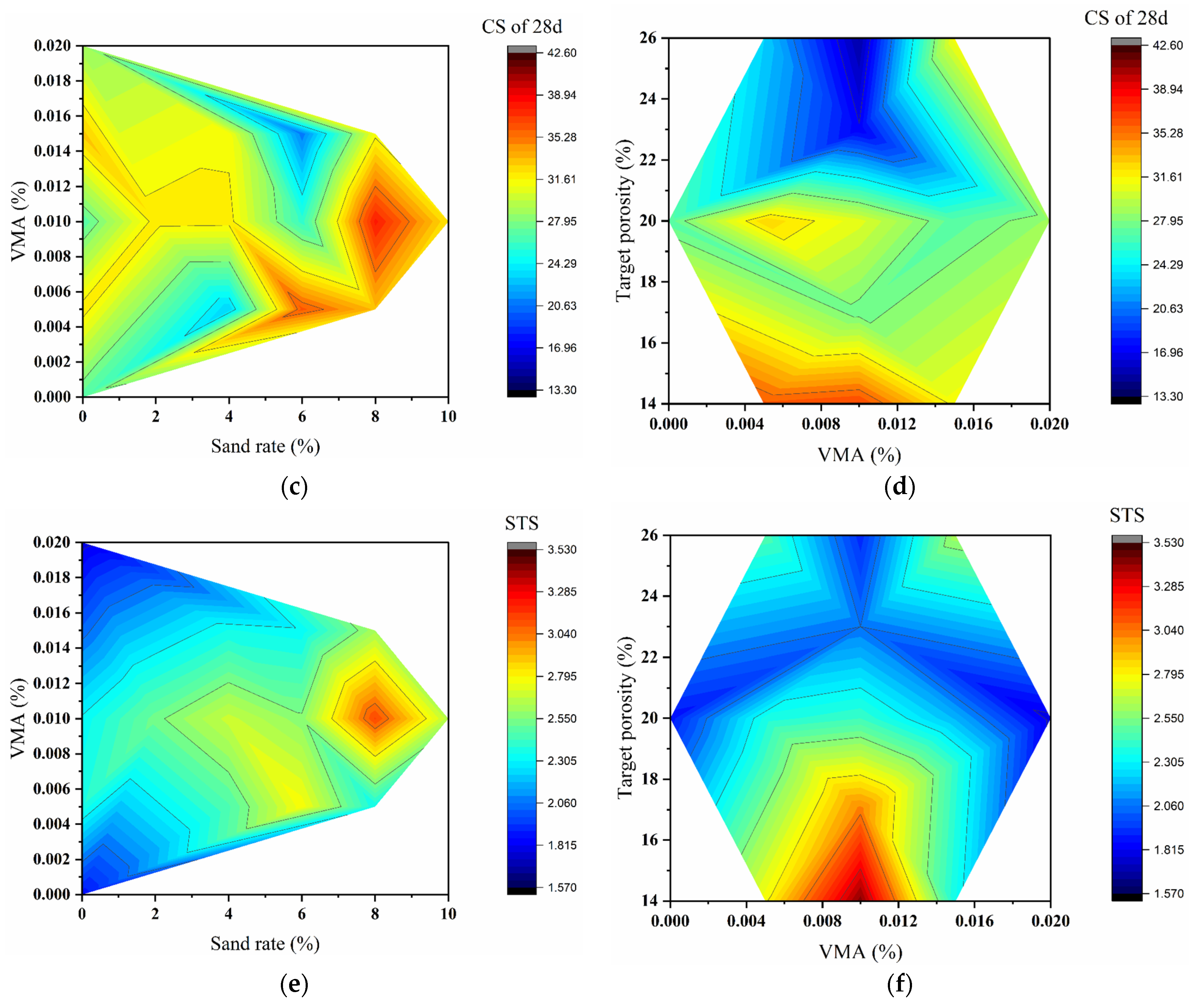
3.2.2. Mechanical Properties: Range Analysis and Contour Mapping
3.2.3. Mix Optimization and Verification
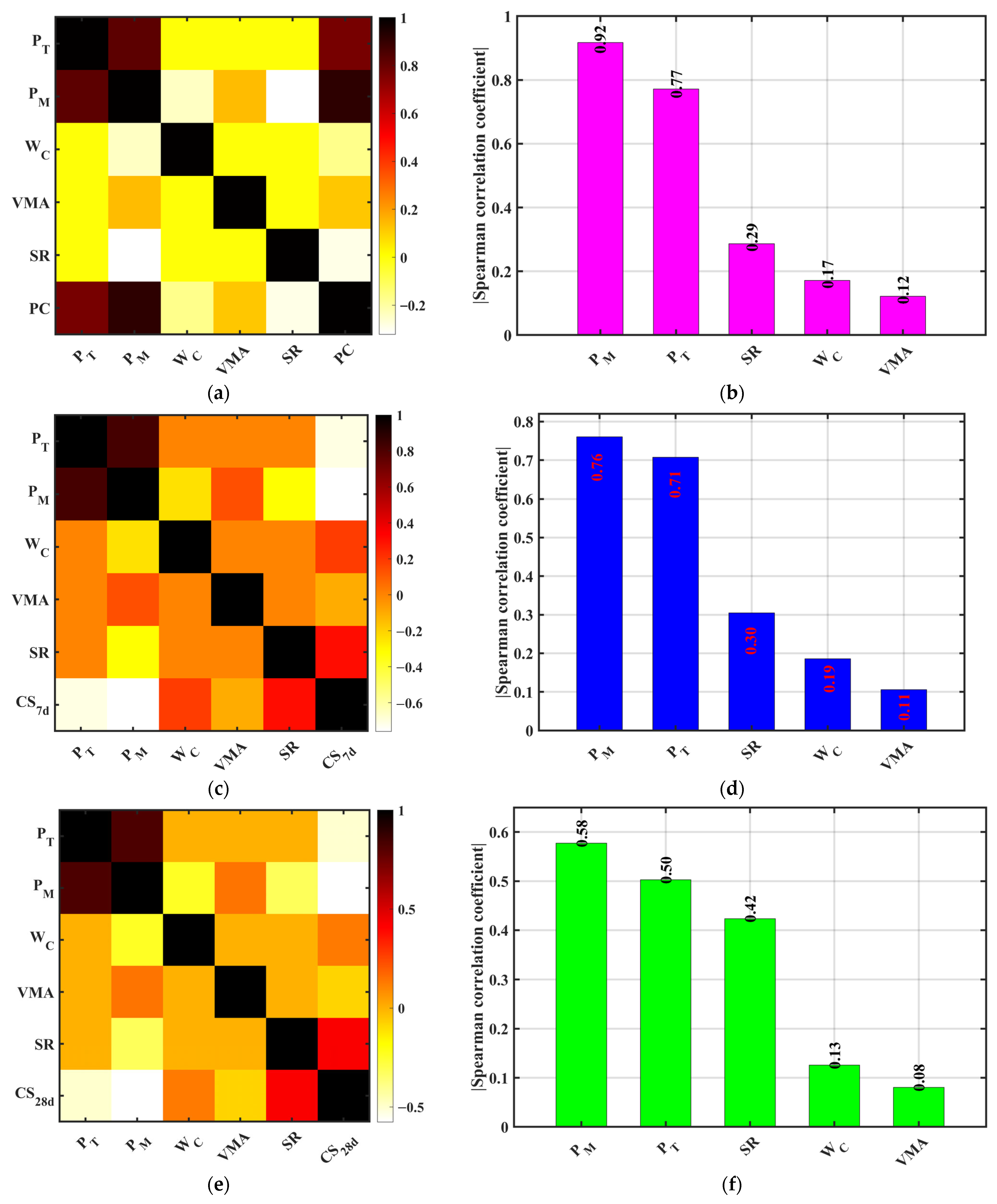
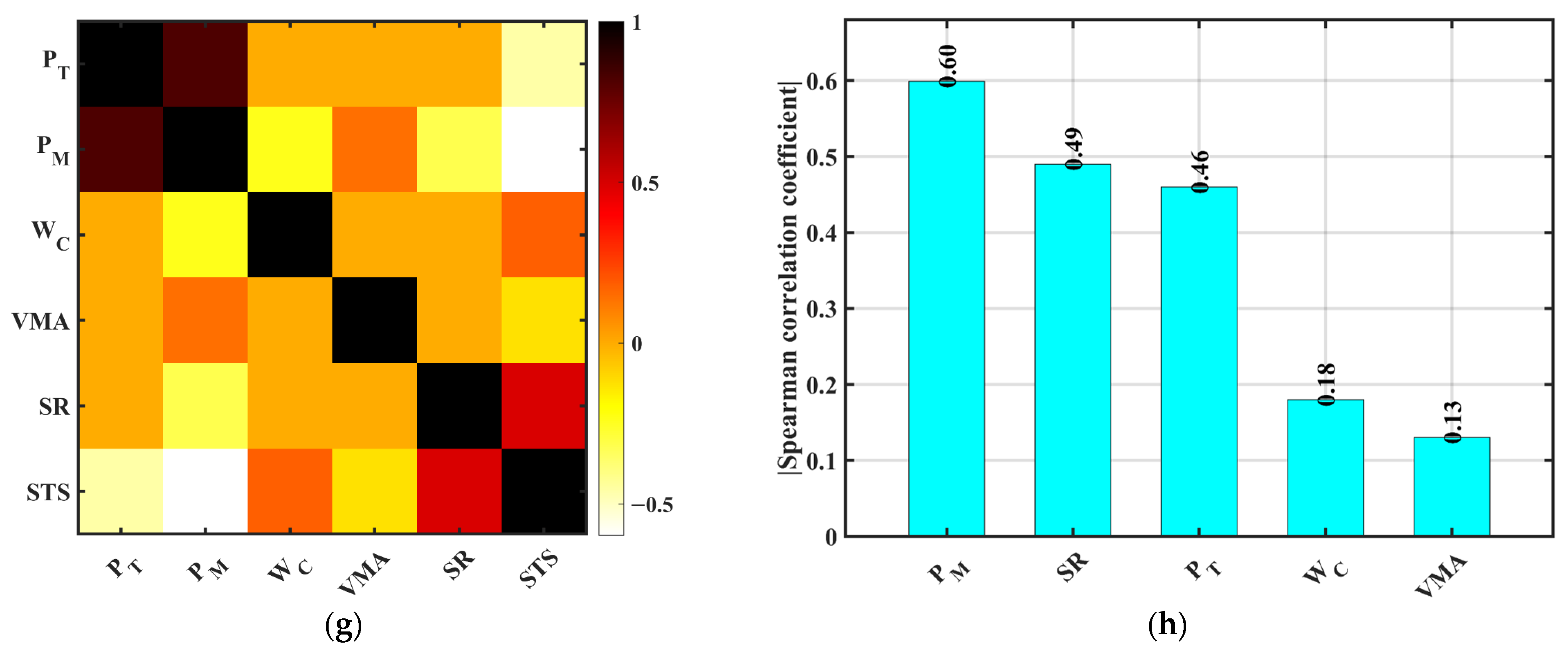
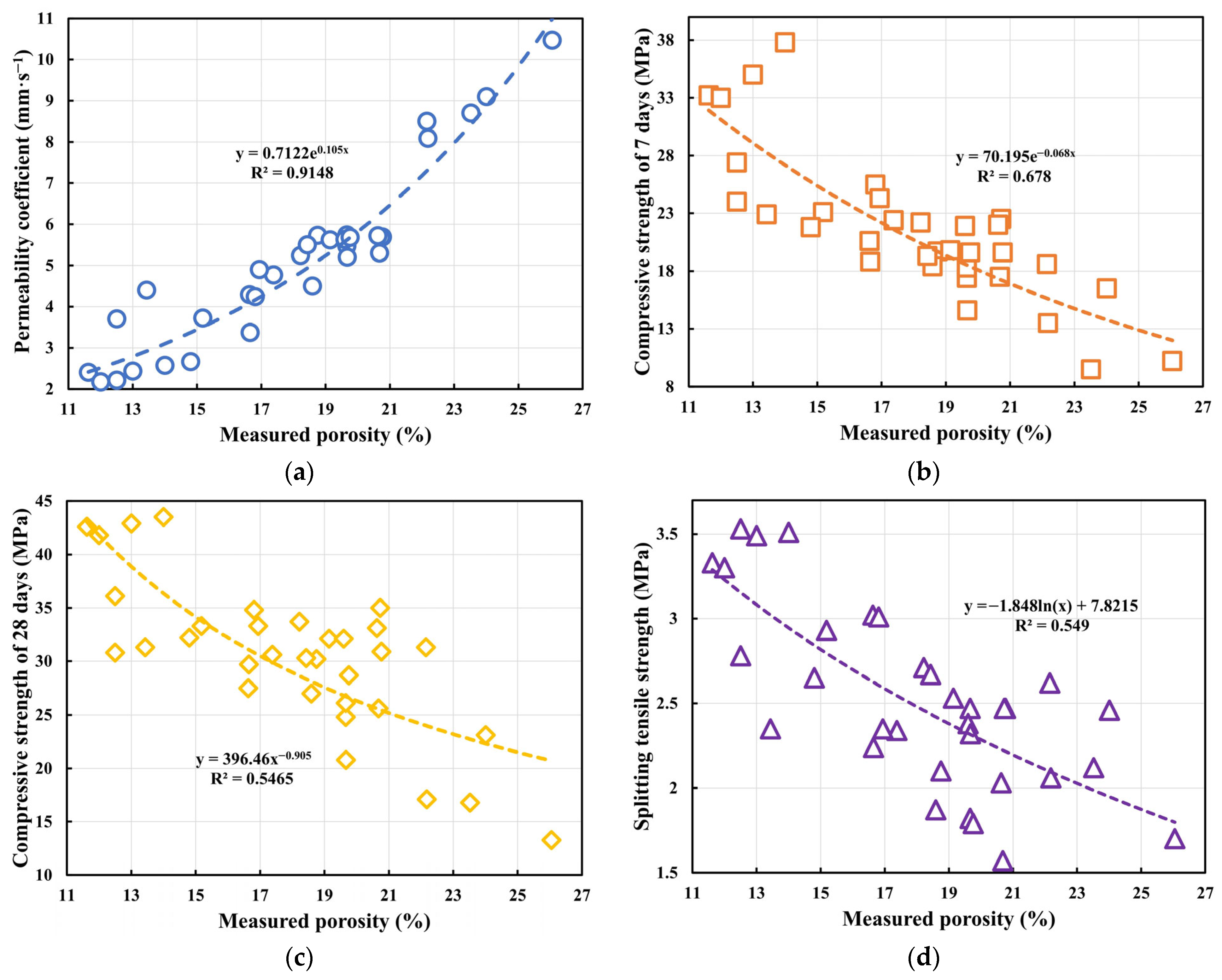
3.3. Correlation Analysis of Pervious Concrete
3.3.1. Spearman Correlation Coefficient Analysis
3.3.2. Correlation Relationships
3.4. Research Novelty
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
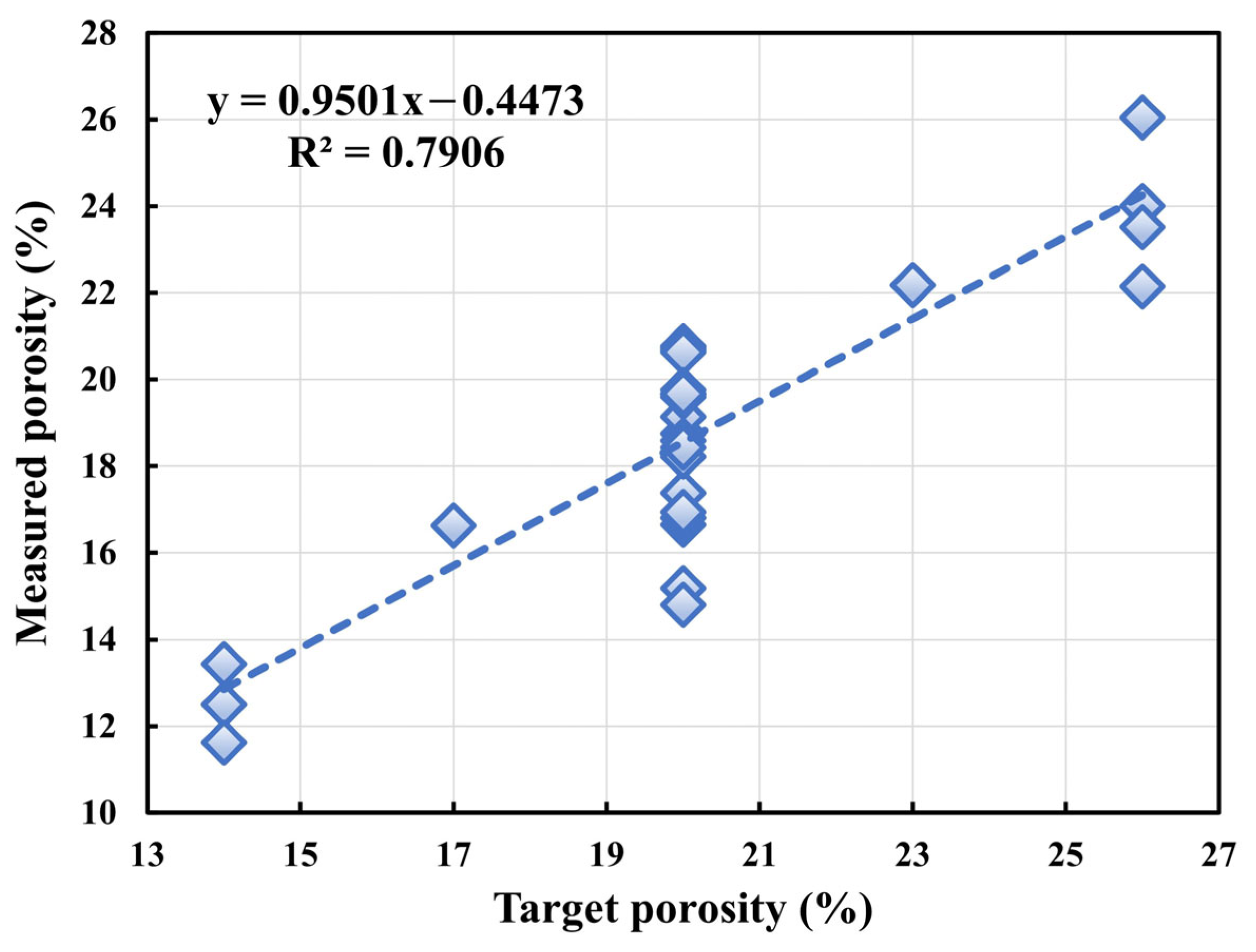
Appendix A. Analysis of Target and Measured Porosity
Appendix A.1. Design Methodology for Target Porosity
Appendix A.2. Correlation and Discrepancy Between Target and Measured Porosity
References
- Debnath, B.; Sarkar, P.P. Pervious concrete as an alternative pavement strategy: A state-of-the-art review. Int. J. Pavement Eng. 2020, 21, 1516–1531. [Google Scholar] [CrossRef]
- Singh, A.; Biligiri, K.P.; Sampath, P.V. Quantification of effective flow resistivity for parametric assessment of pervious concrete by using ultrasonic pulse velocity method. Transp. Res. Rec. 2023, 2677, 64–78. [Google Scholar] [CrossRef]
- Zhang, X.; Lei, C.; Li, Z.; Zhang, A.; Zhao, W.; Zhang, W.; Xu, J.; Guo, P. Effect of cellulose nanofibrils on the physical properties and frost resistance of pervious concrete. Materials 2022, 15, 7906. [Google Scholar] [CrossRef]
- Dos Santos Lima, G.T.; Rocha, J.C.; Cheriaf, M. Investigation of the properties of pervious concrete with a recycled aggregate designed with a new combination of admixture. Constr. Build. Mater. 2022, 340, 127710. [Google Scholar] [CrossRef]
- Nazeer, M.; Kapoor, K.; Singh, S.P. Pervious concrete: A state-of-the-art review. J. Mater. Eng. Struct. 2020, 7, 417–437. [Google Scholar]
- Singh, A.; Sampath, P.V.; Biligiri, K.P. Field performance monitoring of pervious concrete pavements. Road Mater. Pavement 2023, 24, 3013–3028. [Google Scholar] [CrossRef]
- Bittencourt, S.V.; Da Silva Magalhães, M.; Da Nóbrega Tavares, M.E. Mechanical behavior and water infiltration of pervious concrete incorporating recycled asphalt pavement aggregate. Case Stud. Constr. Mater. 2021, 14, e473. [Google Scholar] [CrossRef]
- Seifeddine, K.; Amziane, S.; Toussaint, E. State of the art on the mechanical properties of pervious concrete. Eur. J. Environ. Civ. Eng. 2022, 26, 7727–7755. [Google Scholar] [CrossRef]
- Zhong, R.; Wille, K. Compression response of normal and high strength pervious concrete. Constr. Build. Mater. 2016, 109, 177–187. [Google Scholar] [CrossRef]
- Xu, G.; Shen, W.; Huo, X.; Yang, Z.; Wang, J.; Zhang, W.; Ji, X. Investigation on the properties of porous concrete as road base material. Constr. Build. Mater. 2018, 158, 141–148. [Google Scholar] [CrossRef]
- Yeon, J.H.; Choi, Y.; Yang, C.; Yeon, K. Effect of Polymer Paste Content on the Porosity and Strength of Pervious Polymer Concrete. In International Congress on Polymers in Concrete, 2023; Springer: Cham, Switzerland, 2023; pp. 260–267. [Google Scholar]
- Ichimaru, S. Meso-Mechanical Modeling of Pervious Concrete; University of California, Davis: Davis, CA, USA, 2020. [Google Scholar]
- Qi, R.; Xu, Z.; Jiang, Y.; Liu, X.; Pan, T. Effects of superplasticizer dosage on cement slurry rheological characteristics, pore structure and properties of pervious concrete. Constr. Build. Mater. 2025, 479, 141457. [Google Scholar] [CrossRef]
- Da Costa, F.B.P.; Haselbach, L.M.; Da Silva Filho, L.C.P. Pervious concrete for desired porosity: Influence of w/c ratio and a rheology-modifying admixture. Constr. Build. Mater. 2021, 268, 121084. [Google Scholar] [CrossRef]
- Ji, X.; Pan, T.; Liu, X.; Zhao, W.; Du, L.; Liu, J.; Han, F.; Sha, J. Characterization of thixotropic properties of fresh cement-based materials. Struct. Concrete 2024, 25, 320–333. [Google Scholar] [CrossRef]
- Sonebi, M.; Perrot, A. Effect of mix proportions on rheology and permeability of cement grouts containing viscosity modifying admixture. Constr. Build. Mater. 2019, 212, 687–697. [Google Scholar] [CrossRef]
- Chandrappa, A.K.; Biligiri, K.P. Methodology to develop pervious concrete mixtures for target properties emphasizing the selection of mixture variables. J. Transp. Eng. Part B Pavements 2018, 144, 4018031. [Google Scholar] [CrossRef]
- Torres, A.; Aguayo, F.; Gaedicke, C.; Nerby, P.; Cavazos, M.; Nerby, C. Developing high strength pervious concrete mixtures with local materials. J. Mater. Sci. Chem. Eng. 2019, 8, 20–34. [Google Scholar]
- Zhang, J.; Sun, H.; Shui, X.; Chen, W. Experimental investigation on the properties of sustainable pervious concrete with different aggregate gradation. Int. J. Concr. Struct. M 2023, 17, 64. [Google Scholar] [CrossRef]
- Pan, T.; Jiang, Y.; He, H.; Wang, Y.; Yin, K. Effect of structural build-up on interlayer bond strength of 3D printed cement mortars. Materials 2021, 14, 236. [Google Scholar] [CrossRef]
- Xu, K.; Yang, J.; He, H.; Wei, J.; Zhu, Y. Influences of Additives on the Rheological Properties of Cement Composites: A Review of Material Impacts. Materials 2025, 18, 1753. [Google Scholar] [CrossRef]
- Taheri, B.M.; Ramezanianpour, A.M.; Sabokpa, S.; Gapele, M. Experimental evaluation of freeze-thaw durability of pervious concrete. J. Build. Eng. 2021, 33, 101617. [Google Scholar] [CrossRef]
- Zhang, Q.; Feng, X.; Chen, X.; Lu, K. Mix design for recycled aggregate pervious concrete based on response surface methodology. Constr. Build. Mater. 2020, 259, 119776. [Google Scholar] [CrossRef]
- Liu, R.; Chi, Y.; Chen, S.; Jiang, Q.; Meng, X.; Wu, K.; Li, S. Influence of pore structure characteristics on the mechanical and durability behavior of pervious concrete material based on image analysis. Int. J. Concr. Struct. M 2020, 14, 29. [Google Scholar] [CrossRef]
- Crouch, L.K.; Pitt, J.; Hewitt, R. Aggregate effects on pervious portland cement concrete static modulus of elasticity. J. Mater. Civil. Eng. 2007, 19, 561–568. [Google Scholar] [CrossRef]
- Jiang, C.; Cheng, X. Recycling of waste ceramic foams as fine aggregates in pervious concrete. Rsc. Adv. 2020, 10, 2364–2367. [Google Scholar] [CrossRef] [PubMed]
- Leon Raj, J.; Chockalingam, T. Strength and abrasion characteristics of pervious concrete. Road Mater. Pavement 2020, 21, 2180–2197. [Google Scholar] [CrossRef]
- Bonicelli, A.; Giustozzi, F.; Crispino, M. Experimental study on the effects of fine sand addition on differentially compacted pervious concrete. Constr. Build. Mater. 2015, 91, 102–110. [Google Scholar] [CrossRef]
- Singh, A.; Biligiri, K.P.; Sampath, P.V. Development of framework for ranking pervious concrete pavement mixtures: Application of multi-criteria decision-making methods. Int. J. Pavement Eng. 2023, 24, 2021406. [Google Scholar] [CrossRef]
- Li, F.; Cai, X.; Zhang, Y.; Guo, X.; Jiang, M. Mechanical and permeability analysis and optimization of recycled aggregate pervious concrete based on response surface method. J. Renew. Mater. 2023, 11, 1745. [Google Scholar] [CrossRef]
- Joshaghani, A.; Ramezanianpour, A.A.; Ataei, O.; Golroo, A. Optimizing pervious concrete pavement mixture design by using the Taguchi method. Constr. Build. Mater. 2015, 101, 317–325. [Google Scholar] [CrossRef]
- Chandrappa, A.K.; Biligiri, K.P. Comprehensive investigation of permeability characteristics of pervious concrete: A hydrodynamic approach. Constr. Build. Mater. 2016, 123, 627–637. [Google Scholar] [CrossRef]
- Sun, J.; Zhang, J.; Gu, Y.; Huang, Y.; Sun, Y.; Ma, G. Prediction of permeability and unconfined compressive strength of pervious concrete using evolved support vector regression. Constr. Build. Mater. 2019, 207, 440–449. [Google Scholar] [CrossRef]
- Shan, J.; Zhang, Y.; Wu, S.; Lin, Z.; Li, L.; Wu, Q. Pore characteristics of pervious concrete and their influence on permeability attributes. Constr. Build. Mater. 2022, 327, 126874. [Google Scholar] [CrossRef]
- Yu, F.; Sun, D.; Wang, J.; Hu, M. Influence of aggregate size on compressive strength of pervious concrete. Constr. Build. Mater. 2019, 209, 463–475. [Google Scholar] [CrossRef]
- Song, H.; Yao, J.; Xiang, J. The role of aggregate and cement paste in the deterioration of the transitional interface zone of pervious concrete during freeze-thaw cycles. Case Stud. Constr. Mater. 2022, 16, e1086. [Google Scholar] [CrossRef]
- Bentz, D.P. Influence of water-to-cement ratio on hydration kinetics: Simple models based on spatial considerations. Cement Concrete Res. 2006, 36, 238–244. [Google Scholar] [CrossRef]
- Li, Y.; Mu, J.; Hao, J.; Liu, Y.; Jiang, X.; Luo, X. Research on the particle characteristics of manufactured sands affecting the flow ability of fresh mortar. Constr. Build. Mater. 2023, 382, 131287. [Google Scholar] [CrossRef]
- Bear, J. Dynamics of Fluids in Porous Media; Courier Corporation: North Chelmsford, MA, USA, 2013. [Google Scholar]
- Li, L.G.; Feng, J.; Zhu, J.; Chu, S.; Kwan, A.K.H. Pervious concrete: Effects of porosity on permeability and strength. Mag. Concrete Res. 2021, 73, 69–79. [Google Scholar] [CrossRef]



| Aspect. | Description | Influencing Factors | Common Challenges |
|---|---|---|---|
| Porosity | Typically 15–30% | Aggregate gradation, compaction, paste volume | Trade-off with strength |
| Permeability | Governed by pore connectivity | Porosity, pore size distribution, clogging | Sensitivity to compaction and segregation |
| Strength | Lower than conventional concrete | Paste quality, aggregate interlock, ITZ density | Weak interfacial transition zone (ITZ) |
| Mix Design | Low fine aggregate, high paste coating | w/c ratio, admixtures, sand content | Difficulty in achieving uniform paste distribution |
| Series | No. | Target Porosity (%) | Cement Kg/m3 | Aggregate kg/m3 | W/C Ratio | PCE (%) | VMA (%) | Sand Rate (%) |
|---|---|---|---|---|---|---|---|---|
| TP | TP1 | 14 | 463 | 1627 | 0.3 | 0.12 | 0.01 | – |
| TP2 | 17 | 430 | – | |||||
| TP3 | 20 | 399 | – | |||||
| TP4 | 23 | 366 | – | |||||
| TP5 | 26 | 334 | – | |||||
| WC | WC1 | 20 | 480 | 1627 | 0.26 | 0.12 | 0.01 | – |
| WC2 | 20 | 480 | 1627 | 0.28 | 0.12 | 0.01 | – | |
| WC3 | 20 | 480 | 1627 | 0.30 | 0.12 | 0.01 | – | |
| WC4 | 20 | 480 | 1627 | 0.32 | 0.12 | 0.01 | – | |
| WC5 | 20 | 480 | 1627 | 0.34 | 0.12 | 0.01 | – | |
| SR | SR0 | 20 | 480 | 1627 | 0.30 | 0.12 | 0.01 | 0 |
| SR1 | 20 | 480 | 1594 | 0.30 | 0.12 | 0.01 | 2 | |
| SR2 | 20 | 480 | 1562 | 0.30 | 0.12 | 0.01 | 4 | |
| SR3 | 20 | 480 | 1529 | 0.30 | 0.12 | 0.01 | 6 | |
| SR4 | 20 | 480 | 1497 | 0.30 | 0.12 | 0.01 | 8 | |
| SR5 | 20 | 480 | 1464 | 0.30 | 0.12 | 0.01 | 10 | |
| VMA | VMA1 | 20 | 480 | 1627 | 0.30 | 0.12 | 0 | – |
| VMA2 | 20 | 480 | 1627 | 0.30 | 0.12 | 0.005 | – | |
| VMA3 | 20 | 480 | 1627 | 0.30 | 0.12 | 0.01 | – | |
| VMA4 | 20 | 480 | 1627 | 0.30 | 0.12 | 0.015 | – | |
| VMA5 | 20 | 480 | 1627 | 0.30 | 0.12 | 0.02 | – |
| Level | Factor A | Factor B | Factor C |
|---|---|---|---|
| Sand Rate (%) | VMA (%) | Target Porosity (%) | |
| 1 | 4 | 0.015 | 14 |
| 2 | 6 | 0.01 | 20 |
| 3 | 8 | 0.005 | 26 |
| No. | Factor A | Factor B | Factor C |
|---|---|---|---|
| Sand Rate (%) | VMA (%) | Target Porosity (%) | |
| OED1 | 4 | 0.015 | 14 |
| OED2 | 4 | 0.01 | 20 |
| OED3 | 4 | 0.005 | 26 |
| OED4 | 6 | 0.01 | 26 |
| OED5 | 6 | 0.005 | 14 |
| OED6 | 6 | 0.015 | 20 |
| OED7 | 8 | 0.005 | 20 |
| OED8 | 8 | 0.015 | 26 |
| OED9 | 8 | 0.01 | 14 |
| No. | 7 d /MPa | 28 d /MPa | Splitting Tensile Strength /MPa | Permeability Coefficient /mm·s−1 |
|---|---|---|---|---|
| OED1 | 22.9 | 31.3 | 2.35 | 4.6 |
| OED2 | 19.3 | 30.3 | 2.67 | 5.5 |
| OED3 | 16.5 | 23.1 | 2.46 | 9.1 |
| OED4 | 9.5 | 16.8 | 2.12 | 8.7 |
| OED5 | 27.4 | 36.1 | 2.78 | 4.1 |
| OED6 | 14.6 | 20.8 | 2.32 | 5.2 |
| OED7 | 24.3 | 33.3 | 2.35 | 4.9 |
| OED8 | 18.6 | 31.3 | 2.62 | 8.5 |
| OED9 | 33.2 | 42.6 | 3.33 | 2.4 |
| No. | Factors | Permeability Coefficient /mm·s−1 | |||
|---|---|---|---|---|---|
| A: Sand Rate (%) | B: VMA (%) | C: Target Porosity (%) | Null Column | ||
| OED1 | 1(4) | 1(0.015) | 1(14) | 1 | 4.6 |
| OED2 | 1 | 2(0.01) | 2(20) | 2 | 5.5 |
| OED3 | 1 | 3(0.005) | 3(26) | 3 | 9.1 |
| OED4 | 2(6) | 2 | 3 | 1 | 8.7 |
| OED5 | 2 | 3 | 1 | 2 | 4.1 |
| OED6 | 2 | 1 | 2 | 3 | 5.2 |
| OED7 | 3(8) | 3 | 2 | 1 | 4.9 |
| OED8 | 3 | 1 | 3 | 2 | 8.5 |
| OED9 | 3 | 2 | 1 | 3 | 2.4 |
| K1 | 6.40 | 6.10 | 3.70 | 6.07 | |
| K2 | 6.00 | 5.53 | 5.20 | 6.03 | |
| K3 | 5.27 | 6.03 | 8.77 | 5.57 | |
| R | 1.13 | 0.57 | 5.07 | 0.50 | |
| Factors | Deviation Square Sum | Degrees of Freedom | F Ratio | Significance Level |
|---|---|---|---|---|
| Sand rate | 1.98 | 2 | 4.23 | Non-significant |
| VMA | 0.58 | 2 | 1.23 | Non-significant |
| Target porosity | 40.64 | 2 | 86.66 | Significant |
| Error | 0.47 | 2 |
| No. | Factors | CS of 7 d (MPa) | CS of 28 d (MPa) | STS (MPa) | |||
|---|---|---|---|---|---|---|---|
| Sand Rate (%) | VMA (%) | Target Porosity (%) | Null Column | ||||
| OED1 | 1 (4) | 1 (0.015) | 1 (14) | 1 | 22.9 | 31.3 | 2.35 |
| OED2 | 1 | 2 (0.01) | 2 (20) | 2 | 19.3 | 30.3 | 2.67 |
| OED3 | 1 | 3 (0.005) | 3 (26) | 3 | 16.5 | 23.1 | 2.46 |
| OED4 | 2 (6) | 2 | 3 | 1 | 9.5 | 16.8 | 2.12 |
| OED5 | 2 | 3 | 1 | 2 | 27.4 | 36.1 | 2.78 |
| OED6 | 2 | 1 | 2 | 3 | 14.6 | 20.8 | 2.32 |
| OED7 | 3 (8) | 3 | 2 | 1 | 24.3 | 33.3 | 2.35 |
| OED8 | 3 | 1 | 3 | 2 | 18.6 | 31.3 | 2.62 |
| OED9 | 3 | 2 | 1 | 3 | 33.2 | 42.6 | 3.33 |
| K1 (7 d) | 19.55 | 18.67 | 27.80 | 18.91 | |||
| K2 (7 d) | 17.16 | 20.64 | 19.38 | 21.74 | |||
| K3 (7 d) | 25.36 | 22.76 | 14.89 | 21.41 | |||
| R (7 d) | 8.20 | 4.09 | 12.91 | 2.83 | |||
| K1 (28 d) | 28.23 | 27.80 | 36.67 | 27.13 | |||
| K2 (28 d) | 24.57 | 29.90 | 28.13 | 32.57 | |||
| K3 (28 d) | 35.73 | 30.80 | 23.73 | 28.83 | |||
| R (28 d) | 11.17 | 3.03 | 12.93 | 5.43 | |||
| K1 (STS) | 2.49 | 2.43 | 2.82 | 2.28 | |||
| K2 (STS) | 2.41 | 2.71 | 2.45 | 2.69 | |||
| K3 (STS) | 2.77 | 2.53 | 2.40 | 2.70 | |||
| R (STS) | 0.36 | 0.28 | 0.42 | 0.43 | |||
| Factors | Deviation Square Sum | Degrees of Freedom | F Ratio | Significance Level |
|---|---|---|---|---|
| Sand rate | 106.78 | 2 | 7.43 | Non-significant |
| VMA | 25.04 | 2 | 1.74 | Non-significant |
| Target porosity | 257.83 | 2 | 17.93 | Significant |
| Error | 14.38 | 2 |
| Factors | Deviation Square Sum | Degrees of Freedom | F Ratio | Significance Level |
|---|---|---|---|---|
| Sand rate | 194.30 | 2 | 13.42 | Significant |
| VMA | 15.40 | 2 | 1.00 | Non-significant |
| Target porosity | 257.39 | 2 | 17.91 | Significant |
| Error | 15.40 | 2 |
| Factors | Deviation Square Sum | Degrees of Freedom | F Ratio | Significance Level |
|---|---|---|---|---|
| Sand rate | 0.36 | 2 | 89.75 | Significant |
| VMA | 0.11 | 2 | 28.50 | Significant |
| Target porosity | 1.21 | 2 | 303.25 | Significant |
| Error | 0 | 2 |
| No. | Target Porosity (%) | Cement Kg/m3 | Aggregate kg/m3 | W/C Ratio | PCE (%) | VMA (%) | Sand Rate (%) |
|---|---|---|---|---|---|---|---|
| YZ0 | 15 | 480 | 1497 | 0.3 | 0.12 | 0.01 | 8 |
| YZ1 | 1513 | 7 | |||||
| YZ2 | 1481 | 9 |
| No. | 7 d /MPa | 28 d /MPa | Splitting Tensile Strength /MPa | Permeability Coefficient /mm·s−1 |
|---|---|---|---|---|
| YZ0 | 35.0 | 42.9 | 3.49 | 2.43 |
| YZ1 | 37.8 | 43.5 | 3.51 | 2.57 |
| YZ2 | 33.0 | 41.8 | 3.3 | 2.17 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, F.; Yang, L.; Jiang, Y. Optimum Mix Design and Correlation Analysis of Pervious Concrete. Materials 2025, 18, 4129. https://doi.org/10.3390/ma18174129
Lu F, Yang L, Jiang Y. Optimum Mix Design and Correlation Analysis of Pervious Concrete. Materials. 2025; 18(17):4129. https://doi.org/10.3390/ma18174129
Chicago/Turabian StyleLu, Fenting, Li Yang, and Yaqing Jiang. 2025. "Optimum Mix Design and Correlation Analysis of Pervious Concrete" Materials 18, no. 17: 4129. https://doi.org/10.3390/ma18174129
APA StyleLu, F., Yang, L., & Jiang, Y. (2025). Optimum Mix Design and Correlation Analysis of Pervious Concrete. Materials, 18(17), 4129. https://doi.org/10.3390/ma18174129






