A Numerical Investigation on the Influence of Film-Cooling Hole Inclination Angle on the Stress Field of Surrounding Thermal Barrier Coating
Abstract
1. Introduction
2. Numerical Model
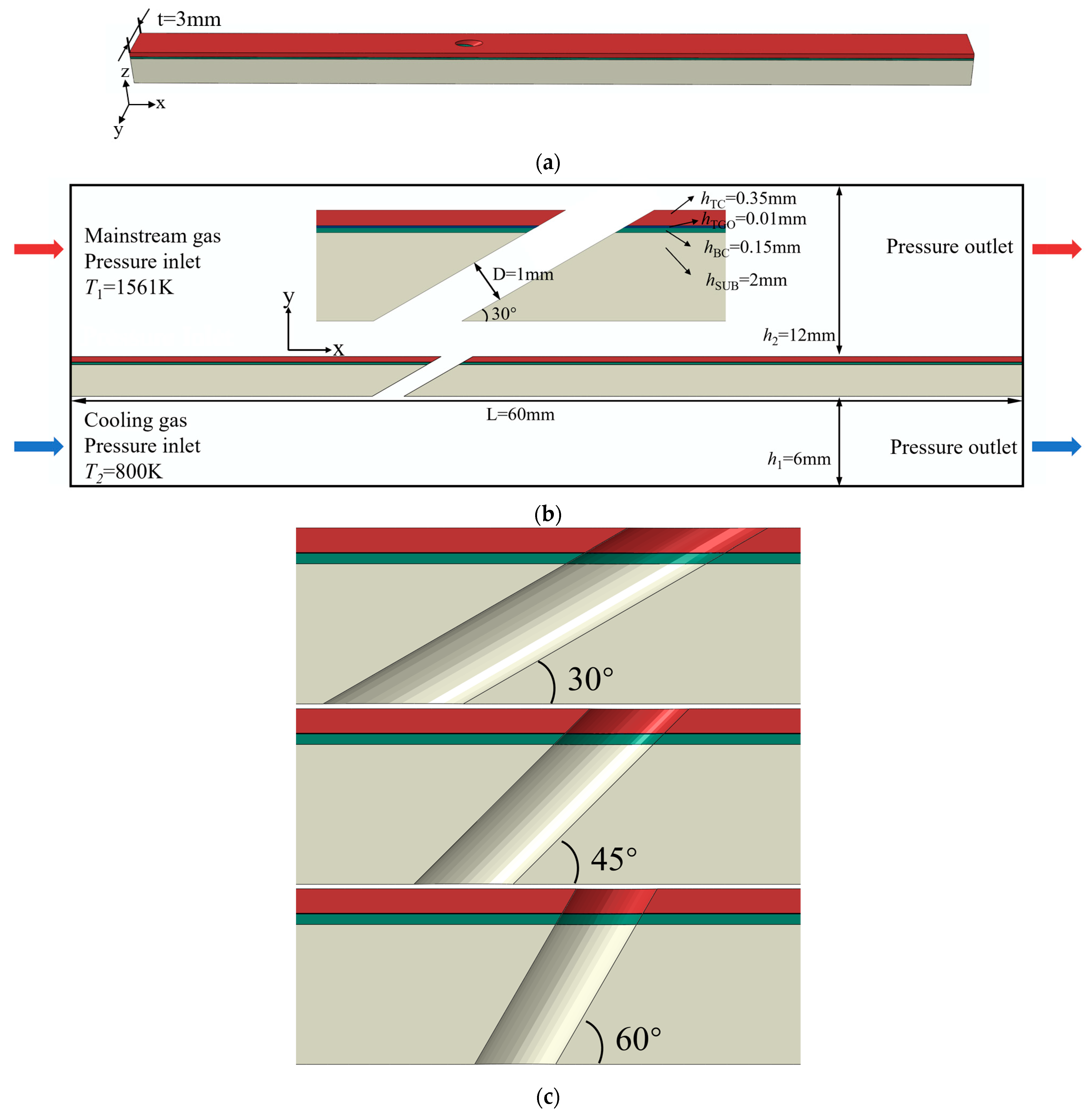
2.1. Geometric Model
2.2. CFD Model
2.3. FE Model
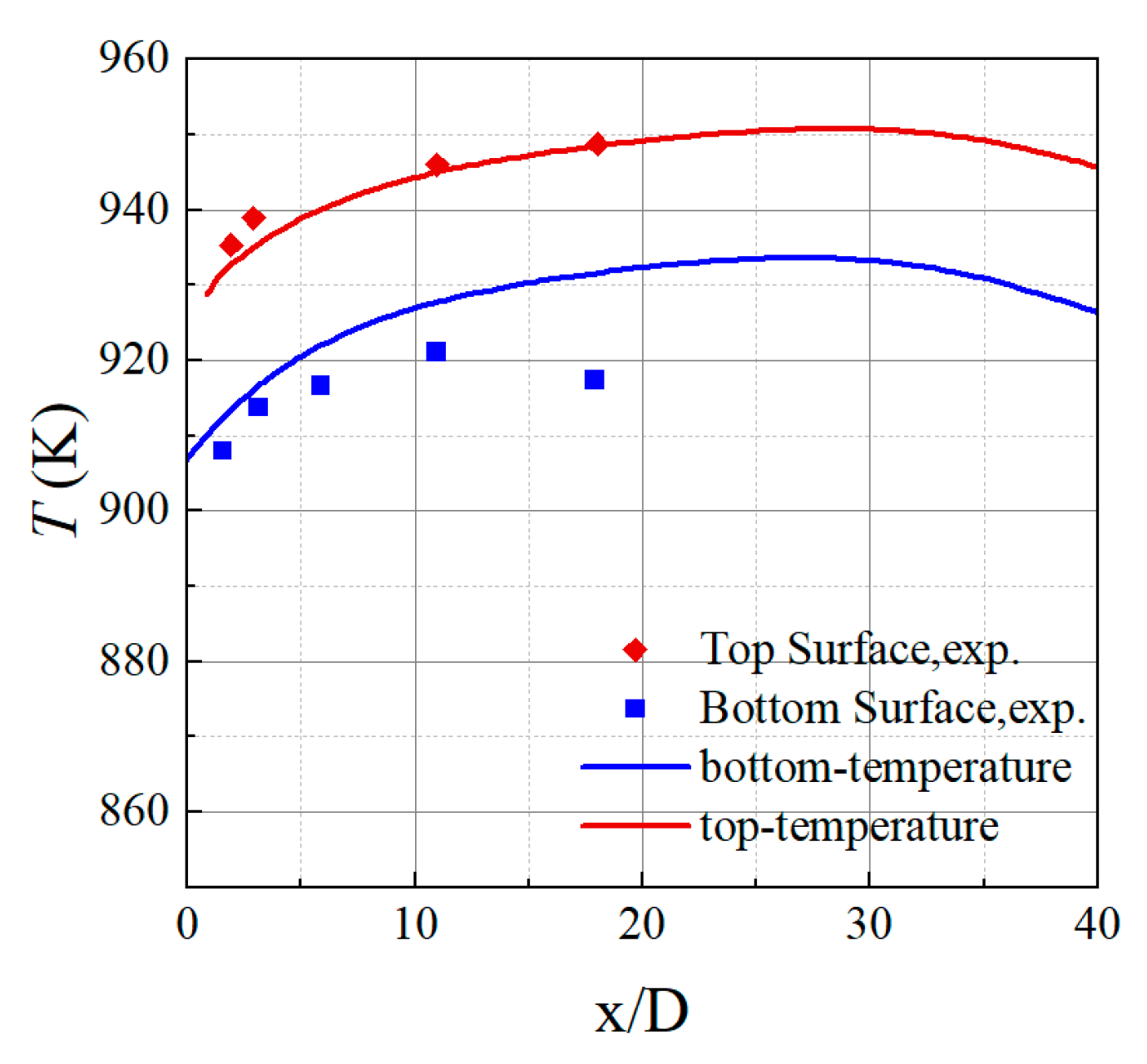
2.4. Experimental Validation
3. Results and Discussion
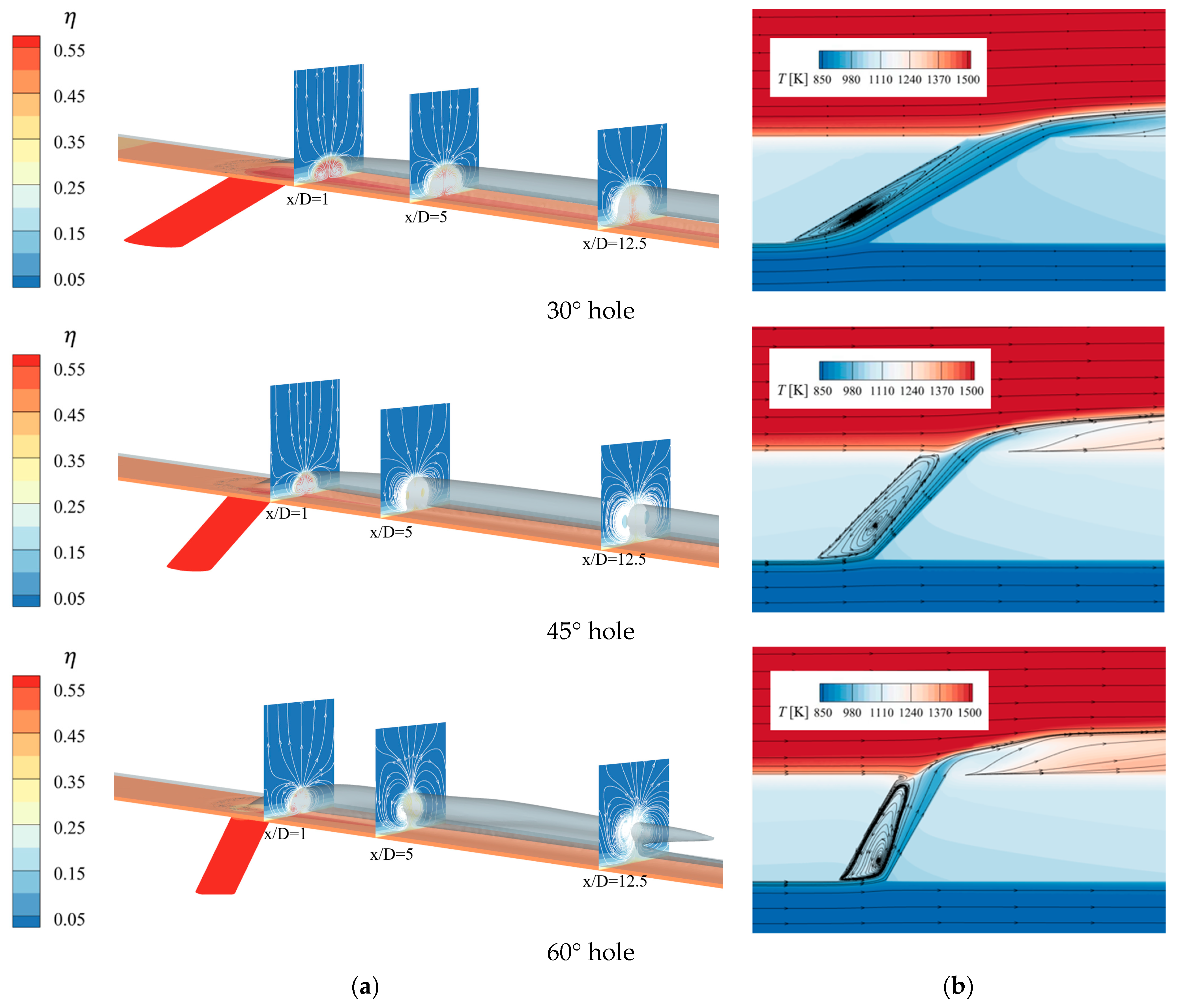
3.1. Flow Characteristics
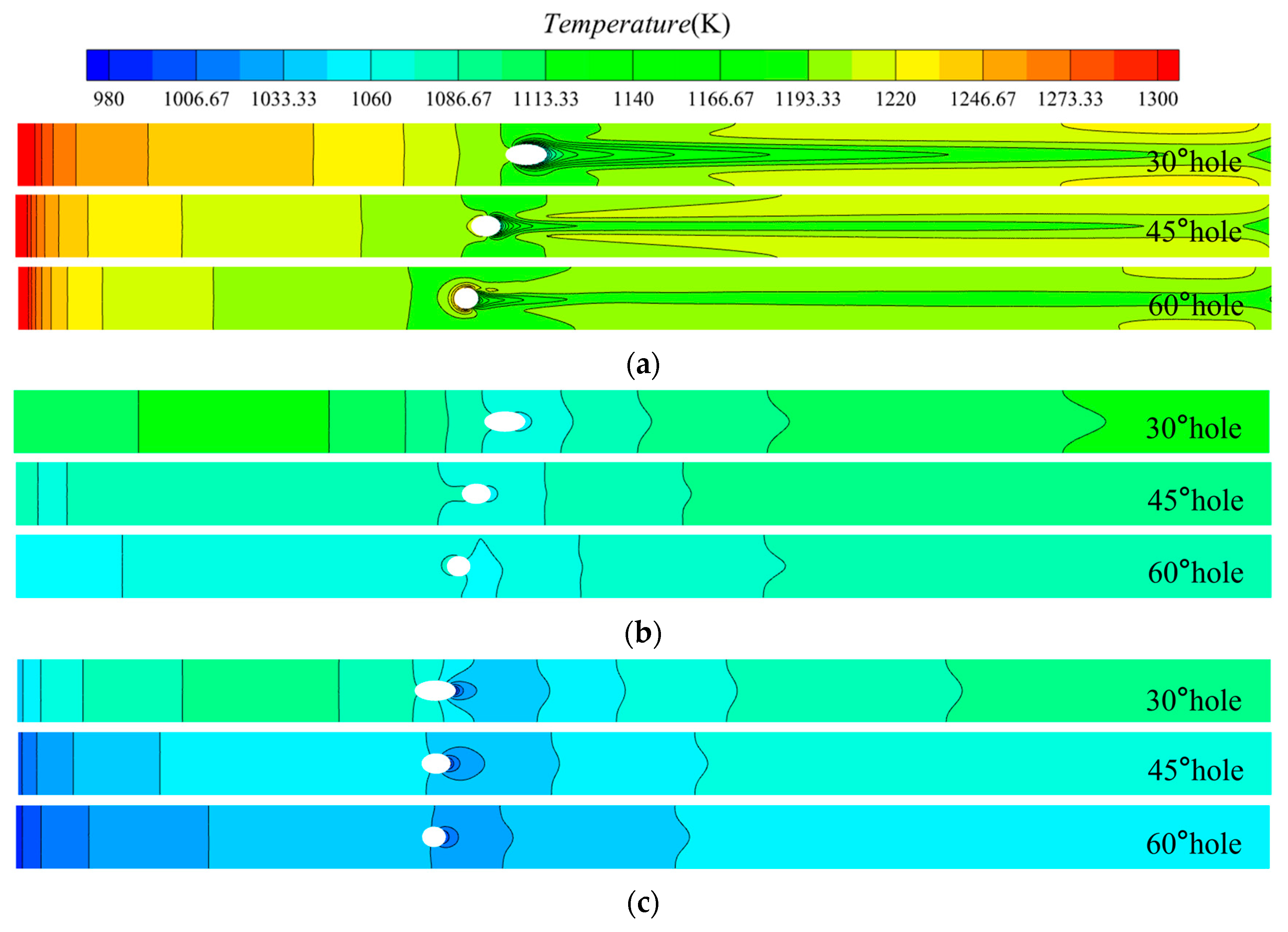
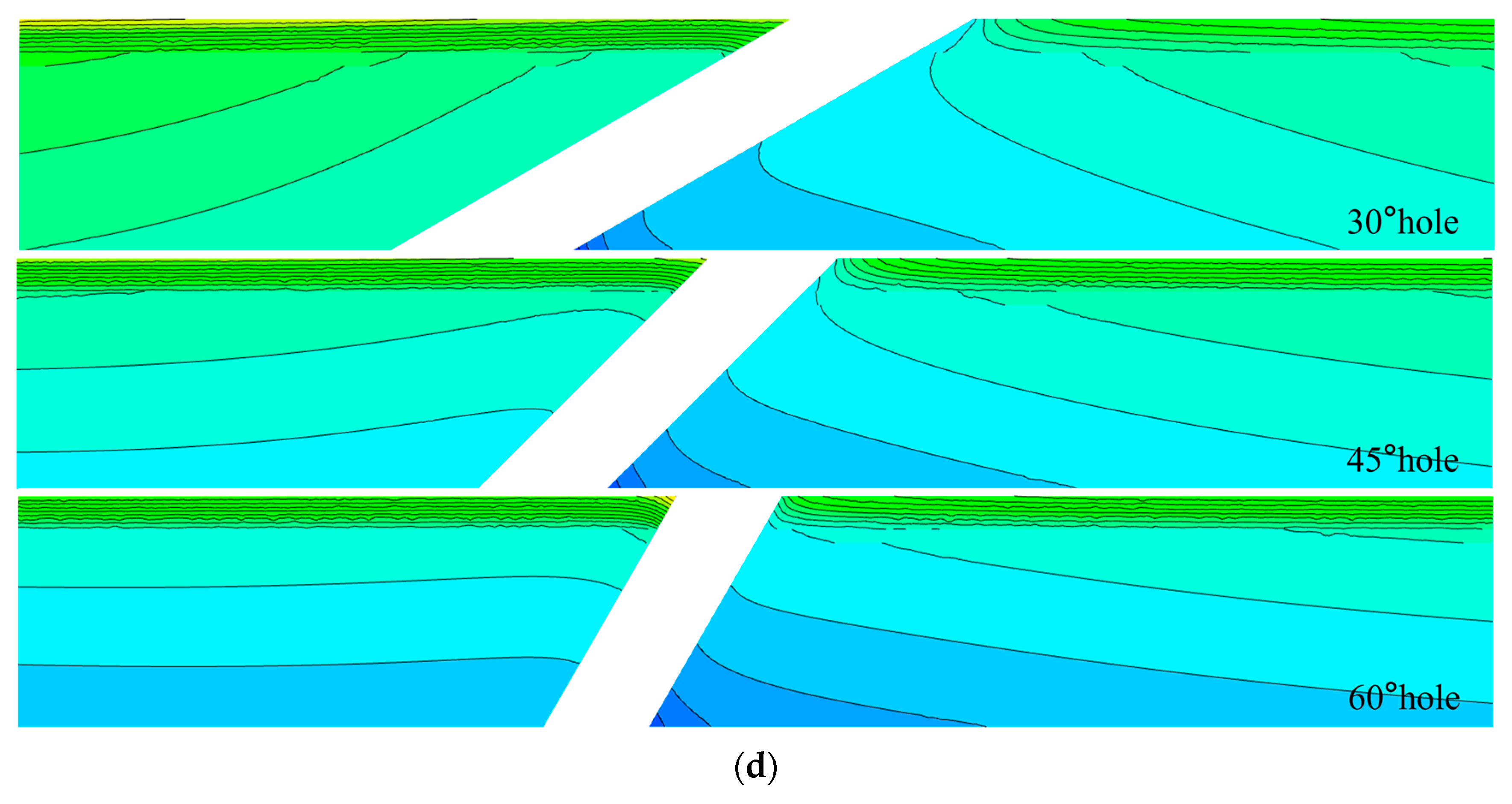
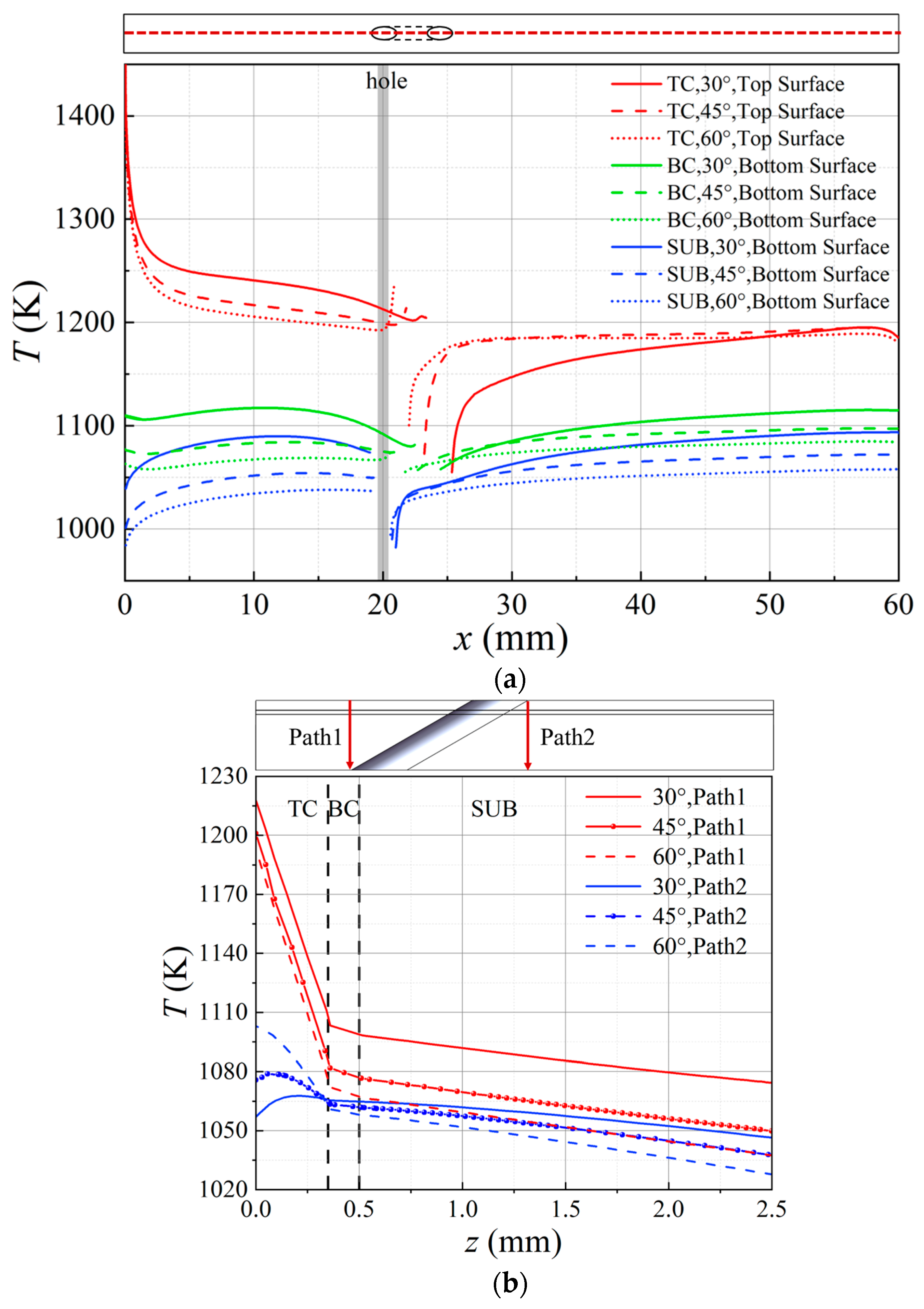
3.2. Temperature Distribution
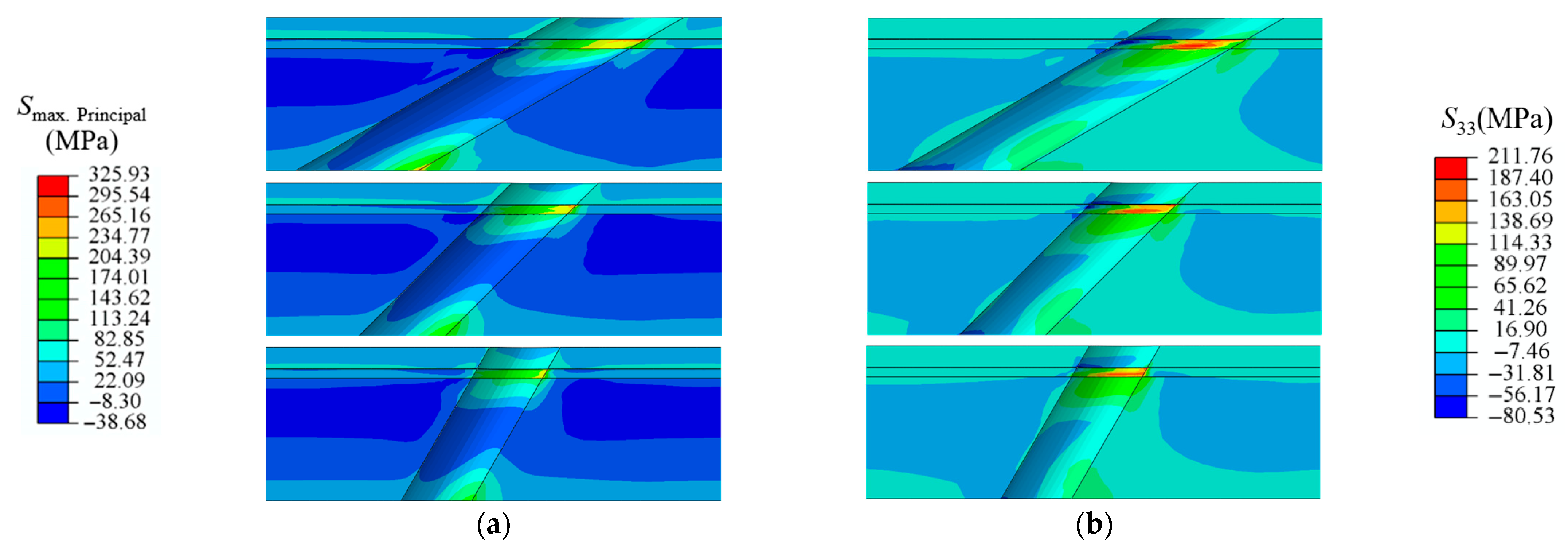
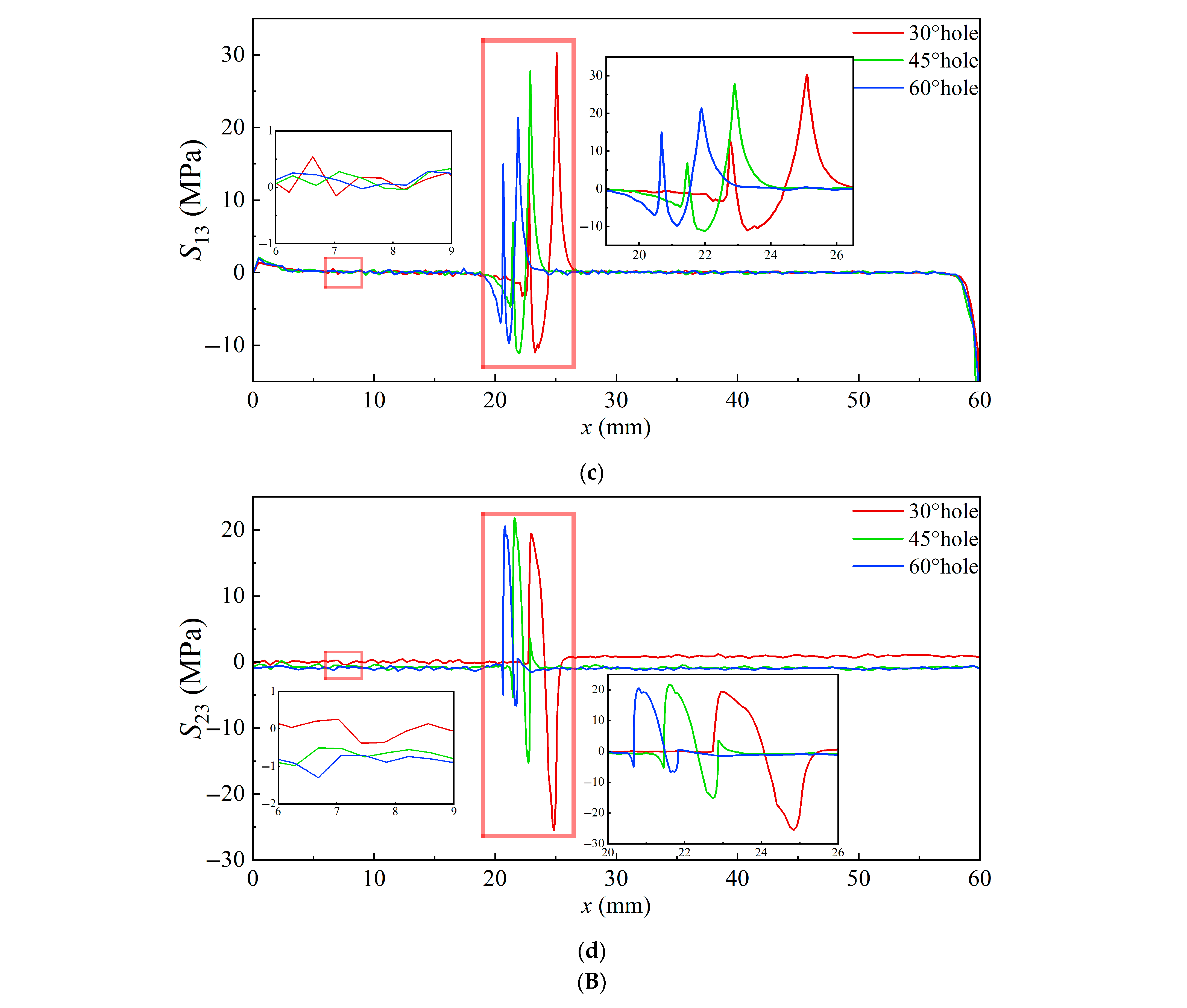
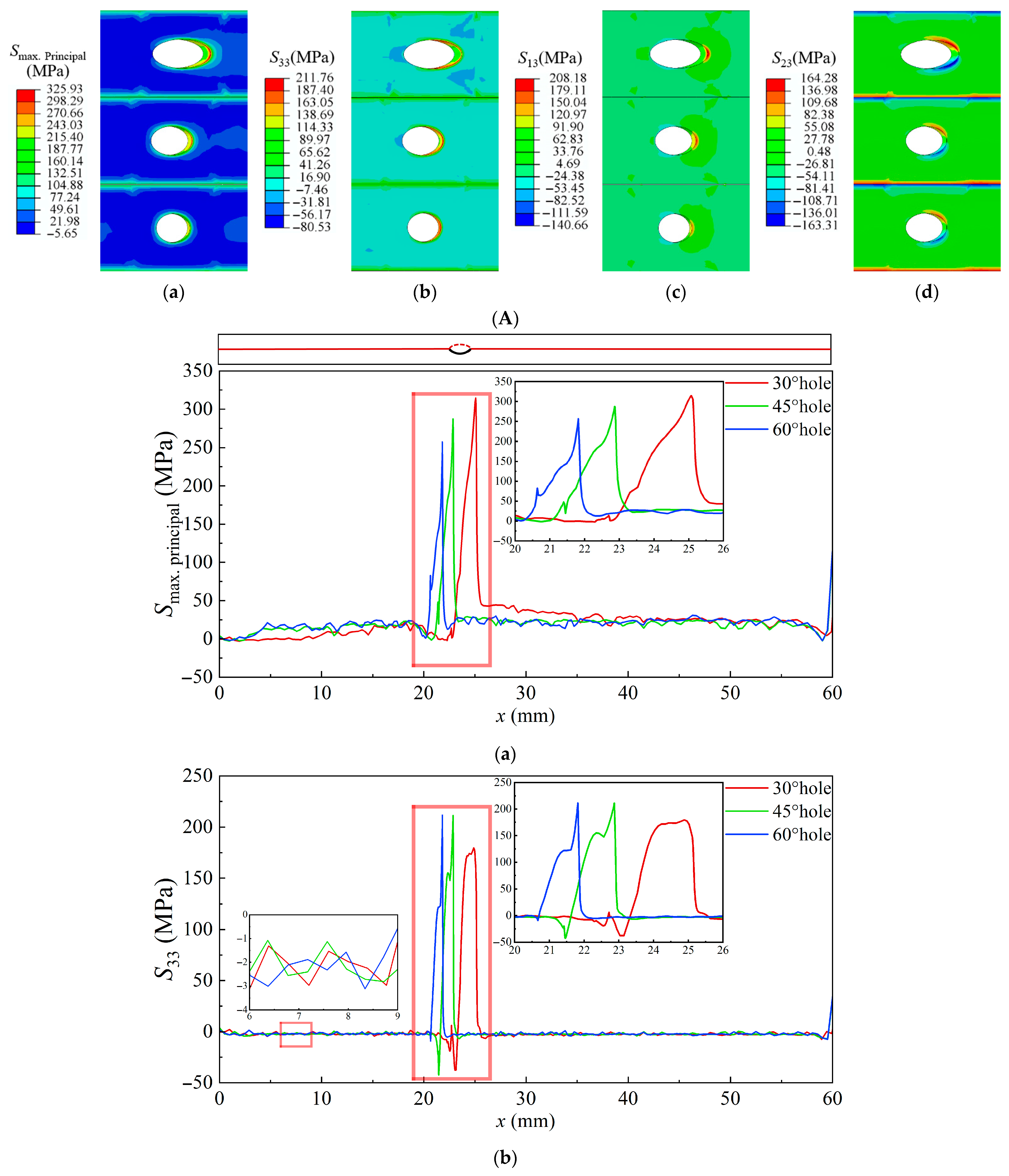
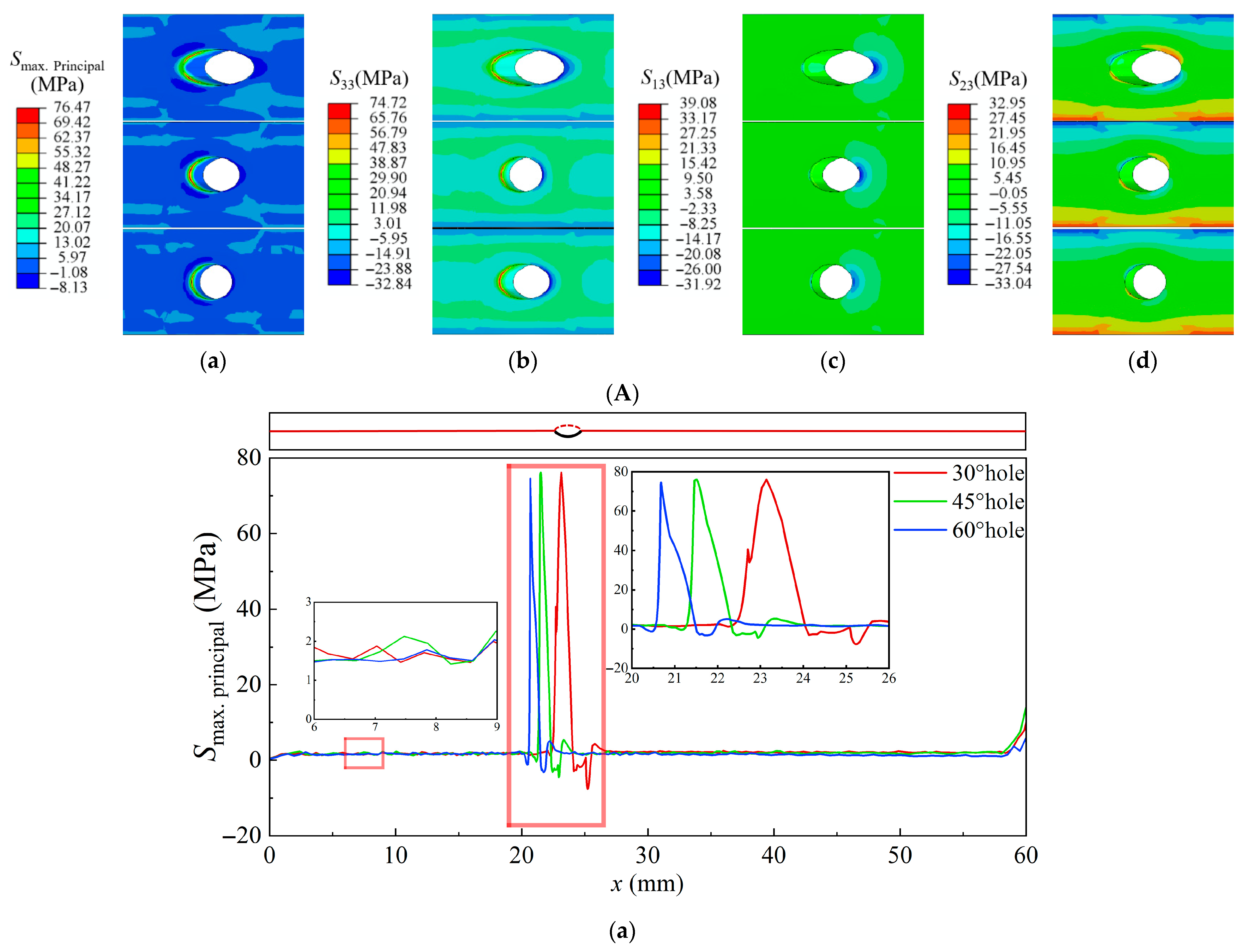
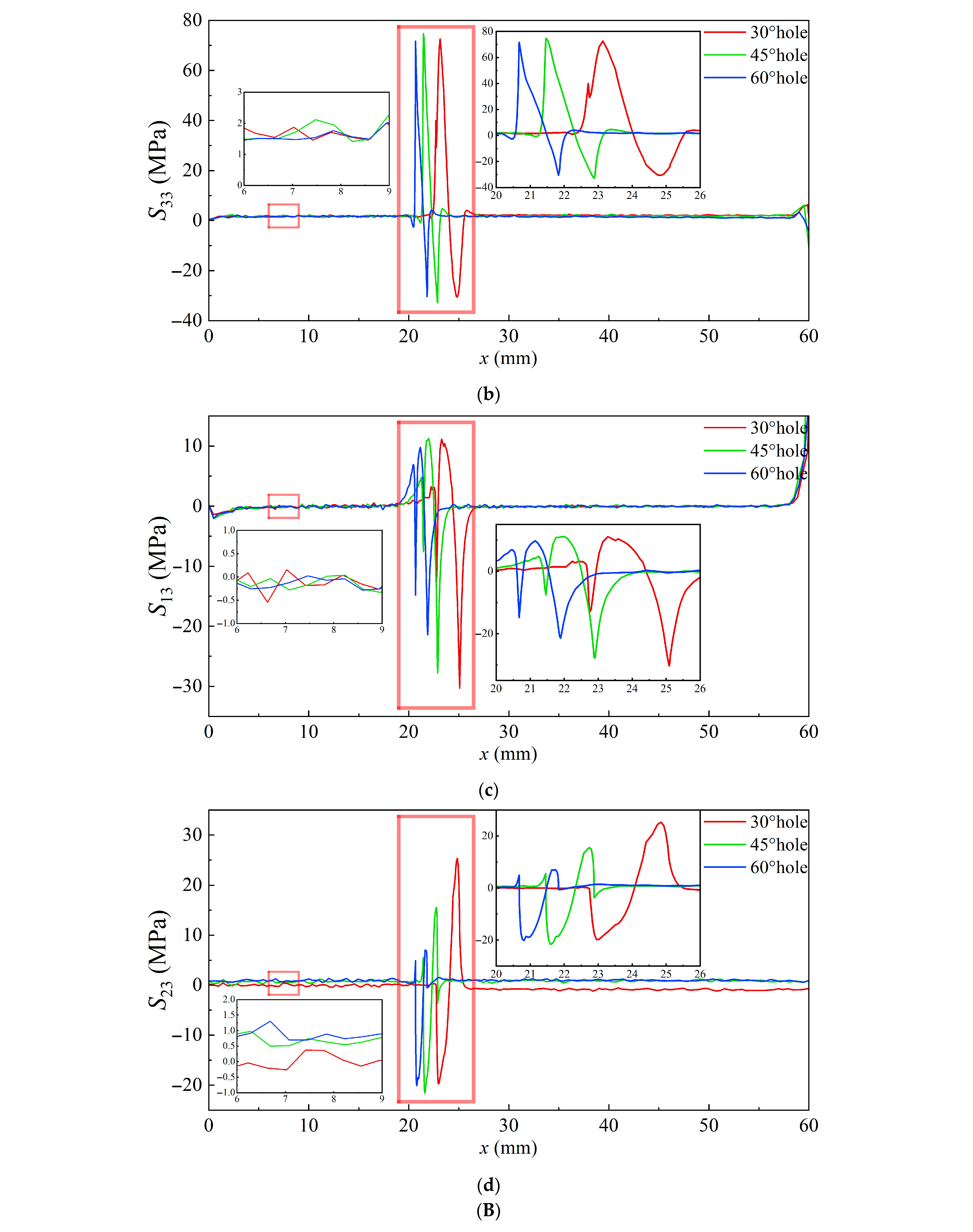
3.3. Thermal Stress at Elevated Temperature
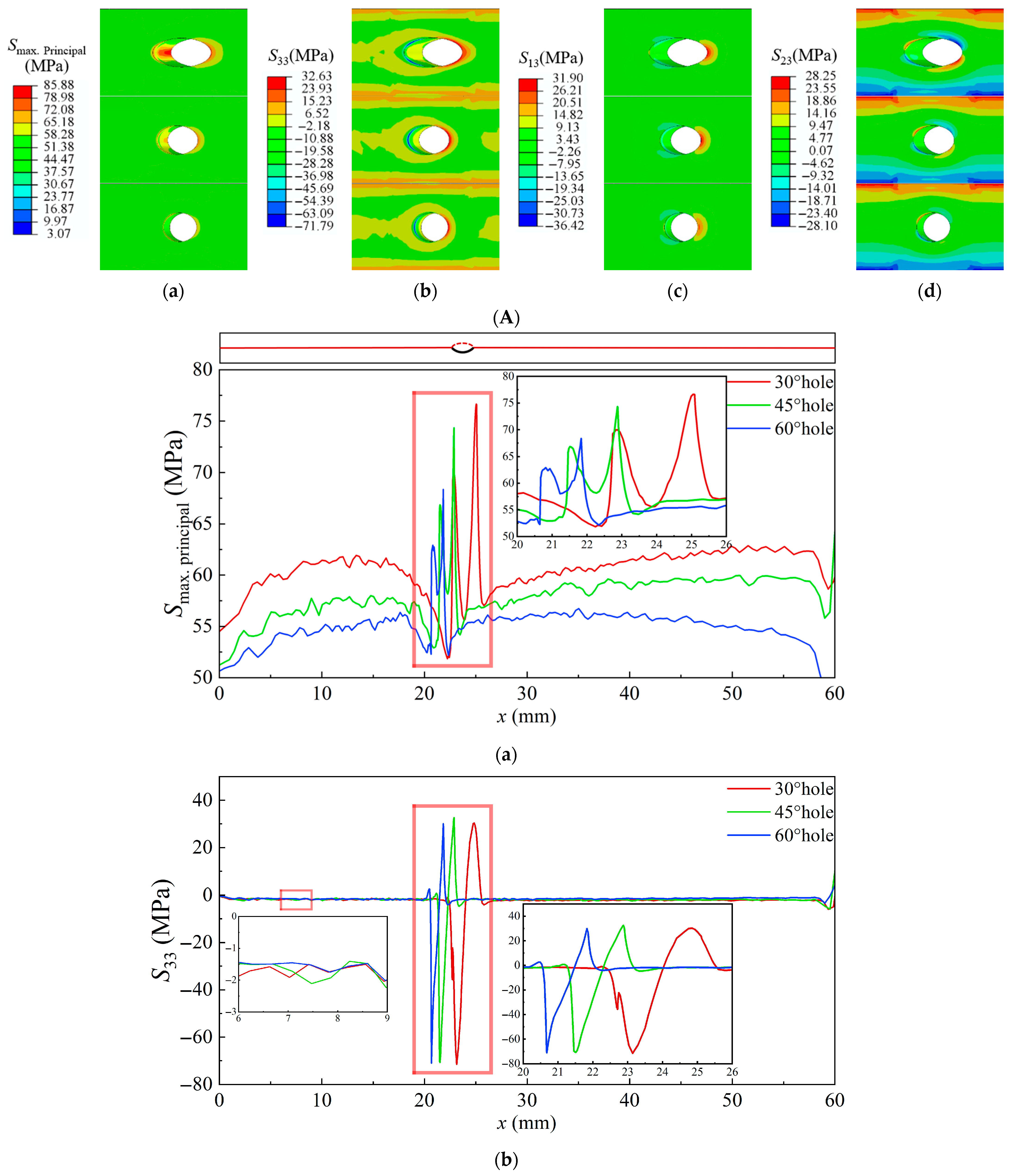
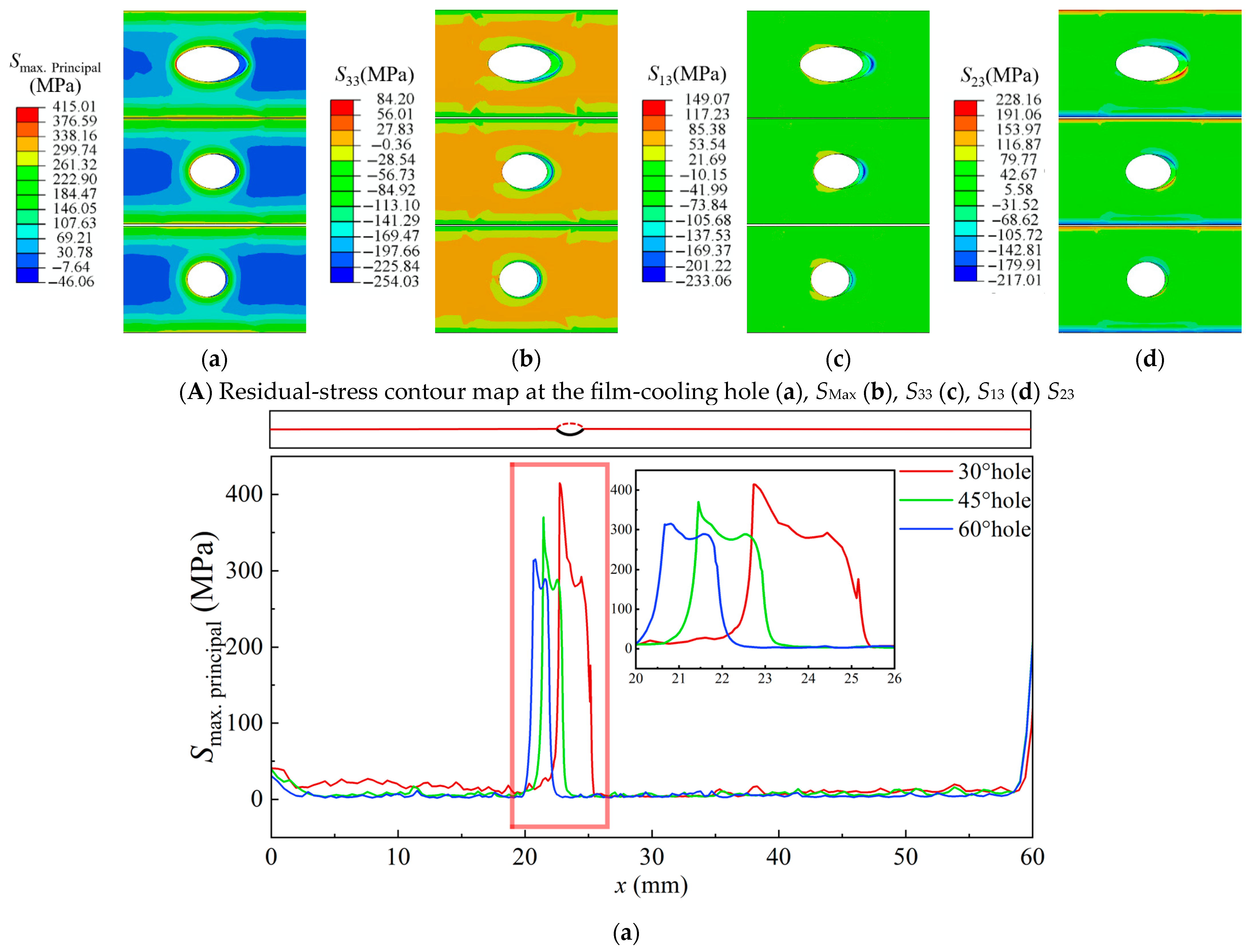
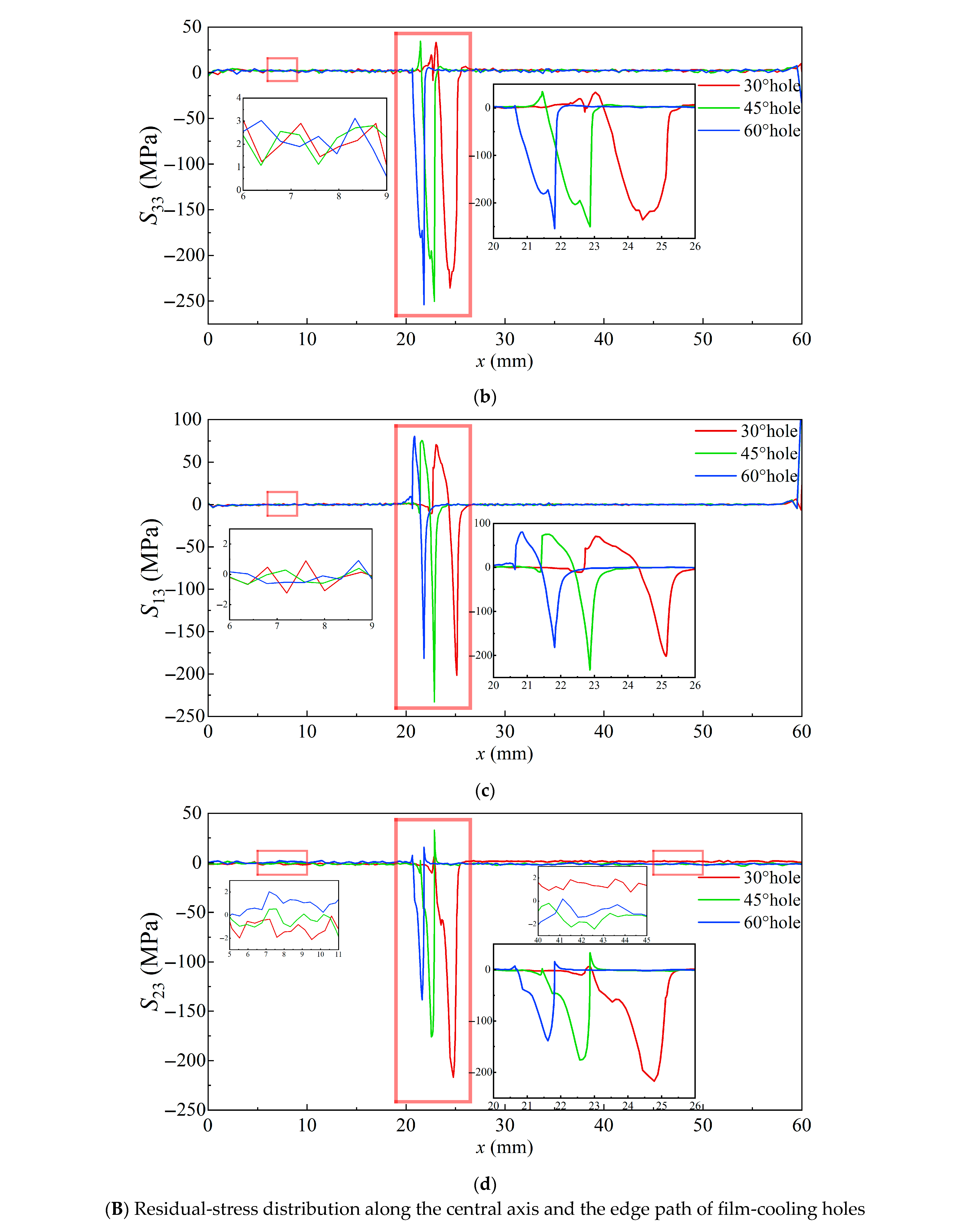
3.4. Residual Stress at Room Temperature
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Anand, V.G.K.; Parammasivam, K.M. Thermal Barrier Coated Surface Modifications for Gas Turbine Film Cooling: A Review. J. Therm. Anal. Calorim. 2021, 146, 545–580. [Google Scholar] [CrossRef]
- Meng, Z.; Liu, Y.; Li, Y.; He, X. The Performance Evaluation for Thermal Protection of Turbine Vane with Film Cooling and Thermal Barrier Coating. Appl. Therm. Eng. 2022, 210, 118405. [Google Scholar] [CrossRef]
- Li, D.; Jiang, P.; Gao, R.; Sun, F.; Jin, X.; Fan, X. Experimental and Numerical Investigation on the Thermal and Mechanical Behaviours of Thermal Barrier Coatings Exposed to CMAS Corrosion. J. Adv. Ceram. 2021, 10, 551–564. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, S.; Wang, C.; Tan, X. Recent Advances in Film Cooling Enhancement: A Review. Chin. J. Aeronaut. 2020, 33, 1119–1136. [Google Scholar] [CrossRef]
- Weeks, M.D.; Subramanian, R.; Vaidya, A.; Mumm, D.R. Defining Optimal Morphology of the Bond Coat–Thermal Barrier Coating Interface of Air-Plasma Sprayed Thermal Barrier Coating Systems. Surf. Coat. Technol. 2015, 273, 50–59. [Google Scholar] [CrossRef]
- Evans, H.E. Oxidation Failure of TBC Systems: An Assessment of Mechanisms. Surf. Coat. Technol. 2011, 206, 1512–1521. [Google Scholar] [CrossRef]
- Beck, T.; Herzog, R.; Trunova, O.; Offermann, M.; Steinbrech, R.W.; Singheiser, L. Damage Mechanisms and Lifetime Behavior of Plasma-Sprayed Thermal Barrier Coating Systems for Gas Turbines—Part II: Modeling. Surf. Coat. Technol. 2008, 202, 5901–5908. [Google Scholar] [CrossRef]
- Tsui, Y.; Clyne, T. An Analytical Model for Predicting Residual Stresses in Progressively Deposited Coatings Part 1: Planar Geometry. Thin Solid Films 1997, 306, 23–33. [Google Scholar] [CrossRef]
- Zhou, Y.; Hashida, T. Coupled Effects of Temperature Gradient and Oxidation on Thermal Stress in Thermal Barrier Coating System. Int. J. Solids Struct. 2001, 38, 4235–4264. [Google Scholar] [CrossRef]
- Mao, W.; Zhou, Y.; Yang, L.; Yu, X. Modeling of Residual Stresses Variation with Thermal Cycling in Thermal Barrier Coatings. Mech. Mater. 2006, 38, 1118–1127. [Google Scholar] [CrossRef]
- Zhang, X.; Xu, B.; Wang, H.; Wu, Y. Effects of Oxide Thickness, Al2O3 Interlayer and Interface Asperity on Residual Stresses in Thermal Barrier Coatings. Mater. Des. 2006, 27, 989–996. [Google Scholar] [CrossRef]
- Hsueh, C.H. Modeling of Elastic Deformation of Multilayers Due to Residual Stresses and External Bending. J. Appl. Phys. 2002, 91, 9652–9656. [Google Scholar] [CrossRef]
- Hsueh, C. Thermal Stresses in Elastic Multilayer Systems. Thin Solid Films 2002, 418, 182–188. [Google Scholar] [CrossRef]
- Yu, Q.; Cen, L. Residual Stress Distribution Along Interfaces in Thermal Barrier Coating System Under Thermal Cycles. Ceram. Int. 2017, 43, 3089–3100. [Google Scholar] [CrossRef]
- Balint, D.S.; Hutchinson, J.W. An Analytical Model of Rumpling in Thermal Barrier Coatings. J. Mech. Phys. Solids 2005, 53, 949–973. [Google Scholar] [CrossRef]
- Rösler, J.; Bäker, M.; Aufzug, K. A Parametric Study of the Stress State of Thermal Barrier Coatings: Part I: Creep Relaxation. Acta Mater. 2004, 52, 4809–4817. [Google Scholar] [CrossRef]
- Bäker, M.; Rösler, J.; Heinze, G. A Parametric Study of the Stress State of Thermal Barrier Coatings Part II: Cooling Stresses. Acta Mater. 2005, 53, 469–476. [Google Scholar] [CrossRef]
- Bednarz, P. Finite Element Simulation of Stress Evolution in Thermal Barrier Coating Systems; Schriften des Forschungszentrums Jülich Reihe Energietechnik/Energy Technolog: Jülich, Germany, 2007. [Google Scholar]
- Ranjbar-Far, M.; Absi, J.; Mariaux, G.; Shahidi, S. Effect of Residual Stresses and Prediction of Possible Failure Mechanisms on Thermal Barrier Coating System by Finite Element Method. J. Therm. Spray Technol. 2010, 19, 1054–1061. [Google Scholar] [CrossRef]
- Ranjbar-Far, M.; Absi, J.; Mariaux, G.; Smith, D. Crack Propagation Modeling on the Interfaces of Thermal Barrier Coating System with Different Thickness of the Oxide Layer and Different Interface Morphologies. Mater. Des. 2011, 32, 4961–4969. [Google Scholar] [CrossRef]
- Xie, F.; Sun, Y.; Li, D.; Bai, Y.; Zhang, W. Modelling of Catastrophic Stress Development Due to Mixed Oxide Growth in Thermal Barrier Coatings. Ceram. Int. 2019, 45, 11353–11361. [Google Scholar] [CrossRef]
- Yu, Q.M.; Zhou, H.L.; Wang, L.B. Influences of Interface Morphology and Thermally Grown Oxide Thickness on Residual Stress Distribution in Thermal Barrier Coating System. Ceram. Int. 2016, 42, 8338–8350. [Google Scholar] [CrossRef]
- Yu, Q.; He, Q. Effect of Material Properties on Residual Stress Distribution in Thermal Barrier Coatings. Ceram. Int. 2018, 44, 3371–3380. [Google Scholar] [CrossRef]
- Bohn, D.; Krewinkel, R. Influence of a Broken-Away TBC on the Flow Structure and Wall Temperature of an Effusion Cooled Multi-Layer Plate Using the Conjugate Calculation Method. In Proceedings of the ASME Turbo Expo 2008: Power for Land, Sea, and Air, Berlin, Germany, 9–13 June 2008; Volume 43147, pp. 351–362. [Google Scholar]
- Mensch, A.; Thole, K.A.; Craven, B.A. Conjugate Heat Transfer Measurements and Predictions of a Blade Endwall with a Thermal Barrier Coating. J. Turbomach. 2014, 136, 121003. [Google Scholar] [CrossRef]
- Mensch, A.; Thole, K.A. Overall Effectiveness of a Blade Endwall with Jet Impingement and Film Cooling. J. Eng. Gas Turbines Power 2014, 136, 031901. [Google Scholar] [CrossRef]
- Kim, K.M.; Shin, S.; Lee, D.H.; Cho, H.H. Influence of Material Properties on Temperature and Thermal Stress of Thermal Barrier Coating Near a Normal Cooling Hole. Int. J. Heat Mass Transf. 2011, 54, 5192–5199. [Google Scholar] [CrossRef]
- Lee, D.H.; Kim, K.M.; Shin, S.; Cho, H.H. Thermal Analysis in a Film Cooling Hole with Thermal Barrier Coating. J. Thermophys. Heat Transf. 2009, 23, 843–847. [Google Scholar] [CrossRef]
- Jiang, J.; Jiang, L.; Cai, Z.; Wang, W.; Zhao, X.; Liu, Y.; Cao, Z. Numerical Stress Analysis of the TBC-Film Cooling System Under Operating Conditions Considering the Effects of Thermal Gradient and TGO Growth. Surf. Coat. Technol. 2019, 357, 433–444. [Google Scholar] [CrossRef]
- Qiao, D.; Zeng, W. Numerical Stress Analysis of TBCs at Film Cooling Hole’s Edge Based on TBC-Film Cooling System. J. Therm. Spray Technol. 2024, 33, 2627–2640. [Google Scholar] [CrossRef]
- Dai, H.; Xie, A.; Gao, L.; Zhang, J.; Zhang, X.; Lin, J. Effect of CMAS Penetration Behavior on Stress Evolution in TBCs Under Three-Dimensional Temperature Gradients. Ceram. Int. 2024, 50, 660–671. [Google Scholar] [CrossRef]
- Meng, Z.; Liu, Y.; Li, Y.; Zhang, Y. An Analytical Model for Predicting Residual Stress in TBC-Film Cooling System Considering Non-Uniform Temperature Field. J. Appl. Phys. 2021, 129, 135301. [Google Scholar] [CrossRef]
- Liu, L.; Fu, S.; Hu, Z.; Wu, J.; Chen, J.; Jin, X.; Fan, X. Thermo-Mechanical Analysis of TBC-Film Cooling System Under High Blowing Ratio Considering the Effects of Curvature. Surf. Coat. Technol. 2023, 470, 129826. [Google Scholar] [CrossRef]
- Jiang, J.; Wu, D.; Wang, W.; Zhao, X.; Ma, X.; Wang, B.; Shi, H.-J. Fracture Behavior of TBCs with Cooling Hole Structure Under Cyclic Thermal Loadings. Ceram. Int. 2020, 46, 3644–3654. [Google Scholar] [CrossRef]
- Aktaa, J.; Sfar, K.; Munz, D. Assessment of TBC Systems Failure Mechanisms Using a Fracture Mechanics Approach. Acta Mater. 2005, 53, 4399–4413. [Google Scholar] [CrossRef]
- Freborg, A.; Ferguson, B.; Brindley, W.; Petrus, G. Modeling Oxidation Induced Stresses in Thermal Barrier Coatings. Mater. Sci. Eng. A 1998, 245, 182–190. [Google Scholar] [CrossRef]
- Wang, W.; Sun, P.; Ren, J.; Jiang, H. Radiative Effectiveness on the Aero-and Thermodynamics in a Highly Thermally Loaded Film Cooling System. In Proceedings of the ASME 2011 Turbo Expo: Turbine Technical Conference and Exposition, Vancouver, BC, Canada, 6–10 June 2011; Volume 54655, pp. 325–334. [Google Scholar]
- Schlichting, K.; Padture, N.; Jordan, E.; Gell, M. Failure Modes in Plasma-Sprayed Thermal Barrier Coatings. Mater. Sci. Eng. A 2003, 342, 120–130. [Google Scholar] [CrossRef]
- Krämer, S.; Faulhaber, S.; Chambers, M.; Clarke, D.; Levi, C.; Hutchinson, J.; Evans, A. Mechanisms of Cracking and Delamination Within Thick Thermal Barrier Systems in Aero-Engines Subject to Calcium-Magnesium-Alumino-Silicate (CMAS) Penetration. Mater. Sci. Eng. A 2008, 490, 26–35. [Google Scholar] [CrossRef]





| T °C | k W/(m·K) | C J/(kg·K) | kg/m3 | E GPa | 10−6/°C | ||
|---|---|---|---|---|---|---|---|
| TC | 25 | 1.05 | 483 | 5650 | 12.4 | 0.2 | 9.68 |
| 800 | 9.88 | ||||||
| 1000 | 10.34 | ||||||
| TGO | 25 | 25.2 | 857 | 3978 | 312 | 0.27 | 5.1 |
| 1000 | 9.8 | ||||||
| BC | 25 | 4.3 | 501 | 7320 | 120 | 0.3 | 10.3 |
| 400 | 6.4 | 592 | 12.5 | ||||
| 800 | 10.2 | 781 | 14.4 | ||||
| 1000 | 11.6 | 764 | 16.0 | ||||
| SUB | 100 | 11.4 | 544 | 8110 | 139 | 0.3 | 12.6 |
| 300 | 14.9 | 13.1 | |||||
| 500 | 18.3 | 14.0 | |||||
| 700 | 21.8 | 14.6 | |||||
| 900 | 25.2 | 15.8 | |||||
| 1100 | 28.7 | 16.3 |
| T (°C) | (MPa) | ||
|---|---|---|---|
| BC | 400 | 1100 | 0 |
| 400 | 2500 | 0.23 | |
| 800 | 300 | 0 | |
| 800 | 375 | 0.022 | |
| 1000 | 11 | 0 | |
| 1000 | 19 | 0.01 | |
| SUB | 27 | 708 | 0 |
| 27 | 716 | 1.998 × 10−3 | |
| 27 | 830 | 0.0402 | |
| 600 | 627 | 0 | |
| 600 | 636 | 1.998 × 10−3 | |
| 600 | 991 | 0.0862 | |
| 1000 | 204 | 0 | |
| 1000 | 205 | 1.998 × 10−3 | |
| 1000 | 355 | 0.2390 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shi, Z.; Jia, Y.; He, X.; Tian, Z.; Liu, Y. A Numerical Investigation on the Influence of Film-Cooling Hole Inclination Angle on the Stress Field of Surrounding Thermal Barrier Coating. Materials 2025, 18, 4079. https://doi.org/10.3390/ma18174079
Shi Z, Jia Y, He X, Tian Z, Liu Y. A Numerical Investigation on the Influence of Film-Cooling Hole Inclination Angle on the Stress Field of Surrounding Thermal Barrier Coating. Materials. 2025; 18(17):4079. https://doi.org/10.3390/ma18174079
Chicago/Turabian StyleShi, Zhengyu, Yuhao Jia, Xing He, Zegang Tian, and Yongbao Liu. 2025. "A Numerical Investigation on the Influence of Film-Cooling Hole Inclination Angle on the Stress Field of Surrounding Thermal Barrier Coating" Materials 18, no. 17: 4079. https://doi.org/10.3390/ma18174079
APA StyleShi, Z., Jia, Y., He, X., Tian, Z., & Liu, Y. (2025). A Numerical Investigation on the Influence of Film-Cooling Hole Inclination Angle on the Stress Field of Surrounding Thermal Barrier Coating. Materials, 18(17), 4079. https://doi.org/10.3390/ma18174079







