Interfacial Adhesion of Mouthrinses to Orthodontic Metal Wires: Surface Film Viscoelasticity Effect
Abstract
1. Introduction
2. Theoretical Background
2.1. Interfacial Adsorptive and Wettability Characteristics
2.2. Interfacial Miscibility of Surface-Active Compounds
2.3. Interfacial Relaxation Processes-Dilatational Viscoelasticity Modulus
3. Materials and Methods
3.1. Dynamic Contact Angle Determination
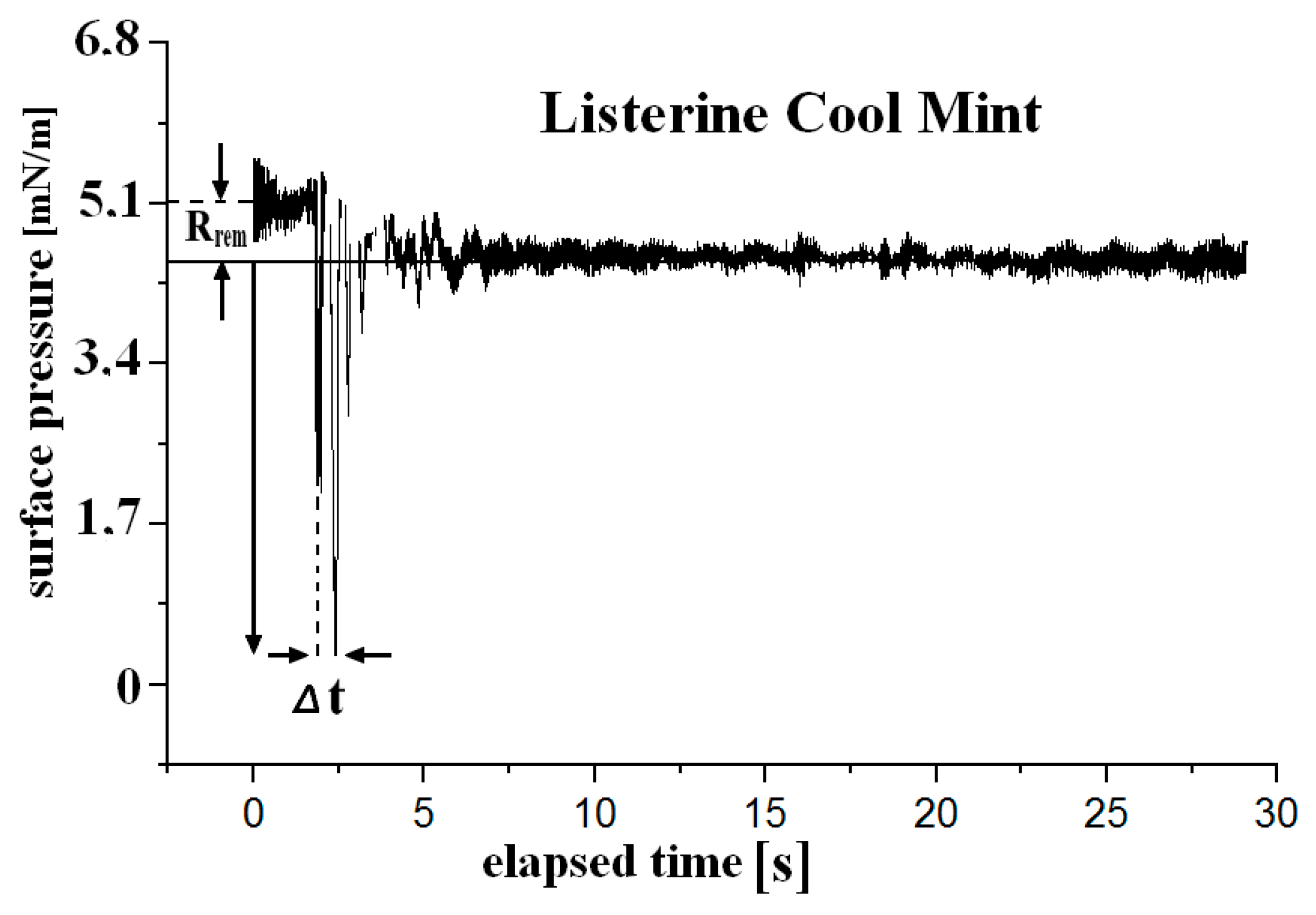
3.2. Surface Rheology: Static and Kinetic Signatures
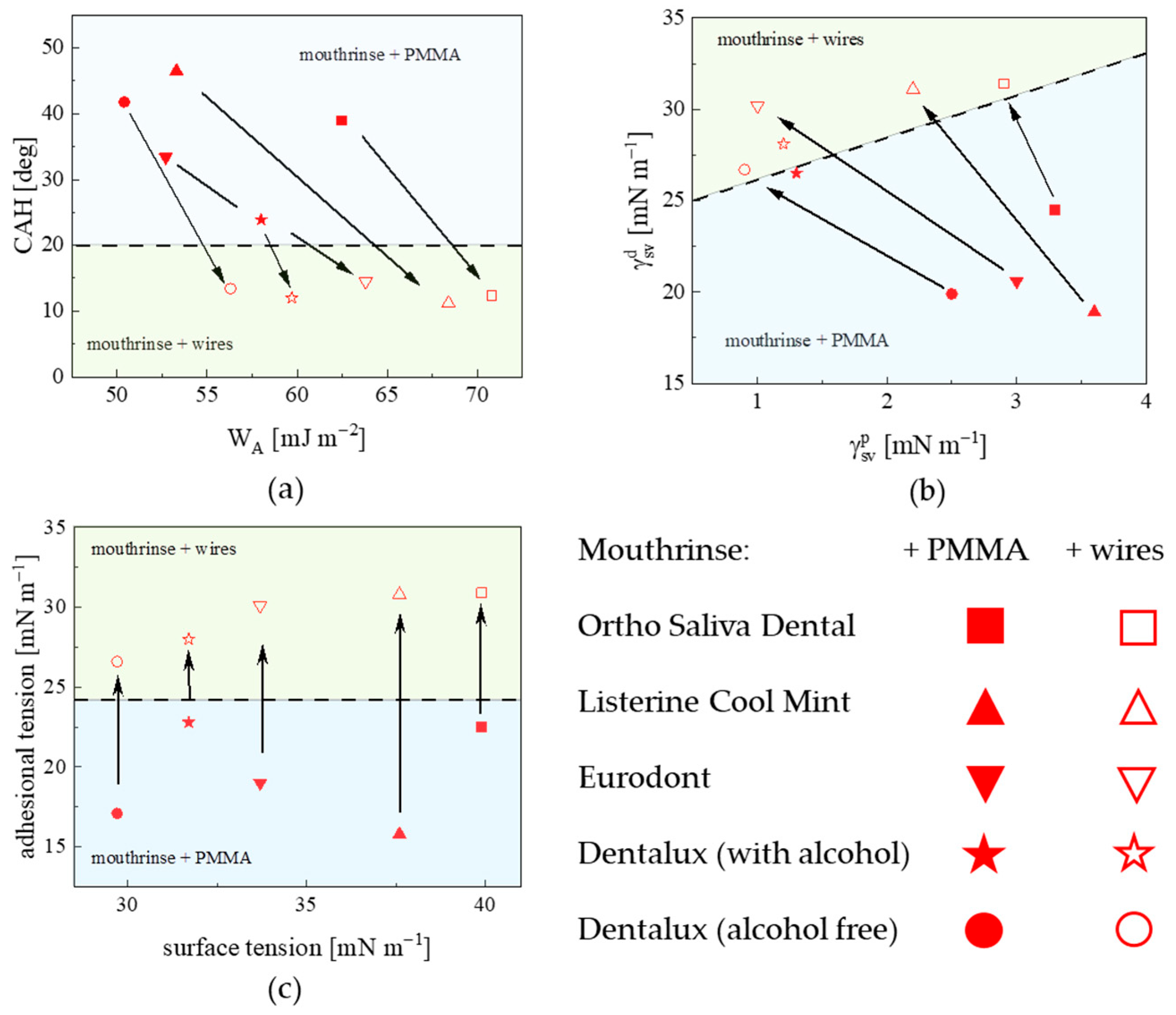
4. Results and Discussion
4.1. Energetics of Wettability
4.2. Metallic Wire Wettability vs. Mouthrinse Dissolution
4.3. Interfacial Molecular Architecture—Components Miscibility
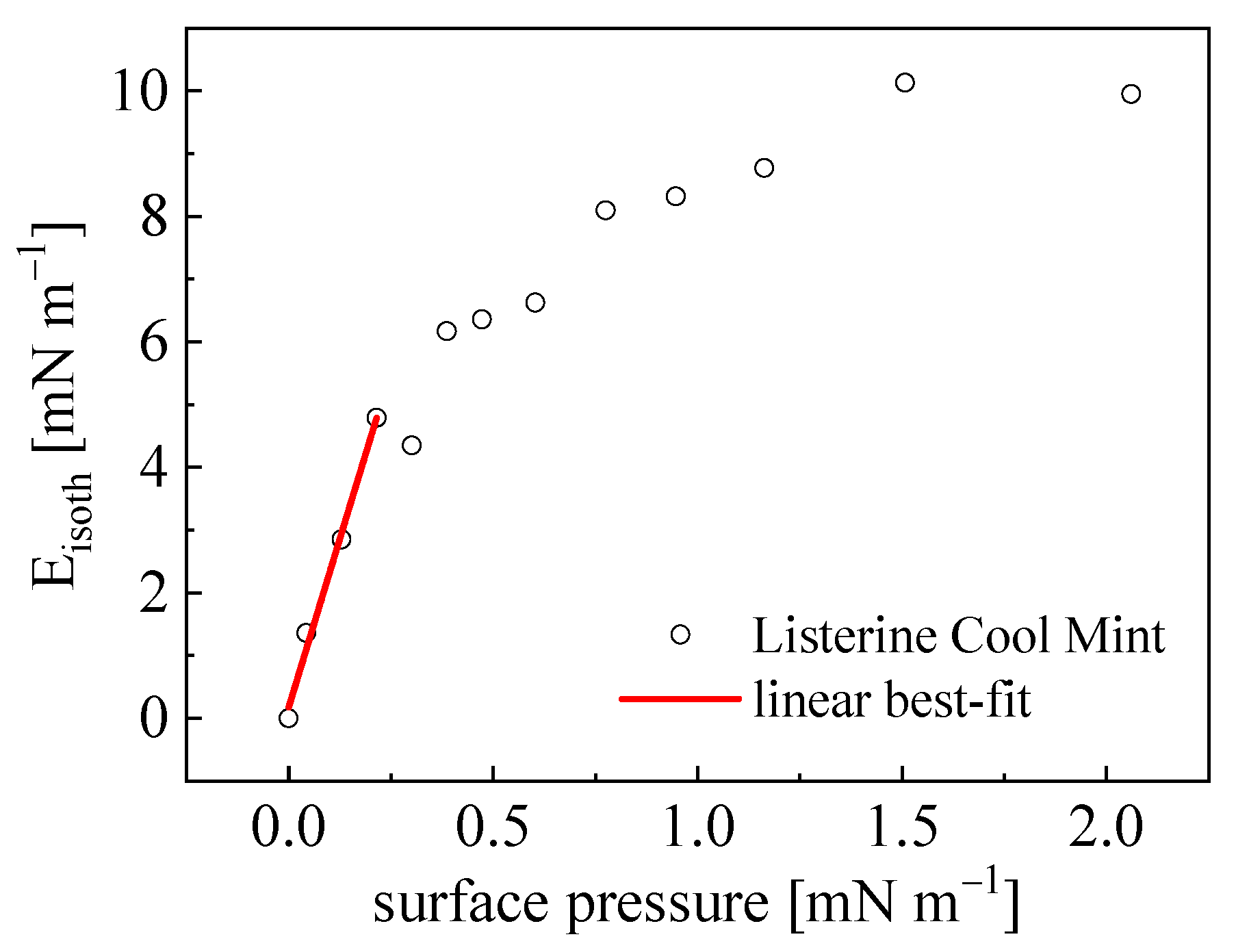
4.4. Interfacial Viscoelasticity Modules
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Pogorzelski, S.; Janowicz, P.; Dorywalski, K.; Boniewicz-Szmyt, K.; Rochowski, P. Wettability, Adsorption and Adhesion in Polymer (PMMA)—Commercially Available Mouthrinse System. Materials 2023, 16, 5753. [Google Scholar] [CrossRef] [PubMed]
- Pogorzelski, S.; Janowicz, P.; Dorywalski, K.; Boniewicz-Szmyt, K.; Rochowski, P. Adsorption, Adhesion, and Wettability of Commercially Available Cleansers at Dental Polymer (PMMA) Surfaces. Materials 2024, 17, 4755. [Google Scholar] [CrossRef] [PubMed]
- Boniewicz-Szmyt, K.; Pogorzelski, S.J. Thermoelastic Surface Properties of Seawater in Coastal Areas of the Baltic Sea. Oceanologia 2016, 58, 25–38. [Google Scholar] [CrossRef]
- Pogorzelski, S.J. Application of 2D Polymer Film Scaling Theory to Natural Sea Surface Films. Colloids Surf. A Physicochem. Eng. Asp. 1996, 114, 297–309. [Google Scholar] [CrossRef]
- Pogorzelski, S.J.; Kogut, A.D. Structural and Thermodynamic Signatures of Marine Microlayer Surfactant Films. J. Sea Res. 2003, 49, 347–356. [Google Scholar] [CrossRef]
- Pogorzelski, S.J.; Rochowski, P.; Szurkowski, J. Pinus sylvestris L. Needle Surface Wettability Parameters as Indicators of Atmospheric Environment Pollution Impacts: Novel Contact Angle Hysteresis Methodology. Appl. Surf. Sci. 2014, 292, 857–866. [Google Scholar] [CrossRef]
- Emelyanenko, A.; Ermolenko, N.; Boinovich, L. Contact Angle and Wetting Hysteresis Measurements by Digital Image Processing of the Drop on a Vertical Filament. Colloids Surf. A Physicochem. Eng. Asp. 2004, 239, 25–31. [Google Scholar] [CrossRef]
- Mann, E.K.; Lee, L.T.; Henon, S.; Langevin, D.; Meunier, J. Polymer-Surfactant Films at the Air-Water Interface. 1. Surface Pressure, Ellipsometry, and Microscopic Studies. Macromolecules 1993, 26, 7037–7045. [Google Scholar] [CrossRef]
- Kato, T.; Iriyama, K.; Araki, T. The Time of Observation of Π−A Isotherms III. Studies on the Morphology of Arachidic Acid Monolayers, Observed by Transmission Electron Microscopy of Replica Samples of One-Layer Langmuir-Blodgett Films Using Plasma-Polymerization. Thin Solid Film. 1992, 210–211, 79–81. [Google Scholar] [CrossRef]
- Boniewicz-Szmyt, K.; Pogorzelski, S.J. Influence of Surfactant Concentration and Temperature Gradients on Spreading of Crude-Oil at Sea. Front. Mar. Sci. 2018, 5, 388. [Google Scholar] [CrossRef]
- Ramé, E.; Garoff, S. Microscopic and Macroscopic Dynamic Interface Shapes and the Interpretation of Dynamic Contact Angles. J. Colloid Interface Sci. 1996, 177, 234–244. [Google Scholar] [CrossRef] [PubMed]
- Schäffer, E.; Wong, P. Contact Line Dynamics near the Pinning Threshold: A Capillary Rise and Fall Experiment. Phys. Rev. E 2000, 61, 5257–5277. [Google Scholar] [CrossRef] [PubMed]
- Bracke, M.; Voeght, F.; Joos, P. The Kinetics of Wetting: The Dynamic Contact Angle. In Trends in Colloid and Interface Science III; Steinkopff: Heidelberg, Germany, 2000; Volume 61, pp. 142–149. [Google Scholar]
- Georgiev, G.A.; Baluschev, S.; Eftimov, P.; Bacheva, M.; Landfester, K. Addressing the Apparent Controversies Between the Contact Angle-Based Models for Estimation of Surface Free Energy: A Critical Review. Colloids Interfaces 2024, 8, 62. [Google Scholar] [CrossRef]
- Krawczyk, J.; Szymczyk, K.; Zdziennicka, A.; Jańczuk, B. Wettability of Polymers by Aqueous Solution of Binary Surfactants Mixture with Regard to Adhesion in Polymer–Solution System II. Critical Surface Tension of Polymers Wetting and Work of Adhesion. Int. J. Adhes. Adhes. 2013, 45, 106–111. [Google Scholar] [CrossRef]
- Yamabe, T.; Moroi, Y.; Abe, Y.; Takahasi, T. Micelle Formation and Surface Adsorption of N-(1,1-Dihydroperfluoroalkyl)-N,N,N-Trimethylammonium Chloride. Langmuir 2000, 16, 9754–9758. [Google Scholar] [CrossRef]
- Jayalakshmi, Y.; Ozanne, L.; Langevin, D. Viscoelasticity of Surfactant Monolayers. J. Colloid Interface Sci. 1995, 170, 358–366. [Google Scholar] [CrossRef]
- Yang, J.; Yu, K.; Tsuji, T.; Jha, R.; Zuo, Y.Y. Determining the Surface Dilational Rheology of Surfactant and Protein Films with a Droplet Waveform Generator. J. Colloid Interface Sci. 2019, 537, 547–553. [Google Scholar] [CrossRef] [PubMed]
- Poirier, A.; Banc, A.; Stocco, A.; In, M.; Ramos, L. Multistep Building of a Soft Plant Protein Film at the Air-Water Interface. J. Colloid Interface Sci. 2018, 526, 337–346. [Google Scholar] [CrossRef] [PubMed]
- Joyner, H.S. (Ed.) Rheology of Semisolid Foods; Food Engineering Series; Springer: Cham, Switzerland, 2019; ISBN 978-3-030-27133-6. [Google Scholar]

| Liquid | CAH [deg] | Π [mN m−1] | WA [mJ m−2] | γLVcosθA [mN m−1] | γSV [mJ m−2] | [mJ m−2] | [mJ m−2] | a = ΓSL/ΓLV |
|---|---|---|---|---|---|---|---|---|
| Ortho Salvia Dental θA = 39.3 θR = 26.8 γLV = 39.9 | 12.5 (0.3) | 4.7 (0.1) | 70.8 (4.1) | 30.9 (1.8) | 34.3 (0.9) | 31.4 (1.1) | 2.9 (0.1) | +0.77 (0.06) |
| Dentalux + alcohol θA = 28.1 θR = 16.0 γLV = 31.7 | 12.1 (0.4) | 2.5 (0.1) | 59.7 (3.6) | 27.9 (1.3) | 29.2 (0.9) | 28.1 (1.2) | 1.2 (0.1) | +0.88 (0.06) |
| Dentalux (alc. free) θA = 26.4 θR = 13.0 γLV = 29.7 | 13.4 (0.5) | 2.3 (0.1) | 56.3 (3.2) | 26.6 (1.3) | 27.6 (0.8) | 26.7 (1.1) | 0.9 (0.1) | +0.89 (0.06) |
| Listerine Cool Mint θA = 34.9 θR = 23.7 γLV = 37.6 | 11.2 (0.2) | 3.6 (0.1) | 68.4 (4.6) | 30.8 (1.2) | 33.4 (1.2) | 31.1 (1.3) | 2.2 (0.2) | +0.82 (0.08) |
| Eurodont θA = 26.7 θR = 12.2 γLV = 33.7 | 14.5 (0.3) | 2.8 (0.1) | 63.8 (4.2) | 30.1 (1.3) | 31.2 (1.0) | 30.2 (1.2) | 1.0 (0.1) | +0.89 (0.07) |
| C/C0 | θA [deg] (0.2°) | θR [deg] (0.2°) | γLV [mN m−1] | Π [mN m−1] | WA [mJ m−2] | [mJ m−2] | [mJ m−2] | [mJ m−2] | γLVcosθA [mN m−1] |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 39.3 | 26.8 | 39.9 (1.1) | 4.7 (0.2) | 70.8 (2.2) | 34.3 (1.4) | 31.4 (1.1) | 2.9 (0.2) | 30.9 (1.3) |
| 0.5 | 42.6 | 25.9 | 40.0 (1.3) | 5.2 (0.2) | 70.9 (2.1) | 33.8 (1.3) | 30.6 (1.2) | 3.1 (0.2) | 29.7 (1.2) |
| 0.25 | 44.2 | 25.3 | 40.2 (1.3) | 7.5 (0.3) | 69.0 (2.1) | 32.7 (1.3) | 29.6 (1.2) | 3.1 (0.2) | 28.8 (1.1) |
| 0.125 | 45.3 | 24.8 | 41.1 (1.3) | 8.4 (0.3) | 70.0 (2.3) | 33.0 (1.2) | 29.8 (1.3) | 3.2 (0.2) | 28.9 (1.3) |
| 0.0625 | 46.2 | 23.2 | 41.8 (1.3) | 9.5 (0.3) | 70.7 (2.4) | 33.1 (1.4) | 29.9 (1.3) | 3.3 (0.2) | 28.9 (1.3) |
| 0.0313 | 48.4 | 23.8 | 42.7 (1.3) | 10.7 (0.4) | 71.1 (2.4) | 33.0 (1.4) | 29.5 (1.2) | 3.5 (0.3) | 28.4 (1.3) |
| 0.0156 | 52.2 | 24.0 | 44.3 (1.3) | 13.3 (0.4) | 71.5 (2.5) | 32.7 (1.4) | 28.8 (1.2) | 3.9 (0.3) | 27.2 (1.2) |
| 0.0078 | 56.1 | 24.3 | 45.8 (1.4) | 16.2 (0.5) | 71.3 (2.3) | 32.0 (1.3) | 27.8 (1.2) | 4.3 (0.3) | 25.5 (1.2) |
| 0.0039 | 55.3 | 24.5 | 48.2 (1.3) | 16.4 (0.5) | 75.6 (2.2) | 34.1 (1.3) | 29.7 (1.3) | 4.4 (0.4) | 27.4 (1.3) |
| 0.001953 | 58.2 | 24.7 | 49.3 (1.3) | 18.8 (0.4) | 75.3 (2.3) | 33.5 (1.3) | 28.7 (1.3) | 4.7 (0.3) | 25.9 (1.4) |
| 0.000976 | 60.3 | 24.9 | 54.3 (1.3) | 22.3 (0.4) | 81.2 (2.4) | 35.7 (1.4) | 30.4 (1.3) | 5.3 (0.3) | 26.9 (1.4) |
| 0.000488 | 61.7 | 25.2 | 67.2 (1.3) | 28.9 (0.3) | 99.1 (2.6) | 43.2 (1.5) | 36.5 (1.4) | 6.7 (0.3) | 31.9 (1.4) |
| 0.000244 | 62.9 | 25.4 | 72.3 (1.4) | 32.4 (0.4) | 105.6 (2.8) | 45.8 (1.6) | 38.4 (1.4) | 7.3 (0.3) | 33.1 (1.4) |
| Liquid | y | SS [mN m−1 K−1] |
|---|---|---|
| Ortho Salvia Dental | 15.3 (0.6) | 0.13 (0.02) |
| Dentalux (+Alc) | 13.1 (0.4) | 0.21 (0.04) |
| Dentalux (Alc. Free) | 12.9 (0.3) | 0.23 (0.04) |
| Listerine Cool Mint | 14.7 (0.3) | 0.14 (0.02) |
| Eurodont | 15.5 (0.7) | 0.12 (0.04) |
| Liquid | ΔA/A0·102 (<3%) | Δt [s]·102 (1 ms) | [s] | τ1 [s] | τ2 [s] | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Ortho Salvia Dental | 12 | 46 | 3.83 (0.07) | 0.74 (0.03) | 0.92 (0.07) | |||||
| 8 | 42 | 5.25 (0.11) | 0.81 (0.05) | 0.87 (0.06) | ||||||
| 8 | 36 | 4.50 (0.09) | 0.59 (0.02) | 0.85 (0.09) | ||||||
| 27 | 28 | 1.04 (0.02) | 0.41 (0.02) | 0.64 (0.05) | ||||||
| Dentalux + alcohol | 12 | 61 | 5.08 (0.10) | 0.71 (0.04) | 0.79 (0.08) | |||||
| Dentalux (alc. free) | 12 | 36 | 3.10 (0.07) | 0.72 (0.03) | 0.92 (0.11) | |||||
| Listerine Cool Mint | 19 11 | 50 66 | 2.62 (0.05) 6.13 (0.13) | 0.63 (0.02) 0.78 (0.04) | 0.65 (0.05) 0.72 (0.07) | |||||
| Eurodont | 24 | 45 | 1.87 (0.03) | 0.89 (0.04) | 3.13 (0.62) | |||||
| Liquid | Ed [mN m−1] | Ei [mN m−1] | |E| [mN m−1] | φ [o] | Rrem [mN m−1] | Eisoth [mN m−1] | ||||
| Ortho Salvia Dental | 24.1 (0.9) | 10.6 (0.3) | 26.3 (1.5) | 23.7 (0.3) | 0.2 (>0.1) | 3.3 (0.2) | ||||
| 37.0 (1.3) | 15.5 (0.4) | 40.1 (1.9) | 22.7 (0.3) | 0.2 (>0.1) | ||||||
| 46.2 (1.8) | 20.2 (0.5) | 50.4 (2.5) | 23.6 (0.3) | 0.3 (>0.1) | ||||||
| 48.4 (1.6) | 21.9 (0.5) | 53.1 (2.5) | 24.3 (0.2) | 0.4 (>0.1) | ||||||
| Dentalux + alcohol | 36.4 (1.4) | 17.5 (0.4) | 40.4 (2.3) | 25.7 (0.3) | 0.1 (>0.1) | 5.6 (0.3) | ||||
| Dentalux (alc. free) | 24.1 (1.0) | 10.6 (0.3) | 26.3 (1.8) | 23.7 (0.2) | 0.3 (>0.1) | 3.4 (0.2) | ||||
| Listerine Cool Mint | 9.3 (0.6) 6.7 (0.5) | 4.4 (0.1) 3.2 (0.1) | 10.3 (1.0) 7.4 (0.8) | 25.2 (0.3) 25.6 (0.3) | 0.7 (>0.1) 0.3 (>0.1) | 1.3 (0.1) | ||||
| Eurodont | 16.1 (1.1) | 6.7 (0.2) | 17.4 (1.6) | 22.5 (0.2) | 1.4 (>0.1) | 7.3 (0.4) | ||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pogorzelski, S.; Dorywalski, K.; Boniewicz-Szmyt, K.; Rochowski, P. Interfacial Adhesion of Mouthrinses to Orthodontic Metal Wires: Surface Film Viscoelasticity Effect. Materials 2025, 18, 4065. https://doi.org/10.3390/ma18174065
Pogorzelski S, Dorywalski K, Boniewicz-Szmyt K, Rochowski P. Interfacial Adhesion of Mouthrinses to Orthodontic Metal Wires: Surface Film Viscoelasticity Effect. Materials. 2025; 18(17):4065. https://doi.org/10.3390/ma18174065
Chicago/Turabian StylePogorzelski, Stanisław, Krzysztof Dorywalski, Katarzyna Boniewicz-Szmyt, and Paweł Rochowski. 2025. "Interfacial Adhesion of Mouthrinses to Orthodontic Metal Wires: Surface Film Viscoelasticity Effect" Materials 18, no. 17: 4065. https://doi.org/10.3390/ma18174065
APA StylePogorzelski, S., Dorywalski, K., Boniewicz-Szmyt, K., & Rochowski, P. (2025). Interfacial Adhesion of Mouthrinses to Orthodontic Metal Wires: Surface Film Viscoelasticity Effect. Materials, 18(17), 4065. https://doi.org/10.3390/ma18174065






