Optical Property Simulations of Gold and Silver Nanostructured Arrays Within a Liquid Crystal Environment
Abstract
1. Introduction
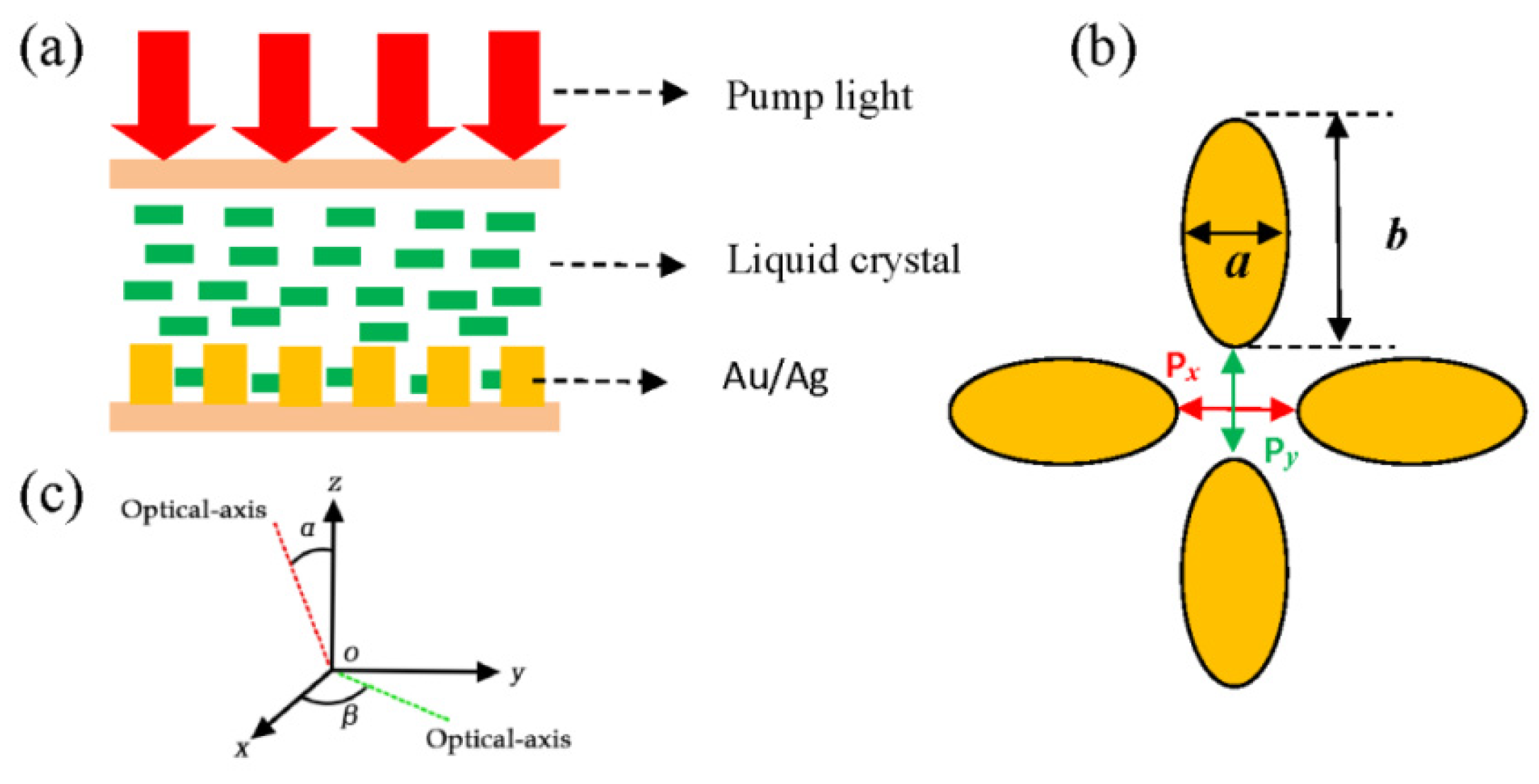
2. Model Overview
3. Results and Discussion
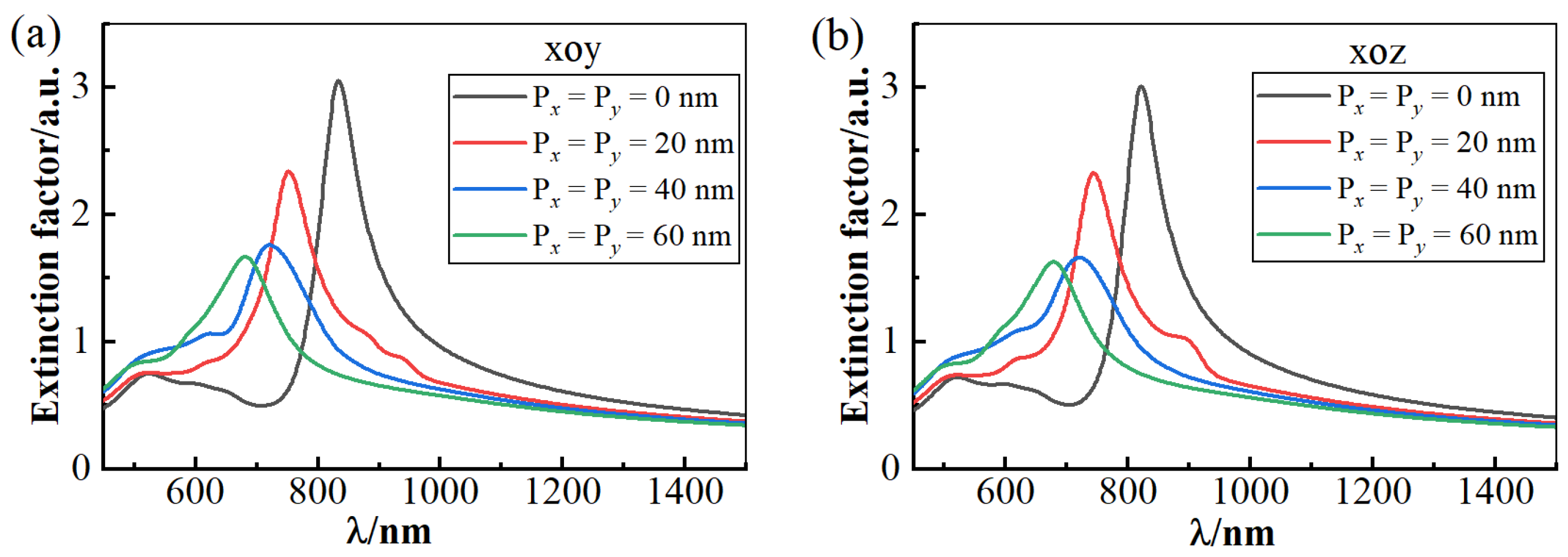
3.1. Extinction Spectrum Analysis
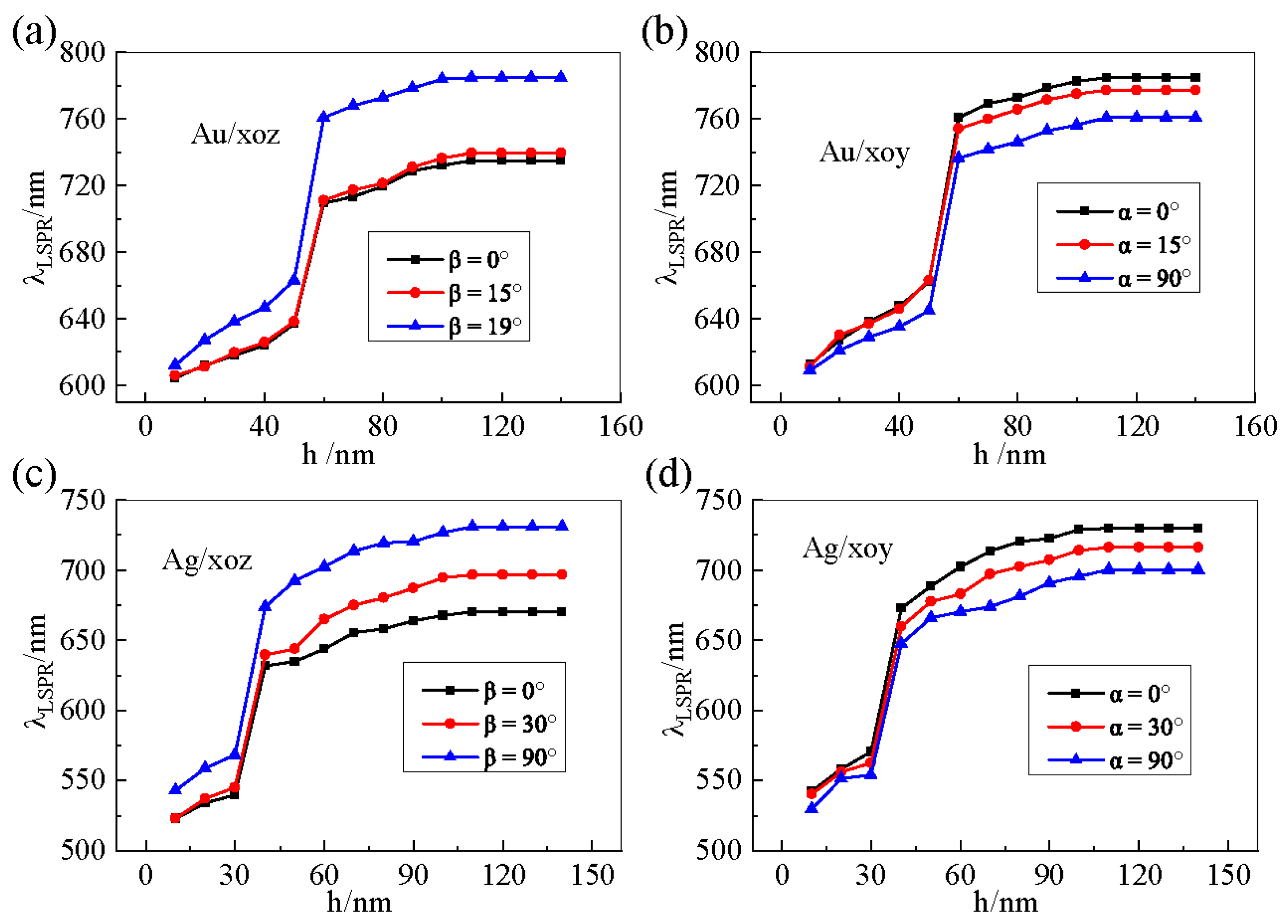
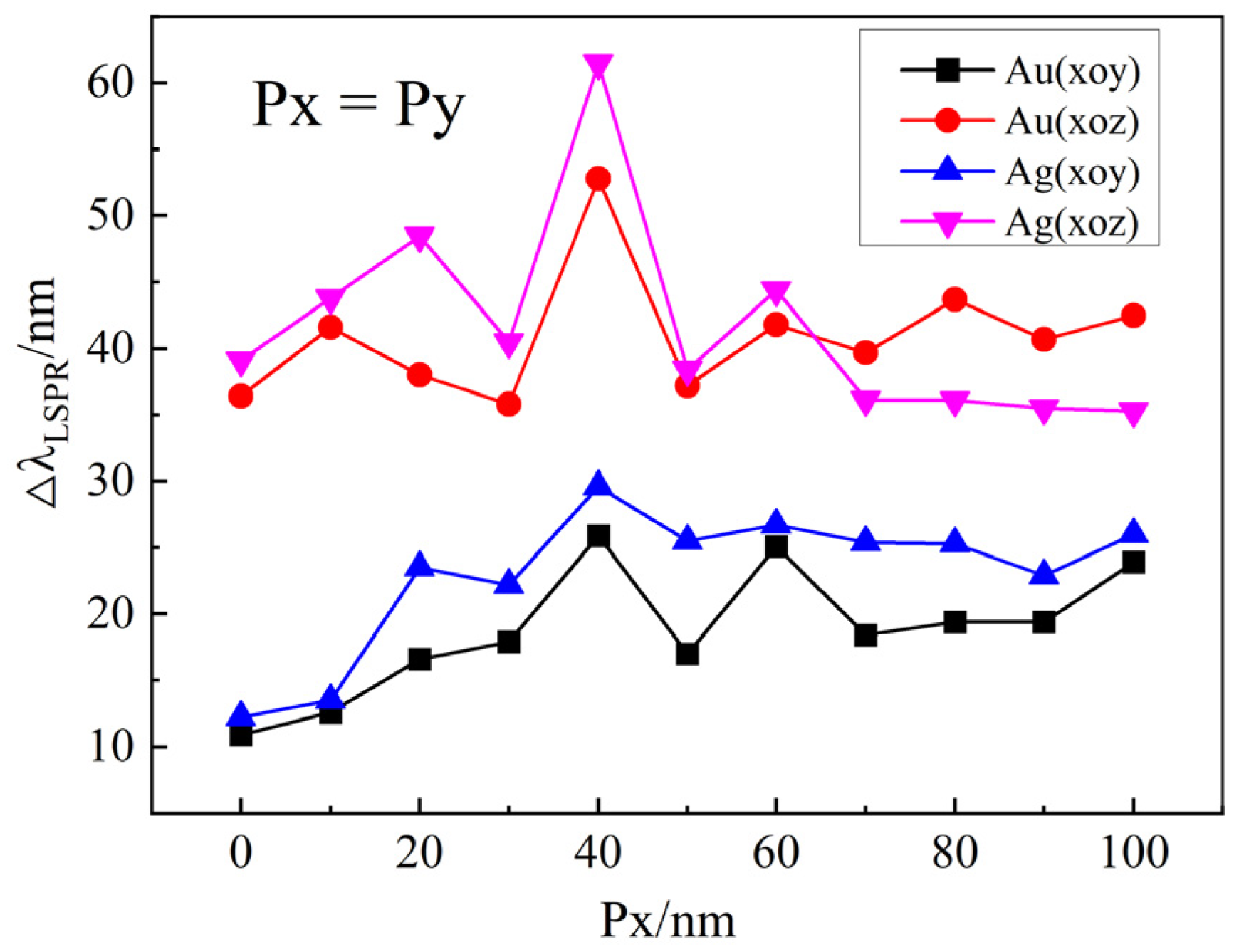
3.2. LSPR Wavelength with Different Liquid Crystal Thicknesses
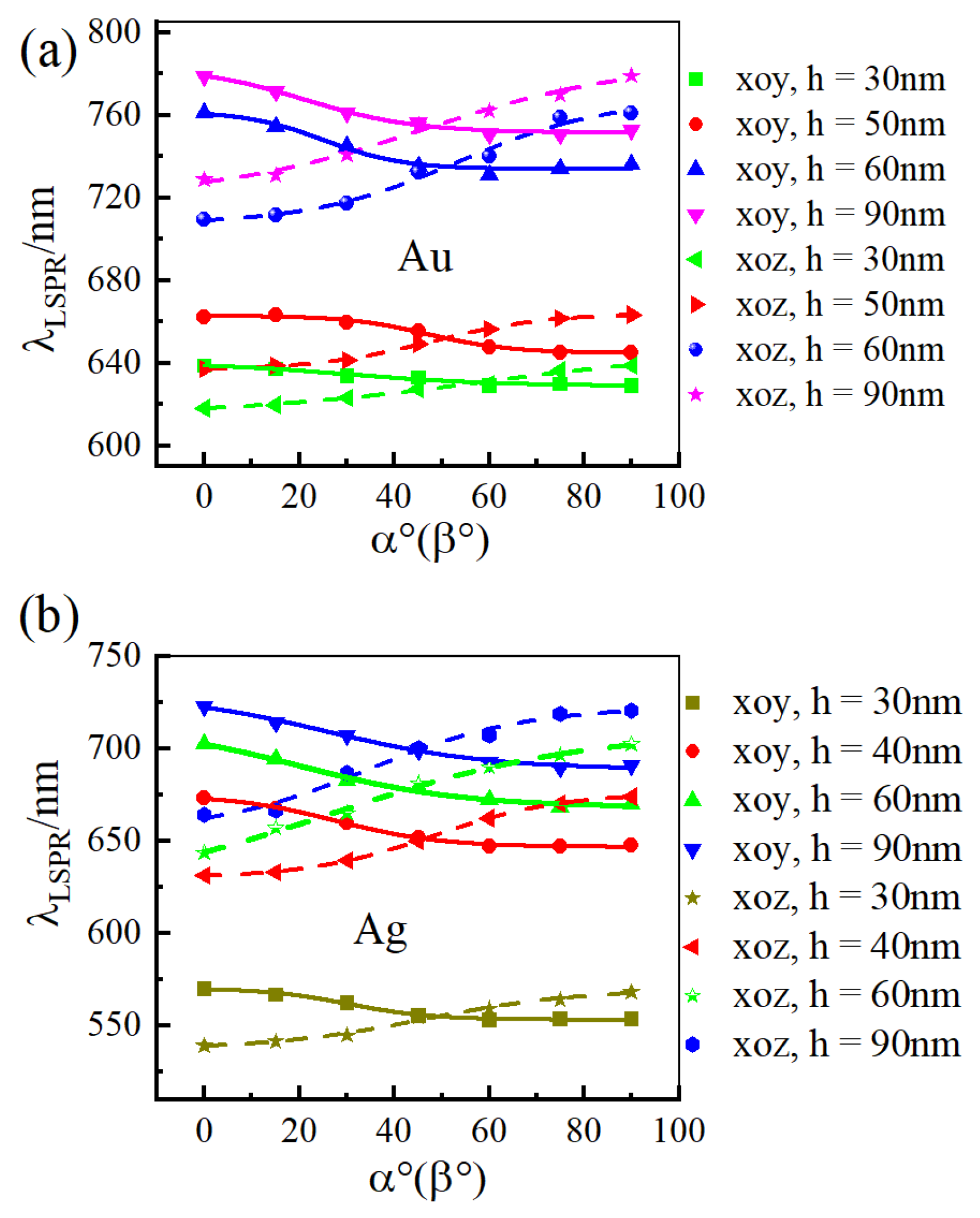
3.3. LSPR Wavelength Variation with the Liquid Crystal Optical Axis Rotation
3.4. LSPR Spectral Sensitivity
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Meng, X.; Fujita, K.; Murai, S.; Matoba, T.; Tanaka, K. Plasmonically Controlled Lasing Resonance with Metallic–Dielectric Core–Shell Nanoparticles. Nano Lett. 2011, 11, 1374–1378. [Google Scholar] [CrossRef]
- Naik, G.V.; Schroeder, J.L.; Ni, X.; Kildishev, A.V.; Sands, T.D.; Boltasseva, A. Titanium nitride as a plasmonic material for visible and near-infrared wavelengths. Opt. Mater. Express 2012, 2, 478–489. [Google Scholar] [CrossRef]
- Hutter, E.; Fendler, J.H. Exploitation of Localized Surface Plasmon Resonance. Adv. Mater. 2004, 16, 1685–1706. [Google Scholar] [CrossRef]
- Abbas, A.; Amin, H.M.A. Silver nanoparticles modified electrodes for electroanalysis: An updated review and a perspective. Microchem. J. 2022, 175, 107166. [Google Scholar] [CrossRef]
- Noginov, M.A.; Zhu, G.; Bahoura, M.; Adegoke, J.; Small, C.E.; Ritzo, B.A.; Drachev, V.P.; Shalaev, V.M. Enhancement of surface plasmons in an Ag aggregate by optical gain in a dielectric medium. Opt. Lett. 2006, 31, 3022–3024. [Google Scholar] [CrossRef] [PubMed]
- Drachev, V.P.; Buin, A.K.; Nakotte, H.; Shalaev, V.M. Size Dependent χ(3) for Conduction Electrons in Ag Nanoparticles. Nano Lett. 2004, 4, 1535–1539. [Google Scholar] [CrossRef]
- Wang, H.; Vial, A. Plasmonic Resonance Tunability and Surface-Enhanced Raman Scattering Gain of Metallic Nanoparticles Embedded in a Liquid Crystal Cell. J. Phys. Chem. C 2013, 117, 24537–24542. [Google Scholar] [CrossRef]
- Li, Z.-Y. Mesoscopic and Microscopic Strategies for Engineering Plasmon-Enhanced Raman Scattering. Adv. Opt. Mater. 2018, 6, 1701097. [Google Scholar] [CrossRef]
- Huang, W.; Qian, W.; Jain, P.K.; El-Sayed, M.A. The Effect of Plasmon Field on the Coherent Lattice Phonon Oscillation in Electron-Beam Fabricated Gold Nanoparticle Pairs. Nano Lett. 2007, 7, 3227–3234. [Google Scholar] [CrossRef] [PubMed]
- Oh, M.; Jeong, M.S.; Cho, J.; Kim, H. Hybrid Functional ITO/Silver Nanowire Transparent Conductive Electrodes for Enhanced Output Efficiency of Ultraviolet GaN-Based Light-Emitting Diodes. Materials 2024, 17, 5385. [Google Scholar] [CrossRef]
- Aslan, K.; Lakowicz, J.R.; Szmacinski, H.; Geddes, C.D. Metal-Enhanced Fluorescence Solution-Based Sensing Platform. J. Fluoresc. 2004, 14, 677–679. [Google Scholar] [CrossRef]
- Akhtar, S.; Shafeeq, S.; Siddique, A.B.; Sabei, F.Y.; Safhi, A.Y.; Ullah, S.; Abbas, A.; Hanbashi, A.; Alshahi, H.; Jali, A.M.; et al. Facile synthesis of bimetallic Ag-Fe core-shell nanoparticles for the selective and efficient dehydrogenation of formic acid. J. Power Sources 2025, 642, 236919. [Google Scholar] [CrossRef]
- Kanwal, M.; Sher, M.; Abbas, A.; Akhtar, S.; Siddique, A.B.; Hasan, M.N.U.; Assad, N.; Alhazmi, H.A.; Amin, H.M.A. Dual colorimetric sensing of Hg(II) and Fe(III) using sulfanilamide-stabilized silver nanoparticles and evaluating their photodegradation and antibacterial properties. J. Water Process Eng. 2025, 75, 107981. [Google Scholar] [CrossRef]
- Demishkevich, E.; Zyubin, A.; Seteikin, A.; Samusev, I.; Park, I.; Hwangbo, C.K.; Choi, E.H.; Lee, G.J. Synthesis Methods and Optical Sensing Applications of Plasmonic Metal Nanoparticles Made from Rhodium, Platinum, Gold, or Silver. Materials 2023, 16, 3342. [Google Scholar] [CrossRef] [PubMed]
- Khurana, K.; Jaggi, N. Localized Surface Plasmonic Properties of Au and Ag Nanoparticles for Sensors: A Review. Plasmonics 2021, 16, 981–999. [Google Scholar] [CrossRef]
- Lee, K.-S.; El-Sayed, M.A. Gold and Silver Nanoparticles in Sensing and Imaging: Sensitivity of Plasmon Response to Size, Shape, and Metal Composition. J. Phys. Chem. B 2006, 110, 19220–19225. [Google Scholar] [CrossRef]
- Stockman, M.I. The spaser as a nanoscale quantum generator and ultrafast amplifier. J. Opt. 2010, 12, 024004. [Google Scholar] [CrossRef]
- Suherman, A.L.; Zampardi, G.; Amin, H.M.A.; Young, N.P.; Compton, R.G. Tannic acid capped gold nanoparticles: Capping agent chemistry controls the redox activity. Phys. Chem. Chem. Phys. 2019, 21, 4444–4451. [Google Scholar] [CrossRef]
- Abbas, A.; Amin, H.; Akhtar, M.; Hussain, M.A.; Batchelor-McAuley, C.; Compton, R.G. Eco-friendly polymer succinate capping on silver nano-particles for enhanced stability: A UV-Vis and electrochemical particle impact study. Chem. Naissensis 2020, 3, 50–70. [Google Scholar] [CrossRef]
- Dridi, M.; Vial, A. Modeling of metallic nanostructures embedded in liquid crystals: Application to the tuning of their plasmon resonance. Opt. Lett. 2009, 34, 2652–2654. [Google Scholar] [CrossRef]
- Dridi, M.; Vial, A. FDTD modelling of gold nanoparticle pairs in a nematic liquid crystal cell. J. Phys. D Appl. Phys. 2010, 43, 415102. [Google Scholar] [CrossRef]
- Jain, P.K.; El-Sayed, M.A. Noble Metal Nanoparticle Pairs: Effect of Medium for Enhanced Nanosensing. Nano Lett. 2008, 8, 4347–4352. [Google Scholar] [CrossRef]
- Chau, Y.-F.; Yeh, H.-H. A comparative study of solid-silver and silver-shell nanodimers on surface plasmon resonances. J. Nanopart. Res. 2011, 13, 637–644. [Google Scholar] [CrossRef]
- Wang, L.; Hasanzadeh Kafshgari, M.; Meunier, M. Optical Properties and Applications of Plasmonic-Metal Nanoparticles. Adv. Funct. Mater. 2020, 30, 2005400. [Google Scholar] [CrossRef]
- Zhang, P.; De Haan, L.T.; Debije, M.G.; Schenning, A.P.H.J. Liquid crystal-based structural color actuators. Light Sci. Appl. 2022, 11, 248. [Google Scholar] [CrossRef] [PubMed]
- Nam, S.; Wang, D.; Kwon, C.; Han, S.H.; Choi, S.S. Biomimetic Multicolor-Separating Photonic Skin using Electrically Stretchable Chiral Photonic Elastomers. Adv. Mater. 2023, 35, 2302456. [Google Scholar] [CrossRef] [PubMed]
- Ye, L.; Liu, B.; Li, F.; Feng, Y.; Cui, Y.; Lu, Y. The influence of Ag nanoparticles on random laser from dye-doped nematic liquid crystals. Laser Phys. Lett. 2016, 13, 105001. [Google Scholar] [CrossRef]
- Fuh, A.Y.-G.; Lin, C.-Y.; Li, M.-S.; Lin, H.-C. Optical Kerr constant of liquid crystals with gold-nanoparticle-doped alignment films. J. Phys. D Appl. Phys. 2012, 45, 445104. [Google Scholar] [CrossRef]
- Coursault, D.; Grand, J.; Zappone, B.; Ayeb, H.; Lévi, G.; Félidj, N.; Lacaze, E. Linear Self-Assembly of Nanoparticles Within Liquid Crystal Defect Arrays. Adv. Mater. 2012, 24, 1461–1465. [Google Scholar] [CrossRef]
- Xie, J.; Zhang, X.; Peng, Z.; Wang, Z.; Wang, T.; Zhu, S.; Wang, Z.; Zhang, L.; Zhang, J.; Yang, B. Low Electric Field Intensity and Thermotropic Tuning Surface Plasmon Band Shift of Gold Island Film by Liquid Crystals. J. Phys. Chem. C 2012, 116, 2720–2727. [Google Scholar] [CrossRef]
- Wang, S.; Lipchus, E.J.; Gharbi, M.A.; Yelleswarapu, C.S. Polarization Z-Scan Studies Revealing Plasmon Coupling Enhancement Due to Dimer Formation of Gold Nanoparticles in Nematic Liquid Crystals. Micromachines 2023, 14, 2206. [Google Scholar] [CrossRef]
- Taflove, A. Computational electromagnetics: The finite difference time domain method. In The Electrical Engineering Handbook; Elsevier: Amsterdam, The Netherlands, 2005. [Google Scholar]
- Tira, C.; Tira, D.; Simon, T.; Astilean, S. Finite-Difference Time-Domain (FDTD) design of gold nanoparticle chains with specific surface plasmon resonance. J. Mol. Struct. 2014, 1072, 137–143. [Google Scholar] [CrossRef]
- Myroshnychenko, V.; Rodríguez-Fernández, J.; Pastoriza-Santos, I.; Funston, A.M.; Novo, C.; Mulvaney, P.; Liz-Marzán, L.M.; García De Abajo, F.J. Modelling the optical response of gold nanoparticles. Chem. Soc. Rev. 2008, 37, 1792–1805. [Google Scholar] [CrossRef]
- Wang, H.; Vial, A. Tunability of LSPR using gold nano-particles embedded in a liquid crystal cell. J. Quant. Spectrosc. Radiat. Transf. 2014, 146, 492–498. [Google Scholar] [CrossRef]
- Chen, H.; Shao, L.; Li, Q.; Wang, J. Gold nanorods and their plasmonic properties. Chem. Soc. Rev. 2013, 42, 2679–2724. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shang, Z.; Zhang, G.; Liu, X.; Huang, H. Optical Property Simulations of Gold and Silver Nanostructured Arrays Within a Liquid Crystal Environment. Materials 2025, 18, 4046. https://doi.org/10.3390/ma18174046
Shang Z, Zhang G, Liu X, Huang H. Optical Property Simulations of Gold and Silver Nanostructured Arrays Within a Liquid Crystal Environment. Materials. 2025; 18(17):4046. https://doi.org/10.3390/ma18174046
Chicago/Turabian StyleShang, Zhenzhen, Guoting Zhang, Xiaoying Liu, and Haishen Huang. 2025. "Optical Property Simulations of Gold and Silver Nanostructured Arrays Within a Liquid Crystal Environment" Materials 18, no. 17: 4046. https://doi.org/10.3390/ma18174046
APA StyleShang, Z., Zhang, G., Liu, X., & Huang, H. (2025). Optical Property Simulations of Gold and Silver Nanostructured Arrays Within a Liquid Crystal Environment. Materials, 18(17), 4046. https://doi.org/10.3390/ma18174046






