Testing the Potential of Magnetic Resonance Dosimetry: The Case of Lithium Carbonate
Highlights
- Lithium carbonate Li2CO3;
- Gamma irradiation;
- Electron paramagnetic resonance (EPR);
- Nuclear magnetic resonance (NMR);
- Paramagnetic defects;
- Testing material for gamma-radiation dosimetry.
Abstract
1. Introduction
2. Materials and Methods
3. Results and Discussion
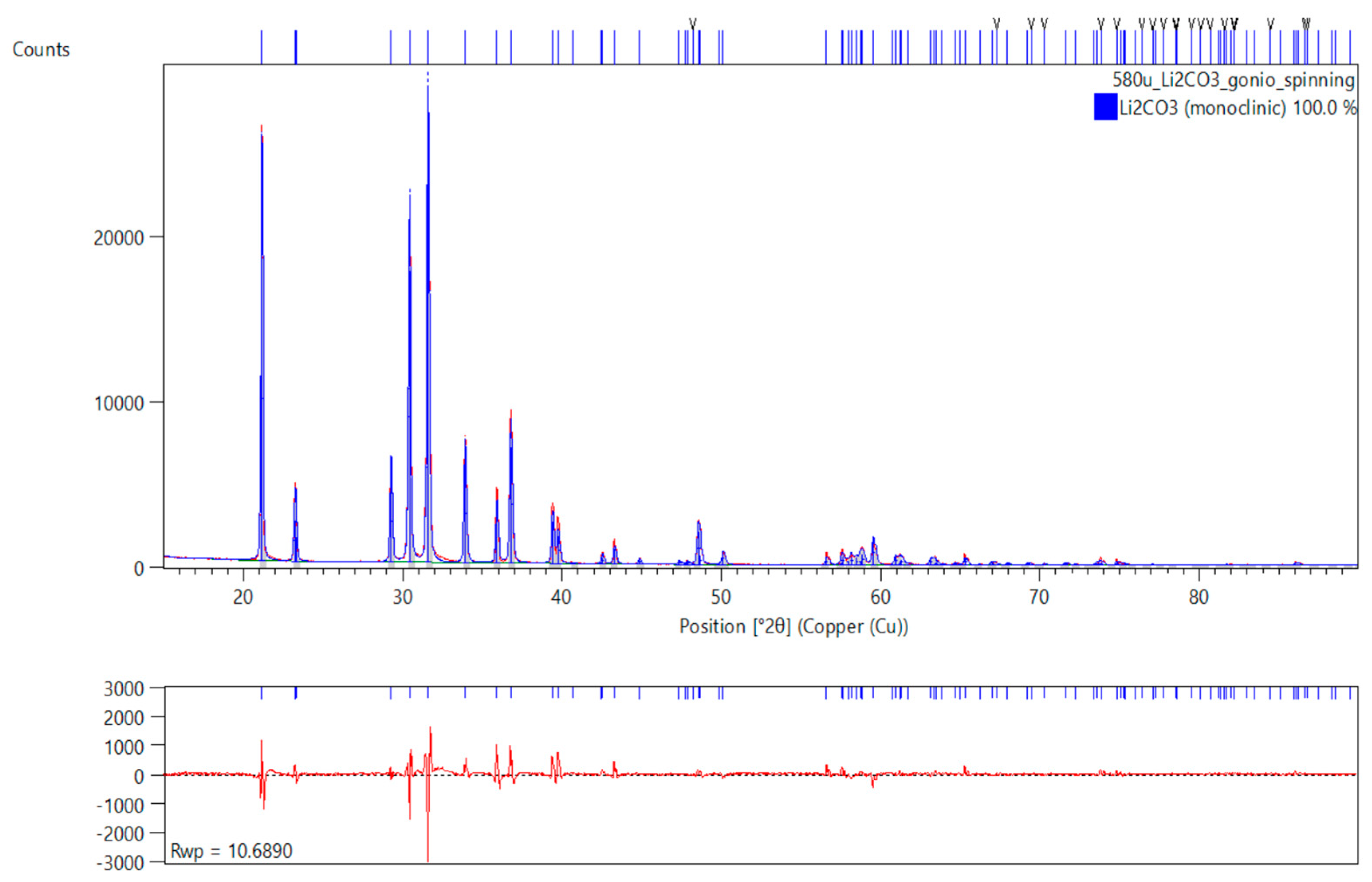
3.1. XRD Data
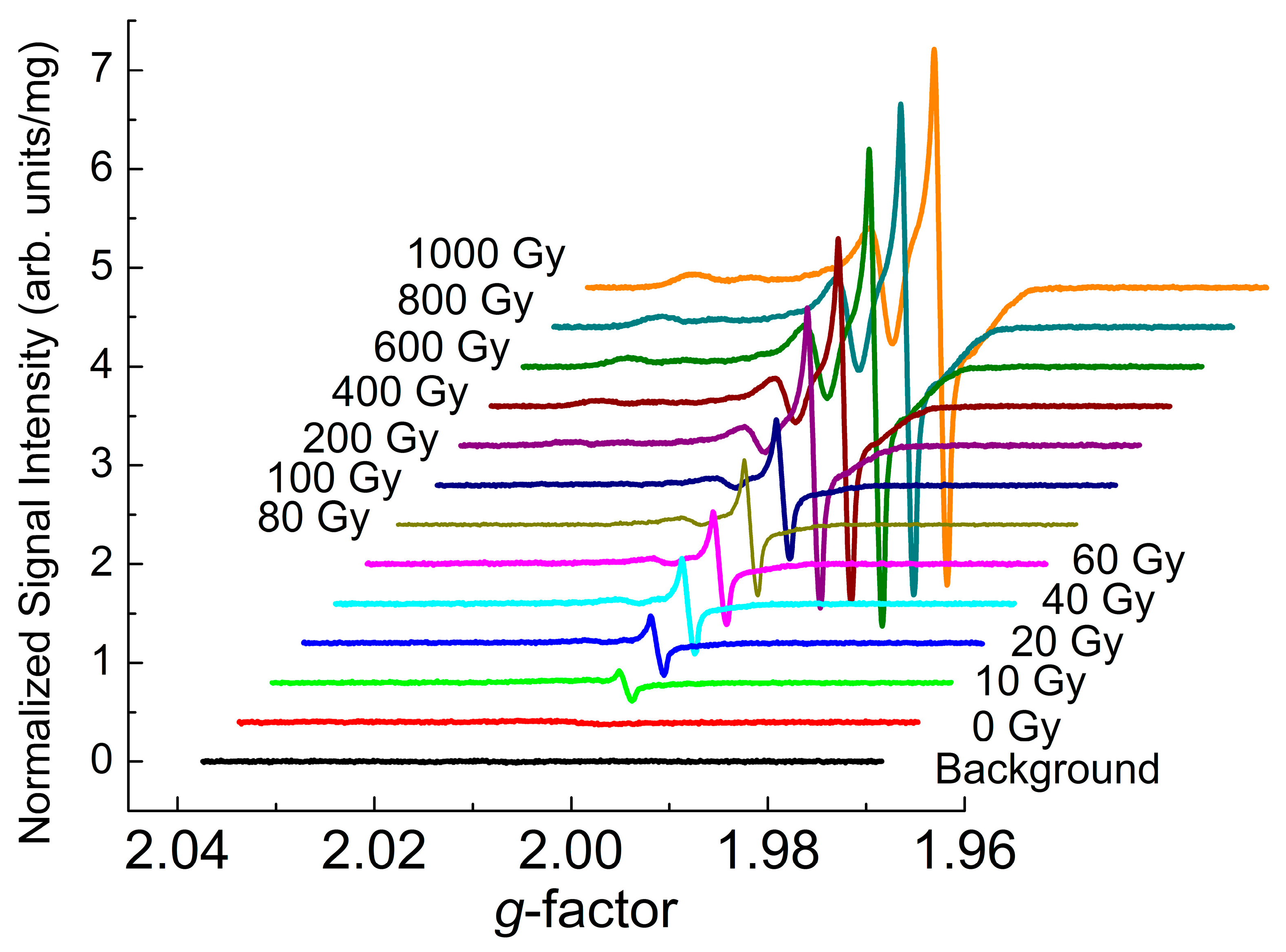
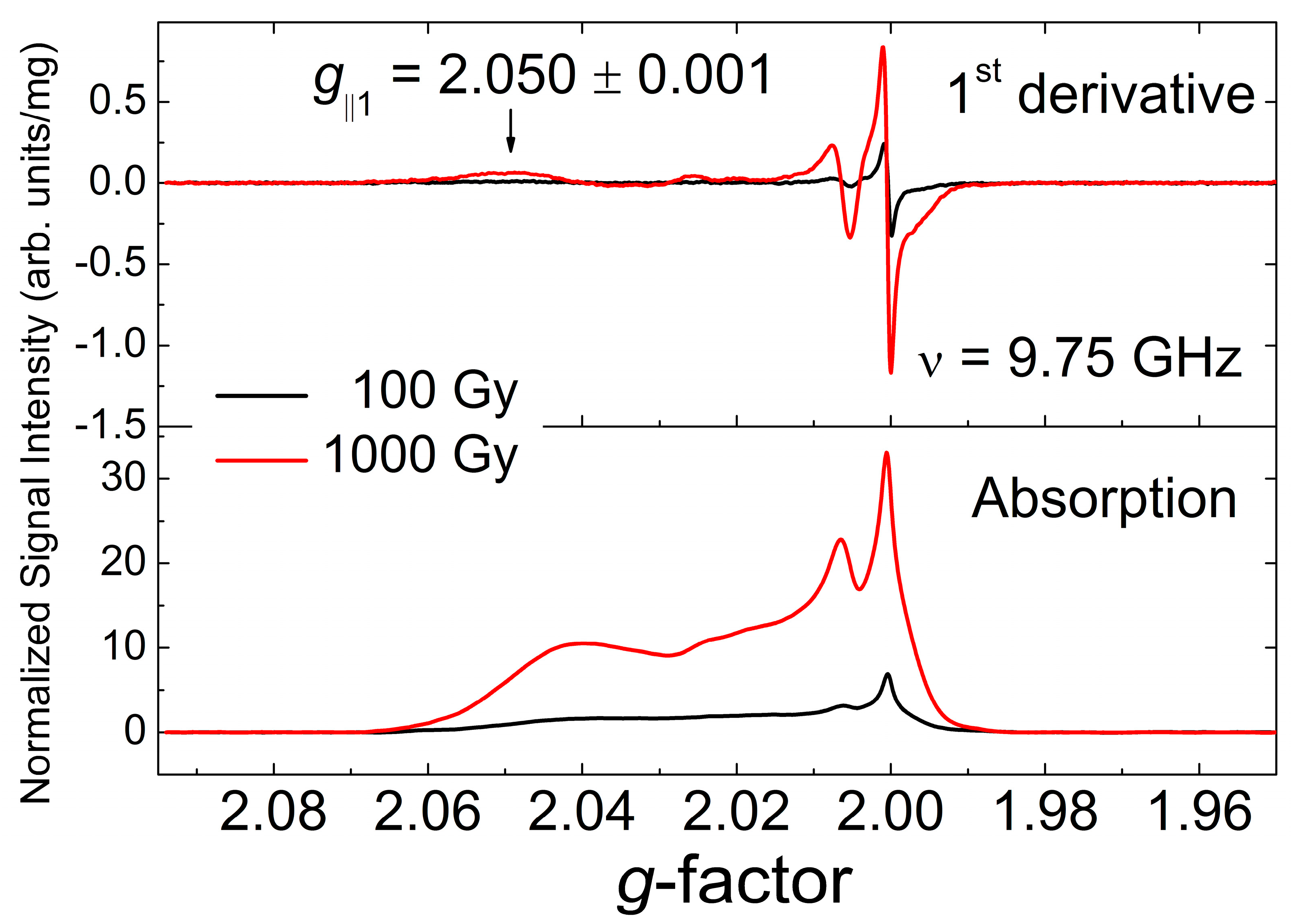
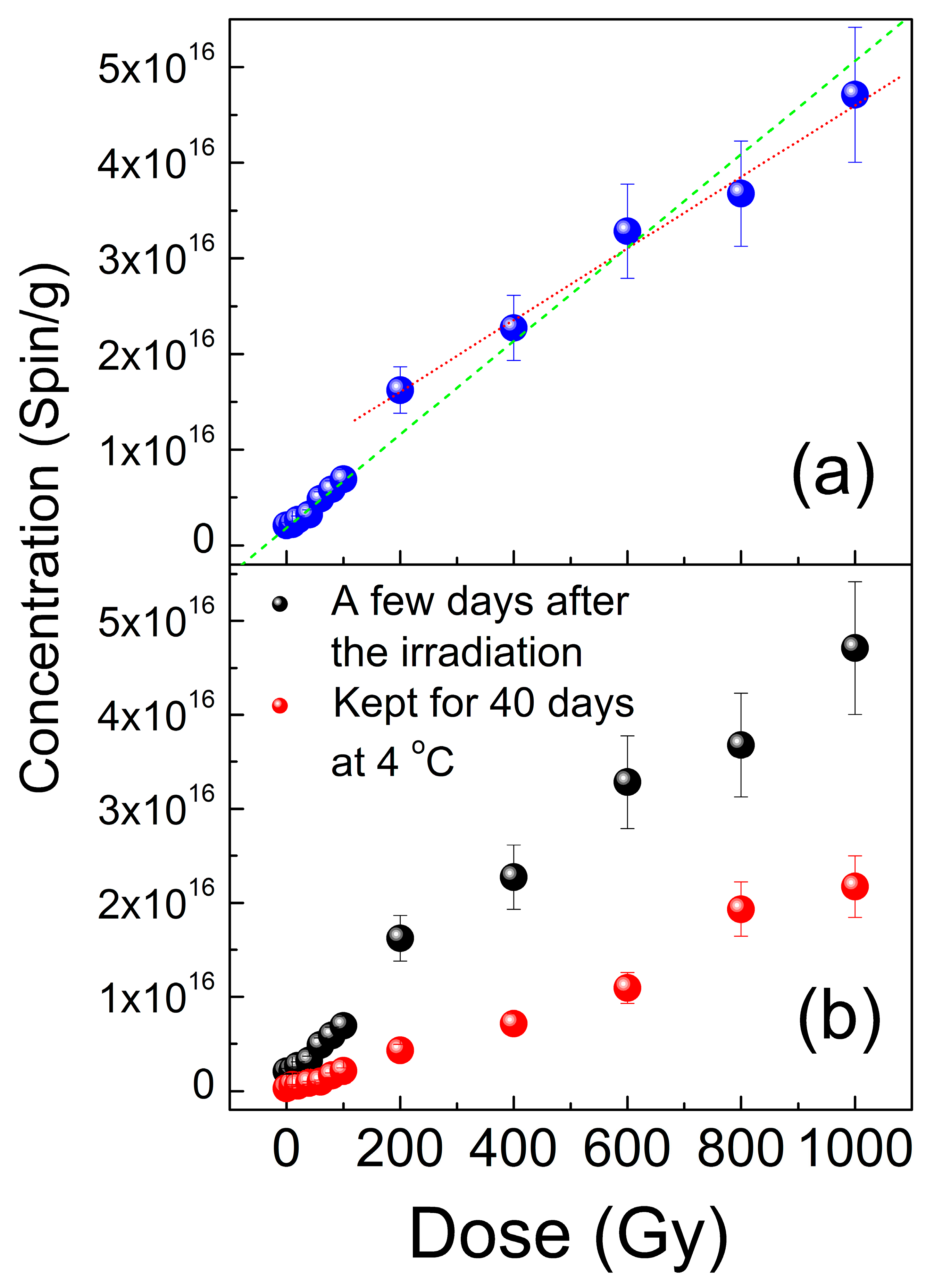
3.2. EPR Data
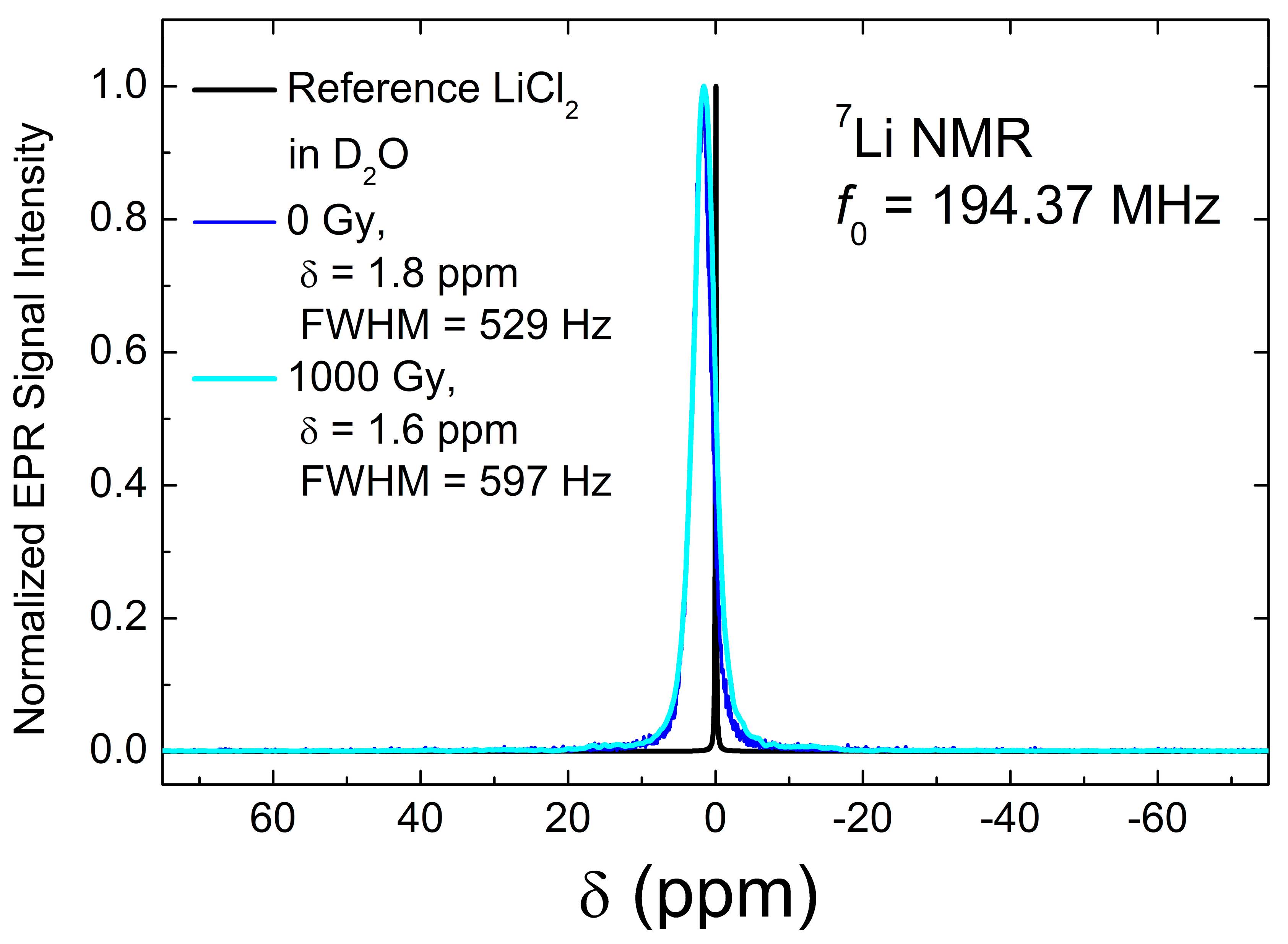
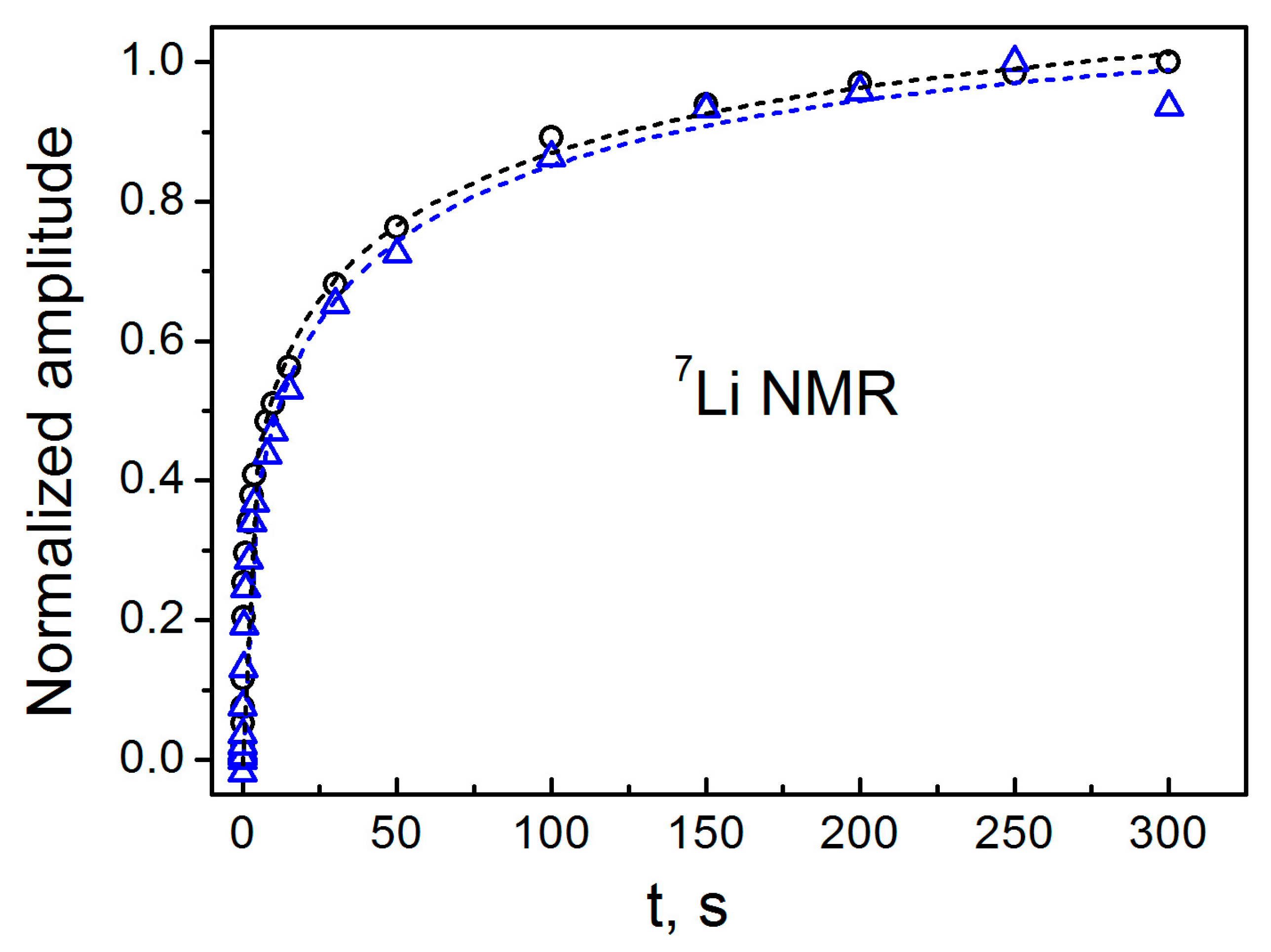
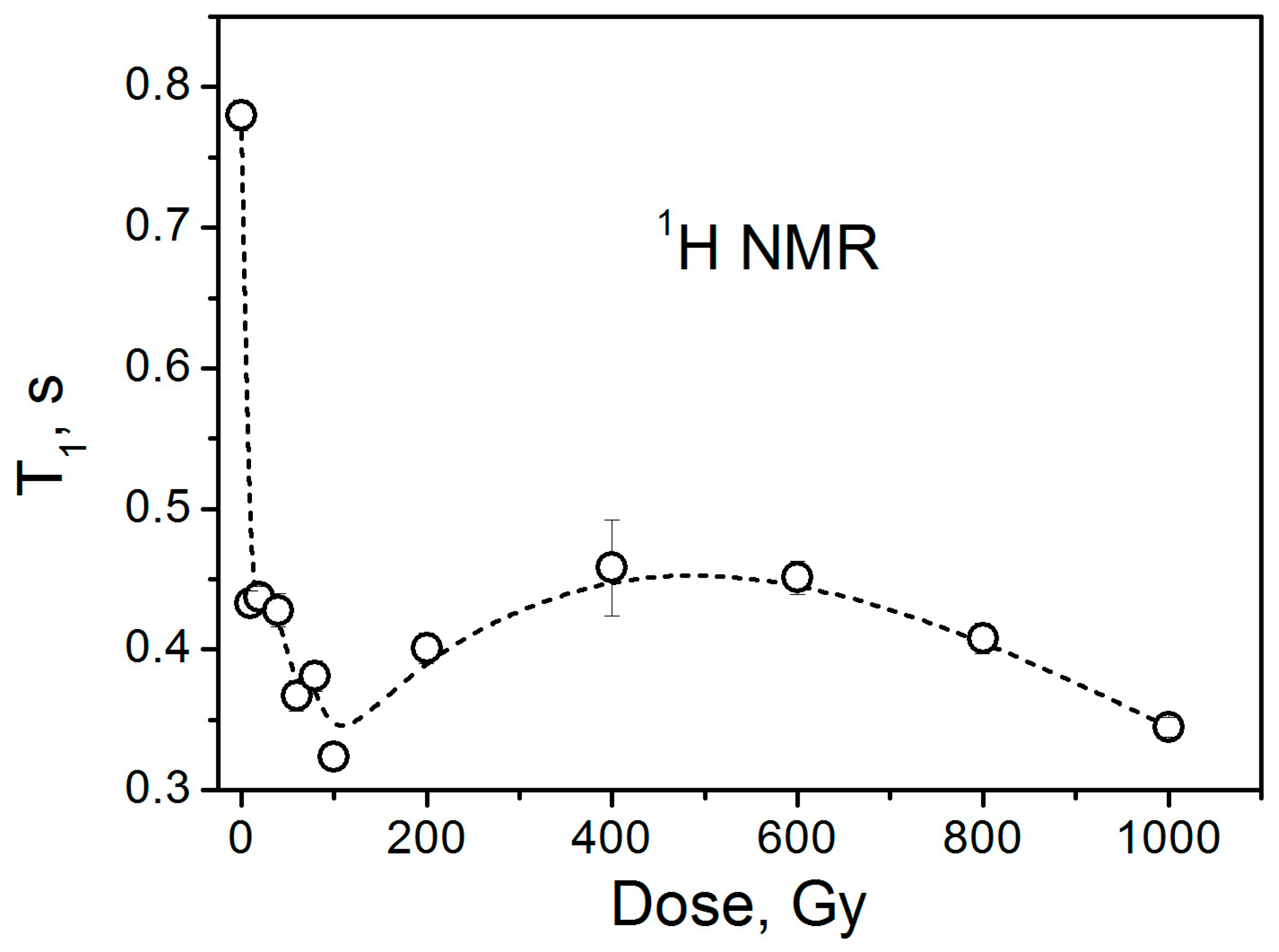
3.3. NMR Data
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Gordy, W. Theory and Applications of Electron Spin Resonance; Wiley: New York, NY, USA, 1980. [Google Scholar]
- Livingston, R. The Potentialities and Limitations of the Paramagnetic Resonance Method in Radiation Research. In Radiation Research Supplement, Vol. 1, Proceedings of the International Congress of Radiation Research, Burlington, VT, USA, 11–15 August 1958; Radiation Research Society: Bozeman, MT, USA, 1959; pp. 463–478. [Google Scholar] [CrossRef]
- Sastry, M.D.; Natarajan, V.; Bhatt, B.C. Electron paramagnetic resonance technique for radiation dosimetry: Emerging trends for laboratory and accidental dosimetry. J. Med. Phys. 1996, 21, 201–207. [Google Scholar] [CrossRef]
- Regulla, D.F.; Deffner, U. Dosimetry by ESR spectroscopy of alanine. Int. J. Appl. Radiat. Isot. 1982, 33, 1101–1114. [Google Scholar] [CrossRef]
- Morton, J.R.; Ahlers, F.J.; Schneider, C.C.J. ESR dosimetry with magnesium sulphate. Rad. Prot. Dosim. 1993, 47, 263–266. [Google Scholar] [CrossRef]
- Ke, W.; Cunpu, S.; Jianbo, C.; Bingzhi, M. Dose estimation of tooth enamel by ESR detection for 11 residents near Chernobyl reactor. Chin. J. Radiol. Med. Prot. 1996, 16, 2–4. [Google Scholar]
- Pass, B.; Shames, A.I. Signal processing for radiation dosimetry using EPR in dental enamel: Comparison of three methods. Radiat. Meas. 2000, 32, 163–167. [Google Scholar] [CrossRef]
- Wieser, A.; Mehta, K.; Amira, S.; Aragno, D.; Bercea, S.; Brik, A.; Bugai, A.; Callens, F.; Chumak, V.; Ciesielski, B.; et al. The second international intercomparison on EPR tooth dosimetry. Radiat. Meas. 2000, 32, 549–557. [Google Scholar] [CrossRef]
- Pass, B.; Shames, A.I. International intercomparisons on EPR tooth dosimetry to assess accuracy and consistency among laboratories. Oral Surg. Oral Med. Oral Pathol. Oral Radiol. Endodontol. 2004, 97, 263–265. [Google Scholar] [CrossRef]
- Wieser, A.; Debuyst, R.; Fattibene, P.; Meghzifene, A.; Onori, S.; Bayankin, S.N.; Blackwell, B.; Brik, A.; Bugay, A.; Chumak, V.; et al. The 3rd international intercomparison on EPR tooth dosimetry: Part 1, general analysis. Appl. Radiat. Isot. 2005, 62, 163–171. [Google Scholar] [CrossRef] [PubMed]
- Fattibene, P.; Callens, F. EPR dosimetry with toot henamel: A review. Appl. Radiat. Isot. 2010, 68, 2033–2116. [Google Scholar] [CrossRef]
- Murali, S.; Natarajan, V.; Venkataramani, R.; Pushparaja Sastry, M.D. ESR dosimetry using inorganic materials: A case study of Li2CO3 and CaSO4:Dy as prospective dosimeters. Appl. Radiat. Isot. 2001, 55, 253–258. [Google Scholar] [CrossRef]
- Marrale, M.; Abbene, L.; d’Errico, F.; Gallo, S.; Longo, A.; Panzeca, S.; Tana, L.; Tranchina, L.; Principato, F. Characterization of the ESR response of alanine dosimeters to low energy Cu-target X-tube photons. Radiat. Measur. 2017, 106, 200–204. [Google Scholar] [CrossRef]
- Gallo, S.; Iacoviello, G.; Panzeca, S.; Veronese, I.; Bartolotta, A.; Dondi, D.; Gueli, A.M.; Loi, G.; Longo, A.; Mones, E.; et al. Characterization of phenolic pellets for ESR dosimetry in photon beam radiotherapy. Radiat. Environ. Biophys. 2017, 56, 471–480. [Google Scholar] [CrossRef]
- Romanyukha, A.; Consani, K.; Tolmachev, S. Variability of radiation doses reconstructed by EPR in teeth of former United States nuclear workers. Int. J. Radiat. Biol. 2025, 1–6. [Google Scholar] [CrossRef] [PubMed]
- Ciesielski, B.; Marciniak, A.; Juniewicz, M. Retrospective EPR dosimetry in glass and tooth enamel—The methodology and results of MUG group in RENEB 2021 inter-laboratory comparison. Radiat. Meas. 2024, 174, 107109. [Google Scholar] [CrossRef]
- Kim, J.S.; Park, B.R.; Kim, H.S.; Eo, I.M.; Yoo, J.; Jang, W.I.; Cho, M.; Kim, H.; Kim, Y.K. X-band EPR dosimetry using minimum mass of tooth enamel for use in radiological accidents. Nucl. Engin. Technol. 2024, 56, 123–131. [Google Scholar] [CrossRef]
- Panda, M.; Joshi, S.; Annalakshmi, O.; Srinivas, V.C.; Venkatraman, B. Spectroscopic and dosimetric comparison of tooth enamel separation methods for EPR retrospective dosimetry. Heliyon 2024, 10, e30571. [Google Scholar] [CrossRef]
- Yalvac, B.; Reulens, N.; Reniers, B. Early results of a remote dosimetry audit program for lung stereotactic body radiation therapy. Phys. Imaging Radiat. Oncol. 2024, 29, 100544. [Google Scholar] [CrossRef]
- Murali, S.; Sarma, K.S.S.; Natarajan, V.; Venkataramani, R.; Pushparaja Sastry, M.D. Alanine—ESR dosimeter: Application for dosimetry in Industrial Electron Beam Accelerator. J. Radiat. Protect. Environ. 2000, 23, 164–169. [Google Scholar]
- Nagy, V.; Sholom, S.V.; Chumak, V.V.; Desrosiers, M.F. Uncertainties in alanine dosimetry in the therapeutic dose range. Appl. Radiat. Isot. 2002, 56, 917–929. [Google Scholar] [CrossRef]
- De Angelis, C.; De Coste, V.; Fattibene, P.; Onori, S.; Petetti, E. Use of alanine for dosimetry intercomparisons among Italian radiotherapy centers. Appl. Radiat. Isot. 2005, 62, 261–265. [Google Scholar] [CrossRef]
- Bergstrand, E.S.; Bjerke, H.; Hole, E.O. An experimental investigation of the electron energy dependence of the EPR alanine dosimetry system. Radiat. Meas. 2005, 39, 21–28. [Google Scholar] [CrossRef]
- Chu, S.; Wieser, A.; Feist, H.; Regular, D.F. ESR/Alanine Dosimetry of High-energy Electrons in Radiotherapy. Appl. Radiat. Isot. 1989, 40, 993–996. [Google Scholar] [CrossRef]
- Olsen, K.J.; Hansen, J.W.; Wille, M. Response of the alanine radiation dosimeter to high-energy photon and electron beams. Phys. Med. Biol. 1990, 35, 43–52. [Google Scholar] [CrossRef]
- Ahlers, F.J.; Schneider, C.C.J. Alanine ESR dosimetry: An assessment of peak-to-peak evaluation. Radiat. Prot. Dosim. 1991, 37, 117–122. [Google Scholar]
- Bartolotta, A.; Fattibene, P.; Onori, S.; Pantaloni, M.; Petetti, E. Sources of uncertainty in therapy level alanine dosimetry. Appl. Radiat. Isot. 1993, 44, 13–17. [Google Scholar] [CrossRef]
- Feist, H.; Regulla, D.; Wieser, A. Is alanine ESR dosimetry now an alternative to ferrous sulfate dosimetry? Appl. Radiat. Isot. 1993, 44, 47–51. [Google Scholar] [CrossRef]
- Gall, K.; Desrosiers, M.; Bensen, D.; Serago, C. Alanine EPR dosimeter response in proton therapy beams. Appl. Radiat. Isot. 1996, 47, 1197–1199. [Google Scholar] [CrossRef]
- Gao, J.; Zaiyong, W. The extension of the range of NIM alanine/ESR dosimetric system to therapy level. Appl. Radiat. Isot. 1996, 47, 1193–1196. [Google Scholar] [CrossRef] [PubMed]
- Mehta, K.; Girzikowsky, R. Alanine-ESR dosimetry for radiotherapy: IAEA experience. Appl. Radiat. Isot. 1996, 47, 1189–1191. [Google Scholar] [CrossRef]
- Nagy, V.Y.; Desrosiers, M.F. Complex time dependence of the EPR signal of irradiated L-a-alanine. Appl. Radiat. Isot. 1996, 47, 789–793. [Google Scholar] [CrossRef]
- Onori, S.; D’Errico, F.; De Angelis, C.; Egger, E.; Fattibene, P.; Janowsky, I. Proton response of alanine-based pellets and films. Appl. Radiat. Isot. 1996, 47, 1201–1204. [Google Scholar] [CrossRef]
- Onori, S.; D’Errico, F.; De Angelis, C.; Egger, E.; Fattibene, P.; Janovsky, I. Alanine dosimetry of proton therapy beams. Med. Phys. 1997, 24, 447–453. [Google Scholar] [CrossRef] [PubMed]
- Rakvin, B. Improvement of sensitivity in the alanine/ESR dosimetry. Appl. Radiat. Isot. 1996, 47, 525–528. [Google Scholar] [CrossRef]
- Ruckerbauer, F.; Sprunck, M.; Regulla, D.F. Numerical signal treatment for optimized alanine/ESR dosimetry in the therapy-level dose range. Appl. Radiat. Isot. 1996, 47, 1263–1268. [Google Scholar] [CrossRef]
- Sharpe, P.H.G.; Rajendran, K.; Sephton, J.P. Progress towards an alanine/ESR therapy level reference dosimetry service at NPL. Appl. Radiat. Isot. 1996, 47, 1171–1175. [Google Scholar] [CrossRef] [PubMed]
- Haskell, E.H.; Hayes, R.B.; Kenner, G.H. A high sensitivity EPR technique for alanine dosimetry. Radiat. Prot. Dosim. 1998, 77, 43–49. [Google Scholar] [CrossRef]
- Fainstein, C.; Winkler, E.; Saravi, M. ESR/alanine gamma-dosimetry in the 10–30 Gy range. Appl. Radiat. Isot. 2000, 52, 1195–1196. [Google Scholar] [CrossRef]
- De Angelis, C.; Mattacchioni, A.; Onori, S.; Aragno, D.; De Paula, U.; Panichelli, V. Electron arc therapy treatment planning verification with alanine/EPR dosimetry. Appl. Radiat. Isot. 2000, 52, 1203–1207. [Google Scholar] [CrossRef]
- Hayes, R.B.; Haskell, E.H.; Wieser, A.; Romanyukha, A.A.; Hardy, B.L.; Barrus, J.K. Assessment of an alanine EPR dosimetry technique with enhanced precision and accuracy. Nucl. Instrum. Methods Phys. Res. Sect. A 2000, 440, 453–461. [Google Scholar] [CrossRef]
- Nagy, V.; Puhl, J.M.; Desrosiers, M.F. Advancements in accuracy of the alanine dosimetry system. Part 2. The influence of the irradiation temperature. Radiat. Phys. Chem. 2000, 57, 1–9. [Google Scholar] [CrossRef]
- Nagy, V.; Sleptchonok, O.F.; Desrosiers, M.F.; Weber, R.T.; Heiss, A.H. Advancements in accuracy of the alanine EPR dosimetry system. Part III: Usefulness of an adjacent reference sample. Radiat. Phys. Chem. 2000, 59, 429–441. [Google Scholar] [CrossRef]
- Sleptchonok, O.F.; Nagy, V.; Desrosiers, M.F. Advancements in accuracy of the alanine dosimetry system. Part 1. The effects of environmental humidity. Radiat. Phys. Chem. 2000, 57, 115–133. [Google Scholar] [CrossRef]
- Anton, M.; Kapsch, R.P.; Krauss, A.; von Voigts-Rhetz, P.; Zink, K.; McEwen, M. Difference in the relative response of the alanine dosimeter to megavoltage x-ray and electron beams. Phys. Med. Biol. 2013, 58, 3259–3282. [Google Scholar] [CrossRef]
- Mierzwinska, G.; Michalec, B.; Oglodek, I.; Petelenzi, B.; Waligorski, M.P.R. Alanine/EPR dosimetry as a potential tool for quality assistance in proton beam radiotherapy. Rom. Rep. Phys. 2014, 66, 54–60. [Google Scholar]
- Michalec, B.; Mierzwińska, G.; Sowa, U.; Ptaszkiewicz, M.; Nowak, T.; Swakoń, J. Alanine dosimetry of 60 MeV proton beam—Preliminary results. Nucleonika 2012, 57, 503–506. [Google Scholar]
- Gu, R.; Wang, J.; Wang, P.; Mao, X.; Lin, B.; Tan, W.; Du, X.; Gao, F.; Wang, T. Alanine/electron spin resonance dosimetry for FLASH radiotherapy. Radiat. Phys. Chem. 2024, 225, 112113. [Google Scholar] [CrossRef]
- Höfel, S.; Liebig, P.; Fix, M.K.; Drescher, M.; Zwicker, F. Adapting a practical EPR dosimetry protocol to measure output factors in small fields with alanine. J. Appl. Clin. Med. Phys. 2023, 24, e14191. [Google Scholar] [CrossRef]
- Michalec, B.; Stolarczyk, L.; Bassler, N.; Rydygier, M.; Spaleniak, A.; Kopec, R. Alanine dosimeters for LET measurement in proton radiotherapy. Radiat. Meas. 2024, 175, 107150. [Google Scholar] [CrossRef]
- Herrera, E.; Urena-Nunez, F.; Delfın Loya, A. Lithium carbonate (Li2CO3) as a material for thermal neutron fluence measurements. Appl. Radiat. Isot. 2005, 63, 241–246. [Google Scholar] [CrossRef]
- Popoca, R.; Urena-Nunez, F. Dosimetric evaluation of lithium carbonate (Li2CO3) as a dosemeter for gamma-radiation dose measurements. Radiat. Protect. Dosim. 2009, 134, 102–106. [Google Scholar] [CrossRef] [PubMed]
- Rech, A.B.; Kinoshita, A.; Donate, P.M.; Baffa, O. ESR dosimetry with lithium, potassium, and sodium compounds. Appl. Radiat. Isot. 2022, 181, 110105. [Google Scholar] [CrossRef] [PubMed]
- Bailiff, I.K.; Sholom, S.; McKeever, S.W.S. Retrospective and emergency dosimetry in response to radiological incidents and nuclear mass-casualty events: A review. Radiat. Meas. 2016, 94, 83–139. [Google Scholar] [CrossRef]
- Swartz, H.M.; Williams, B.B.; Zaki, B.I.; Hartford, A.C.; Jarvis, L.A.; Chen, E.; Comi, R.J.; Ernstoff, M.S.; Hou, H.; Khan, N.; et al. Clinical EPR: Unique Opportunities and Some Challenges. Acad. Radiol. 2014, 21, 197–206. [Google Scholar] [CrossRef] [PubMed]
- Koo, C.U.; Oh, J.; Choi, K.; Ye, S.J. Wearable Resonator for In Vivo Electron Paramagnetic Resonance Tooth Dosimetry. Appl. Magn. Reson. 2025, 56, 887–902. [Google Scholar] [CrossRef]
- Drager, E.; Roberts, K.; Decker, R.D.; Bahar, N.; Wilson, L.D.; Contessa, J.; Husain, Z.; Williams, B.; Flood, A.B.; Swartz, H.M.; et al. In Vivo Verification of Electron Paramagnetic Resonance Biodosimetry Using Patients Undergoing Radiation Therapy Treatment. Int. J. Radiat. Oncol. Biol. Phys. 2024, 119, 292–301. [Google Scholar] [CrossRef] [PubMed]
- Abragam, A. The Principles of Nuclear Magnetism; Oxford University Press: Oxford, UK, 1961. [Google Scholar]
- Goldman, M. Spin Temperature and Nuclear Magnetic Resonance in Solids; Oxford University Press: Oxford, UK, 1970. [Google Scholar]
- Shames, A.I.; Panich, A.M.; Porro, S.; Rovere, M.; Musso, S.; Tagliaferro, A.; Baidakova, M.V.; Osipov, V.Y.; Vul’, A.Y.; Enoki, T.; et al. Defects localization and nature in bulk and thin film utrananocrystalline diamond. Diamond Relat. Mater. 2007, 16, 1806–1812. [Google Scholar] [CrossRef]
- Gore, J.C.; Kang, Y.S.; Schulz, R.J. Measurement of radiation dose distributions by nuclear magnetic resonance (NMR) imaging. Phys. Med. Biol. 1984, 29, 1189–1197. [Google Scholar] [CrossRef]
- Appleby, A.; Christman, E.A.; Leghrouz, A. Imaging of spatial radiation dose distribution in agarose gels using magnetic resonance. Med. Phys. 1986, 14, 382–384. [Google Scholar] [CrossRef]
- Schulz, R.J.; de Guzman, A.F.; Nguyen, D.B.; Gore, J.C. Dose-response curves for Fricke-infused agarose gels as obtained by nuclear magnetic resonance. Phys. Med. Biol. 1990, 35, 1611–1622. [Google Scholar] [CrossRef]
- Audet, C.; Schreiner, L.J. Radiation dosimetry by NMR relaxation time measurements of irradiated polymer solutions. In Proceedings of the International Society for Magnetic Resonance in Medicine, Tenth Annual Meeting, San Francisco, CA, USA, 10–16 August 1991; p. 705. [Google Scholar]
- Maryanski, M.J.; Gore, J.C.; Kennen, R.P.; Schulz, R.J. NMR Relaxation enhancement in gels polymerized and cross-linked by ionizing radiation: A new approach to 3D dosimetry by MRI. Magn. Reson. Imaging 1993, 11, 253–258. [Google Scholar] [CrossRef]
- Pereira, E.L.M.; Cardoso, G.P.; Gontijo, R.M.G.; Oliveira, A.H.; Batista, A.S.M. Evaluation of the radioinduced alteration of gel compound relaxation times obtained by MRI for application as dosimetric system. In Proceedings of the ISSSD 2019, Zacatecas, Mexico, 7–11 October 2019; Volume 2, pp. 224–233. [Google Scholar]
- McJury, M.; Oldham, M.; Cosgrove, V.P.; Murthy, P.S.; Doran, S.; Leach, M.O.; Webb, S. Radiation dosimetry using polymer gels: Methods and applications. Br. J. Radiol. 2000, 73, 919–929. [Google Scholar] [CrossRef] [PubMed]
- Locarno, S.; Gallo, S.; Arosio, P.; Biordi, C.; Dallasega, D.; Gargano, M.; Ludwig, N.; Orsini, F.; Pignoli, E.; Veronese, I.; et al. Dosimetric Double Network Hydrogel Based on Poly(vinyl-alcohol)/Phenylalanine-Derivatives with Enhanced Mechanical Properties. ACS Appl. Polym. Mater. 2023, 5, 1902–1914. [Google Scholar] [CrossRef]
- De Deene, Y.; Jirasek, A. Gel dosimetry: An overview of dosimetry systems and readout methods. Radiat. Meas. 2024, 179, 107321. [Google Scholar] [CrossRef]
- Lepage, M.; Whittaker, A.K.; Rintoul, L.; Baldock, C. 13C-NMR, 1H-NMR, and FT-Raman Study of Radiation-Induced Modifications in Radiation Dosimetry Polymer Gels. J. Appl. Polym. Sci. 2001, 79, 1572–1581. [Google Scholar] [CrossRef]
- Schreiner, L.J. NMR mechanisms in gel dosimetry. J. Phys. Conf. Ser. 2009, 164, 012032. [Google Scholar] [CrossRef]
- Back, S.A.J.; Lepage, M.; Baldock, C. Investigation of the NMR relaxation rate dose-response of a ceric sulphate dosimeter. Appl. Radiat. Isot. 2002, 56, 895–899. [Google Scholar] [CrossRef]
- Baldock, C. Review of gel dosimetry: A personal reflection. J. Phys. Conf. Ser. 2017, 777, 012029. [Google Scholar] [CrossRef]
- De Deene, Y. Radiation Dosimetry by Use of Radiosensitive Hydrogels and Polymers: Mechanisms, State-of-the-Art and Perspective from 3D to 4D. Gels 2022, 8, 599. [Google Scholar] [CrossRef]
- Marrale, M.; d’Errico, F. Hydrogels for Three-Dimensional Ionizing-Radiation Dosimetry. Gels 2021, 7, 74. [Google Scholar] [CrossRef]
- Moftah, B.; Rabaeh, K.A.; Moussa, A.A.; Kafi, M.A.A.; Issa, A.S.B. Magnetic properties of polymeric acrylic acid hydrogel dosimeter for radiotherapy applications. Sci. Rep. 2025, 15, 13178. [Google Scholar] [CrossRef] [PubMed]
- Furman, G.B.; Goren, S.D.; Panich, A.M.; Shames, A.I. Spin Diffusion and Nuclear Spin-Lattice Relaxation in Irradiated Solids: A multiple-pulse NQR study. Solid. State Nucl. Magn. Reson. 1999, 14, 145–155. [Google Scholar] [CrossRef]
- Hart, E.J. Radiation chemistry of aqueous ferrous sulfate-cupric sulfate solutions; effect of gamma-rays. Radiat. Res. 1955, 2, 33–46. [Google Scholar] [CrossRef]
- Fricke, H.; Hart, E.J. Radiation Dosimetry; Attix, F.H., Roesch, W.C., Tochilin, E., Eds.; Academic Press: New York, NY, USA, 1966; p. 167. [Google Scholar]
- Osipov, V.Y.; Shames, A.I.; Enoki, T.; Takai, K.; Baidakova, M.V.; Vul, A.Y. Paramagnetic defects and exchange coupled spins in pristine ultrananocrystalline diamonds. Diam. Relat. Mater. 2007, 16, 2035–2038. [Google Scholar] [CrossRef]
- Zemann, J. Die Kristallstruktur von Li2CO3. Acta Cryst. 1957, 10, 664–666. [Google Scholar] [CrossRef]
- Effenberger, H.; Zemann, J. Verfeinerung der Kristallstruktur des Lithiumkarbonates, Li2CO3. Zeit. Krist. 1979, 150, 133–138. [Google Scholar] [CrossRef]
- Callens, F.; Vanhaelewyn, G.; Matthys, P.; Boesman, E. EPR of Carbonate Derived Radicals: Applications in Dosimetry, Dating and Detection of Irradiated Food. Appl. Magn. Reson. 1998, 14, 235–254. [Google Scholar] [CrossRef]
- Schramm, D.U.; Rossi, A.M. EPR and ENDOR studies on CO2− radicals in γ-irradiated B-type carbonated apatites. Phys. Chem. Chem. Phys. 2000, 2, 1339–1343. [Google Scholar] [CrossRef]
- Callens, F.; Debuyst, R.; Dejehet, F.; Idrissi, S.; Moens, P. Location and motion of isotropic paramagnetic centers in synthetic monohydracalcite. Jpn. J. Appl. Phys. 1994, 33, 4044–4050. [Google Scholar] [CrossRef]
- Glinskaya, L.G.; Zanin, Y.N. Factors stabilizing the paramagnetic radicals CO2−, CO3−, and CO33− in natural carbonated apatites. J. Struct. Chem. 1998, 39, 671–686. [Google Scholar] [CrossRef]
- Hughes, R.C.; Soos, Z.G. EPR of CO2− defects in calcite: Motional and nonsecular contributions. J. Chem. Phys. 1970, 52, 6302–6310. [Google Scholar] [CrossRef]
- Sasakura, H.; Takeuchi, N.; Miyagi, M.; Matsuda, H.; Kami, H.; Nobusawa, T. Coloration of irradiated sodium-silicate glass containing impurities. Jpn. J. Appl. Phys. 1964, 3, 767–772. [Google Scholar] [CrossRef]
- Srinivas, B.; Rao, V.R.S. Physico-chemical and catalytic properties of gamma-irradiated lanthanum nickelate (LaNiO3). J. Rad. Nucl. Chem. 1996, 210, 3–14. [Google Scholar] [CrossRef]
- Alessi, A.; Agnello, S.; Buscarino, G.; Pan, Y.; Mashkovtsev, R.I. EPR on Radiation-Induced Defects in SiO2. In Applications of EPR in Radiation Research; Lund, A., Shiotani, M., Eds.; Springer: Heidelberg, Germany, 2014; Chapter 7; pp. 255–295. [Google Scholar]
- Pound, R.V. Nuclear Electric Quadrupole Interactions in Solids. Phys. Rev. 1950, 79, 685–702. [Google Scholar] [CrossRef]
- Andrew, E.R.; Tunstall, D.P. Spin-Lattice Relaxation in Imperfect Cubic Crystals and in Non-cubic Crystals. Proc. Phys. Soc. 1961, 78, 1. [Google Scholar] [CrossRef]
- Horvatić, M. Magnetic nuclear spin-lattice relaxation in NMR of orthorhombic crystals in the presence of strong quadrupole coupling. J. Phys. Condens. Matter 1992, 4, 5811–5824. [Google Scholar] [CrossRef]
- Auler, T.; Butaud, P.; Gillet, J.A. A fictitious-spin calculation of the nuclear magnetic relaxation of nuclei of spin I = 3/2 in the presence of strong quadrupole coupling. J. Phys. Condens. Matter 1996, 8, 6425–6434. [Google Scholar] [CrossRef]
- Phillips, J.C. Stretched exponential relaxation in molecular and electronic glasses. Rep. Prog. Phys. 1996, 59, 1133–1207. [Google Scholar] [CrossRef]
- Panich, A.M.; Shames, A.I.; Tsindlekht, M.I.; Osipov, V.Y.; Patel, M.; Savaram, K.; He, H. Structure and Magnetic Properties of Pristine and Fe-Doped Micro and Nanographenes. J. Phys. Chem. C 2016, 120, 3042–3053. [Google Scholar] [CrossRef]
- Panich, A.M. Nuclear magnetic resonance studies of nanodiamond surface modification. Diam. Relat. Mater. 2017, 79, 21–31. [Google Scholar] [CrossRef]
- Bloembergen, N. On the interaction of nuclear spins in a crystalline lattice. Physica 1949, 15, 386–426. [Google Scholar] [CrossRef]
- Blumberg, W.E. Nuclear spin–lattice relaxation caused by paramagnetic impurities. Phys. Rev. 1960, 119, 79–84. [Google Scholar] [CrossRef]
- Khutsishvili, G.R. Spin diffusion and nuclear magnetic relaxation in crystal with paramagnetic impurity. Sov. Phys. Usp. 1969, 11, 802–815. [Google Scholar] [CrossRef]
- Panich, A.M.; Teske, C.L.; Bensch, W. Nuclear spin diffusion in the semiconductor TlTaS3. Phys. Rev. B 2006, 73, 115209. [Google Scholar] [CrossRef]
- Panich, A.M. Proton spin diffusion in a nanodiamond. J. Phys. Condens. Matter 2014, 26, 165301. [Google Scholar] [CrossRef]
- Dunstan, M.T.; Griffin, J.M.; Blanc, F.; Leskes, M.; Grey, C.P. Ion Dynamics in Li2CO3 Studied by Solid-State NMR and First-Principles Calculations. J. Phys. Chem. C 2015, 119, 24255–24264. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shames, A.; Panich, A.; Friedlander, L.; Iliashevsky, O.; Cohen, H.; Moreh, R. Testing the Potential of Magnetic Resonance Dosimetry: The Case of Lithium Carbonate. Materials 2025, 18, 3986. https://doi.org/10.3390/ma18173986
Shames A, Panich A, Friedlander L, Iliashevsky O, Cohen H, Moreh R. Testing the Potential of Magnetic Resonance Dosimetry: The Case of Lithium Carbonate. Materials. 2025; 18(17):3986. https://doi.org/10.3390/ma18173986
Chicago/Turabian StyleShames, Alexander, Alexander Panich, Lonia Friedlander, Olga Iliashevsky, Haim Cohen, and Raymond Moreh. 2025. "Testing the Potential of Magnetic Resonance Dosimetry: The Case of Lithium Carbonate" Materials 18, no. 17: 3986. https://doi.org/10.3390/ma18173986
APA StyleShames, A., Panich, A., Friedlander, L., Iliashevsky, O., Cohen, H., & Moreh, R. (2025). Testing the Potential of Magnetic Resonance Dosimetry: The Case of Lithium Carbonate. Materials, 18(17), 3986. https://doi.org/10.3390/ma18173986









