Next Article in Journal
Green and Efficient Lithium Extraction from Spent NCM Batteries via Electromagnetic Radiation
Previous Article in Journal
Experimental Investigation on the Bonding Performance of Steel Bars in Desert Sand Concrete After Freeze–Thaw Cycles
Previous Article in Special Issue
Co-Doped ErFeO3 for Dual-Band Laser Absorption with High-Temperature Stability
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Materials
Volume 18
Issue 17
10.3390/ma18173976
materials-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Tailoring the Electronic and Structural Properties of Lead-Free A2ZrX6 “Defect” Perovskites: A DFT Study on A-Site Cation and Halogen Substitutions

by
Christina Kolokytha
1,2,
Demeter Tzeli
1,2,* and
Nektarios N. Lathiotakis
1,*
1
Theoretical and Physical Chemistry Institute, National Hellenic Research Foundation, 48 Vassileos Constantinou Ave., GR-11635 Athens, Greece
2
Laboratory of Physical Chemistry, Department of Chemistry, National and Kapodistrian University of Athens, GR-15784 Zografou, Greece
*
Authors to whom correspondence should be addressed.
Materials 2025, 18(17), 3976; https://doi.org/10.3390/ma18173976
Submission received: 9 July 2025 / Revised: 13 August 2025 / Accepted: 19 August 2025 / Published: 25 August 2025
(This article belongs to the Special Issue Application and Theoretical Research of Perovskite Structural Materials)
Browse Figures
Versions Notes

Abstract

Lead-free A2ZrX6 “defect” perovskites hold significant potential for many optoelectronic applications due to their stability and tunable properties. Extending a previous work, we present a first-principles density functional theory (DFT) study, utilizing PBE and HSE06 functionals, to systematically investigate the impact of A-site cation and X-site halogen substitutions on the structural and electronic properties of these materials. We varied the A-site cation, considering ammonium, methylammonium, dimethylammonium, trimethylammonium, and phosphonium, and the X-site halogen, trying Cl, Br, and I. Our calculations reveal that both these substitutions significantly affect the band gap and the lattice parameters. Increasing A-site cation size generally enlarges the unit cell, while halogen electronegativity directly correlates with the band gap, yielding the lowest values for iodine-containing systems. We predict a broad range of band gaps (from ~4.79 eV for (PH4)2ZrCl6 down to ~2.11 eV for MA2ZrI6 using HSE06). The (PH4)2ZrX6 compounds maintain cubic crystal symmetry, unlike the triclinic of the ammonium-derived systems. Finally, our calculations show that the MA cation yields the smallest band gap among the ones studied, a result that is attributed to its size and the charges of the hydrogen atoms attached to nitrogen. Thus, our findings offer crucial theoretical insights into A2ZrX6 structure–property relationships, demonstrating how A-site cation and halogen tuning enables control over electronic and structural characteristics, thus guiding future experimental efforts for tailored lead-free perovskite design.

1. Introduction

Metal-halide perovskites remain a focal point of intense research, due to their great potential in various applications, including photovoltaics [1,2,3], light-emitting diodes (LEDs) [4,5,6], photodetectors (PDs) [7], laser crystals [4], transistors [8], memories [9], superconductors [10],photocatalysts [11], and other optoelectronic devices [12,13]. Typical metal-halide perovskites are of the form ABX3 where the A-site is occupied by inorganic (e.g., cesium) or organic (e.g., methylammonium (MA), formamidinium (FA)) cations, the B-site typically houses a divalent metal (e.g., Pb2+, Sn2+, Ge2+), and the X-site hosts a halogen anion (Cl, Br, I).
In photovoltaics, metal-halide perovskites have rapidly achieved Power Conversion Efficiency (PCE) that exceeds 25% in single-junction laboratory devices, and even higher in tandem configurations [14]. In organic–inorganic hybrid perovskites, high efficiency is achieved in parallel with low fabrication cost; however, these systems are facing challenges with operational stability [15]. In light-emitting diodes (LEDs), they have also achieved external quantum efficiency (EQE) exceeding 20% in the green and red spectrum, approaching the efficiencies of established OLEDs [16,17]. As photo-detectors [7,17], they have the potential to replace traditional photo-detection materials such as silicon, III–V, or II–VI semiconductors. The potential of metal-halide perovskites in these applications is based on their compelling features, including low fabrication cost through solution-based manufacturing, inherent flexibility, and tunable optoelectronic properties. Among them, lead-halide perovskites have demonstrated exceptional performance. However, the adoption of technologies based on these materials is challenged by concerns regarding the toxicity of lead and the inherent instability of lead-halide perovskites when exposed to environmental stressors like moisture and oxygen [18,19]. To address these challenges, it is crucial to develop environmentally stable, robust, and non-toxic perovskite materials capable of matching or surpassing the performance of their lead-containing counterparts [20,21].
A promising direction in lead-free perovskite research concerns the so-called double perovskites materials, with the general formula A2BB’O6, where A-site cations occupy interstitial spaces within a three-dimensional network of alternating BO6 and B’O6 octahedra [22]. Double perovskites have demonstrated strong and unusual magnetic interactions, enhanced stability, and are considered as viable options to replace lead halide perovskites [22,23,24]. Closely related structures are the “defect perovskites”, for which the B’ site is vacant and a tetravalent metal cation (Sn+4, Ti+4, Zr+4) occupies the B position to maintain charge neutrality [13,25,26]. They are also known as vacancy-ordered double perovskites, with the general formula A2BX6, and have also received significant attention [13,25,26]. Unlike their ABX3 counterparts, they feature isolated [BX6] octahedra, which often translates to enhanced structural stability, while due to the “vacancy” sites a large variety of A cations can be accommodated. Within this class, metal halide perovskites based on non-toxic and abundant Zirconium (A2ZrX6) represent an attractive proposition for optoelectronic applications [5,27,28,29,30].
Zhu et al. [31] developed Zr-based perovskites achieving high photoluminescence quantum yields (PLQYs). However, despite their promise, challenges remain in optimizing synthesis and addressing issues like color purity and long-term stability under light exposure. The electronic properties of Cs2BX6, with B = Sn, Te, Zr, were studied theoretically [26] and it was found that they can be tailored for hole and electron transport. Cs2ZrX6 (X = Cl, Br) perovskite derivatives were synthesized and studied, theoretically, by Abfalterer et al. [27], showing good agreement between theory and experiment. For these compounds, indirect band gaps of the order of 4–5 eV were found. Dai et al. [32] reported the synthesis of ((CH3)4N)2ZrCl6 and demonstrated that it exhibits excitation-dependent fluorescence across the visible region. Lin et al. [33] focused on the optical property regulation of 0D A2ZrCl6 through non-protonated cation substitution (A = [(CH3)3SO]+ and [(CH3)4N]+) combined with different guest ions (i.e., Sb3+, Bi3+, and Mn2+), providing insights into compositional engineering. Another zirconium-containing perovskite, ((CH3)2S)2ZrCl6, was recently created, by Tagiara et al. [34] and exhibited broad photoluminescence. Finally, a newly developed zero-dimensional organic–inorganic hybrid perovskite [5], ((C2H5)4N)2ZrCl6, was found to exhibit multiple emissions in red, green, and blue, attributed to different mechanisms, like self-trapped excitons, Zr(IV) d–d transitions, and thermally activated delayed fluorescence (TADF), and boasted a high photoluminescence quantum yield.
Inspired by recent experimental results [34], in a previous work [35], we studied theoretically “defect” perovskites, with the chemical formula A2ZrX6, where the A-site cation is either methylammonium, formamidinium, or trimethyl-sulfonium, and the X-site anions are halogen, X = Cl, Br, and I, using hybrid density functional theory (DFT). The target of our study was the exploration of the effect of the A-site cation as well as the X-site anion on the electronic properties. We found that all compounds exhibit wide band gaps ranging from 5.22 eV down to 2.11 eV. One main point was that both the A-site cation as well as the X-site anion can be used to tailor the electronic properties [35]. Among the studied systems, the particular one that combines methylammonium cation and iodine anion was found to yield the lowest band gap.
Motivated by the findings of our previous work [35], especially the pronounced influence of ion substitution on band gaps, the present study extends the theoretical investigation of A-site cation substitutions in A2ZrX6 perovskites, employing DFT methods. Prompted by the approximately 2 eV band gap calculated for methylammonium (MA), CH3NH3+, in the A-site, we expand our focus to include other ammonium-derived cations, namely ammonium, NH4+, dimethylammonium (DMA), (CH3)2NH2+, and trimethylammonium (TMA), (CH3)3NH+, as well as the related phosphonium cation, PH4+. For completeness, in order to have all ammonium-derived cations up to TMA, our results, already presented in Ref. [35] concerning MA, are also included. These cations are combined with halide anions X = Cl, Br, and I. For these systems, we predict the structural properties, as well as basic electronic properties (densities of states, band gaps). Although there are several reports of utilizing such cations in metal-halide perovskites [36], there is a scarcity of results concerning these cations in Zr-based systems. It is our ambition to motivate such experimental and theoretical studies through this work, by demonstrating the tunability of the electronic properties of these systems. Furthermore, our study aims to categorize the considered perovskite materials based on their bandgap to determine their suitability for specific applications. Materials with bandgaps in the range 1.5–2.8 eV are suitable for solar cells, LEDs, and thin-film transistors. Specifically, a 2.5 eV bandgap is optimal for blue light absorption, while a 1.9 eV band gap targets red light. On the other hand, a bandgap of 1.5 eV enables broad absorption across visible and near-infrared regions and can be versatile for energy and optoelectronic applications.

2. Computational Methodology

We performed DFT calculations using the Vienna Ab initio Simulation Package (VASP) plane-wave code [37,38], version 6.1, employing the projected augmented wave (PAW) formalism [39]. First, every perovskite structure was fully energetically optimized, allowing the relaxation of every atomic position and the unit cell shape and volume, using the Perdew–Burke–Ernzerhof (PBE) generalized gradient approximation (GGA). For the electronic properties of the optimized structures, apart from GGA-PBE functional, which systematically underestimates band gaps, we employed the Heyd–Scuseria–Ernzehof (HSE06) screened hybrid functional [40]. It has been established that hybrid functionals predict accurately optoelectronic properties [41,42]. In our previous work [35], we demonstrated that the strategy of using the PBE functional for the energetic optimization of the structures and HSE06 for the electronic properties of these systems is accurate compared to experimental results. The convergence criterion for the electronic self-consistency cycle was set at 10−5 eV, while the ionic relaxation was terminated when the total energy change was less than 10−4 eV. Furthermore, we used the value of 400 eV for the maximum energy cutoff and 2 × 2 × 2 reciprocal space sampling, and these choices were also validated in our previous work.

3. Results and Discussion

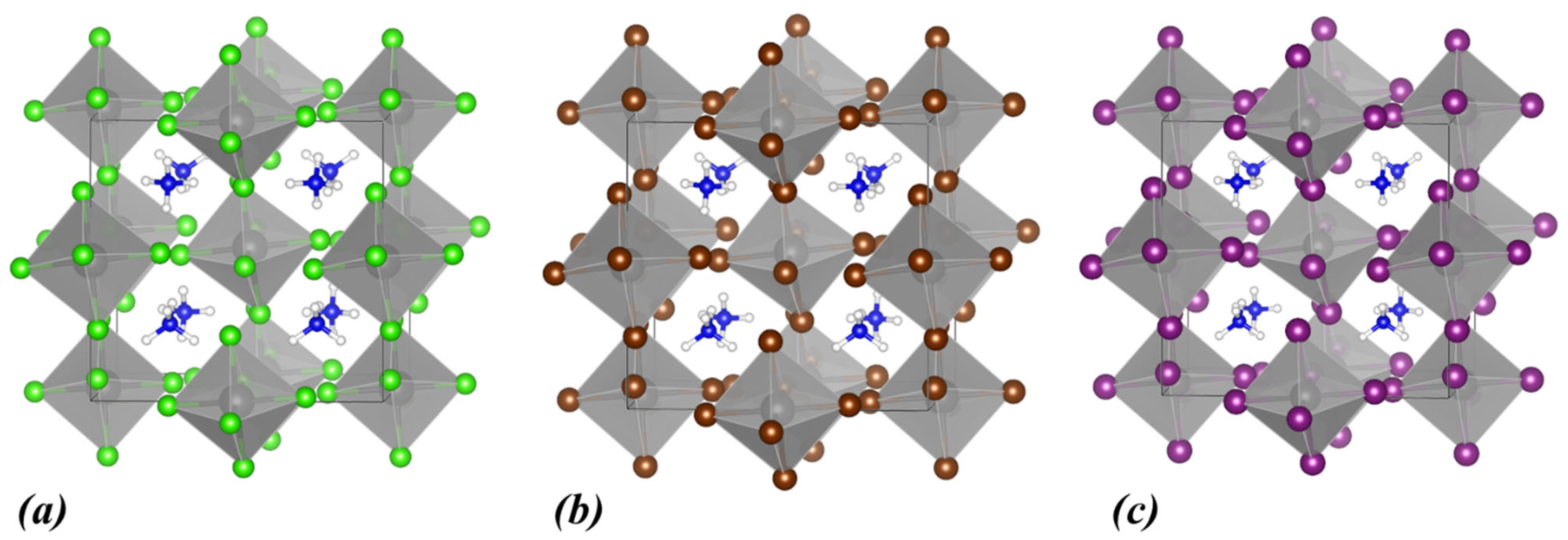
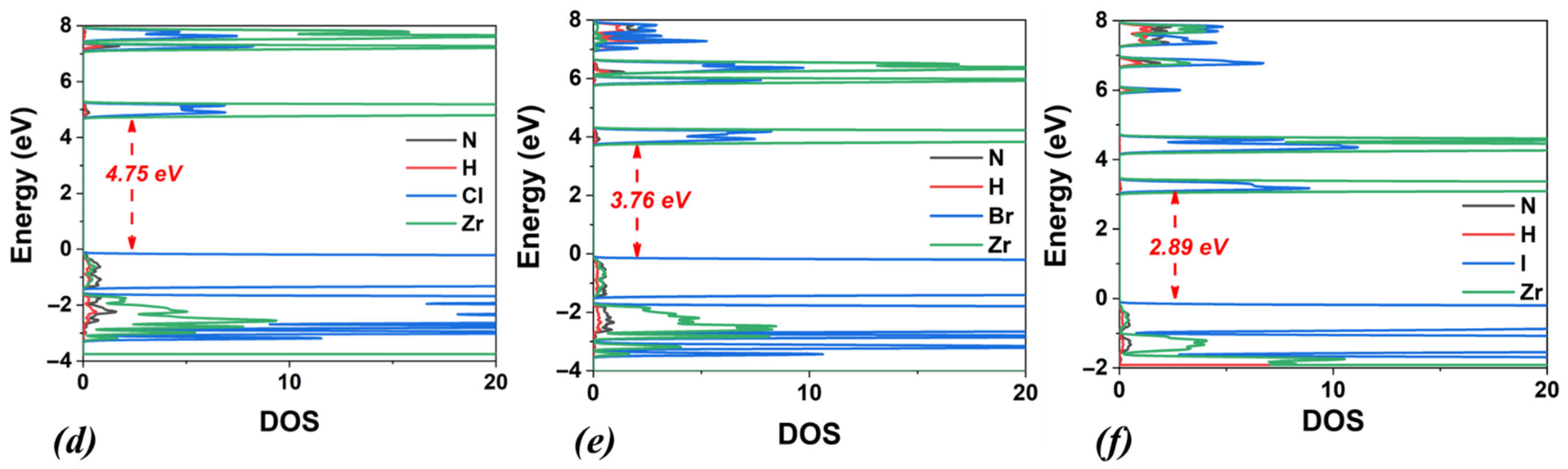
3.1. (NH4)2ZrX6, X: Cl, Br, I

Initially, our computational study focused on the (NH4)2ZrX6 system, i.e., with ammonium as the A-site cation and X = Cl, Br, and I. The energy optimized structures are shown in Figure 1, while the obtained structural and electronic properties are included in Table 1. The calculated band structures and densities of states (DOSs) using the PBE functional for all halogen structures are shown in Figure 2a–c together with the DOS obtained with HSE06 (Figure 2d–f).
Regarding the structural properties of (NH4)2ZrX6, as seen in Table 1, the symmetry of the crystal structure is triclinic. Moreover, for chlorine the lattice constants are the smallest compared to the rest of the halogens. For Br, the lattice constants increase by approximately 0.5 Å. Finally, for I, an additional increase of about 0.8 Å, in the lattice constants is predicted. Overall, we can conclude that as the ionic radius of the halogen atoms increases (RI > RBr > RCl), the lattice constants increase accordingly.
Concerning the electronic properties, the bandgap energy values calculated by the PBE functional are underestimated compared to those obtained by the HSE06, as expected (see Table 1) by approximately 1–1.2 eV. Moreover, as the electronegativity of the halogen decreases (Cl > Br > I), the bandgap energy shows a reduction by approximately 1 eV, for both functionals. In particular, for the perovskite (NH4)2ZrCl6, the bandgap energies are 3.58 eV (PBE) and 4.75 eV (HSE06). When Cl anions are replaced by Br, the bandgap energies decrease by 0.8 eV (to 2.73 eV) using PBE and by 1.0 eV (to 3.76 eV) using HSE06. Finally, for the perovskite (NH4)2ZrI6, the calculated values of the bandgap energy are 1.74 eV (PBE) and 2.89 eV (HSE06), showing a decrease of 1.0 eV (PBE) and 0.9 eV (HSE06), compared to (NH4)2ZrBr6.

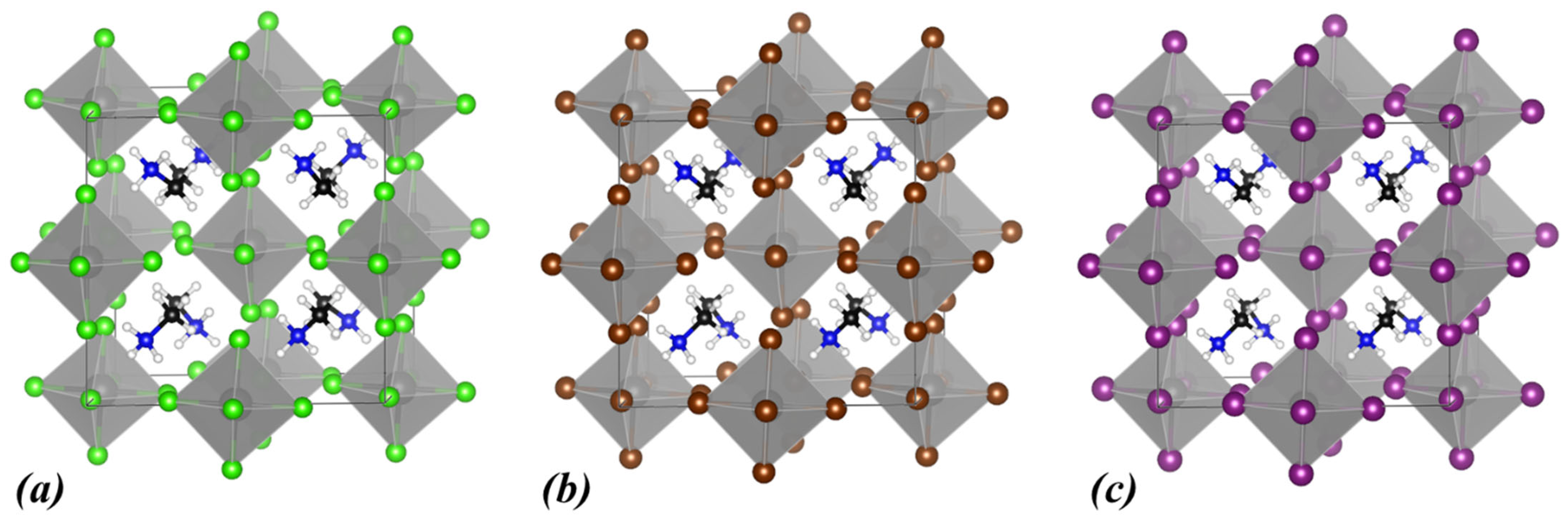
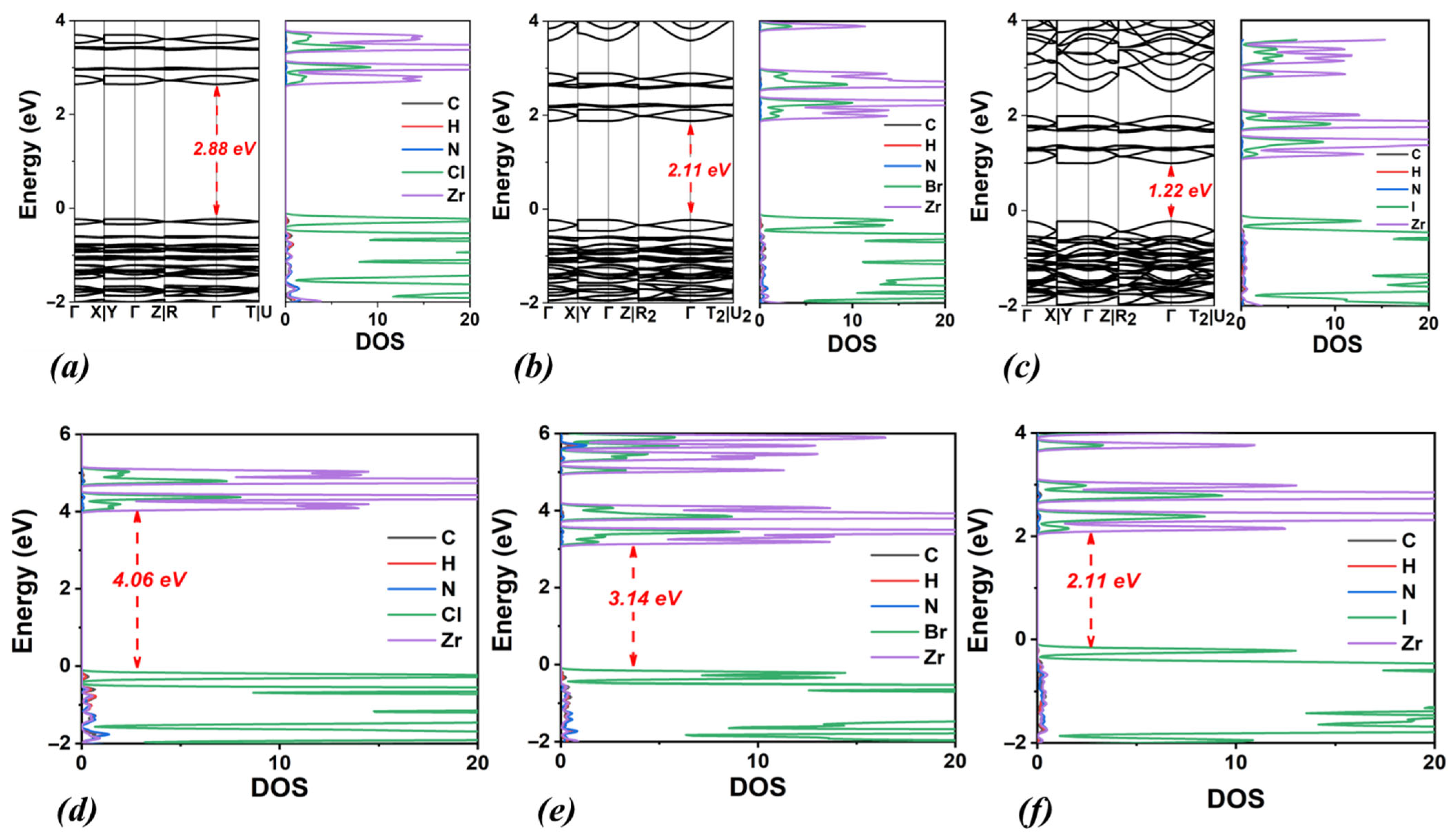
3.2. MA2ZrX6, X: Cl, Br, I

Our next focus is the MA cation at the A-site, formed by replacing a hydrogen atom of the NH4 ion with a methyl group. The energetically optimal structures of MA2ZrCl6 are shown in Figure 3, while the structural and electronic properties are included in Table 2 and Figure 4. In the case of MA2ZrCl6, the calculated values of the bandgap energy are 2.88 eV (PBE) and 4.06 eV (HSE06) which are lower than those of (NH4)2ZrCl6 by 1.3 eV and 0.7 eV, respectively. Furthermore, for the bandgap energy of MA2ZrBr6, we calculated the values 2.11 eV (PBE) and 3.14 eV (HSE06), which are lower than those of (NH4)2ZrBr6 by 0.6 eV, for both approximations. Finally, for the bandgap energy of MA2ZrI6, we found the values 1.22 eV (PBE) and 2.11 eV (HSE06) which are lower by 0.6 eV and 0.7 eV, respectively, compared to (NH4)2ZrI6. In conclusion, by replacing NH4+ with MA+, the bandgap energies drop substantially for all the halogen options.
In addition, replacing NH4+ with MA+ at the A-site, significantly affects the structural properties. For all studied halogens (Cl, Br, and I), the lattice constants of the MA2ZrX6 structures are consistently larger than their (NH4)2ZrX6 counterparts (see Table 1 and Table 2). Specifically, the lattice constants for MA2ZrCl6 increase by 0.7–0.9 Å compared to (NH4)2ZrCl6. Similarly, MA2ZrBr6 shows an increase of 0.6–1.0 Å relative to (NH4)2ZrBr6, and MA2ZrI6 exhibits a comparable increase of 0.6–1.0 Å over (NH4)2ZrI6. This expansion of the unit cell can be attributed to the larger molecular weight of the MA+ (32 g/mol) compared to NH4+ (18 g/mol). Despite the increase in unit cell size, the crystal symmetry remains triclinic.

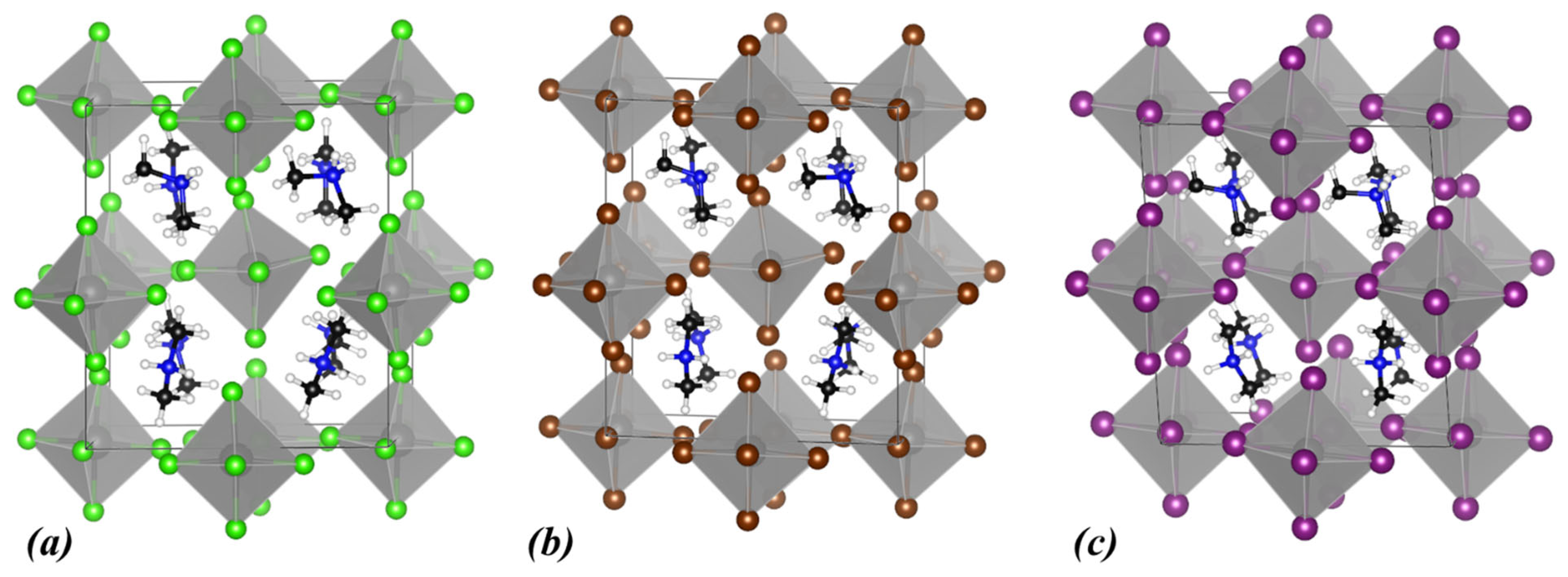
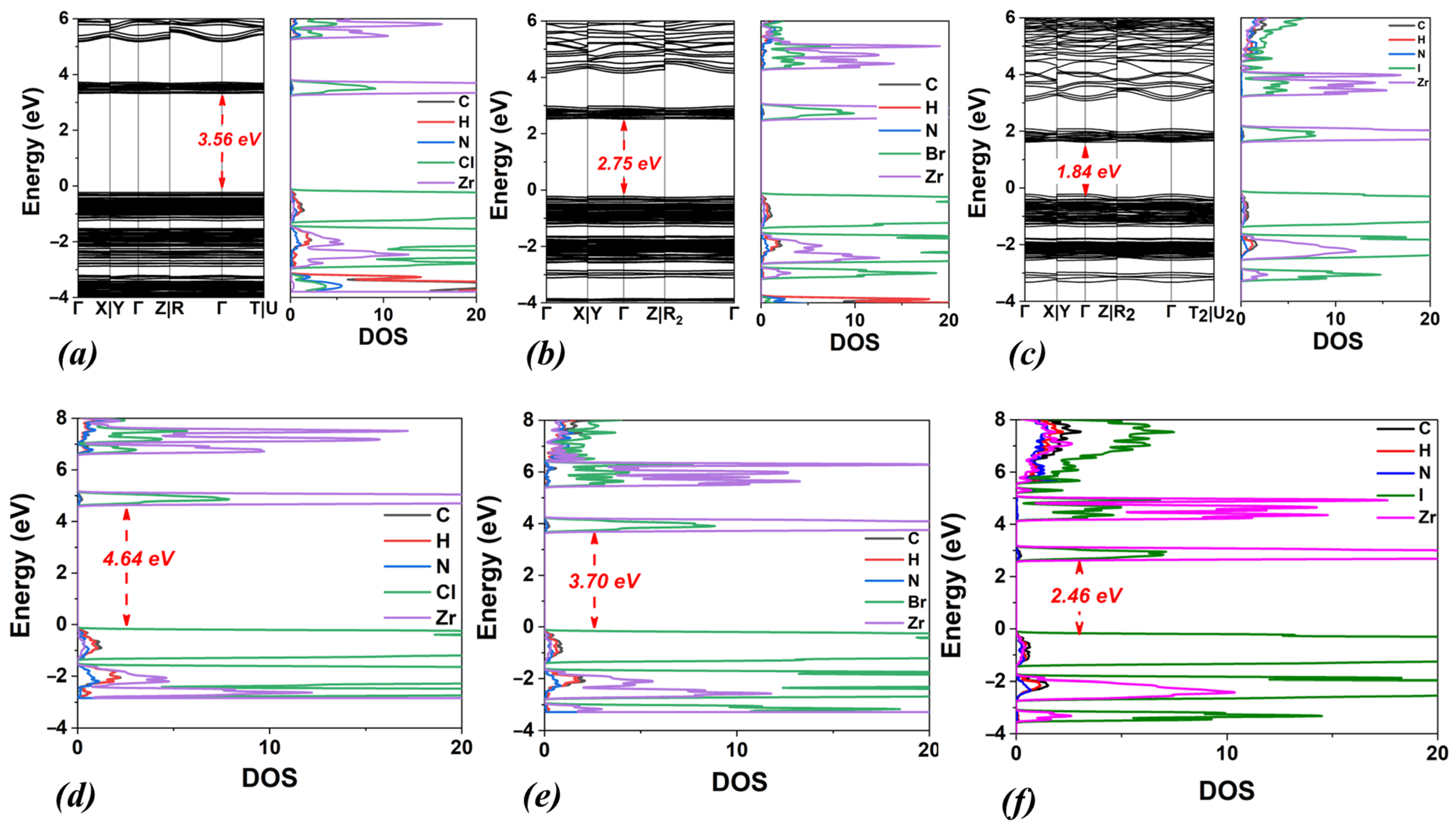
3.3. DMA2ZrX6, X: Cl, Br, I

Next, we present results for DMA cation at the A-site, formed by replacing one more hydrogen in the MA+ with a methyl group. In Figure 5, the optimal structures for the three halogens are shown, and in Table 3 as well as in Figure 6, we present the structural characteristics and electronic properties.
Regarding the electronic properties, for DMA2ZrCl6, the bandgap energies are 3.56 eV (PBE) and 4.64 eV (HSE06). Compared to (NH4)2ZrCl6 (Figure 2, Table 1), DMA2ZrCl6 shows a slight decrease in bandgap energy, ranging from 0.02 to 0.11 eV. Instead, relative to MA2ZrCl6 (Table 2, Figure 4), the band gap of DMA2ZrCl6 increases by approximately 0.7 eV (PBE) and 0.6 eV (HSE06). For DMA2ZrBr6, the band gap values are 2.75 eV (PBE) and 3.70 eV (HSE06). Compared to (NH4)2ZrBr6 (see Table 1), the bandgap slightly increases by 0.02 eV for the PBE functional and decreases marginally, by 0.06 eV, for HSE06. On the contrary, relative to MA2ZrBr6 (Table 2), DMA2ZrBr6 shows a sizable increase in band gap by 0.64 eV (PBE) and 0.56 eV (HSE06). Finally, for DMA2ZrI6, the calculated bandgap values are 1.84 eV (PBE) and 2.46 eV (HSE06). These values are larger than those for MA2ZrI6 by 0.6 eV and 0.35 eV for PBE and HSE06, respectively. Following the bandgap trend with halogen substitutions, the DMA2ZrI6 bandgap values are substantially smaller than DMA2ZrBr6 and DMA2ZrCl6, as seen in Table 3. Overall, across all halogens, the band gap values of DMA2ZrX6 systems generally lie between those of the (NH4)2ZrX6 and MA2ZrX6 (for HSE06).
Regarding the structural properties of the DMA2ZrX6 compounds (Table 3), the crystal symmetry consistently remains triclinic. In the case of DMA2ZrCl6, the lattice constants are 11.21 Å, 12.68 Å, 11.41 Å for a, b and c, respectively, and they are higher than those of MA2ZrCl6 by ~2 Å and (NH4)2ZrCl6 by ~2.5 Å. In the case of Br in the X-site, the lattice constants are 11.55 Å, 13.29 Å, 11.64 Å, i.e., they are 0.2–0.8 Å larger than those of Cl anion in the X-site. Compared to MA2ZrBr6, one lattice parameter (b in Table 3) is significantly enlarged, while the other two are only marginally smaller. DMA2ZrBr6 lattice parameters are also significantly larger than those of and (NH4)2ZrBr6 by 0.5 Å, 2.7 Å and 1.1 Å, for a, b, c, respectively. For DMA2ZrI6, the lattice constants values are 12.20 Å, 13.84 Å, 12.30 Å and they are significantly enlarged compared to DMA2ZrBr6 by 0.5–0.7 Å. They are also substantially larger than both (NH4)2ZrI6 and MA2ZrI6 by 0.8–2.0 Å, and 0.4–1.5 Å, respectively.

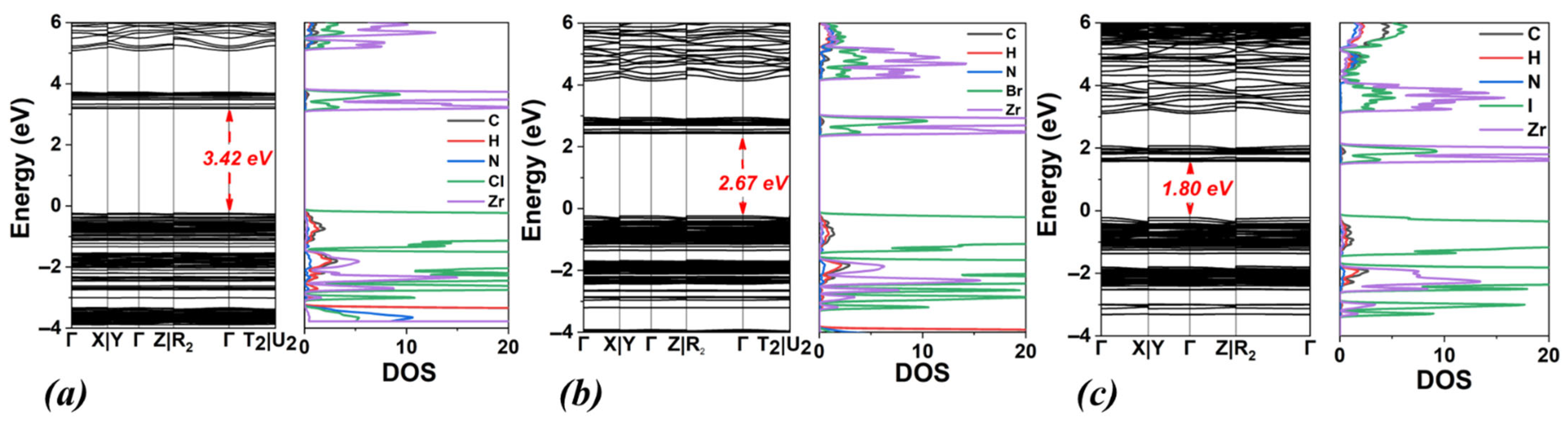
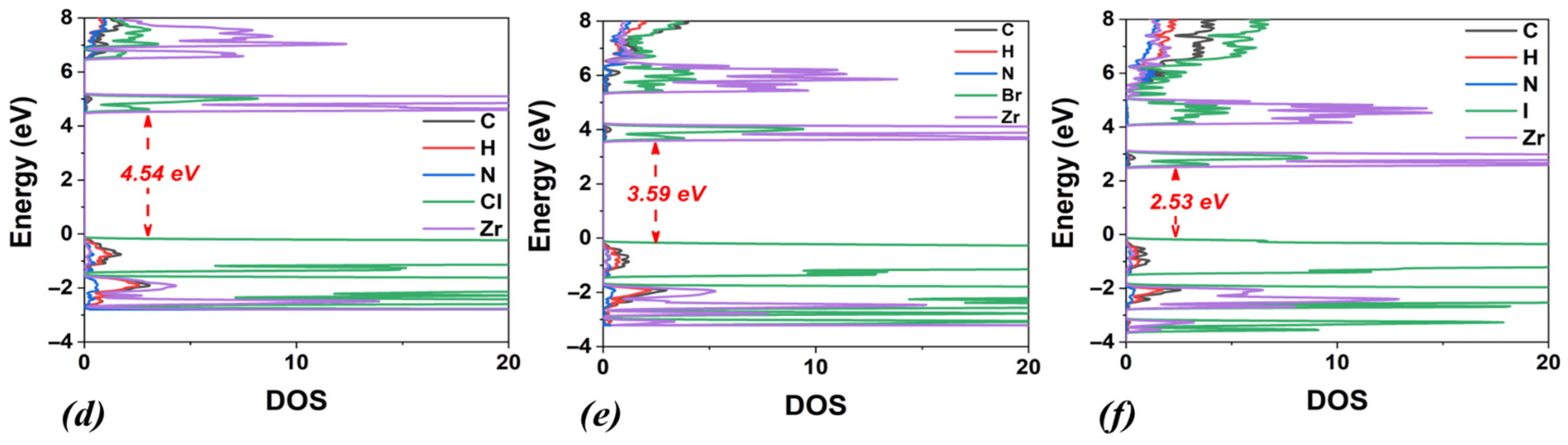
3.4. TMA2ZrX6, X: Cl, Br, I

Next, we investigated the TMA2ZrX6 series, where trimethylammonium (TMA+) occupies the A-site. The structures obtained for all halogens are shown in Figure 7. The electronic and structural properties for these structures are presented in Table 4 and Figure 8.
Figure 4 clearly illustrates that as the halogen electronegativity decreases, the band gap energy consistently decreases for both PBE and HSE06 functionals. Specifically, replacing chlorine (Cl) with bromine (Br) at the X-site causes the band gap energy to decrease by 0.8 eV (PBE) and 1.0 eV (HSE06). A similar reduction is observed when bromine (Br) is replaced by iodine (I), with the band gap energy decreasing by another 0.8 eV (PBE) and 1.0 eV (HSE06). Notably, the HSE06 functional consistently predicts a greater decrease in band gap energies compared to PBE.
For TMA2ZrCl6, the band gap energies are 3.42 eV (PBE) and 4.54 eV (HSE06). These values are slightly lower (by ~0.1 eV) than those of DMA2ZrCl6 (3.56 eV with PBE and 4.64 eV with HSE06). Similarly, TMA2ZrBr6 exhibits band gap energies of 2.67 eV (PBE) and 3.59 eV (HSE06), which are also lower by ~0.1 eV compared to DMA2ZrBr6 (2.75 eV with PBE and 3.70 eV with HSE06). Finally, for TMA2ZrI6, the calculated bandgap energy values are 1.80 eV (PBE) and 2.53 eV (HSE06).
Regarding the structural properties of the TMA2ZrX6 compounds (Table 4), the lattice constants are significantly influenced by the increasing molecular weight of the halogen at the X-site. Specifically, for TMA2ZrCl6, the lattice constants are a =11.64 Å, b =13.21 Å, and c =12.04 Å. When Cl is replaced by Br, all three lattice parameters increase by approximately 0.4 Å. Further substitution of Br with iodine I results in even larger lattice constants, a =12.67 Å, b =14.25 Å, and c =13.03 Å, representing an additional increase of 0.4–0.6 Å. Compared to DMA2ZrX6, the lattice parameters of TMA2ZrX6 are substantially enlarged: in the cases of Cl and Br anions, they are increased by 0.5 Å on the average, while, in the case of I, this expansion is more than 1.0 Å, for all parameters a, b and c.

3.5. (PH4)2ZrX6, X: Cl, Br, I

The last crystal structure that we studied is (PH4)2ZrX6, where the phosphonium cation (PH4+) serves as the A-site cation. The structures we obtained from geometry optimization are shown in Figure 9, while our results are included in Table 5 and Figure 10.
Notably, (PH4)2ZrX6 compounds exhibit a unique structural feature: their crystal symmetry remains cubic regardless of the halogen (Table 5). This contrasts with the triclinic crystal symmetry observed for all the ammonium-derived A-site cations investigated (NH4+, MA+, DMA+, and TMA+).
Regarding their electronic properties (Figure 10 and Table 5), the calculated bandgap energy of (PH4)2ZrCl6 has values of 3.57 eV (PBE) and 4.79 eV (HSE06). These values are comparable to those of (NH4)2ZrCl6, DMA2ZrCl6, and TMA2ZrCl6 (Figure 2, Figure 6 and Figure 8, respectively). However, they are notably higher (by approximately 0.8 eV, for both PBE and HSE06) than the calculated bandgap energies for MA2ZrCl6 (Figure 4). Similarly, the calculated bandgap energy of (PH4)2ZrBr6 has values of 2.70 eV (PBE) and 3.79 eV (HSE06), which are close to those of (NH4)2ZrBr6, DMA2ZrBr6, and TMA2ZrBr6, but significantly lower than that of MA2ZrBr6. In the case of iodine anion, the band gap of (PH4)2ZrBr6 is found to be smaller, by ~0.4 eV, than that of (NH4)2ZrBr6 and very close (~0.1 eV larger) to that of TMA2ZrBr6, according to HSE06.
Upon halogen substitution, the band gap energies generally decrease. Specifically, replacing Cl with Br in (PH4)2ZrBr6 leads to a decrease of 0.8 eV (PBE) and 1.0 eV (HSE06). When Br is further replaced by I, a significant decrease in the bandgap energy, of 1.0 eV (PBE) and 1.2 eV (HSE06), is found.
Regarding the structural properties of the (PH4)2ZrX6 series (Table 5), it is observed that the increase in the molecular weight of the halogen significantly influences the lattice constants. Importantly, these compounds maintain their cubic crystal symmetry throughout the series. Specifically, for (PH4)2ZrCl6, the cubic lattice constant is a=10.34 Å. When chlorine (Cl−) is replaced by bromine (Br−), the lattice constant increases by 0.65 Å. Finally, upon substituting bromine (Br−) with iodine (I−), the lattice constant for (PH4)2ZrI6 increases further by 0.74 Å.

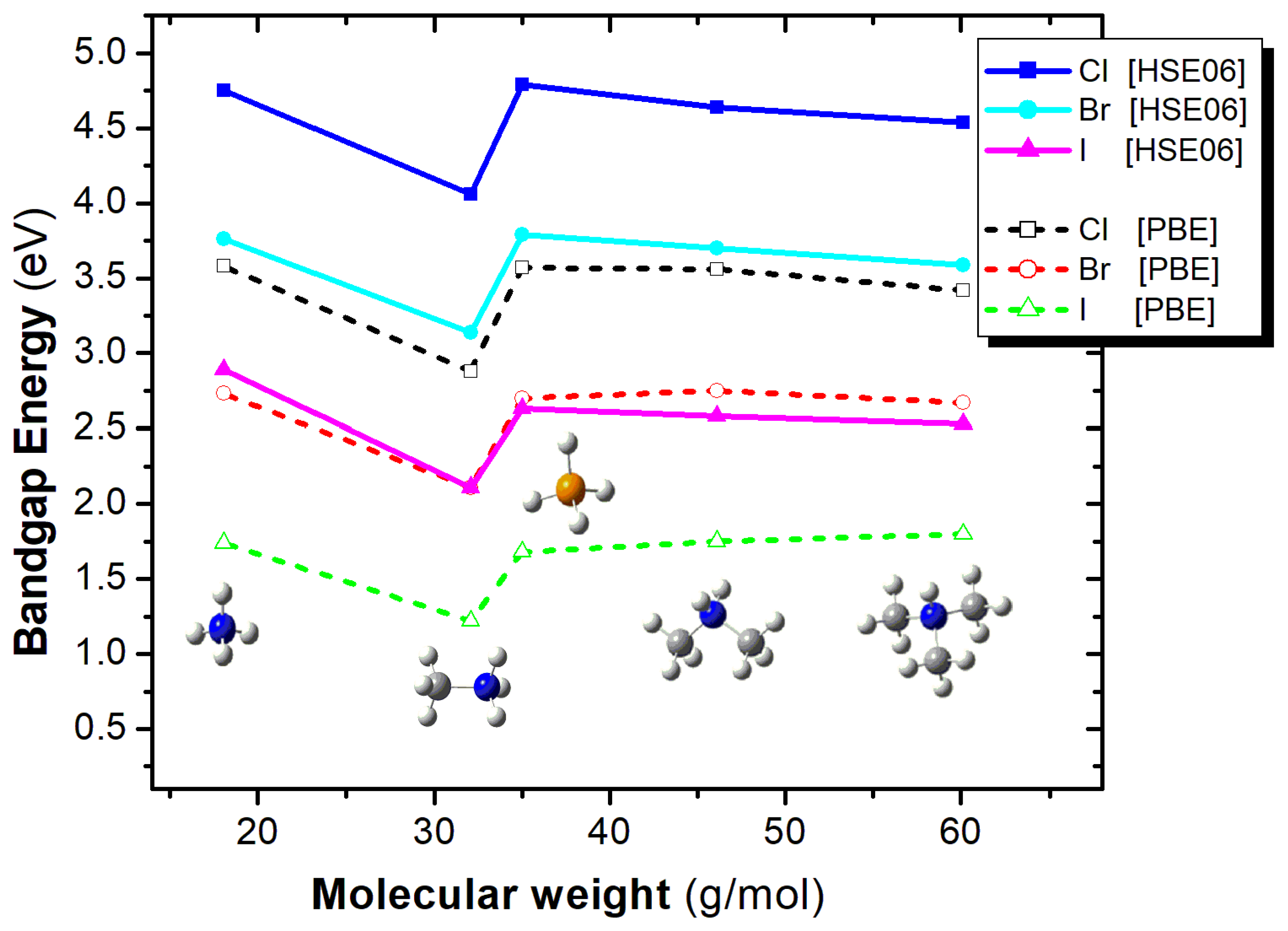
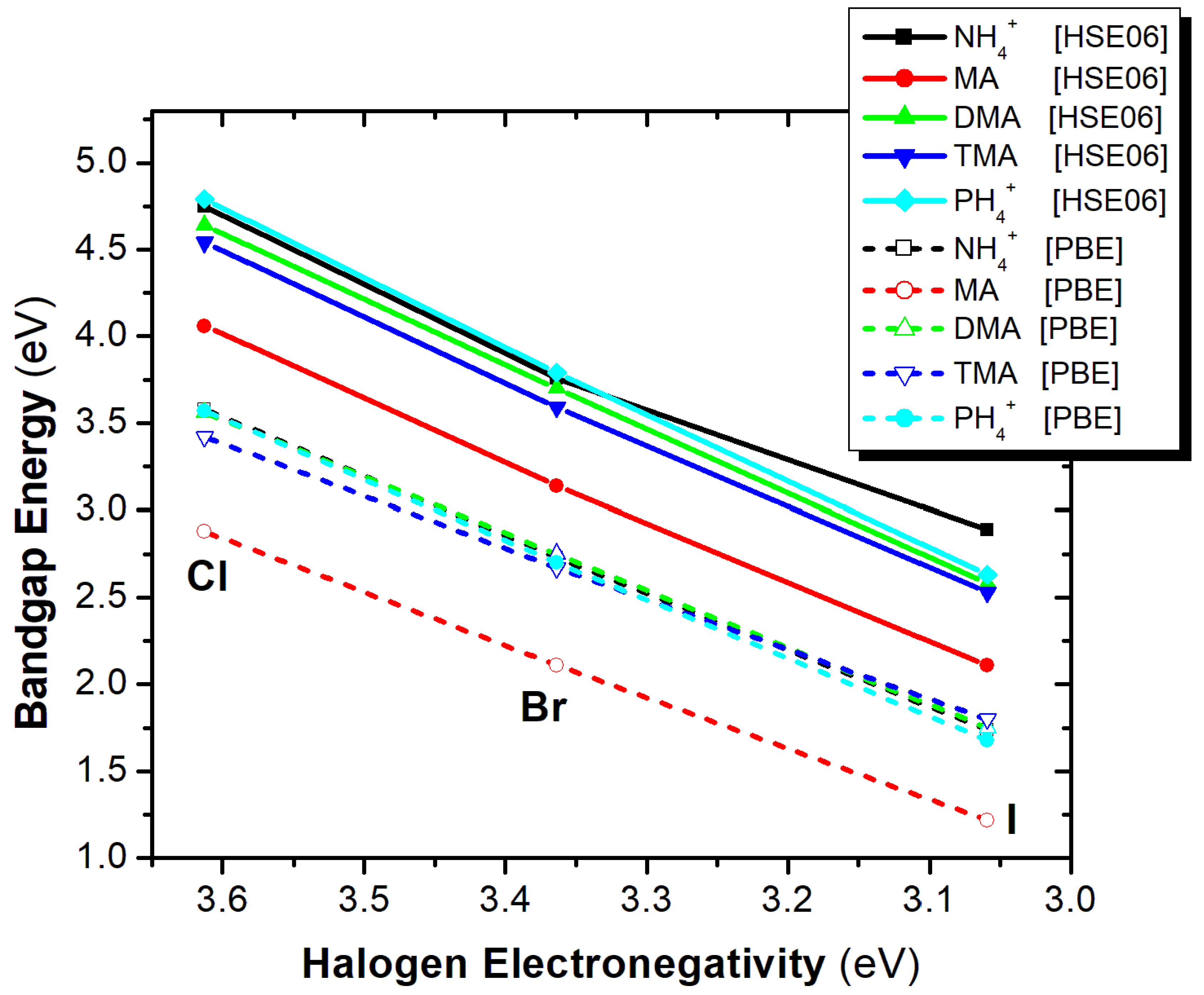
3.6. The Effect of A-Cation and X-Anion

Let us now shed more light on the effect of the A-site substitution and the X-site substitution on the bandgap energy. Regarding the A-site effect, for both functionals and for all X anions, MA in A-site results in the smallest bandgap energy, while the remaining four cations, i.e., NH4+, PH4+, DMA, and TMA, result in similar bandgap energies, as seen in Figure 11. Specifically, the bandgap energy has been plotted as a function of the molecular weight of the A-site cation, since molecular weight can be used as a proxy for the size of the molecular ion, which is responsible for the observed changes in the lattice parameters (Figure 11).
In order to explain the A-cation effect and specifically why MA present the smallest bandgap, the NH4+, MA, DMA, and TMA cations were energetically optimized using the B3LYP/6-31G(d,p) methodology [43,44] to calculate the atomic charges via the natural population analysis and the volume of these cations. It was found that the charges on the H atoms bonded on the N atoms are +0.50 e, while the N atom has a charge of about –1.0 e. The three H atoms of the MA attached to the N atom of MA have a similar charge of +0.49 e. On the contrary, the H atoms attached to N of the DMA and TMA have a charge of +0.37 e and +0.36 e, respectively. Thus, while all NH4+, MA, DMA, and TMA are positively charged by +1.0 e, the NH4+ and MA have the most positively charged H atoms that may affect the bandgap [45]. Comparing the NH4+ and MA cations, they have different volumes, i.e., about 4.7 Å and 5.7 Å. The second one fits better and a better size match at the A-site can reduce the band gap, though the relationship is not always linear and depends on other structural factors too [46]. As a result of the cation size and the charges of the H atoms attached to N, the systems with MA have the smallest band gap among the considered A-site cations.
The A-site cations’ shape and charge distribution also influence crystal symmetry. The NH4+ and PH4+ are both tetrahedral. The rest, especially DMA+ and TMA+, are elongated. Thus, it is not surprising that for NH4+ and PH4+ cations the optimal crystal structures are close to cubic. However, in the case of PH4+, the structure remains cubic, while for NH4+, it is, to a small extent, distorted towards triclinic symmetry. This difference can be attributed to the distribution of positive charge. Indeed, by performing the natural population analysis mentioned above, we found that, for NH4+, each hydrogen atom carries a positive charge of around +0.5 e, compared to only +0.1 e for PH4+. These tetrahedrally oriented charges, significantly larger for NH4+, lead to enhanced interactions with the octahedrally oriented halogen atoms and can explain the distortion of the cubic lattice towards triclinic. The interactions of PH4+ hydrogens with halogens are much weaker, and the structure prefers cubic symmetry. According to our previous work [35], compounds with trimethyl sulfonium cation (TMS+) at the A-site also adopt a cubic structure, which can also be attributed to the shape of the cation and the low positive charge (~ +0.2 e) on hydrogen atoms.
Regarding the effect of the X-site substitution, as the electronegativity of the X-site halogen is decreased, i.e., Cl > Br > I, the bandgap also decreases (see Figure 12). Both PBE and HSE06 functionals exhibit similar trends, with the smallest bandgap values observed for X = I. The observed linearity of these trends suggests a strong predictive capability, allowing for the reliable estimation of missing bandgap values for halogens in these or similar compounds.

4. Conclusions

In this density functional theory (DFT) study, we investigate the impact of A-site cation and X-site halogen substitutions on the structural and optoelectronic properties of lead-free A2ZrX6 “defect” perovskites. Following our previous work [35], we extend the A-site cation substitutions by considering four ammonium-derived cations (ammonium, methylammonium, dimethylammonium, trimethylammonium) as well as phosphonium. These cations are combined with three X-site halogens: Cl, Br, I. We demonstrate a significant tunability in the properties of these promising materials.
We show that both the size and composition of the A-site cation, as well as the electronegativity of the X-site anion, significantly influence the electronic band gap and lattice parameters. Our results offer a quantitative measure of this tunability. Specifically, we found that larger A-site cations lead to enlarged lattice constants. Furthermore, the bandgap energy is found to depend linearly on halogen electronegativity, with iodine-containing compounds systematically exhibiting, the lowest band gaps for all studied compounds. We find a broad range of predicted band gap values, spanning from wide bandgap materials (~4.79 eV for (PH4)2ZrCl6) suitable for UV detection or insulation, down to the lower end of the visible spectrum (~2.11 eV for MA2ZrI6), which holds promise for optoelectronic applications, like LEDs. It is worth mentioning that the (PH4)2ZrX6 series maintain cubic crystal symmetry across all halogens, in contrast to the triclinic symmetry found for the other ammonium-derived A-site cations.
The theoretical insights, presented in this work, demonstrate at a quantitative level, the vast potential of A-site cation and halogen substitution as powerful strategies for precisely tailoring the electronic and structural characteristics of A2ZrX6 “defect” perovskites. Finally, our calculations show that the MA cation yields the smallest band gap among the ones studied, a result that is attributed to its size and the charges of the hydrogen atoms attached to nitrogen. Our findings provide valuable theoretical predictions for future experimental synthesis and optimization efforts aimed at developing novel, high-performance, and lead-free perovskite materials for diverse optoelectronic applications.

Author Contributions

Conceptualization, C.K., N.N.L., and D.T.; Methodology, C.K., N.N.L., and D.T.; Validation, C.K., N.N.L. and D.T.; Formal analysis, C.K., N.N.L., and D.T.; Investigation, C.K., N.N.L. and D.T.; Resources, N.N.L., and D.T.; Data curation, C.K., N.N.L., and D.T.; Writing—original draft, C.K., N.N.L., and D.T.; Writing—review & editing, C.K., N.N.L., and D.T.; Visualization, C.K., and D.T.; Supervision, N.N.L., and D.T.; Project administration, N.N.L., and D.T.; Funding acquisition, N.N.L. All authors have read and agreed to the published version of the manuscript.

Funding

This work was carried out within the framework of the Action ‘Flagship Research Projects in challenging interdisciplinary sectors with practical applications in Greek Industry’, implemented through the National Recovery and Resilience Plan Greece 2.0 and funded by the European Union—NextGenerationEU (Acronym: 3GPV-4INDUSTRY, project code: TAEDR-0537347). We acknowledge support in computational time granted by the National Infrastructures for Research and Technology S.A. (GRNET S.A.) in the National HPC facility - ARIS - under project ID: pr017022.

Data Availability Statement

The original contributions presented in this study are included in the article. Further inquiries can be directed at the corresponding authors.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Stranks, S.D.; Snaith, H.J. Metal-Halide Perovskites for Photovoltaic and Light-Emitting Devices. Nat. Nanotechnol. 2015, 10, 391–402. [Google Scholar] [CrossRef]
  2. Kojima, A.; Teshima, K.; Shirai, Y.; Miyasaka, T. Organometal Halide Perovskites as Visible-Light Sensitizers for Photovoltaic Cells. J. Am. Chem. Soc. 2009, 131, 6050–6051. [Google Scholar] [CrossRef]
  3. Snaith, H.J. Perovskites: The Emergence of a New Era for Low-Cost, High-Efficiency Solar Cells. J. Phys. Chem. Lett. 2013, 4, 3623–3630. [Google Scholar] [CrossRef]
  4. Cui, J.; Liu, Y.; Deng, Y.; Lin, C.; Fang, Z.; Xiang, C.; Bai, P.; Du, K.; Zuo, X.; Wen, K.; et al. Efficient Light-Emitting Diodes Based on Oriented Perovskite Nanoplatelets. Sci. Adv. 2021, 7, abg8458. [Google Scholar] [CrossRef]
  5. Wang, C.; Meng, W.; Luo, G.; Xu, G.; Peng, M.; Xu, B.; Nie, S.; Deng, Z. RGB Tri-Luminescence in Organic–Inorganic Zirconium Halide Perovskites. Chem. Sci. 2024, 15, 2954–2962. [Google Scholar] [CrossRef]
  6. Koutsoubogeras, J.; Tsoureas, N.; Tagiara, N.S.; Kaltzoglou, A. Synthesis, Crystal Structure and Optoelectronic Properties of [(CH3)3S]SnBr3. J. Coord. Chem. 2025. [Google Scholar] [CrossRef]
  7. Wang, Y.; Gao, M.-L.; Wu, J.-L.; Zhang, X.-W. Metal Halide Perovskite Photodetectors: Material Features and Device Engineering. Chin. Phys. B 2019, 28, 018502. [Google Scholar] [CrossRef]
  8. Xing, G.; Mathews, N.; Sun, S.; Lim, S.S.; Lam, Y.M.; Grätzel, M.; Mhaisalkar, S.; Sum, T.C. Long-Range Balanced Electron- and Hole-Transport Lengths in Organic-Inorganic CH3NH3PbI3. Science 2013, 342, 344–347. [Google Scholar] [CrossRef]
  9. Waser, R.; Dittmann, R.; Staikov, G.; Szot, K. Redox-Based Resistive Switching Memories—Nanoionic Mechanisms, Prospects, and Challenges. Adv. Mater. 2009, 21, 2632–2663. [Google Scholar] [CrossRef]
  10. Reyren, N.; Thiel, S.; Caviglia, A.D.; Kourkoutis, L.F.; Hammerl, G.; Richter, C.; Schneider, C.W.; Kopp, T.; Rüetschi, A.-S.; Jaccard, D.; et al. Superconducting Interfaces Between Insulating Oxides. Science 2007, 317, 1196–1199. [Google Scholar] [CrossRef]
  11. Zhang, Z.; Liang, Y.; Huang, H.; Liu, X.; Li, Q.; Chen, L.; Xu, D. Stable and Highly Efficient Photocatalysis with Lead-Free Double-Perovskite of Cs2AgBiBr6. Angew. Chem. 2019, 131, 7341–7345. [Google Scholar] [CrossRef]
  12. Sharif, R.; Khalid, A.; Ahmad, S.W.; Rehman, A.; Qutab, H.G.; Akhtar, H.H.; Mahmood, K.; Afzal, S.; Saleem, F. A Comprehensive Review of the Current Progresses and Material Advances in Perovskite Solar Cells. Nanoscale Adv. 2023, 5, 3803–3833. [Google Scholar] [CrossRef] [PubMed]
  13. Cucco, B.; Katan, C.; Even, J.; Kepenekian, M.; Volonakis, G. Fine Structure of Excitons in Vacancy-Ordered Halide Double Perovskites. ACS Mater. Lett. 2023, 5, 52–59. [Google Scholar] [CrossRef]
  14. NREL Best Research-Cell Efficiency Chart. Available online: https://www.nrel.gov/pv/cell-efficiency (accessed on 1 July 2025).
  15. Zhu, H.; Teale, S.; Lintangpradipto, M.N.; Mahesh, S.; Chen, B.; McGehee, M.D.; Sargent, E.H.; Bakr, O.M. Long-Term Operating Stability in Perovskite Photovoltaics. Nat. Rev. Mater. 2023, 8, 569–586. [Google Scholar] [CrossRef]
  16. Ma, C.; Ni, M.; Liu, X.; Zhan, K.; Chen, M.; Li, S.; Li, F.; Wang, H.; Dang, Y. Recent Progress in Perovskite Light-Emitting Diodes with High External Quantum Efficiency and Stability. CrystEngComm 2025, 27, 3853–3876. [Google Scholar] [CrossRef]
  17. Zhang, J.; Ma, C. Recent Progress and Future Opportunities for Optical Manipulation in Halide Perovskite Photodetectors. Nanomaterials 2025, 15, 816. [Google Scholar] [CrossRef]
  18. Hidalgo, J.; Kaiser, W.; An, Y.; Li, R.; Oh, Z.; Castro-Méndez, A.-F.; LaFollette, D.K.; Kim, S.; Lai, B.; Breternitz, J.; et al. Synergistic Role of Water and Oxygen Leads to Degradation in Formamidinium-Based Halide Perovskites. J. Am. Chem. Soc. 2023, 145, 24549–24557. [Google Scholar] [CrossRef]
  19. Kore, B.P.; Jamshidi, M.; Gardner, J.M. The Impact of Moisture on the Stability and Degradation of Perovskites in Solar Cells. Mater. Adv. 2024, 5, 2200–2217. [Google Scholar] [CrossRef]
  20. Ahmed, I.; Prakash, K.; Mobin, S.M. Lead-Free Perovskites for Solar Cell Applications: Recent Progress, Ongoing Challenges, and Strategic Approaches. Chem. Commun. 2025, 61, 6691–6721. [Google Scholar] [CrossRef]
  21. Meyer, E.; Mutukwa, D.; Zingwe, N.; Taziwa, R. Lead-Free Halide Double Perovskites: A Review of the Structural, Optical, and Stability Properties as Well as Their Viability to Replace Lead Halide Perovskites. Metals 2018, 8, 667. [Google Scholar] [CrossRef]
  22. Vasala, S.; Karppinen, M. A2B′B″O6 Perovskites: A Review. Prog. Solid State Chem. 2015, 43, 1–36. [Google Scholar] [CrossRef]
  23. Ghosh, S.; Shankar, H.; Kar, P. Recent Developments of Lead-Free Halide Double Perovskites: A New Superstar in the Optoelectronic Field. Mater. Adv. 2022, 3, 3742–3765. [Google Scholar] [CrossRef]
  24. Nabi, M.; Padelkar, S.S.; Jasieniak, J.J.; Simonov, A.N.; Alam, A. Lead-Free Magnetic Double Perovskites for Photovoltaic and Photocatalysis Applications. Phys. Rev. Appl. 2024, 21, 014063. [Google Scholar] [CrossRef]
  25. Maughan, A.E.; Ganose, A.M.; Scanlon, D.O.; Neilson, J.R. Perspectives and Design Principles of Vacancy-Ordered Double Perovskite Halide Semiconductors. Chem. Mater. 2019, 31, 1184–1195. [Google Scholar] [CrossRef]
  26. Rahim, W.; Cheng, A.; Lyu, C.; Shi, T.; Wang, Z.; Scanlon, D.O.; Palgrave, R.G. Geometric Analysis and Formability of the Cubic A2BX6 Vacancy-Ordered Double Perovskite Structure. Chem. Mater. 2020, 32, 9573–9583. [Google Scholar] [CrossRef]
  27. Abfalterer, A.; Shamsi, J.; Kubicki, D.J.; Savory, C.N.; Xiao, J.; Divitini, G.; Li, W.; Macpherson, S.; Gałkowski, K.; MacManus-Driscoll, J.L.; et al. Colloidal Synthesis and Optical Properties of Perovskite-Inspired Cesium Zirconium Halide Nanocrystals. ACS Mater. Lett. 2020, 2, 1644–1652. [Google Scholar] [CrossRef]
  28. Guo, Y.; Wang, B.; Zhang, X.; An, K.; Zang, Z.; Li, R. Molecule Design Enabled High Efficiency Flexible Zirconium-Based Lead-Free Perovskite Scintillator. Appl. Phys. Lett. 2025, 126, 081901. [Google Scholar] [CrossRef]
  29. You, M.-X.; Lyu, Z.; Xu, Q.; Sun, D.; Tan, T.; Luo, P.; Lu, Z.; You, H. Enhanced and Tunable Emission from Organic–Inorganic Metal Halide Perovskites A2ZrCl6:Sb3+ via A-Site Organic Cation Manipulation. ACS Appl. Mater. Interfaces 2025, 17, 35714–35722. [Google Scholar] [CrossRef]
  30. Wang, Z.; Lai, J.; Huang, Q.; Wu, D.; Qi, F.; Zhang, N.; Pu, Y.; Tian, C.; Chen, W.; Liu, Y.; et al. Ultrahigh PLQY Lead-Free Organic–Inorganic Hybrid Zirconium-Based Perovskites in Anticounterfeiting Applications. Adv. Opt. Mater. 2023, 11, 2300399. [Google Scholar] [CrossRef]
  31. Zhu, C.; Jin, J.; Wang, Z.; Xu, Z.; Folgueras, M.C.; Jiang, Y.; Uzundal, C.B.; Le, H.K.D.; Wang, F.; Zheng, X.; et al. Supramolecular Assembly of Blue and Green Halide Perovskites with Near-Unity Photoluminescence. Science 2024, 383, 86–93. [Google Scholar] [CrossRef]
  32. Dai, G.; Ma, Z.; Qiu, Y.; Li, Z.; Fu, X.; Jiang, H.; Ma, Z. Excitation-Dependent Luminescence of 0D ((CH3)4N)2ZrCl6 across the Full Visible Region. J. Phys. Chem. Lett. 2022, 13, 7553–7560. [Google Scholar] [CrossRef]
  33. Lin, J.-W.; Lu, X.; Liu, Z.; Lin, Y.-P.; Yang, J.; Ge, Y.; Zhou, C.; Wang, X.; Li, J.-R.; Du, K.-Z.; et al. Optical Property Regulation through Host–Guest Interaction in a Zero-Dimensional Zr Chloride. Chem. Mater. 2024, 36, 4600–4606. [Google Scholar] [CrossRef]
  34. Tagiara, N.S.; Psycharis, V.; Kaltzoglou, A. Synthesis, Crystal Structure and Luminescence of [(CH3)3S]2ZrCl6. J. Coord. Chem. 2024, 77, 286–294. [Google Scholar] [CrossRef]
  35. Kolokytha, C.; Lathiotakis, N.N.; Kaltzoglou, A.; Petsalakis, I.D.; Tzeli, D. The Effect of A-Cation and X-Anion Substitutions on the Electronic and Structural Properties of A2ZrX6 ‘Defect’ Perovskite Materials: A Theoretical Density Functional Theory Study. Materials 2025, 18, 726. [Google Scholar] [CrossRef]
  36. Wang, C.; Liu, Y.; Feng, X.; Zhou, C.; Liu, Y.; Yu, X.; Zhao, G. Phase Regulation Strategy of Perovskite Nanocrystals from 1D Orthomorphic NH4PbI3 to 3D Cubic (NH4)0.5Cs0.5Pb(I0.5Br0.5)3 Phase Enhances Photoluminescence. Angew. Chem. Int. Ed. 2019, 58, 11642–11646. [Google Scholar] [CrossRef]
  37. Kresse, G.; Furthmüller, J. Efficiency of Ab-Initio Total Energy Calculations for Metals and Semiconductors Using a Plane-Wave Basis Set. Comput. Mater. Sci. 1996, 6, 15–50. [Google Scholar] [CrossRef]
  38. Kresse, G.; Furthmüller, J. Efficient Iterative Schemes for Ab. Initio Total-Energy Calculations Using a Plane-Wave Basis Set. Phys. Rev. B 1996, 54, 11169–11186. [Google Scholar] [CrossRef]
  39. Blöchl, P.E. Projector Augmented-Wave Method. Phys. Rev. B 1994, 50, 17953–17979. [Google Scholar] [CrossRef]
  40. Krukau, A.V.; Vydrov, O.A.; Izmaylov, A.F.; Scuseria, G.E. Influence of the Exchange Screening Parameter on the Performance of Screened Hybrid Functionals. J. Chem. Phys. 2006, 125, 224106. [Google Scholar] [CrossRef]
  41. Franchini, C. Hybrid Functionals Applied to Perovskites. J. Phys. Condens. Matter 2014, 26, 253202. [Google Scholar] [CrossRef]
  42. El-Mellouhi, F.; Brothers, E.N.; Lucero, M.J.; Bulik, I.W.; Scuseria, G.E. Structural Phase Transitions of the Metal Oxide Perovskites SrTiO3, LaAlO3, and LaTiO3 Studied with a Screened Hybrid Functional. Phys. Rev. B 2013, 87, 035107. [Google Scholar] [CrossRef]
  43. Becke, A.D. Density-Functional Thermochemistry. III. The Role of Exact Exchange. J. Chem. Phys. 1993, 98, 5648–5652. [Google Scholar] [CrossRef]
  44. Blaudeau, J.-P.; McGrath, M.P.; Curtiss, L.A.; Radom, L. Extension of Gaussian-2 (G2) Theory to Molecules Containing Third-Row Atoms K and Ca. J. Chem. Phys. 1997, 107, 5016–5021. [Google Scholar] [CrossRef]
  45. Kageshima, Y.; Kumagai, H.; Teshima, K.; Domen, K.; Nishikiori, H. Neutral Buffered Electrolytes Guarantee Ideal Band-Edge Pinning for Semiconductor Photoanodes. Chem. Sci. 2025, 16, 14088–14097. [Google Scholar] [CrossRef]
  46. Man, G.J.; Kamal, C.; Kalinko, A.; Phuyal, D.; Acharya, J.; Mukherjee, S.; Nayak, P.K.; Rensmo, H.; Odelius, M.; Butorin, S.M. A-Site Cation Influence on the Conduction Band of Lead Bromide Perovskites. Nat. Commun. 2022, 13, 3839. [Google Scholar] [CrossRef]
Materials 18 03976 g001
Figure 1. Calculated crystal structures of (a) (NH4)2ZrCl6, (b) (NH4)2ZrBr6, and (c) (NH4)2ZrI6. In the polyhedral structures, Zr is depicted as grey spheres, and the halogen atoms are shown as green (Cl), brown (Br), and purple (I) spheres. Within the ammonium cation, N atoms are shown as blue and H atoms as white spheres.
Figure 1. Calculated crystal structures of (a) (NH4)2ZrCl6, (b) (NH4)2ZrBr6, and (c) (NH4)2ZrI6. In the polyhedral structures, Zr is depicted as grey spheres, and the halogen atoms are shown as green (Cl), brown (Br), and purple (I) spheres. Within the ammonium cation, N atoms are shown as blue and H atoms as white spheres.
Materials 18 03976 g001
Materials 18 03976 g002aMaterials 18 03976 g002b
Figure 2. Calculated band structures and densities of states (DOSs) using the PBE functional for (a) (NH4)2ZrCl6, (b) (NH4)2ZrBr6 and (c) (NH4)2ZrI6. Corresponding DOSs calculated using the HSE06 functional are also shown for (d) (NH4)2ZrCl6, (e) (NH4)2ZrBr6 and (f) (NH4)2ZrI6.
Figure 2. Calculated band structures and densities of states (DOSs) using the PBE functional for (a) (NH4)2ZrCl6, (b) (NH4)2ZrBr6 and (c) (NH4)2ZrI6. Corresponding DOSs calculated using the HSE06 functional are also shown for (d) (NH4)2ZrCl6, (e) (NH4)2ZrBr6 and (f) (NH4)2ZrI6.
Materials 18 03976 g002aMaterials 18 03976 g002b
Materials 18 03976 g003
Figure 3. Calculated crystal structures of (a) MA2ZrCl6, (b) MA2ZrBr6, and (c) MA2ZrI6. In the polyhedral structures, Zr is depicted as grey spheres, and the halogen atoms are shown as green (Cl), brown (Br), and purple (I) spheres. Within MA+, N atoms are shown as blue, C atoms as black, and H atoms as white spheres.
Figure 3. Calculated crystal structures of (a) MA2ZrCl6, (b) MA2ZrBr6, and (c) MA2ZrI6. In the polyhedral structures, Zr is depicted as grey spheres, and the halogen atoms are shown as green (Cl), brown (Br), and purple (I) spheres. Within MA+, N atoms are shown as blue, C atoms as black, and H atoms as white spheres.
Materials 18 03976 g003
Materials 18 03976 g004
Figure 4. Calculated band structures and densities of states (DOSs) using the PBE functional for (a) MA2ZrCl6, (b) MA2ZrBr6 and (c) MA2ZrI6. Corresponding DOSs calculated using the HSE06 functional are also shown for (d) MA2ZrCl6, (e) MA2ZrBr6, and (f) MA2ZrI6.
Figure 4. Calculated band structures and densities of states (DOSs) using the PBE functional for (a) MA2ZrCl6, (b) MA2ZrBr6 and (c) MA2ZrI6. Corresponding DOSs calculated using the HSE06 functional are also shown for (d) MA2ZrCl6, (e) MA2ZrBr6, and (f) MA2ZrI6.
Materials 18 03976 g004
Materials 18 03976 g005
Figure 5. Calculated crystal structures of (a) DMA2ZrCl6, (b) DMA2ZrBr6, and (c) DMA2ZrI6. In the polyhedral structures, Zr is depicted as grey spheres, and the halogen atoms are shown as green (Cl), brown (Br), and purple (I) spheres. Within DMA+, N atoms are shown as blue, C atoms as black, and H atoms as white spheres.
Figure 5. Calculated crystal structures of (a) DMA2ZrCl6, (b) DMA2ZrBr6, and (c) DMA2ZrI6. In the polyhedral structures, Zr is depicted as grey spheres, and the halogen atoms are shown as green (Cl), brown (Br), and purple (I) spheres. Within DMA+, N atoms are shown as blue, C atoms as black, and H atoms as white spheres.
Materials 18 03976 g005
Materials 18 03976 g006
Figure 6. Calculated band structures and densities of states (DOSs) using the PBE functional for (a) DMA2ZrCl6, (b) DMA2ZrBr6, and (c) DMA2ZrI6. Corresponding DOS calculated using the HSE06 functional are also shown for (d) DMA2ZrCl6, (e) DMA2ZrBr6 and (f) DMA2ZrI6.
Figure 6. Calculated band structures and densities of states (DOSs) using the PBE functional for (a) DMA2ZrCl6, (b) DMA2ZrBr6, and (c) DMA2ZrI6. Corresponding DOS calculated using the HSE06 functional are also shown for (d) DMA2ZrCl6, (e) DMA2ZrBr6 and (f) DMA2ZrI6.
Materials 18 03976 g006
Materials 18 03976 g007
Figure 7. Calculated crystal structures of (a) TMA2ZrCl6, (b) TMA2ZrBr6, and (c) TMA2ZrI6. In the polyhedral structures, Zr is depicted as grey spheres, and the halogen atoms are shown as green (Cl), brown (Br), and purple (I) spheres. Within TMA+, N atoms are shown as blue, C atoms as black, and H atoms as white spheres.
Figure 7. Calculated crystal structures of (a) TMA2ZrCl6, (b) TMA2ZrBr6, and (c) TMA2ZrI6. In the polyhedral structures, Zr is depicted as grey spheres, and the halogen atoms are shown as green (Cl), brown (Br), and purple (I) spheres. Within TMA+, N atoms are shown as blue, C atoms as black, and H atoms as white spheres.
Materials 18 03976 g007
Materials 18 03976 g008aMaterials 18 03976 g008b
Figure 8. Calculated band structures and densities of states (DOSs) using the PBE functional for (a) TMA2ZrCl6, (b) TMA2ZrBr6, and (c) TMA2ZrI6. Corresponding DOSs calculated using the HSE06 functional are also shown for (d) TMA2ZrCl6, (e) TMA2ZrBr6 and (f) TMA2ZrI6.
Figure 8. Calculated band structures and densities of states (DOSs) using the PBE functional for (a) TMA2ZrCl6, (b) TMA2ZrBr6, and (c) TMA2ZrI6. Corresponding DOSs calculated using the HSE06 functional are also shown for (d) TMA2ZrCl6, (e) TMA2ZrBr6 and (f) TMA2ZrI6.
Materials 18 03976 g008aMaterials 18 03976 g008b
Materials 18 03976 g009
Figure 9. Calculated crystal structures of (a) (PH4)2ZrCl6, (b) (PH4)2ZrBr6, and (c) (PH4)2ZrI6. In the polyhedral structures, Zr is depicted as grey spheres, and the halogen atoms are shown as green (Cl), brown (Br), and purple (I) spheres. Within the (PH4)+, P atoms are shown as pink and H atoms as white spheres.
Figure 9. Calculated crystal structures of (a) (PH4)2ZrCl6, (b) (PH4)2ZrBr6, and (c) (PH4)2ZrI6. In the polyhedral structures, Zr is depicted as grey spheres, and the halogen atoms are shown as green (Cl), brown (Br), and purple (I) spheres. Within the (PH4)+, P atoms are shown as pink and H atoms as white spheres.
Materials 18 03976 g009
Materials 18 03976 g010
Figure 10. Calculated band structures and densities of states (DOSs) using the PBE functional for (a) (PH4)2ZrCl6, (b) (PH4)2ZrBr6, and (c) (PH4)2ZrI6. Corresponding DOSs calculated using the HSE06 functional are also shown for (d) (PH4)2ZrCl6, (e) (PH4)2ZrBr6, and (f) (PH4)2ZrI6.
Figure 10. Calculated band structures and densities of states (DOSs) using the PBE functional for (a) (PH4)2ZrCl6, (b) (PH4)2ZrBr6, and (c) (PH4)2ZrI6. Corresponding DOSs calculated using the HSE06 functional are also shown for (d) (PH4)2ZrCl6, (e) (PH4)2ZrBr6, and (f) (PH4)2ZrI6.
Materials 18 03976 g010
Materials 18 03976 g011
Figure 11. Bandgap energy as a function of the molecular weight of the A-site cation, for the A2ZrX6 crystal, calculated using the HSE06 (solid lines) and PBE (dash lines) functionals. Color assignment: blue for N, grey for carbon, white for hydrogen, yellow for S and orange for P.
Figure 11. Bandgap energy as a function of the molecular weight of the A-site cation, for the A2ZrX6 crystal, calculated using the HSE06 (solid lines) and PBE (dash lines) functionals. Color assignment: blue for N, grey for carbon, white for hydrogen, yellow for S and orange for P.
Materials 18 03976 g011
Materials 18 03976 g012
Figure 12. Bandgap energy as a function of halogen electronegativity of the A2ZrX6 compounds, calculated using the HSE06 (solid lines) and PBE (dash lines) functionals.
Figure 12. Bandgap energy as a function of halogen electronegativity of the A2ZrX6 compounds, calculated using the HSE06 (solid lines) and PBE (dash lines) functionals.
Materials 18 03976 g012
Table 1. Calculated bandgap energy, Egap, (in eV), using PBE and HSE06 functionals, crystal symmetry, the lattice constants (a, b, c) (in Å) and the lattice angles (α, β, γ) (in °) for the structures (NH4)2ZrX6.
Table 1. Calculated bandgap energy, Egap, (in eV), using PBE and HSE06 functionals, crystal symmetry, the lattice constants (a, b, c) (in Å) and the lattice angles (α, β, γ) (in °) for the structures (NH4)2ZrX6.
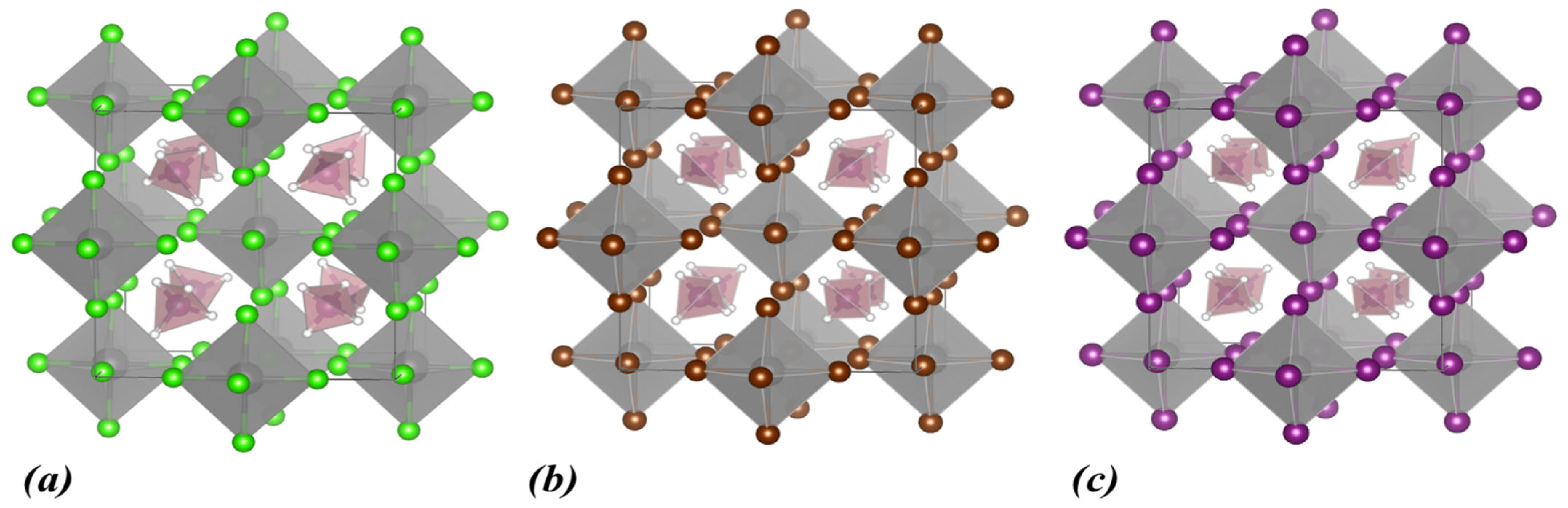
Lattice Constants Lattice Angles
StructureEgap
PBE		Egap
HSE06		Symmetry of Crystalabcαβγ
(NH4)2ZrCl63.584.75triclinic10.5210.1010.0490.0090.0089.68
(NH4)2ZrBr62.733.76triclinic11.0610.5810.5490.0090.0089.80
(NH4)2ZrI61.742.89triclinic11.8711.3511.3490.0090.0090.04
Table 2. Calculated bandgap energy, Egap, (in eV), using PBE and HSE06 functionals, crystal symmetry, the lattice constants (a, b, c) (in Å) and the lattice angles (α, β, γ) (in °) for the structures MA2ZrX6.
Table 2. Calculated bandgap energy, Egap, (in eV), using PBE and HSE06 functionals, crystal symmetry, the lattice constants (a, b, c) (in Å) and the lattice angles (α, β, γ) (in °) for the structures MA2ZrX6.
Lattice ConstantsLattice Angles
StructureEgap
PBE		Egap
HSE06		Symmetry of Crystalabcαβγ
MA2ZrCl62.884.06triclinic11.2610.8411.1890.0090.0089.98
MA2ZrBr62.113.14triclinic11.6411.2311.5990.0090.0089.99
MA2ZrI61.222.11triclinic12.3011.9212.2889.9990.0089.99
Table 3. Calculated bandgap energy, Egap, (in eV), using PBE and HSE06 functionals, crystal symmetry, the lattice constants (a, b, c) (in Å) and the lattice angles (α, β, γ) (in °) for the structures DMA2ZrX6.
Table 3. Calculated bandgap energy, Egap, (in eV), using PBE and HSE06 functionals, crystal symmetry, the lattice constants (a, b, c) (in Å) and the lattice angles (α, β, γ) (in °) for the structures DMA2ZrX6.
Lattice Constants Lattice Angles
StructureEgap
PBE		Egap
HSE06		Symmetry of Crystalabcαβγ
DMA2ZrCl63.564.64triclinic11.2112.6811.4189.2188.6889.07
DMA2ZrBr62.753.70triclinic11.5513.2911.6489.3089.2891.20
DMA2ZrI61.842.46triclinic12.2013.8412.3089.3089.4792.14
Table 4. Calculated bandgap energy, Egap, (in eV), using PBE and HSE06 functionals, crystal symmetry, the lattice constants (a, b, c) (in Å) and the lattice angles (α, β, γ) (in °) for the structures TMA2ZrX6.
Table 4. Calculated bandgap energy, Egap, (in eV), using PBE and HSE06 functionals, crystal symmetry, the lattice constants (a, b, c) (in Å) and the lattice angles (α, β, γ) (in °) for the structures TMA2ZrX6.
Lattice Constants Lattice Angles
StructureEgap PBEEgap HSE06Symmetry of Crystalabcαβγ
TMA2ZrCl63.424.54triclinic11.6413.2112.0491.0798.3290.12
TMA2ZrBr62.673.59triclinic12.0713.6312.4291.0897.9890.64
TMA2ZrI61.802.53triclinic12.6714.2513.0391.0397.1691.01
Table 5. Calculated bandgap energy, Egap, (in eV), using PBE and HSE06 functionals, crystal symmetry and the lattice constants (a, b, c) (in Å) for the structures (PH4)2ZrX6.
Table 5. Calculated bandgap energy, Egap, (in eV), using PBE and HSE06 functionals, crystal symmetry and the lattice constants (a, b, c) (in Å) for the structures (PH4)2ZrX6.
Lattice Constants
StructureEgap
PBE		Egap
HSE06		Symmetry of Crystalabc
(PH4)2ZrCl63.574.79cubic10.3410.341034
(PH4)2ZrBr62.703.79cubic10.9910.9910.99
(PH4)2ZrI61.682.63cubic11.7311.7311.73
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Kolokytha, C.; Tzeli, D.; Lathiotakis, N.N. Tailoring the Electronic and Structural Properties of Lead-Free A2ZrX6 “Defect” Perovskites: A DFT Study on A-Site Cation and Halogen Substitutions. Materials 2025, 18, 3976. https://doi.org/10.3390/ma18173976

AMA Style

Kolokytha C, Tzeli D, Lathiotakis NN. Tailoring the Electronic and Structural Properties of Lead-Free A2ZrX6 “Defect” Perovskites: A DFT Study on A-Site Cation and Halogen Substitutions. Materials. 2025; 18(17):3976. https://doi.org/10.3390/ma18173976

Chicago/Turabian Style

Kolokytha, Christina, Demeter Tzeli, and Nektarios N. Lathiotakis. 2025. "Tailoring the Electronic and Structural Properties of Lead-Free A2ZrX6 “Defect” Perovskites: A DFT Study on A-Site Cation and Halogen Substitutions" Materials 18, no. 17: 3976. https://doi.org/10.3390/ma18173976

APA Style

Kolokytha, C., Tzeli, D., & Lathiotakis, N. N. (2025). Tailoring the Electronic and Structural Properties of Lead-Free A2ZrX6 “Defect” Perovskites: A DFT Study on A-Site Cation and Halogen Substitutions. Materials, 18(17), 3976. https://doi.org/10.3390/ma18173976

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop