Low Cycle Fatigue Life Prediction for Hydrogen-Charged HRB400 Steel Based on CPFEM
Abstract
1. Introduction
2. LCF Testing of Hydrogen-Charged HRB400 Steel
2.1. Materials and Testing Methods
2.2. Low Cycle Fatigue Response
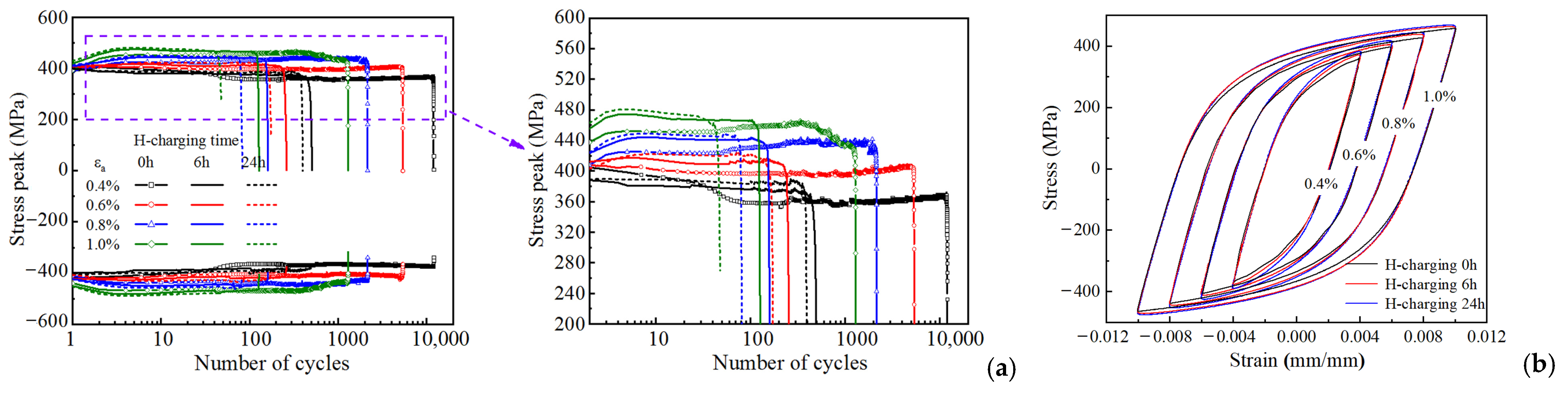
2.2.1. Cyclic Stress Response
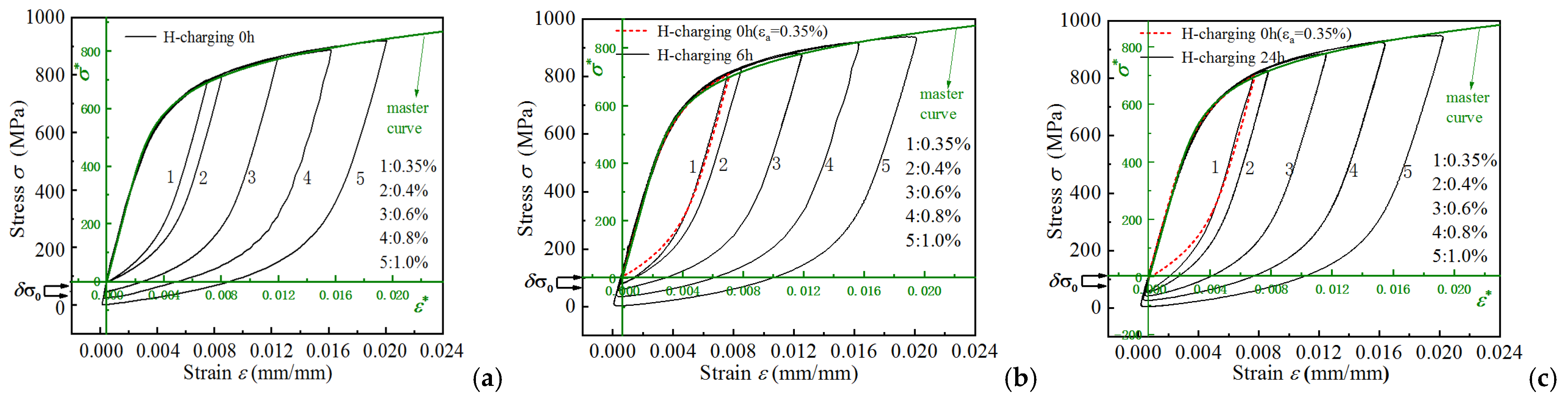
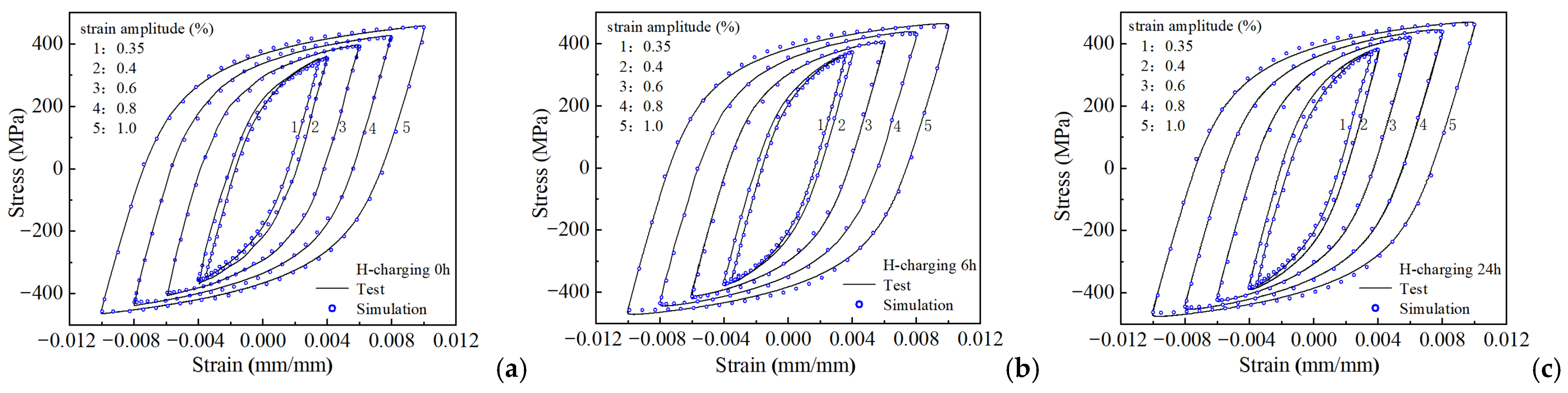
2.2.2. Analysis of Hysteresis Loop
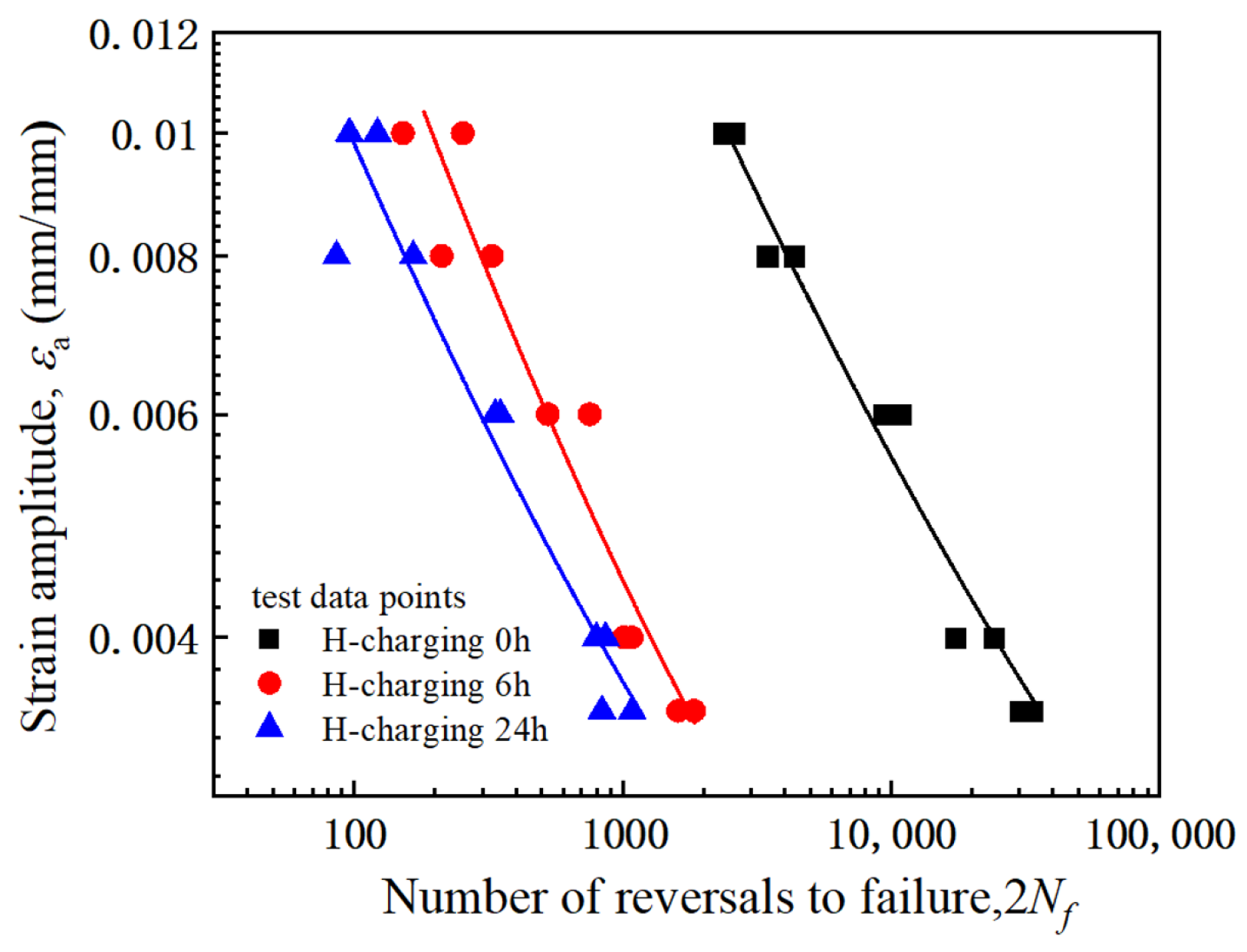
2.2.3. Strain-Life Relationships
3. Theory of Crystal Plastic Finite Element Method (CPFEM)
3.1. Crystal Plasticity Constitutive Model
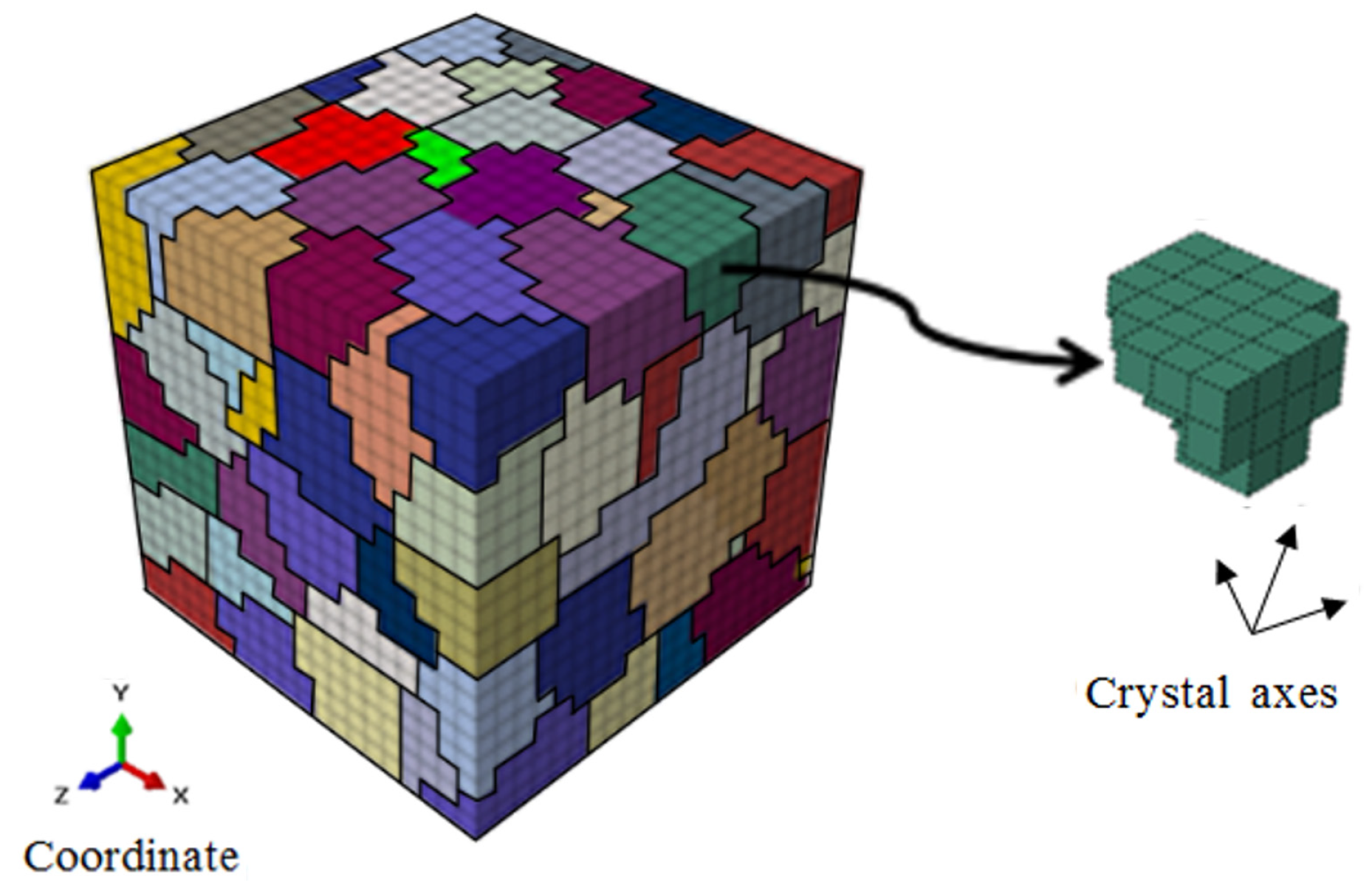
3.2. RVE Model Formulation
3.3. FIP Based on Microscale Deformation Inhomogeneity
3.4. FIP Considering Hydrogen Effects
4. Results and Discussion
4.1. Calibration and Validation of Model Parameters
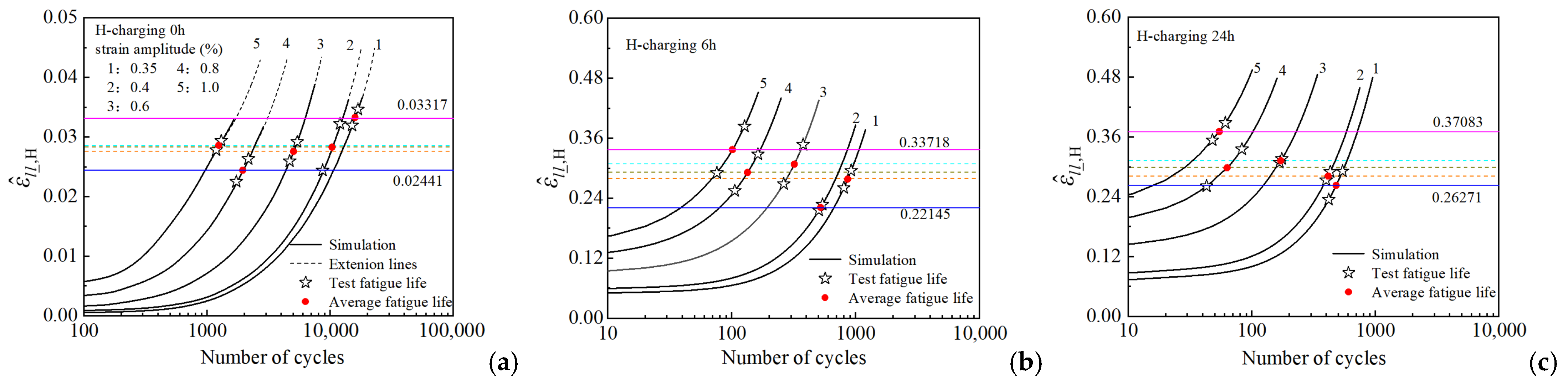
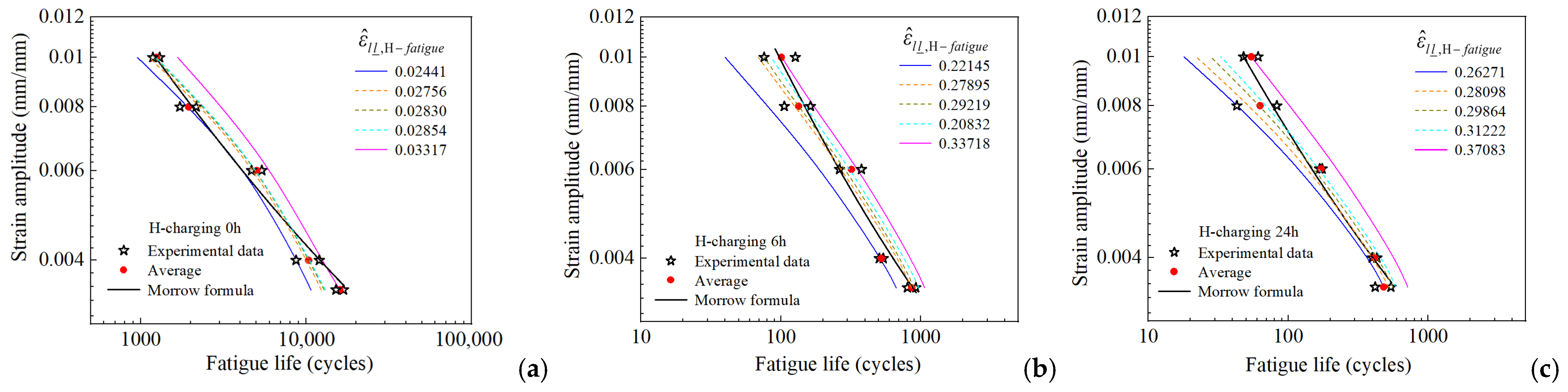
4.2. Determination of the FIP Critical Value
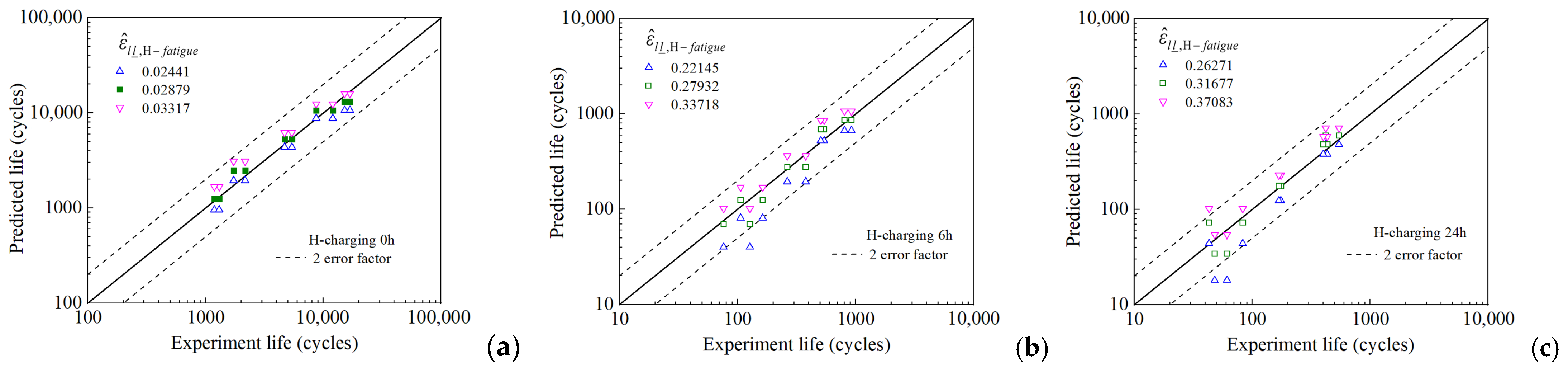
4.3. Fatigue Life Prediction and Validation
5. Conclusions
- (1)
- Hydrogen charging significantly modifies the cyclic hardening/softening characteristics and cyclic hysteresis behavior of HRB400 steel. It increases the elastic regime within the stabilized hysteresis loop and markedly reduces its LCF life.
- (2)
- The hydrogen-charged HRB400 steel specimens (charged for 0 h, 6 h, and 24 h) all exhibited non-Masing behavior. Their hysteretic response was dependent on the applied strain amplitude, manifesting as distinct elastic ranges under different strain amplitudes.
- (3)
- The cyclically stabilized stress–strain hysteresis loops of HRB400 steel were simulated using the CPFEM. The simulation results demonstrated excellent concurrence with the experimental measurements.
- (4)
- The proposed FIP is effective and feasible for predicting the LCF life of hydrogen-containing metals, with the discrepancies between the predicted and measured results generally within the two-fold error range.
- (5)
- The proposed low-cycle fatigue life prediction method theoretically requires only a single measured fatigue life at a specific strain amplitude to determine the critical value of the FIP, thereby enabling predictions of the LCF life under other cyclic loading conditions. This method presents the advantages of simplicity and efficiency. Furthermore, the prediction accuracy improves with the increase in the amount of measured fatigue life data.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Guo, Z.Z.; Ma, Y.F.; Wang, L.; Zhang, J.R.; Harik, I.E. Corrosion Fatigue Crack Propagation Mechanism of High-Strength Steel Bar in Various Environments. J. Mater. Civil Eng. 2020, 32, 04020115. [Google Scholar] [CrossRef]
- Fu, Z.; Sun, Y.; Hu, Y.; Chen, R.; Wang, P.; Kan, Q. Low-Cycle Fatigue Behavior of U71Mn Rail Steel with Pre-Corrosion. Eng. Fail. Anal. 2025, 168, 109118. [Google Scholar] [CrossRef]
- Siegwart, M.; Lyness, J.F.; McFarland, B.J.; Doyle, G. The Effect of Electrochemical Chloride Extraction on Pre-Stressed Concrete. Constr. Build. Mater. 2005, 19, 585–594. [Google Scholar] [CrossRef]
- Li, Q.D.; Ghadiani, H.; Jalilvand, V.; Alam, T.; Farhat, Z.; Islam, M.A. Hydrogen Impact: A Review on Diffusibility, Embrittlement Mechanisms, and Characterization. Materials 2024, 17, 965. [Google Scholar] [CrossRef] [PubMed]
- Mohtadi-Bonab, M.A. Effect of Different Parameters on Hydrogen Affected Fatigue Failure in Pipeline Steels. Eng. Fail. Anal. 2022, 137, 106262. [Google Scholar] [CrossRef]
- Behvar, A.; Haghshenas, M.; Djukic, M.B. Hydrogen Embrittlement and Hydrogen-Induced Crack Initiation in Additively Manufactured Metals: A Critical Review on Mechanical and Cyclic Loading. Int. J. Hydrogen Energy 2024, 58, 1214–1239. [Google Scholar] [CrossRef]
- Yang, G.; Guo, Z.; Li, Z.; Liang, L.; Zhang, Y.; Guo, H.; Wang, C.; Xu, K.; Li, L. Effect of Hydrogen on Low-Cycle Fatigue Properties and the Mechanism of Hysteresis Energy Method Lifetime Prediction of X80 Pipeline Steel. Corros. Sci. 2025, 243, 112599. [Google Scholar] [CrossRef]
- Michler, T.; Naumann, J.; Sattler, E. Influence of High-Pressure Gaseous Hydrogen on S-N Fatigue in Two Austenitic Stainless Steels. Int. J. Fatigue 2013, 51, 1–7. [Google Scholar] [CrossRef]
- Zheng, J.; Hu, J.; Ma, K.; Zhao, Y.; Zhang, R.; Gu, C.; Hua, Z. Study on Low Cycle Fatigue Properties of Cr-Mo Steel in 50 MPa Gaseous Hydrogen. Int. J. Hydrogen Energy 2024, 84, 1042–1049. [Google Scholar] [CrossRef]
- Li, W.X.; Zhao, S.W.; He, P.F.; Wang, B.J. Experimental and Numerical Study on High-Cycle Fatigue Performance of Austenitic Stainless Steel with Pre-Charged Hydrogen. Int. J. Fatigue 2024, 185, 108359. [Google Scholar] [CrossRef]
- Manonukul, A.; Dunne, F.P.E. High-and Low-Cycle Fatigue Crack Initiation Using Polycrystal Plasticity. Proc. R. Soc. A Math. Phys. Eng. Sci. 2004, 460, 1881–1903. [Google Scholar] [CrossRef]
- Sweeney, C.A.; McHugh, P.E.; McGarry, J.P.; Leen, S.B. Micromechanical Methodology for Fatigue in Cardiovascular Stents. Int. J. Fatigue 2012, 44, 202–216. [Google Scholar] [CrossRef]
- Wan, V.V.C.; Jiang, J.; MacLachlan, D.W.; Dunne, F.P.E. Microstructure-Sensitive Fatigue Crack Nucleation in a Polycrystalline Ni Superalloy. Int. J. Fatigue 2016, 90, 181–190. [Google Scholar] [CrossRef]
- Lu, R.; Li, K.S.; Wang, J.; Yang, J.; Zhang, X.C.; Tu, S.T. Understanding the Small Creep-Fatigue Crack Growth Mechanism of Polycrystalline Alloy Based on Crystal Plasticity and Extended Finite Element Method. Eng. Fract. Mech. 2024, 306, 110172. [Google Scholar] [CrossRef]
- Korsunsky, A.M.; Dini, D.; Dunne, F.P.E.; Walsh, M.J. Comparative Assessment of Dissipated Energy and Other Fatigue Criteria. Int. J. Fatigue 2007, 29, 1990–1995. [Google Scholar] [CrossRef]
- Zhang, P.; Zhang, L.; Baxevanakis, K.P.; Lu, S.; Zhao, L.G.; Bullough, C. Discrete Crystal Plasticity Modelling of Slip-Controlled Cyclic Deformation and Short Crack Growth under Low Cycle Fatigue. Int. J. Fatigue 2021, 145, 106095. [Google Scholar] [CrossRef]
- Jin, L.L.; Zeng, B.; Lu, D.M.; Gao, Y.J.; Zhang, K.S. Prediction of Strain Fatigue Life of HRB400 Steel Based on Meso-Deformation Inhomogeneity. Materials 2020, 13, 1464. [Google Scholar] [CrossRef] [PubMed]
- Zhang, K.S.; Ju, J.W.; Li, Z.; Bai, Y.L.; Brocks, W. Micromechanics Based Fatigue Life Prediction of a Polycrystalline Metal Applying Crystal Plasticity. Mech. Mater. 2015, 85, 16–37. [Google Scholar] [CrossRef]
- Cen, C.X.; Lu, D.M.; Qin, D.W.; Zhang, K.S. Torsional Fatigue Life Prediction of 30CrMnSiNi2A Based on Meso-Inhomogeneous Deformation. Materials 2021, 14, 1846. [Google Scholar] [CrossRef]
- Stark, A.; Sonnweber-Ribic, P.; Elsässer, C. Theoretical Study of Individual and Combined Effects of HELP- and HEDE-Based Damage Models on the Fatigue Behavior of Ferritic Steel by Hydrogen. Int. J. Hydrogen Energy 2025, 109, 27–39. [Google Scholar] [CrossRef]
- Moshtaghi, M.; Safyari, M.; Khonsari, M.M. Hydrogen-Enhanced Entropy (HEENT): A Concept for Hydrogen Embrittlement Prediction. Int. J. Hydrogen Energy 2024, 53, 434–440. [Google Scholar] [CrossRef]
- Li, X.; Zhang, J.; Cui, Y.; Djukic, M.B.; Feng, H.; Wang, Y. Review of the Hydrogen Embrittlement and Interactions between Hydrogen and Microstructural Interfaces in Metallic Alloys: Grain Boundary, Twin Boundary, and Nano-Precipitate. Int. J. Hydrogen Energy 2024, 72, 74–109. [Google Scholar] [CrossRef]
- Meda, U.S.; Bhat, N.; Pandey, A.; Subramanya, K.N.; Lourdu Antony Raj, M.A. Challenges associated with hydrogen storage systems due to the hydrogen embrittlement of high strength steels. Int. J. Hydrogen Energy 2023, 48, 17894–17913. [Google Scholar] [CrossRef]
- Komatsu, A.; Fujinami, M.; Hatano, M.; Matsumoto, K.; Sugeoi, M.; Chiari, L. Straining-temperature dependence of vacancy behavior in hydrogen-charged austenitic stainless steel 316L. Int. J. Hydrogen Energy 2021, 46, 6960–6969. [Google Scholar] [CrossRef]
- Wang, S.; Nagao, A.; Sofronis, P.; Robertson, I.M. Hydrogen-Modified Dislocation Structures in a Cyclically Deformed Ferritic-Pearlitic Low Carbon Steel. Acta Mater. 2018, 144, 164–176. [Google Scholar] [CrossRef]
- Martin, M.L.; Dadfarnia, M.; Nagao, A.; Wang, S.; Sofronis, P. Enumeration of the Hydrogen-Enhanced Localized Plasticity Mechanism for Hydrogen Embrittlement in Structural Materials. Acta Mater. 2019, 165, 734–750. [Google Scholar] [CrossRef]
- An, T.; Peng, H.T.; Bai, P.P.; Zheng, S.Q.; Wen, X.L.; Zhang, L. Influence of Hydrogen Pressure on Fatigue Properties of X80 Pipeline Steel. Int. J. Hydrogen Energy 2017, 42, 15669–15678. [Google Scholar] [CrossRef]
- Hwang, B.K.; Cha, S.J.; Kim, H.T.; Lee, S.J.; Kim, J.H.; Lee, J.M. Notch Sensitivity of Hydrogen-Charged 316L Stainless Steel: Experimental Insights into Mechanical Degradation and Fracture Mechanics. Materials 2025, 18, 1274. [Google Scholar] [CrossRef]
- Campari, A.; Ustolin, F.; Alvaro, A.; Paltrinieri, N. Inspection of Hydrogen Transport Equipment: A Data-Driven Approach to Predict Fatigue Degradation. Reliab. Eng. Syst. Saf. 2024, 251, 110342. [Google Scholar] [CrossRef]
- Hu, J.; Ma, K.; Zhang, Z.; Zhang, R.; Zheng, J. Machine Learning-Based Prediction of Hydrogen-Assisted Fatigue Crack Growth Rate in Cr–Mo Steel. Int. J. Hydrogen Energy 2025, 122, 1–11. [Google Scholar] [CrossRef]
- Yang, S.Y.; De-Jesus, A.M.P.; Meng, D.B.; Nie, P.; Darabi, R.; Azinpour, E.; Zhu, S.P.; Wang, Q. Very High-Cycle Fatigue Behavior of Steel in Hydrogen Environment: State of the Art Review and Challenges. Eng. Fail. Anal. 2024, 166, 108898. [Google Scholar] [CrossRef]
- Zeng, B.; Zhang, G.; Zhang, K.; Qin, S.; Li, Y. Effect of Hydrogen on Low-Cycle Fatigue Behavior of HRB400 Steel under Asymmetric Cyclic Loading. Int. J. Hydrogen Energy 2023, 48, 422–435. [Google Scholar] [CrossRef]
- Asaro, R.J.; Rice, J.R. Strain Localization in Ductile Single Crystals. J. Mech. Phys. Solids 1977, 25, 309–338. [Google Scholar] [CrossRef]
- Hill, R.; Rice, J.R. Constitutive Analysis of Elastic-Plastic Crystals at Arbitrary Strain. J. Mech. Phys. Solids 1972, 20, 401–413. [Google Scholar] [CrossRef]
- Peirce, D.; Asaro, R.J.; Needleman, A. Material Rate Dependence and Localized Deformation in Crystalline Solids. Acta Metall. Sin. 1983, 31, 1951–1976. [Google Scholar] [CrossRef]
- Hutchinson, J.W. Bounds and Self-Consistent Estimates for Creep of Polycrystalline Materials. Proc. R. Soc. A Math. Phys. 1976, 348, 101–127. [Google Scholar]
- Feng, L.; Zhang, G.; Zhang, K. Discussion of Cyclic Plasticity and Viscoplasticity of Single Crystal Nickel-Based Superalloy in Large Strain Analysis: Comparison of Anisotropic Macroscopic Model and Crystallographic Model. Int. J. Mech. Sci. 2004, 46, 1157–1171. [Google Scholar] [CrossRef]
- Frederick, C.O.; Armstrong, P.J. A Mathematical Representation of the Multiaxial Bauschinger Effect. Mater. High Temp. 2007, 24, 1–26. [Google Scholar] [CrossRef]
- Zhang, K.S.; Shi, Y.K.; Ju, J.W. Grain-Level Statistical Plasticity Analysis on Strain Cycle Fatigue of a FCC Metal. Mech. Mater. 2013, 64, 76–90. [Google Scholar] [CrossRef]
- Pan, J.; Rice, J.R. Rate Sensitivity of Plastic Flow and Implications for Yield-Surface Vertices. Int. J. Solids Struct. 1983, 19, 973–987. [Google Scholar] [CrossRef]
- Hutchinson, J.W. Elastic-Plastic Behaviour of Polycrystalline Metals and Composites. Proc. R. Soc. A Math. Phys. 1970, 319, 247–272. [Google Scholar]
- Chang, Y.W.; Asaro, R.J. An Experimental Study of Shear Localization in Aluminum-Copper Single Crystals. Acta Metall. 1981, 29, 241–257. [Google Scholar] [CrossRef]
- Needleman, A.; Asaro, R.J.; Lemonds, J.; Peirce, D. Finite Element Analysis of Crystalline Solids. Comput. Methods Appl. Mech. Eng. 1985, 52, 689–708. [Google Scholar] [CrossRef]
- Ma, Y.S.; Sun, D.Z.; Andrieux, F.; Zhang, K.S. Influences of Initial Porosity Stress Triaxiality and Lode Parameter on Plastic Deformation and Ductile Fracture. Acta Mech. Solida Sin. 2017, 30, 493–506. [Google Scholar] [CrossRef]
- Chen, Y.S.; Lu, H.Z.; Liang, J.T.; Rosenthal, A.; Liu, H.W.; Sneddon, G. Observation of Hydrogen Trapping at Dislocations, Grain Boundaries, and Precipitates. Science 2020, 367, 171–175. [Google Scholar] [CrossRef]
- Shibata, A.; Yonemura, T.; Momotani, Y.; Park, M.; Takagi, S.; Madi, Y.; Besson, J.; Tsuji, N. Effects of Local Stress, Strain, and Hydrogen Content on Hydrogen-Related Fracture Behavior in Low-Carbon Martensitic Steel. Acta Mater. 2021, 210, 116828. [Google Scholar] [CrossRef]
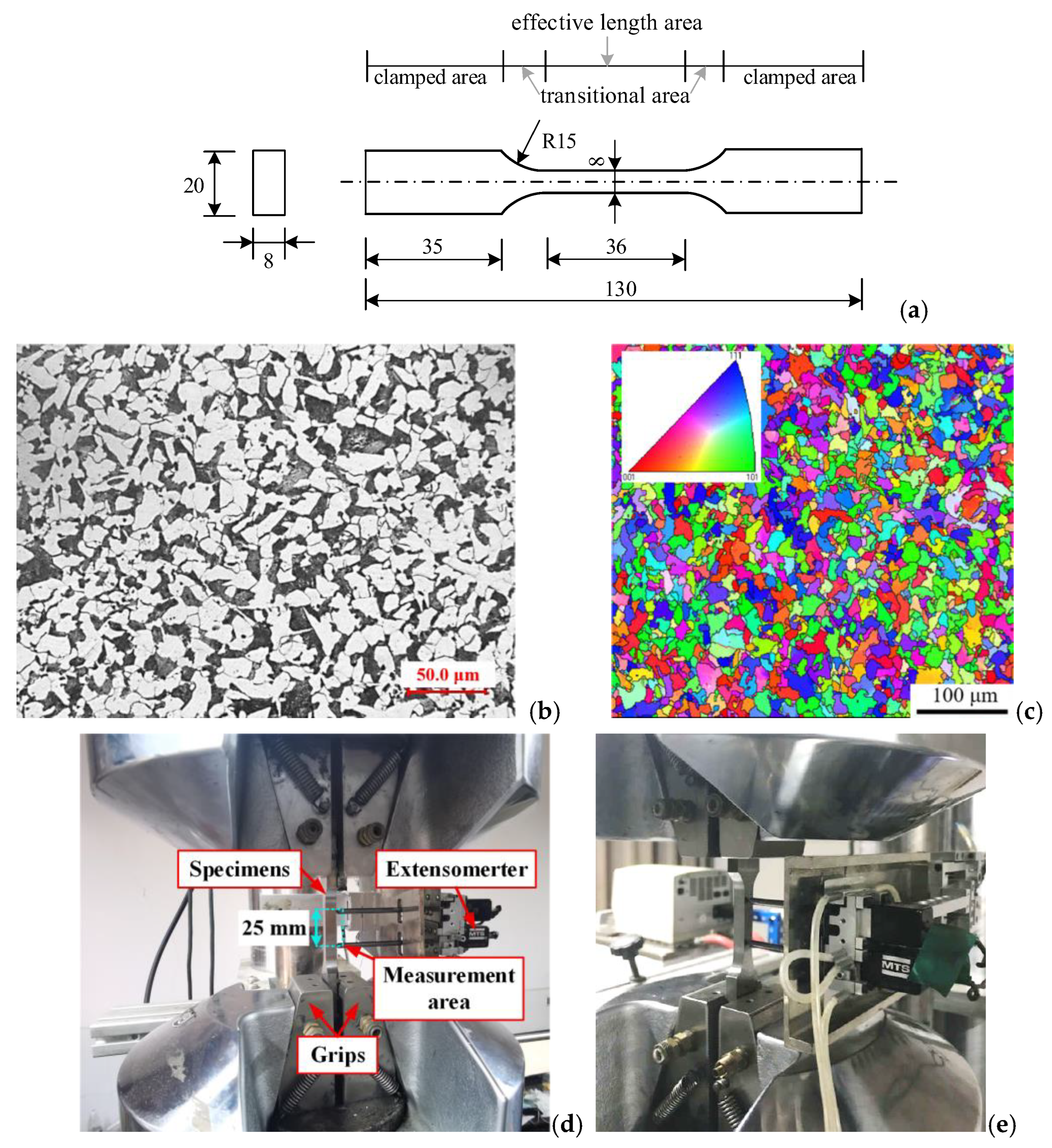
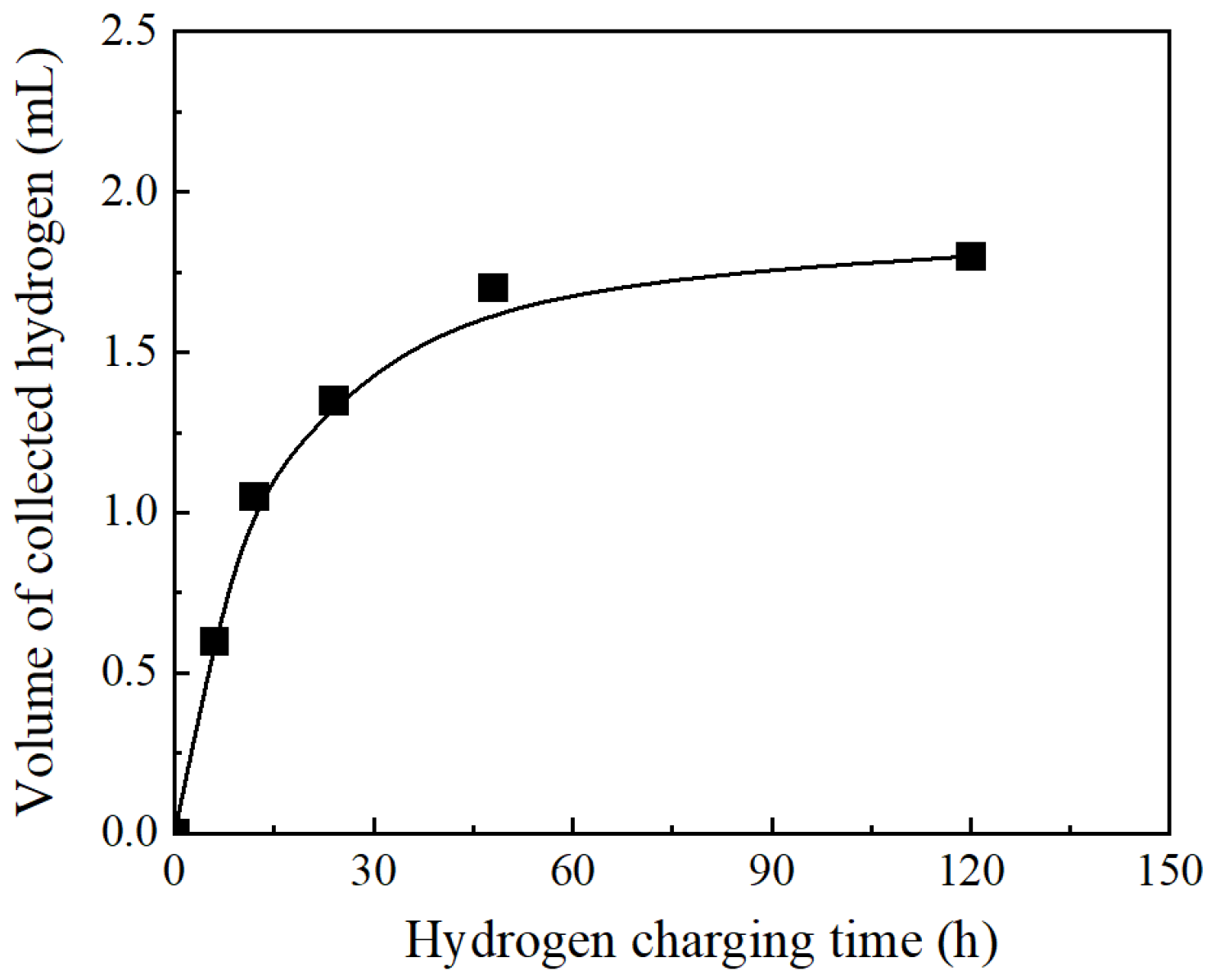



| Group Number | Electrolyte | Current Density | Hydrogen Charging Time |
|---|---|---|---|
| H-charging 0 h | — | — | 0 h |
| H-charging 6 h | 0.5 mol/mL H2SO4 + 0.001 g/mL (NH2)2CS | 5 mA/cm2 | 6 h |
| H-charging 24 h | 0.5 mol/mL H2SO4 + 0.001 g/mL (NH2)2CS | 5 mA/cm2 | 24 h |
| Hydrogen-Charged Time | (MPa) | b | c | |
|---|---|---|---|---|
| 0 h | 1408.1 | −0.128 | 0.579 | −0.558 |
| 6 h | 1155.5 | −0.153 | 0.271 | −0.682 |
| 24 h | 958.8 | −0.135 | 0.116 | −0.602 |
GPa | GPa | GPa | MPa | MPa | MPa | GPa | GPa | s−1 | s−1 | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 293.4 | 158.0 | 67.6 | 90 | 94 | 110 | 35 | 0.57 | 0 | 0 | 0 | 0.001 | 1 | 200 |
| 0.35% | 0.4% | 0.6% | 0.8% | 1.0% | |
|---|---|---|---|---|---|
| H-charging 0 h | 91 | 91 | 94 | 98 | 102 |
| H-charging 6 h | 99 | 99 | 102 | 105 | 108 |
| H-charging 24 h | 103 | 103 | 105 | 108 | 111 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zeng, B.; Wei, X.-F.; Tan, J.-Z.; Zhang, K.-S. Low Cycle Fatigue Life Prediction for Hydrogen-Charged HRB400 Steel Based on CPFEM. Materials 2025, 18, 3920. https://doi.org/10.3390/ma18163920
Zeng B, Wei X-F, Tan J-Z, Zhang K-S. Low Cycle Fatigue Life Prediction for Hydrogen-Charged HRB400 Steel Based on CPFEM. Materials. 2025; 18(16):3920. https://doi.org/10.3390/ma18163920
Chicago/Turabian StyleZeng, Bin, Xue-Fei Wei, Ji-Zuan Tan, and Ke-Shi Zhang. 2025. "Low Cycle Fatigue Life Prediction for Hydrogen-Charged HRB400 Steel Based on CPFEM" Materials 18, no. 16: 3920. https://doi.org/10.3390/ma18163920
APA StyleZeng, B., Wei, X.-F., Tan, J.-Z., & Zhang, K.-S. (2025). Low Cycle Fatigue Life Prediction for Hydrogen-Charged HRB400 Steel Based on CPFEM. Materials, 18(16), 3920. https://doi.org/10.3390/ma18163920






