Compressive Mechanical Properties of Lattice Structures with Varied Structural Parameters Prepared by Stereolithography
Abstract
1. Introduction
2. Materials and Methods
2.1. Sample Preparation
2.2. Mechanical Property Testing
2.3. Finite Element Modeling
2.4. Formulation of Structural Efficiency and Stress Concentration Coefficient
3. Results and Discussion
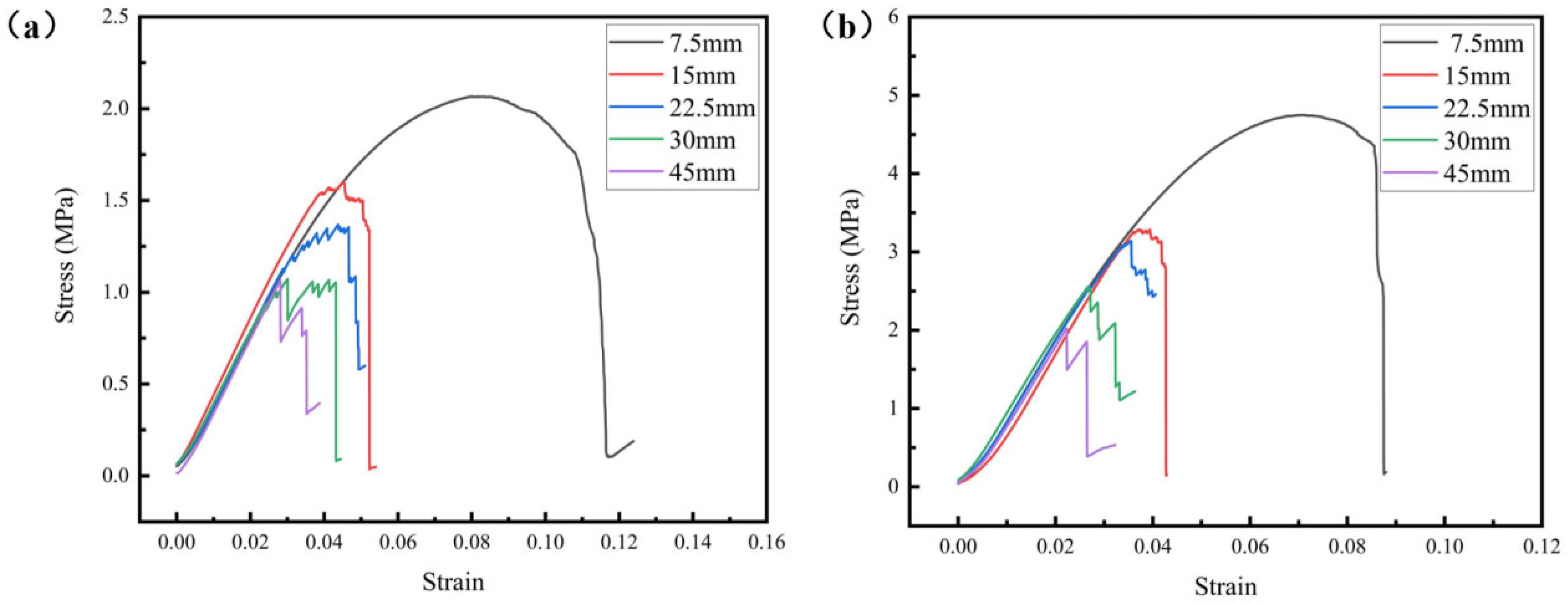
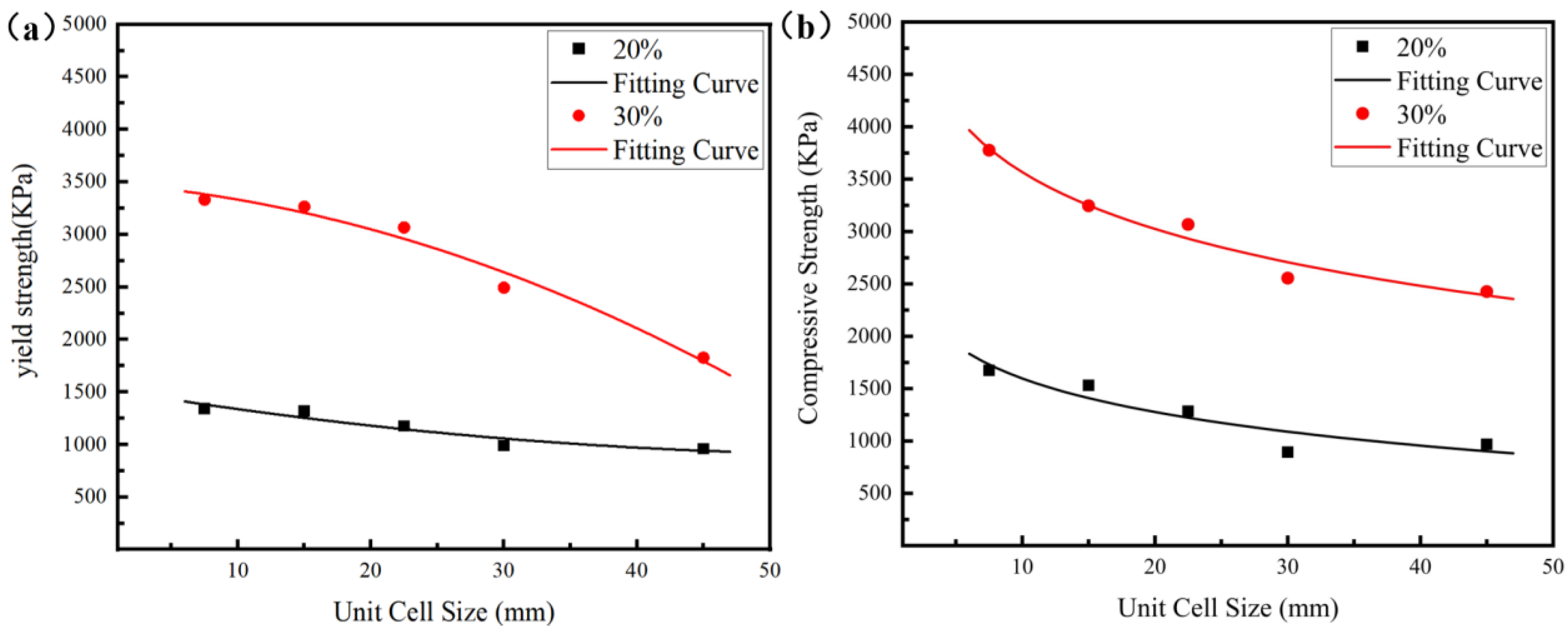
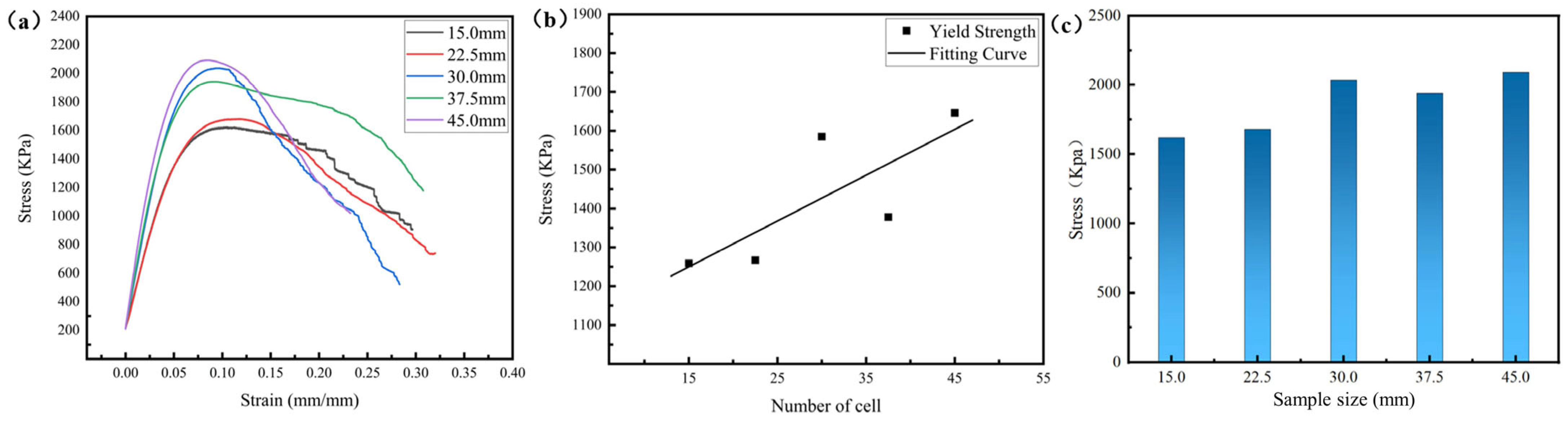
3.1. Mechanical Properties of Diamond Lattice Structures
3.2. Stress Distribution of Diamond Lattice Structures
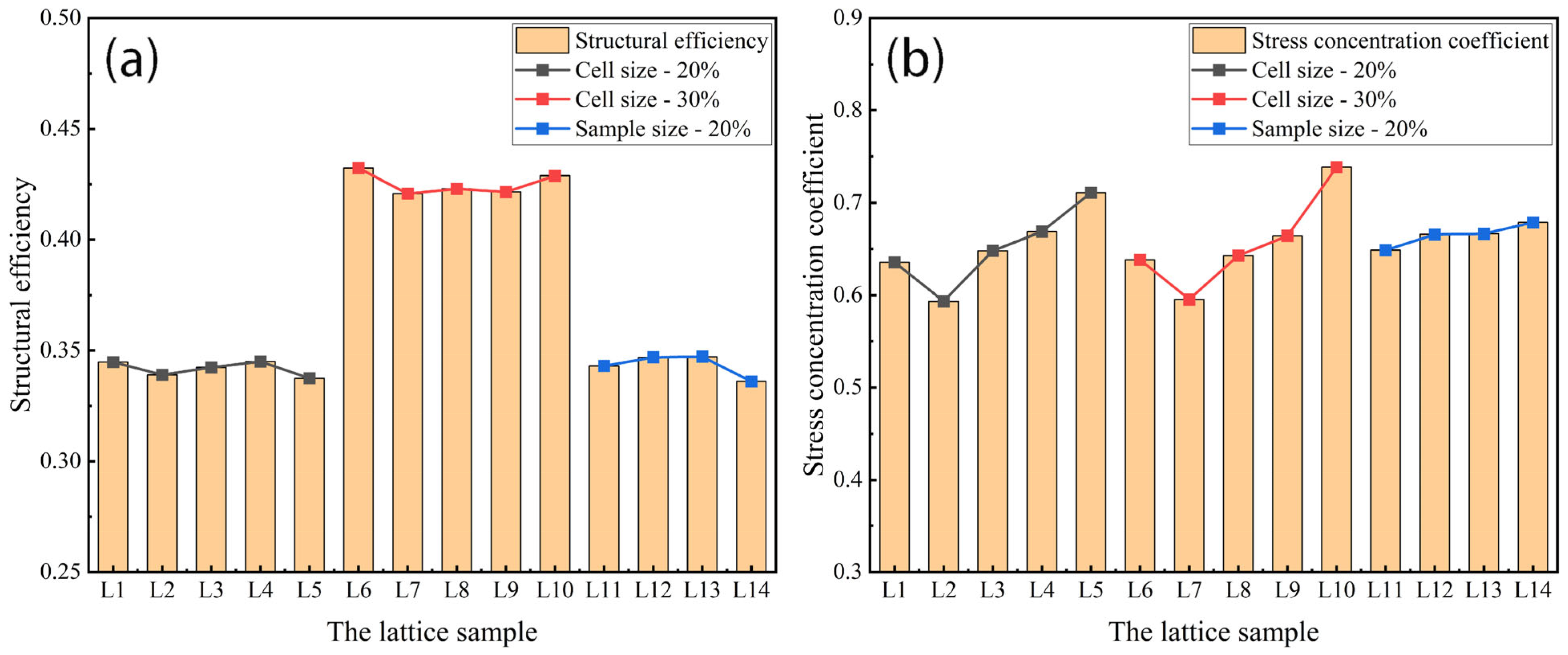
3.3. Structural Efficiency and Stress Concentration Coefficient
4. Conclusions
- The findings of this study emphasize the obvious influence of relative density, cell size, and sample size on the mechanical properties of diamond lattice structures.
- The lattice samples with a relative density of 30% exhibited a 142% increase in compressive strength compared to those with a relative density of 20%.
- Greater relative density results in higher structural efficiency, and both greater relative density and higher structural efficiency lead to an increase in the compressive strength of diamond lattice structures with a greater relative density.
- Both smaller cell sizes and larger sample sizes can enable a lattice structure to contain more cells, thereby increasing the stress concentration coefficient and improving the mechanical properties of the lattices to a certain extent.
- The structural efficiency is closely related to the cell type and relative density, which hardly change as the cell size or sample size changes.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Mizzi, L.; Dudek, K.K.; Frassineti, A.; Spaggiari, A.; Ulliac, G.; Kadic, M. Lightweight 3D Hierarchical Metamaterial Microlattices. Adv. Sci. 2025, 12, 2410293. [Google Scholar] [CrossRef] [PubMed]
- Mohsenizadeh, M.; Gasbarri, F.; Munther, M.; Beheshti, A.; Davami, K. Additively-manufactured lightweight Metamaterials for energy absorption. Mater. Des. 2018, 139, 521–530. [Google Scholar] [CrossRef]
- Wu, R.; Roberts, P.C.; Lyu, S.; Zheng, F.; Soutis, C.; Diver, C.; Zhou, D.; Li, L.; Deng, Z. Lightweight self-forming super-elastic mechanical metamaterials with adaptive stiffness. Adv. Funct. Mater. 2021, 31, 2008252. [Google Scholar] [CrossRef]
- Afshar, M.; Pourkamali, A.A.; Montazerian, H. Compressive characteristics of radially graded porosity scaffolds architectured with minimal surfaces. Mat. Sci. Eng. C-Mater. 2018, 92, 254–267. [Google Scholar] [CrossRef]
- Ataollahi, S. A review on additive manufacturing of lattice structures in tissue engineering. Bioprinting 2023, 35, e00304. [Google Scholar] [CrossRef]
- Bai, L.; Zhang, J.; Chen, X.; Yi, C.; Chen, R.; Zhang, Z. Configuration Optimization Design of Ti6Al4V Lattice Structure Formed by SLM. Materials 2018, 11, 1856. [Google Scholar] [CrossRef]
- Bai, L.; Zhang, J.; Xiong, Y.; Chen, X.; Sun, Y.; Gong, C.; Pu, H.; Wu, X.; Luo, J. Influence of unit cell pose on the mechanical properties of Ti6Al4V lattice structures manufactured by selective laser melting. Addit. Manuf. 2020, 34, 101222. [Google Scholar] [CrossRef]
- Ahmadi, S.M.; Yavari, S.A.; Wauthle, R.; Pouran, B.; Schrooten, J.; Weinans, H.; Zadpoor, A.A. Additively Manufactured Open-Cell Porous Biomaterials Made from Six Different Space-Filling Unit Cells: The Mechanical and Morphological Properties. Materials 2015, 8, 1871–1896. [Google Scholar] [CrossRef]
- Al-Saedi, D.S.J.; Masood, S.H.; Faizan-Ur-Rab, M.; Alomarah, A.; Ponnusamy, P. Mechanical properties and energy absorption capability of functionally graded F2BCC lattice fabricated by SLM. Mater. Des. 2018, 144, 32–44. [Google Scholar] [CrossRef]
- Ahmadi, S.M.; Kumar, R.; Borisov, E.V.; Petrov, R.; Leeflang, S.; Li, Y.; Tumer, N.; Huizenga, R.; Ayas, C.; Zadpoor, A.A.; et al. From microstructural design to surface engineering: A tailored approach for improving fatigue life of additively manufactured meta-biomaterials. Acta Biomater. 2019, 83, 153–166. [Google Scholar] [CrossRef]
- Dar, U.A.; Mian, H.H.; Abid, M.; Topa, A.; Sheikh, M.Z.; Bilal, M. Experimental and numerical investigation of compressive behavior of lattice structures manufactured through projection micro stereolithography. Mater. Today Commun. 2020, 25, 101563. [Google Scholar] [CrossRef]
- Zhang, J.; Chen, X.; Sun, Y.; Wang, Y.; Bai, L. Sound-absorption and mechanical properties of multisheet Gyroid lattice structures by stereolithography. Compos. Struct. 2023, 325, 117589. [Google Scholar] [CrossRef]
- Bobbert, F.S.L.; Lietaert, K.; Eftekhari, A.A.; Pouran, B.; Ahmadi, S.M.; Weinans, H.; Zadpoor, A.A. Additively manufactured metallic porous biomaterials based on minimal surfaces: A unique combination of topological, mechanical, and mass transport properties. Acta Biomater. 2017, 53, 572–584. [Google Scholar] [CrossRef] [PubMed]
- Cutolo, A.; Neirinck, B.; Lietaert, K.; de Formanoir, C.; Van Hooreweder, B. Influence of layer thickness and post-process treatments on the fatigue properties of CoCr scaffolds produced by laser powder bed fusion. Addit. Manuf. 2018, 23, 498–504. [Google Scholar] [CrossRef]
- Boniotti, L.; Beretta, S.; Patriarca, L.; Rigoni, L.; Foletti, S. Experimental and numerical investigation on compressive fatigue strength of lattice structures of AlSi7Mg manufactured by SLM. Int. J. Fatigue 2019, 128, 105181. [Google Scholar] [CrossRef]
- Bertocco, A.; Esposito, L.; Aurino, A.; Borrelli, D.; Caraviello, A. Influence of SLM parameters on the compressive behaviour of lattice structures in 17-4PH stainless steel. IOP Conf. Ser. Mater. Sci. Eng. 2021, 1038, 12035. [Google Scholar] [CrossRef]
- Brodie, E.G.; Wegener, T.; Richter, J.; Medvedev, A.; Niendorf, T.; Molotnikov, A. A mechanical comparison of alpha and beta phase biomedical TiTa lattice structures. Mater. Des. 2021, 212, 110220. [Google Scholar] [CrossRef]
- Leary, M.; Mazur, M.; Williams, H.; Yang, E.; Alghamdi, A.; Lozanovski, B.; Zhang, X.; Shidid, D.; Farahbod-Sternahl, L.; Witt, G.; et al. Inconel 625 lattice structures manufactured by selective laser melting (SLM): Mechanical properties, deformation and failure modes. Mater. Des. 2018, 157, 179–199. [Google Scholar] [CrossRef]
- Li, P.; Warner, D.H.; Fatemi, A.; Phan, N. Critical assessment of the fatigue performance of additively manufactured Ti–6Al–4V and perspective for future research. Int. J. Fatigue 2016, 85, 130–143. [Google Scholar] [CrossRef]
- Liu, L.; Kamm, P.; García-Moreno, F.; Banhart, J.; Pasini, D. Elastic and failure response of imperfect three-dimensional metallic lattices: The role of geometric defects induced by Selective Laser Melting. J. Mech. Phys. Solids 2017, 107, 160–184. [Google Scholar] [CrossRef]
- Wei, K.; Yang, Q.; Ling, B.; Xie, H.; Qu, Z.; Fang, D. Mechanical responses of titanium 3D kagome lattice structure manufactured by selective laser melting. Extreme Mech. Lett. 2018, 23, 41–48. [Google Scholar] [CrossRef]
- Zhao, M.; Zhang, D.Z.; Li, Z.; Zhang, T.; Zhou, H.; Ren, Z. Design, mechanical properties, and optimization of BCC lattice structures with taper struts. Compos. Struct. 2022, 295, 115830. [Google Scholar] [CrossRef]
- Zhao, M.; Li, X.; Zhang, D.Z.; Zhai, W. TPMS-based interpenetrating lattice structures: Design, mechanical properties and multiscale optimization. Int. J. Mech. Sci. 2023, 244, 108092. [Google Scholar] [CrossRef]
- Bai, L.; Xu, Y.; Chen, X.; Xin, L.; Zhang, J.; Li, K.; Sun, Y. Improved mechanical properties and energy absorption of Ti6Al4V laser powder bed fusion lattice structures using curving lattice struts. Mater. Des. 2021, 211, 110140. [Google Scholar] [CrossRef]
- Zhao, J.; Liu, R.; Cai, J.; Estakhrianhaghighi, E.; Sasmito, A.P.; Hou, J.; Akbarzadeh, A. Enhanced Mechanical Properties of Lattice Structures Enabled by Tailoring Oblique Truss Orientation Angle. Adv. Eng. Mater. 2024, 26, 2301646. [Google Scholar] [CrossRef]
- Li, C.; Lei, H.; Liu, Y.; Zhang, X.; Xiong, J.; Zhou, H.; Fang, D. Crushing behavior of multi-layer metal lattice panel fabricated by selective laser melting. Int. J. Mech. Sci. 2018, 145, 389–399. [Google Scholar] [CrossRef]
- Zhao, S.; Zong, X.; Wu, N. Design of Load Path-oriented BCCz Lattice Sandwich Structures. J. Phys. Conf. Ser. 2022, 2239, 12014. [Google Scholar] [CrossRef]
- Dar, U.A.; Mian, H.H.; Abid, M.; Nutkani, M.B.; Jamil, A.; Sheikh, M.Z. Quasi-Static Compression and Deformation Behavior of Additively Manufactured Flexible Polymeric Lattice Structure. J. Mater. Eng. Perform. 2022, 31, 3107–3119. [Google Scholar] [CrossRef]
- Wang, W.; Feng, D.; Yang, L.; Li, S.; Wang, C.C.L. Topology optimization of self-supporting lattice structure. Addit. Manuf. 2023, 67, 103507. [Google Scholar] [CrossRef]
- Tyagi, S.A.; Manjaiah, M. Additive manufacturing of titanium-based lattice structures for medical applications—A review. Bioprinting 2023, 30, e00267. [Google Scholar] [CrossRef]
- Timercan, A.; Terriault, P.; Brailovski, V. Axial tension/compression and torsional loading of diamond and gyroid lattice structures for biomedical implants: Simulation and experiment. Mater. Des. 2023, 225, 111585. [Google Scholar] [CrossRef]
- Pozo, S.; Golecki, T.; Gomez, F.; Carrion, J.; Spencer, B.F. Minimum-thickness method for 2.5D topology optimization applied to structural design. Eng. Struct. 2023, 286, 116065. [Google Scholar] [CrossRef]
- Yu, G.; Li, Z.; Li, S.; Zhang, Q.; Hua, Y.; Liu, H.; Zhao, X.; Dhaidhai, D.T.; Li, W.; Wang, X. The select of internal architecture for porous Ti alloy scaffold: A compromise between mechanical properties and permeability. Mater. Des. 2020, 192, 108754. [Google Scholar] [CrossRef]
- Corvi, A.; Collini, L.; Sciancalepore, C.; Kumar, A. Analysis and modelling of damage mechanism in FDM 3D-printed lattice structure under compression loading. J. Mech. Sci. Technol. 2023, 37, 1089–1095. [Google Scholar] [CrossRef]
- Cutolo, A.; Beevers, E.; Van Hooreweder, B. A design strategy to enhance the mechanical response of diamond-based lattice structures produced by laser powder bed fusion. Mater. Sci. Eng. A-Struct. 2023, 876, 145120. [Google Scholar] [CrossRef]
- Magarò, P.; Alaimo, G.; Carraturo, M.; Sgambitterra, E.; Maletta, C. A novel methodology for the prediction of the stress–strain response of laser powder bed fusion lattice structure based on a multi-scale approach. Mater. Sci. Eng. A-Struct. 2023, 863, 144526. [Google Scholar] [CrossRef]
- ASTM D695-2015; Standard Test Method for Compressive Properties of Rigid Plastics. ASTM International: West Conshohocken, PA, USA, 2015.
- Liang, Z.; Meng, Y.; Zhao, J.; Sun, Z.; Guo, Y.; Xia, J.; Chang, H.; Zhou, L.; Alexandrov, I.V. A theoretical method to analyze the effect of stress distribution on compressive strength of periodic lattices. Mater. Des. 2025, 250, 113580. [Google Scholar] [CrossRef]
- Zhang, L.; Feih, S.; Daynes, S.; Chang, S.; Wang, M.Y.; Wei, J.; Lu, W.F. Energy absorption characteristics of metallic triply periodic minimal surface sheet structures under compressive loading. Addit. Manuf. 2018, 23, 505–515. [Google Scholar] [CrossRef]
- Zhang, X.Z.; Tang, H.P.; Wang, J.; Jia, L.; Fan, Y.X.; Leary, M.; Qian, M. Additive manufacturing of intricate lattice materials: Ensuring robust strut additive continuity to realize the design potential. Addit. Manuf. 2022, 58, 103022. [Google Scholar] [CrossRef]
- Maiti, S.K.; Gibson, L.J.; Ashby, M.F. Deformation and energy absorption diagrams for cellular solids. Acta Metall. 1984, 32, 1963–1975. [Google Scholar] [CrossRef]
- Xiao, L.; Song, W.; Wang, C.; Liu, H.; Tang, H.; Wang, J. Mechanical behavior of open-cell rhombic dodecahedron Ti–6Al–4V lattice structure. Mater. Sci. Eng. A-Struct. 2015, 640, 375–384. [Google Scholar] [CrossRef]
- Chen, W.; Voisin, T.; Zhang, Y.; Forien, J.B.; Spadaccini, C.M.; McDowell, D.L.; Zhu, T.; Wang, Y.M. Microscale residual stresses in additively manufactured stainless steel. Nat. Commun. 2019, 10, 4338. [Google Scholar] [CrossRef]



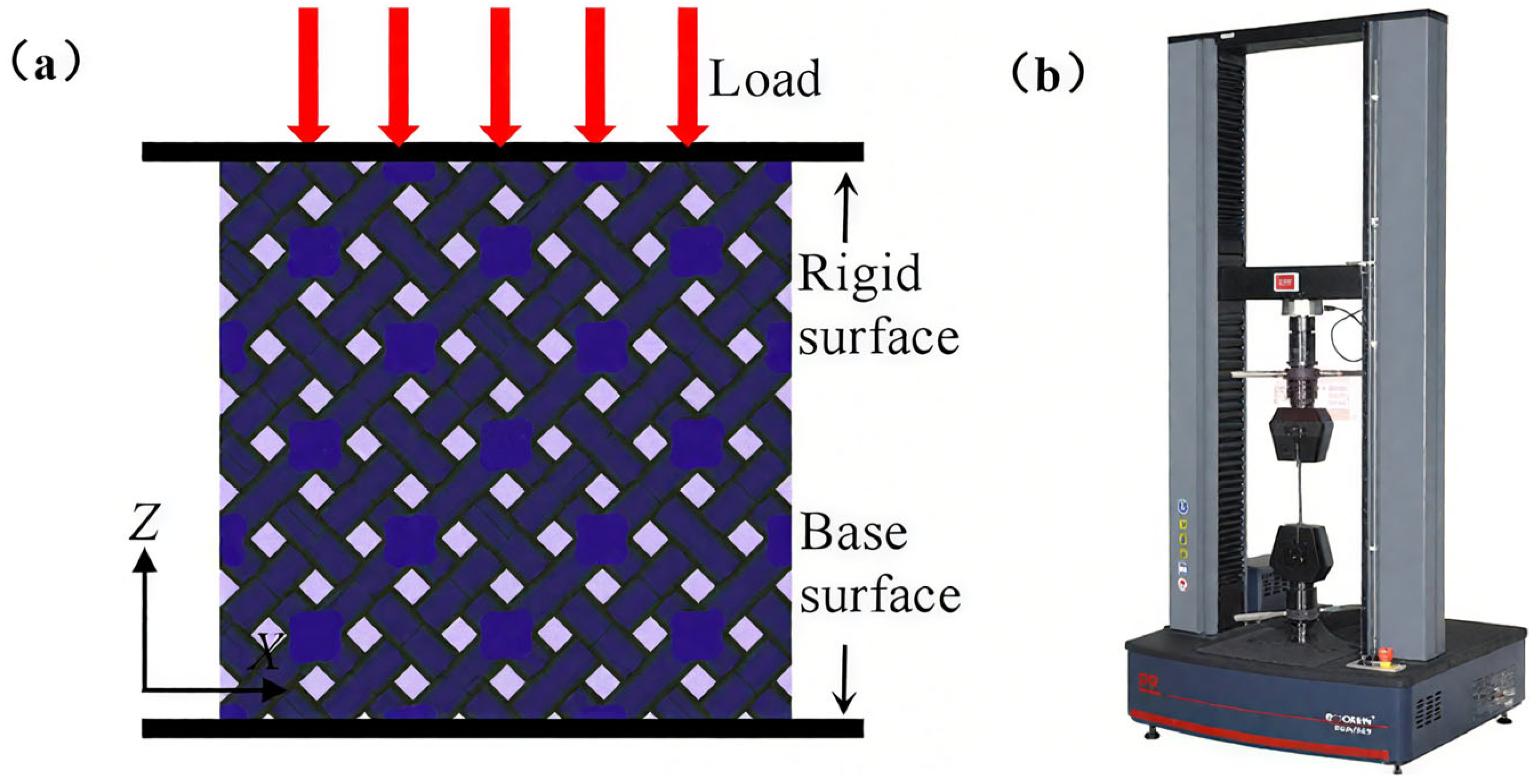


| The Lattices with Different Cell Sizes and Relative Densities | The Lattices with Different Sample Sizes | ||||
|---|---|---|---|---|---|
| Sample Size | Cell Size | Relative Density | Sample Size | Cell Size | Relative Density |
| 45 mm | 45 mm | 20% and 30% | 45 mm | 7.5 mm | 20% |
| 45 mm | 30 mm | 20% and 30% | 37.5 mm | 7.5 mm | 20% |
| 45 mm | 22.5 mm | 20% and 30% | 30 mm | 7.5 mm | 20% |
| 45 mm | 15 mm | 20% and 30% | 22.5 mm | 7.5 mm | 20% |
| 45 mm | 7.5 mm | 20% and 30% | 15 mm | 7.5 mm | 20% |
| Fracture Strain | Displacement at Failure | Density | Young’s Modulus | Poisson’s Ratio | Yield Stress 1 | Plastic Strain 1 | Yield Stress 2 | Plastic Strain 2 |
|---|---|---|---|---|---|---|---|---|
| 0.16 | 0.0025 | 1.3 × 10−9 t/mm3 | 2250 MPa | 0.3 | 39.3 MPa | 0 | 45.5 | 0.16 |
| Sample | Sample Sizes (mm) | Cell Size (mm) | Relative Density (%) | Structural Efficiency | Stress Concentration Coefficient | Simulated Strength (KPa) | Calculated Strength by Formula (4) (KPa) |
|---|---|---|---|---|---|---|---|
| L1 | 45.0 | 45.0 | 18.85 | 0.3449 | 0.6356 | 1798 | 1775 |
| L2 | 45.0 | 30.0 | 19.98 | 0.3391 | 0.5934 | 1545 | 1726 |
| L3 | 45.0 | 22.5 | 19.35 | 0.3425 | 0.6482 | 1746 | 1844 |
| L4 | 45.0 | 15.0 | 19.41 | 0.3451 | 0.6688 | 1796 | 1924 |
| L5 | 45.0 | 7.5 | 19.41 | 0.3375 | 0.7110 | 1894 | 2000 |
| L6 | 45.0 | 45.0 | 27.82 | 0.4323 | 0.6383 | 3418 | 3296 |
| L7 | 45.0 | 30.0 | 29.72 | 0.4208 | 0.5954 | 3362 | 3197 |
| L8 | 45.0 | 22.5 | 28.96 | 0.4230 | 0.6429 | 3578 | 3382 |
| L9 | 45.0 | 15.0 | 29.16 | 0.4216 | 0.6642 | 3738 | 3507 |
| L10 | 45.0 | 7.5 | 28.50 | 0.4280 | 0.7384 | 4182 | 3867 |
| L11 | 15.0 | 7.5 | 19.33 | 0.3431 | 0.6488 | 1819 | 1847 |
| L12 | 22.5 | 7.5 | 19.39 | 0.3470 | 0.6657 | 1872 | 1924 |
| L13 | 30.0 | 7.5 | 19.41 | 0.3473 | 0.6663 | 1901 | 1928 |
| L14 | 37.5 | 7.5 | 19.42 | 0.3361 | 0.6785 | 1953 | 1902 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, J.; Gu, H.; Zhang, J.; Dai, G.; Li, B.; Sun, Z.; Liang, Z. Compressive Mechanical Properties of Lattice Structures with Varied Structural Parameters Prepared by Stereolithography. Materials 2025, 18, 3898. https://doi.org/10.3390/ma18163898
Sun J, Gu H, Zhang J, Dai G, Li B, Sun Z, Liang Z. Compressive Mechanical Properties of Lattice Structures with Varied Structural Parameters Prepared by Stereolithography. Materials. 2025; 18(16):3898. https://doi.org/10.3390/ma18163898
Chicago/Turabian StyleSun, Jianhua, Hai Gu, Jie Zhang, Guoqing Dai, Bin Li, Zhonggang Sun, and Zulei Liang. 2025. "Compressive Mechanical Properties of Lattice Structures with Varied Structural Parameters Prepared by Stereolithography" Materials 18, no. 16: 3898. https://doi.org/10.3390/ma18163898
APA StyleSun, J., Gu, H., Zhang, J., Dai, G., Li, B., Sun, Z., & Liang, Z. (2025). Compressive Mechanical Properties of Lattice Structures with Varied Structural Parameters Prepared by Stereolithography. Materials, 18(16), 3898. https://doi.org/10.3390/ma18163898






