A New Concrete Freeze–Thaw Damage Model Based on Hydraulic Pressure Mechanism and Its Application
Abstract
1. Introduction
2. A Theoretical Model for Freeze–Thaw Damage of Concrete
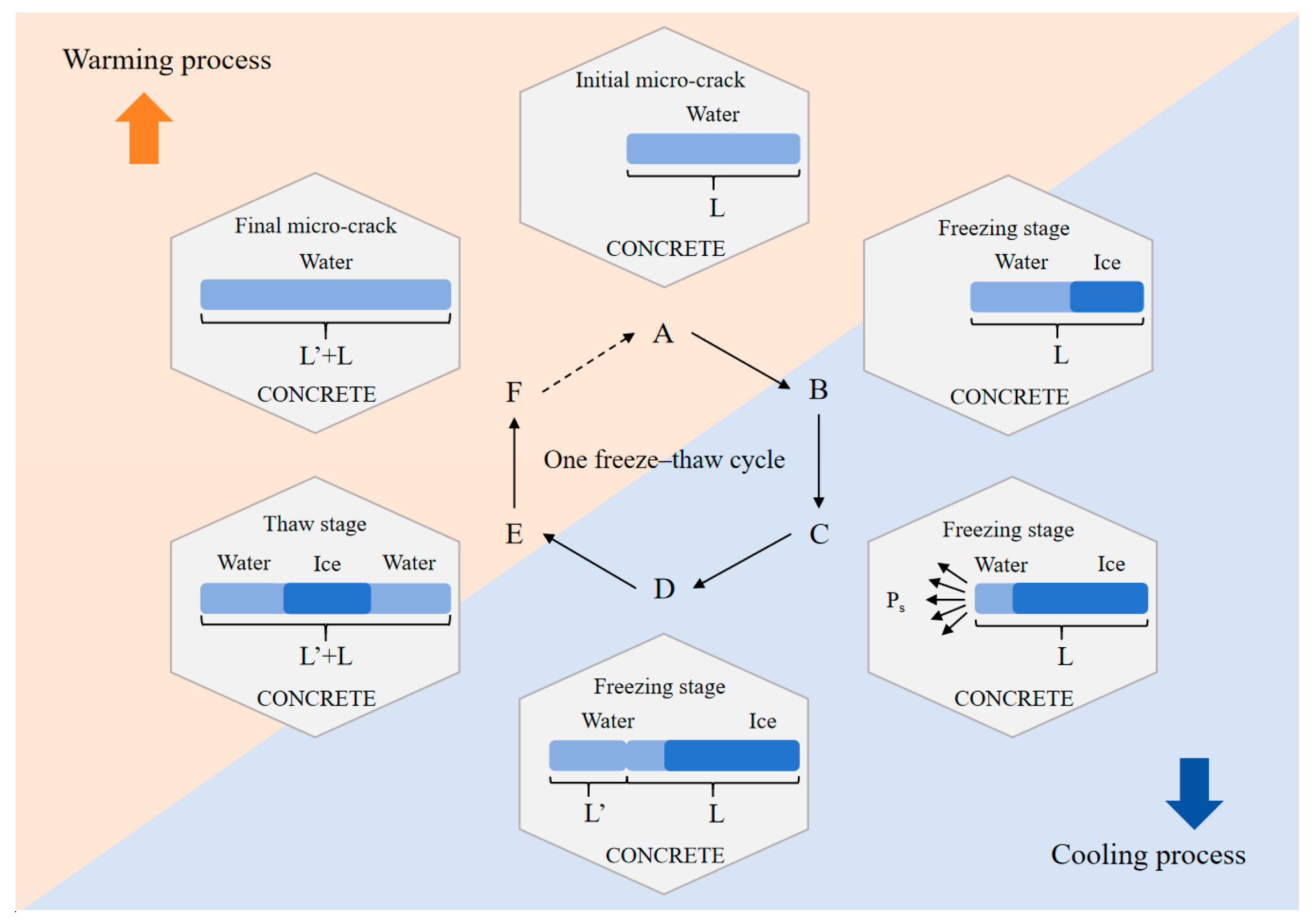
2.1. Hydraulic Pressure Theory
- (1)
- Hydraulic pressure in concrete: Freeze–thaw damage in concrete is caused by the hydraulic pressure generated by the phase transformation of the liquid phase in the concrete. During freeze–thaw cycles, hydraulic pressure is generated with pore water frozen only under the circumstance that the volume percentage of the liquid phase of concrete is higher than a specific value. Therefore, material properties related to the volume percentage of the liquid phase in concrete (e.g., concrete saturation [33,34,35], water-to-binder ratio [36,37], etc.) have an important effect on freeze–thaw damage of concrete.
- (2)
- Strength of concrete: If concrete strength is not enough to resist hydraulic pressure, new defects will be generated inside concrete. Therefore, material properties related to the strength of concrete (e.g., concrete admixtures [38,39], water-to-binder ratio [36,37], etc.) have an important impact on freeze–thaw damage of concrete.
- (3)
- Initial defects inside concrete: Stress concentration commonly appears at the tips of micro-cracks under hydraulic pressure, so micro-cracks inside concrete can easily extend during freeze–thaw cycles. Therefore, properties of initial defects in concrete (e.g., the number, morphology and distribution of defects inside concrete [2,40,41], etc.) also affect freeze–thaw damage of concrete.
2.2. A Freeze–Thaw Damage Model Based on Hydraulic Pressure Theory
2.2.1. Theory Parameters
- (1)
- Defects inside concrete (DEF): DEF defined in this model refers to internal material defects, which increase with the number of freeze–thaw cycles.
- (2)
- New defects (NDs): NDs represent the new defects that are generated during one freeze–thaw cycle.
2.2.2. Assumption on Characteristics of Concrete
2.2.3. Mode for Development of Defects Based on Micro-Cracks in Concrete
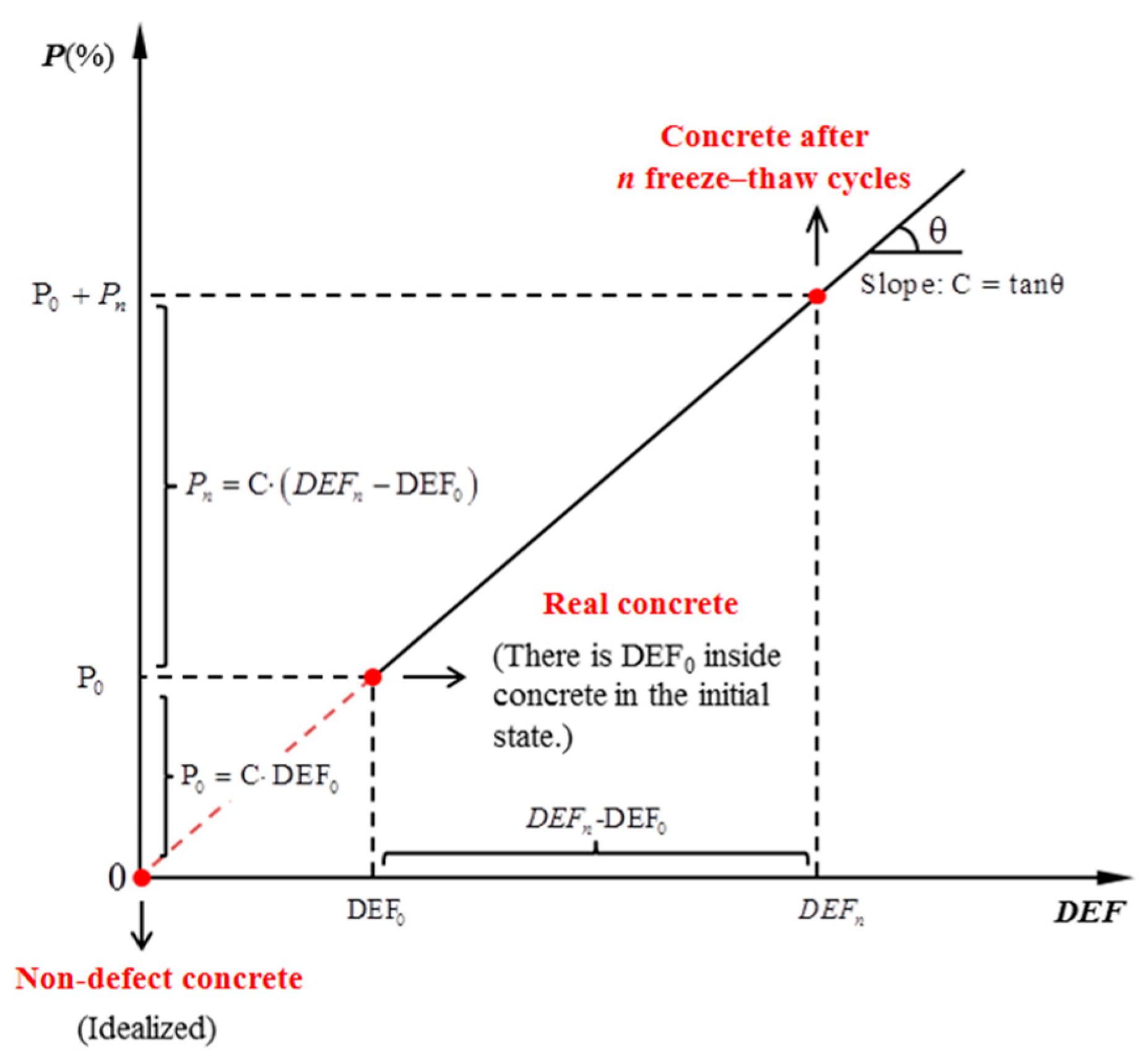
2.2.4. Defect Development Equation
2.3. Explanation of the Freeze–Thaw Damage Model
3. An Equation for the Loss of Relative Dynamic Elastic Modulus Based on Freeze–Thaw Damage Model
4. Experimental Investigation for the Loss of Relative Dynamic Elastic Modulus of Concrete
4.1. Materials and Preparation
4.2. Test Methods
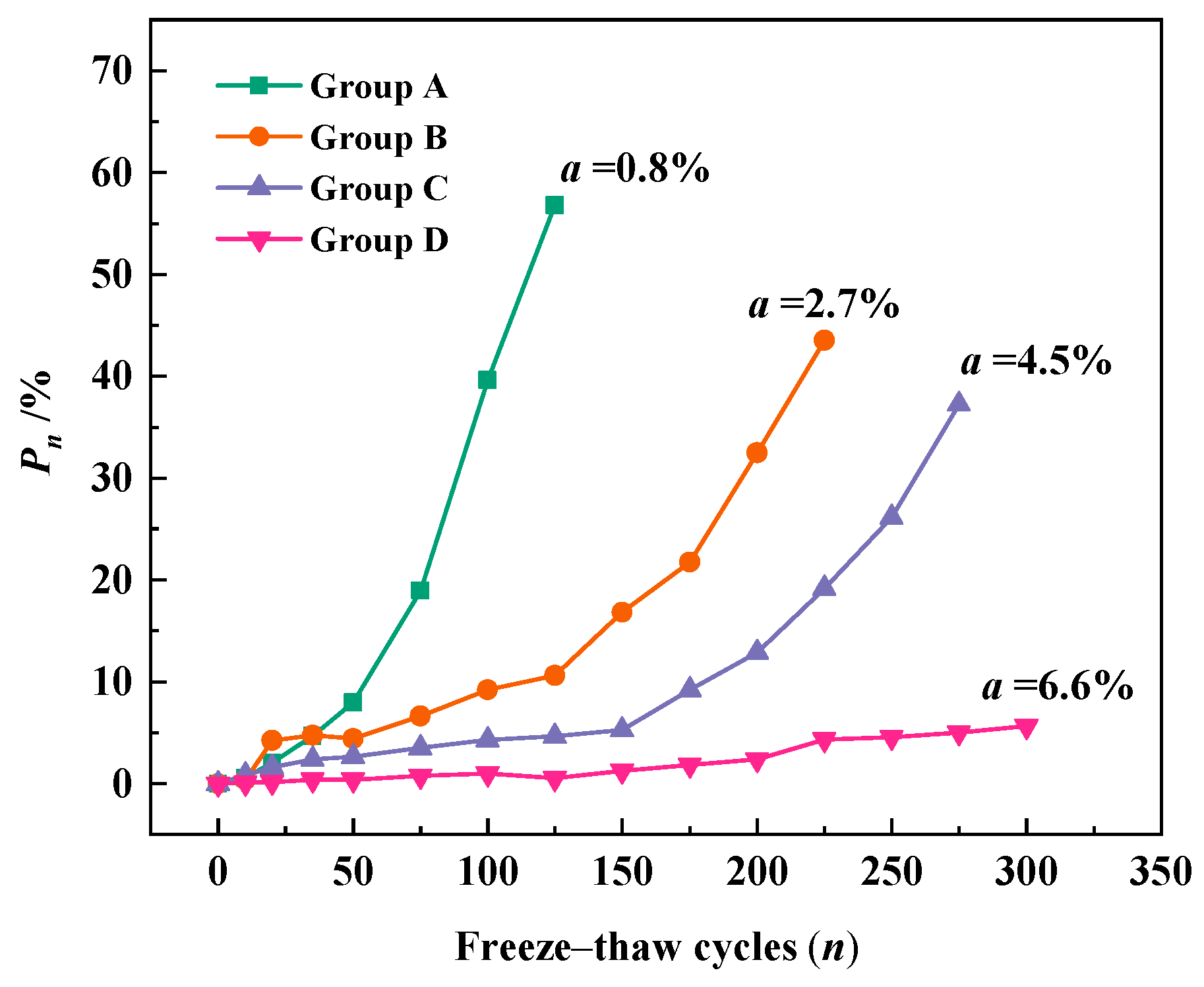
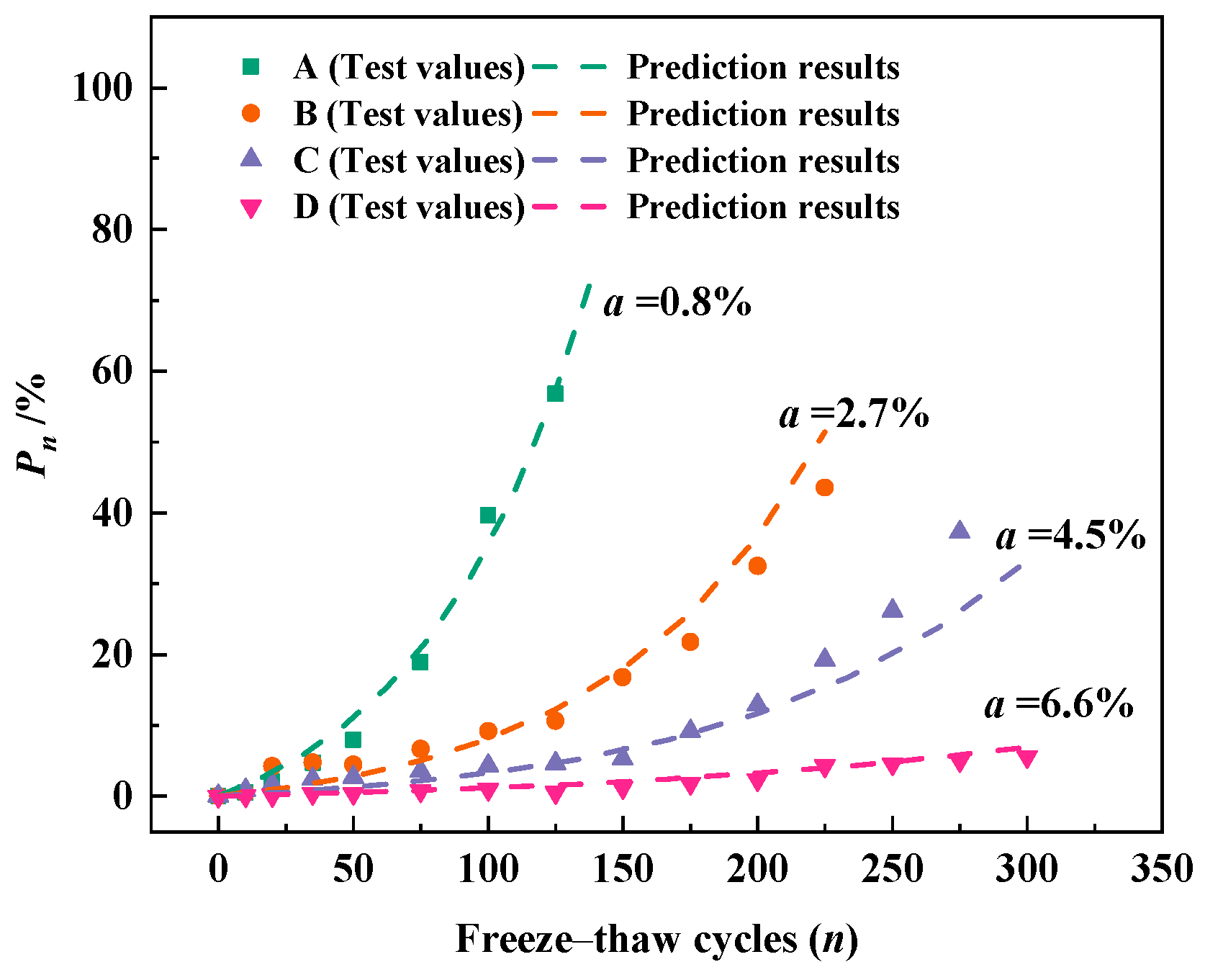
4.3. Test Results and Analysis
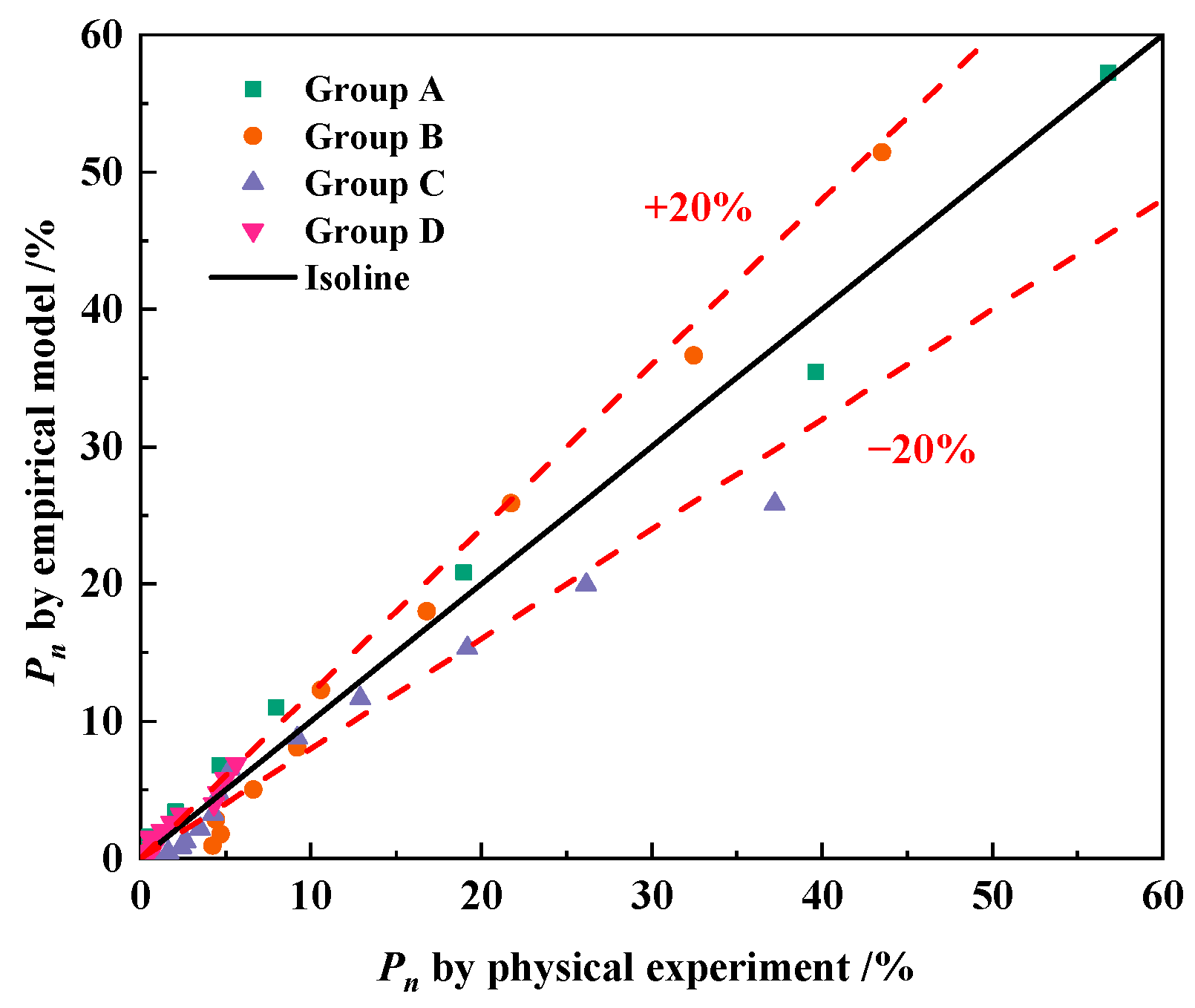
4.4. Relative Dynamic Elastic Modulus Loss Prediction Model of Concrete Considering the Effect of Air Content
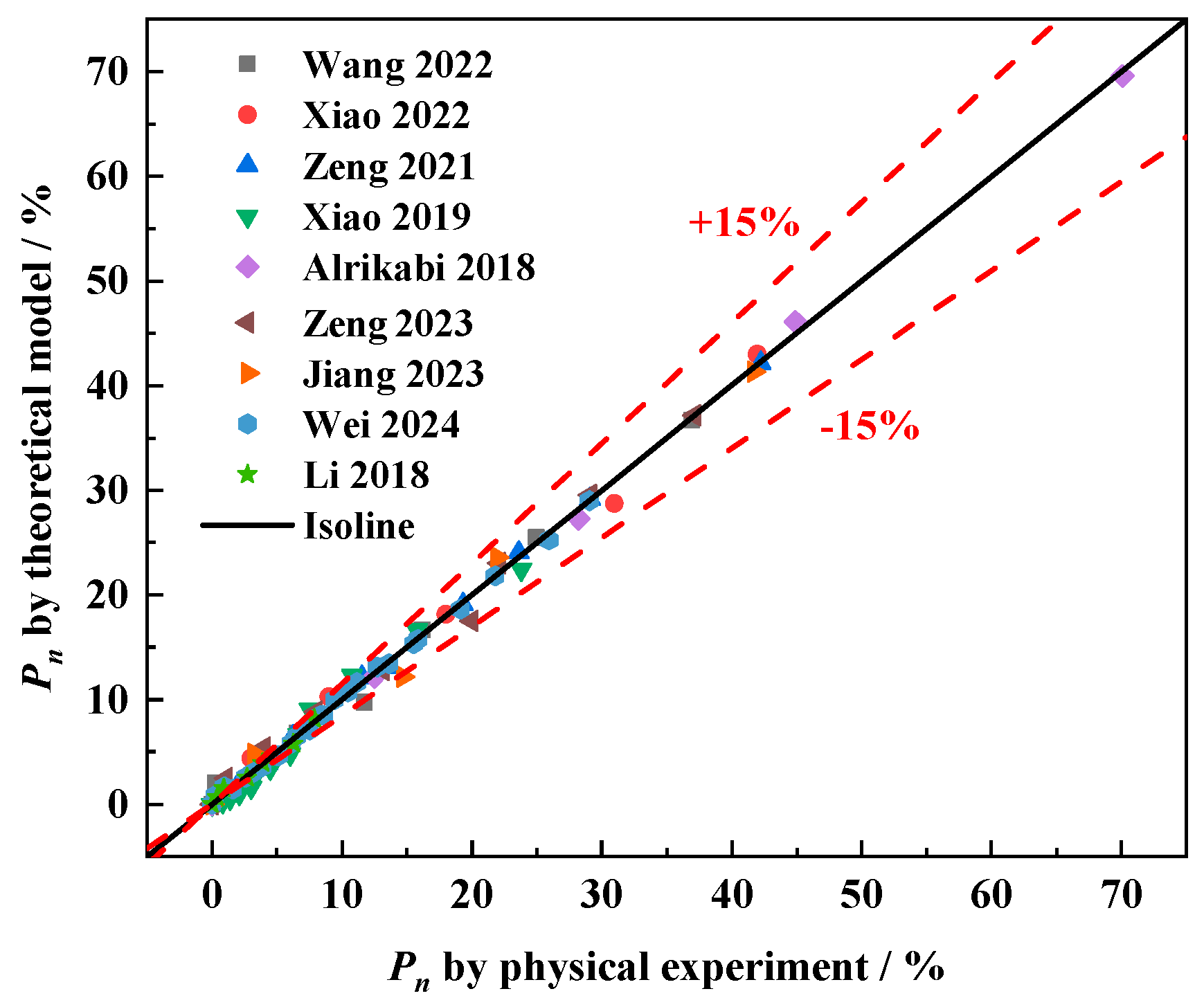
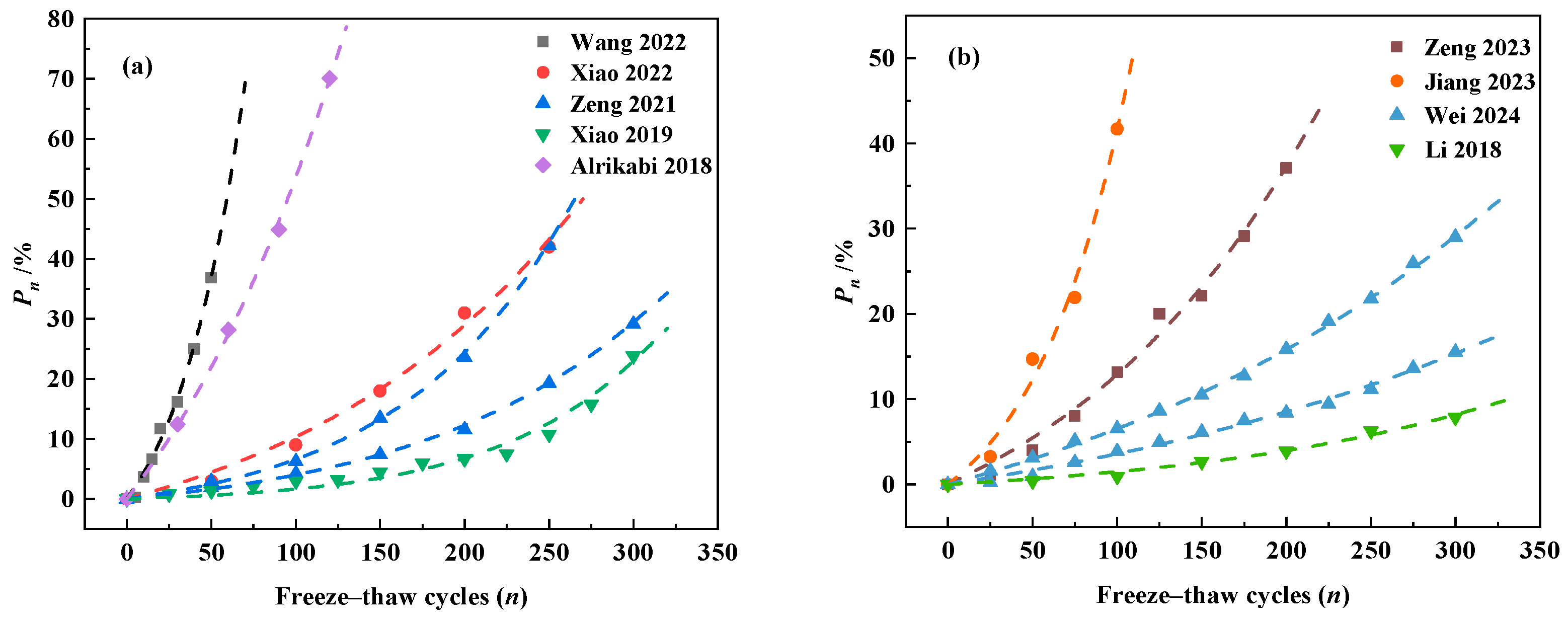
5. Additional Validation of the Relative Dynamic Elastic Modulus Loss Equation
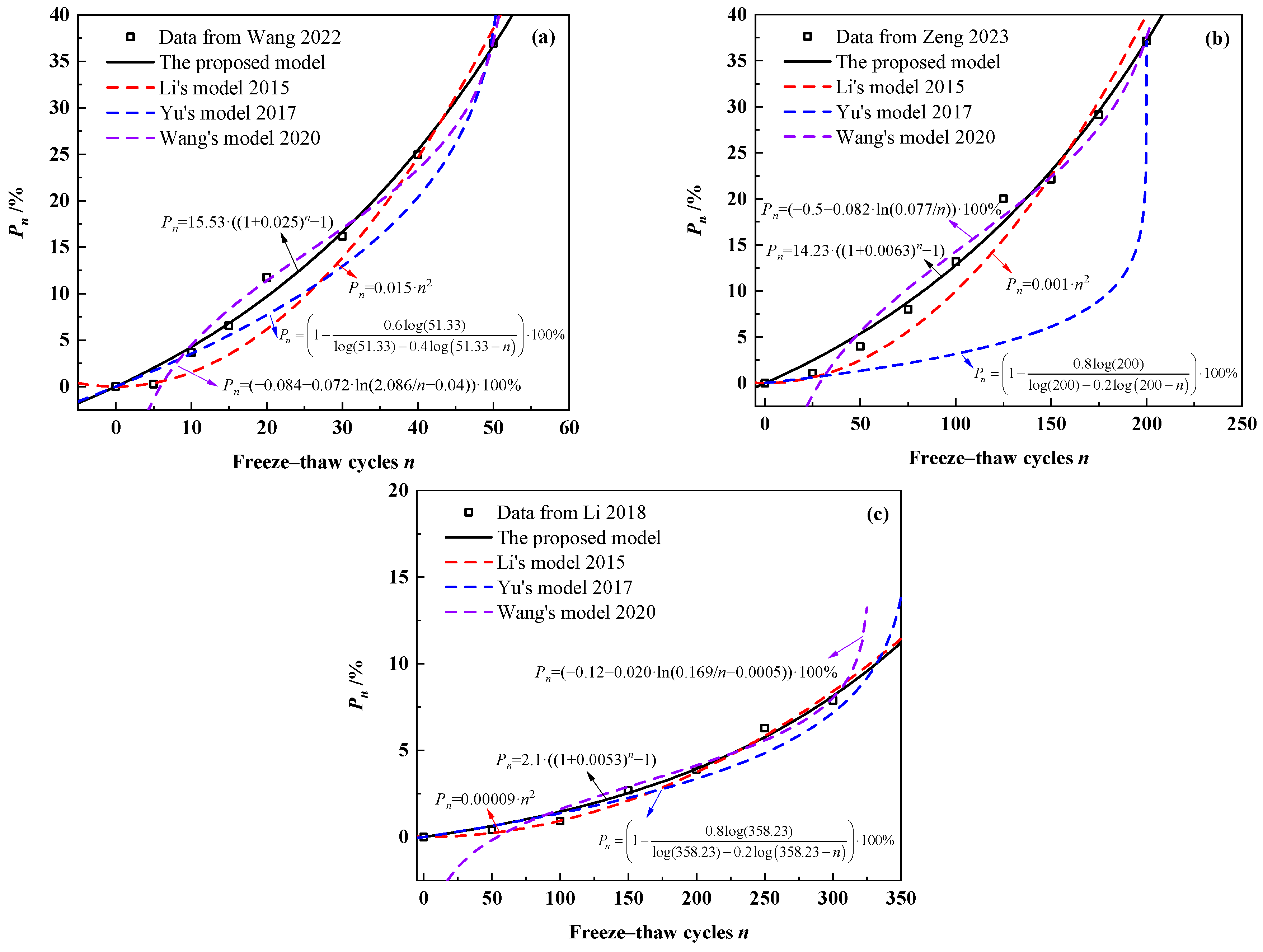
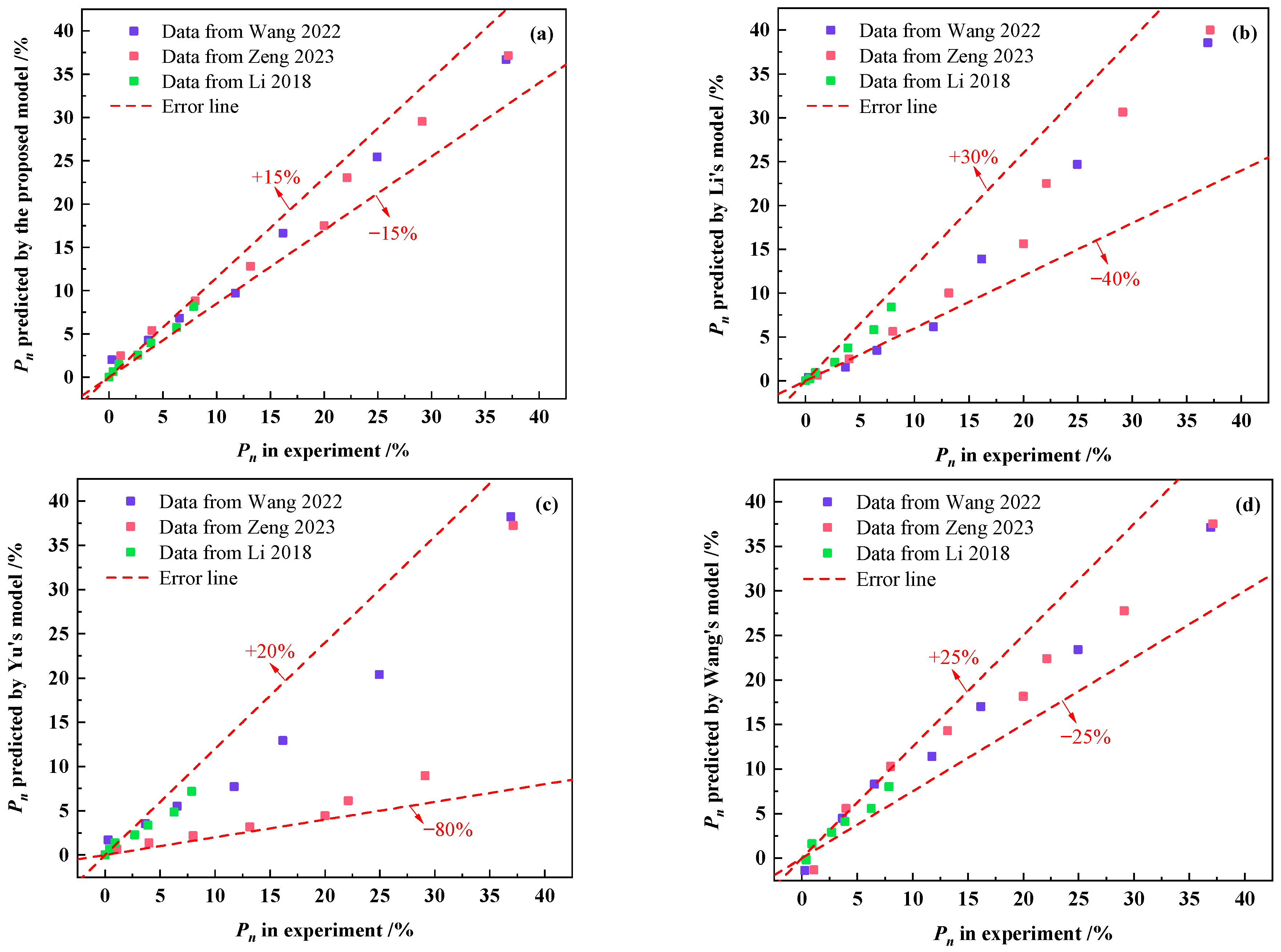
6. The Comparison Between the Proposed Model and Similar Models
7. Conclusions
- (1)
- A new freeze–thaw damage model was established based on the hydraulic pressure mechanism. The total amount of defects inside concrete is related to the initial defects inside concrete and the ability of defect development.
- (2)
- Based on the defect evolution equation proposed in this paper, the relative dynamic elastic modulus loss equation is established. It can be seen from the equation that the loss of relative dynamic elastic modulus increases exponentially during the freeze–thaw cycle.
- (3)
- The relative dynamic elastic modulus loss equation of concrete during freeze–thaw cycle was established considering the change of air content in concrete. The higher the air content of concrete, the smaller the parameters K and P0 in the dynamic elastic modulus damage equation.
- (4)
- The model established in this study is suitable for describing the loss of relative dynamic elastic modulus of various types of concrete during the freeze–thaw process under different freeze–thaw conditions and is universally adaptable.
- (5)
- The defect development capacity (K) in the model ranges from 0.001 to 0.050, and the initial loss of relative dynamic elastic modulus (P0) ranges from 0.1 to 100 (%).
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| OPC | Ordinary Portland cement |
| DEF | Defects |
| ND | New defects |
| RCA | Recycled coarse aggregate |
| BF | Basalt fiber |
| FA | Fly ash |
| SF | Steer fiber |
| WRA | Water-reducing agent |
| AEA | Air-entraining agent |
References
- Mehta, P. Concrete durability-fifty year’s progress. In Proceedings of the 2nd International Conference on Concrete Durability, Montreal, QC, Canada, 4–9 August 1991; ACI SP126-1. American Concrete Institution: Farmington Hills, MI, USA, 1991; pp. 1–31. [Google Scholar] [CrossRef]
- Powers, T. A Working Hypothesis for Further Studies of Frost Resistance of Concrete. ACI Mater. J. 1945, 16, 245–272. [Google Scholar] [CrossRef]
- Powers, T.; Helmuth, R. Theory of Volume Changes in Hardened Portland Cement Paste During Freezing. In Proceedings of the Highway Research Board Proceedings, Washington, DC, USA, 13–16 January 1953; Volume 32, pp. 285–297. [Google Scholar]
- Powers, T. Void Space as a Basis for Producing Air-Entrained Concrete. ACI Mater. J. 1954, 50, 741–760. [Google Scholar] [CrossRef]
- Xie, W.; Shao, C.; Xu, Y.; Chen, H.; Zheng, S. Study of the Mesodamage Analysis Method for Frozen-Thawed Concrete Based on CT Image Recognition. J. Mater. Civ. Eng. 2024, 36, 04024067. [Google Scholar] [CrossRef]
- Yang, T.; Yang, S.; Sun, Z.; Wang, S.; Pang, R. Deterioration mechanism of alkali-activated slag and fly ash blended recycled aggregate concrete under freeze-thaw cycles. J. Build. Eng. 2025, 99, 111555. [Google Scholar] [CrossRef]
- Zhang, C.; Liu, T.; Jiang, C.; Chen, Z.; Zhou, K.; Chen, L. The Freeze-Thaw Strength Evolution of Fiber-Reinforced Cement Mortar Based on NMR and Fractal Theory: Considering Porosity and Pore Distribution. Materials 2022, 15, 7316. [Google Scholar] [CrossRef]
- Deng, C.; Yu, L.; Wang, H.; Liu, Z.; Fan, D. Frost Resistance Differences of Concrete in Frequent Natural Freeze-Thaw versus Standard Rapid Method. Buildings 2024, 18, 2489. [Google Scholar] [CrossRef]
- Wang, D.; Zhou, X.; Meng, Y.; Chen, Z. Durability of Concrete Containing Fly Ash and Silica Fume Against Combined Freezing-Thawing and Sulfate Attack. Constr. Build. Mater. 2017, 147, 398–406. [Google Scholar] [CrossRef]
- Tan, Y.; Yu, H. Freeze Thaw Durability of Air-Entrained Concrete under Various Types of Salt Lake Brine Exposure. Mag. Concr. Res. 2018, 70, 928–937. [Google Scholar] [CrossRef]
- Guo, T.; Weng, X. Evaluation of the Freeze-Thaw Durability of Surface-Treated Airport Pavement Concrete under Adverse Conditions. Constr. Build. Mater. 2019, 206, 519–530. [Google Scholar] [CrossRef]
- Lehner, P.; Hrabová, K. Relationship of Time-Dependent Parameters from Destructive and Non-Destructive Tests of Structural Concrete. Mathematics 2022, 10, 460. [Google Scholar] [CrossRef]
- Lehner, P.; Gołaszewski, J. Relationship of Different Properties from Non-Destructive Testing of Heavy Concrete from Magnetite and Serpentinite. Materials 2021, 14, 4288. [Google Scholar] [CrossRef] [PubMed]
- ASTM C666/C66M-15; Standard Test Method for Resistance of Concrete to Rapid Freezing and Thawing. American Society of Testing Materials: Conshohocken, PA, USA, 2015.
- GB/T 50082-2009; Standard for Test Methods of Long-Term Performance and Durability of Ordinary Concrete. China Architecture and Building Press: Beijing, China, 2009.
- Wang, Y.; Liu, Z.; Zhang, B.; Fu, K. A Time-Dependent Diffusive Model for the Simulation of Chloride Penetration in Concrete Considering the Effect of Natural Salt Freeze-Thaw Cycles. Cold Reg. Sci. Technol. 2022, 201, 103622. [Google Scholar] [CrossRef]
- Liu, Z.; El-Tawil, S.; Hansen, W.; Wang, F. Effect of Slag Cement on the Properties of Ultra-High Performance Concrete. Constr. Build. Mater. 2018, 190, 830–837. [Google Scholar] [CrossRef]
- Li, Y.; Wang, R.; Li, S.; Zhao, Y.; Qin, Y. Resistance of Recycled Aggregate Concrete Containing Low- and High-Volume Fly Ash Against the Combined Action of Freeze-Thaw Cycles and Sulfate Attack. Constr. Build. Mater. 2018, 166, 23–34. [Google Scholar] [CrossRef]
- Wang, H.; Liu, J.; Gao, X.; Li, Y.; Cai, J.; Wang, J. Influence of Salt Freeze-Thaw Cycles on the Damage and the Following Electrical and Self-Sensing Performance of Carbon Nanofibers Concrete. Mater. Res. Express 2018, 6, 025705. [Google Scholar] [CrossRef]
- Li, Y. Study on the Physical and Mechanical Properties and Damage Mechanism of Concrete Mixed with Mineral Admixture in Marine Corrosion and Freeze-Thawing Environment. Ph.D. Thesis, China University of Mining and Technology, Beijing, China, 2015. [Google Scholar]
- Xiao, Q.; Li, Q.; Cao, Z.; Tian, W. The Deterioration Law of Recycled Concrete Under the Combined Effects of Freeze-Thaw and Sulfate Attack. Constr. Build. Mater. 2019, 200, 344–355. [Google Scholar] [CrossRef]
- Yu, H.; Ma, H.; Yan, K. An Equation for Determining Freeze-Thaw Fatigue Damage in Concrete and a Model for Predicting the Service Life. Constr. Build. Mater. 2017, 137, 104–116. [Google Scholar] [CrossRef]
- Wang, X.; Wu, Y.; Shen, X.; Wang, H.; Liu, S.; Yan, C. An Experimental Study of a Freeze-Thaw Damage Model of Natural Pumice Concrete. Powder Technol. 2018, 339, 651–658. [Google Scholar] [CrossRef]
- Løland, K. Continuous Damage Model for Load-Response Estimation of Concrete. Cem. Concr. Res. 1989, 10, 395–402. [Google Scholar] [CrossRef]
- Wang, B.; Pan, J.; Fang, R.; Wang, Q. Damage Model of Concrete Subjected to Coupling Chemical Attacks and Freeze-Thaw Cycles in Saline Soil Area. Constr. Build. Mater. 2020, 242, 118205. [Google Scholar] [CrossRef]
- Qu, G.; Zheng, M.; Wang, X.; Zhu, R.; Su, Y.; Chang, G. A Freeze-Thaw Damage Evolution Equation and a Residual Strength Prediction Model for Porous Concrete Based on the Weibull Distribution Function. J. Mater. Civ. Eng. 2023, 35, 04023074. [Google Scholar] [CrossRef]
- Longarini, N.; Crespi, P.; Zucca, M.; Giordano, N.; Silvestro, G. The advantages of fly ash use in concrete structures. Inz. Miner. 2014, 15, 141–145. [Google Scholar]
- Huang, Y.; Shao, C.; Yu, Z.; Wei, H.; Li, Z.; Zhu, Z. Study of Freeze-Thaw Deterioration of Saturated and Unsaturated Hydraulic Concrete Based on Measured Strain. J. Build. Eng. 2024, 97, 110771. [Google Scholar] [CrossRef]
- Yuan, J.; Wu, Y.; Zhang, J. Characterization of Air Voids and Frost Resistance of Concrete Based on Industrial Computerized Tomographical Technology. Constr. Build. Mater. 2018, 168, 975–983. [Google Scholar] [CrossRef]
- Shang, H.; Yi, T.; Guo, X. Study on Strength and Ultrasonic Velocity of Air-Entrained Concrete and Plain Concrete in Cold Environment. Adv. Mater. Sci. Eng. 2014, 2014, 706986. [Google Scholar] [CrossRef]
- Deng, X.; Liu, Y.; Wang, R. Investigating Freeze-Proof Durability of Air-Entrained C30 Recycled Coarse Aggregate Concrete. Arch. Civ. Eng. 2021, 67, 507–524. [Google Scholar] [CrossRef]
- Hang, M.; Cui, L.; Wu, J.; Sun, Z. Freezing-Thawing Damage Characteristics and Calculation Models of Aerated Concrete. J. Build. Eng. 2020, 28, 101072. [Google Scholar] [CrossRef]
- Liu, L.; Ye, G.; Schlangen, E.; Chen, H.; Qian, Z.; Sun, W.; van Breugel, K. Modeling of the Internal Damage of Saturated Cement Paste due to Ice Crystallization Pressure During Freezing. Cem. Concr. Compos. 2011, 33, 562–571. [Google Scholar] [CrossRef]
- Liu, L.; Shen, D.; Chen, H.; Sun, W.; Qian, Z.; Zhao, H.; Jiang, J. Analysis of Damage Development in Cement Paste due to Ice Nucleation at Different Temperatures. Cem. Concr. Compos. 2014, 53, 1–9. [Google Scholar] [CrossRef]
- Koci, V.; Madera, J.; Jerman, M.; Cerny, R. Experimental Determination of Frost Resistance of Autoclaved Aerated Concrete at Different Levels of Moisture Saturation. Int. J. Thermophys. 2018, 39, 1328–1339. [Google Scholar] [CrossRef]
- Dabrowski, M.; Glinicki, M.; Gibas, K.; Jozwiak-Niedzwiedzka, D. Effects of Calcareous Fly Ash in Blended Cements on Chloride Ions Migration and Strength of Air Entrained Concrete. Constr. Build. Mater. 2016, 126, 1044–1053. [Google Scholar] [CrossRef]
- Karagol, F.; Yegin, Y.; Polat, R.; Benli, A.; Demirboga, R. The Influence of Lightweight Aggregate, Freezing-Thawing Procedure and Air Entraining Agent on Freezing-Thawing Damage. Struct. Concr. 2018, 19, 1328–1340. [Google Scholar] [CrossRef]
- Cui, Y.; Chen, Y.; Cen, G.; Peng, G. Comparative Study on the Effect of Organic and Inorganic Fiber on the Anti-wheel Impact Performance of Airport Pavement Concrete under Freeze-thaw Environment. Constr. Build. Mater. 2019, 211, 284–297. [Google Scholar] [CrossRef]
- Li, G.; Shen, X. A Study of the Durability of Aeolian Sand Powder Concrete Under the Coupling Effects of Freeze-Thaw and Dry-Wet Conditions. JOM 2019, 71, 1962–1974. [Google Scholar] [CrossRef]
- Gong, F.; Maekawa, K. Proposal of Poro-Mechanical Coupling among ASR, Corrosion and Frost Action for Damage Assessment of Structural Concrete with Water. Eng. Struct. 2019, 188, 418–429. [Google Scholar] [CrossRef]
- Tian, W.; Han, N. Pore Characteristics (>0.1 mm) of Non-Air Entrained Concrete Destroyed by Freeze-Thaw Cycles Based on CT Scanning and 3D Printing. Cold Reg. Sci. Technol. 2018, 151, 314–322. [Google Scholar] [CrossRef]
- Luo, Q.; Liu, D.; Qiao, P.; Feng, Q.; Sun, L. Microstructural Damage Characterization of Concrete under Freeze-Thaw Action. Int. J. Damage Mech. 2017, 27, 1551–1568. [Google Scholar] [CrossRef]
- Lazniewska-Piekarczyk, B. The Influence of Admixtures Type on the Air-Voids Parameters of Non-Air-Entrained and Air-Entrained High Performance SCC. Constr. Build. Mater. 2013, 41, 109–124. [Google Scholar] [CrossRef]
- Tolegenova, A.; Skripkiunas, G.; Rishko, L.; Akmalaiuly, K. Both Plasticizing and Air-Entraining Effect on Cement-Based Material Porosity and Durability. Materials 2022, 15, 4382. [Google Scholar] [CrossRef]
- GB/T 50080-2016; Ordinary Concrete Mix Performance Test Method Standard. Ministry of Housing and Urban-Rural Development of the People’s Republic of China: Beijing, China, 2016.
- Wang, Y.; Song, Y.; Yan, B.; Yuan, C.; Wang, D.; Guo, W. Experimental Study of Chloride Transport Law in Concrete Considering the Coupling Effects of Dry-Wet Ratio and Freeze-Thaw Damage. Constr. Build. Mater. 2022, 351, 651–658. [Google Scholar] [CrossRef]
- Zhang, P.; Wittmann, F.; Vogel, M.; Mueller, H.; Zhao, T. Influence of Freeze-Thaw Cycles on Capillary Absorption and Chloride Penetration into Concrete. Cem. Concr. Res. 2017, 100, 60–67. [Google Scholar] [CrossRef]
- Xiao, Q.; Wu, Z.; Qiu, J.; Dong, Z.; Shi, S. Capillary Water Absorption Performance and Damage Constitutive Model of Recycled Concrete under Freeze-Thaw Action. Constr. Build. Mater. 2022, 353, 129120. [Google Scholar] [CrossRef]
- Zeng, Y.; Zhou, X.; Tang, A. Shear Performance of Fibers-Reinforced Lightweight Aggregate Concrete Produced with Industrial Waste Ceramsite-Lytag after Freeze-Thaw Action. J. Clean. Prod. 2021, 328, 129626. [Google Scholar] [CrossRef]
- Al Rikabi, F.; Sargand, F.; Khoury, I.; Hussein, H. Material Properties of Synthetic Fiber-Reinforced Concrete under Freeze-Thaw Conditions. J. Mater. Civ. Eng. 2018, 30, 04018090. [Google Scholar] [CrossRef]
- Zeng, W.; Zhao, X.; Zou, B.; Chen, C. Topographical Characterization and Permeability Correlation of Steel Fiber Reinforced Concrete Surface under Freeze-Thaw Cycles and NaCl Solution Immersion. J. Build. Eng. 2023, 80, 108042. [Google Scholar] [CrossRef]
- Jiang, M.; Liu, X.; Hang, M.; Xu, Y.; Lai, G.; Li, S. Performance and Deterioration Mechanism of Concrete Incorporated with Corrosion-Inhibiting Admixtures under the Coupling Effect of Composite Salt and Freeze-Thaw Cycles. J. Build. Eng. 2023, 69, 106329. [Google Scholar] [CrossRef]
- Wei, Y.; Chen, X.; Chai, J.; Qin, Y. Correlation Between Mechanical Properties and Pore Structure Deterioration of Recycled Concrete under Sulfate Freeze-Thaw Cycles: An Experimental Study. Constr. Build. Mater. 2024, 412, 134794. [Google Scholar] [CrossRef]
- Jin, S.J.; Li, Z.L.; Zhang, J.; Wang, Y.L. Experimental Study on the Performance of the Basalt Fiber Concrete Resistance to Freezing and Thawing. Appl. Mech. Mater. 2014, 584–586, 1304–1308. [Google Scholar] [CrossRef]
- Zaharieva, R.; Buyle-Bodin, F.; Wirquin, E. Frost Resistance of Recycled Aggregate Concrete. Cem. Concr. Res. 2004, 34, 1927–1932. [Google Scholar] [CrossRef]





| Researchers Reference | Freeze–Thaw Damage Models | Parameters |
|---|---|---|
| Yan Li 2015 [20] | Dn: loss of relative dynamic elastic modulus eg: relative dynamic elastic modulus acceleration n: number of freeze–thaw cycles | |
| Hongfa Yu 2017 [22] | Dn: loss of relative dynamic elastic modulus N: the standard fatigue life of concrete subjected to freeze–thaw cycles n: number of freeze–thaw cycles β: concrete material parameter | |
| Xiaoxiao Wang 2018 [23] | Dn: loss of relative dynamic elastic modulus D0: initial damage of the concrete at the time of loading C: maximum strain of the concrete prior to damage localization β: material parameters σmax: maximum hydraulic pressure εt: strain value where the stress is 80% of the concrete tensile strength E0: initial elastic modulus of the concrete Et: tangent modulus when the strain is εt | |
| Boxin Wang 2020 [25] | Dn: loss of relative dynamic elastic modulus n: number of freeze–thaw cycles α; β; γ; k: undetermined parameters that can be confirmed by test | |
| Guanglei Qu 2023 [26] | Dn: loss of relative dynamic elastic modulus n: number of freeze–thaw cycles F(n): strength of concrete after n freezing and thawing F0: initial strength of concrete k: strength loss rate α: empirical parameter β: empirical parameter μ: empirical parameter |
| Mixture Notation | Group | Air Content (%) | W/C | Mix Proportion (kg/m3) | Sand Ratio | |||
|---|---|---|---|---|---|---|---|---|
| Water | Cement | Sand | Coarse Aggregate | |||||
| Ordinary Portland concrete | A | 0.8 | 0.45 | 195.0 | 435.0 | 566.7 | 1204.3 | 0.32 |
| Air-entrained concrete | B | 2.7 | ||||||
| C | 4.5 | |||||||
| D | 6.6 | |||||||
| Group | Mixture Notation | Pn = P0 ((1 + k)n − 1) | Air Content (%) | ||
|---|---|---|---|---|---|
| P0 | K | R2 | |||
| A | Ordinary Portland concrete | 9.05 | 0.0161 | 0.99 | 0.8 |
| B | Air-entrained concrete | 2.96 | 0.0124 | 0.99 | 2.7 |
| C | 2.40 | 0.0100 | 0.99 | 4.5 | |
| D | 1.35 | 0.0056 | 0.99 | 6.6 | |
| n 1 | The Loss of Relative Dynamic Elastic Modulus (%) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Wang [46] | Xiao [48] | Zeng [49] | Xiao [21] | Alrikabi [50] | Zeng [51] | Jiang [52] | Wei [53] | Li [18] | |||
| 0 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 5 | 0.26 | - | - | - | - | - | - | - | - | - | - |
| 10 | 3.68 | - | - | - | - | - | - | - | - | - | - |
| 15 | 6.57 | - | - | - | - | - | - | - | - | - | - |
| 20 | 11.74 | - | - | - | - | - | - | - | - | - | - |
| 25 | - | - | - | - | 0.83 | - | 1.09 | 3.24 | 0.20 | 1.60 | - |
| 30 | 16.17 | - | - | - | - | 12.48 | - | - | - | - | - |
| 35 | - | - | - | - | - | - | - | - | - | - | - |
| 40 | 24.95 | - | - | - | - | - | - | - | - | - | - |
| 50 | 36.92 | 2.99 | 2.92 | 1.89 | 1.37 | - | 4.00 | 14.69 | 0.95 | 3.10 | 0.40 |
| 60 | - | - | - | - | - | 28.19 | - | - | - | - | - |
| 75 | - | - | - | - | 2.10 | - | 8.01 | 21.93 | 2.58 | 5.12 | - |
| 80 | - | - | - | - | - | - | - | - | - | - | - |
| 90 | - | - | - | - | - | 44.9 | - | - | - | - | - |
| 100 | - | 8.98 | 6.24 | 4.26 | 3.00 | - | 13.17 | 41.70 | 3.85 | 6.53 | 0.91 |
| 120 | - | - | - | - | - | 70.08 | - | - | - | - | - |
| 125 | - | - | - | - | 3.18 | - | 20.02 | - | 4.96 | 8.61 | - |
| 150 | - | 18.00 | 13.45 | 7.42 | 4.48 | - | 22.13 | - | 6.13 | 10.47 | 2.69 |
| 175 | - | - | - | - | 6.00 | - | 29.12 | - | 7.50 | 12.72 | - |
| 200 | - | 30.96 | 23.60 | 11.53 | 6.68 | - | 37.13 | - | 8.39 | 15.86 | 3.89 |
| 225 | - | - | - | - | 7.52 | - | - | - | 9.43 | 19.12 | - |
| 250 | - | 41.98 | 42.24 | 19.30 | 10.77 | - | - | - | 11.16 | 21.79 | 6.28 |
| 275 | - | - | - | - | 15.79 | - | - | - | 13.64 | 25.94 | - |
| 300 | - | - | - | 29.13 | 23.81 | - | - | - | 15.53 | 29.04 | 7.88 |
| Freeze–thaw condition | Pure water | Pure water | Pure water | Pure water | Pure water | Pure water | 3.5% NaCl | 6% NaCl 3% Na2SO4 | 5% Na2SO4 | 5% Na2SO4 | 5% Mg2SO4 |
| W/C | 0.5 | 0.45 | 0.29 | 0.29 | 0.45 | 0.32 | 0.50 | 0.45 | 0.38 | 0.38 | 0.5 |
| Adulteration | / | RCA 2 | Lytag 3 | Lytag BF 4 | RCA | FA 5 | FA SF 6 | FA | FA | FA RCA | / |
| Admixtures | / | WRA 7 AEA 8 | WRA | AEA | WRA | WRA | WRA | WRA AEA | WRA AEA | ||
| Wang [46] | Xiao [48] | Zeng [49] | Xiao [21] | Alrikabi [50] | Zeng [51] | Jiang [52] | Wei [53] | Li [18] | |||
|---|---|---|---|---|---|---|---|---|---|---|---|
| P0(%) | 15.53 | 12.78 | 3.73 | 3.64 | 0.74 | 49.54 | 14.23 | 8.67 | 9.18 | 14.97 | 2.10 |
| K | 0.0246 | 0.0059 | 0.0101 | 0.0074 | 0.0115 | 0.0073 | 0.0064 | 0.0177 | 0.0033 | 0.0036 | 0.0053 |
| Correlation (R2) | 0.99 | 0.99 | 0.99 | 0.99 | 0.97 | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, L.; Wang, Y.; Wang, Y.; Cheng, T. A New Concrete Freeze–Thaw Damage Model Based on Hydraulic Pressure Mechanism and Its Application. Materials 2025, 18, 3708. https://doi.org/10.3390/ma18153708
Xu L, Wang Y, Wang Y, Cheng T. A New Concrete Freeze–Thaw Damage Model Based on Hydraulic Pressure Mechanism and Its Application. Materials. 2025; 18(15):3708. https://doi.org/10.3390/ma18153708
Chicago/Turabian StyleXu, Lantian, Yuchi Wang, Yuanzhan Wang, and Tianqi Cheng. 2025. "A New Concrete Freeze–Thaw Damage Model Based on Hydraulic Pressure Mechanism and Its Application" Materials 18, no. 15: 3708. https://doi.org/10.3390/ma18153708
APA StyleXu, L., Wang, Y., Wang, Y., & Cheng, T. (2025). A New Concrete Freeze–Thaw Damage Model Based on Hydraulic Pressure Mechanism and Its Application. Materials, 18(15), 3708. https://doi.org/10.3390/ma18153708