A Modified Two-Temperature Calibration Method and Facility for Emissivity Measurement
Abstract
1. Introduction
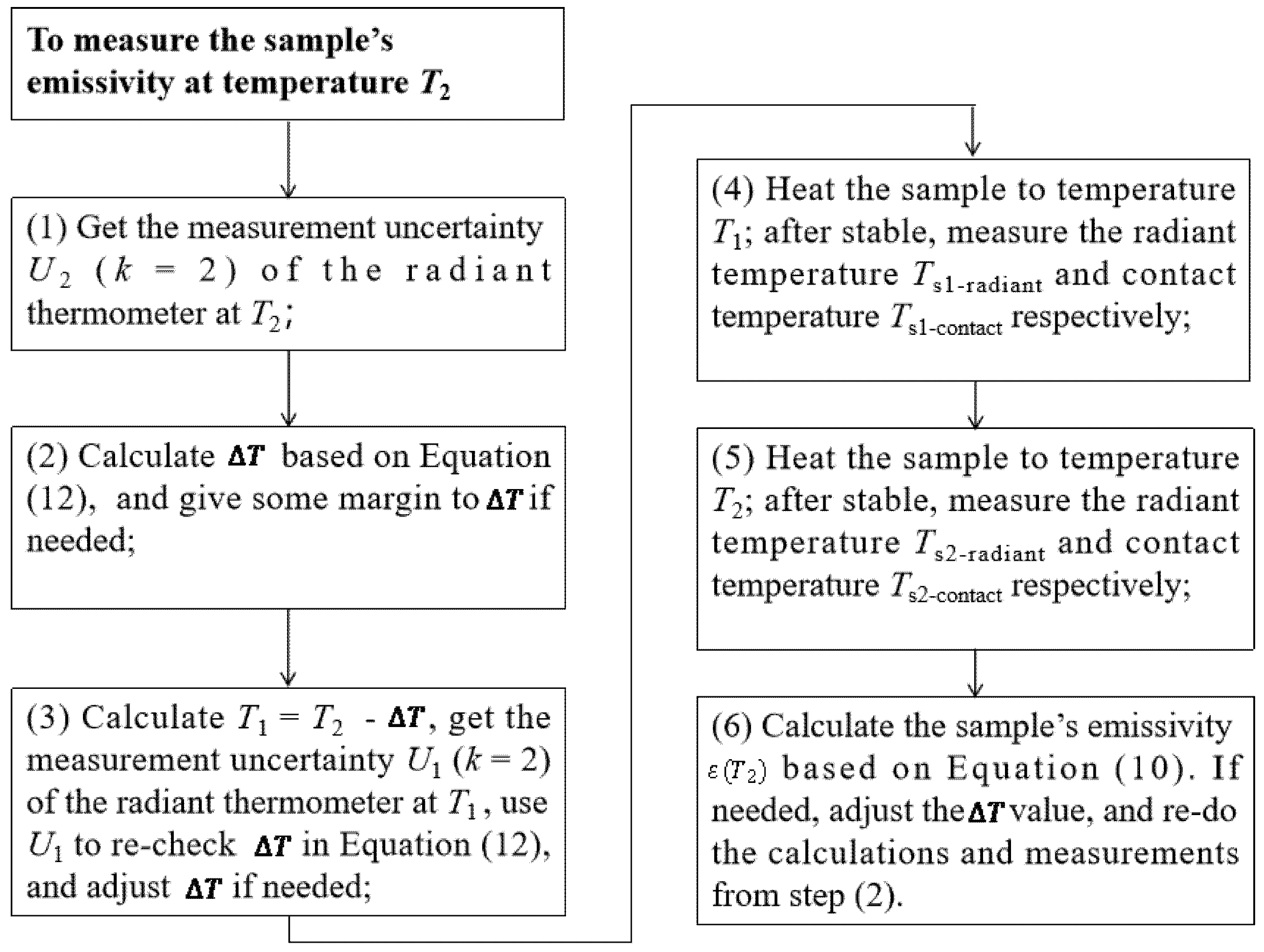
2. The Principle of the Developed Modified Two-Temperature Calibration Method
3. Experiments and Uncertainty Estimation
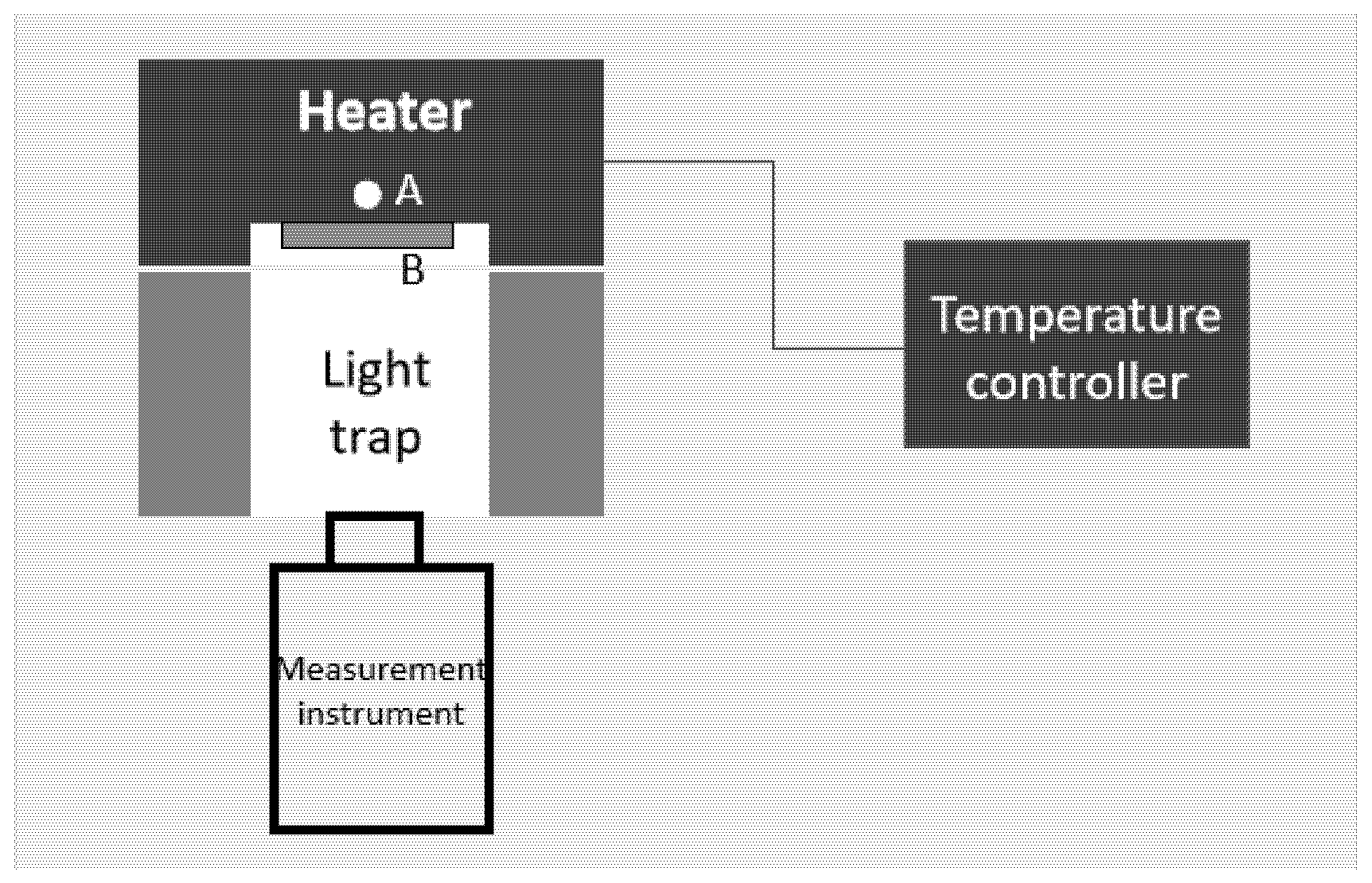
3.1. Experimental Facility and Results
3.2. Uncertainty Estimation
4. Comparisons and Discussions
5. Novel Points and Limitations of This Study
5.1. Novel Points of This Study
5.2. Limitations of This Study and Future Directions
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ravindra, N.M.; Sopori, B.; Gokce, O.H.; Cheng, S.X.; Shenoy, A.; Jin, L.; Abedrabbo, S.; Chen, W.; Zhang, Y. Emissivity Measurements and Modeling of Silicon-Related Materials: An Overview. Int. J. Thermophys. 2001, 22, 1593–1611. [Google Scholar] [CrossRef]
- Hanssen, L.; Mekhontsev, S.; Khromchenko, V. Infrared Spectral Emissivity Characterization Facility at NIST. In Thermosense XXVI; SPIE: Bellingham, WA, USA, 2004; pp. 1–12. [Google Scholar]
- Ivanov, V.; Lisiansky, B.; Morozova, S.; Sapritsky, V.; Melenevsky, U.; Xi, L.; Pei, L. Medium-background radiometric facility for calibration of sources or sensors. Metrologia 2000, 37, 599–602. [Google Scholar] [CrossRef]
- Honnerová, P.; Martan, J.; Kučera, M.; Honner, M.; Hameury, J. New experimental device for high-temperature normal spectral emissivity measurements of coatings. Meas. Sci. Technol. 2014, 25, 095501. [Google Scholar] [CrossRef]
- Zhu, C.; Hobbs, M.J.; Willmott, J.R. An accurate instrument for emissivity measurements by direct and indirect methods. Meas. Sci. Technol. 2020, 31, 044007. [Google Scholar] [CrossRef]
- Vishnevetsky, I.; Rotenberg, E.; Kribus, A.; Yakir, D. Method for accurate measurement of infrared emissivity for opaque low-reflectance materials. Appl. Opt. 2019, 58, 4599–4609. [Google Scholar] [CrossRef] [PubMed]
- Monte, C.; Gutschwager, B.; Morozova, S.; Hollandt, J. Radiation thermometry and emissivity measurements under vacuum at the PTB. Int. J. Thermophys. 2008, 30, 203–219. [Google Scholar] [CrossRef]
- Parfentiev, N.A.; Lisiansky, B.E.; Melenevsky, U.A.; Gutschwager, B.; Monte, C.; Hollandt, J. Vacuum Variable Medium Temperature Blackbody. Int. J. Thermophys. 2010, 31, 1809–1820. [Google Scholar] [CrossRef]
- Hao, X.P.; Song, J.; Xu, M.; Sun, J.P.; Gong, L.Y.; Yuan, Z.D. Vacuum radiance-temperature standard facility for infrared remote sensing at nim. Int. J. Thermophys. 2018, 39, 78. [Google Scholar] [CrossRef]
- Del Campo LPerez-Saez, R.B.; Esquisabel, X.; Fernández, I.; Manuel, J.T. New experimental device for infrared spectral directional emissivity measurements in a controlled environment. Rev. Sci. Instrum. 2006, 77, 113111. [Google Scholar] [CrossRef]
- Zhang, K.; Yu, K.; Liu, Y.; Zhao, Y. An improved algorithm for spectral emissivity measurements at low temperatures based on the multi-temperature calibration method. Int. J. Heat Mass. Tran. 2017, 114, 1037–1044. [Google Scholar] [CrossRef]
- Zhang, K.; Liu, Y. Modified two-temperature calibration method for emissivity measurements at high temperatures. Appl. Therm. Eng. 2020, 168, 114854. [Google Scholar] [CrossRef]
- ISO 14253-1: 2013; Geometrical Product Specifications (GPS)—Inspection by Measurement of Workpieces and Measuring Equipment—Part 1: Decision Rules for Proving Conformity or Nonconformity with Specifications. International Organization for Standardization: Geneva, Switzerland, 2013.
- Lohrengel, J.; Todtenhaupt, R. Thermal conductivity, degree of total emissivity and spectral emissivity of the nextel velvet coating. PTB-Mitteilungen 1996, 106, 259–265. [Google Scholar]
- Moreira, T.A.; Colmanetti, A.R.A.; Tibiriá, C.B. Heat transfer coefficient: A review of measurement techniques. J. Braz. Soc. Mech. Sci. Eng. 2019, 41, 264. [Google Scholar] [CrossRef]
- Carlomagno, G.M.; Cardone, G. Infrared thermography for convective heat transfer measurements. Exp. Fluids 2010, 49, 1187–1218. [Google Scholar] [CrossRef]
- Ishii, J.; Ono, A. Uncertainty estimation for emissivity measurements near room temperature with a Fourier transform spectrometer. Meas. Sci. Technol. 2001, 12, 2103. [Google Scholar] [CrossRef]
- Ishii, J.; Ono, A. Low-Temperature Infrared Radiation Thermometry at NMIJ. In Temperature: Its Measurement and Control in Science and Industry, Volume VII, Proceedings of theEighth Temperature Symposium, Chicago, IL, USA, 21–24 October 2002; American Institute of Physics: College Park, MD, USA, 2003. [Google Scholar]
- Ma, J.; Zhang, Y.; Wu, L.; Li, H.; Song, L. An apparatus for spectral emissivity measurements of thermal control materials at low temperatures. Materials 2019, 12, 1141. [Google Scholar] [CrossRef] [PubMed]
- Rubin, M.; Arasteh, D.; Hartmann, J. A correlation between normal and hemispherical emissivity of low-emissivity coatings on glass. Int. J. Heat Mass. Tran. 1987, 14, 561–565. [Google Scholar] [CrossRef]
- Singh, S.M. Remarks on the use of a Stefan-Boltzmann-type relation for estimating surface temperatures. Int. J. Remote Sens. 1985, 6, 741–747. [Google Scholar] [CrossRef]

| Parameters | Sample 1 | Sample 2 | Sample 3 |
|---|---|---|---|
| Material | Aluminum plate | Aluminum plate with gray coating | Stainless steel with black coating |
| Thickness (mm) | 0.5 | 2.2 (Aluminum) 0.1 (self-made gray coating) | 3 (Stainless steel) 0.1 (black coating) |
| ) | 0.100 | 0.500 | 0.900 |
| ) | 10.0 | 10.0 | 10.0 |
| ) | 15.0 | 15.0 | 15.0 |
| Thermal conductivity (W·m−1·K−1) | 205 | 205 (Aluminum) 20 (self-made gray coating) | 15 (Stainless steel) 0.2 (black coating) |
| Samples | Set Value (°C) | Contact Thermometer (°C) | Radiant (°C) | ||
|---|---|---|---|---|---|
| Sample 1 | 50 | 51.77 | 28.7 | 0.110 | |
| 60 | 62.50 | 30.3 | |||
| 70 | 73.28 | 31.3 | 0.114 | ||
| 85 | 89.30 | 34.2 | |||
| Sample 2 | 50 | 51.53 | 40.2 | 0.529 | |
| 60 | 62.28 | 46.6 | |||
| 70 | 73.08 | 52.9 | 0.527 | ||
| 85 | 89.32 | 63.3 | |||
| Sample 3 | 50 | 51.75 | 50.1 | 0.932 | |
| 60 | 62.48 | 60.3 | |||
| 70 | 73.28 | 70.5 | 0.933 | ||
| 85 | 89.36 | 85.9 | |||
| Uncertainty Component | Sample 1 | Sample 2 | Sample 3 | |||
|---|---|---|---|---|---|---|
| Repeatability (%) | 1.08 | 0.60 | 0.20 | 0.33 | 0.19 | 0.11 |
| Reproducibility (%) | 2.62 | 2.17 | 0.74 | 0.86 | 0.59 | 0.34 |
| measurement (%) | 0.00003 | 0.00007 | 0.00014 | 0.00030 | 0.00026 | 0.00054 |
| measurement (%) | 0.00003 | 0.00008 | 0.00015 | 0.00035 | 0.00027 | 0.00062 |
| measurement (%) | 0.0024 | 0.0059 | 0.0025 | 0.0072 | 0.0027 | 0.0085 |
| measurement (%) | 0.0024 | 0.0061 | 0.0026 | 0.0079 | 0.0029 | 0.0097 |
| (%) | 0.0002 | 0.0003 | 0.0015 | 0.0044 | 0.0031 | 0.0069 |
| (%) | 0.0002 | 0.0004 | 0.0015 | 0.0048 | 0.0033 | 0.0079 |
| (%) | N.S. * | N.S. * | 0.00002 | 0.00002 | 0.00294 | 0.00342 |
| (%) | N.S. * | N.S. * | 0.00002 | 0.00002 | 0.00447 | 0.00529 |
| Uniformity (%) | 3.64 | 3.54 | 1.70 | 2.66 | 0.32 | 0.43 |
| Stray radiation and air convection on the sample surface (%) | 1.0 | 1.0 | 0.5 | 0.5 | 0.1 | 0.1 |
| Combined uncertainty (urel, %) | 4.8 | 4.4 | 2.0 | 2.9 | 0.71 | 0.57 |
| Combined relative expanded uncertainty (Urel, %, k = 2) | 9.6 | 8.8 | 4.0 | 5.8 | 1.5 | 1.2 |
| Samples | The Indirect Method | The Conventional Two-Temperature Calibration Method | The Developed Method | ||
|---|---|---|---|---|---|
| Sample 1 | ) | ||||
| Sample 2 | |||||
| Sample 3 | |||||
| Samples | En Values of the Indirect Method | En Values of the Conventional Two-Temperature Calibration Method | En Values of the Developed Method |
|---|---|---|---|
| Sample 1 | ) | ) | ) |
| ) | ) | ) | |
| Sample 2 | ) | ) | ) |
| ) | ) | ) | |
| Sample 3 | ) | ) | ) |
| ) | ) | ) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, S.; Li, S.; Dai, C.; Liu, J.; Wang, Y.; Sun, R.; Feng, G.; Wang, J. A Modified Two-Temperature Calibration Method and Facility for Emissivity Measurement. Materials 2025, 18, 3392. https://doi.org/10.3390/ma18143392
He S, Li S, Dai C, Liu J, Wang Y, Sun R, Feng G, Wang J. A Modified Two-Temperature Calibration Method and Facility for Emissivity Measurement. Materials. 2025; 18(14):3392. https://doi.org/10.3390/ma18143392
Chicago/Turabian StyleHe, Shufang, Shuai Li, Caihong Dai, Jinyuan Liu, Yanfei Wang, Ruoduan Sun, Guojin Feng, and Jinghui Wang. 2025. "A Modified Two-Temperature Calibration Method and Facility for Emissivity Measurement" Materials 18, no. 14: 3392. https://doi.org/10.3390/ma18143392
APA StyleHe, S., Li, S., Dai, C., Liu, J., Wang, Y., Sun, R., Feng, G., & Wang, J. (2025). A Modified Two-Temperature Calibration Method and Facility for Emissivity Measurement. Materials, 18(14), 3392. https://doi.org/10.3390/ma18143392







