Life Prediction Model for High-Cycle and Very-High-Cycle Fatigue of Ti-6Al-4V Titanium Alloy Under Symmetrical Loading
Abstract
1. Introduction
2. Experimental Material and Procedures
2.1. Materials and Static Tensile Test
2.2. High-Cycle Fatigue Test and Results
2.3. Very-High-Cycle Fatigue Test and Results
3. Life Prediction Model of the Ti-6Al-4V Titanium Alloy in the High-Cycle Fatigue Regime
3.1. Constitutive Model of Continuous Damage Mechanics
3.2. High-Cycle Fatigue Model Based on Continuous Damage Theory
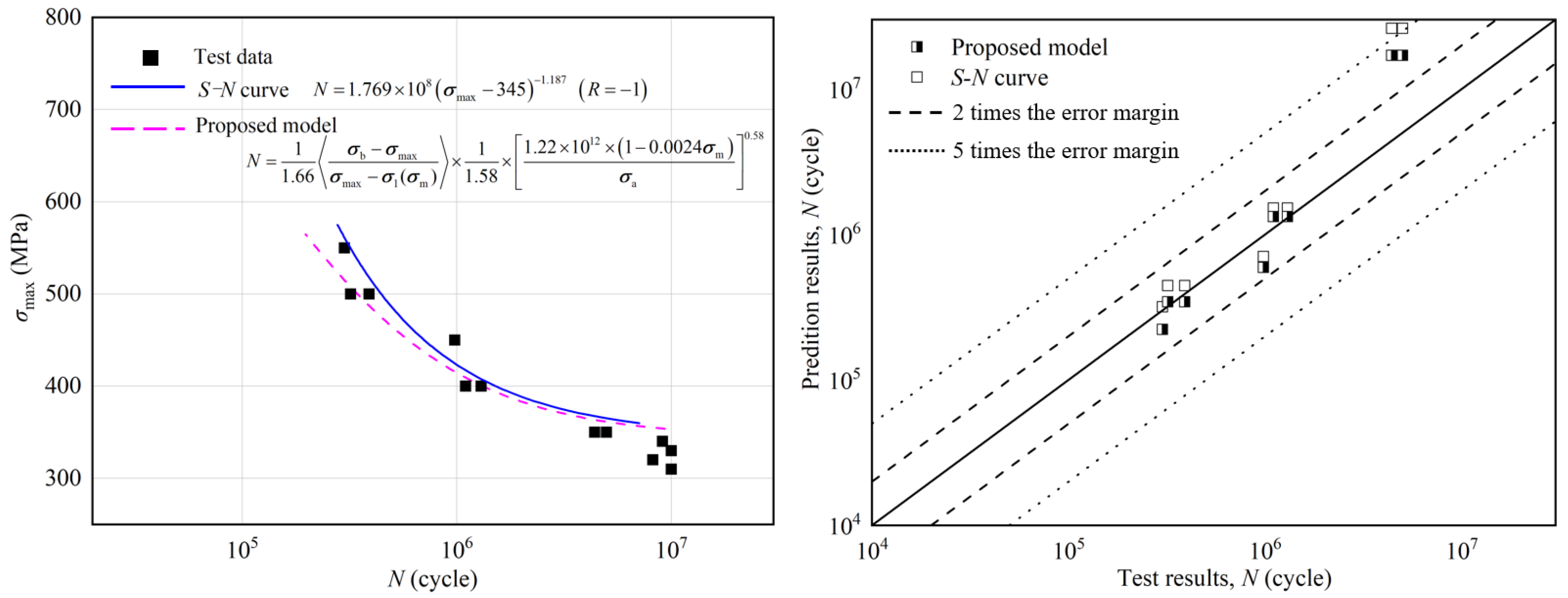
3.3. Discussion
4. Life Prediction Model of Ti-6Al-4V Titanium Alloy in the Very-High-Cycle Fatigue Regime
4.1. Very-High-Cycle Fatigue Model Based on Continuous Damage Theory
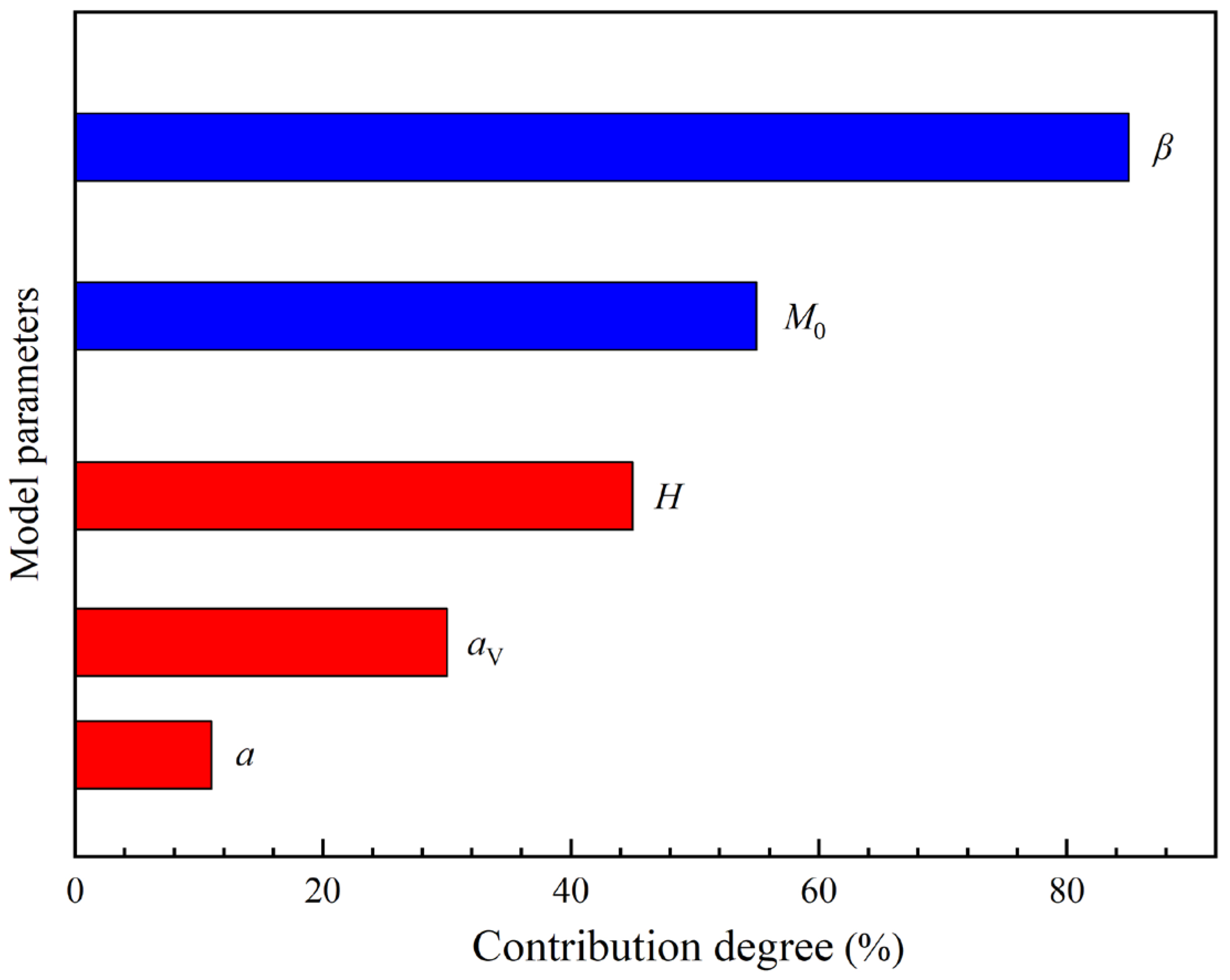
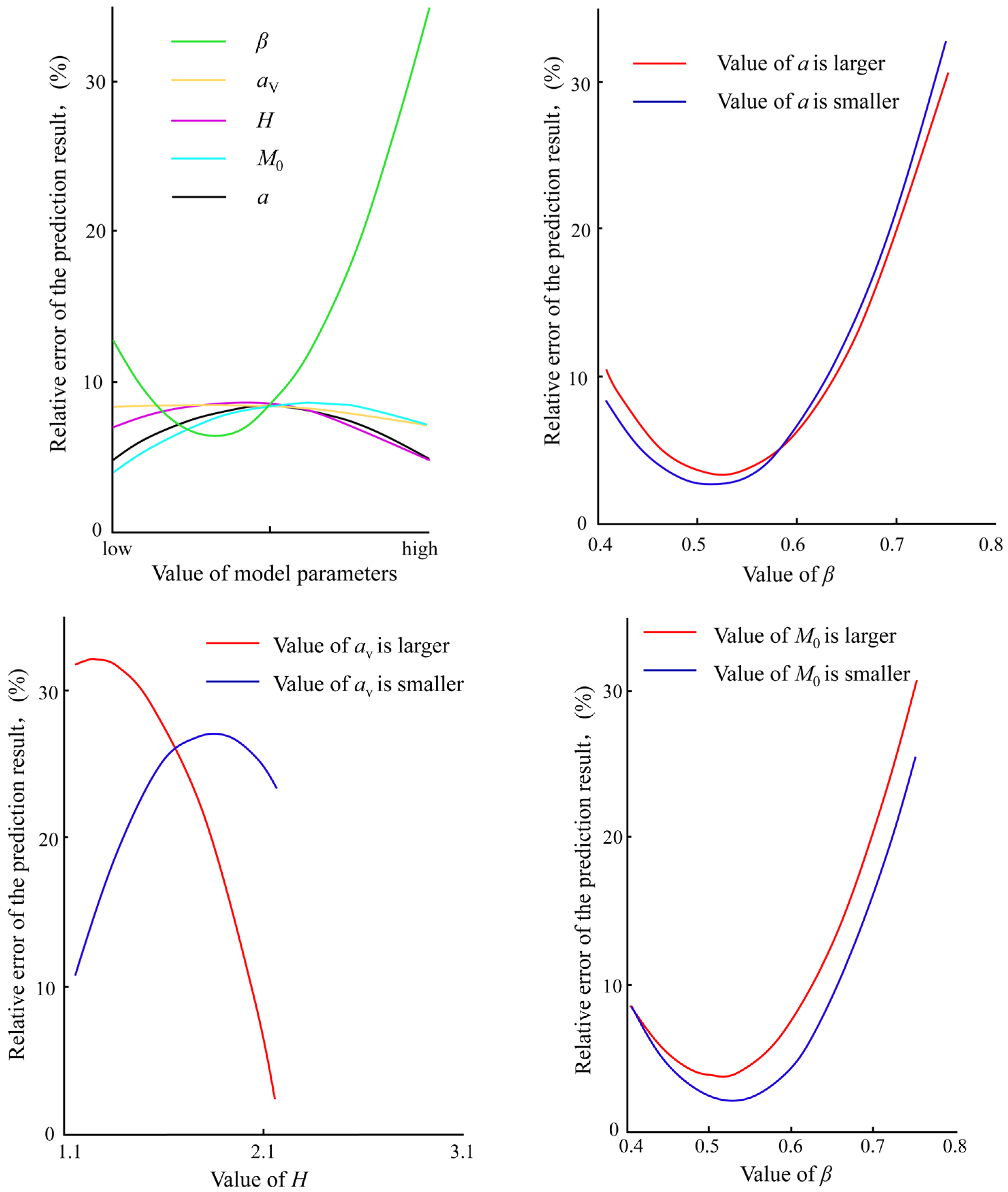
4.2. Parameter Optimization of the Fatigue Model Based on Sensitivity Analysis
5. Conclusions
- Through the microscopic observation of the high-cycle fatigue crack propagation zone of the titanium alloy, obvious fatigue striations can be observed. Due to the crystal lattice, some fatigue striations are not parallel. High-cycle fatigue cracks initiate at several adjacent positions on the surface of the specimen. For the fracture morphology of very-high-cycle fatigue, the fatigue cracks all initiate inside the specimen, and typical “fish-eye” fracture morphology characteristics are formed.
- The high-cycle fatigue model based on nonlinear continuum damage mechanics is a smooth curve within the entire load range (500 MPa to 750 MPa) of the test. When the applied load is close to the fatigue limit, the fatigue characteristics of the material change continuously with the loading parameters. At the same time, the influence of the applied stress on the fatigue damage development process of the material is considered, and the prediction accuracy is higher than that of the S-N curve.
- For the very-high-cycle fatigue model based on nonlinear continuum damage mechanics, by introducing the internal stress parameter to describe the variation law of the plastic strain energy during the very-high-cycle fatigue damage evolution process of the titanium alloy material, the law of damage accumulation and development of high-cycle/very-high-cycle fatigue of the titanium alloy is revealed. In addition, the prediction accuracy of the model after parameter optimization is significantly improved, and the average error of its prediction results is reduced from 59% to 38%.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wu, Y.; He, W.; Ma, H.; Nie, X.; Liang, X.; Pan, J.; Wang, S.; Shang, M.; Cheng, L. Titanium Alloy Materials with Very High Cycle Fatigue: A Review. Materials 2024, 17, 2987. [Google Scholar] [CrossRef]
- Zhao, C.; Wang, Y.; Hu, R.; Shang, G.; Wu, Y.; Lu, Y. Microstructural Influences on High Cycle Fatigue Crack Initiation Mechanism in Ti-Al-Mo-Cr-V-Nb-Zr-Sn Metastable β Titanium Alloy. Materials 2025, 18, 336. [Google Scholar] [CrossRef] [PubMed]
- MIL-HDBK, 1783BW/CHANGE2; Engine Structural Integrity Programs (EN-SIP). US Department of Defense: Pentagon City, VA, USA, 2004.
- Sonsino, C.M. Course of SN-curves especially in the high cycle fatigue regime with regard to component design and safety. Int. J. Fatigue 2007, 29, 2246–2258. [Google Scholar] [CrossRef]
- Zhang, Y.H.; Maddox, S.J.; Manteghi, S. Verification of Class B SN curve for fatigue design of steel forgings. Int. J. Fatigue 2016, 92, 246–264. [Google Scholar] [CrossRef]
- Zhou, S.Z.; Guo, S.; Chen, B.Z.; Zhang, J.; Zhao, W.Z. Master S-N curve fitting and life prediction method for very high cycle fatigue of welded structures. Trans. China Weld. Inst. 2022, 43, 76–82. (In Chinese) [Google Scholar]
- Wang, Z.P.; Zhu, M.L.; Xuan, F.Z. High cycle fatigue property and lifetime modeling of CrMoV and NiCrMoV dissimilar steel welded joint. Trans. China Weld. Inst. 2024, 45, 67–73. (In Chinese) [Google Scholar]
- Li, J.K.; Liu, Y.J.; Wang, Q.Y.; Hou, F. High-temperature ultra-high cycle fatigue test of TC17 titanium alloy. J. Aero Power 2014, 7, 1567–1573. (In Chinese) [Google Scholar]
- Liu, X.L.; Sun, C.Q.; Hong, Y.S. Effects of stress ratio on high cycle and very-high cycle fatigue behavior of a Ti-6Al-4Valloy. Mater. Sci. Eng. A 2015, 622, 228–235. [Google Scholar] [CrossRef]
- Morrissey, R.; Nicholas, T. Staircase testing of a titanium alloy in the gigacycle regime. Int. J. Fatigue 2006, 28, 1577–1582. [Google Scholar] [CrossRef]
- Zuo, Z.H.; Wang, Z.G.; Han, E.H. Effect of microstructure on ultra-high cycle fatigue behavior of Ti-6Al-4V. Mater. Sci. Eng. A 2008, 473, 147–152. [Google Scholar] [CrossRef]
- Oguma, H.; Nakamura, T. Fatigue crack propagation properties of Ti-6Al-4V in vacuum environments. Int. J. Fatigue 2013, 50, 89–93. [Google Scholar] [CrossRef]
- Su, H.; Liu, X.; Sun, C.; Hong, Y. Nanograin layer formation at crack initiation region for very-high cycle fatigue of a Ti-6Al-4V alloy. Fatigue Frac Eng. Mater. Struct. 2017, 40, 979–993. [Google Scholar] [CrossRef]
- Furuya, Y.; Nishikawa, H.; Hirukawa, H.; Nagashima, N.; Takeuchi, E. Catalogue of NIMS fatigue data sheets. Sci. Technol. Adv. Mater. 2019, 20, 1055–1072. [Google Scholar] [CrossRef] [PubMed]
- Yang, K.; He, C.; Huang, Q.; Huang, Z.Y.; Wang, C.; Wang, Q.Y.; Liu, Y.J.; Zhong, B. Very high cycle fatigue behaviors of a turbine engine blade alloy at various stress ratios. Int. J. Fatigue 2017, 99, 35–43. [Google Scholar] [CrossRef]
- Pan, X.N.; Su, H.; Hong, Y.S. The behavior of crack initiation and early growth in high cycle and very-high cycle fatigue regimes for a titanium alloy. Int. J. Fatigue 2018, 115, 67–78. [Google Scholar] [CrossRef]
- Hagiwara, M.; Kitashima, T.; Emura, S. Relationship between microstructures, facet morphologies at the high cycle fatigue (HCF) crack initiation site, and HCF strength in Ti-6242S. Mater. Sci. Eng. A 2018, 727, 43–50. [Google Scholar] [CrossRef]
- Yu, D.; Zhang, D.F.; Dai, Q.W.; Lan, W.; Peng, J.; Xu, J.Y.; Qi, F.G.; Pan, F.S. Effect of stress ratio on high cycle fatigue properties in Mg-6Zn-1Mn alloy. Mater. Sci. Eng. A 2018, 711, 624–632. [Google Scholar] [CrossRef]
- Tan, C.S.; Sun, Q.Y.; Xiao, L.; Zhao, Y.Q.; Sun, J. Cyclic deformation and microcrack initiation during stress controlled high cycle fatigue of a titanium alloy. Mater. Sci. Eng. A 2018, 711, 212–222. [Google Scholar] [CrossRef]
- Sun, K.P.; Sun, Q.C.; Zhang, Y.Z.; Shi, B.W.; Zhao, B.B. A pragmatic approach to predict fatigue strength concerning the short crack behavior in VHCF. Int. J. Fatigue 2020, 135, 105561. [Google Scholar] [CrossRef]
- Liu, F.L.; He, C.; Chen, Y.; Zhang, H.; Wang, Q.Y.; Liu, Y.J. Effects of defects on tensile and fatigue behaviors of selective laser melted titanium alloy in very high cycle regime. Int. J. Fatigue 2020, 140, 105795. [Google Scholar] [CrossRef]
- Chen, Y.; He, C.; Liu, F.L.; Wang, C.; Xie, Q.; Wang, Q.Y.; Liu, Y.J. Effect of microstructure inhomogeneity and crack initiation environment on the very high cycle fatigue behavior of a magnesium alloy. Int. J. Fatigue 2020, 131, 105376. [Google Scholar] [CrossRef]
- Chen, J.; Cheng, L.; Jiao, S.B.; Lu, K.J. On the ultra-high cycle fatigue behavior of titanium alloy TC4. J. Exp. Mech. 2018, 33, 272–280. (In Chinese) [Google Scholar]
- Yang, H.P.; Yan, W.B.; Zhuang, W.; Wang, Y.M. Effect of texture characteristics on the high cycle fatigue properties of a Ti-6Al-4V alloy. Mater. Res. Express 2021, 8, 1–11. [Google Scholar] [CrossRef]
- Hou, S.Q.; Cai, X.J.; Xu, J.Q. A life evaluation formula for high cycle fatigue under uniaxial and multiaxial loadings with mean stresses. Int. J. Mech. Sci. 2015, 93, 229–239. [Google Scholar] [CrossRef]
- Wang, H. Study of Fatigue Behavior and Mechanism of Fatigue Failure in the Ultra-High Cycle Regime in 40Cr and 50 Axles Steels. Ph.D. Thesis, Southwest Jiaotong University, Chengdu, 2024. (In Chinese). [Google Scholar]
- Guo, H.F.; Yan, J.W.; Zhang, R.; He, Z.H.; Zhao, Z.H.; Zhao, Z.Q.; Qu, T.; Wan, M.; Liu, J.S.; Li, C.D. Failure Analysis on 42CrMo Steel Bolt Fracture. Adv. Mater. Sci. Eng. 2019, 2019, 8. [Google Scholar] [CrossRef]
- Shen, Z.S.; Huang, Z.Y.; Wang, J.; Zheng, L.Q.; Qian, H.J.; Zhu, Q.Y. Investigation of fretting fatigue performance for IN718 dovetail joint in very high cycle regime. Int. J. Fatigue 2025, 195, 108874. [Google Scholar] [CrossRef]
- Zhang, H.; Zhao, Y.F.; Zhang, M.; Li, M.L.; Liu, L.; Cui, Y.L.; Shang, X.D. The Fatigue Behavior and Mechanism of Large FV520B-I Specimens in a Very High Cycle Regime. J. Mater. Eng. Perform. 2024, 33, 950–960. [Google Scholar] [CrossRef]
- Zhou, Q.K.; Huang, Z.Y.; Qian, H.J.; Wang, J.; Shen, Z.S.; Pan, K.; Chen, Y.H. Fracture mechanism of Ti60 alloy at high temperature in very high cycle fatigue regime and fatigue life prediction. Fatigue Frac. Eng. Mater. Struct. 2024, 47, 3285. [Google Scholar] [CrossRef]
- Bathias, C.; Drouillac, L.; Francois, P.L. How and why the fatigue S-N curve does not approach ahorizontal asymptote. Int. J. Fatigue 2021, 23, S143–S151. [Google Scholar] [CrossRef]
- GB/T 3620.1-2016; Designation and Chemical Composition of Titanium and Titanium Alloys. China Standard Press: Beijing, China, 2016. (In Chinese)
- GB/T 228.1-2010; Metallic materials-Tensile testing-Part 1: Method of test at room temperature. China Standard Press: Beijing, China, 2010. (In Chinese)
- Lemaitre, J. Evaluation of dissipation and damage in metals submitted to dynamic loading. Mech. Behav. Mater. 1972, 76, 540–549. [Google Scholar]
- Feng, M.H. A Visco-Elastic-Plstic Unified Constitutive Theory for Deformation. Ph.D. Dissertation, Dalian University of Technology, Dalian, China, 2000. (In Chinese). [Google Scholar]
- Hirth, J.P.; Lothe, J. Theory of Dislocation; John Wiley: New York, NY, USA, 1982. [Google Scholar]

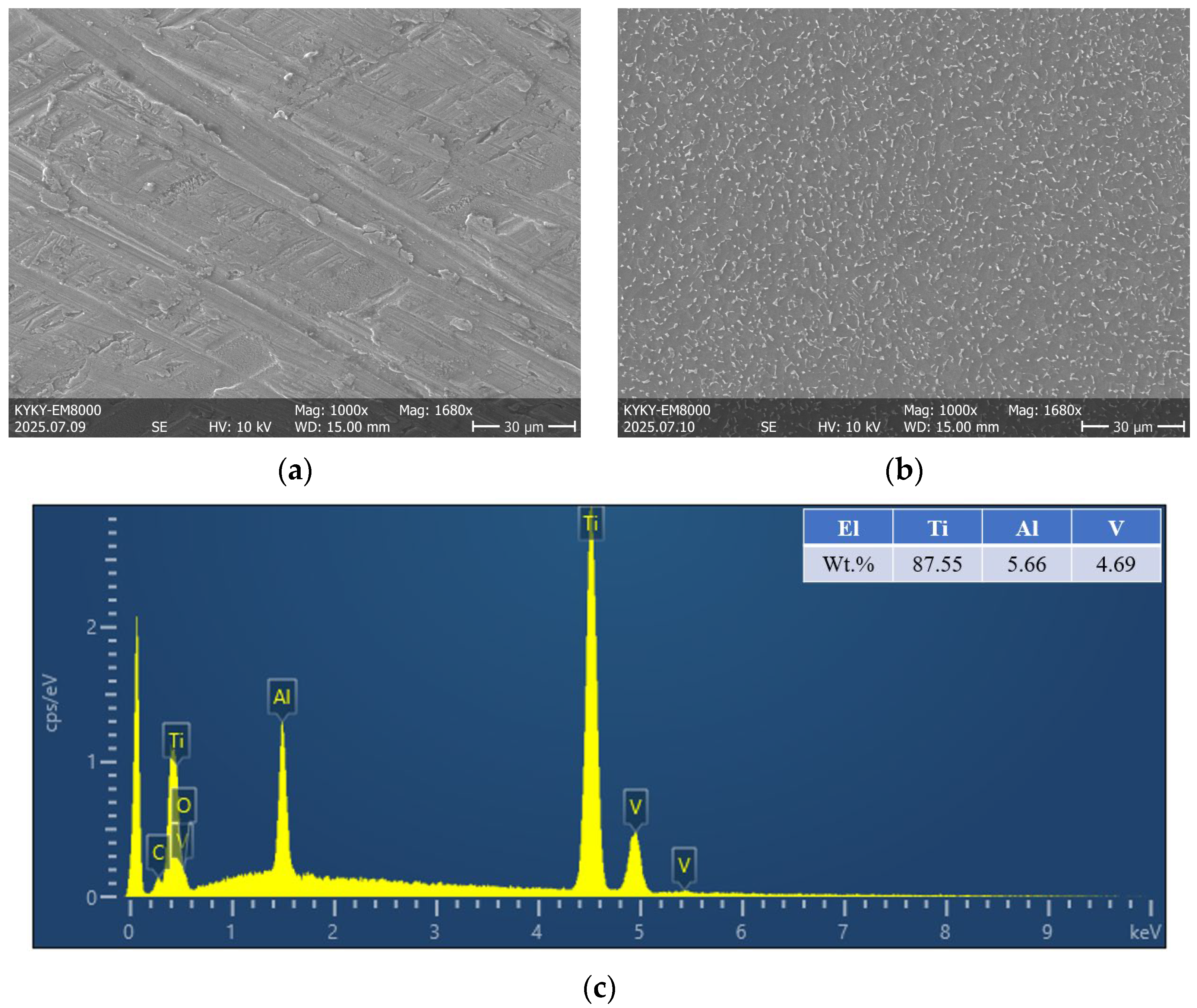

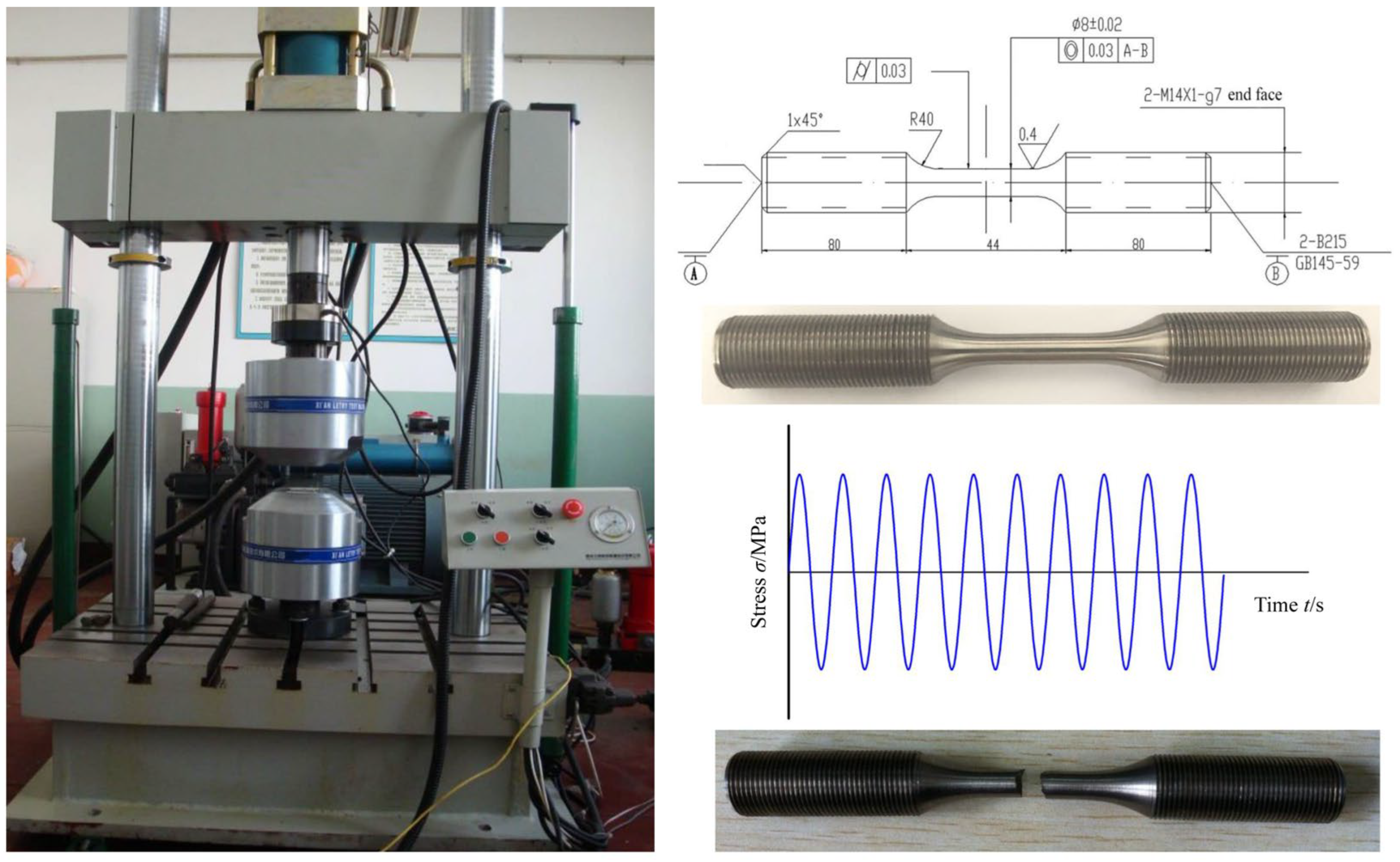

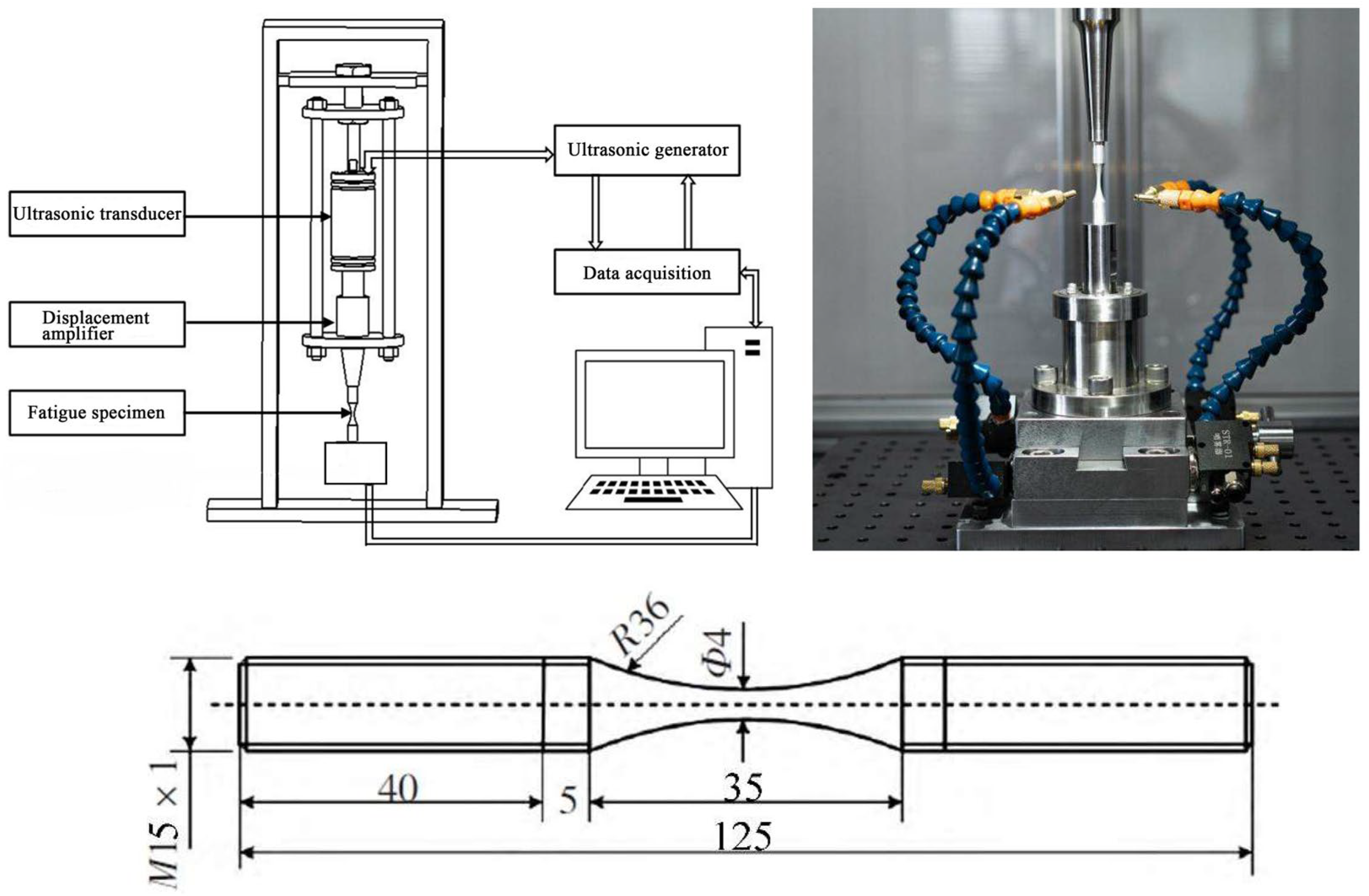


| Chemical Composition (Weight Percent) | ||||||||
|---|---|---|---|---|---|---|---|---|
| Main Constituents/% | Impurity (No More Than)/% | |||||||
| Ti | Al | V | Fe | C | H | O | N | Other Elements |
| Residual | 5.5~6.75 | 3.5~4.5 | 0.30 | 0.08 | 0.015 | 0.2 | 0.05 | 0.40 |
| No. | Stress /MPa | Cycles | State | No. | Stress /MPa | Cycles | State |
|---|---|---|---|---|---|---|---|
| 1 | 550 | 3.00 × 105 | fractured | 7 | 350 | 4.40 × 106 | fractured |
| 2 | 500 | 3.20 × 105 | fractured | 8 | 350 | 5.00 × 106 | fractured |
| 3 | 500 | 3.90 × 105 | fractured | 9 | 340 | 9.10 × 106 | fractured |
| 4 | 450 | 9.80 × 105 | fractured | 10 | 330 | 1.00 × 107 | Un-fractured |
| 5 | 400 | 1.10 × 106 | fractured | 11 | 320 | 8.20 × 106 | fractured |
| 6 | 400 | 1.30 × 106 | fractured | 12 | 310 | 1.00 × 107 | Un-fractured |
| No. | Stress /MPa | Cycles | State | No. | Stress /MPa | Cycles | State |
|---|---|---|---|---|---|---|---|
| 1 | 730 | 3.85 × 103 | fractured | 15 | 640 | 4.84 × 105 | fractured |
| 2 | 700 | 8.79 × 103 | fractured | 16 | 630 | 2.94 × 106 | fractured |
| 3 | 650 | 2.05 × 104 | fractured | 17 | 635 | 1.88 × 107 | fractured |
| 4 | 650 | 4.40 × 104 | fractured | 18 | 640 | 1.38 × 105 | fractured |
| 5 | 650 | 3.57 × 104 | fractured | 19 | 620 | 5.26 × 107 | fractured |
| 6 | 650 | 1.25 × 105 | fractured | 20 | 640 | 8.84 × 105 | fractured |
| 7 | 630 | 2.88 × 105 | fractured | 21 | 635 | 9.56 × 105 | fractured |
| 8 | 600 | 1.20 × 108 | Un-fractured | 22 | 635 | 2.55 × 105 | fractured |
| 9 | 630 | 1.39 × 105 | fractured | 23 | 632 | 1.06 × 108 | Un-fractured |
| 10 | 610 | 1.20 × 108 | Un-fractured | 24 | 635 | 1.20 × 106 | fractured |
| 11 | 620 | 4.18 × 105 | fractured | 25 | 640 | 1.21 × 107 | fractured |
| 12 | 620 | 1.70 × 107 | fractured | 26 | 640 | 1.03 × 106 | fractured |
| 13 | 630 | 9.50 × 107 | fractured | 27 | 550 | 1.00 × 109 | Un-fractured |
| 14 | 650 | 5.14 × 104 | fractured | 28 | 500 | 1.00 × 109 | Un-fractured |
| Model Parameters | Results Before Optimization | Results After Optimization |
|---|---|---|
| β | 0.40 | 0.42 |
| H | 2.23 | 1.88 |
| M0 | 3.12 × 1011 | 4.08 × 1011 |
| αV | 0.43 | 0.44 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fu, X.; Zhang, L.; Yang, W.; Yin, Z.; Zhou, J.; Wang, H. Life Prediction Model for High-Cycle and Very-High-Cycle Fatigue of Ti-6Al-4V Titanium Alloy Under Symmetrical Loading. Materials 2025, 18, 3354. https://doi.org/10.3390/ma18143354
Fu X, Zhang L, Yang W, Yin Z, Zhou J, Wang H. Life Prediction Model for High-Cycle and Very-High-Cycle Fatigue of Ti-6Al-4V Titanium Alloy Under Symmetrical Loading. Materials. 2025; 18(14):3354. https://doi.org/10.3390/ma18143354
Chicago/Turabian StyleFu, Xi, Lina Zhang, Wenzhao Yang, Zhaoming Yin, Jiakang Zhou, and Hongwei Wang. 2025. "Life Prediction Model for High-Cycle and Very-High-Cycle Fatigue of Ti-6Al-4V Titanium Alloy Under Symmetrical Loading" Materials 18, no. 14: 3354. https://doi.org/10.3390/ma18143354
APA StyleFu, X., Zhang, L., Yang, W., Yin, Z., Zhou, J., & Wang, H. (2025). Life Prediction Model for High-Cycle and Very-High-Cycle Fatigue of Ti-6Al-4V Titanium Alloy Under Symmetrical Loading. Materials, 18(14), 3354. https://doi.org/10.3390/ma18143354






