Effect of Crestal Position on Bone–Implant Stress Interface of Three-Implant Splinted Prostheses: A Finite Element Analysis
Abstract
1. Introduction
2. Materials and Methods
2.1. FEA Modeling
2.2. Load and Boundary Conditions
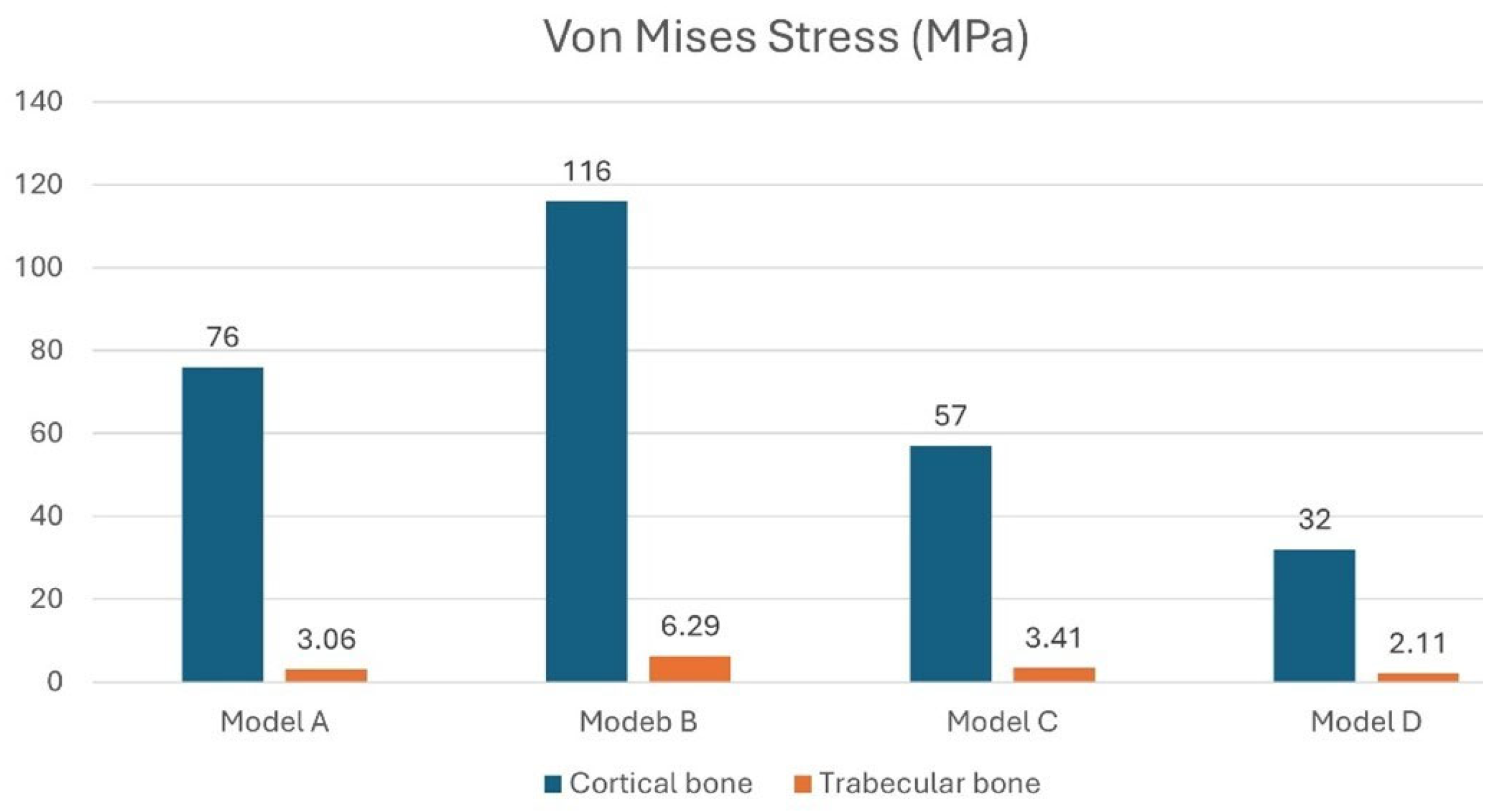
3. Results
3.1. Effect of Inclined Load
3.2. Stress on the Implants
4. Discussion
Limitations
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Schierz, O.; Reissmann, D.R. Dental patient-reported outcomes—The promise of dental implants. J. Evid. Based Dent. Pract. 2021, 21, 101541. [Google Scholar] [CrossRef]
- French, D.; Ofec, R.; Levin, L. Long term clinical performance of 10 871 dental implants with up to 22 years of follow-up: A cohort study in 4247 patients. Clin. Implant Dent. Relat. Res. 2021, 23, 289–297. [Google Scholar] [CrossRef]
- Schiegnitz, E.; Müller, L.K.; Sagheb, K.; Theis, L.; Cagiran, V.; Kämmerer, P.W.; Wegener, J.; Wagner, W.; Al-Nawas, B. Clinical long-term and patient-reported outcomes of dental implants in oral cancer patients. Int. J. Implant Dent. 2021, 7, 93. [Google Scholar] [CrossRef]
- Chia-Chun Yuan, J.; Shyamsunder, N.; Adelino Ricardo Barão, V.; Lee, D.J.; Sukotjo, C. Publication bias in five dental implant journals: An observation from 2005 to 2009. Int. J. Oral Maxillofac. Implant. 2011, 26, 1024. [Google Scholar]
- Lin, G.H.; Tran, C.; Brzyska, K.; Kan, J.Y.; Wang, H.L.; Curtis, D.A.; Kao, R.T. The significance of vertical platform discrepancies and splinting on marginal bone levels for adjacent dental implants. Clin. Implant Dent. Relat. Res. 2023, 25, 321–329. [Google Scholar] [CrossRef]
- Elias, C.N. Factors affecting the success of dental implants. In Implant Dentistry: A Rapidly Evolving Practice; InTech: Rijeka, Croatia, 2011; pp. 319–364. [Google Scholar]
- Steigenga, J.T.; Al-Shammari, K.F.; Nociti, F.H.; Misch, C.E.; Wang, H.L. Dental implant design and its relationship to long-term implant success. Implant Dent. 2003, 12, 306–317. [Google Scholar] [CrossRef]
- Vehemente, V.A.; Chuang, S.K.; Daher, S.; Muftu, A.; Dodson, T.B. Risk factors affecting dental implant survival. J. Oral Implantol. 2002, 28, 74–81. [Google Scholar] [CrossRef]
- Sartoretto, S.C.; Shibli, J.A.; Javid, K.; Cotrim, K.; Canabarro, A.; Louro, R.S.; Lowenstein, A.; Mourão, C.F.; Moraschini, V. Comparing the long-term success rates of tooth preservation and dental implants: A critical review. J. Funct. Biomater. 2023, 14, 142. [Google Scholar] [CrossRef]
- Heimes, D.; Becker, P.; Pabst, A.; Smeets, R.; Kraus, A.; Hartmann, A.; Sagheb, K.; Kämmerer, P.W. How does dental implant macrogeometry affect primary implant stability? A narrative review. Int. J. Implant Dent. 2023, 9, 20. [Google Scholar] [CrossRef]
- Lee, S.J.; Alamri, O.; Cao, H.; Wang, Y.; Gallucci, G.O.; Lee, J.D. Occlusion as a predisposing factor for peri-implant disease: A review article. Clin. Implant Dent. Relat. Res. 2023, 25, 734–742. [Google Scholar] [CrossRef]
- Di Fiore, A.; Montagner, M.; Sivolella, S.; Stellini, E.; Yilmaz, B.; Brunello, G. Peri-implant bone loss and overload: A systematic review focusing on occlusal analysis through digital and analogic methods. J. Clin. Med. 2022, 11, 4812. [Google Scholar] [CrossRef]
- Nimbalkar, S.; Dhatrak, P.; Gherde, C.; Joshi, S. A review article on factors affecting bone loss in dental implants. Mater. Today Proc. 2021, 43, 970–976. [Google Scholar] [CrossRef]
- Kowalski, J.; Lapinska, B.; Nissan, J.; Lukomska-Szymanska, M. Factors influencing marginal bone loss around dental implants: A narrative review. Coatings 2021, 11, 865. [Google Scholar] [CrossRef]
- Galindo-Moreno, P.; Catena, A.; Pérez-Sayáns, M.; Fernández-Barbero, J.E.; O’Valle, F.; Padial-Molina, M. Early marginal bone loss around dental implants to define success in implant dentistry: A retrospective study. Clin. Implant Dent. Relat. Res. 2022, 24, 630–642. [Google Scholar] [CrossRef] [PubMed]
- Sargolzaie, N.; Zarch, H.H.; Arab, H.; Koohestani, T.; Ramandi, M.F. Marginal bone loss around crestal or sub-crestal dental implants: Prospective clinical study. J. Korean Assoc. Oral Maxillofac. Surg. 2022, 48, 159–166. [Google Scholar] [CrossRef]
- Albrektsson, T.; Albrektsson, B. Osseointegration of bone implants: A review of an alternative mode of fixation. Acta Orthop. Scand. 1987, 58, 567–577. [Google Scholar] [CrossRef]
- Misch, C.E. Stress treatment theorem for implant dentistry. In Contemporary Implant Dentistry, 3rd ed.; Mosby, Elsevier: Bengaluru, India, 2007; pp. 68–91. [Google Scholar]
- Ali, B.; Meddah, H.M.; Merdji, A. Effects of overloading in mastication on the mechanical behaviour of dental implants. Mater. Des. 2013, 47, 210–217. [Google Scholar] [CrossRef]
- Prados-Privado, M.; Martínez-Martínez, C.; Gehrke, S.A.; Prados-Frutos, J.C. Influence of bone definition and finite element parameters in bone and dental implants stress: A literature review. Biology 2020, 9, 224. [Google Scholar] [CrossRef]
- Himmlova, L.; Dostálová, T.J.; Kácovský, A.; Konvickova, S. Influence of implant length and diameter on stress distribution: A finite element analysis. J. Prosthet. Dent. 2004, 91, 20–25. [Google Scholar] [CrossRef]
- Bahuguna, R.; Anand, B.; Kumar, D.; Aeran, H.; Anand, V.; Gulati, M. Evaluation of stress patterns in bone around dental implant for different abutment angulations under axial and oblique loading: A finite element analysis. Natl. J. Maxillofac. Surg. 2013, 4, 46–51. [Google Scholar] [CrossRef]
- Alkan, I.; Sertgöz, A.; Ekici, B. Influence of occlusal forces on stress distribution in preloaded dental implant screws. J. Prosthet. Dent. 2004, 91, 319–325. [Google Scholar] [CrossRef]
- Menacho-Mendoza, E.; Cedamanos-Cuenca, R.; Díaz-Suyo, A. Stress analysis and factor of safety in three dental implant systems by finite element analysis. Saudi Dent. J. 2022, 34, 579–584. [Google Scholar] [CrossRef]
- Alshenaiber, R.; Silikas, N.; Barclay, C. Does the length of mini dental implants affect their resistance to failure by overloading? Dent. J. 2022, 10, 117. [Google Scholar] [CrossRef]
- Verma, P.K.; Vasudev, H.; Kumar, V. Dental Implant Materials and Designs and Failure during Implant Placement and Loading: A Review. In Advanced Manufacturing Processes; CRC Press: Boca Raton, FL, USA, 2025; pp. 138–150. [Google Scholar]
- Shigemitsu, R.; Ogawa, T.; Matsumoto, T.; Yoda, N.; Gunji, Y.; Yamakawa, Y.; Ikeda, K.; Sasaki, K. Stress distribution in the peri-implant bone with splinted and non-splinted implants by in vivo loading data-based finite element analysis. Odontology 2013, 101, 222–226. [Google Scholar] [CrossRef]
- Toniollo, M.B.; dos Reis, K.E.M.; Sakamoto, S.P.d.S.; Terada, A.S.S.D.; Paranhos, L.R.; Macedo, A.P.; da Silva, R.C.D.; Limirio, P.H.J.O. Von Mises equivalent stresses developed in fixed partial denture infrastructures on implants according to changes in their prosthetic materials. J. Oral Implantol. 2025, 51, 267–274. [Google Scholar] [CrossRef] [PubMed]
- Pellizzer, E.P.; de Mello, C.C.; Junior, J.F.S.; de Souza Batista, V.E.; de Faria Almeida, D.A.; Verri, F.R. Analysis of the biomechanical behavior of short implants: The photo-elasticity method. Mater. Sci. Eng. C 2015, 55, 187–192. [Google Scholar] [CrossRef] [PubMed]
- Ceddia, M.; Solarino, G.; Tucci, M.; Lamberti, L.; Trentadue, B. Stress analysis of tibial bone using three different materials for bone fixation plates. J. Compos. Sci. 2024, 8, 334. [Google Scholar] [CrossRef]
- Ceddia, M.; Solarino, G.; Cassano, G.D.; Trentadue, B. Finite Element Study on Stability in the Femoral Neck and Head Connection to Varying Geometric Parameters with the Relates Implications on the Effect of Wear. J. Compos. Sci. 2023, 7, 387. [Google Scholar] [CrossRef]
- Hosseini-Faradonbeh, S.A.; Katoozian, H.R. Biomechanical evaluations of the long-term stability of dental implant using finite element modeling method: A systematic review. J. Adv. Prosthodont. 2022, 14, 182. [Google Scholar] [CrossRef]
- Ghosh, R.; Chanda, S.; Chakraborty, D. Application of finite element analysis to tissue differentiation and bone remodelling approaches and their use in design optimization of orthopaedic implants: A review. Int. J. Numer. Methods Biomed. Eng. 2022, 38, e3637. [Google Scholar] [CrossRef]
- Santonocito, D.; Nicita, F.; Risitano, G. A parametric study on a dental implant geometry influence on bone remodelling through a numerical algorithm. Prosthesis 2021, 3, 157–172. [Google Scholar] [CrossRef]
- Poovarodom, P.; Rungsiyakull, C.; Suriyawanakul, J.; Li, Q.; Sasaki, K.; Yoda, N.; Rungsiyakull, P. Effect of implant placement depth on bone remodeling on implant-supported single zirconia abutment crown: A 3D finite element study. J. Prosthodont. Res. 2023, 67, 278–287. [Google Scholar] [CrossRef]
- Falcinelli, C.; Valente, F.; Vasta, M.; Traini, T. Finite element analysis in implant dentistry: State of the art and future directions. Dent. Mater. 2023, 39, 539–556. [Google Scholar] [CrossRef]
- Gasik, M.; Lambert, F.; Bacevic, M. Biomechanical properties of bone and mucosa for design and application of dental implants. Materials 2021, 14, 2845. [Google Scholar] [CrossRef] [PubMed]
- de Matos, J.D.M.; Queiroz, D.A.; Nakano, L.J.N.; Andrade, V.C.; Ribeiro, N.d.C.R.; Borges, A.L.S.; Bottino, M.A.; Lopes, G.d.R.S. Bioengineering tools applied to dentistry: Validation methods for in vitro and in silico analysis. Dent. J. 2022, 10, 145. [Google Scholar] [CrossRef] [PubMed]
- Kshirsagar, M.; Dhatrak, P. Strain based in vitro analysis of dental implant using artificial bone model and validation by numerical technique. Med. Eng. Phys. 2023, 111, 103931. [Google Scholar] [CrossRef] [PubMed]
- Ingawale, S.M.; Krishnan, D.G.; Goswami, T. Validation of Experimental and Finite Element Biomechanical Evaluation of Human Cadaveric Mandibles. Lubricants 2022, 10, 169. [Google Scholar] [CrossRef]
- Corrêa, C.B.; Ribeiro, A.L.R.; Reis, J.M.D.S.N.; Vaz, L.G. Photoelasticity in Dentistry: A literature review. Rev. Sul-Bras. Odontol. 2014, 11, 178–184. [Google Scholar]
- Andrade, C.S.; de Abreu Costa, L.; Menechelli, L.G.; Lemos, C.A.; Okamoto, R.; Verri, F.R.; de Souza Batista, V.E. Biomechanical effects of different materials for an occlusal device on implant-supported rehabilitation in a tooth clenching situation: A 3D finite element analysis. J. Prosthodont. 2024, 33, 706–713. [Google Scholar] [CrossRef]
- Guichet, D.L.; Yoshinobu, D.; Caputo, A.A. Effect of splinting and interproximal contact tightness on load transfer by implant restorations. J. Prosthet. Dent. 2002, 87, 528–535. [Google Scholar] [CrossRef] [PubMed]
- Lemos, C.A.A.; Verri, F.R.; Santiago, J.F., Júnior; Almeida, D.A.F.; Batista, V.E.S.; Noritomi, P.Y.; Pellizzer, D.P. Retention System and Splinting on Morse Taper Implants in the Posterior Maxilla by 3D Finite Element Analysis. Braz. Dent J. 2018, 29, 30–35. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Toniollo, M.B.; Macedo, A.P.; Silveira Rodrigues, R.C.; Ribeiro, R.F.; da Gloria Chiarello de Mattos, M. A Three-Dimensional Finite Element Analysis of the Stress Distribution Generated by Splinted and Nonsplinted Prostheses in the Rehabilitation of Various Bony Ridges with Regular or Short Morse Taper Implants. Int. J. Oral Maxillofac. Implant. 2017, 32, 372. [Google Scholar] [CrossRef]
- Ravidà, A.; Saleh, M.H.; Muriel, M.C.; Maska, B.; Wang, H.L. Biological and technical complications of splinted or nonsplinted dental implants: A decision tree for selection. Implant Dent. 2018, 27, 89–94. [Google Scholar] [CrossRef]
- Mendonça, J.A.; Francischone, C.E.; Senna, P.M.; Matos de Oliveira, A.E.; Sotto-Maior, B.S. A retrospective evaluation of the survival rates of splinted and non-splinted short dental implants in posterior partially edentulous jaws. J. Periodontol. 2014, 85, 787–794. [Google Scholar] [CrossRef]
- Yi, Y.; Heo, S.J.; Koak, J.Y.; Kim, S.K.; Koo, K.T. Splinting or Nonsplinting Adjacent Implants? A Retrospective Study Up to 15 Years: Part II—Success and Survival Rate Analysis. Int. J. Oral Maxillofac. Implant. 2023, 38, 443. [Google Scholar] [CrossRef]
- Wagenberg, B.; Froum, S.J. A Retrospective Study of 1,925 Consecutively Placed Immediate Implants from 1988 to 2004. Int. J. Oral Maxillofac. Implant. 2006, 21, 71. [Google Scholar] [CrossRef]
- Cruz, R.S.; Lemos, C.A.A.; de Luna Gomes, J.M.; e Oliveira, H.F.F.; Pellizzer, E.P.; Verri, F.R. Clinical comparison between crestal and sub-crestal dental implants: A systematic review and meta-analysis. J. Prosthet. Dent. 2022, 127, 408–417. [Google Scholar] [CrossRef] [PubMed]
- Comuzzi, L.; Ceddia, M.; Di Pietro, N.; Inchingolo, F.; Inchingolo, A.M.; Romasco, T.; Trentadue, B. Crestal and sub-crestal placement of morse cone implant–abutment connection implants: An in vitro finite element analysis (fea) study. Biomedicines 2023, 11, 3077. [Google Scholar] [CrossRef] [PubMed]
- Di Pietro, N.; Ceddia, M.; Romasco, T.; De Bortoli Junior, N.; Mello, B.F.; Tumedei, M.; Specchiulli, A.; Piattelli, A.; Trentadue, B. Finite element analysis (FEA) of the stress and strain distribution in cone-morse implant–abutment connection implants placed equi-crestally and sub-crestally. Appl. Sci. 2023, 13, 8147. [Google Scholar] [CrossRef]
- Koodaryan, R.; Hafezeqoran, A. The effect of implant diameter on stress distribution around implants: A finite element analysis. Int. J. Implant. Dent. 2017, 3, 26. [Google Scholar]
- Miyamoto, Y.; Sato, Y.; Ogawa, T. Biomechanical behavior of dental implants with different diameters and lengths: A finite element analysis. Clin. Implant. Dent. Relat. Res. 2020, 22, 388–395. [Google Scholar]
- Taheri, R.A.; Jarrahi, A.; Farnoosh, G.; Karimi, A. A comparative finite element simulation of stress in dental implant–bone interface using isotropic and orthotropic material models in three mastication cycles. J. Braz. Soc. Mech. Sci. Eng. 2018, 40, 489. [Google Scholar] [CrossRef]
- Ceddia, M.; Trentadue, B. Evaluation of rotational stability and stress shielding of a stem optimized for hip replacements—A finite element study. Prosthesis 2023, 5, 678–693. [Google Scholar] [CrossRef]
- Ceddia, M.; Solarino, G.; Giannini, G.; De Giosa, G.; Tucci, M.; Trentadue, B. A Finite Element Analysis Study of Influence of Femoral Stem Material in Stress Shielding in a Model of Uncemented Total Hip Arthroplasty: Ti-6Al-4V versus Carbon Fibre-Reinforced PEEK Composite. J. Compos. Sci. 2024, 8, 254. [Google Scholar] [CrossRef]
- Cipollina, A.; Ceddia, M.; Di Pietro, N.; Inchingolo, F.; Tumedei, M.; Romasco, T.; Trentadue, B. Finite element analysis (FEA) of a premaxillary device: A new type of subperiosteal implant to treat severe atrophy of the maxilla. Biomimetics 2023, 8, 336. [Google Scholar] [CrossRef]
- López-López, E.; Erauw, J.P.; Moreno, R.; Baudín, C.; Cambier, F. Elastic behaviour of zirconium titanate bulk material at room and high temperature. J. Eur. Ceram. Soc. 2012, 32, 4083–4089. [Google Scholar] [CrossRef]
- Ficarella, E.; Minooei, M.; Santoro, L.; Toma, E.; Trentadue, B.; De Spirito, M.; Papi, M.; Pruncu, C.I.; Lamberti, L. Visco-Hyperelastic Characterization of the Equine Immature Zona Pellucida. Materials 2021, 14, 1223. [Google Scholar] [CrossRef]
- Almasri, M.; Elkhaweldi, N.; Alqahtani, F. The effect of implant diameter on stress distribution in the peri-implant bone: A finite element study. Int. J. Implant. Dent. 2021, 7, 37. [Google Scholar]
- Calvo-Guirado, J.L.; Cegarra-Delgado, A.; Maté-Sánchez de Val, J.E.; Gómez-Moreno, G.; Guardia, J. Influence of implant diameter on stress distribution in peri-implant bone: A finite element analysis. Clin. Oral Implant. Res. 2019, 30, 539–547. [Google Scholar]
- Kious, A.; Cheng, A. Biomechanical evaluation of implant diameter and length on stress distribution using finite element analysis. J. Oral Implantol. 2014, 40, 269–276. [Google Scholar]
- Figueiredo, L.C.; Neves, A.A.; de Mattos, M.G. Effect of implant diameter and bone quality on stress distribution: A finite element analysis. Braz. Oral Res. 2020, 34, 46–54. [Google Scholar] [CrossRef]
- Mahantesh, T.; Girish, H.C. Effect of implant diameter and length on stress distribution in peri-implant bone: A finite element study. Int. J. Oral Maxillofac. Implant. 2016, 31, e25–e31. [Google Scholar]
- Kaur, G.; Kaur, S.; Kaur, H. Finite element analysis of the effect of implant diameter and length on stress distribution in the peri-implant bone. J. Indian Prosthodont. Soc. 2022, 22, 61–68. [Google Scholar]
- Alrahlah, A.; Iqbal, A. The effect of implant diameter and length on stress distribution in the peri-implant bone: A finite element study. J. Prosthodont. 2021, 30, 440–448. [Google Scholar]
- Rodríguez-Ciurana, X.; Vela-Nebot, X.; Segalà-Torres, M.; Rodado-Alonso, C.; Méndez-Blanco, V.; Mata-Bugueroles, M. Biomechanical repercussions of bone resorption related to biologic width: A finite element analysis of three implant-abutment configurations. Int. J. Periodontics Restor. Dent. 2009, 29, 479. [Google Scholar]
- Hériveaux, Y.; Le Cann, S.; Fraulob, M.; Vennat, E.; Nguyen, V.H.; Haïat, G. Mechanical micromodeling of stress-shielding at the bone-implant interphase under shear loading. Med. Biol. Eng. Comput. 2022, 60, 3281–3293. [Google Scholar] [CrossRef]
- Mameno, T.; Wada, M.; Otsuki, M.; Okuno, I.; Ozeki, K.; Tahara, A.; Ikebe, K. Risk indicators for marginal bone resorption around implants in function for at least 4 years: A retrospective longitudinal study. J. Periodontol. 2020, 91, 37–45. [Google Scholar] [CrossRef]
- Renouard, F.; Nisand, D. Short implants in the severely resorbed maxilla: A 2-year retrospective clinical study. Clin. Implant. Dent. Relat. Res. 2005, 7, s104–s110. [Google Scholar] [CrossRef]
- Tonin, B.S.H.; Peixoto, R.F.; Fu, J.; De Mattos, M.D.G.C.; Macedo, A.P. Influence of the frameworks of implant-supported prostheses and implant connections on stress distribution. Dent. Med. Probl. 2023, 60, 551–557. [Google Scholar] [CrossRef]
- Krawiec, M.; Olchowy, C.; Kubasiewicz-Ross, P.; Hadzik, J.; Dominiak, M. Role of implant loading time in the prevention of marginal bone loss after implant-supported restorations: A targeted review. Dent. Med. Probl. 2022, 59, 475–481. [Google Scholar] [CrossRef]
- Hariharan, R.; Shankar, C.; Rajan, M.; Azhagarasan, N.S. Evaluation of accuracy of multiple dental implant impressions using various splinting materials. Int. J. Oral Maxillofac. Implant. 2010, 25, 38. [Google Scholar]
- Baig, M.R. Multi-implant impressions. To splint or not to splint: A critical review. Int. J. Prosthodont. 2019, 32, 66–67. [Google Scholar] [CrossRef]
- Vigolo, P.; Zaccaria, M. Clinical evaluation of marginal bone level change of multiple adjacent implants restored with splinted and nonsplinted restorations: A 5-year prospective study. Int. J. Oral Maxillofac. Implant. 2010, 25, 1189–1194. [Google Scholar] [PubMed]
- Huang, H.L.; Huang, J.S.; Ko, C.C.; Hsu, J.T.; Chang, C.H.; Chen, M.Y. Effects of splinted prosthesis supported a wide implant or two implants: A three-dimensional finite element analysis. Clin. Oral Implant. Res. 2005, 16, 466–472. [Google Scholar] [CrossRef] [PubMed]
- Iplikçioğlu, H.; Akça, K. Comparative evaluation of the effect of diameter, length and number of implants supporting three-unit fixed partial prostheses on stress distribution in the bone. J. Dent. 2002, 30, 41–46. [Google Scholar] [CrossRef] [PubMed]
- Al Amri, M.D. Crestal bone loss around submerged and nonsubmerged dental implants: A systematic review. J. Prosthet. Dent. 2016, 115, 564–570. [Google Scholar] [CrossRef]
- Saleh, M.H.; Ravida, A.; Suárez-López del Amo, F.; Lin, G.H.; Asa’ad, F.; Wang, H.L. The effect of implant-abutment junction position on crestal bone loss: A systematic review and meta-analysis. Clin. Implant. Dent. Relat. Res. 2018, 20, 617–633. [Google Scholar] [CrossRef]
- Chu, C.M.; Hsu, J.T.; Fuh, L.J.; Huang, H.L. Biomechanical evaluation of subcrestal placement of dental implants: In vitro and numerical analyses. J. Periodontol. 2011, 82, 302–310. [Google Scholar] [CrossRef]
- Li, R.; Wu, Z.; Chen, S.; Li, X.; Wan, Q.; Xie, G.; Pei, X. Biomechanical behavior analysis of four types of short implants with different placement depths using the finite element method. J. Prosthet. Dent. 2023, 129, 447.e1–447.e10. [Google Scholar] [CrossRef]
- Yi, Y.; Heo, S.J.; Koak, J.Y.; Kim, S.K.; Koo, K.T. Splinting or Nonsplinting Adjacent Implants? A Retrospective Study Up to 15 Years: Part I—Biologic and Mechanical Complication Analysis. Int. J. Oral Maxillofac. Implant. 2023, 38, 435. [Google Scholar] [CrossRef]
- Prete, B.R.; Silva, M.A.; Wong, B.C.; Deporter, D.A. A pattern of peri-implantitis affecting middle implants in 3-implant splinted prostheses. Clin. Adv. Periodontics 2024, 14, 284–289. [Google Scholar] [CrossRef]
- Berthaume, M.A.; Dechow, P.C.; Iriarte-Diaz, J.; Ross, C.F.; Strait, D.S.; Wang, Q.; Grosse, I.R. Probabilistic finite element analysis of a craniofacial finite element model. J. Theor. Biol. 2012, 300, 242–253. [Google Scholar] [CrossRef]
- Taddei, F.; Cristofolini, L.; Martelli, S.; Gill, H.S.; Viceconti, M. Subject-specific finite element models of long bones: An in vitro evaluation of the overall accuracy. J. Biomech. 2006, 39, 2457–2467. [Google Scholar] [CrossRef] [PubMed]
- Sandino, C.; Planell, J.A.; Lacroix, D. A finite element study of mechanical stimuli in scaffolds for bone tissue engineering. J. Biomech. 2008, 41, 1005–1014. [Google Scholar] [CrossRef] [PubMed]
- Hambli, R. Micro-CT finite element model and experimental validation of trabecular bone damage and fracture. Bone 2013, 56, 363–374. [Google Scholar] [CrossRef] [PubMed]
- Kayabaşı, O.; Yüzbasıoğlu, E.; Erzincanlı, F. Static, dynamic and fatigue behaviors of dental implant using finite element method. Adv. Eng. Softw. 2006, 37, 649–658. [Google Scholar] [CrossRef]
- Demirbas, A.E.; Ekici, R.; Karakaya, M.; Alkan, A. Bone stress and damage distributions during dental implant insertion: A novel dynamic FEM analysis. Comput. Methods Biomech. Biomed. Eng. 2022, 25, 1381–1392. [Google Scholar] [CrossRef]
- Ceddia, M.; Romasco, T.; Marchioli, G.; Comuzzi, L.; Cipollina, A.; Piattelli, A.; Lamberti, L.; Di Pietro, N.; Trentadue, B. Finite Element Analysis of Implant Stability Quotient (ISQ) and Bone Stresses for Implant Inclinations of 0°, 15°, and 20°. Materials 2025, 18, 1625. [Google Scholar] [CrossRef]
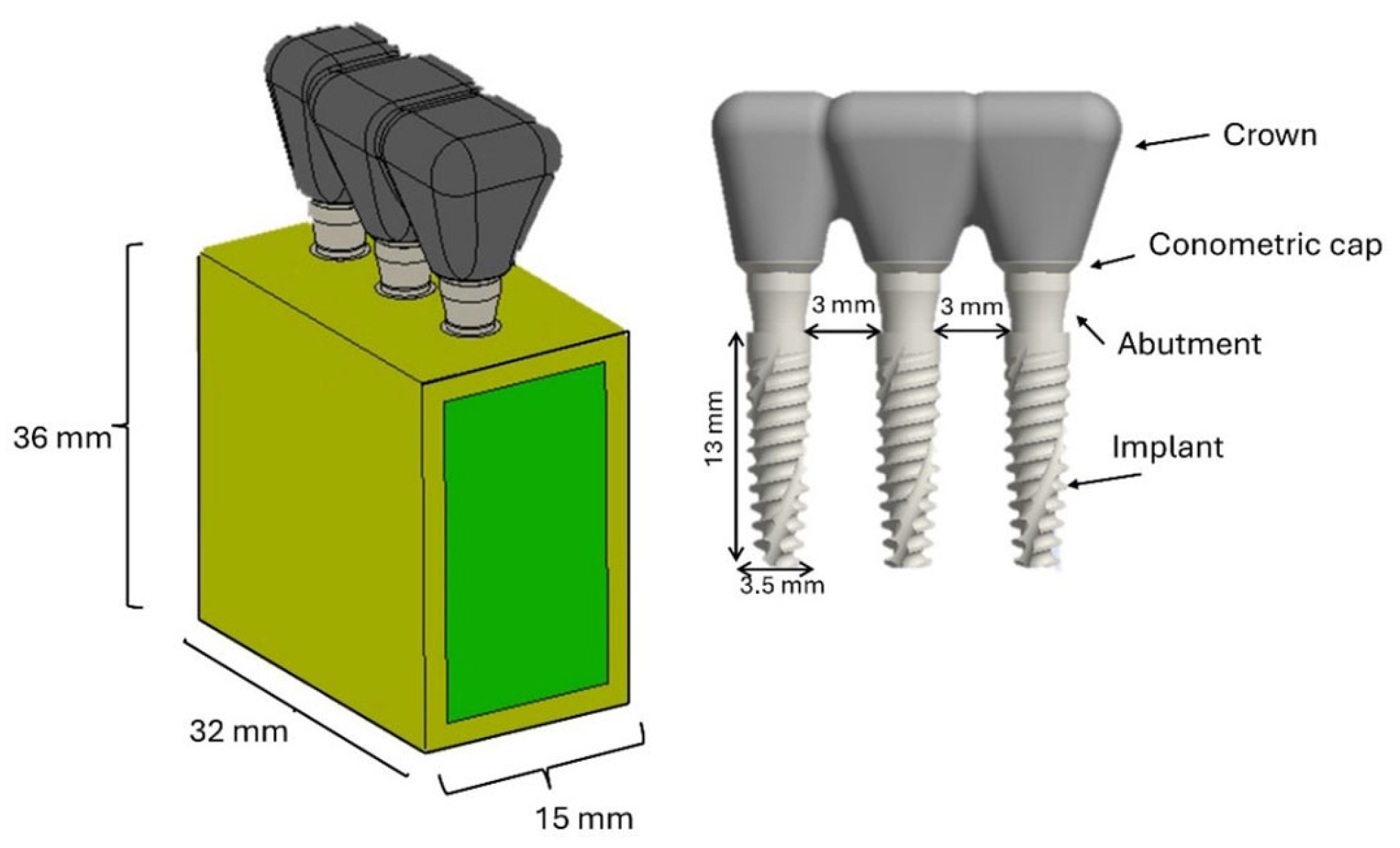


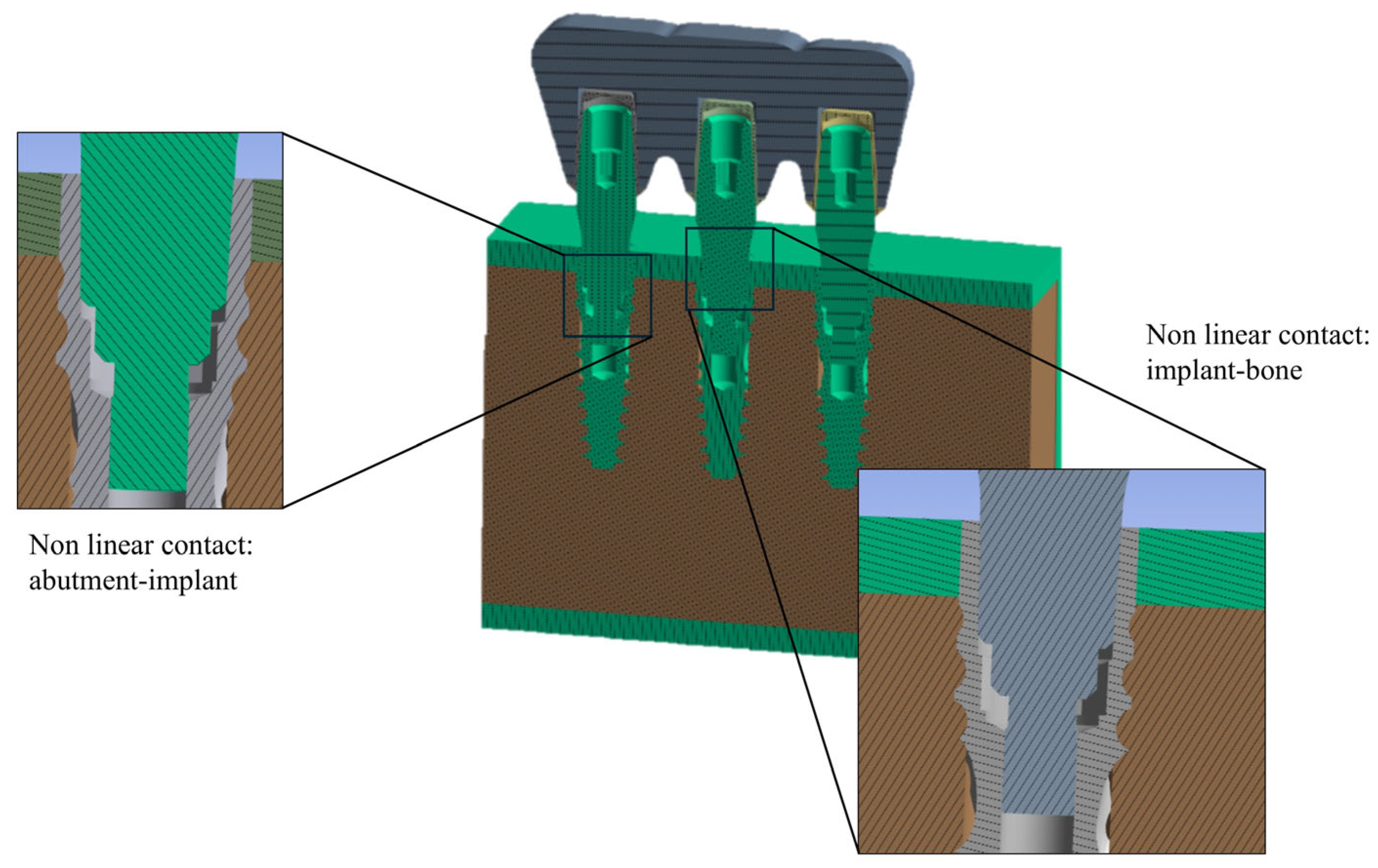
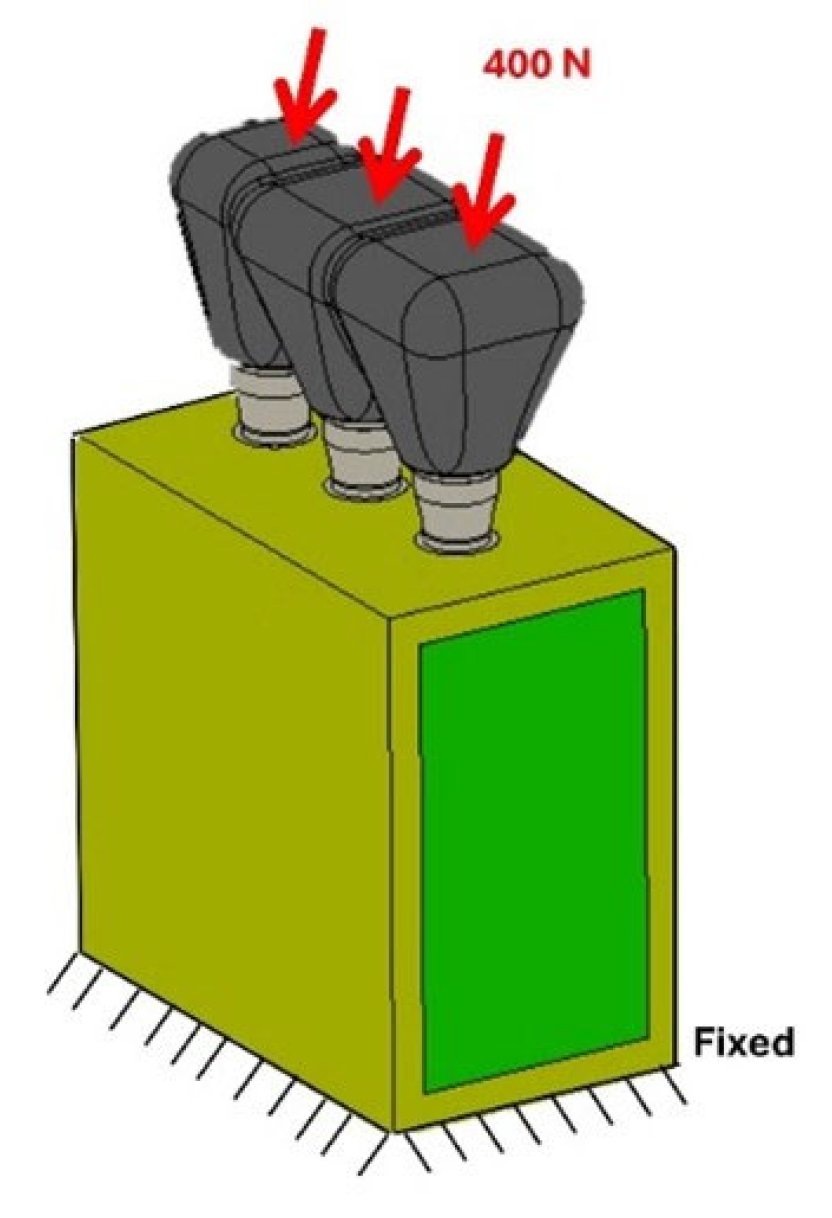

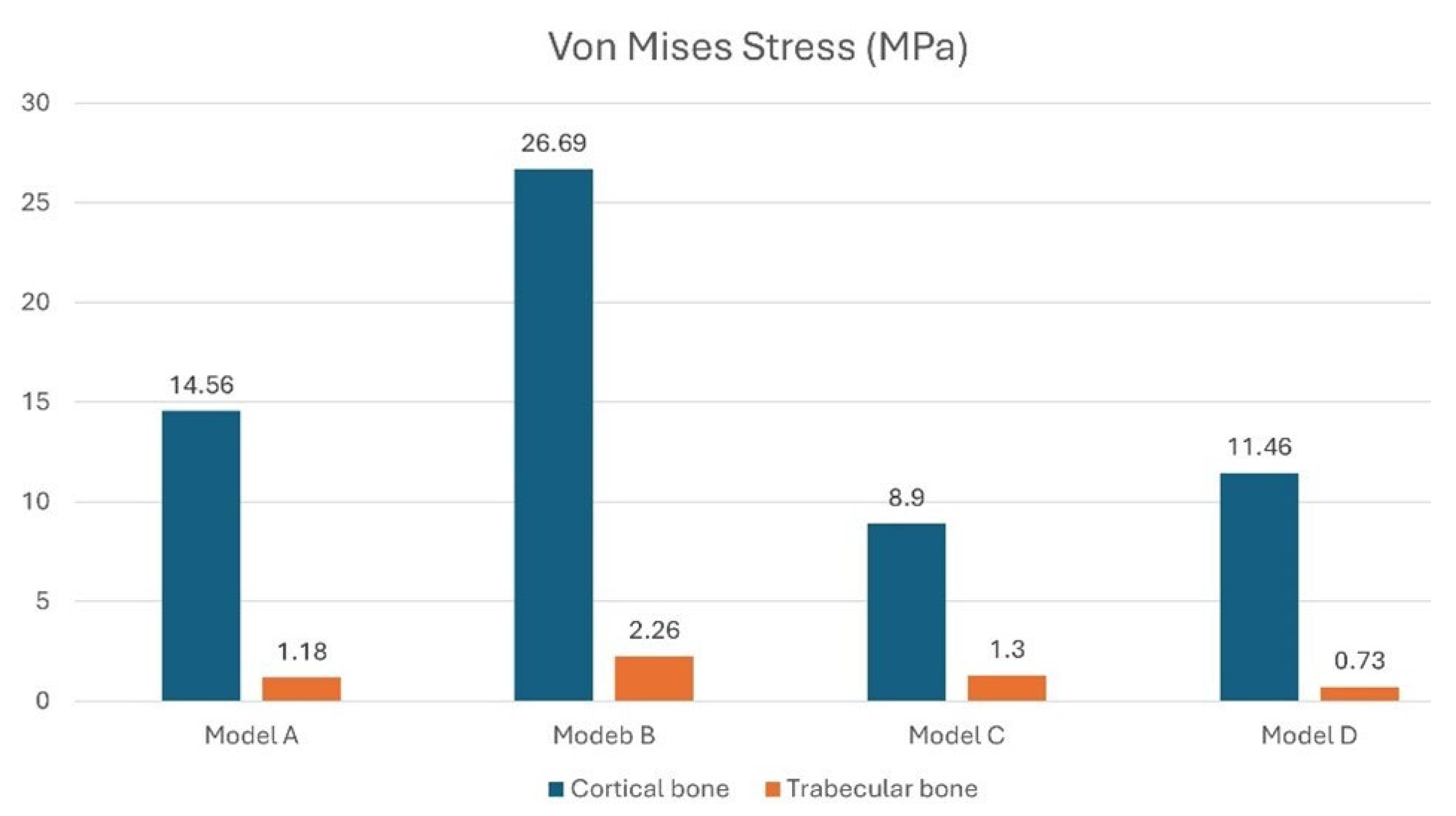


| Material | Young’s Modulus E (MPa) | Shear Modulus G (MPa) | |
|---|---|---|---|
| Cortical bone | Ex = 12,600 Ey = 12,600 Ez = 19,400 | Gxy = 4850 Gyz = 5700 Gxz = 5700 | |
| Cancellous bone | Ex = 1148 Ey = 210 Ez = 1148 | Gxy = 68 Gyz = 68 Gxz = 434 | |
| Titanium (Ti6Al4V) | 110,000 | 0.35 | |
| Ceramic (ZrO2) | 150,000 | 0.3 | |
| Cement | 280 | 0.3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ceddia, M.; Marchioli, G.; Romasco, T.; Comuzzi, L.; Piattelli, A.; Deporter, D.A.; Di Pietro, N.; Trentadue, B. Effect of Crestal Position on Bone–Implant Stress Interface of Three-Implant Splinted Prostheses: A Finite Element Analysis. Materials 2025, 18, 3344. https://doi.org/10.3390/ma18143344
Ceddia M, Marchioli G, Romasco T, Comuzzi L, Piattelli A, Deporter DA, Di Pietro N, Trentadue B. Effect of Crestal Position on Bone–Implant Stress Interface of Three-Implant Splinted Prostheses: A Finite Element Analysis. Materials. 2025; 18(14):3344. https://doi.org/10.3390/ma18143344
Chicago/Turabian StyleCeddia, Mario, Giulia Marchioli, Tea Romasco, Luca Comuzzi, Adriano Piattelli, Douglas A. Deporter, Natalia Di Pietro, and Bartolomeo Trentadue. 2025. "Effect of Crestal Position on Bone–Implant Stress Interface of Three-Implant Splinted Prostheses: A Finite Element Analysis" Materials 18, no. 14: 3344. https://doi.org/10.3390/ma18143344
APA StyleCeddia, M., Marchioli, G., Romasco, T., Comuzzi, L., Piattelli, A., Deporter, D. A., Di Pietro, N., & Trentadue, B. (2025). Effect of Crestal Position on Bone–Implant Stress Interface of Three-Implant Splinted Prostheses: A Finite Element Analysis. Materials, 18(14), 3344. https://doi.org/10.3390/ma18143344









