Mechanical Response Analysis of Ultra-Thin Asphalt Wearing Course Pavement Under Non-Uniform Loading Pressure
Abstract
1. Introduction
2. Finite Element Modeling
2.1. Model Construction
- (1)
- For the asphalt layers (Ultra-thin, Surface, Middle, and Bottom layers), a viscoelastic material model was used. This model accurately captures the time-dependent nature of asphalt concrete, where the stress at any given moment is a function of the entire history of strain. This is essential for modeling phenomena such as stress relaxation and creep.
- (2)
- For the cement-stabilized base layers (Upper Base, Lower Base), a linear elastic material model was employed. This model assumes a direct, time-independent linear relationship between stress and strain (Hooke’s Law), which is a standard and effective representation for these stiffer, unbound, or stabilized materials.
2.2. Load Boundary Conditions
- (1)
- Uniform load: A standard dual-wheel axle load of 100 kN was adopted, determining the corresponding pressure as 0.707 MPa. According to the equivalence principle, the wheel load was simplified as a rectangular uniform load, with single wheel dimensions set as 0.2 m × 0.25 m and a center distance of 0.3 m between the two wheels, as shown in the dark area in Figure 3.
- (2)
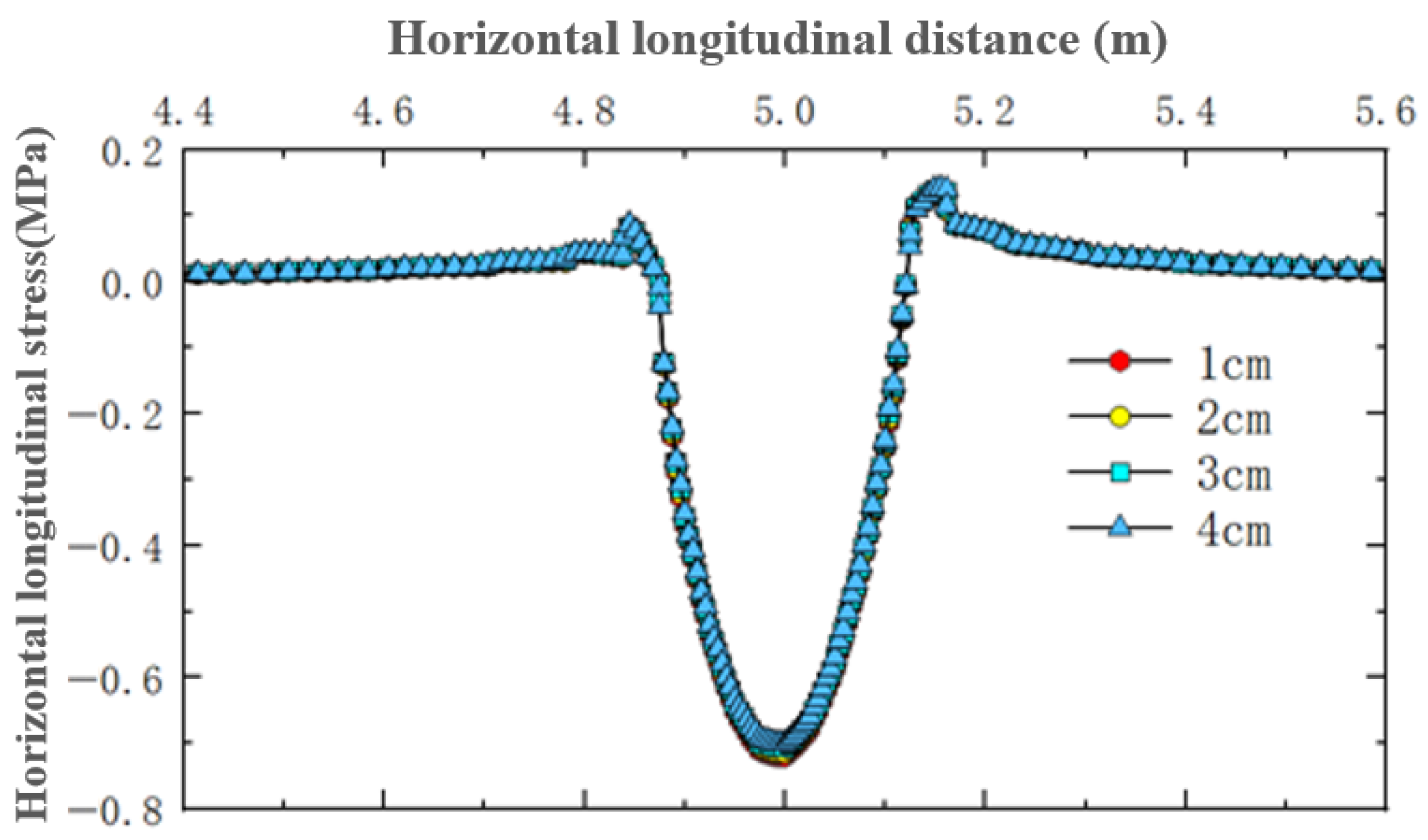
- Non-uniform load: To simulate the actual pressure distribution of tires on the pavement, the tire-pavement contact stress distributions were obtained from the TireView database developed by the Texas Transportation Institute. TireView provides comprehensive contact pressure distributions in longitudinal, lateral, and vertical directions for various tire types under different loading conditions [18]. The actual pressure distribution is shown in Figure 4. The non-uniform load simulated based on the actual pressure distribution was also applied within the range of 0.2 m × 0.25 m, with an equivalent average contact pressure of 0.736 MPa, and pressure peaks located at y = ±0.1085 m. The simulated load is shown in Figure 5.
3. Comparative Analysis of Ultra-Thin Layer Pavement Structure Stress Under Uniform and Non-Uniform Loads
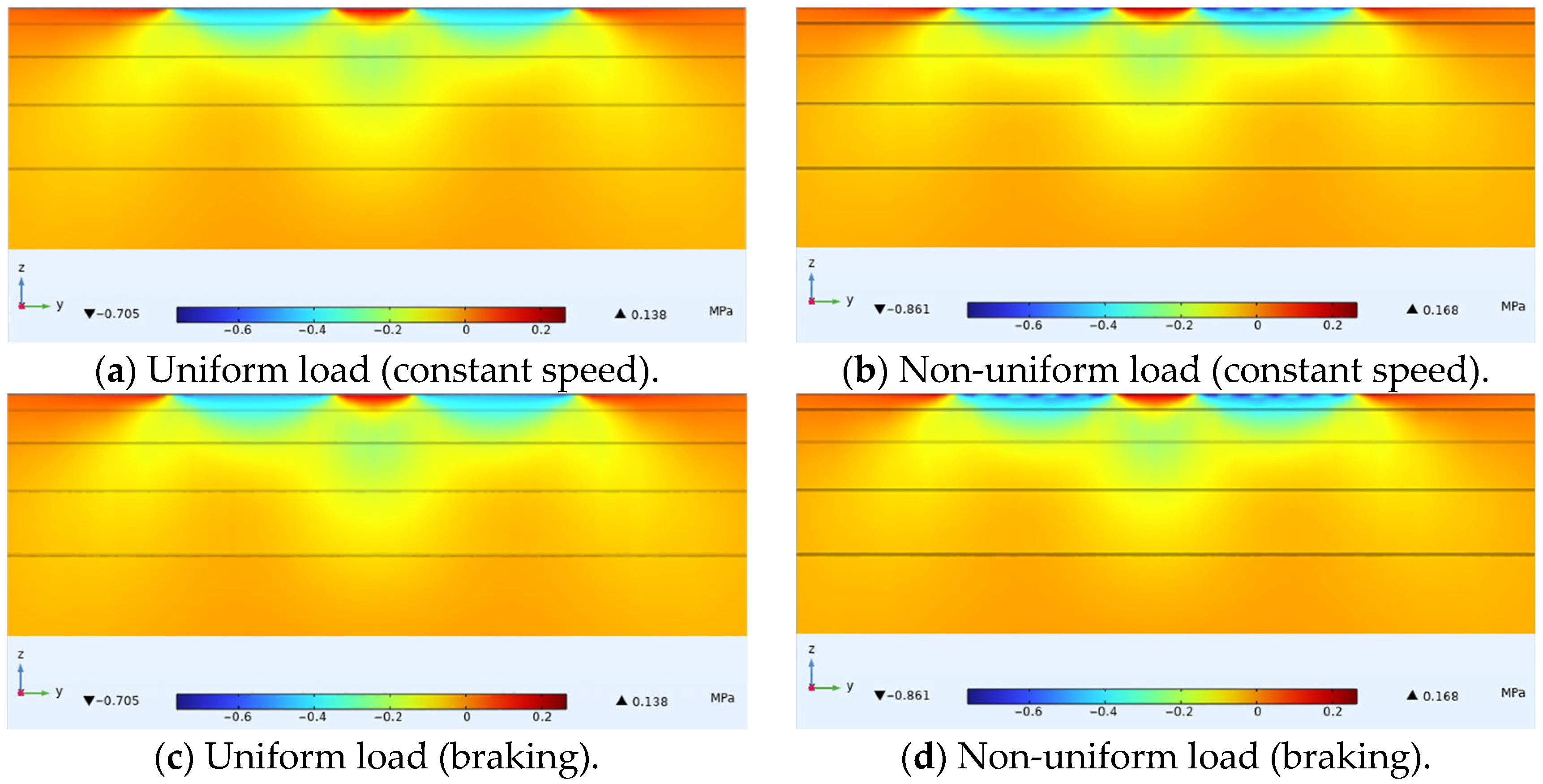
3.1. Vertical Stress
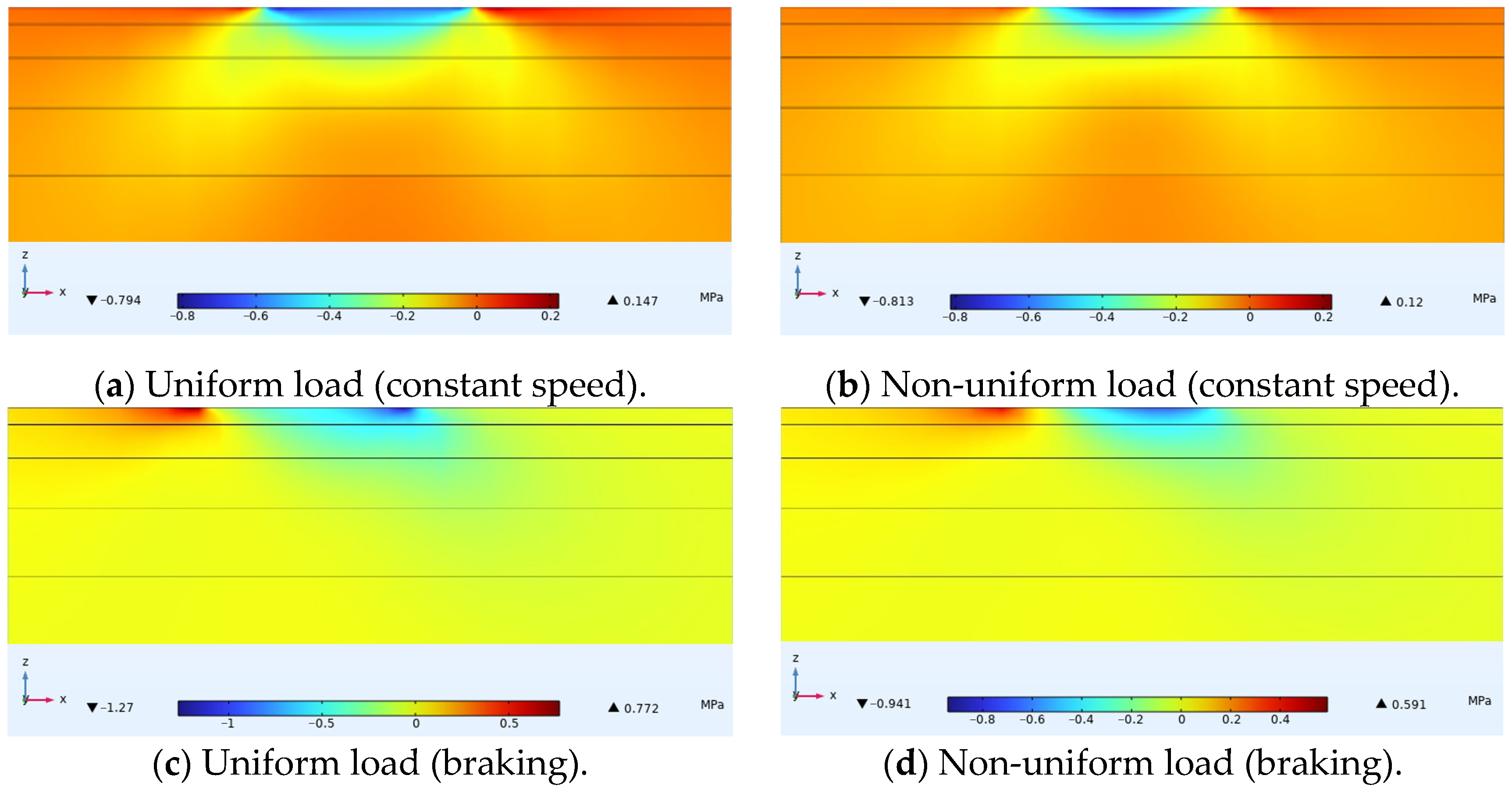
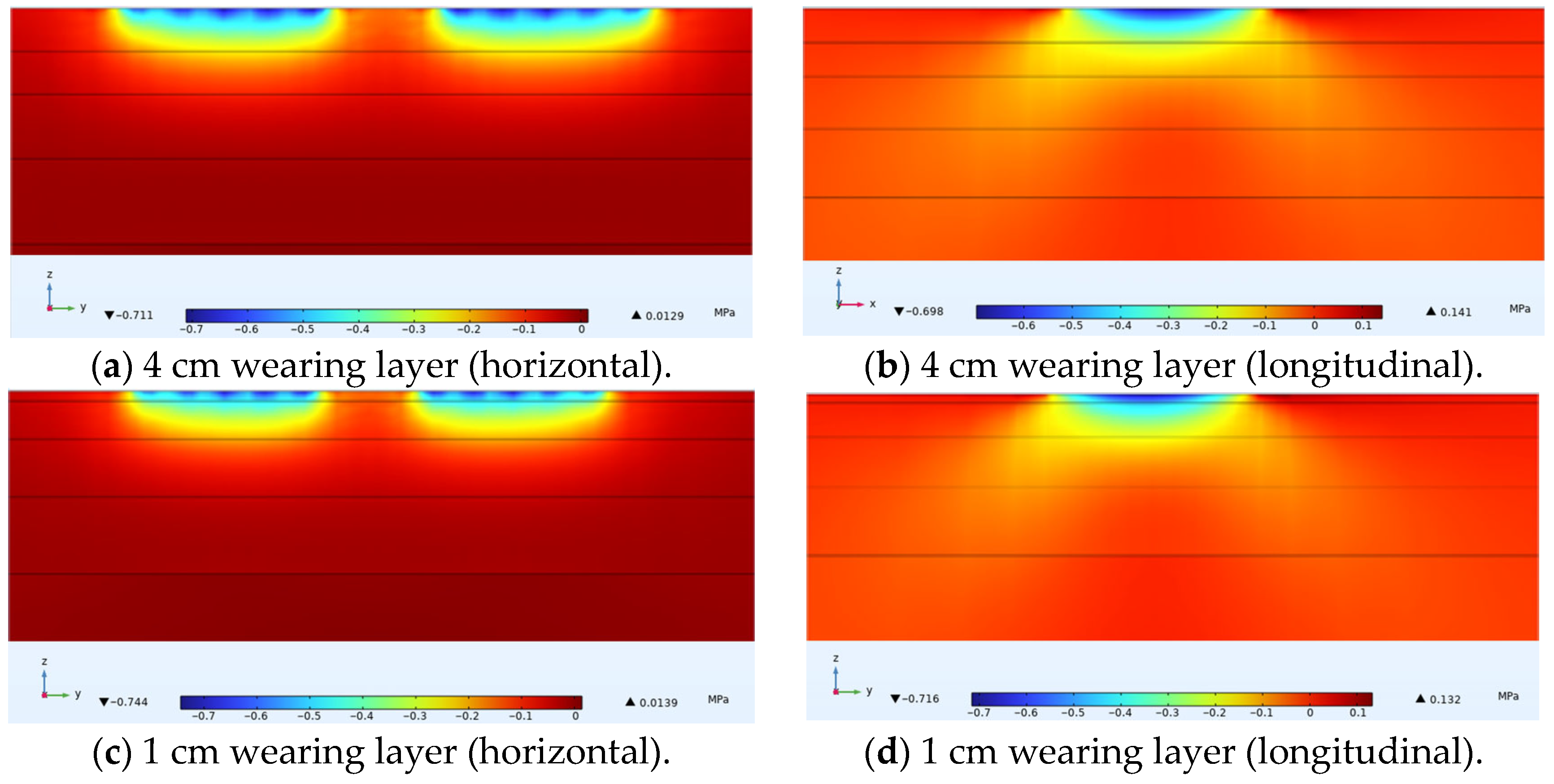
3.2. Horizontal Transverse Stress
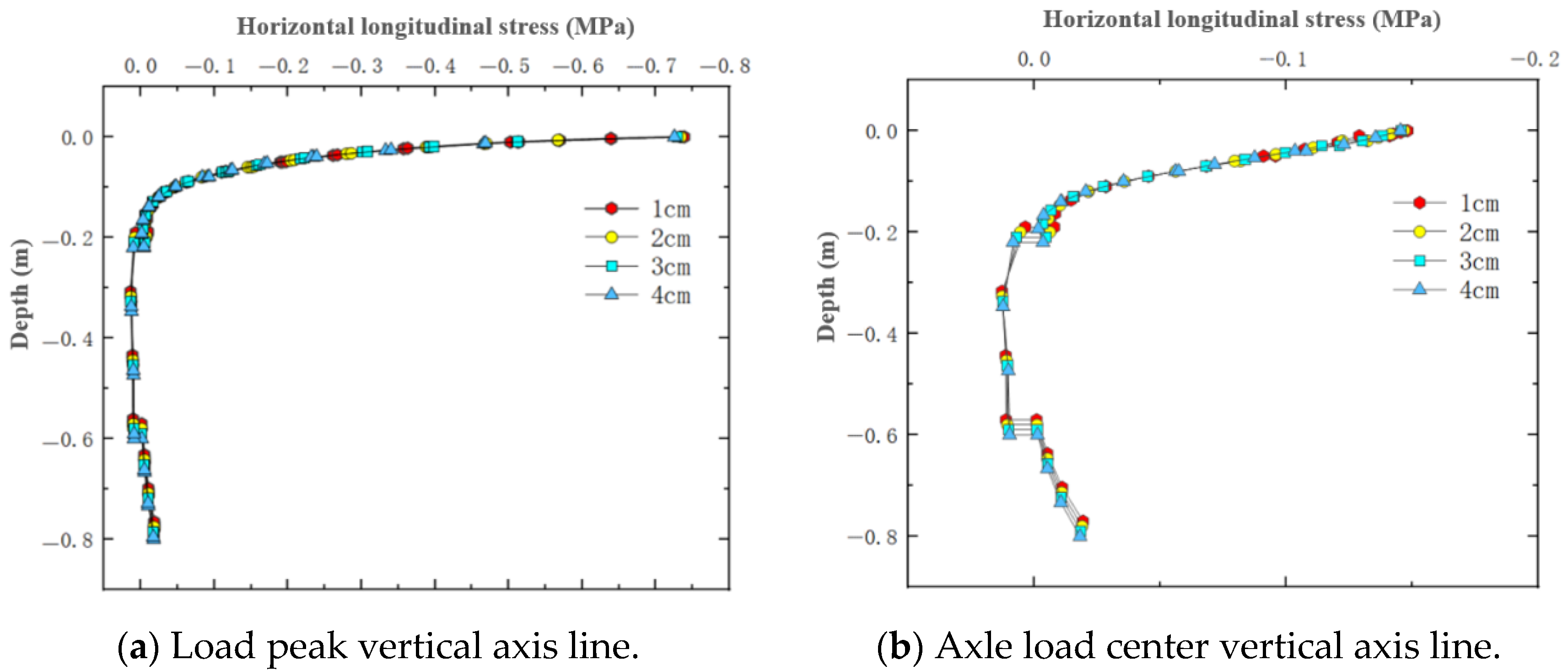
3.3. Horizontal Longitudinal Stress
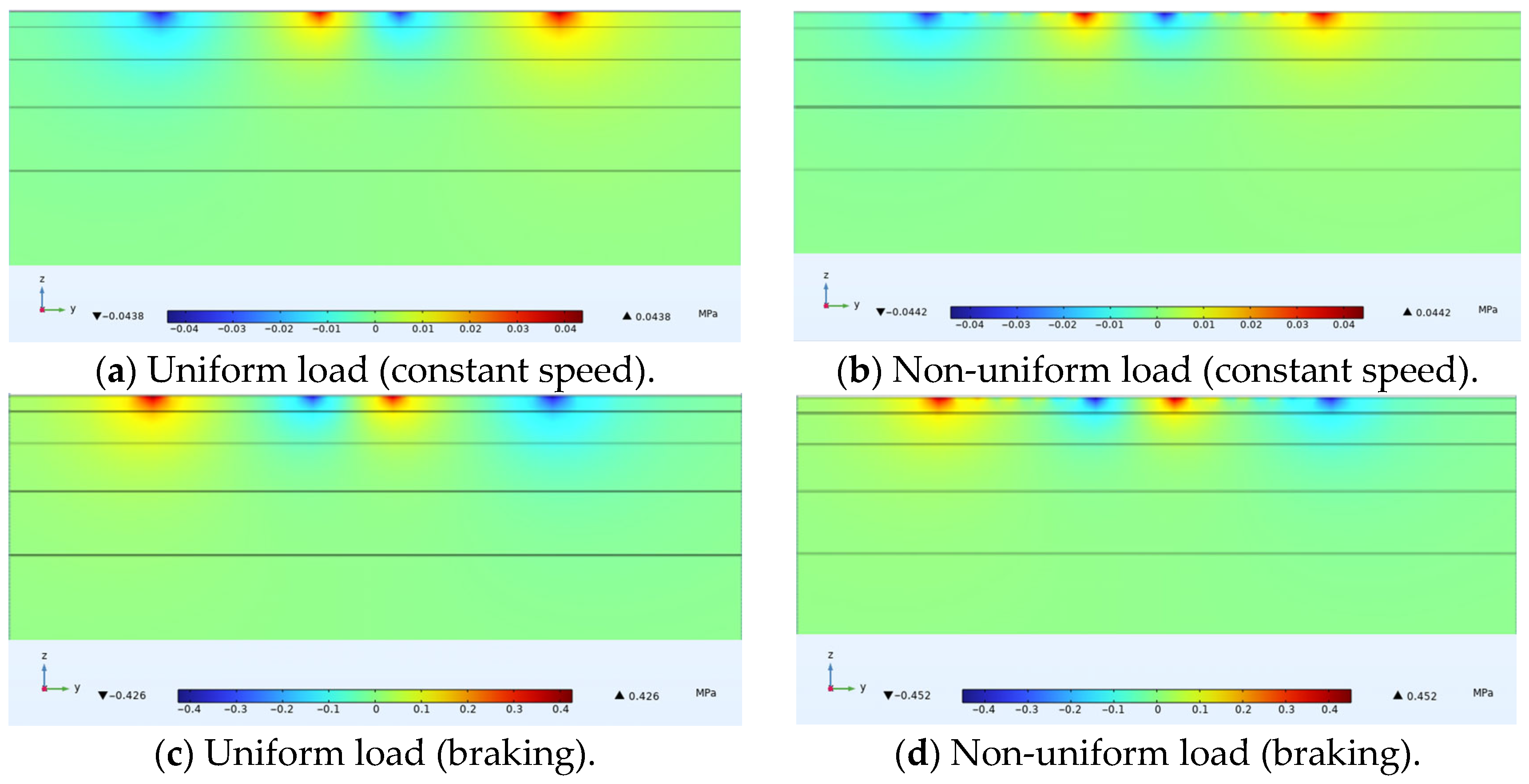
3.4. Shear Stress
4. Calculation and Analysis of Pavement Structure Stress Under Non-Uniform Constant Speed Loads with Different Thin Layer
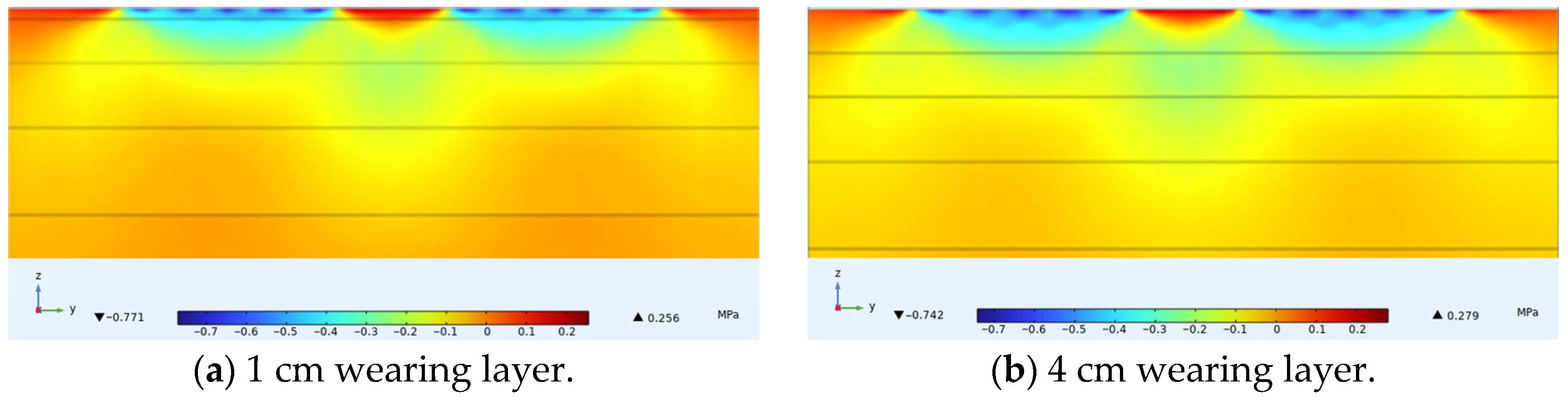
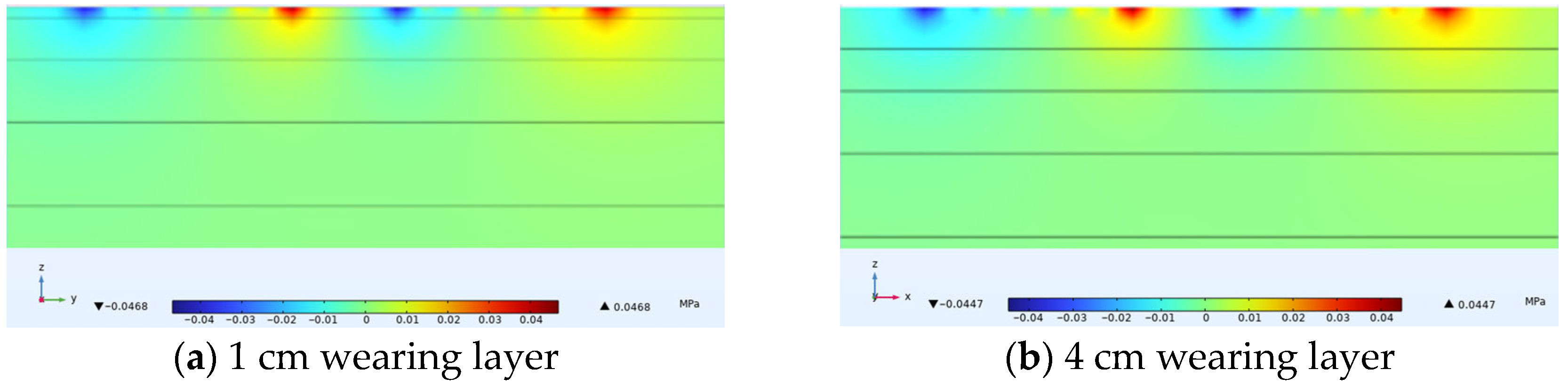
4.1. Vertical Stress Under Varying Thin Layer Thicknesses
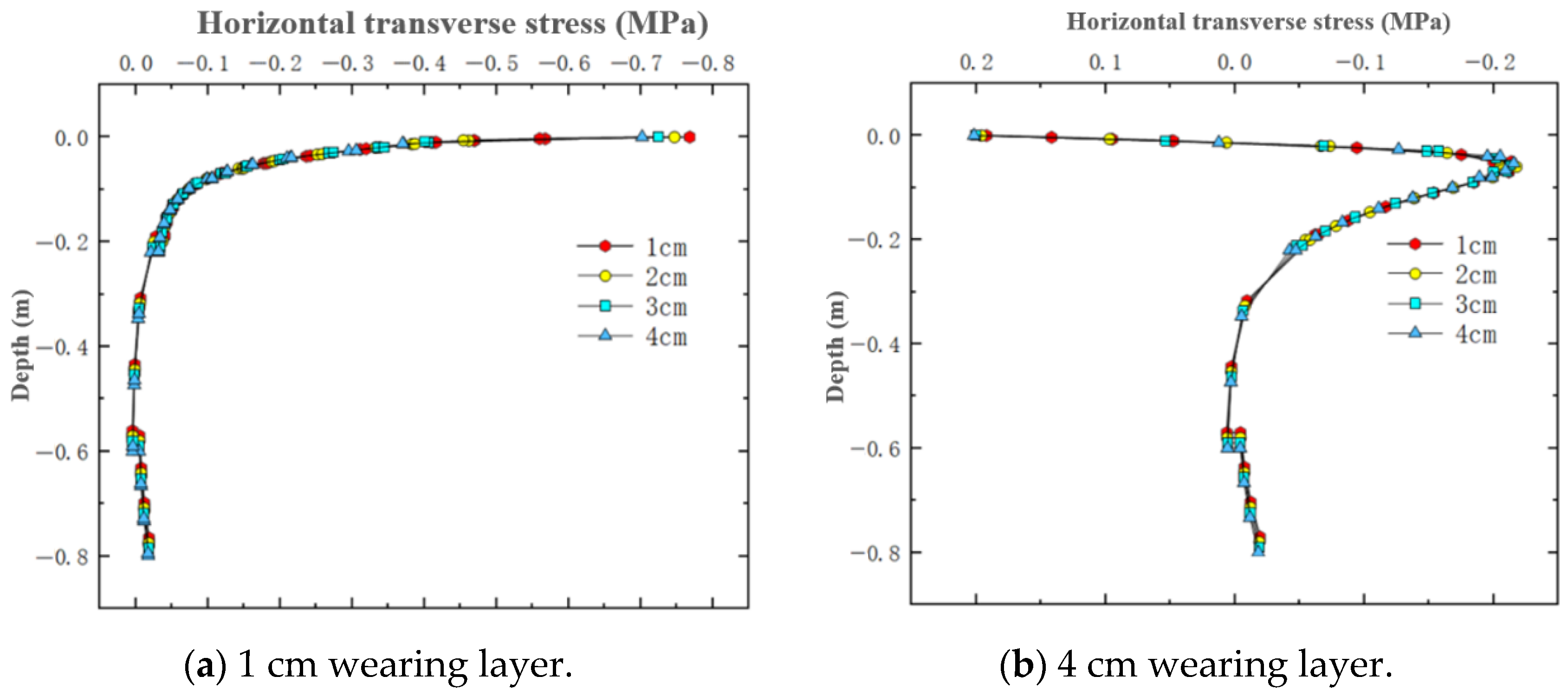
4.2. Horizontal Transverse Stress Under Varying Thin Layer Thicknesses
4.3. Horizontal Longitudinal Stress Under Varying Thin Layer Thicknesses
4.4. Shear Stress Under Varying Thin Layer Thicknesses
5. Non-Uniform Load Influence Factor
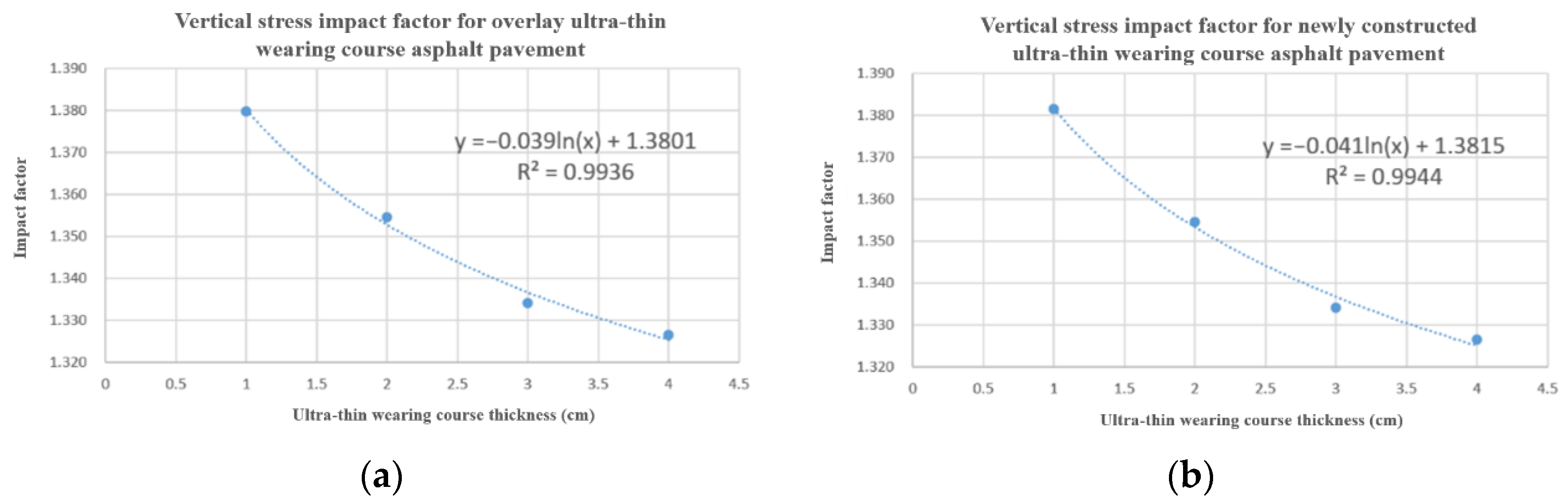
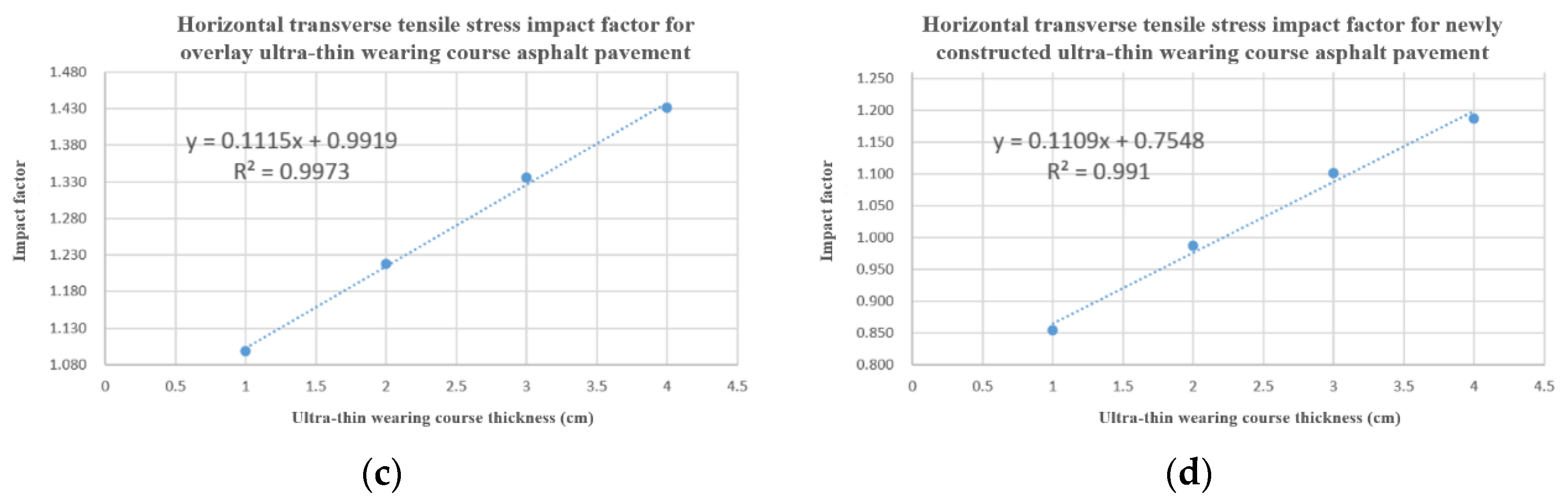
5.1. Definition of Influence Factors
5.2. Establishment of Empirical Influence Factor Model
5.3. Design Recommendations
6. Conclusions
- (1)
- Compared with traditional uniform load assumptions, non-uniform loading pressure significantly altered the internal stress distribution within the ultra-thin wearing layer. This study found that vertical stress peaks increased by 35.4% and horizontal transverse compressive stress increased by 22.1%. Moreover, this stress amplification became more prominent as the wearing course thickness decreased. These results indicated that existing load simplification methods significantly underestimated the actual stress levels in ultra-thin wearing courses.
- (2)
- The model simulation results for varied wearing layer thicknesses showed that as the thickness decreased, the influence of non-uniform loading pressure became more significant. When the thickness reached 1 cm, local stress concentration was particularly pronounced. This finding provided important insight for the thickness optimization design of ultra-thin wearing courses.
- (3)
- Based on numerous numerical simulation results, a Non-uniform Load Influence Factor (NLIF) that considers thickness effects was established, along with corresponding design recommendations. This model enables practical engineering applications by modifying the dynamic stability calculation formula for asphalt mixture rutting tests, effectively transforming non-uniform load effects from the pavement structure scale to the material test scale. As such, it allows for the consideration of non-uniform loading influences through calculation adjustments without requiring changes to existing test equipment and procedures.
- (1)
- Field validation via micro-strain sensors embedded in 1–2 cm ultra-thin layers.
- (2)
- Multiphysics integration of thermo-mechanical effects and moisture-induced damage.
- (3)
- Standardization pathways for NLIF adoption in AASHTO/JTG design frameworks.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wang, W.; Liu, B.; Jin, D.; Yu, M.; Zeng, J. Durability Investigation of Ultra-Thin Polyurethane Wearing Course for Asphalt Pavement. Materials 2024, 17, 4977. [Google Scholar] [CrossRef] [PubMed]
- Pei, Y.; Li, P.; Jiang, S.Q.; Yao, S.; Ding, Z.; Augusto, C.F. Mix design optimization of high-viscosity asphalt mixtures for ultra-thin pavement considering geometric properties and interface slip behavior for aggregate system. Constr. Build. Mater. 2025, 464, 140085. [Google Scholar] [CrossRef]
- Yu, J.; Yang, N.; Yu, H. Research and application status of high-performance asphalt ultra-thin wearing layer technology. J. Cent. South Univ. 2021, 52, 2287–2298. [Google Scholar]
- Liu, H. Performance Comparision on Ultra-Thin Wearing Course of Asphalt Mixture. Master’s Thesis, Chang’an University, Xi’an, China, 2011. [Google Scholar]
- Guo, M.; Zhang, R.; Du, X.L.; Liu, P.F. A State-of-the-Art Review on the Functionality of Ultra-Thin Overlays Towards a Future Low Carbon Road Maintenance. Engineering 2024, 32, 82–98. [Google Scholar] [CrossRef]
- Fu, Z.H. Discussion on Asphalt Pavement Structure Design under Moving Non-Uniform Load. TranspoWorld 2023, 36, 46–48. [Google Scholar] [CrossRef]
- Zheng, J.C.; Chen, X.H. Analysis of Mechanical Response and Fatigue Life of Asphalt Pavement under Different Heterogeneous Load. J. Guangdong Commun. Polytech. 2021, 20, 1–6. [Google Scholar]
- Ye, Y.L.; Xu, Q.L.; Ning, X.J.; YU, S.X. Analysis on longitudinal cracking of flexible base asphalt pavement under non-uniform distributed tire pressure. J. Chang. Univ. (Nat. Sci. Ed.) 2019, 39, 35–46. [Google Scholar] [CrossRef]
- Brosseaud, Y.; Bellanger, J.; Gourdon, J. Thinner and Thinner Asphalt Layers for the Maintenance of French Roads. Transp. Res. Rec. 1992, 1334, 9–11. [Google Scholar]
- Ulf, S.; Jørgen, K.; Luc, G.; Hans, B.; Anneleen, B.; Krishna, P.B.; Robert, K.; Erik, N.; Erik, O.; Stefan, V. Optimization of Thin Asphalt Layers: State-of-the-Art Review; ERA-NET Road Project; European Commission: Brussels, Belgium, 2011. [Google Scholar]
- Vanelstraete, A. O 5 EE-191 Laboratory Tests for Internal Cohesion and Raveling of Thin and Ultra-Thin Wearing Courses. In Proceedings of the 5th Eurasphalt & Eurobitume Congress, Istanbul, Turkey, 13–15 June 2012. [Google Scholar]
- Mogawer, W.S.; Austerman, A.J.; Underwood, S. Effect of Binder Modification on the Performance of an Ultra-Thin Overlay Pavement Preservation Strategy. Transp. Res. Rec. 2016, 2550, 1–7. [Google Scholar] [CrossRef]
- Sol-Sánchez, M.; García-Travé, G.; Ayar, P.; Moreno-Navarro, F.; Rubio-Gámez, M.C. Evaluating the mechanical performance of Very Thin Asphalt Overlay (VTAO) as a sustainable rehabilitation strategy in urban pavements. Mater. Construcción 2017, 67, e132. [Google Scholar] [CrossRef]
- Liu, H. Detecting Evaluation of Road Performance of Ultra-thin Asphalt Overlay. Shanxi Sci. Technol. Transp. 2022, 1, 23–25. [Google Scholar]
- Zhang, Q.; Lu, Z.; Chen, A.; Wu, S.; Feng, J.; Xu, H.; Li, Y. Study on the Performance of Epoxy-Modified Asphalt and Steel Slag Ultra-Thin Friction Course. Materials 2024, 17, 4513. [Google Scholar] [CrossRef] [PubMed]
- Cui, W.; Wu, K.; Cai, X.; Tang, H.; Huang, W. Optimizing Gradation Design for Ultra-Thin Wearing Course Asphalt. Materials 2020, 13, 189. [Google Scholar] [CrossRef] [PubMed]
- JTG D50-2017; Specifications for Design of Highway Asphalt Pavement. China Communication Press: Beijing, China, 2017.
- Fernando, E.G.; Musani, D.; Park, D.W.; Liu, W. Evaluation of Effects of Tire Size and Inflation Pressure on Tire Contact Stresses and Pavement Response; Texas Transportation Institute: College Station, TX, USA, 2006; Tech. Rep. FHWA/TX-06/0-4361-1. [Google Scholar]
- Magazzù, A.; Marcuello, C. Investigation of Soft Matter Nanomechanics by Atomic Force Microscopy and Optical Tweezers: A Comprehensive Review. Nanomaterials 2023, 13, 963. [Google Scholar] [CrossRef] [PubMed]
- Yu, J.; Chen, Y.; Wei, X.; Dong, N.; Yu, H. Performance Evaluation of Ultra-Thin Wearing Course with Different Polymer Modified Asphalt Binders. Polymers 2022, 14, 3235. [Google Scholar] [CrossRef] [PubMed]
- JTG E20-2011; Standard Test Methods of Bitumen and Bituminous Mixtures for Highway Engineering. China Communications Press: Beijing, China, 2011.

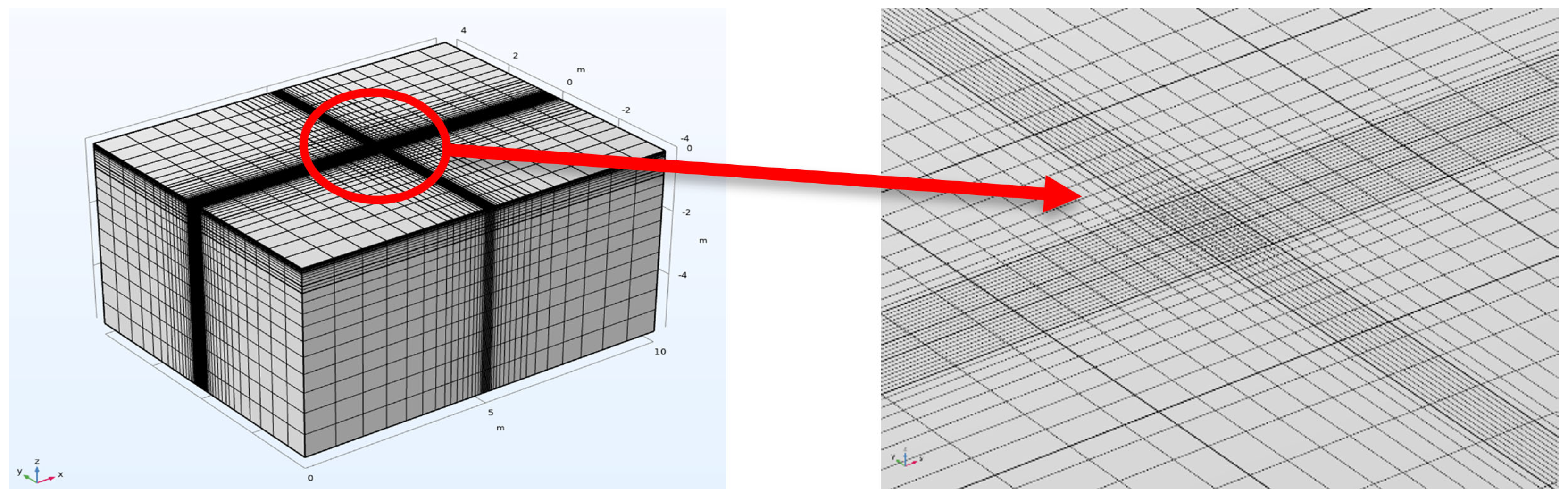
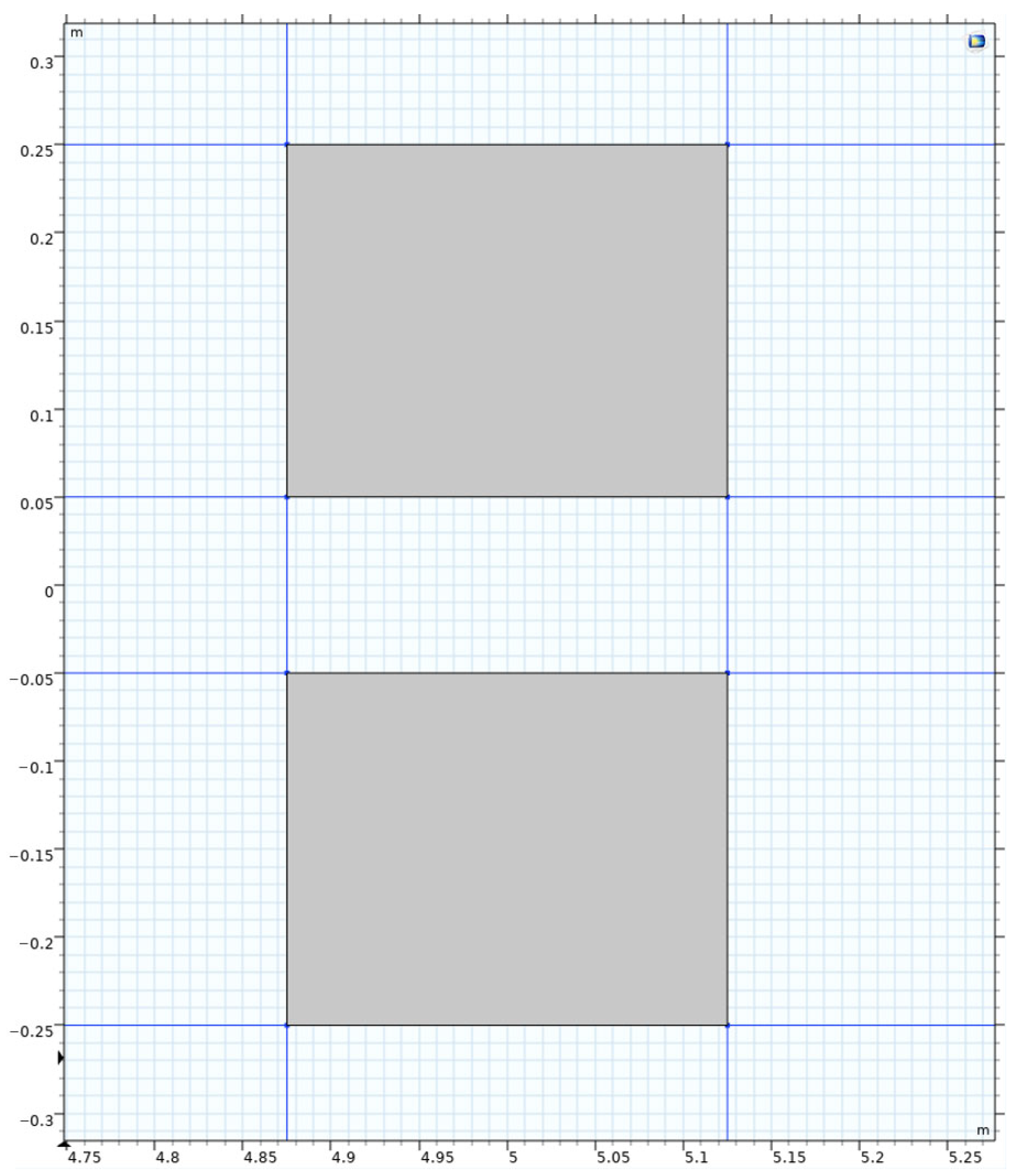
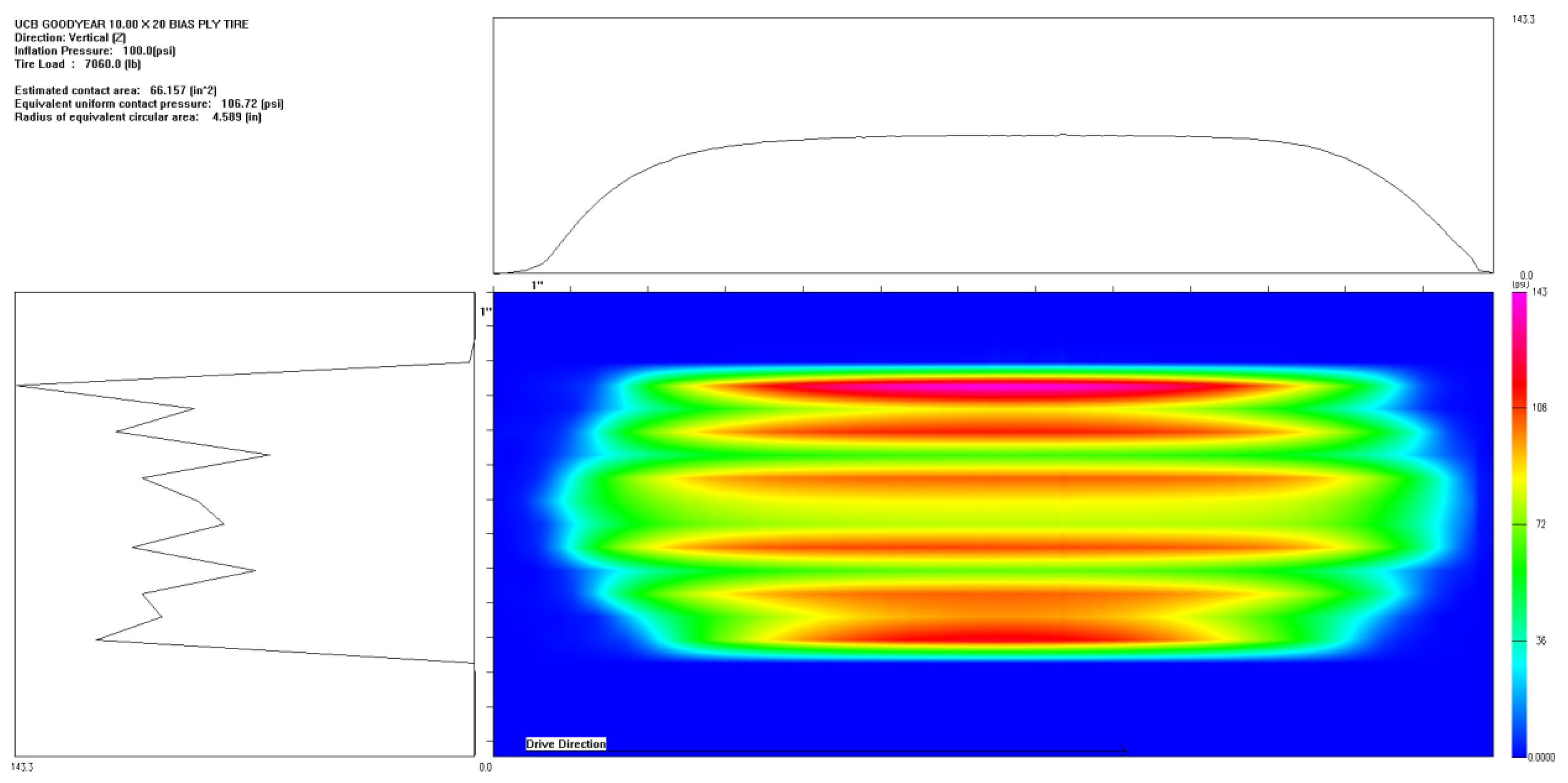
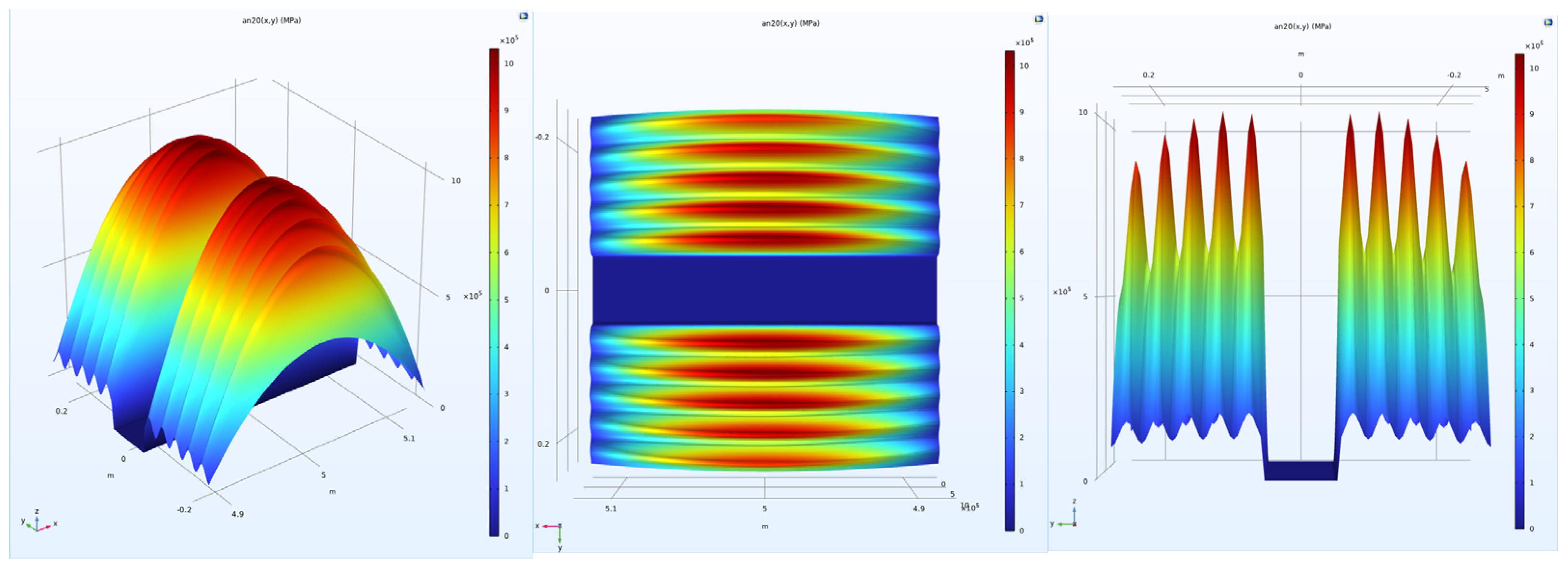





| Structural Layer | Thickness (cm) | Modulus (MPa) | Poisson’s Ratio |
|---|---|---|---|
| Ultra-thin Layer | 1, 2, 3, 4 | 11,000 | 0.25 |
| Asphalt Surface Layer | 4 | 10,375 | 0.25 |
| Asphalt Middle Layer | 6 | 11,224 | 0.25 |
| Asphalt Bottom Layer | 8 | 11,197 | 0.25 |
| Upper Base | 38 | 13,000 | 0.25 |
| Lower Base | 20 | 9000 | 0.25 |
| Subgrade | 500 | 40 | 0.4 |
| Load | Condition | Surface Layer Structure (cm) | Vertical Stress (MPa) | Horizontal Stress (MPa) | Shear Stress (MPa) | |||
|---|---|---|---|---|---|---|---|---|
| Transverse Compressive Stress | Transverse Tensile Stress | Longitudinal Compressive Stress | Longitudinal Tensile Stress | |||||
| Uniform Load | Overlay | 1 + 4 + 6 + 8 | 0.79 | 0.71 | 0.142 | 0.797 | 0.151 | 0.0451 |
| 2 + 4 + 6 + 8 | 0.79 | 0.705 | 0.138 | 0.794 | 0.147 | 0.0445 | ||
| 3 + 4 + 6 + 8 | 0.787 | 0.699 | 0.134 | 0.788 | 0.143 | 0.0439 | ||
| 4 + 4 + 6 + 8 | 0.784 | 0.694 | 0.13 | 0.782 | 0.139 | 0.0433 | ||
| New Construction | 1 + 6 + 8 | 0.789 | 0.708 | 0.158 | 0.795 | 0.168 | 0.0438 | |
| 2 + 6 + 8 | 0.79 | 0.707 | 0.153 | 0.794 | 0.163 | 0.0437 | ||
| 3 + 6 + 8 | 0.787 | 0.704 | 0.149 | 0.792 | 0.158 | 0.0435 | ||
| 4 + 6 + 8 | 0.784 | 0.699 | 0.145 | 0.788 | 0.154 | 0.043 | ||
| Non-uniform Load | Overlay | 1 + 4 + 6 + 8 | 1.09 | 0.872 | 0.156 | 0.821 | 0.123 | 0.0468 |
| 2 + 4 + 6 + 8 | 1.07 | 0.861 | 0.168 | 0.813 | 0.12 | 0.0461 | ||
| 3 + 4 + 6 + 8 | 1.05 | 0.847 | 0.179 | 0.804 | 0.116 | 0.0454 | ||
| 4 + 4 + 6 + 8 | 1.04 | 0.833 | 0.186 | 0.795 | 0.113 | 0.0447 | ||
| New Construction | 1 + 6 + 8 | 1.09 | 0.863 | 0.135 | 0.823 | 0.137 | 0.0456 | |
| 2 + 6 + 8 | 1.07 | 0.856 | 0.151 | 0.816 | 0.133 | 0.0454 | ||
| 3 + 6 + 8 | 1.05 | 0.848 | 0.164 | 0.807 | 0.129 | 0.0451 | ||
| 4 + 6 + 8 | 1.04 | 0.837 | 0.172 | 0.799 | 0.126 | 0.0445 | ||
| Wearing Layer Thickness (cm) | Vertical Stress | Horizontal Stress | Shear Stress | |||
|---|---|---|---|---|---|---|
| Transverse Compressive Stress | Transverse Tensile Stress | Longitudinal Compressive Stress | Longitudinal Tensile Stress | |||
| 1 | 1.3797468354 | 1.2281690141 | 1.0985915493 | 1.0301129235 | 0.8145695364 | 1.0376940133 |
| 2 | 1.3544303797 | 1.2212765957 | 1.2173913043 | 1.0239294710 | 0.8163265306 | 1.0359550562 |
| 3 | 1.3341804320 | 1.2117310443 | 1.3358208955 | 1.0203045685 | 0.8111888112 | 1.0341685649 |
| 4 | 1.3265306122 | 1.2002881844 | 1.4307692308 | 1.0166240409 | 0.8129496403 | 1.0323325635 |
| Wearing Layer Thickness (cm) | Vertical Stress | Horizontal Stress | Shear Stress | |||
|---|---|---|---|---|---|---|
| Transverse Compressive Stress | Transverse Tensile Stress | Longitudinal Compressive Stress | Longitudinal Tensile Stress | |||
| 1 | 1.3814955640 | 1.2189265537 | 0.8544303797 | 1.0352201258 | 0.8154761905 | 1.0410958904 |
| 2 | 1.3544303797 | 1.2107496464 | 0.9869281046 | 1.0277078086 | 0.8159509202 | 1.0389016018 |
| 3 | 1.3341804320 | 1.2045454545 | 1.1006711409 | 1.0189393939 | 0.8164556962 | 1.0367816092 |
| 4 | 1.3265306122 | 1.1974248927 | 1.1862068966 | 1.0139593909 | 0.8181818182 | 1.0348837209 |
| Vertical Stress | Horizontal Stress | Shear Stress | |||
|---|---|---|---|---|---|
| Transverse Compressive Stress | Transverse Tensile Stress | Longitudinal Compressive Stress | Longitudinal Tensile Stress | ||
| 0.0549649518 | 0.0307441214 | 0.5763388510 | 0.0212607349 | 0.0069930070 | 0.0087633269 |
| Corresponding Stress | Corresponding Formula |
|---|---|
| Vertical Stress | |
| Horizontal Transverse Compressive Stress | |
| Horizontal Transverse Tensile Stress | |
| Horizontal Longitudinal Compressive Stress | |
| Horizontal Longitudinal Tensile Stress | |
| Shear Stress |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, W.; Dou, Y.; Chen, C.; Yang, Y.; Xu, X.; Li, L.; Xiao, J.; Chen, F. Mechanical Response Analysis of Ultra-Thin Asphalt Wearing Course Pavement Under Non-Uniform Loading Pressure. Materials 2025, 18, 3335. https://doi.org/10.3390/ma18143335
Zhou W, Dou Y, Chen C, Yang Y, Xu X, Li L, Xiao J, Chen F. Mechanical Response Analysis of Ultra-Thin Asphalt Wearing Course Pavement Under Non-Uniform Loading Pressure. Materials. 2025; 18(14):3335. https://doi.org/10.3390/ma18143335
Chicago/Turabian StyleZhou, Wei, Yingying Dou, Chupeng Chen, Yi Yang, Xinquan Xu, Lintao Li, Jiangyin Xiao, and Feng Chen. 2025. "Mechanical Response Analysis of Ultra-Thin Asphalt Wearing Course Pavement Under Non-Uniform Loading Pressure" Materials 18, no. 14: 3335. https://doi.org/10.3390/ma18143335
APA StyleZhou, W., Dou, Y., Chen, C., Yang, Y., Xu, X., Li, L., Xiao, J., & Chen, F. (2025). Mechanical Response Analysis of Ultra-Thin Asphalt Wearing Course Pavement Under Non-Uniform Loading Pressure. Materials, 18(14), 3335. https://doi.org/10.3390/ma18143335





