State-of-the-Art Review of Studies on the Flexural Behavior and Design of FRP-Reinforced Concrete Beams
Abstract
1. Introduction
2. FRP-Reinforced Concrete (RC) Beams
2.1. Fiber-Reinforced Polymer (FRP)
2.2. Major Types of Concrete
| Source | Type of Concrete | Key Findings |
|---|---|---|
| [16,26,92,93,94,95] | OPC | ACI 318 underestimated the deflection of FRP RC beams up to 70%. The proposed model could predict the deflection of FRP beams with an error of less than 10%. ACI 440.1R overestimated crack widths but underestimated the deflection of FRP beams. FRP RC beams experienced large deformation to achieve predicted moment capacity. |
| [96,97,98] | UHPC | The load and deflection at the first crack were not dependent on the reinforcement ratio. ACI 440.1R overestimated the deflection of FRP-reinforced UHPC beams. UHPC could improve the ductility of the beam because of its high compressive strain and high tensile strength. The ductility model of FRP normal concrete beams could not be used for FRP UHPC beams. |
| [45,48,49,52] | SWSSC | GB 50608 underestimated the moment capacity of FRP beams. The moment capacity of FRP-reinforced SWSSC beams increased when shear/span ratio was reduced. Compression-cast FRP beams have higher cracking instances due to the higher strength of concrete. With the same applied loads, the maximum crack with compression-cast FRP beams is smaller than that of FRP OPC beams. A model for predicting the ultimate moment was proposed. A cracking moment is governed by the tensile strength of concrete. Both ACI 440.1R and GB 50608 should be modified to predict the deflection of FRP beams better. |
| [33,38,40,51,99,100] | GPC | Both ACI 440.1R and CSA S806 underestimated the ultimate moment of FRP GPC beams. It was better to use CFRP than GFRP, BFRP, and AFRP as tensile reinforcement of concrete beams. GPC could be an alternative material to replace traditional concrete. Beams with steel stirrups had better performance than beams with FRP stirrups. GPC had higher compressive strain than normal concrete. ACI 440.2R underestimated the experimental load of the GFRP-reinforced T-beam. The structural behavior of geopolymer concrete was similar to normal concrete. |
| [34,50,88] | LWAC | CFRP bars could be a good option to replace steel reinforcement. The proposed equations to predict the ultimate moment of FRP-reinforced LWAC could give reliable results compared to experiments. Research on anchoring measures at ends of CFRP bars should be conducted. A model to predict the crack width of CFRP LWAC beams was proposed. GFRP LWAC beams had large deflection and crack width. The flexural capacity of BFRP LWAC beams could be predicted by specifications for FRP-reinforced OPC beams. The ultimate moments of BFRP LWAC beams reduced significantly when exposed to high temperature. |
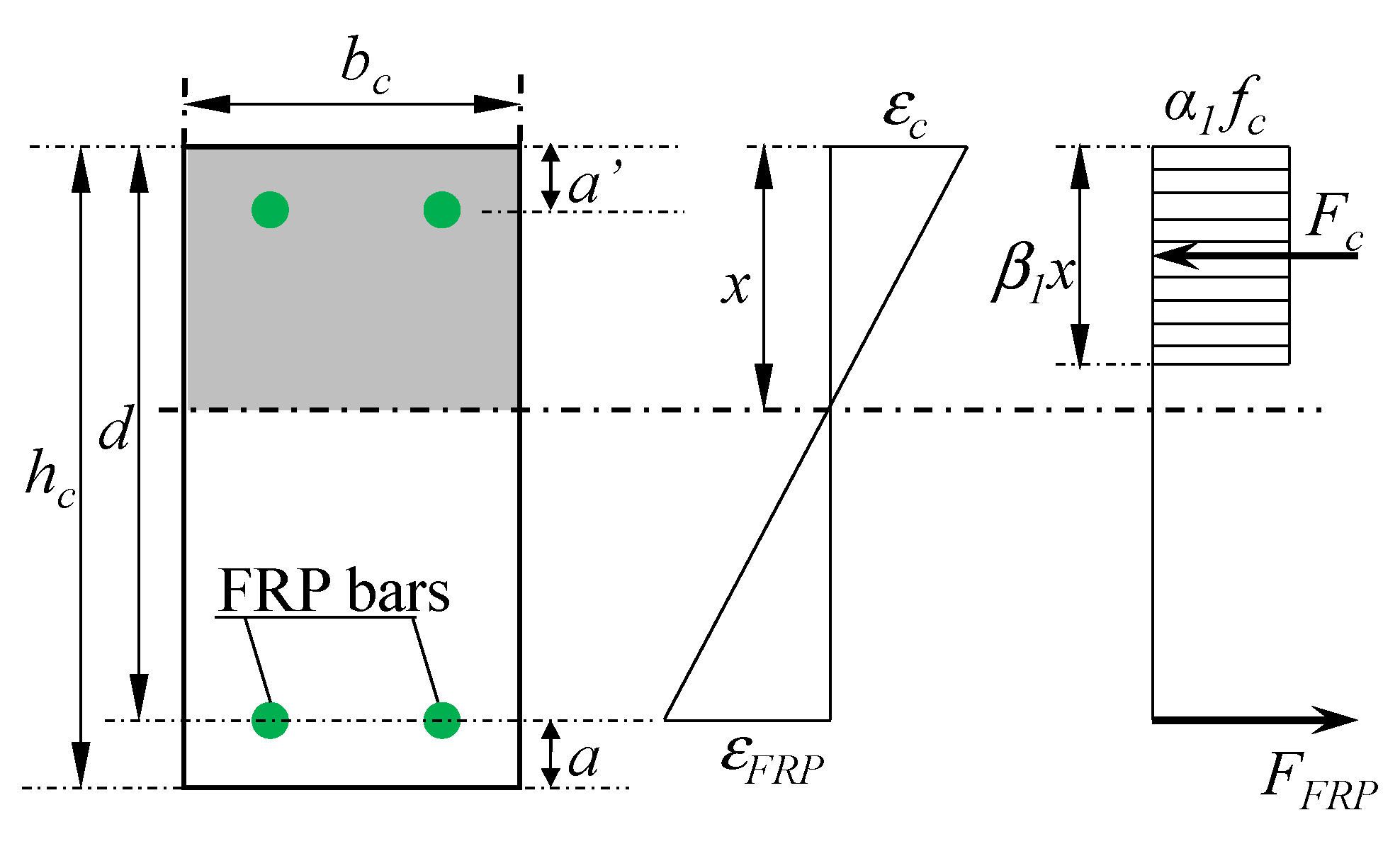
2.3. Concrete Stress–Strain Relationship
2.4. Bond Between FRP Bars and Concrete
2.5. Failure Mechanism of FRP RC Beams
3. Experimental Studies on FRP RC Beams
3.1. Beams Reinforced with GFRP Bars
3.2. Beams Reinforced with CFRP Bars
3.3. Beams Reinforced with BFRP/AFRP Bars
4. Numerical Studies on FRP RC Beams
4.1. Finite Element (FE) Analysis
4.2. Discrete Element (DE) Analysis
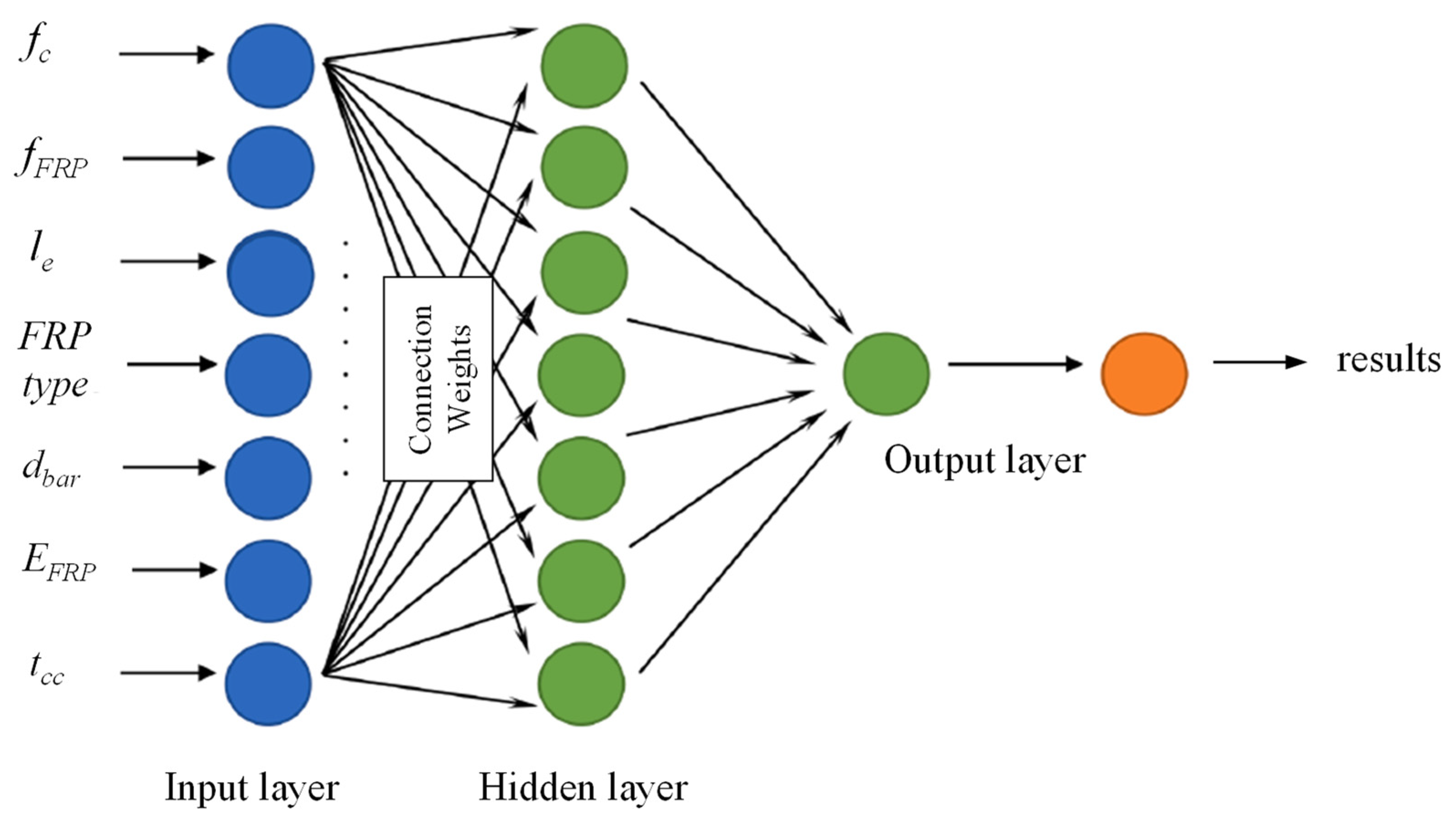
4.3. Artificial Intelligence/Machine Learning (AI/ML)
5. Design Guidelines
6. Conclusions and Recommendations
- (1)
- Many experimental and numerical studies on FRP RC beams with the consideration of different types of concrete and FRP have been carried out. Based on these studies, 93 tested beams have been collected, and it can be a good source of reference for other future studies.
- (2)
- The application of the AI/ML and the DE method to investigate the behavior of FRP RC beams are still limited. More studies using these approaches can be conducted.
- (3)
- Although numerous experimental studies and studies using FE simulation have been found, few studies consider the effect of the bond and the radial stress between concrete and FRP bars on the behavior of FRP RC beams. In addition, research focusing on the behavior of FRP RC deep beams and FRP RC continuous beams is still limited.
- (4)
- Almost all studies focus on beams with rectangular sections; beams with other shapes of section can be investigated. In addition, most studies investigate the strength limit state of FRP RC beams; few research explores the serviceability performance of FRP RC beams.
- (5)
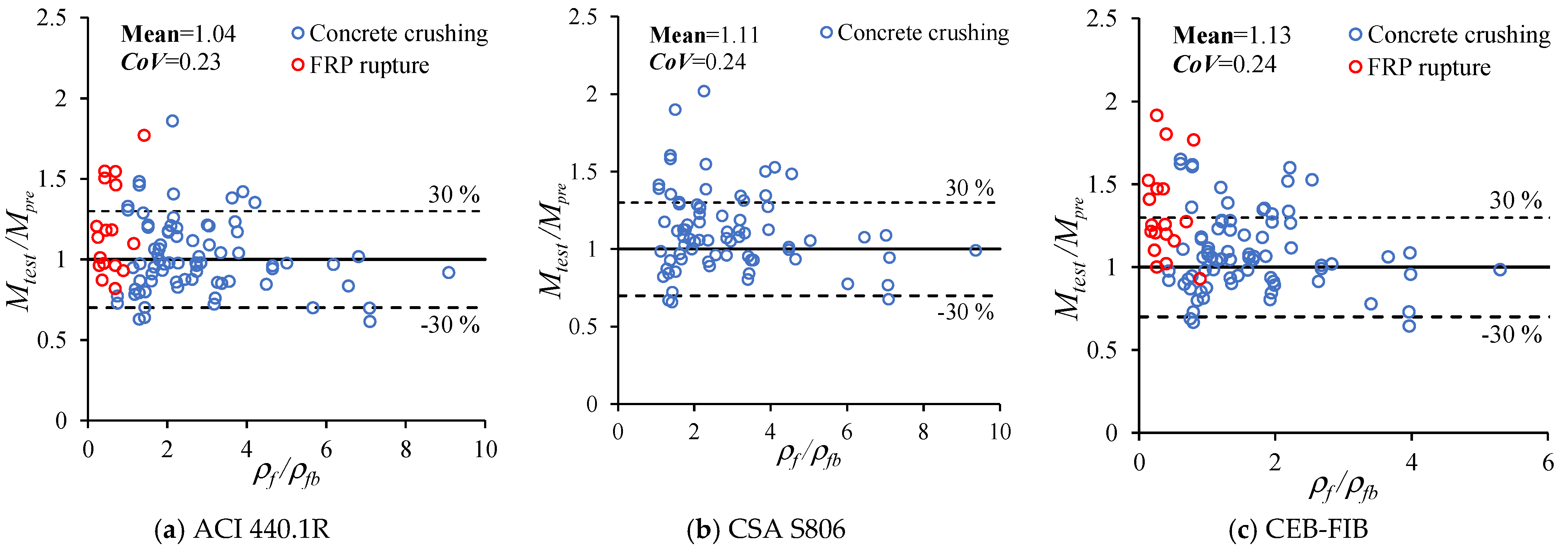
- Three prevalent design standards of FRP RC beams are summarized in the study. Among these standards, ACI 440.1R can give the best prediction of moment capacity of FRP RC beams as the Mtest/Mpre ratio has the mean and CoV of 1.04 and 0.23, respectively.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Abdoli, M.; Mostofinejad, D. Torsional behavior of frp-strengthened reinforced concrete members considering various wrapping configurations: Theoretical analysis and modeling. Constr. Build. Mater. 2023, 401, 132636. [Google Scholar] [CrossRef]
- Abed, M.A.; Anagreh, A.; Tošić, N.; Alkhabbaz, O.; Alshwaiki, M.E.; Černý, R. Structural performance of lightweight aggregate concrete reinforced by glass or basalt fiber reinforced polymer bars. Polymers 2022, 14, 2142. [Google Scholar] [CrossRef] [PubMed]
- Belarbi, A.; Dawood, M.; Acun, B. 20—Sustainability of fiber-reinforced polymers (frps) as a construction material. In Sustainability of Construction Materials, 2nd ed.; Khatib, J.M., Ed.; Woodhead Publishing: Sawston, UK, 2016; pp. 521–538. [Google Scholar]
- Liu, Z.; Sun, C.; Qu, J.; Mokhov, A. State-of-the-art review of the performance of fiber-reinforced-composite-confined concrete columns at ambient temperatures. Materials 2025, 18, 1151. [Google Scholar] [CrossRef]
- Ortiz, J.D.; Khedmatgozar Dolati, S.S.; Malla, P.; Nanni, A.; Mehrabi, A. Frp-reinforced/strengthened concrete: State-of-the-art review on durability and mechanical effects. Materials 2023, 16, 1990. [Google Scholar] [CrossRef]
- Saleem, S.; Pimanmas, A.; Rattanapitikon, W.; Ali, F.I. Investigating dilation response in pet frp-confined reinforced concrete: Experimental study. Constr. Build. Mater. 2024, 442, 137645. [Google Scholar] [CrossRef]
- Tran, H.; Thai, H.T.; Ngo, T.; Uy, B.; Li, D.; Mo, J. Advanced analysis of steel-concrete composite buildings. Ce/Papers 2023, 6, 423–434. [Google Scholar] [CrossRef]
- Tran, H.; Thai, H.-T.; Uy, B. Monte carlo and subset simulations-based reliability analysis of composite frames using opensees. In Proceedings of the 2022 Eurasian OpenSees Days; Di Trapani, F., Demartino, C., Marano, G.C., Monti, G., Eds.; Springer Nature: Cham, Switzerland, 2023; pp. 214–223. [Google Scholar]
- Tran, H.; Thai, H.-T.; Uy, B. System reliability-based design of composite frames with concrete—Filled steel plate shear walls. Structures 2024, 64, 106576. [Google Scholar] [CrossRef]
- Zhou, Y.; Fan, Z.; Du, J.; Sui, L.; Xing, F. Bond behavior of frp-to-concrete interface under sulfate attack: An experimental study and modeling of bond degradation. Constr. Build. Mater. 2015, 85, 9–21. [Google Scholar] [CrossRef]
- Zhu, H.; Cheng, S.; Gao, D.; Neaz, S.M.; Li, C. Flexural behavior of partially fiber-reinforced high-strength concrete beams reinforced with frp bars. Constr. Build. Mater. 2018, 161, 587–597. [Google Scholar] [CrossRef]
- Zomorodian, M.; Yang, G.; Belarbi, A.; Ayoub, A. Cracking behavior and crack width predictions of frp strengthened rc members under tension. Eng. Struct. 2016, 125, 313–324. [Google Scholar] [CrossRef]
- Manalo, A.C.; Mendis, P.; Bai, Y.; Jachmann, B.; Sorbello, C.D. Fiber-reinforced polymer bars for concrete structures: State-of-the-practice in australia. J. Compos. Constr. 2021, 25, 05020007. [Google Scholar] [CrossRef]
- Manalo, A.; Benmokrane, B.; Park, K.-T.; Lutze, D. Recent developments on frp bars as internal reinforcement in concrete structures. Concr. Aust. 2014, 40, 46–56. [Google Scholar]
- Micelli, F.; Belarbi, A.; Donne, G.P.D.; Zerbe, L.; Vieira, D. Experimental tests on prestressed rc beams with gfrp reinforcement. In Proceedings of the 11th International Conference on FRP Composites in Civil Engineering, CICE 2023, Rio de Janeiro, Brazil, 23–26 July 2023. [Google Scholar]
- Alsayed, S.H. Flexural behaviour of concrete beams reinforced with gfrp bars. Cem. Concr. Compos. 1998, 20, 1–11. [Google Scholar] [CrossRef]
- Ashour, A.F. Flexural and shear capacities of concrete beams reinforced with gfrp bars. Constr. Build. Mater. 2006, 20, 1005–1015. [Google Scholar] [CrossRef]
- Benmokrane, B.; Chaallal, O.; Masmoudi, R. Glass fibre reinforced plastic (gfrp) rebars for concrete structures. Constr. Build. Mater. 1995, 9, 353–364. [Google Scholar] [CrossRef]
- Chen, G.; An, R.; Xu, J.; Fu, S. Finite element analysis of the reinforcement ratio effect on tension stiffening in frp reinforced concrete beams. Compos. Struct. 2022, 298, 116020. [Google Scholar] [CrossRef]
- Confrere, A.; Michel, L.; Ferrier, E.; Chanvillard, G. Experimental behaviour and deflection of low-strength concrete beams reinforced with frp bars. Struct. Concr. 2016, 17, 858–874. [Google Scholar] [CrossRef]
- Micelli, F.; Aiello, M.A. Residual tensile strength of dry and impregnated reinforcement fibres after exposure to alkaline environments. Compos. Part B Eng. 2019, 159, 490–501. [Google Scholar] [CrossRef]
- Micelli, F.; Corradi, M.; Aiello, M.A.; Borri, A. Properties of aged gfrp reinforcement grids related to fatigue life and alkaline environment. Appl. Sci. 2017, 7, 897. [Google Scholar] [CrossRef]
- Micelli, F.; Mazzotta, R.; Leone, M.; Aiello, M.A. Review study on the durability of frp-confined concrete. J. Compos. Constr. 2015, 19, 04014056. [Google Scholar] [CrossRef]
- Micelli, F.; Rizzo, A.; Galati, D. Anchorage of composite laminates in rc flexural beams. Struct. Concr. 2010, 11, 117–126. [Google Scholar] [CrossRef]
- Mostafa, O.M.; Rahman, M.K.; Al-Zahrani, M.M.; Adekunle, S.K.; Al-Osta, M.A.; Najamuddin, S.K. Flexural behavior and bond coefficient of bfrp bar reinforced normal and high strength concrete beams. Constr. Build. Mater. 2023, 401, 132896. [Google Scholar] [CrossRef]
- Muhammad, M.A.; Ahmed, F.R. Evaluation of deflection and flexural performance of reinforced concrete beams with glass fiber reinforced polymer bars. Case Stud. Constr. Mater. 2023, 18, e01855. [Google Scholar] [CrossRef]
- Selcuk, S.; Ahmetoglu, U.; Gokce, E.C. Basalt fiber reinforced polymer composites (bfrp) other than rebars: A review. Mater. Today Commun. 2023, 37, 107359. [Google Scholar] [CrossRef]
- Tran, H.; Thai, H.-T.; Ngo, T.; Uy, B.; Li, D.; Mo, J. Nonlinear inelastic simulation of high-rise buildings with innovative composite coupling shear walls and cfst columns. Struct. Des. Tall Spec. Build. 2021, 30, e1883. [Google Scholar] [CrossRef]
- Elsevier. Frp Reinforced Concrete. Available online: https://www.sciencedirect.com (accessed on 28 November 2024).
- Abed, F.; Al-Mimar, M.; Ahmed, S. Performance of bfrp rc beams using high strength concrete. Compos. Part C Open Access 2021, 4, 100107. [Google Scholar] [CrossRef]
- Abushanab, A.; Alnahhal, W.; Farraj, M. Structural performance and moment redistribution of basalt frc continuous beams reinforced with basalt frp bars. Eng. Struct. 2021, 240, 112390. [Google Scholar] [CrossRef]
- Abushanab, A.; Alnahhal, W.; Farraj, M. Experimental and finite element studies on the structural behavior of bfrc continuous beams reinforced with bfrp bars. Compos. Struct. 2022, 281, 114982. [Google Scholar] [CrossRef]
- Ahmed, H.Q.; Jaf, D.K.; Yaseen, S.A. Flexural strength and failure of geopolymer concrete beams reinforced with carbon fibre-reinforced polymer bars. Constr. Build. Mater. 2020, 231, 117185. [Google Scholar] [CrossRef]
- Deng, Z.; Zhong, X.; Liu, B.; Wen, K. Study on flexural behavior of coral concrete beams reinforced with cfrp bars. Structures 2022, 39, 378–386. [Google Scholar] [CrossRef]
- Dong, Z.; Wu, G.; Zhu, H.; Zhao, X.-L.; Wei, Y.; Qian, H. Flexural behavior of seawater sea-sand coral concrete–uhpc composite beams reinforced with bfrp bars. Constr. Build. Mater. 2020, 265, 120279. [Google Scholar] [CrossRef]
- El-Nemr, A.; Ahmed, E.A.; El-Safty, A.; Benmokrane, B. Evaluation of the flexural strength and serviceability of concrete beams reinforced with different types of gfrp bars. Eng. Struct. 2018, 173, 606–619. [Google Scholar] [CrossRef]
- Ge, W.; Ashour, A.F.; Cao, D.; Lu, W.; Gao, P.; Yu, J.; Ji, X.; Cai, C. Experimental study on flexural behavior of ecc-concrete composite beams reinforced with frp bars. Compos. Struct. 2019, 208, 454–465. [Google Scholar] [CrossRef]
- George, G.; Shreeram, P.K.; Minalan, A.S.; Lokesh, K.; Mano, M.; Prince, A. Numerical investigation on the flexural behavior of geopolymer concrete beam reinforced with different types of fiber-reinforced polymer bars. Mater. Today Proc. 2023, in press. [Google Scholar]
- Guo, B.; Lin, X.; Wu, Y.; Zhang, L. Machine learning-driven evaluation and optimisation of compression yielded frp-reinforced concrete beam with t section. Eng. Struct. 2023, 275, 115240. [Google Scholar] [CrossRef]
- Hasan, M.A.; Sheehan, T.; Ashour, A.; Elkezza, O. Flexural behaviour of geopolymer concrete t-beams reinforced with gfrp bars. Structures 2023, 49, 345–364. [Google Scholar] [CrossRef]
- Huang, Z.; Chen, W.; Tran, T.T.; Pham, T.M.; Hao, H.; Chen, Z.; Elchalakani, M. Experimental and numerical study on concrete beams reinforced with basalt frp bars under static and impact loads. Compos. Struct. 2021, 263, 113648. [Google Scholar] [CrossRef]
- Kazemi, M.; Madandoust, R.; Chastre, C.; Reza Esfahani, M.; Courard, L. Numerical study on the flexural behaviour of normal- and high-strength concrete beams reinforced with gfrp bar, using different amounts of transverse reinforcement. Structures 2021, 34, 3113–3124. [Google Scholar] [CrossRef]
- Metwally, I.M. Three-dimensional nonlinear finite element analysis of concrete deep beam reinforced with gfrp bars. HBRC J. 2017, 13, 25–38. [Google Scholar] [CrossRef]
- Nassif, M.K.; Erfan, A.M.; Fadel, O.T.; El-sayed, T.A. Flexural behavior of high strength concrete deep beams reinforced with gfrp bars. Case Stud. Constr. Mater. 2021, 15, e00613. [Google Scholar] [CrossRef]
- Ren, F.; Liu, T.; Chen, G.; Xie, P.; Xiong, M.-X.; Yuan, T.; Chen, Y.; Guo, S. Flexural behavior and modelling of frp-bar reinforced seawater sea sand concrete beams exposed to subtropical coastal environment. Constr. Build. Mater. 2021, 309, 125071. [Google Scholar] [CrossRef]
- Shen, X.; Li, B.; Shi, W.; Chen, Y.-T. Numerical study on flexural behaviour of frp reinforced concrete beams with compression yielding blocks. Case Stud. Constr. Mater. 2022, 17, e01169. [Google Scholar] [CrossRef]
- Thériault, M.; Benmokrane, B. Effects of frp reinforcement ratio and concrete strength on flexural behavior of concrete beams. J. Compos. Constr. 1998, 2, 7–16. [Google Scholar] [CrossRef]
- Wang, Z.; Xie, J.; Li, J.; Liu, P.; Shi, C.; Lu, Z. Flexural behaviour of seawater–sea sand concrete beams reinforced with gfrp bars: Effects of the reinforcement ratio, stirrup ratio, shear span ratio and prestress level. J. Build. Eng. 2022, 54, 104566. [Google Scholar] [CrossRef]
- Yuan, F.; Liu, P.; Li, H.; Wu, Y. Experimental investigations on the flexural behavior of compression-cast seawater sea-sand concrete beams reinforced with cfrp bars. Constr. Build. Mater. 2024, 445, 137754. [Google Scholar] [CrossRef]
- Zhang, B.; Yang, Z.; Jiang, X.a.; Zhu, H.; Wang, W.; Dong, Y.-R.; Peng, H. Flexural behavior of coral aggregate concrete beams reinforced with bfrp bars under seawater corrosion environments. Constr. Build. Mater. 2024, 447, 138091. [Google Scholar] [CrossRef]
- Zinkaah, O.H.; Alridha, Z.; Alhawat, M. Numerical and theoretical analysis of frp reinforced geopolymer concrete beams. Case Stud. Constr. Mater. 2022, 16, e01052. [Google Scholar] [CrossRef]
- Dong, Z.; Wu, G.; Zhao, X.-L.; Zhu, H.; Lian, J.-L. Durability test on the flexural performance of seawater sea-sand concrete beams completely reinforced with frp bars. Constr. Build. Mater. 2018, 192, 671–682. [Google Scholar] [CrossRef]
- De, B.; Bera, M.; Bhattacharjee, D.; Ray, B.C.; Mukherjee, S. A comprehensive review on fiber-reinforced polymer composites: Raw materials to applications, recycling, and waste management. Prog. Mater. Sci. 2024, 146, 101326. [Google Scholar] [CrossRef]
- Khodadadi, N.; Roghani, H.; Harati, E.; Mirdarsoltany, M.; De Caso, F.; Nanni, A. Fiber-reinforced polymer (frp) in concrete: A comprehensive survey. Constr. Build. Mater. 2024, 432, 136634. [Google Scholar] [CrossRef]
- Sathishkumar, T.P.; Satheeshkumar, S.; Naveen, J. Glass fiber-reinforced polymer composites—A review. J. Reinf. Plast. Compos. 2014, 33, 1258–1275. [Google Scholar] [CrossRef]
- Morampudi, P.; Namala, K.K.; Gajjela, Y.K.; Barath, M.; Prudhvi, G. Review on glass fiber reinforced polymer composites. Mater. Today Proc. 2021, 43, 314–319. [Google Scholar] [CrossRef]
- Agarwal, A.; Garg, S.; Rakesh, P.; Singh, I.; Mishra, B. Tensile behavior of glass fiber reinforced plastics subjected to different environmental conditions. Indian J. Eng. Mater. Sci. 2010, 17, 471–476. [Google Scholar]
- Aktaş, A.; Uzun, İ. Sea water effect on pinned-joint glass fibre composite materials. Compos. Struct. 2008, 85, 59–63. [Google Scholar] [CrossRef]
- Ashrafi, H.; Bazli, M.; Najafabadi, E.P.; Vatani Oskouei, A. The effect of mechanical and thermal properties of frp bars on their tensile performance under elevated temperatures. Constr. Build. Mater. 2017, 157, 1001–1010. [Google Scholar] [CrossRef]
- Gu, H.; Hongxia, S. Delamination behaviour of glass/polyester composites after water absorption. Mater. Des. 2008, 29, 262–264. [Google Scholar] [CrossRef]
- Hamad, R.J.A.; Megat Johari, M.A.; Haddad, R.H. Mechanical properties and bond characteristics of different fiber reinforced polymer rebars at elevated temperatures. Constr. Build. Mater. 2017, 142, 521–535. [Google Scholar] [CrossRef]
- Olmos, D.; López-Morón, R.; González-Benito, J. The nature of the glass fibre surface and its effect in the water absorption of glass fibre/epoxy composites. The use of fluorescence to obtain information at the interface. Compos. Sci. Technol. 2006, 66, 2758–2768. [Google Scholar] [CrossRef]
- Robert, M.; Benmokrane, B. Behavior of gfrp reinforcing bars subjected to extreme temperatures. J. Compos. Constr. 2010, 14, 353–360. [Google Scholar] [CrossRef]
- Wang, Y.C.; Wong, P.M.H.; Kodur, V. An experimental study of the mechanical properties of fibre reinforced polymer (frp) and steel reinforcing bars at elevated temperatures. Compos. Struct. 2007, 80, 131–140. [Google Scholar] [CrossRef]
- Al-Furjan, M.S.H.; Shan, L.; Shen, X.; Zarei, M.S.; Hajmohammad, M.H.; Kolahchi, R. A review on fabrication techniques and tensile properties of glass, carbon, and kevlar fiber reinforced rolymer composites. J. Mater. Res. Technol. 2022, 19, 2930–2959. [Google Scholar] [CrossRef]
- Bakis, C.E.; Bank Lawrence, C.; Brown, V.L.; Cosenza, E.; Davalos, J.F.; Lesko, J.J.; Machida, A.; Rizkalla, S.H.; Triantafillou, T.C. Fiber-reinforced polymer composites for construction—State-of-the-art review. J. Compos. Constr. 2002, 6, 73–87. [Google Scholar] [CrossRef]
- Zhang, R.; Li, Z.; Sun, Q.; Yu, G.; Wang, X.; Wu, L. Design and characterization of the carbon fiber tube reinforced polymer composite for full ocean depth submersibles. Compos. Sci. Technol. 2022, 217, 109074. [Google Scholar] [CrossRef]
- Cousin, P.; Hassan, M.; Vijay, P.V.; Robert, M.; Benmokrane, B. Chemical resistance of carbon, basalt, and glass fibers used in frp reinforcing bars. J. Compos. Mater. 2019, 53, 3651–3670. [Google Scholar] [CrossRef]
- Feih, S.; Mouritz, A.P. Tensile properties of carbon fibres and carbon fibre–polymer composites in fire. Compos. Part A Appl. Sci. Manuf. 2012, 43, 765–772. [Google Scholar] [CrossRef]
- Ji, Y.; Kim Yail, J. Effects of sulfuric acid on durability characteristics of cfrp composite sheets. J. Mater. Civ. Eng. 2017, 29, 04017159. [Google Scholar] [CrossRef]
- Li, H.; Zhang, K.; Fan, X.; Cheng, H.; Xu, G.; Suo, H. Effect of seawater ageing with different temperatures and concentrations on static/dynamic mechanical properties of carbon fiber reinforced polymer composites. Compos. Part B Eng. 2019, 173, 106910. [Google Scholar] [CrossRef]
- Uğur Yüncüoğlu, E.; Turgut Ince, S.; Bağcı, E. Strength of carbon fiber/epoxy in sea water. Mater. Test. 2021, 63, 811–815. [Google Scholar] [CrossRef]
- Yuan, X.W.; Li, W.G.; Xiao, Z.M.; Zhang, Y.M. Prediction of temperature-dependent transverse strength of carbon fiber reinforced polymer composites by a modified cohesive zone model. Compos. Struct. 2023, 304, 116310. [Google Scholar] [CrossRef]
- Bashtannik, P.I.; Kabak, A.I.; Yakovchuk, Y.Y. The effect of adhesion interaction on the mechanical properties of thermoplastic basalt plastics. Mech. Compos. Mater. 2003, 39, 85–88. [Google Scholar] [CrossRef]
- Bhat, T.; Chevali, V.; Liu, X.; Feih, S.; Mouritz, A.P. Fire structural resistance of basalt fibre composite. Compos. Part A Appl. Sci. Manuf. 2015, 71, 107–115. [Google Scholar] [CrossRef]
- Chen, W.; Hao, H.; Jong, M.; Cui, J.; Shi, Y.; Chen, L.; Pham, T.M. Quasi-static and dynamic tensile properties of basalt fibre reinforced polymer. Compos. Part B Eng. 2017, 125, 123–133. [Google Scholar] [CrossRef]
- Fiore, V.; Scalici, T.; Di Bella, G.; Valenza, A. A review on basalt fibre and its composites. Compos. Part B Eng. 2015, 74, 74–94. [Google Scholar] [CrossRef]
- Greco, A.; Maffezzoli, A.; Casciaro, G.; Caretto, F. Mechanical properties of basalt fibers and their adhesion to polypropylene matrices. Compos. Part B Eng. 2014, 67, 233–238. [Google Scholar] [CrossRef]
- Lopresto, V.; Leone, C.; De Iorio, I. Mechanical characterisation of basalt fibre reinforced plastic. Compos. Part B Eng. 2011, 42, 717–723. [Google Scholar] [CrossRef]
- Plappert, D.; Ganzenmüller, G.C.; May, M.; Beisel, S. Mechanical properties of a unidirectional basalt-fiber/epoxy composite. J. Compos. Sci. 2020, 4, 101. [Google Scholar] [CrossRef]
- Scalici, T.; Pitarresi, G.; Badagliacco, D.; Fiore, V.; Valenza, A. Mechanical properties of basalt fiber reinforced composites manufactured with different vacuum assisted impregnation techniques. Compos. Part B Eng. 2016, 104, 35–43. [Google Scholar] [CrossRef]
- Wang, M.; Zhang, Z.; Li, Y.; Li, M.; Sun, Z. Chemical durability and mechanical properties of alkali-proof basalt fiber and its reinforced epoxy composites. J. Reinf. Plast. Compos. 2008, 27, 393–407. [Google Scholar] [CrossRef]
- Xing, D.; Xi, X.-Y.; Ma, P.-C. Factors governing the tensile strength of basalt fibre. Compos. Part A Appl. Sci. Manuf. 2019, 119, 127–133. [Google Scholar] [CrossRef]
- Sim, J.; Park, C.; Moon, D.Y. Characteristics of basalt fiber as a strengthening material for concrete structures. Compos. Part B Eng. 2005, 36, 504–512. [Google Scholar] [CrossRef]
- Elchalakani, M.; Yang, B.; Mao, K.; Pham, T. 2—Mechanical properties of fiber reinforced polymer (frp) and steel bars. In Geopolymer Concrete Structures with Steel and Frp Reinforcements; Elchalakani, M., Yang, B., Mao, K., Pham, T., Eds.; Woodhead Publishing: Sawston, UK, 2023; pp. 75–135. [Google Scholar]
- Puttegowda, M.; Rangappa, S.M.; Jawaid, M.; Shivanna, P.; Basavegowda, Y.; Saba, N. 15—Potential of natural/synthetic hybrid composites for aerospace applications. In Sustainable Composites for Aerospace Applications; Jawaid, M., Thariq, M., Eds.; Woodhead Publishing: Sawston, UK, 2018; pp. 315–351. [Google Scholar]
- Dong, Z.; Han, T.; Zhang, B.; Zhu, H.; Wu, G.; Wei, Y.; Zhang, P. A review of the research and application progress of new types of concrete-filled frp tubular members. Constr. Build. Mater. 2021, 312, 125353. [Google Scholar] [CrossRef]
- Liu, X.; Sun, Y.; Wu, T.; Liu, Y. Flexural cracks in steel fiber-reinforced lightweight aggregate concrete beams reinforced with frp bars. Compos. Struct. 2020, 253, 112752. [Google Scholar] [CrossRef]
- Lotfy, A.; Hossain, K.M.A.; Lachemi, M. Durability properties of lightweight self-consolidating concrete developed with three types of aggregates. Constr. Build. Mater. 2016, 106, 43–54. [Google Scholar] [CrossRef]
- Polat, R.; Demirboğa, R.; Karakoç, M.B.; Türkmen, İ. The influence of lightweight aggregate on the physico-mechanical properties of concrete exposed to freeze–thaw cycles. Cold Reg. Sci. Technol. 2010, 60, 51–56. [Google Scholar] [CrossRef]
- Zhang, B.; Zhu, H.; Dong, Z.; Yang, Z. Mechanical properties and durability of frp-reinforced coral aggregate concrete structures: A critical review. Mater. Today Commun. 2023, 35, 105656. [Google Scholar] [CrossRef]
- Duic, J.; Kenno, S.; Das, S. Performance of concrete beams reinforced with basalt fibre composite rebar. Constr. Build. Mater. 2018, 176, 470–481. [Google Scholar] [CrossRef]
- Kassem, C.; Farghaly Ahmed, S.; Benmokrane, B. Evaluation of flexural behavior and serviceability performance of concrete beams reinforced with frp bars. J. Compos. Constr. 2011, 15, 682–695. [Google Scholar] [CrossRef]
- Thiagarajan, G. Experimental and analytical behavior of carbon fiber-based rods as flexural reinforcement. J. Compos. Constr. 2003, 7, 64–72. [Google Scholar] [CrossRef]
- Toutanji, H.; Deng, Y. Deflection and crack-width prediction of concrete beams reinforced with glass frp rods. Constr. Build. Mater. 2003, 17, 69–74. [Google Scholar] [CrossRef]
- Tan, H.; Hou, Z.; Li, Y.; Xu, X. A flexural ductility model for uhpc beams reinforced with frp bars. Structures 2022, 45, 773–786. [Google Scholar] [CrossRef]
- Yoo, D.-Y.; Banthia, N.; Yoon, Y.-S. Flexural behavior of ultra-high-performance fiber-reinforced concrete beams reinforced with gfrp and steel rebars. Eng. Struct. 2016, 111, 246–262. [Google Scholar] [CrossRef]
- Yoo, D.-Y.; Banthia, N.; Yoon, Y.-S. Predicting service deflection of ultra-high-performance fiber-reinforced concrete beams reinforced with gfrp bars. Compos. Part B Eng. 2016, 99, 381–397. [Google Scholar] [CrossRef]
- Maranan, G.B.; Manalo, A.C.; Benmokrane, B.; Karunasena, W.; Mendis, P. Evaluation of the flexural strength and serviceability of geopolymer concrete beams reinforced with glass-fibre-reinforced polymer (gfrp) bars. Eng. Struct. 2015, 101, 529–541. [Google Scholar] [CrossRef]
- Rahman, S.K.; Al-Ameri, R. Structural assessment of basalt frp reinforced self-compacting geopolymer concrete using artificial neural network (ann) modelling. Constr. Build. Mater. 2023, 397, 132464. [Google Scholar] [CrossRef]
- Akhnoukh, A.K.; Buckhalter, C. Ultra-high-performance concrete: Constituents, mechanical properties, applications and current challenges. Case Stud. Constr. Mater. 2021, 15, e00559. [Google Scholar] [CrossRef]
- Bahmani, H.; Mostofinejad, D. Microstructure of ultra-high-performance concrete (uhpc)—A review study. J. Build. Eng. 2022, 50, 104118. [Google Scholar] [CrossRef]
- Ferrier, E.; Michel, L.; Zuber, B.; Chanvillard, G. Mechanical behaviour of ultra-high-performance short-fibre-reinforced concrete beams with internal fibre reinforced polymer bars. Compos. Part B Eng. 2015, 68, 246–258. [Google Scholar] [CrossRef]
- Han, S.; Zhou, A.; Ou, J. Relationships between interfacial behavior and flexural performance of hybrid steel-frp composite bars reinforced seawater sea-sand concrete beams. Compos. Struct. 2021, 277, 114672. [Google Scholar] [CrossRef]
- Su, C.; Wang, X.; Ding, L.; Chen, Z.; Liu, S.; Wu, Z. Experimental study on the seismic behavior of seawater sea sand concrete beams reinforced with steel-frp composite bars. Eng. Struct. 2021, 248, 113269. [Google Scholar] [CrossRef]
- Hognestad, E.; Hanson, N.W.; McHenry, D.; McHenry, D. Concrete Stress Distribution in Ultimate Strength Design; Portland Cement Association, Research and Development Laboratories: Skokie, IL, USA, 1955. [Google Scholar]
- Kent Dudley, C.; Park, R. Flexural members with confined concrete. J. Struct. Div. 1971, 97, 1969–1990. [Google Scholar] [CrossRef]
- Popovics, S. A numerical approach to the complete stress-strain curve of concrete. Cem. Concr. Res. 1973, 3, 583–599. [Google Scholar] [CrossRef]
- Sargin, M.; Ghosh, S.K.; Handa, V.K. Effects of lateral reinforcement upon the strength and deformation properties of concrete. Mag. Concr. Res. 1971, 23, 99–110. [Google Scholar] [CrossRef]
- Wee, T.H.; Chin, M.S.; Mansur, M.A. Stress-strain relationship of high-strength concrete in compression. J. Mater. Civ. Eng. 1996, 8, 70–76. [Google Scholar] [CrossRef]
- Nepomuceno, E.; Sena-Cruz, J.; Correia, L.; D’Antino, T. Review on the bond behavior and durability of frp bars to concrete. Constr. Build. Mater. 2021, 287, 123042. [Google Scholar] [CrossRef]
- Cosenza, E.; Manfredi, G.; Realfonzo, R. Behavior and modeling of bond of frp rebars to concrete. J. Compos. Constr. 1997, 1, 40–51. [Google Scholar] [CrossRef]
- El-Nemr, A.; Ahmed, E.A.; Barris, C.; Joyklad, P.; Hussain, Q.; Benmokrane, B. Bond performance of fiber reinforced polymer bars in normal- and high-strength concrete. Constr. Build. Mater. 2023, 393, 131957. [Google Scholar] [CrossRef]
- Gooranorimi, O.; Suaris, W.; Nanni, A. A model for the bond-slip of a gfrp bar in concrete. Eng. Struct. 2017, 146, 34–42. [Google Scholar] [CrossRef]
- Tighiouart, B.; Benmokrane, B.; Gao, D. Investigation of bond in concrete member with fibre reinforced polymer (frp) bars. Constr. Build. Mater. 1998, 12, 453–462. [Google Scholar] [CrossRef]
- Brad, W.W.; Carol, K.S. Development length of glass fiber-reinforced polymer bars in concrete. ACI Struct. J. 2006, 103, 11. [Google Scholar]
- San-José, J.T.; Vegas, I.; Meyer, F. Structural analysis of frp reinforced polymer concrete material. Constr. Build. Mater. 2006, 20, 971–981. [Google Scholar] [CrossRef]
- Escórcio, P.; França, P.M. Experimental study of a rehabilitation solution that uses gfrp bars to replace the steel bars of reinforced concrete beams. Eng. Struct. 2016, 128, 166–183. [Google Scholar] [CrossRef]
- He, Z.; Ou, J.; Wang, B. The trilinear moment vs. Curvature relationship of concrete beams reinforced with fiber reinforced polymer (frp) rebars. Compos. Struct. 2007, 77, 30–35. [Google Scholar] [CrossRef]
- Lau, D.; Pam, H.J. Experimental study of hybrid frp reinforced concrete beams. Eng. Struct. 2010, 32, 3857–3865. [Google Scholar] [CrossRef]
- Maranan, G.B.; Manalo, A.C.; Benmokrane, B.; Karunasena, W.; Mendis, P.; Nguyen, T.Q. Flexural behavior of geopolymer-concrete beams longitudinally reinforced with gfrp and steel hybrid reinforcements. Eng. Struct. 2019, 182, 141–152. [Google Scholar] [CrossRef]
- Pawłowski, D.; Szumigała, M. Flexural behaviour of full-scale basalt frp rc beams—Experimental and numerical studies. Procedia Eng. 2015, 108, 518–525. [Google Scholar] [CrossRef]
- Cai, J.; Pan, J.; Zhou, X. Flexural behavior of basalt frp reinforced ecc and concrete beams. Constr. Build. Mater. 2017, 142, 423–430. [Google Scholar] [CrossRef]
- De Domenico, D.; Pisano, A.A.; Fuschi, P. A fe-based limit analysis approach for concrete elements reinforced with frp bars. Compos. Struct. 2014, 107, 594–603. [Google Scholar] [CrossRef]
- Mohamed, K.; Farghaly, A.S.; Benmokrane, B.; Neale, K.W. Nonlinear finite-element analysis for the behavior prediction and strut efficiency factor of gfrp-reinforced concrete deep beams. Eng. Struct. 2017, 137, 145–161. [Google Scholar] [CrossRef]
- Yang, W.-r.; He, X.-j.; Dai, L. Damage behaviour of concrete beams reinforced with gfrp bars. Compos. Struct. 2017, 161, 173–186. [Google Scholar] [CrossRef]
- Khodaie, S.; Matta, F.; Alnaggar, M. Discrete meso-scale modeling and simulation of shear response of scaled glass frp reinforced concrete beams without stirrups. Eng. Fract. Mech. 2019, 216, 106486. [Google Scholar] [CrossRef]
- Concha, N.C. Neural network model for bond strength of frp bars in concrete. Structures 2022, 41, 306–317. [Google Scholar] [CrossRef]
- Murad, Y.; Tarawneh, A.; Arar, F.; Al-Zu’bi, A.; Al-Ghwairi, A.; Al-Jaafreh, A.; Tarawneh, M. Flexural strength prediction for concrete beams reinforced with frp bars using gene expression programming. Structures 2021, 33, 3163–3172. [Google Scholar] [CrossRef]
- GB50010-2010; Code for Design of Concrete Structures. Chinese Standard: Beijing, China, 2010.
- Cusatis, G.; Mencarelli, A.; Pelessone, D.; Baylot, J. Lattice discrete particle model (ldpm) for failure behavior of concrete. II: Calibration and validation. Cem. Concr. Compos. 2011, 33, 891–905. [Google Scholar] [CrossRef]
- Cusatis, G.; Pelessone, D.; Mencarelli, A. Lattice discrete particle model (ldpm) for failure behavior of concrete. I: Theory. Cem. Concr. Compos. 2011, 33, 881–890. [Google Scholar] [CrossRef]
- Jin, C.; Buratti, N.; Stacchini, M.; Savoia, M.; Cusatis, G. Lattice discrete particle modeling of fiber reinforced concrete: Experiments and simulations. Eur. J. Mech. —A/Solids 2016, 57, 85–107. [Google Scholar] [CrossRef]
- Li, Y.; Yao, W.; Yu, Y.; He, H. A three dimension lattice-spring model with rotational degree of freedom and its application in fracture simulation of elastic brittle materials. Int. J. Solids Struct. 2020, 202, 208–216. [Google Scholar] [CrossRef]
- Huang, L.; Chen, J.; Tan, X. Bp-ann based bond strength prediction for frp reinforced concrete at high temperature. Eng. Struct. 2022, 257, 114026. [Google Scholar] [CrossRef]
- Nguyen, H.D.; Zhang, Q.; Choi, E.; Duan, W. An improved deflection model for frp rc beams using an artificial intelligence-based approach. Eng. Struct. 2020, 219, 110793. [Google Scholar] [CrossRef]
- ACI440.1R-15; Guide for the Design and Construction of Structural Concrete Reinforced with Fiber—Reinforced Polymer (frp) bars. American Concrete Institute: Farmington Hills, MI, USA, 2015.
- CEB-FIB. Frp Reinforcement in rc Structures; Fib International: Lausanne, Switzerland, 2007. [Google Scholar]
- CSA-S806; Design and Construction of Building Components with Fiber-Reinforced Polymers. Canadian Standards Association: Toronto, ON, Canada, 2007.
- Tran, H. 93 frp rc Beams. 2025. Available online: https://drive.google.com/file/d/12KkVluClvDYDoyWxpfV1rfh4NeRMGu_r/view?usp=sharing (accessed on 28 November 2024).

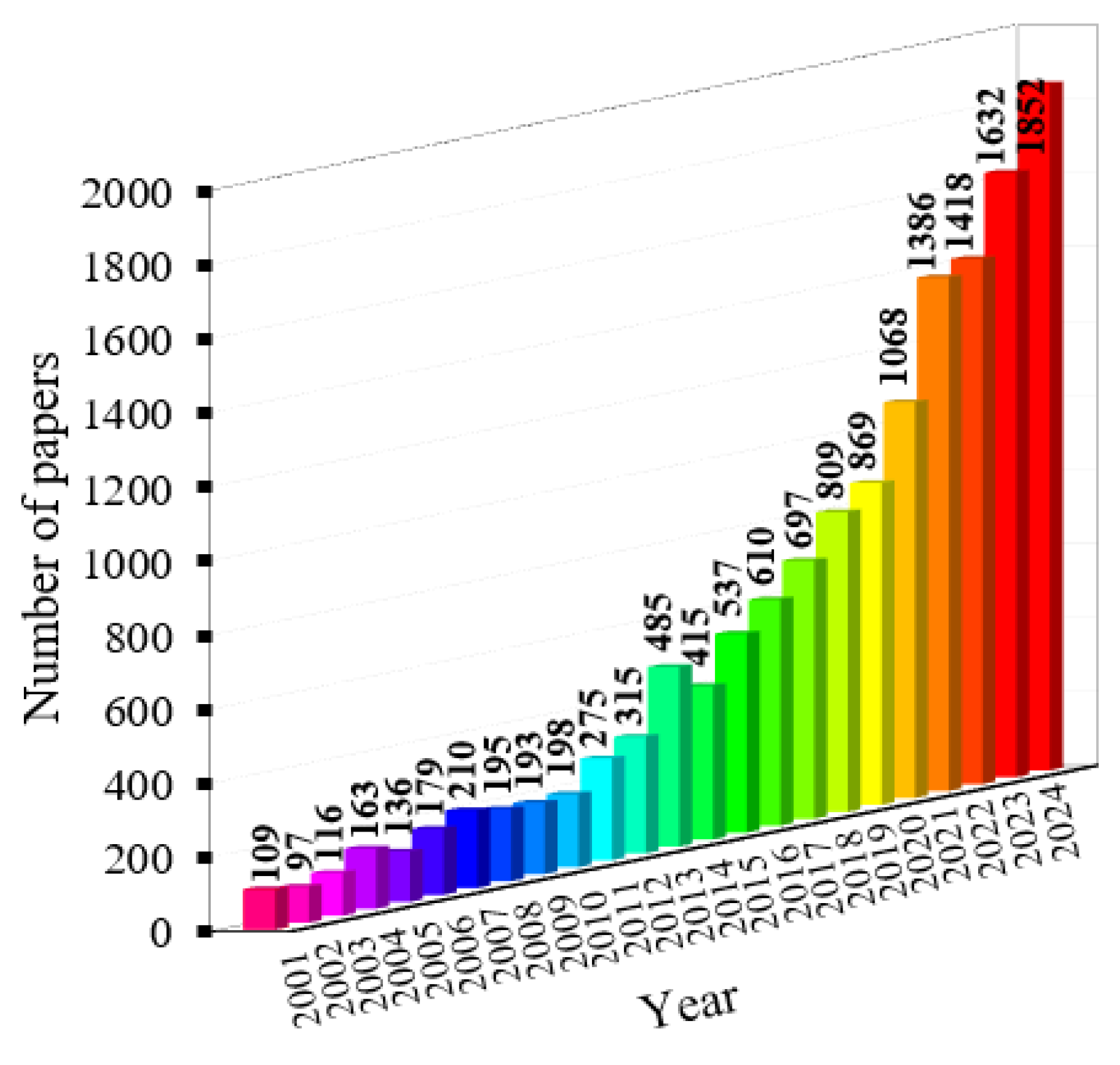


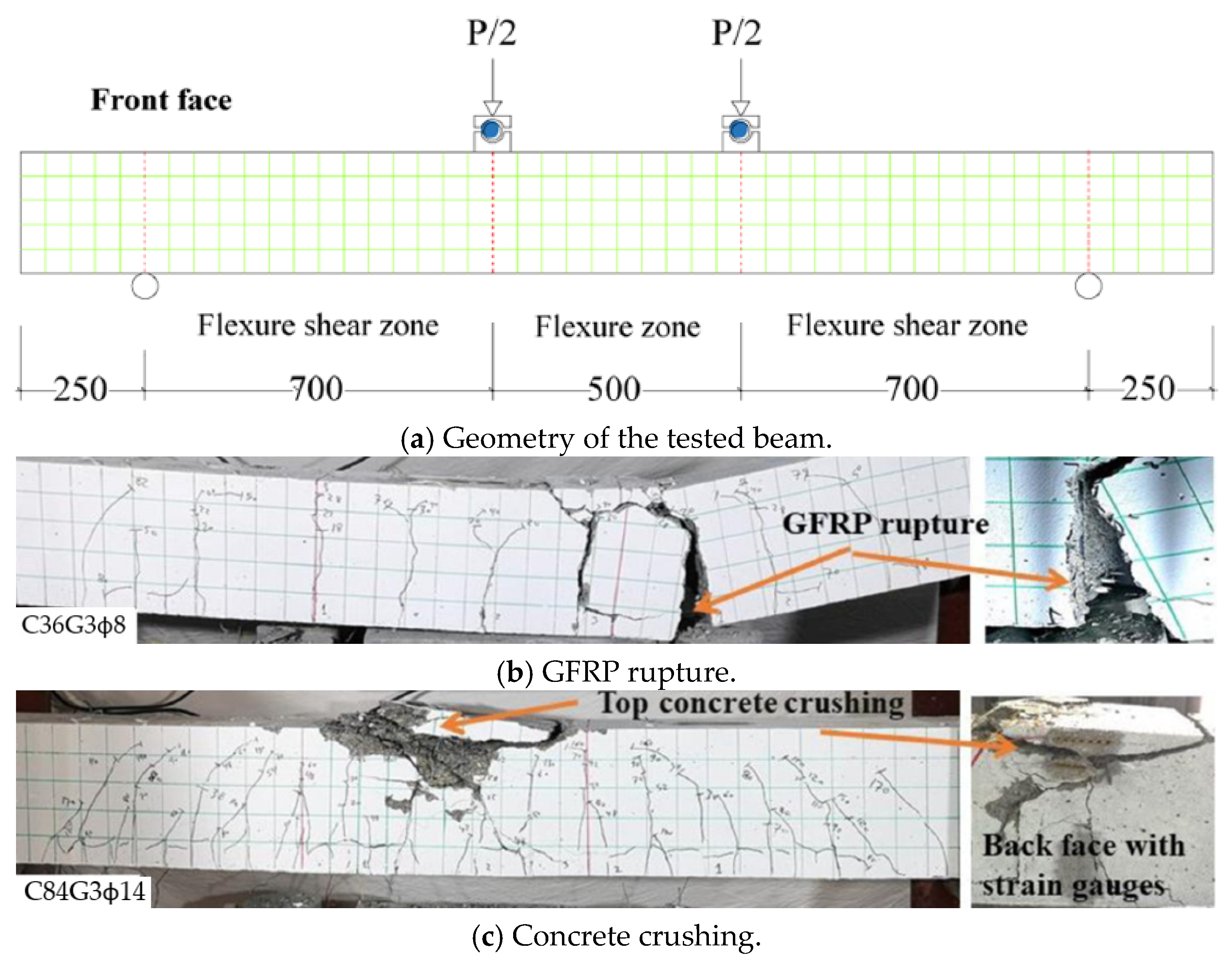
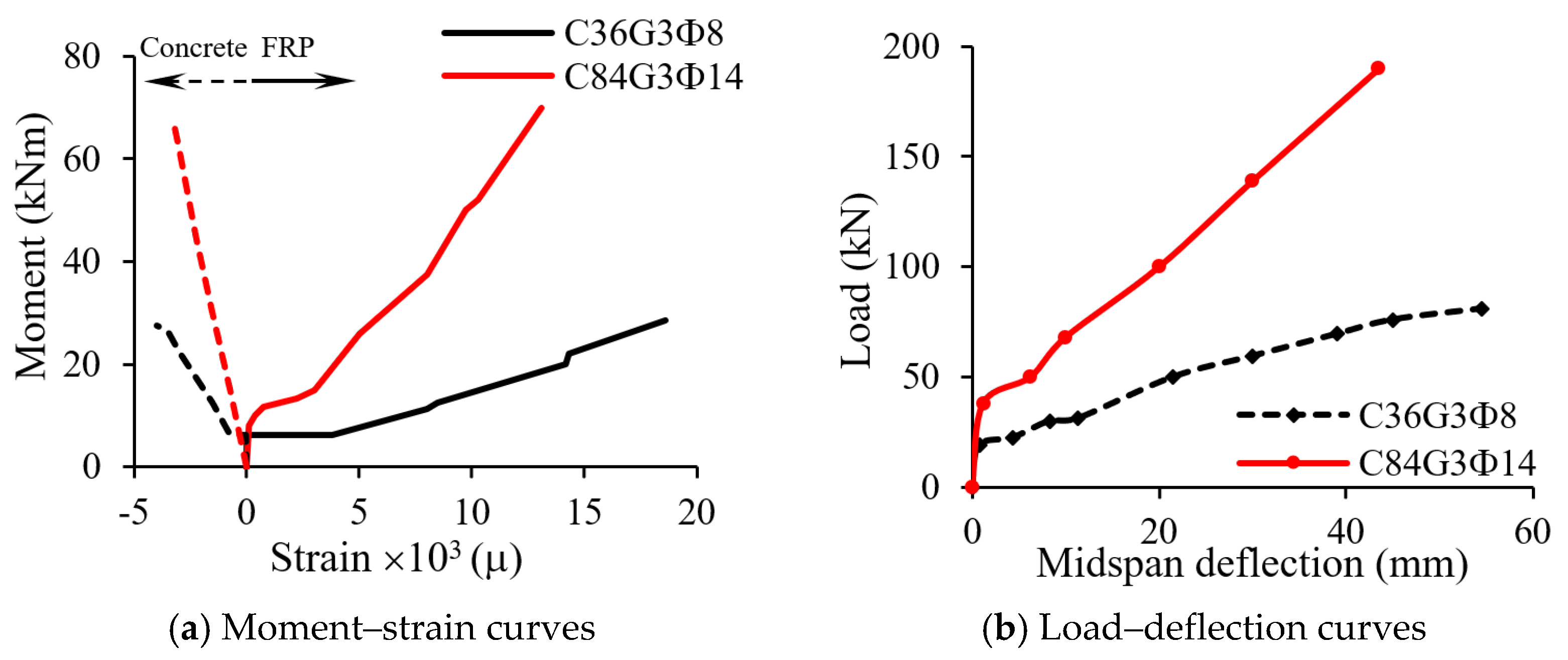

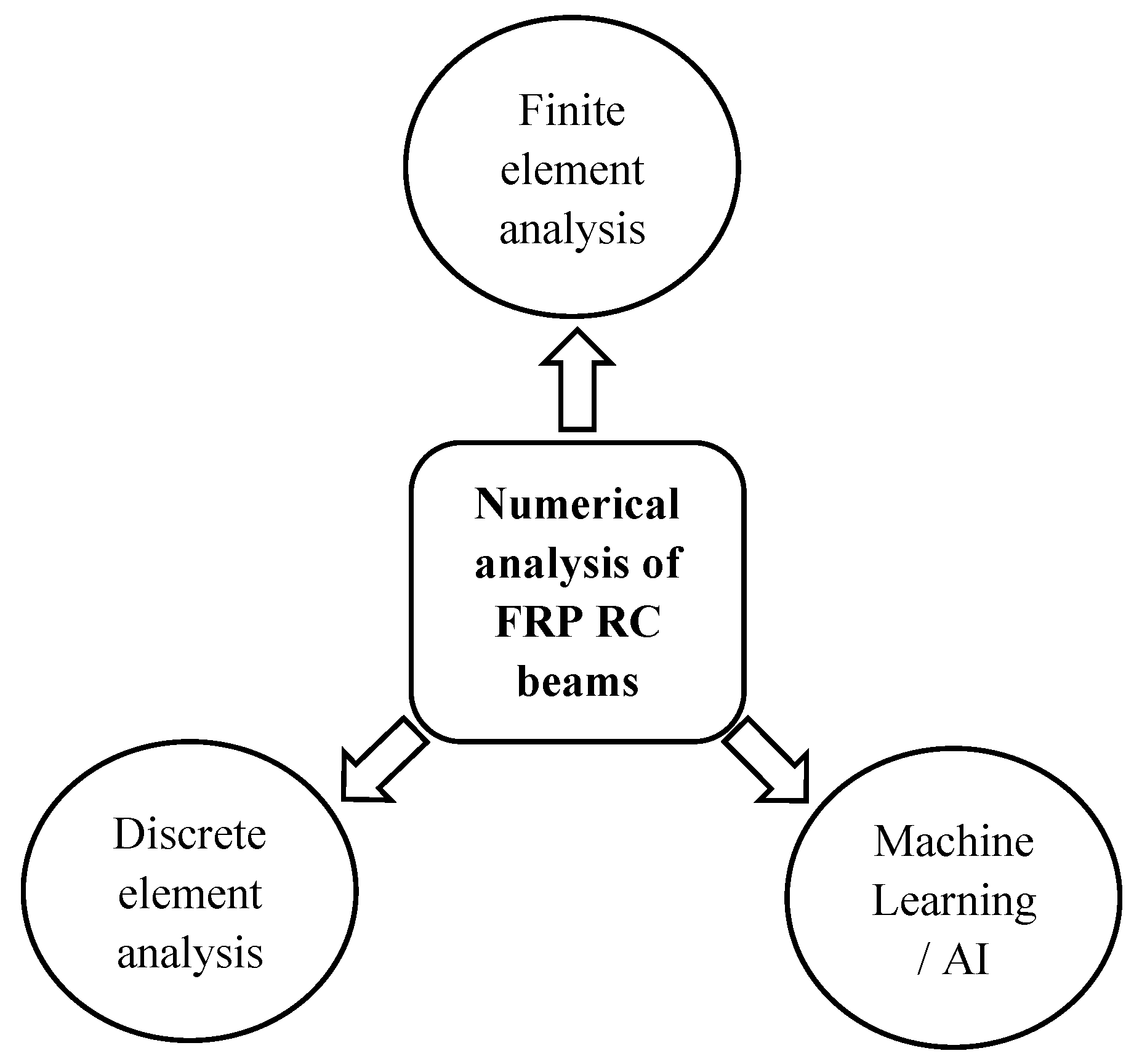

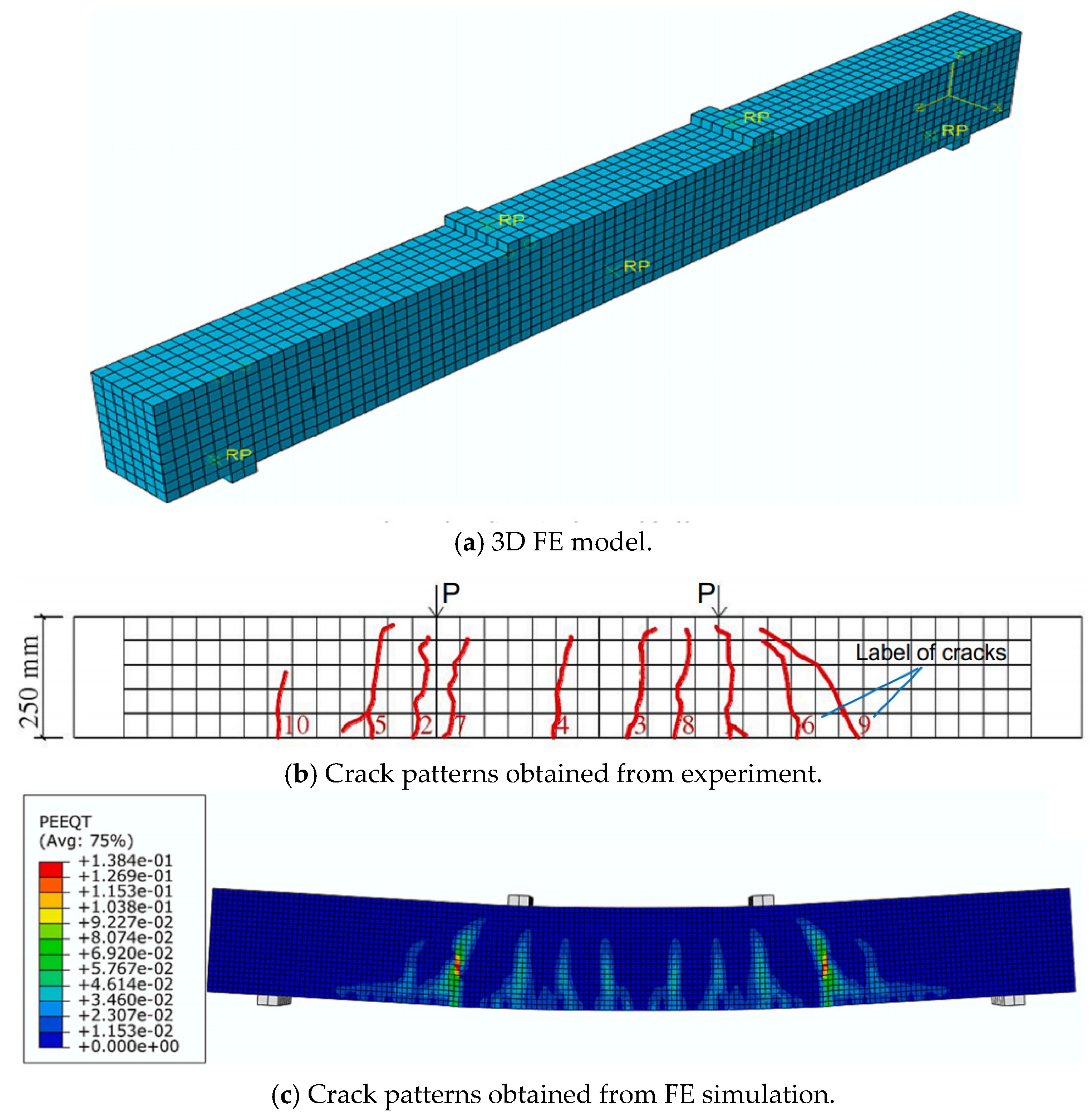

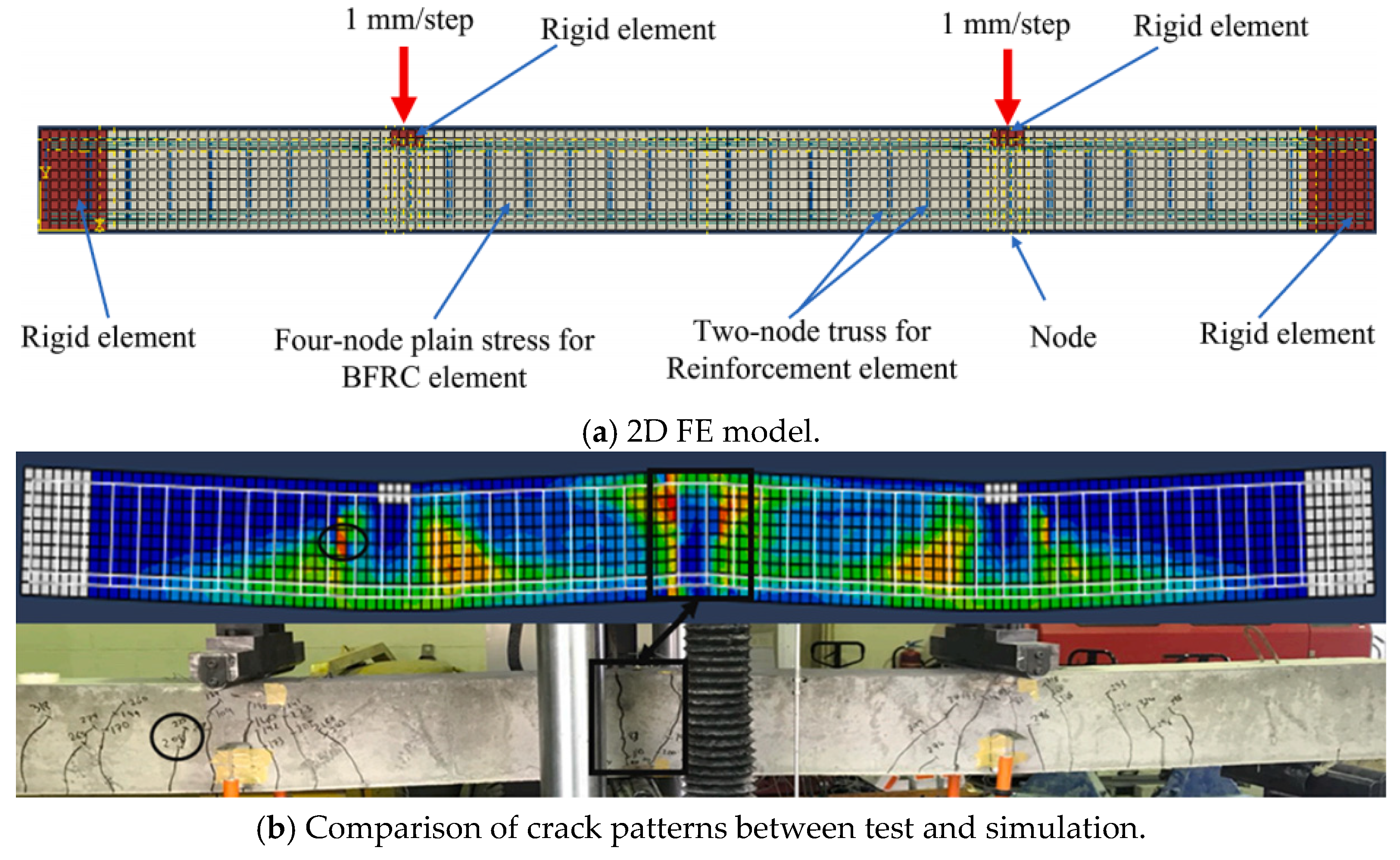
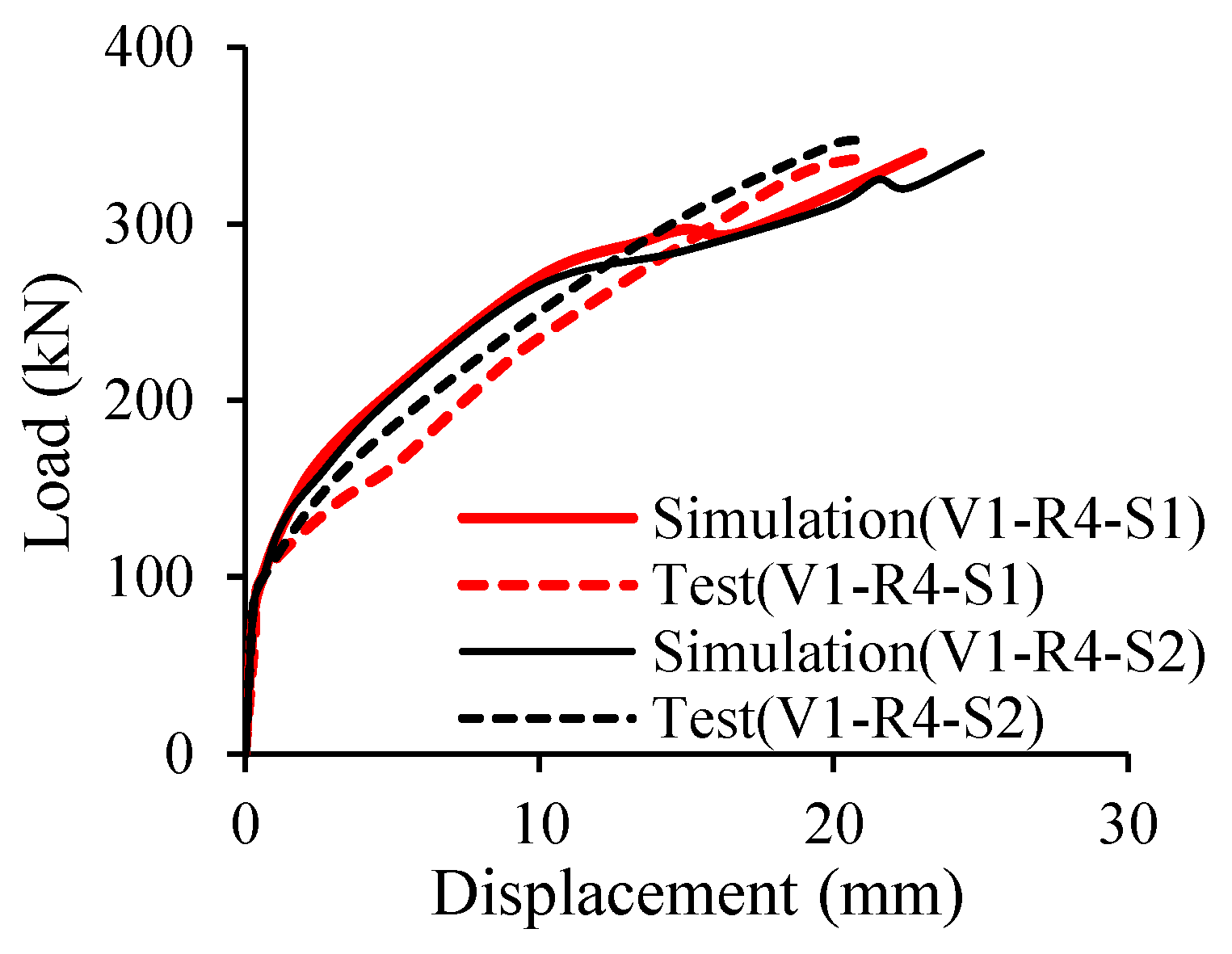

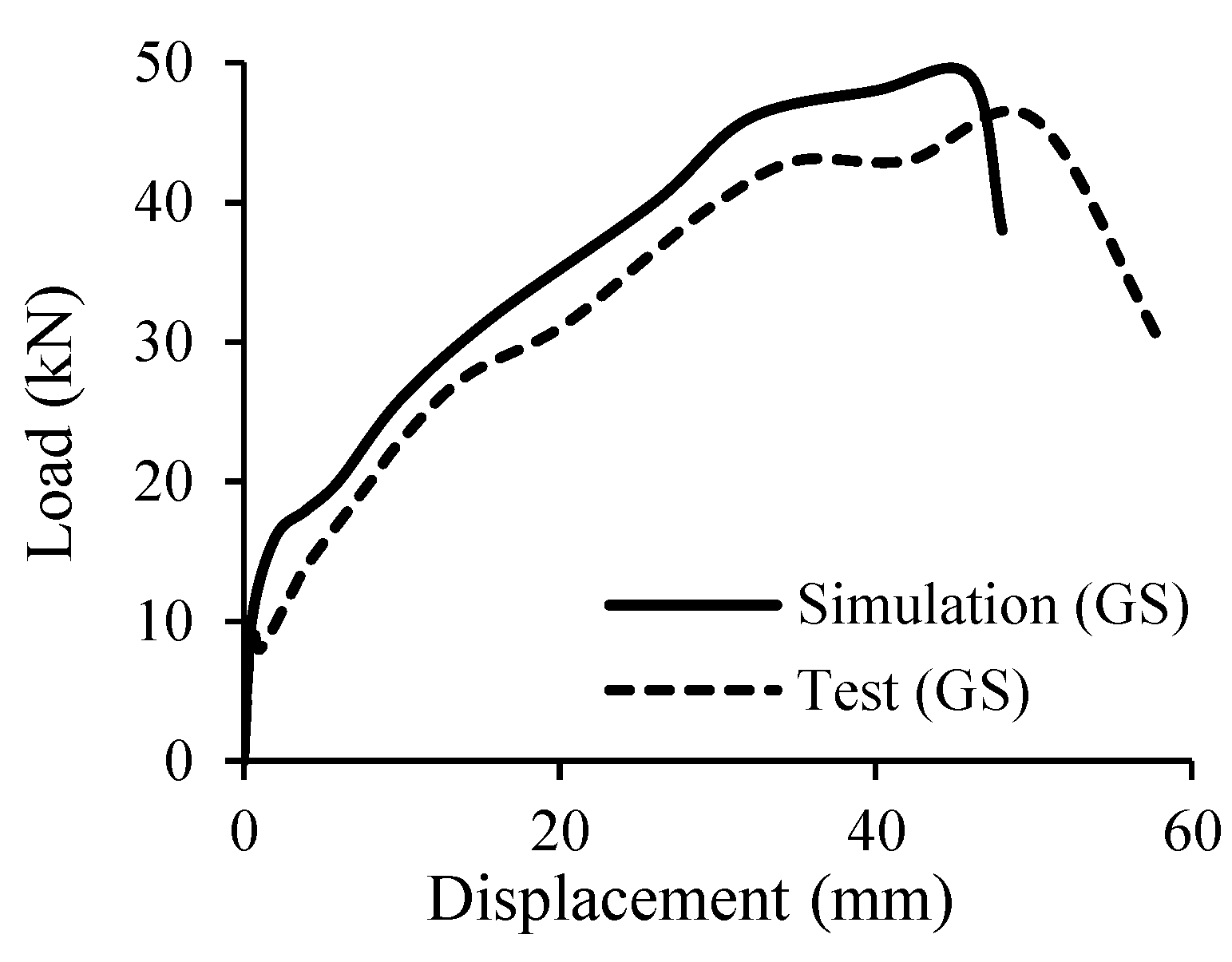
| Types of Bars | Density (kg/m3) | Tensile Strength (MPa) | Young Modulus (GPa) | Price (USD/kg) | Melting Point (°C) | Number of Specimens |
|---|---|---|---|---|---|---|
| GFRP | 1250–2500 | 483–4890 | 35–86.9 | 1.75 | 880 | 67 (72%) |
| CFRP | 1500–2100 | 600–3900 | 37–784 | 11.7 | 1600 | 22 (23.7%) |
| BFRP | 2630–2800 | upto 4840 | 40–110 | 7.6 | 1500–1700 | 2 (2.15%) |
| AFRP | 1250–1450 | 1700–3600 | 41–175 | - | 500 | 2 (2.15%) |
| Steel | 7850 | 250–690 | 200 | 0.6 | 1300–1600 | - |
| Fiber | Density (g/cm3) | Tensile Strength (MPa) | Young’s Modulus (GPa) | Elongation (%) | Coefficient of Thermal Expansion (10−7/°C) |
|---|---|---|---|---|---|
| A-glass | 2.44 | 3310 | 68.9 | 4.8 | 73 |
| AR-glass | 2.7 | 3241 | 73.1 | 4.4 | 65 |
| C-glass | 2.52 | 3310 | 68.9 | 4.8 | 63 |
| D-glass | 2.11–2.14 | 2415 | 51.7 | 4.6 | 25 |
| E-glass | 2.58 | 3445 | 72.3 | 4.8 | 54 |
| EGR-glass | 2.72 | 3445 | 80.3 | 4.8 | 59 |
| R-glass | 2.54 | 4135 | 85.5 | 4.8 | 33 |
| S2-glass | 2.46 | 4890 | 86.9 | 5.7 | 16 |
| σ–ε Relationship | Methodology | Source |
|---|---|---|
| Empirical approach | [109] | |
| Numerical approach | [108] | |
| Empirical approach | [28,107] | |
| Empirical approach | [106] | |
| Empirical approach | [110] |
| Type of Surface | α | β |
|---|---|---|
| Sand coated with deformed surface | 5.24 | 0.33 |
| Deformed surface | 2.57 | 0.54 |
| Sand coated | 3.33 | 0.41 |
| Smooth surface | 0.18 | 0.96 |
| Source | Key Investigated Parameters | Objectives of the Study | Type of Test |
|---|---|---|---|
| [48,51,92] | Type and strength of reinforcement, reinforcement ratio, stirrup ratio, concrete compressive strength. | Evaluate the flexural performance of beams reinforced with FRP in terms of crack patterns, deformability, and failure mode. | Four-point bending, three-point bending. |
| [25,94,104] | Type and strength of reinforcement, reinforcement ratio, surface of reinforcement, compressive strength of concrete. | Explore the bond between FRP bars and concrete. Investigate the behavior and deflection response of FRP-reinforced concrete beams. | Four-point bending, pull-out test. |
| [49,117] | Dosage of aggregates, reinforcement ratio, concrete compressive strength. | Investigate the flexural response of beams reinforced with FRP bars. Propose a model to predict the ultimate moment of FRP beams. | Four-point bending, compression test. |
| [37] | Type and strength of reinforcement, reinforcement ratio, cementitious composite thickness. | Assess the behavior of FRP-reinforced cementitious composite concrete beams in terms of crack width, ultimate load, and failure mode. | Four-point bending. |
| [26,30,34,40,44] | Type and strength of reinforcement, reinforcement ratio, type of concrete. | Investigate the flexural behavior and serviceability performance of BFRP-reinforced normal/high strength concrete beams. | Four-point bending. |
| [88,103] | Type and ratio of reinforcement, span length of beams, steel–fibers ratio, concrete compressive strength. | Investigate the cracking behavior of FRP-reinforced beams. Propose equations to predict crack widths of FRP RC beams. | Four-point bending. |
| [47,95,118] | Reinforcement ratio, concrete compressive strength. | Assess the behavior of FRP-reinforced beams in terms of crack width, ultimate load, and failure mode. Evaluate the design standards. | Four-point bending, three-point bending. |
| [36,93] | Type and strength of reinforcement, reinforcement ratio, surface of reinforcement, compressive strength of concrete. | Investigate the flexural behavior and serviceability performance of FRP-reinforced beams in terms of crack width, ultimate load, and failure mode. Evaluate the design standards. | Four-point bending. |
| Refs. | Numerical Analysis Method | Types of Software | Modeling of Concrete | Parameters | Key Findings |
|---|---|---|---|---|---|
| [19,42,43,46,51,123,124,125,126] | Finite element analysis | ABAQUS v6.13, DIANA v10.4, ATENA v5.4, self-developed program | Concrete damage plasticity model, concrete smear crack model, Fracture plastic model. | Strength of concrete, transverse reinforcement ratio, reinforcement ratio, type of FRP bars, compression yielded block, shear span-to-depth ratio, shear reinforcement, engineering cementitious concrete, and size of loading-plate. | Transverse reinforcements transfer stresses to flexural reinforcements, and they can affect the crack patterns. The bond quality of GFRP in high-strength concrete is higher than that in normal-strength concrete, CY block can increase the strength and ductility of the beam up to 30%, Compressive strength affects the capacity of beams without web reinforcement significantly, BFRP ECC beams were superior to BFRP concrete beams with higher ductility, higher load-carrying capacity, and better crack controlling ability. |
| [127] | Discrete element analysis | Self-developed program | Using the stress–strain relationship of concrete. | Reinforcement ratio, section dimension, and size of loading plate. | The developed program predicted the behavior of FRP RC beams well. |
| [39,128,129] | AI/ML | Self-developed program | Not used | Concrete compressive strength, section dimensions, FRP tensile strength, and elastic modulus. | The developed AI/ML model predicted the capacity of FRP RC beams well. |
| ACI 440.1R | CSA S806 | CEB-FIB | |
|---|---|---|---|
| ρfb | If fc 28 MPa: If fck > 28 MPa: | If fc < 50 MPa: If fc 50 MPa: | |
| MCR (Concrete crushing) | |||
| MFR (FRP rupture) | Not allowed |
| Source | bc (mm) | hc (mm) | fc (MPa) | Af (mm2) | Ef (GPa) | ff (MPa) | Mtest (kNm) |
|---|---|---|---|---|---|---|---|
| Benmokrane et al. [18] | 200 | 300–550 | 43–55 | 573 | 42–49 | 641–689 | 50.6–181.5 |
| Thériault et al. [47] | 130 | 180 | 46.2–97.4 | 237.7–475.3 | 38 | 773 | 19.7–29.5 |
| Thiagarajan [94] | 152.4 | 152.4 | 43.9–53.3 | 63.3–142.4 | 140 | 1900 | 10.2–17.5 |
| Toutanji et al. [95] | 180 | 300 | 35 | 253.4–506.7 | 40 | 695 | 59–71 |
| Ashour [17] | 150 | 200–300 | 34–59 | 56.6–113.1 | 38 | 650 | 5.9–16.8 |
| He et al. [119] | 150 | 300 | 21.3–33.1 | 226.9–314 | 52 | 1230 | 46.6–66.8 |
| Lau et al. [120] | 280 | 380 | 33.9–42.5 | 339.3–1963.5 | 38–40.2 | 582–603 | 80.4–237.9 |
| Kassem et al. [93] | 200 | 300 | 39.1–40.8 | 254.5–1013.4 | 36–122 | 617–1988 | 70.9–90.4 |
| Escorcio et al. [118] | 250 | 400 | 47.9–48.2 | 339–2455 | 60 | 1100–1350 | 85.9–206.2 |
| El-Nemr et al. [36] | 200 | 400 | 29–48 | 258–1194 | 46.4–69.3 | 666–1639 | 81–171 |
| Ahmed et al. [33] | 110 | 300 | 20–50 | 28.27–169.7 | 148 | 2000 | 20.9–67.9 |
| Maranan et al. [99,121] | 200 | 300 | 38.2 | 520–992.8 | 62.6 ̶ 65.6 | 1105–1312 | 91.4–104.8 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tran, H.; Nguyen-Thoi, T.; Dinh, H.-B. State-of-the-Art Review of Studies on the Flexural Behavior and Design of FRP-Reinforced Concrete Beams. Materials 2025, 18, 3295. https://doi.org/10.3390/ma18143295
Tran H, Nguyen-Thoi T, Dinh H-B. State-of-the-Art Review of Studies on the Flexural Behavior and Design of FRP-Reinforced Concrete Beams. Materials. 2025; 18(14):3295. https://doi.org/10.3390/ma18143295
Chicago/Turabian StyleTran, Hau, Trung Nguyen-Thoi, and Huu-Ba Dinh. 2025. "State-of-the-Art Review of Studies on the Flexural Behavior and Design of FRP-Reinforced Concrete Beams" Materials 18, no. 14: 3295. https://doi.org/10.3390/ma18143295
APA StyleTran, H., Nguyen-Thoi, T., & Dinh, H.-B. (2025). State-of-the-Art Review of Studies on the Flexural Behavior and Design of FRP-Reinforced Concrete Beams. Materials, 18(14), 3295. https://doi.org/10.3390/ma18143295








