Methodology for the Early Detection of Damage Using CEEMDAN-Hilbert Spectral Analysis of Ultrasonic Wave Attenuation
Abstract
1. Introduction
- Enhanced Sensitivity to Early Damage: Unlike conventional methods, the proposed technique effectively handles nonlinear, nonstationary ultrasonic signals and resolves decomposition challenges (mode-mixing and noise-sensitivity), significantly improving early damage sensitivity.
- Superior Frequency Resolution: By focusing on ultrasonic wave attenuation, the method achieves a higher frequency resolution, enabling more precise damage characterization in concrete specimens compared to full-structure analyses.
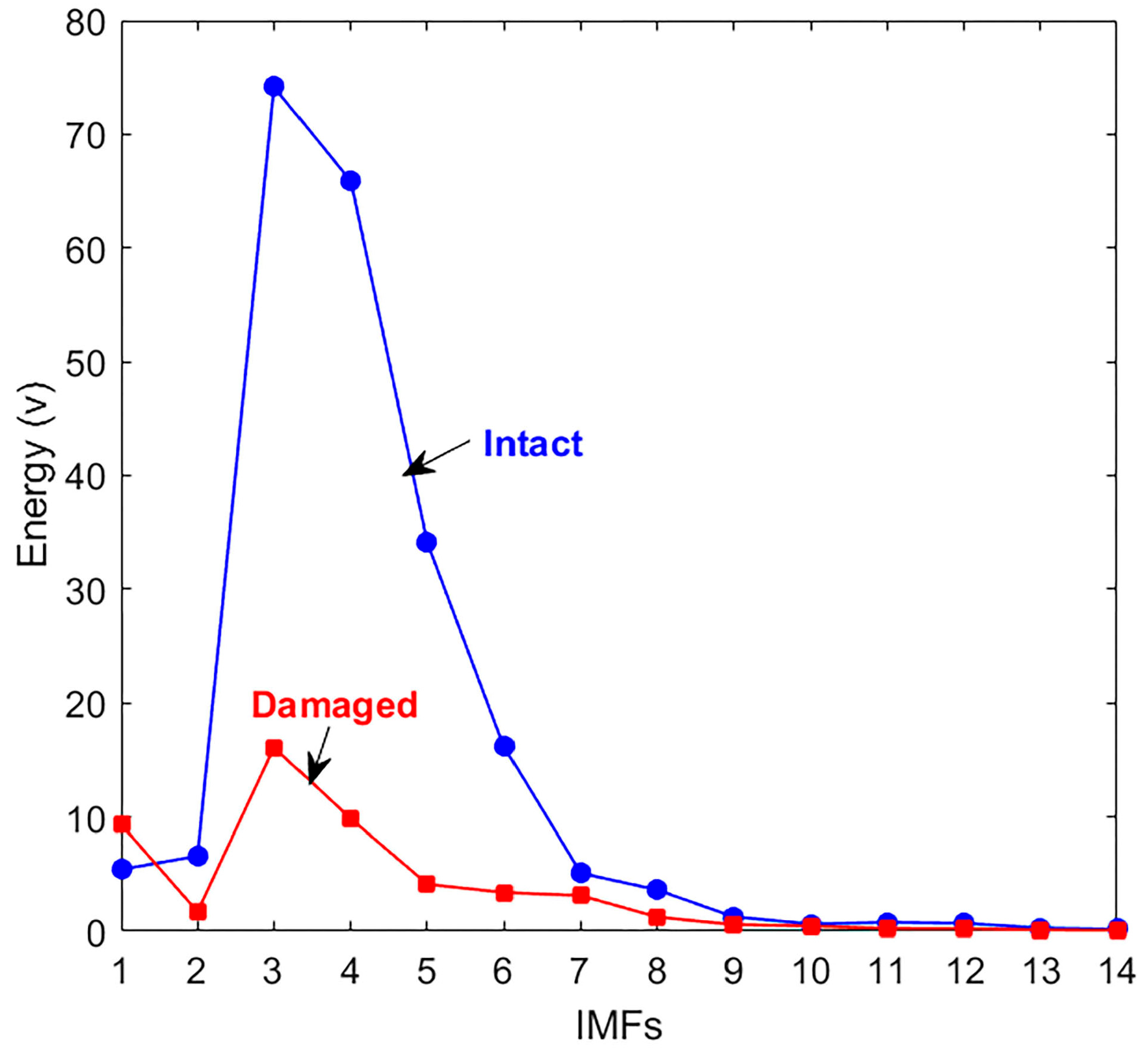
- Energy-Preserving IMF Selection: A systematic selection of the most effective Intrinsic Mode Functions (IMFs) retains over 20% of the original signal’s energy, ensuring meaningful feature extraction while minimizing noise interference.
- Time-Domain Damage Assessment: A modified energy-based damage index exclusively correlates positive IMF energy loss with severity, enabling robust time-domain assessment.
- Experimental Validation and Robustness: The method has been validated on PMMA specimens with controlled cracks and on concrete under freeze–thaw cycles, demonstrating its robustness. A dedicated CEEMDAN repeatability analysis confirms consistency under noise, reinforcing reliability.
2. Methods
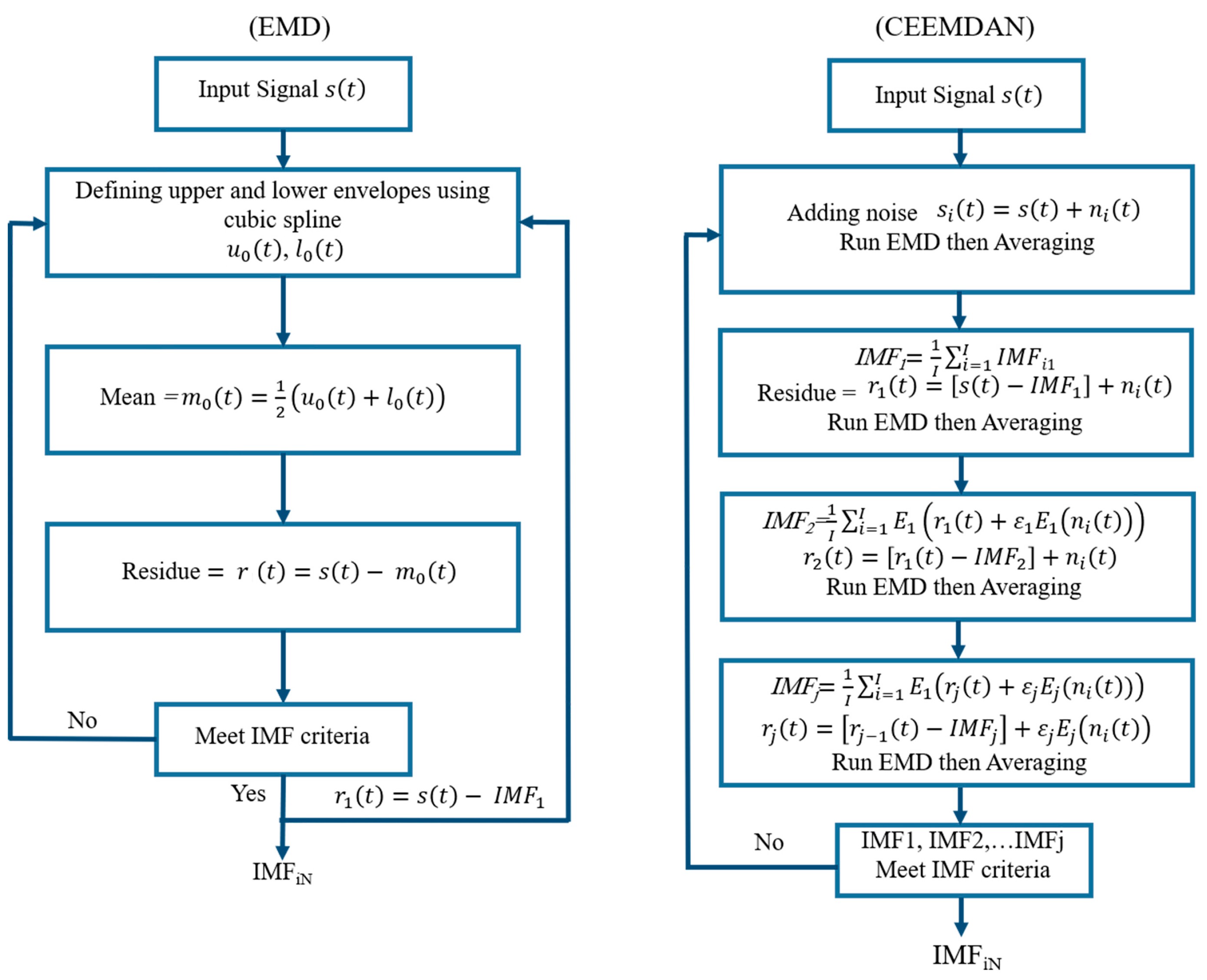
2.1. Hilbert–Huang Transform (HHT)
2.1.1. Complete Ensemble Empirical Mode Decomposition with Adaptive Noise (CEEMDAN)
2.1.2. Hilbert Spectral Analysis (HSA)
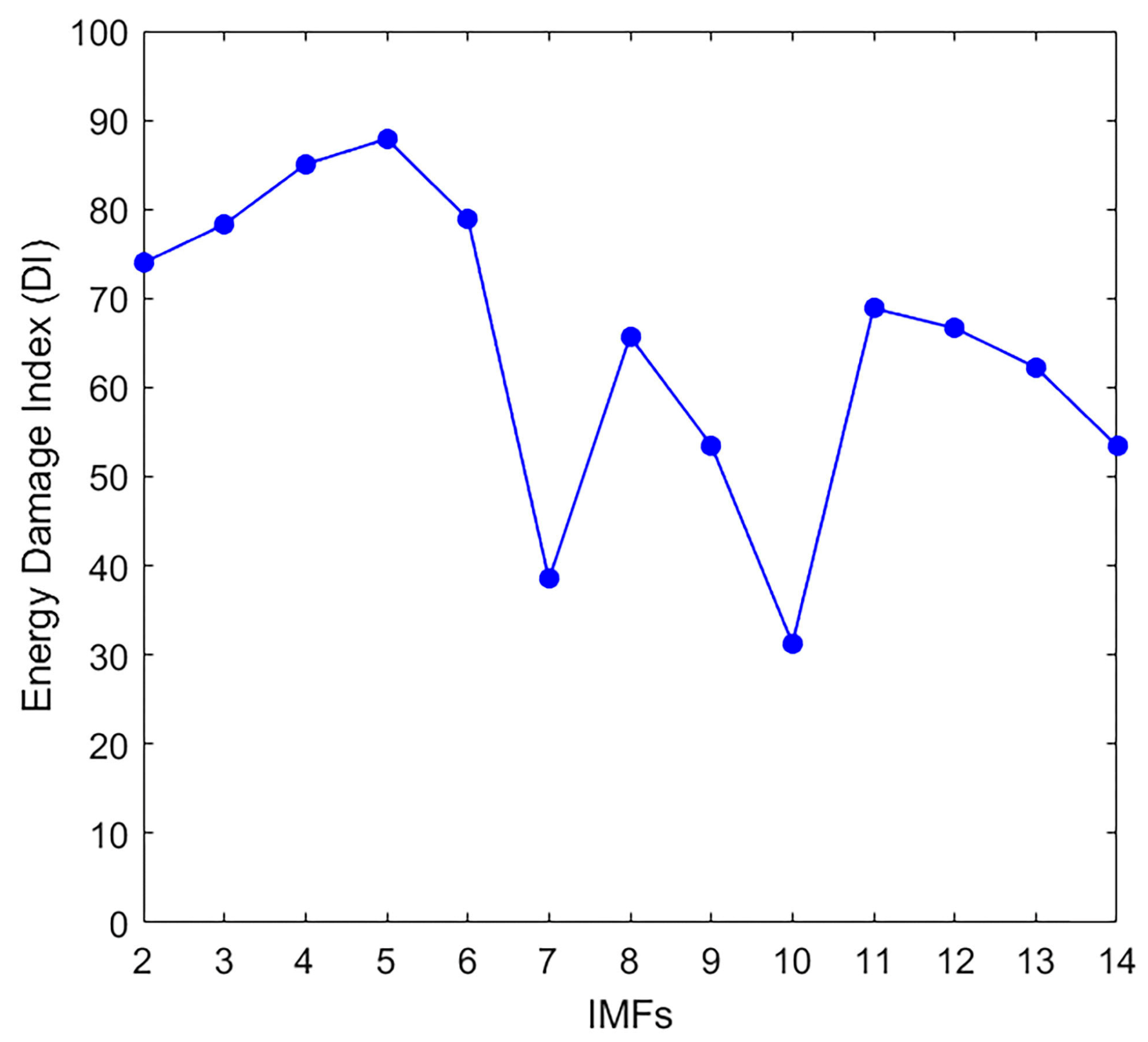
2.2. Selection of the Effective IMFs
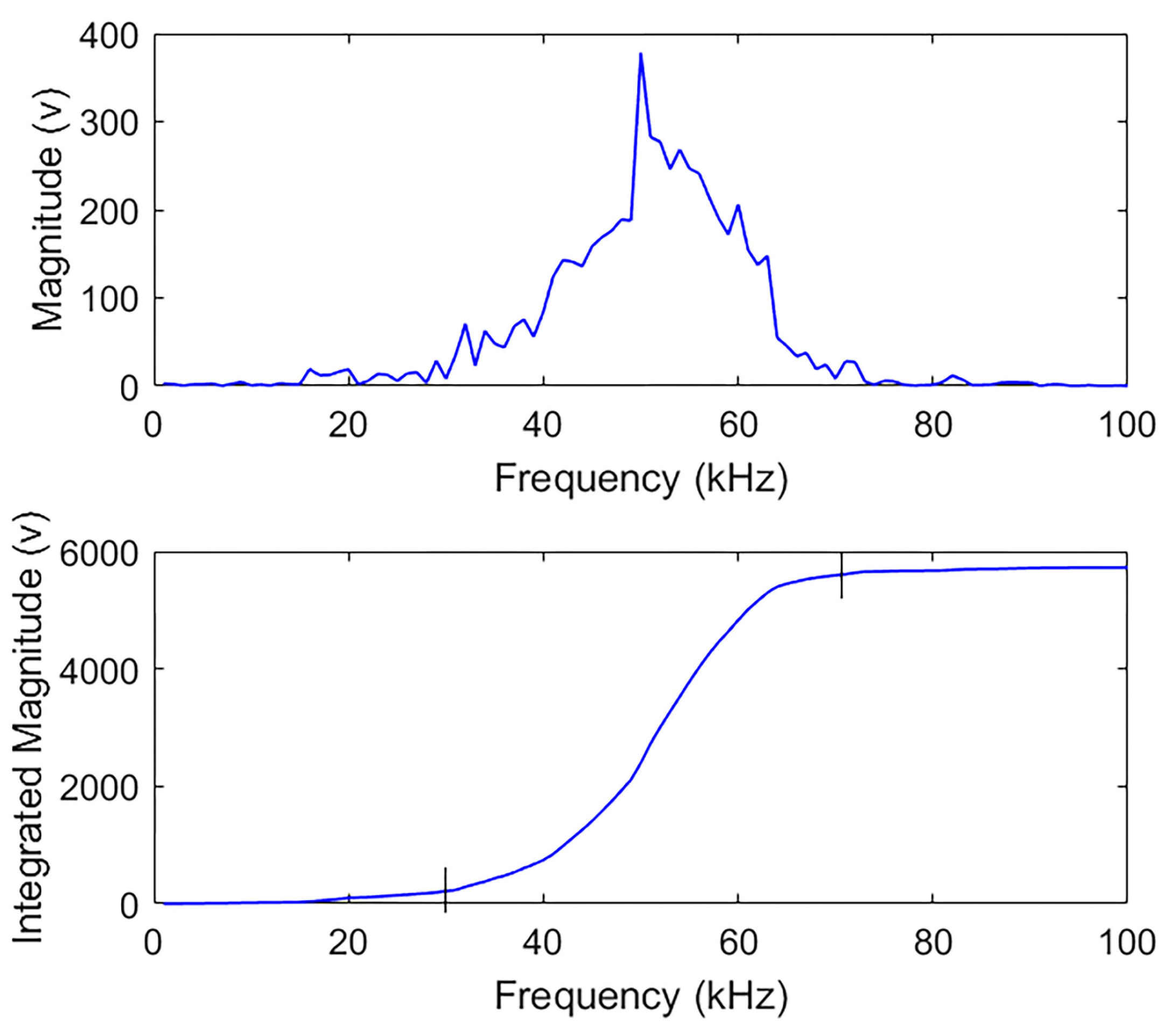
2.3. Damage Index (DI)
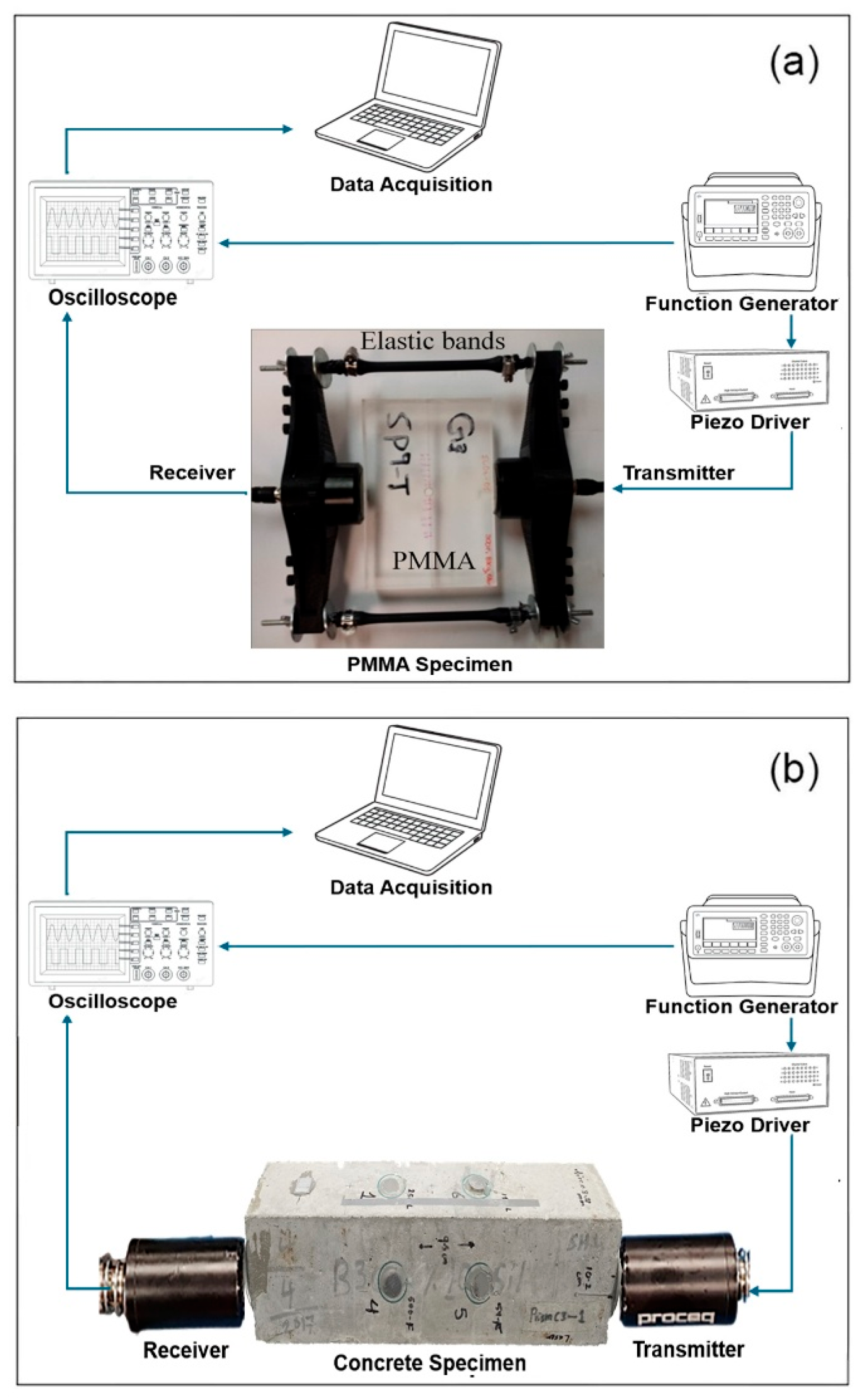
3. Experimental Procedure
3.1. Methodology
3.2. Experimental Setup
4. Results and Discussion
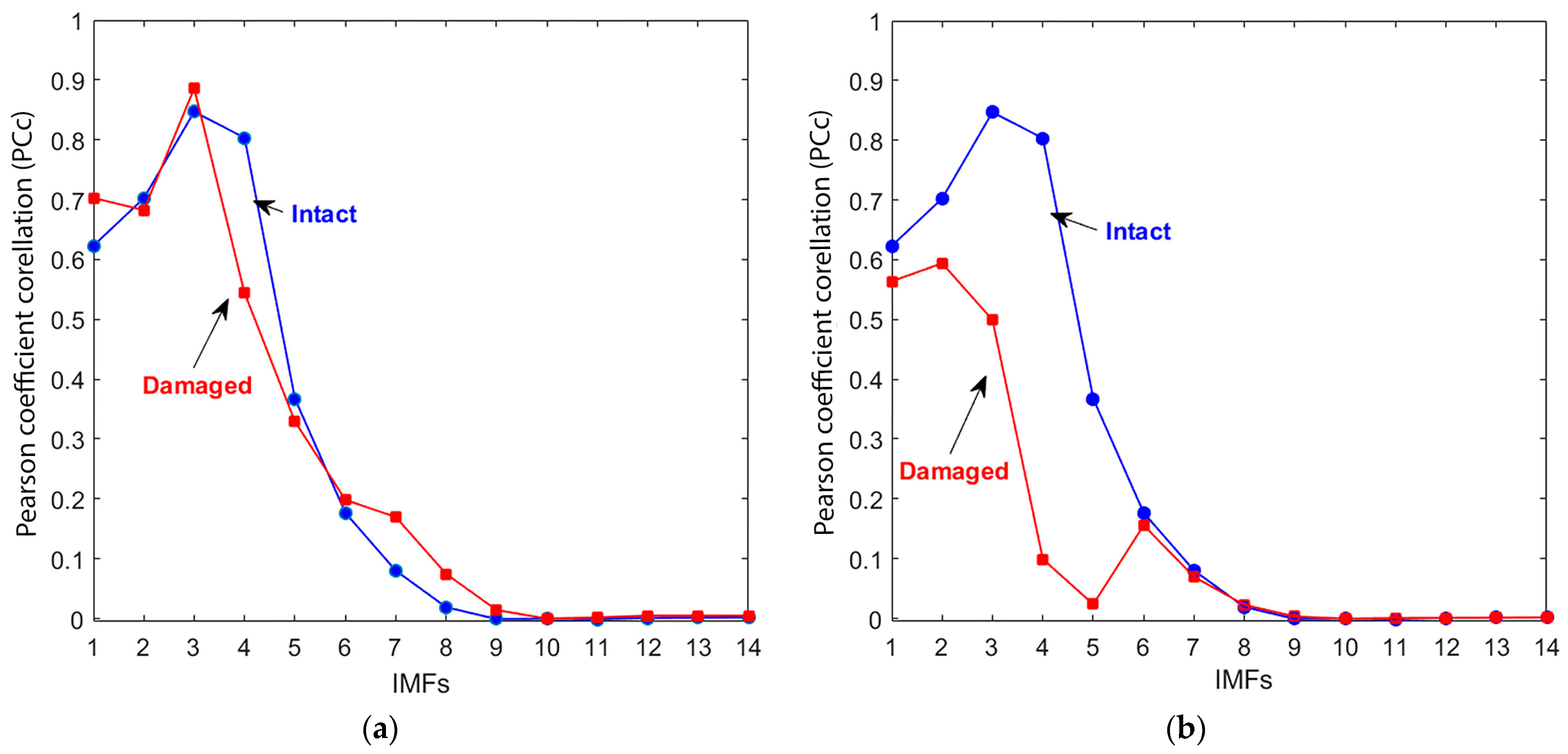
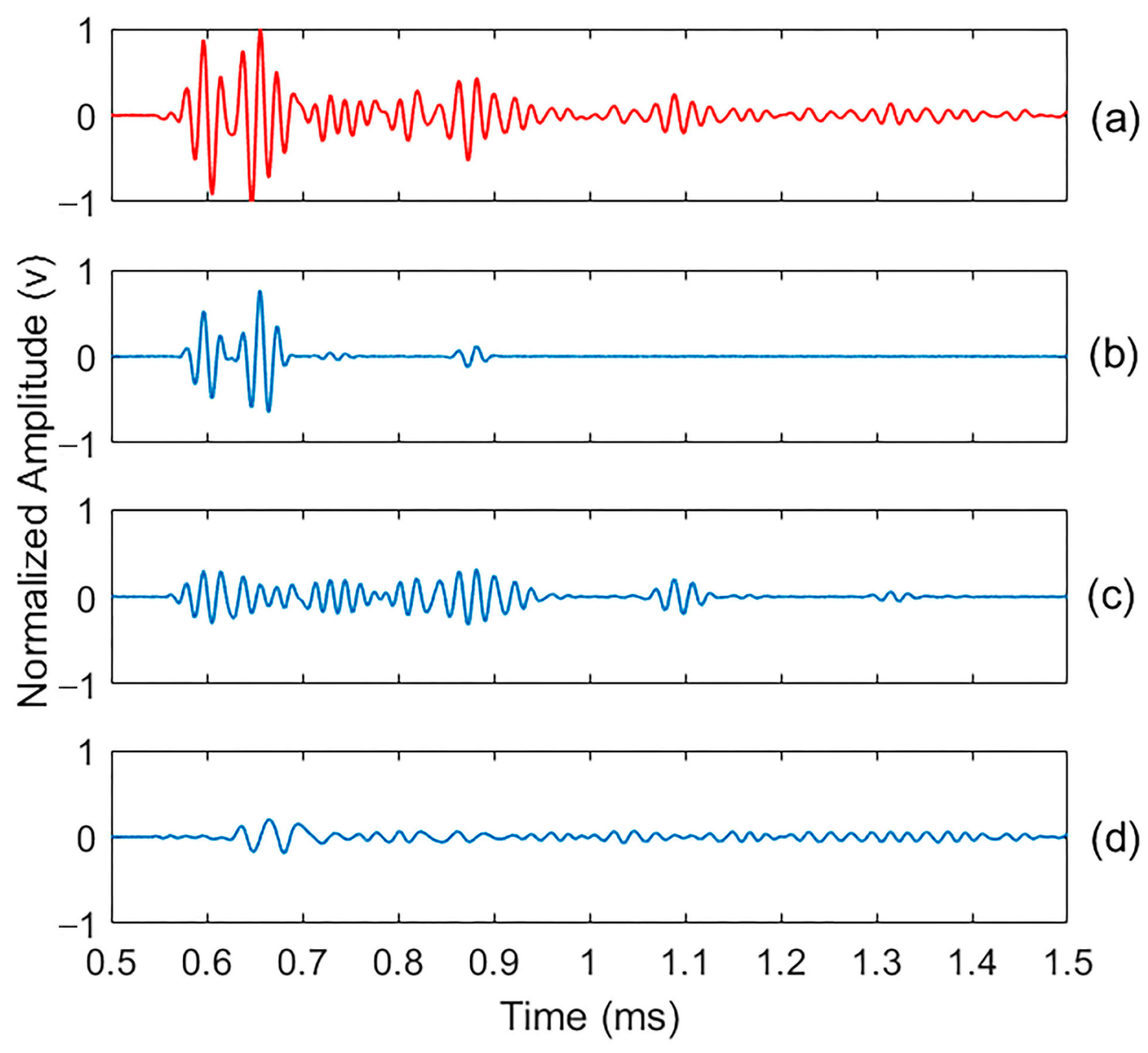
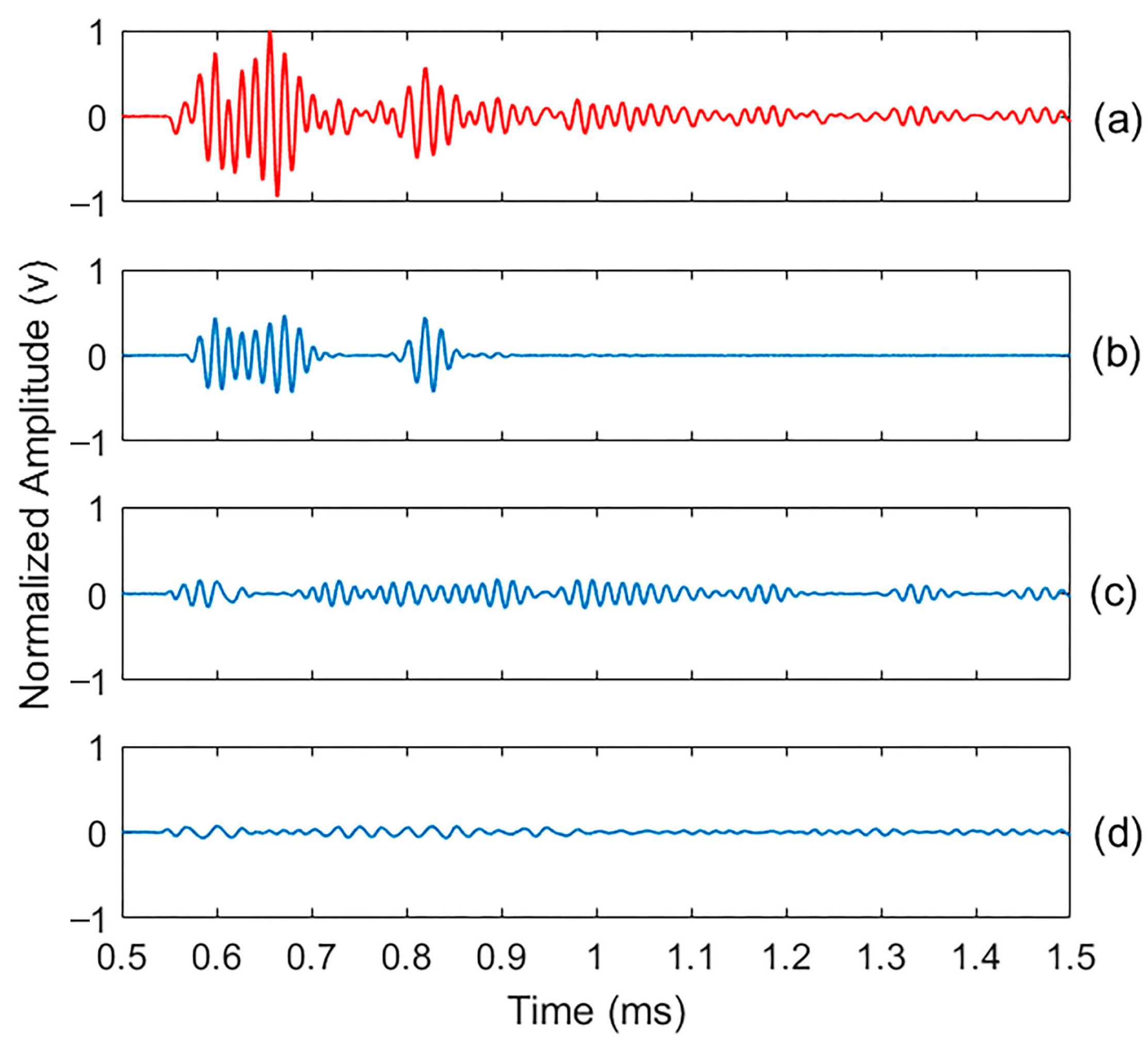
4.1. Validation of Decomposition Completeness
4.2. Testing of HHT on PMMA Samples
4.3. Application of HHT in Concrete Samples
4.3.1. Damage Identification in Time Domain
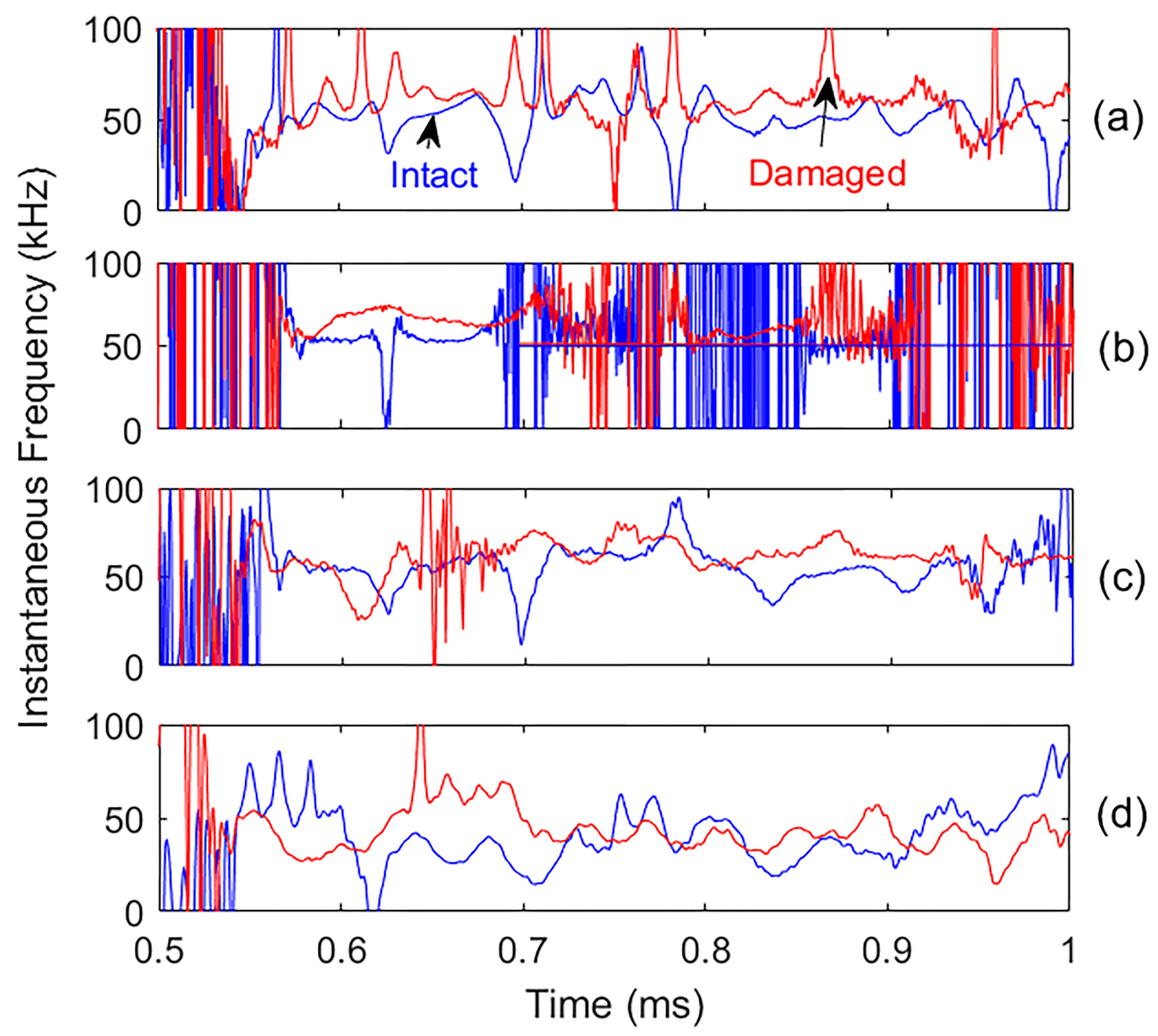
4.3.2. Damage Identification in Time–Frequency Domain
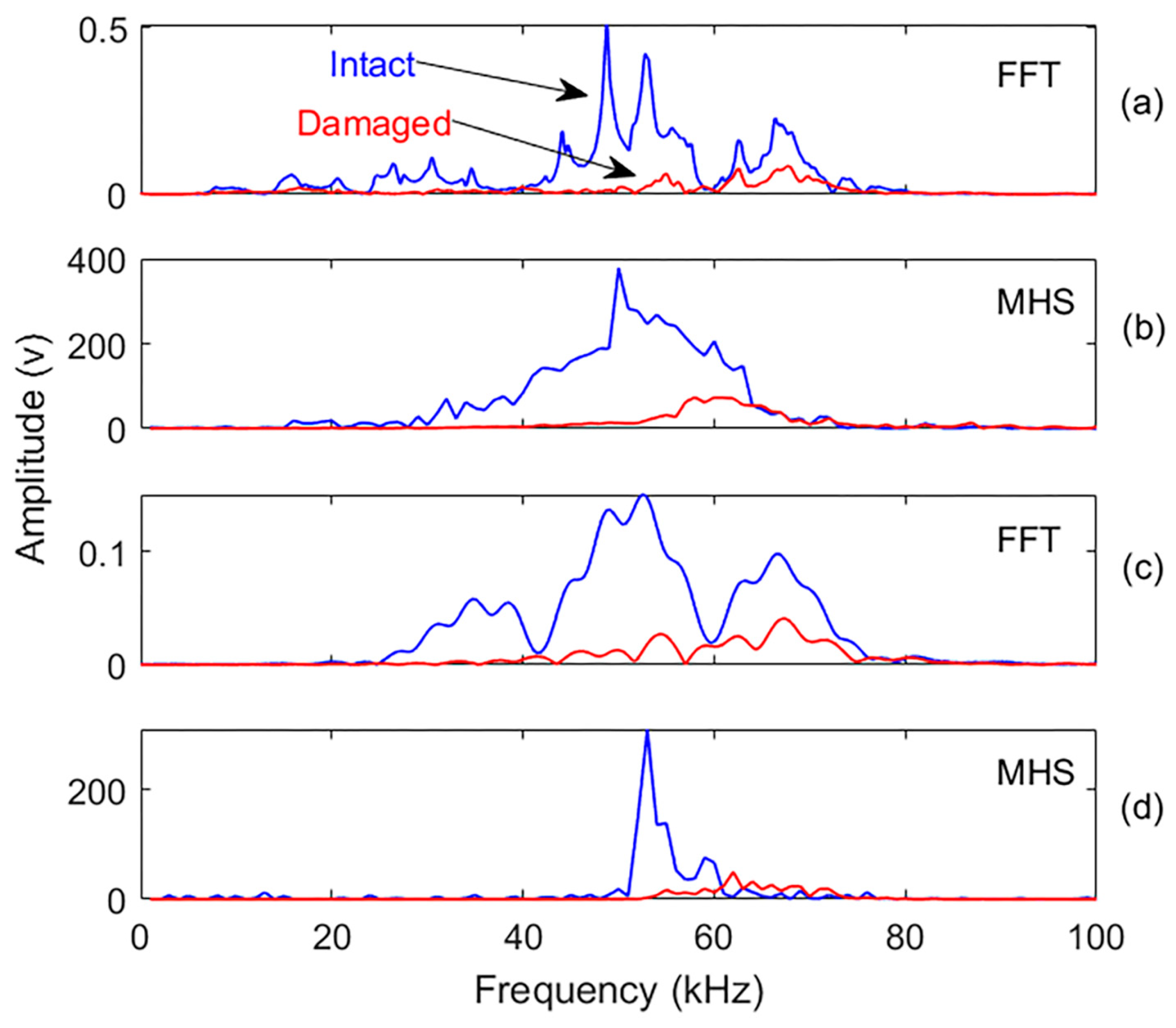
4.3.3. Damage Identification in the Frequency Domain
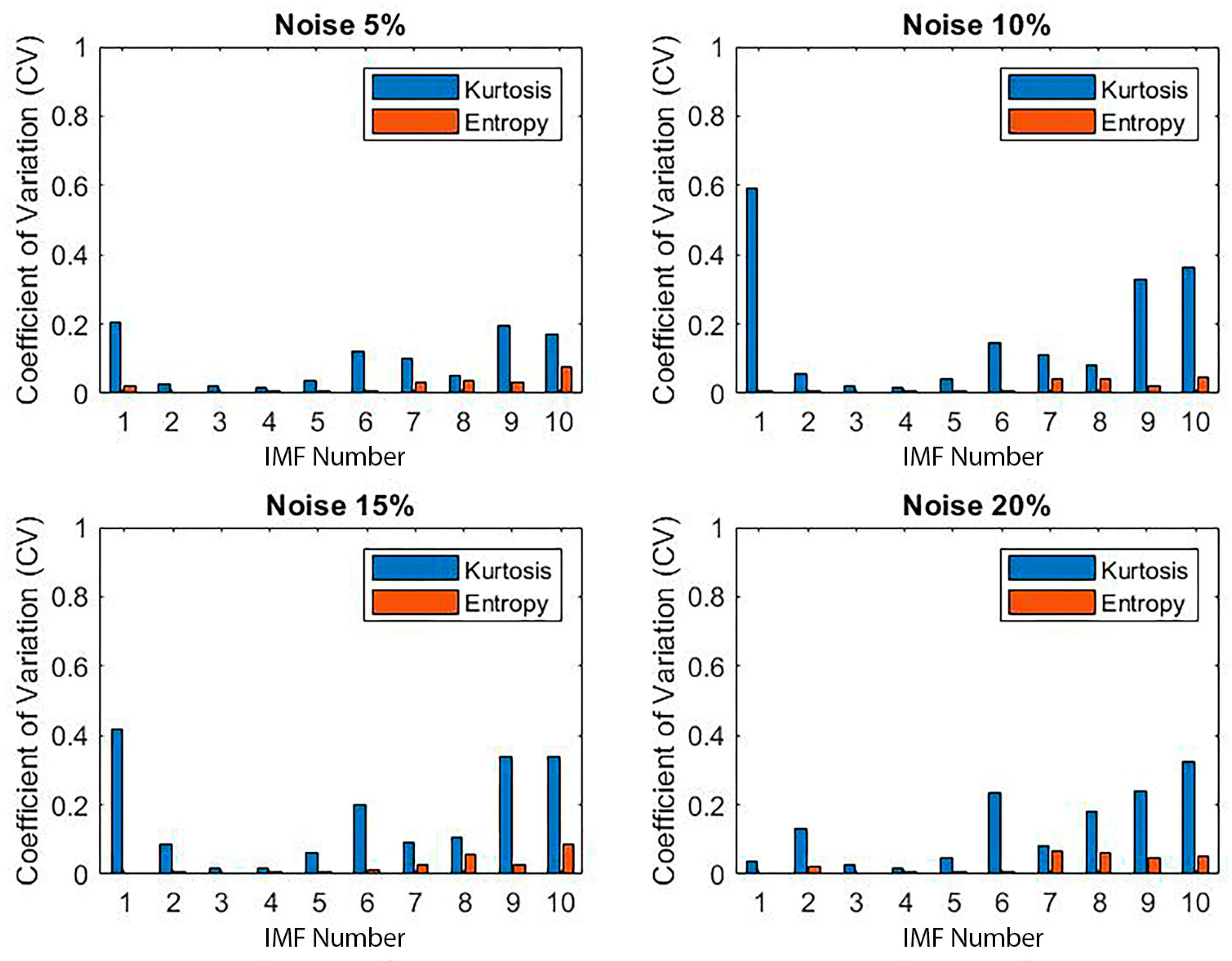
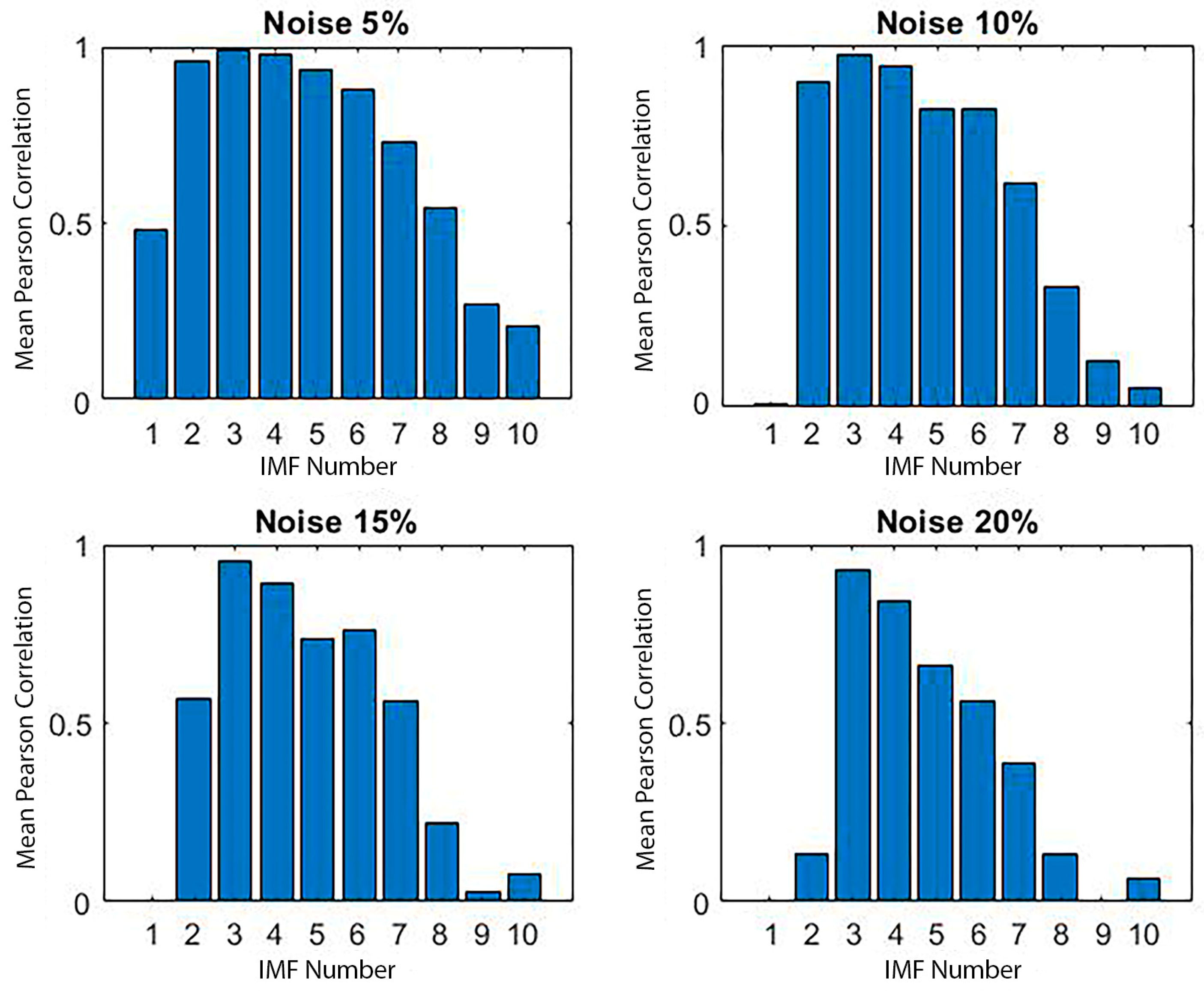
4.4. Evaluation of Decomposition Robustness
- Assessing feature variability across multiple decomposition trials;
- Evaluating consistency under increasing noise perturbations, focusing on CEEMDAN’s noise-assisted characteristics.
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wang, Y.; Cui, J.; Deng, J.; Zhou, H. Experimental Study of Thermally Damaged Concrete under a Hygrothermal Environment by Using a Combined Infrared Thermal Imaging and Ultrasonic Pulse Velocity Method. Materials 2023, 16, 1040. [Google Scholar] [CrossRef] [PubMed]
- Dérobert, X.; Villain, G.; Palma-Lopes, S.; Bouvard-Coconet, V.; Decitre, J.M.; Jabbour, J.; Qu, S.; Geffard, J.L.; Durand, O.; Gugole, G.; et al. Electromagnetical and ultrasonic characterizations of concretes subjected to internal swelling reactions. NDT E Int. 2024, 148, 103217. [Google Scholar] [CrossRef]
- Wang, D.; Yang, C.; Lin, Y.; Lü, L. An ultrasonic approach for characterising subsurface fractures in concrete. Nondestruct. Test. Eval. 2023, 39, 2002–2014. [Google Scholar] [CrossRef]
- Wang, P.; Zeng, J.; Lou, D.; Zheng, W.; Zheng, S.; Chen, B.; Gao, Z. Nonlinear Ultrasonic Characterization of Processing Defects in Wire Arc Additive Manufacturing 316L Stainless Steel. Materials 2025, 18, 805. [Google Scholar] [CrossRef]
- Shah, A.A.; Ribakov, Y.; Zhang, C. Efficiency and sensitivity of linear and non-linear ultrasonics to identifying micro and macro-scale defects in concrete. Mater. Des. 2013, 50, 905–916. [Google Scholar] [CrossRef]
- Yang, H.; Lin, Y. A simplified procedure for evaluation of damage-depth in concrete exposed to high temperature using the impact-echo method. NDT E Int. 2025, 149, 103270. [Google Scholar] [CrossRef]
- Li, Z.; Yang, Y.; Wang, Y.; Wang, W.; Zhang, B. Effect of Macro Fibers on Chloride Permeability and Damage of Concrete Under Uniaxial Compression. Materials 2025, 18, 784. [Google Scholar] [CrossRef]
- Radecki, R.; Staszewski, W.J. Evaluation of Material Integrity Using Higher-Order Harmonic Generation in Propagating Shear Horizontal Ultrasonic Waves. Materials 2024, 17, 3960. [Google Scholar] [CrossRef]
- Jhang, K.Y. Nonlinear ultrasonic techniques for non-destructive assessment of micro damage in material: A review. Int. J. Precis. Eng. Manuf. 2009, 10, 123–135. [Google Scholar] [CrossRef]
- Jhang, K.Y.; Lissenden, C.J.; Solodov, I.; Ohara, Y.; Gusev, V. Measurement of Nonlinear Ultrasonic Characteristics; Springer: Berlin/Heidelberg, Germany, 2020; p. 287. [Google Scholar] [CrossRef]
- Jáquez-Muñoz, J.M.; Gaona-Tiburcio, C.; Méndez-Ramírez, C.T.; Martínez-Ramos, C.; Baltazar-Zamora, M.A.; Santiago-Hurtado, G.; Estupinan-Lopez, F.; Landa-Ruiz, L.; Nieves-Mendoza, D.; Almeraya-Calderon, F. Electrochemical Noise Analysis: An Approach to the Effectivity of Each Method in Different Materials. Materials 2024, 17, 4013. [Google Scholar] [CrossRef]
- Amiri, G.G.; Darvishan, E. Damage detection of moment frames using ensemble Empirical Mode Decomposition and clustering techniques. KSCE J. Civ. Eng. 2015, 19, 1302–1311. [Google Scholar] [CrossRef]
- Liu, N.; Schumacher, T.; Li, Y.; Xu, L.; Wang, B. Damage Detection in Reinforced Concrete Member Using Local Time-Frequency Transform Applied to Vibration Measurements. Buildings 2023, 13, 148. [Google Scholar] [CrossRef]
- Melhem, H.; Kim, H. Damage detection in concrete by Fourier and wavelet analyses. J. Eng. Mech. 2003, 129, 571–577. [Google Scholar] [CrossRef]
- Huang, N.E.; Wu, Z. A Review on Hilbert-Huang Transform: Method and Its Applications to Geophysical Studies. Rev. Geophys. 2008, 42, 1–23. [Google Scholar] [CrossRef]
- de Lima Seiffert, H.L.; Balbo, J.T. Suppression of surface waves with the ensemble empirical mode decomposition to enhance ultrasound images of reinforced concrete elements. NDT E Int. 2020, 116, 102329. [Google Scholar] [CrossRef]
- Yim, H.J.; Kwak, H.G.; Kim, J.H. Wave attenuation measurement technique for nondestructive evaluation of concrete. Nondestruct. Test. Eval. 2011, 27, 81–94. [Google Scholar] [CrossRef]
- Jiang, Z.Y.; Ponniah, J.; Cascante, G. Improved ultrasonic pulse velocity technique for bituminous material characterization. In Proceedings of the Annual Conference of the Transportation Association of Canada Charlottetown, Charlottetown, PE, USA, 17–20 September 2006. [Google Scholar]
- Fartosy, S.; Gomez-Rodriguez, D.; Cascante, G.; Basu, D.; Dusseault, M.B. Effects of a Fracture on Ultrasonic Wave Velocity and Attenuation in a Homogeneous Medium. Geotech. Test. J. 2020, 43, 394–413. [Google Scholar] [CrossRef]
- Nie, Z.; Wang, K.; Zhao, M. Application of Wavelet and EEMD joint denoising in non-linear ultrasonic testing of concrete. Adv. Mater. Sci. Eng. 2018, 2018, 7872036. [Google Scholar] [CrossRef]
- Wiciak, P.; Cascante, G.; Polak, M.A. Novel application of wavelet synchrosqueezed transform (WSST) in laser-vibrometer measurements for condition assessment of cementitious materials. NDT E Int. 2021, 120, 102424. [Google Scholar] [CrossRef]
- Rodríguez Roblero, M.J. Condition Assessment of Concrete Elements Through Two Non-destructive Ultrasonic Techniques. Ph.D. Thesis, University of Waterloo, Waterloo, ON, Canada.
- Zhu, X.Q.; Law, S.S. Non-linear characteristics of damaged reinforced concrete beam from Hilbert-Huang transform. J. Struct. Eng. 2007, 133, 1186–1191. [Google Scholar] [CrossRef]
- Antonio, O.V.M., Jr.; Hirose, S. Ultrasonic imaging of concrete using Wavelet transform and Hilbert-Huang transform as signal processing tools. J. Appl. Mech. 2010, 13, 99–110. [Google Scholar]
- Antonio, O.V.M., Jr.; Hirose, S. Ultrasonic imaging of concrete by synthetic aperture focusing technique based on hilbert-huang transform of time domain data. Mater. Trans. 2012, 53, 621–626. [Google Scholar] [CrossRef]
- Musolino, A.; Raugi, M.; Tucci, M.; Turcu, F. Time, Wavelet and Hilbert-Huang domain analysis of signals from ultrasonic based equipment for the non-destructive evaluation of concrete and brick masonry walls. In Proceedings of the International Conference on Computational Science and Its Applications, Perugia, Italy, 30 June–3 July 2008; Springer: Berlin/Heidelberg, Germany, 2008; pp. 566–581. [Google Scholar]
- Bandara, S.; Rajeev, P.; Gad, E.; Sriskantharajah, B.; Flatley, I. Damage detection of in service timber poles using Hilbert-Huang transform. NDT E Int. 2019, 107, 102141. [Google Scholar] [CrossRef]
- Mousavi, A.A.; Zhang, C.; Masri, S.F.; Gholipour, G. Structural damage localization and quantification based on a CEEMDAN Hilbert transform neural network approach: A model steel truss bridge case study. Sensors 2020, 20, 1271. [Google Scholar] [CrossRef]
- Vergura, S.; Carpentieri, M. Phase Coherence Index, HHT and Wavelet Analysis to Extract Features from Active and Passive Distri-bution Networks. Appl. Sci. 2018, 8, 71. [Google Scholar] [CrossRef]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.C.; Shih, H.H.; Zheng, Q.; Yen, N.-C.; Tung, C.C.; Liu, H.H. The empirical mode decomposition and the Hilbert spectrum for non-linear and non-stationary time series analysis. Math. Phys. Eng. Sci. 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Marcos-Andrade, D.; Beltran-Carbajal, F.; Esquivel-Cruz, E.; Rivas-Cambero, I.; Gabbar, H.A.; Castelan-Perez, A. Power Signal Analysis for Early Fault Detection in Brushless DC Motor Drivers Based on the Hilbert–Huang Transform. World Electr. Veh. J. 2024, 15, 159. [Google Scholar] [CrossRef]
- Lv, Y.; Yuan, R.; Wang, T.; Li, H.; Song, G. Health Degradation Monitoring and Early Fault Diagnosis of a Rolling Bearing Based on CEEMDAN and Improved MMSE. Materials 2018, 11, 1009. [Google Scholar] [CrossRef]
- Wu, Z.; Huang, N.E. Ensemble empirical mode decomposition: A noise-assisted data analysis method. Adv. Adapt. Data Anal. 2009, 1, 1–41. [Google Scholar] [CrossRef]
- Lin, C.C.; Liu, P.L.; Yeh, P.L. Application of empirical mode decomposition in the impact-echo test. NDT E Int. 2009, 42, 589–598. [Google Scholar] [CrossRef]
- Li, M.; Wang, H.; Tang, G.; Yuan, H.; Yang, Y. An improved method based on CEEMD for fault diagnosis of rolling bearing. Adv. Mech. Eng. 2014, 6, 676205. [Google Scholar] [CrossRef]
- Barnhart, B.L. The Hilbert-Huang transform: Theory, applications, development. Ph.D. Thesis, The University of Iowa, Iowa, IA, USA, 2011. [Google Scholar]
- Song, H.; Bai, Y.; Pinheiro, L.; Dong, C.; Huang, X.; Liu, B. analysis of ocean internal waves imaged by multichannel reflection seismics, using ensemble empirical mode decomposition. J. Geophys. Eng. 2012, 9, 302. [Google Scholar] [CrossRef]
- Flandrin, P.; Rilling, G.; Gonçalvès, P. Empirical mode decomposition as a filter bank. IEEE Signal Process. Lett. 2004, 11, 112–114. [Google Scholar] [CrossRef]
- Torres, M.E.; Colominas, M.A.; Schlotthauer, G.; Flandrin, P. A complete ensemble empirical mode decomposition with adaptive noise. In Proceedings of the 2011 IEEE international conference on Acoustics, speech and signal processing (ICASSP), Prague, Czech Republic, 22–27 May 2011; pp. 4144–4147. [Google Scholar] [CrossRef]
- Xu, Y.; Luo, M.; Li, T.; Song, G. ECG Signal De-noising and Baseline Wander Correction Based on CEEMDAN and Wavelet Threshold. Sensors 2017, 17, 2754. [Google Scholar] [CrossRef] [PubMed]
- Cui, M.; Hou, E.; Hou, P. VMD-SE-CEEMDAN-BO-CNNGRU: A Dual-Stage Mode Decomposition Hybrid Deep Learning Model for Microseismic Time Series Prediction. Mathematics 2025, 13, 2121. [Google Scholar] [CrossRef]
- Hossain, G.; Myers, M.H.; Kozm, R. Study of Phase Relationships in ECoG Signals Using Hilbert-Huang Transforms. In Proceedings of the Advances in Brain Inspired Cognitive Systems—5th International Conference, BICS, Shenyang, China, 11–14 July 2012; Volume 7366, pp. 174–182. [Google Scholar]
- Sandoval, S.; De Leon, P.L.; Liss, J.M. Hilbert spectral analysis of vowels using intrinsic mode functions. In Proceedings of the 2015 IEEE Workshop on Automatic Speech Recognition and Understanding (ASRU), Scottsdale, AZ, USA, 13–17 December 2015; pp. 569–575. [Google Scholar]
- Rao, A.R.; Hsu, E.C. Hilbert-Huang Transform Analysis Of Hydrological And Environmental Time Series; Springer: Dordrecht, The Netherlands, 2008; Volume 60, p. 248. [Google Scholar]
- Hou, S.; Guo, W. Faulty Line Selection Based on Modified CEEMDAN Optimal Denoising Smooth Model and Duffing Oscillator for Un-Effectively Grounded System. Math. Probl. Eng. 2020, 2020, 21. [Google Scholar] [CrossRef]
- Rostami, J.; Chen, J.; Tse, P.W. A signal processing approach with a smooth empirical mode decomposition to reveal hidden trace of corrosion in highly contaminated guided wave signals for concrete-covered pipes. Sensors 2017, 17, 302. [Google Scholar] [CrossRef]
- Carrasco-López, S.; Herrera-Trejo, M.; Castro-Román, M.; Castro-Uresti, F.; Castro-Cedeño, E.I. Analysis of the Steelmaking Process via Data Mining and Pearson Correlation. Materials 2024, 17, 2786. [Google Scholar] [CrossRef]
- Kovačević, M.; Lozančić, S.; Nyarko, E.K.; Hadzima-Nyarko, M. Modeling of Compressive Strength of Self-Compacting Rubberized Concrete Using Machine Learning. Materials 2021, 14, 4346. [Google Scholar] [CrossRef]
- Cheraghi, N.; Riley, M.J.; Taheri, F. A novel approach for detection of damage in adhesively bonded joints in plastic pipes based on vibration methods using piezoelectric sensors. In Proceedings of the IEEE International Conference on Systems, Waikoloa, HI, USA, 12 October 2005; Volume 4, pp. 3472–3478. [Google Scholar]
- Li, C.; Wang, Q.; Zhu, R.; Zhu, Y.; Hu, Y. Damage Identification for Pile Foundation in High-Piled Wharf Using Composite Energy Factors Driven by Dynamic Response under Wave Impact Excitation. Ocean Eng. 2024, 291, 116286. [Google Scholar] [CrossRef]
- Cheraghi, N.; Taheri, F. A damage index for structural health monitoring based on the empirical mode decomposition. J. Mech. Mater. Struct. 2007, 2, 43–61. [Google Scholar] [CrossRef]
- Cheraghi, N.; Taheri, F. Application of the empirical mode decomposition for system identification and structural health monitoring. Int. J. Appl. Math. Eng. Sci. 2008, 2, 61–72. [Google Scholar]
- Rezaei, D.; Taheri, F. Experimental validation of a novel structural damage detection method based on empirical mode decomposition. Smart Mater. Struct. 2009, 18, 045004. [Google Scholar] [CrossRef]
- ASTM C666/C666M-15; Standard Test Method for Resistance of Concrete to Rapid Freezing and Thawing. ASTM International: West Conshohocken, PA, USA, 2015. Available online: https://www.astm.org (accessed on 1 November 2023).
- Wang, C.; Zhang, M.; Pei, W.; Lai, Y.; Zhang, R.; Sun, J.; Zhao, T. Deterioration process and damage constitutive model of concrete under freeze-thaw circumstances of severely cold regions. Cold Reg. Sci. Technol. 2024, 226, 104290. [Google Scholar] [CrossRef]
- He, J.; Deng, Y.; Shi, X. Quantitative analysis of pore structures and microcracks in self-healing concrete after freeze-thaw exposure: An X-ray computed tomography-based approach. Cem. Concr. Compos. 2025, 162, 106105. [Google Scholar] [CrossRef]
- Krautkrämer, J.; Krautkrämer, H. Ultrasonic testing by determination of material properties. In Ultrasonic Testing of Materials; Springer: Berlin/Heidelberg, Germany, 1990; pp. 528–550. [Google Scholar]
- Zhang, Z.; Wu, H.; Chen, L.; Bao, X. Signal-to-Noise Ratio Enhancement Based on Empirical Mode Decomposition in Phase-Sensitive Optical Time Domain Reflectometry Systems. Sensors 2017, 17, 1870. [Google Scholar] [CrossRef]
- Karatoprak, E.; Seker, S. An Improved Empirical Mode Decomposition Method Using Variable Window Median Filter for Early Fault Detection in Electric Motors. Math. Probl. Eng. 2019, 2019, 8015295. [Google Scholar] [CrossRef]
- Zhao, Z.; Shen, Q.; Ren, F. Heart sound biometric system based on marginal spectrum analysis. Sensors 2013, 3, 2530–2551. [Google Scholar] [CrossRef]







| Method | Handles Non-Stationarity? | Handles Nonlinearity? | Adaptive? | Time-Frequency Resolution |
|---|---|---|---|---|
| FFT | No | No | No | Poor |
| Wavelet | Partial | Partial | Semi | Moderate |
| HHT | Yes | Yes | Yes | High |
| MHS | FFT | |||
|---|---|---|---|---|
| Signals | Effective Frequency Range | DI Value (%) | Effective Frequency Range | DI Value (%) |
| Original | 30–70 kHz | 74 | 30–60 kHz | 68 |
| IMF1 | 40–60 kHz | 76 | 30–60 kHz | 68 |
| IMF2 | 20–60 kHz | 78 | 40–60 kHz | 71 |
| IMF3 | 20–60 kHz | 88 | 20–60 kHz | 85 |
| Signals | DI Value (%) |
|---|---|
| Original | 78 |
| IMF3 | 78 |
| IMF4 | 85 |
| IMF5 | 87 |
| Signals | Effective Time Range (ms) | DI Value (%) |
|---|---|---|
| Original | 0.55–1.00 | 78 |
| IMF3 | 0.55–0.70 | 77 |
| IMF4 | 0.55–1.00 | 87 |
| IMF5 | 0.50–1.50 | 87 |
| MHS | FFT | |||
|---|---|---|---|---|
| Signals | Effective Frequency Range | DI Value (%) | Effective Frequency Range | DI Value (%) |
| Original | 30–70 kHz | 82 | 30–80 kHz | 72 |
| IMF3 | 50–70 kHz | 83 | 30–80 kHz | 74 |
| IMF4 | 40–70 kHz | 78 | 40–80 kHz | 72 |
| IMF5 | 30–70 kHz | 88 | 20–60 kHz | 87 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shakir, A.M.; Cascante, G.; Ameen, T.H. Methodology for the Early Detection of Damage Using CEEMDAN-Hilbert Spectral Analysis of Ultrasonic Wave Attenuation. Materials 2025, 18, 3294. https://doi.org/10.3390/ma18143294
Shakir AM, Cascante G, Ameen TH. Methodology for the Early Detection of Damage Using CEEMDAN-Hilbert Spectral Analysis of Ultrasonic Wave Attenuation. Materials. 2025; 18(14):3294. https://doi.org/10.3390/ma18143294
Chicago/Turabian StyleShakir, Ammar M., Giovanni Cascante, and Taher H. Ameen. 2025. "Methodology for the Early Detection of Damage Using CEEMDAN-Hilbert Spectral Analysis of Ultrasonic Wave Attenuation" Materials 18, no. 14: 3294. https://doi.org/10.3390/ma18143294
APA StyleShakir, A. M., Cascante, G., & Ameen, T. H. (2025). Methodology for the Early Detection of Damage Using CEEMDAN-Hilbert Spectral Analysis of Ultrasonic Wave Attenuation. Materials, 18(14), 3294. https://doi.org/10.3390/ma18143294






