Effects of Aging on Mode I Fatigue Crack Growth Characterization of Double Cantilever Beam Specimens with Thick Adhesive Bondline for Marine Applications
Abstract
1. Introduction
2. Materials and Methods
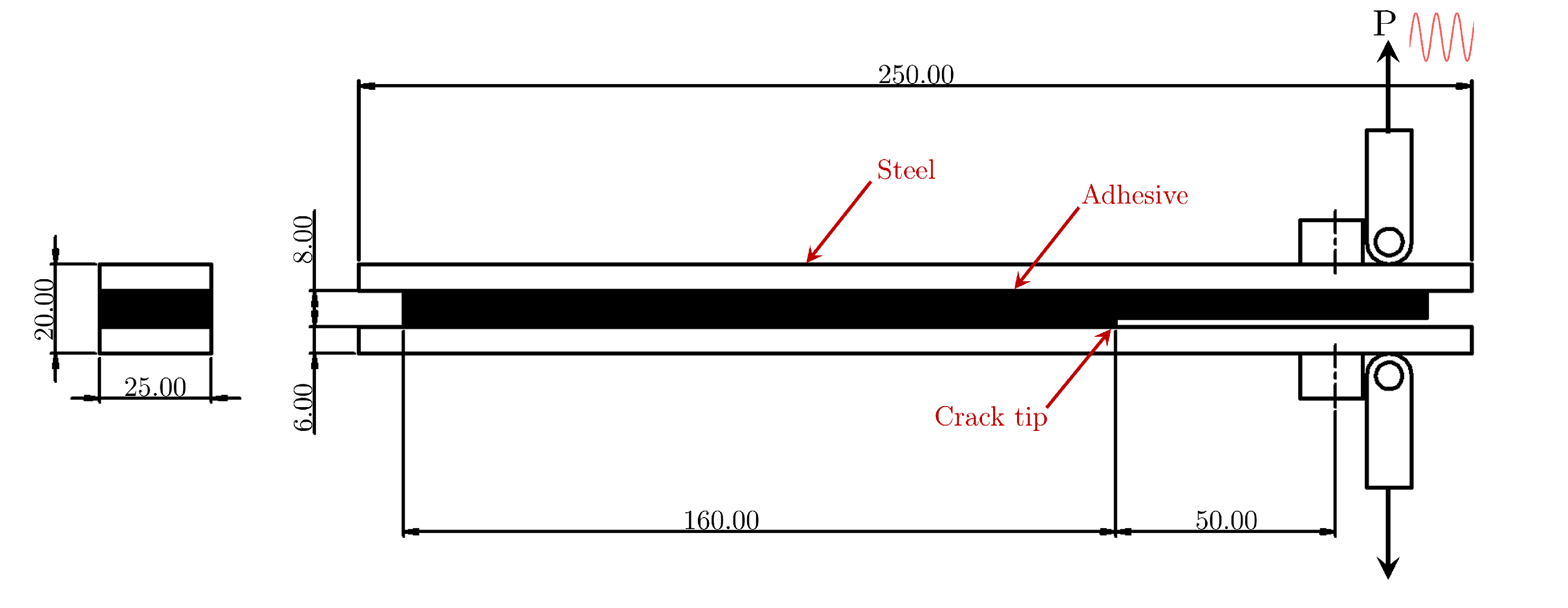
2.1. Specimen Configuration and Preparation
2.2. Aging Procedure
2.3. Experimental Procedure
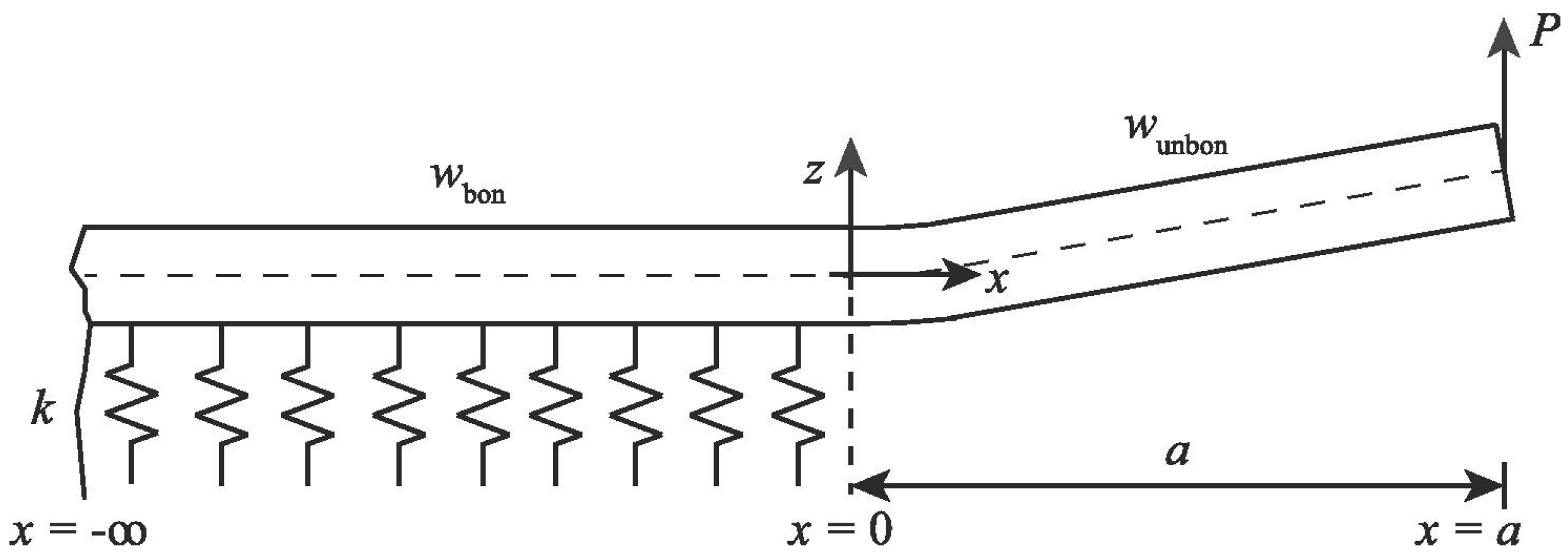
2.4. Data Reduction
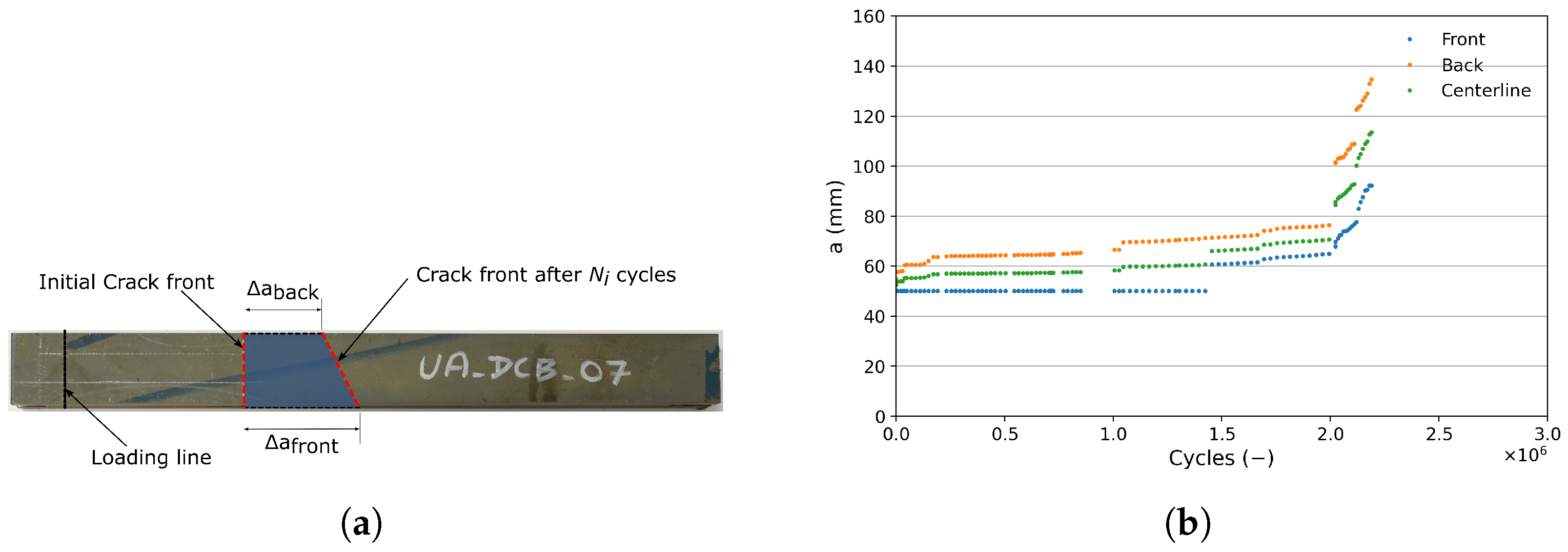
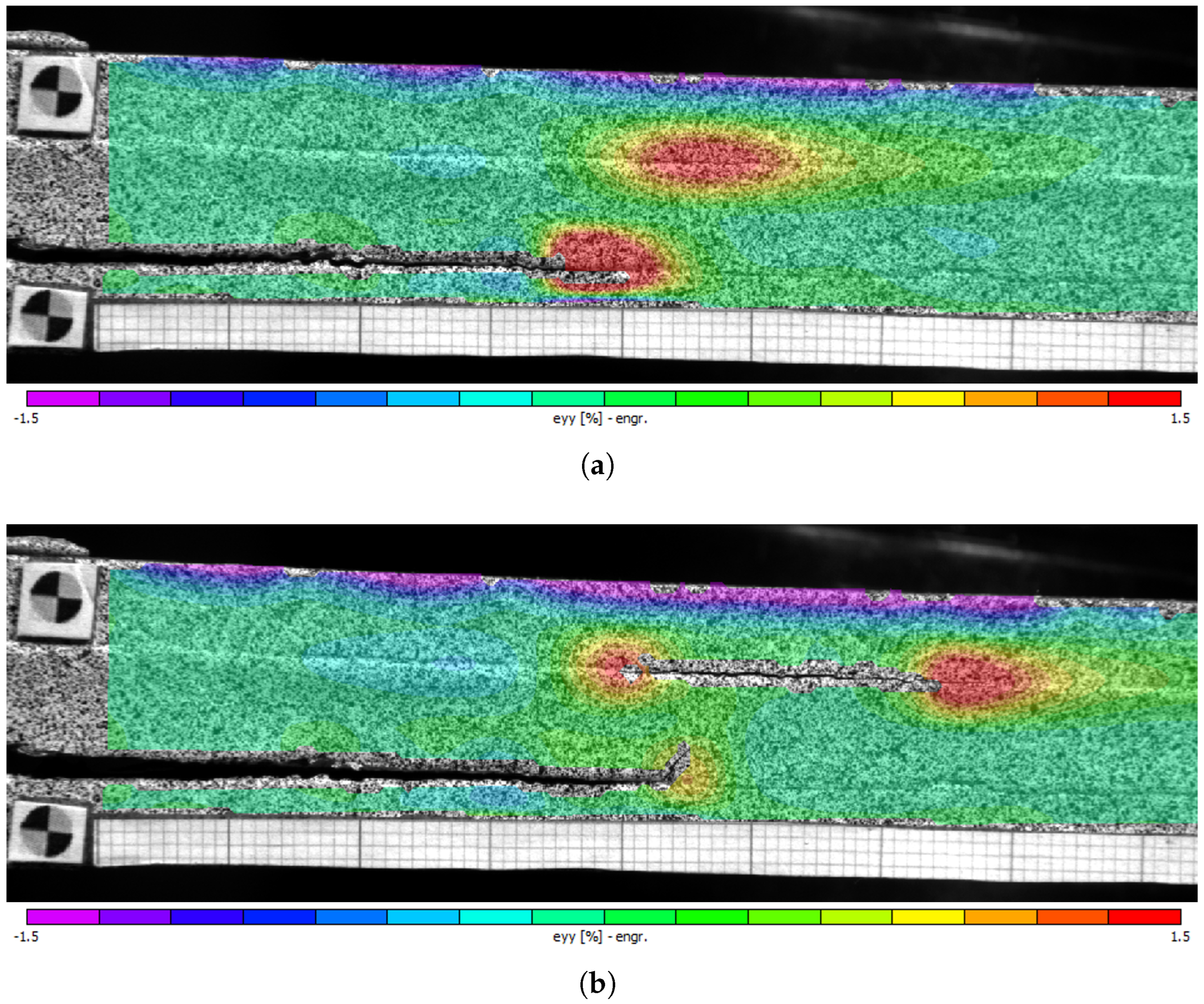
2.5. Crack Length Measurement and Fracture Surface Analysis
2.6. Statistical Analysis
2.6.1. Moderated Multiple Regression
3. Results and Discussions
3.1. Unaged Specimens
3.2. Aged Specimens
3.2.1. Salt-Spray-Aged Specimens
3.2.2. Immersion-Aged Specimens
3.3. Data Analysis
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Siengchin, S. A Review on Lightweight Materials for Defence Applications: Present and Future Developments. Def. Technol. 2023, 24, 1–17. [Google Scholar] [CrossRef]
- Rubino, F.; Nisticò, A.; Tucci, F.; Carlone, P. Marine Application of Fiber Reinforced Composites: A Review. J. Mar. Sci. Eng. 2020, 8, 26. [Google Scholar] [CrossRef]
- Mouritz, A.P.; Gellert, E.; Burchill, P.; Challis, K. Review of Advanced Composite Structures for Naval Ships and Submarines. Compos. Struct. 2001, 53, 21–42. [Google Scholar] [CrossRef]
- Chalmers, D. The Potential for the Use of Composite Materials in Marine Structures. Mar. Struct. 1994, 7, 441–456. [Google Scholar] [CrossRef]
- Chen, D.; Yan, R.; Lu, X. Mechanical Properties Analysis of the Naval Ship Similar Model with an Integrated Sandwich Composite Superstructure. Ocean Eng. 2021, 232, 109101. [Google Scholar] [CrossRef]
- Hashim, S.A. Adhesive Bonding of Thick Steel Adherends for Marine Structures. Mar. Struct. 1999, 12, 405–423. [Google Scholar] [CrossRef]
- Eyres, D.; Bruce, G. Shipyard Layout. In Ship Construction; Butterworth-Heinemann: Waltham, MA, USA, 2012; pp. 119–124. [Google Scholar] [CrossRef]
- Eyres, D.; Bruce, G. Launching. In Ship Construction; Butterworth-Heinemann: Waltham, MA, USA, 2012; pp. 161–172. [Google Scholar] [CrossRef]
- Jarry, E.; Shenoi, R.A. Performance of Butt Strap Joints for Marine Applications. Int. J. Adhes. Adhes. 2006, 26, 162–176. [Google Scholar] [CrossRef]
- Zuo, P.; Vassilopoulos, A.P. Review of Fatigue of Bulk Structural Adhesives and Thick Adhesive Joints. Int. Mater. Rev. 2021, 66, 313–338. [Google Scholar] [CrossRef]
- Delzendehrooy, F.; Akhavan-Safar, A.; Barbosa, A.Q.; Beygi, R.; Cardoso, D.; Carbas, R.J.; Marques, E.A.; Da Silva, L.F. A Comprehensive Review on Structural Joining Techniques in the Marine Industry. Compos. Struct. 2022, 289, 115490. [Google Scholar] [CrossRef]
- ASTM D3166-99; Test Method for Fatigue Properties of Adhesives in Shear by Tension Loading (Metal/Metal). ASTM International: West Conshohocken, PA, USA, 2020. [CrossRef]
- ISO 9664:1993; Adhesives—Test Methods for Fatigue Properties of Structural Adhesives in Tensile Shear. International Organization for Standardization: Vernier, Switzerland; Geneva, Switzerland, 1993.
- Marques, D.; Madureira, F.; Tita, V. Data Reduction Methods in the Fatigue Analysis of the Double Cantilever Beam, Part I: Fundaments and Virtual Fatigue Testing. Compos. Struct. 2023, 324, 117527. [Google Scholar] [CrossRef]
- ASTM D6115-97; Standard Test Method for Mode I Fatigue Delamination Growth Onset of Unidirectional Fiber-Reinforced Polymer Matrix Composites. ASTM International: West Conshohocken, PA, USA, 2019. [CrossRef]
- ASTM B117-19; Standard Practice for Operating Salt Spray (Fog) Apparatus. ASTM International: West Conshohocken, PA, USA, 2019. [CrossRef]
- ASTM E647-24; Standard Test Method for Measurement of Fatigue Crack Growth Rates. ASTM International: West Conshohocken, PA, USA, 2024. [CrossRef]
- Mall, S.; Ramamurthy, G. Effect of Bond Thickness on Fracture and Fatigue Strength of Adhesively Bonded Composite Joints. Int. J. Adhes. Adhes. 1989, 9, 33–37. [Google Scholar] [CrossRef]
- Kinloch, A.J.; Osiyemi, S.O. Predicting the Fatigue Life of Adhesively-Bonded Joints. J. Adhes. 1993, 43, 79–90. [Google Scholar] [CrossRef]
- Jethwa, J.K.; Kinloch, A.J. The Fatigue and Durability Behaviour of Automotive Adhesives. Part I: Fracture Mechanics Tests. J. Adhes. 1997, 61, 71–95. [Google Scholar] [CrossRef]
- Ashcroft, I.A.; Shaw, S.J. Mode I Fracture of Epoxy Bonded Composite Joints 2. Fatigue Loading. Int. J. Adhes. Adhes. 2002, 22, 151–167. [Google Scholar] [CrossRef]
- Pirondi, A.; Nicoletto, G. Fatigue Crack Growth in Bonded DCB Specimens. Eng. Fract. Mech. 2004, 71, 859–871. [Google Scholar] [CrossRef]
- Abel, M.L.; Adams, A.N.; Kinloch, A.J.; Shaw, S.J.; Watts, J.F. The Effects of Surface Pretreatment on the Cyclic-Fatigue Characteristics of Bonded Aluminium-Alloy Joints. Int. J. Adhes. Adhes. 2006, 26, 50–61. [Google Scholar] [CrossRef]
- Sekiguchi, Y.; Sato, C. Effect of Bond-Line Thickness on Fatigue Crack Growth of Structural Acrylic Adhesive Joints. Materials 2021, 14, 1723. [Google Scholar] [CrossRef]
- Azari, S.; Ameli, A.; Papini, M.; Spelt, J.K. Adherend Thickness Influence on Fatigue Behavior and Fatigue Failure Prediction of Adhesively Bonded Joints. Compos. Part A 2013, 48, 181–191. [Google Scholar] [CrossRef]
- Fernlund, G.; Spelt, J.K. Mixed Mode Energy Release Rates for Adhesively Bonded Beam Specimens. J. Compos. Technol. Res. 1994, 16, 234–243. [Google Scholar] [CrossRef]
- Rocha, A.V.; Akhavan-Safar, A.; Carbas, R.; Marques, E.A.; Goyal, R.; El-zein, M.; da Silva, L.F. Fatigue Crack Growth Analysis of Different Adhesive Systems: Effects of Mode Mixity and Load Level. Fatigue Fract. Eng. Mater. Struct. 2020, 43, 330–341. [Google Scholar] [CrossRef]
- Xu, X.X.; Crocombe, A.D.; Smith, P.A. Fatigue Crack Growth Rates in Adhesive Joints Tested at Different Frequencies. J. Adhes. 1996, 58, 191–204. [Google Scholar] [CrossRef]
- Abou-Hamda, M.M.; Megahed, M.M.; Hammouda, M.M.I. Fatigue Crack Growth in Double Cantilever Beam Specimen with an Adhesive Layer. Eng. Fract. Mech. 1998, 60, 605–614. [Google Scholar] [CrossRef]
- Yamada, S.E. The J-Integral for Augmented Double Cantilever Beams and Its Application to Bonded Joints. Eng. Fract. Mech. 1998, 29, 673–682. [Google Scholar] [CrossRef]
- Fan, J.; Ikeda, K.; Vassilopoulos, A.P.; Michaud, V. Void Content and Displacement Ratio Effects on Fatigue Crack Growth in Thick Adhesively Bonded Composite Joints under Constant Amplitude Loading. Int. J. Fatigue 2024, 188, 108508. [Google Scholar] [CrossRef]
- Krenk, S. Energy Release Rate of Symmetric Adhesive Joints. Eng. Fract. Mech. 1992, 43, 549–559. [Google Scholar] [CrossRef]
- Kim, H.B.; Naito, K.; Oguma, H. Fatigue Crack Growth Properties of a Two-Part Acrylic-Based Adhesive in an Adhesive Bonded Joint: Double Cantilever-Beam Tests under Mode I Loading. Int. J. Fatigue 2017, 98, 286–295. [Google Scholar] [CrossRef]
- Imanaka, M.; Ishii, K.; Hara, K.; Ikeda, T.; Kouno, Y. Fatigue Crack Propagation Rate of CFRP/Aluminum Adhesively Bonded DCB Joints with Acrylic and Epoxy Adhesives. Int. J. Adhes. Adhes. 2018, 85, 149–156. [Google Scholar] [CrossRef]
- Interreg 2 Seas. Enabling Qualication of Hybrid Structures for Lightweight and Safe Maritime Transport. Available online: https://keep.eu/projects/18525/Enabling-Qualification-of-H-EN/ (accessed on 23 June 2025).
- ISO 8501-1:2007; Preparation of Steel Substrates before Application of Paints and Related Products–Visual Assessment of Surface Cleanliness–Part 1: Rust Grades and Preparation Grades of Uncoated Steel Substrates and of Steel Substrates after Overall Removal of Previous Coatings. International Organization for Standardization: Vernier, Switzerland; Geneva, Switzerland, 2017.
- Jaiswal, P.; Iyer Kumar, R.; Mouton, L.; Starink, L.; Katsivalis, I.; Cedric, V.; De Waele, W. Durability of an Adhesively Bonded Joint between Steel Ship Hull and Sandwich Superstructure Pre-Exposed to Saline Environment. J. Adhes. 2024, 100, 985–1014. [Google Scholar] [CrossRef]
- Iyer Kumar, R.; Jaiswal, P.; De Waele, W. Fatigue Damage and Life Evaluation of Thick Bi-material Double Strap Joints for Use in Marine Applications. Fatigue Fract. Eng. Mater. Struct. 2022, 45, 2099–2111. [Google Scholar] [CrossRef]
- Saleh, M.N.; Venkatesan, P.; Askarinejad, S.; Katsivalis, I.; Teixeira De Freitas, S.; De Waele, W. Material Properties as a Function of Environmental and Operational Conditions. Available online: https://keep.eu/media/project_documents/18525/report/outputs_1_4_-_qualify_d1.3.2_public_version.pdf (accessed on 24 June 2025).
- Saleh, M.N.; Budzik, M.K.; Saeedifar, M.; Zarouchas, D.; Teixeira De Freitas, S. On the Influence of the Adhesive and the Adherend Ductility on Mode I Fracture Characterization of Thick Adhesively-Bonded Joints. Int. J. Adhes. Adhes. 2022, 115, 103123. [Google Scholar] [CrossRef]
- Kanninen, M.F. An Augmented Double Cantilever Beam Model for Studying Crack Propagation and Arrest. Int. J. Fract. 1973, 9, 83–92. [Google Scholar] [CrossRef]
- Penado, F.E. A Closed Form Solution for the Energy Release Rate of the Double Cantilever Beam Specimen with an Adhesive Layer. J. Compos. Mater. 1993, 27, 383–407. [Google Scholar] [CrossRef]
- Heide-Jørgensen, S.; Budzik, M.K. Crack Growth along Heterogeneous Interface during the DCB Experiment. Int. J. Solids Struct. 2017, 120, 278–291. [Google Scholar] [CrossRef]
- Lopes Fernandes, R.; Teixeira de Freitas, S.; Budzik, M.K.; Poulis, J.A.; Benedictus, R. From Thin to Extra-Thick Adhesive Layer Thicknesses: Fracture of Bonded Joints under Mode I Loading Conditions. Eng. Fract. Mech. 2019, 218, 106607. [Google Scholar] [CrossRef]
- Marques, D.; Madureira, F.; Tita, V. Data Reduction Methods in the Fatigue Analysis of the Double Cantilever Beam, Part II: Evaluation and Case Studies. Compos. Struct. 2023, 324, 117528. [Google Scholar] [CrossRef]
- Iyer Kumar, R.; De Waele, W. Development of Test Method for Fatigue Crack Growth Using DCB Specimens with Thick Adhesive Bondline. Pro. Struct. Integr. 2024, 54, 164–171. [Google Scholar] [CrossRef]
- Schindelin, J.; Arganda-Carreras, I.; Frise, E.; Kaynig, V.; Longair, M.; Pietzsch, T.; Preibisch, S.; Rueden, C.; Saalfeld, S.; Schmid, B.; et al. Fiji: An Open-Source Platform for Biological-Image Analysis. Nat. Methods 2012, 9, 676–682. [Google Scholar] [CrossRef]
- Andrade, J.; Estévez-Pérez, M. Statistical Comparison of the Slopes of Two Regression Lines: A Tutorial. Anal. Chim. Acta 2014, 838, 1–12. [Google Scholar] [CrossRef]
- Ng, M.; Wilcox, R.R. Comparing the Regression Slopes of Independent Groups. Br. J. Math. Stat. Psychol. 2010, 63, 319–340. [Google Scholar] [CrossRef]
- Hu, D.; Su, X.; Liu, X.; Mao, J.; Shan, X.; Wang, R. Bayesian-Based Probabilistic Fatigue Crack Growth Evaluation Combined with Machine-Learning-Assisted GPR. Eng. Fract. Mech. 2020, 229, 106933. [Google Scholar] [CrossRef]
- He, G.Y.; Zhao, Y.X.; Yan, C.L. Parameter Estimation in Multiaxial Fatigue Short Crack Growth Model Using Hierarchical Bayesian Linear Regression. Fatigue Fract. Eng. Mater. Struct. 2023, 46, 845–865. [Google Scholar] [CrossRef]
- He, G.; Zhao, Y.; Yan, C. Uncertainty Quantification in Multiaxial Fatigue Life Prediction Using Bayesian Neural Networks. Eng. Fract. Mech. 2024, 298, 109961. [Google Scholar] [CrossRef]
- Johnson, T.A. Fatigue Fracture of Polymethylmethacrylate. J. Appl. Phys. 1972, 43, 1311–1313. [Google Scholar] [CrossRef]
- Saeed, H.; Chaudhuri, S.; De Waele, W. Front Face Strain Compliance for Quantification of Short Crack Growth in Fatigue Testing. J. Strain Anal. Eng. Des. 2023, 58, 649–660. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Core Team: Vienna, Austria, 2024. [Google Scholar]
- Wickham, H.; Averick, M.; Bryan, J.; Chang, W.; McGowan, L.; François, R.; Grolemund, G.; Hayes, A.; Henry, L.; Hester, J.; et al. Welcome to the Tidyverse. J. Open Source Softw. 2019, 4, 1686. [Google Scholar] [CrossRef]
- Wickham, H.; François, R.; Henry, L.; Müller, K.; Vaughan, D. Dplyr: A Grammar of Data Manipulation. Available online: https://dplyr.tidyverse.org/ (accessed on 24 June 2025).
- Wickham, H.; Hester, J.; Bryan, J. Readr: Read Rectangular Text Data. Available online: https://readr.tidyverse.org (accessed on 24 June 2025).
- Abril-Pla, O.; Andreani, V.; Carroll, C.; Dong, L.; Fonnesbeck, C.J.; Kochurov, M.; Kumar, R.; Lao, J.; Luhmann, C.C.; Martin, O.A.; et al. PyMC: A Modern, and Comprehensive Probabilistic Programming Framework in Python. PeerJ Comput. Sci. 2023, 9, e1516. [Google Scholar] [CrossRef]









| Specimen | Block Loading Sequence | Number of Cycles to Failure |
|---|---|---|
| UA-DCB-03 | 45% | 783,211 |
| UA-DCB-04 | 45%, 47.5%, 50% | 2,042,765 |
| UA-DCB-05 | 45%, 50%, 55% | 2,137,778 |
| UA-DCB-06 | 45%, 50% | 1,010,026 |
| UA-DCB-07 | 30%, 40%, 45%, 50% | 3,390,261 |
| UA-DCB-08 | 45%, 50% | 1,430,000 |
| Specimen | Block Loading Sequence | Number of Cycles to Failure | Aging Methodology |
|---|---|---|---|
| A-DCB-01 | 45%, 50%, 55% | 2,498,006 | Salt-spray |
| A-DCB-02 | 45%, 50%, 55%, 60%, 65%, 70% | 2,383,010 | Salt-spray + Immersion |
| A-DCB-03 | 50%, 55%, 60% | 2,917,432 | Salt-spray |
| A-DCB-04 | 50%, 55%, 60% | 165,024 | Salt-spray + Immersion |
| A-DCB-05 | 45%, 50%, 55%, 60%, 65%, 70%, 80% | 631,651 | Salt-spray + Immersion |
| A-DCB-06 | 55% | 878,172 | Salt-spray |
| Condition | C | m |
|---|---|---|
| Unaged specimens | 2.3726 × 10−14 | 3.3911 |
| Aged specimens (combined) | 1.0907 × 10−10 | 2.0978 |
| - Salt-spray-aged specimens | 8.8870 × 10−13 | 2.8334 |
| - Immersion-aged specimens | 9.2916 × 10−8 | 1.1497 |
| Specimen Condition | Coefficient | Mean | SD | 2.5% CI | 97.5% CI |
|---|---|---|---|---|---|
| Unaged | −30.858 | 1.214 | −33.072 | −28.284 | |
| m | 3.307 | 0.201 | 2.897 | 3.690 | |
| Aged (combined) | −22.572 | 1.259 | −25.100 | −20.150 | |
| m | 2.036 | 0.210 | 1.630 | 2.453 | |
| - Salt spray | −27.425 | 1.115 | −29.670 | −25.205 | |
| m | 2.780 | 0.186 | 2.383 | 3.127 | |
| - Immersion | −15.289 | 2.493 | −20.070 | −10.467 | |
| m | 1.000 | 0.419 | 0.197 | 1.805 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Iyer Kumar, R.; De Waele, W. Effects of Aging on Mode I Fatigue Crack Growth Characterization of Double Cantilever Beam Specimens with Thick Adhesive Bondline for Marine Applications. Materials 2025, 18, 3286. https://doi.org/10.3390/ma18143286
Iyer Kumar R, De Waele W. Effects of Aging on Mode I Fatigue Crack Growth Characterization of Double Cantilever Beam Specimens with Thick Adhesive Bondline for Marine Applications. Materials. 2025; 18(14):3286. https://doi.org/10.3390/ma18143286
Chicago/Turabian StyleIyer Kumar, Rahul, and Wim De Waele. 2025. "Effects of Aging on Mode I Fatigue Crack Growth Characterization of Double Cantilever Beam Specimens with Thick Adhesive Bondline for Marine Applications" Materials 18, no. 14: 3286. https://doi.org/10.3390/ma18143286
APA StyleIyer Kumar, R., & De Waele, W. (2025). Effects of Aging on Mode I Fatigue Crack Growth Characterization of Double Cantilever Beam Specimens with Thick Adhesive Bondline for Marine Applications. Materials, 18(14), 3286. https://doi.org/10.3390/ma18143286








